Abstract
The present work aims at studying the effect of geometric parameters of isogrid structures on their buckling behavior. To this purpose, isogrid structures in polyamide reinforced with short carbon fibers, with different rib widths, rib thicknesses, and cell heights, were additively manufactured using the fused deposition modeling technology; then, they were subjected to compression test until the occurrence of buckling. It was observed that isogrid structures can undergo to different failure modes, local and global buckling, depending on the values of geometrical parameters. Furthermore, the geometrical parameters that lead to the highest strength are different to those providing the highest specific strength. However, the specific strength of the 3D printed composite material is higher than those of 1XXX and 3XXX aluminum alloys. Rib thickness was characterized by the highest effect on both strength and specific strength while the cell height results in the lowest contribution. Finally, optical and scanning electron microscopies were carried out in order to analyze the fractured ribs and to obtain high magnification three-dimensional topography of fractured surfaces after buckling. The effect of moisture content on polyamide reinforced composites and the comparison between 3D printed and traditionally produced isogrid structures will be investigated in future researches.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the aerospace industry, the need to develop lightweight and reliable structures has forced researchers to study new materials and structures. One of the main issues which designers faced concerns the strength to compressive loads of thin structures, such as fuselage panels, due to the occurrence of buckling phenomena [1]. This problem can be avoided using thicker sheets even though the increase in weight could lead to a decrease in the specific strength [2, 3]. For this reason, reinforcing methods to stiffen structures while reducing weight have been developed. Among them, a very effective approach consists in using reinforcing ribs in form of regular lattice structures.
The first appearance of isogrid structures was in a patent of McDonnell-Douglas Corporation in the 1960s. They were machined from a workpiece in aluminum alloy and consists of a skin with stiffeners that form equilateral triangles. An application of these structures was reported by Huybrechts et al. [4]. Unfortunately, the isogrid structures in aluminum alloys are obtained by means of expensive processes which also require long manufacturing times and involve a large amount of material waste. The availability of carbon fiber reinforced polymers (CFRPs), characterized by very high specific strength and modulus, allowed to develop isogrid structures with performances and efficiency higher than the ones provided by structures in aluminum alloys. Most of the lattice structures have been developed for cylindrical or conical geometries and can be manufactured through automated processes such as filament winding [5] and automated fiber placement [6]. They are composed of a regular cell pattern obtained by two systems of ribs with rectangular cross section: two sets of helical ribs, oriented with respect to the axis of revolution with angles equal in magnitude but with opposite signs, and hoop ribs. The type of the elementary lattice cell influences the strength and stiffness of the lattice structure. An external or internal skin, without a structural role, can be co-cured with the isogrid structure. Buckling is the most important failure mode of axisymmetric isogrid structures. It can be subdivided into global and local buckling. The former causes the collapse of the whole structure, while the latter produces the localized failure mode involving local failure of stiffener. The failure mode depends on both the type of applied load and the geometric parameters of isogrid structure, such as the rib thickness, rib width, cell height, winding angle, and skin thickness. Several analytical and numerical methods have been developed to predict the different buckling loads and modes of stiffened cylinders [7, 8].
Notwithstanding the improvement in automated manufacturing processes of CFRPs has allowed to produce flat isogrid lattice panels at low cost, making them a competitive alternative to traditional stiffened or sandwich panels; the isogrid panels did not find the same interest as the cylindrical and conical ones, whose development was driven by the aerospace industry. For this reason, few studies are available in order to develop optimal design concepts for such kind of structures. To this purpose, Totaro focused on the formulation of the main design constraint equations for lattice panels in which local and global buckling were the most important failure modes and on the approach to minimum mass solutions through the analytical minimization of corresponding safety factors [9]. Shroff et al. have developed a failure model to predict the extent and type of damage of isogrid panels [10].
Recent advancements in the additive manufacturing (AM) allowed to use such technology also for the production of parts in composite materials. AM processes give the opportunity to reduce manufacturing time and costs for certain products, especially those with personalized geometries [11,12,13]. AM of CFRP is currently performed by means of processes such as stereolithography (SL), laminated object manufacturing (LOM), fused deposition modeling (FDM), selective laser sintering (SLS), and photo-solidification [14, 15]. Among them, FDM is the most used method owing to its simplicity, reliability, and low cost, as shown by Wang et al. in their review of the 3D printing methods for CFRPs [16]. The FDM process is based on the extrusion of a heated thermoplastic filament through a nozzle and allows to build the part by means of a layer by layer deposition [17,18,19]. In order to improve the properties of FDM 3D printed component, reinforced filaments, filled up to 30% of short carbon fibers, are typically used [20,21,22,23].
The 3D printing processes could be used to manufacture isogrid structures in CFRPs. Such structures can result in higher specific performances and lower manufacturing times than those realized in aluminum alloys. On the other hand, if compared with continuous carbon fiber structures, isogrid structures realized with short carbon fibers typically result in lower performances. However, the AM process allows to overcome the critical design aspect of continuous carbon fiber isogrid structures represented by the nodal points in which the increase in reinforcement content due to intersection of three tows leads to undesired bending of fibers. Furthermore, an amount of fibers in the nodal point three times higher than of the rest of ribs cannot be compacted by keeping a constant rib height [9, 24]. For this reason, 3D printing of composite materials is attracting the interest of different industries as a method for metal replacement and, especially in the aerospace sector, as a system able to substitute the traditional manufacturing processes of composite materials. Detailed investigations of 3D printed composite structures properties are mandatory.
The only relevant paper available in literature concerning 3D printed isogrid structures was proposed by Li et al. [25] who investigated such structures by means of experiments and FEM analysis to build a multi-failure theory. They proposed a failure mode map which can be used for the optimal design of isogrid structures. However, the isogrid panels were produced by the LOM printing method in unreinforced plastic (PVC). No work is available in the scientific literature concerning the FDM 3D printing of isogrid structures in CFRP, although it may represent the turning point for a wide diffusion of these structures. In order to overcome this issue, the authors have recently assessed the feasibility of FDM 3D printing of isogrid structures in CFRP by presenting a preliminary investigation [26].
In the present investigation, flat isogrid lattice panels, without the skin, in short carbon fiber reinforced polyamide, were manufactured by means of FDM 3D printing, with different values of geometric parameters. The effect of width and height of the ribs and cell height on the buckling behavior of structures subjected to compressive load was studied. To this purpose, compression tests were performed; the maximum load and the limit buckling displacement were derived from the load vs. displacement curves. In addition, sensitivity analysis was performed in order to investigate the contribution of each geometric parameter on the mechanical properties of the structures. Furthermore, fracture surfaces of isogrid structures were analyzed by means of microstructural investigations carried out using both optical and scanning electron microscopes in order to evaluate the failure mode after the buckling phenomena. The main goal was to define the failure mode map of isogrid lattice panel as a function of geometric parameters, thus allowing engineers to easily identify the best configuration for the design of high-performance isogrid structures.
2 Fabrication and testing
2.1 3D printer and material
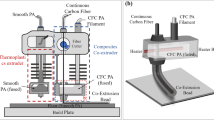
The Roboze One+400 3D printer, used to obtain isogrid structures in CFRP, is shown in Fig. 1. The printing process, based on the FDM technology, was carried out using a composite filament, 1.75 mm in diameter, and an extruder with a diameter of 0.6 mm.
The composite material investigated was polyamide resin with a weight content of short carbon fibers equal to 20%; the composite density was equal to 1.43 g/cm3.
Before printing, the composite material was heated in an oven at 120 °C for 4 h in order to improve printing quality and reduce void formation. During extrusion, the CFRP was kept in a controlled atmosphere at 70 °C. The extrusion temperature was 240 °C, while the plate temperature was 45 °C to avoid the sample detachment. The main phases of the 3D printing process are shown in Fig. 2.
Isogrid structures were drawn by a CAD software and exported as .STL files. They were imported in a slicing software which translates the 3D model in instructions for the 3D printer by creating a .GCODE file. The software allowed to set up the printing parameters such as infill, infill angle offset, printing speed, and internal fill pattern. The main process parameters used for printing the isogrid structures are reported in Table 1.
Different isogrid structures were manufactured in order to investigate the effect of geometric parameters on their compressive behavior. In particular, structures were obtained by choosing the rib width (X), rib thickness (Z), and cell height (T) (Fig. 3) in the ranges 3–5 mm, 4–15 mm, and 18–25.5 mm, respectively. All isogrid structures were characterized by the same values of length and width equal to 106 and 80 mm, respectively.
The weight of each structure was measured after 15 days from its manufacture using an analytical balance with a readability of 0.1 mg.
2.2 Tensile tests
The mechanical behavior of the polyamide resin reinforced with short carbon fibers was characterized by means of tensile tests. They were carried out on dog bone samples obtained using the Roboze One+400 3D printer by choosing as printing direction the loading one and the highest infill pattern (Fig. 4). Wang et al. [16], in their review paper, reported that during the extrusion, short carbon fibers tend to align in the printing direction. The first and the last layers were printed with a printing direction of 45° in order to facilitate raft removing and to guarantee the best surface quality. The tensile sample was characterized by a cross section with thickness and width values equal to 2 mm and 10 mm, respectively, and a gauge length of 80 mm. It was printed by including the end tabs in order to avoid failures caused by the clamping force. Tests were carried out on the servo-hydraulic universal testing machine MTS 810. During test, load (P) and nominal strain (e) along the loading direction were acquired using a load cell and an extensometer, respectively. The nominal stress (s) was obtained by the ratio between load and initial area of cross section. The elastic modulus was calculated as the slope of the straight line joining the stress values corresponding to the strain levels equal to 0.05 and 0.25%. The repeatability of the results was ensured by performing at least three tensile tests.
2.3 Buckling test of isogrid structures
Buckling tests of isogrid panels were performed on the universal testing machine MTS 810 with a movable platen speed equal to 0.5 mm/min (Fig. 5). The load (P) vs. displacement (Δh) curves were acquired during testing by means of a load cell and a linear variable displacement transducer (LVDT), respectively. The isogrid structures were positioned with the shortest side in contact with the flat, smooth platens. Repeatability of results was assured by repeating the buckling tests at least three times for each combination of geometric parameters investigated. Moreover, a sensitivity analysis was carried out in order to evaluate the contribution of each parameter on the investigated mechanical performances in terms of peak load and limiting buckling displacement.
2.4 Optical and scanning electron microscopies
The fractured surface of isogrid structures subjected to buckling tests was analyzed using the optical microscope Leica DMi8. Furthermore, the scanning electron microscope FESEM ZEISS SUPRATM 40, with compact GEMINI® objective lens, was also utilized to acquire high magnification three-dimensional topography of fractured surfaces of deformed isogrid structures. The fractured samples were coated by means of a metallization process in order to make conductive the composite material.
3 Results and discussion
3.1 Tensile tests
Figure 6 shows the nominal stress-nominal strain curves obtained by subjecting three different samples in polyamide resin reinforced with short carbon fibers, produced by means of 3D printing, to tension test. It appears the excellent repeatability of the s-e curves characterized by large overlapping zones for the entire deformation range investigated. The values of elastic modulus (E), ultimate tensile strength (UTS), and ultimate elongation (UE) are equal to 13.5 GPa, 127 MPa, and 2.1%, respectively. The Young modulus tends to decrease as strain increases exhibiting the typical behavior of short fiber reinforced polyamide in which the structure of long, covalently bonded matrix atoms, with high molecular weights, is responsible for the failure mechanisms [27]. Such behavior is consistent with what observed by Bernasconi et al. on a short glass fiber reinforced polyamide 6.6 [28]. However, as far as the values of specific strength and stiffness of the composite material are concerned, they are equal to 89.2 MPa/(g/cm3) and 9.5 GPa/(g/cm3), respectively. It appears that the former is higher and the latter lower than those of several Al alloys of 1XXX and 3XXX series.
3.2 Buckling tests
3.2.1 Analysis of P-Δh curves
The isogrid structures subjected to buckling test showed the occurrence of both global and local buckling failure modes. In particular, Fig. 7a shows an isogrid panel, characterized by relatively small rib thickness, undergoing global buckling which takes place before stress reaches yielding of composite material, according to the results shown in Fig. 6. Such failure mode, characterized by instability that extends to the whole structure, is consistent with what observed by Wang et al. [29]. Figure 7b shows local buckling which occurs with small values of rib width. In such case, the instability extends to a local zone of the structure.
A typical load-displacement curve of an isogrid structure subjected to buckling test is reported in Fig. 8. The P-Δh curve exhibits an increase in load with platen displacement up to a peak value (Pmax) reached at to the onset of buckling of structure (global buckling) or ribs (local buckling). The value of the displacement at which to the peak load occurs was defined by authors as limit buckling displacement (LBD).
The effect of geometric parameters of isogrid structures on load vs. displacement curves is shown in Fig. 9.
It is shown that, irrespective of displacement, for given values of rib width and cell height, the increase in the rib thickness leads to a rise in the load applied to the isogrid structure during buckling test; a similar effect on compressive load is obtained by increasing the rib width, for the given rib thickness and cell height. Furthermore, the P-Δh curves show that, for the given values of rib width and rib thickness, an increase in the cell height causes a slight decrease in the applied load. Finally, the thicker structures investigated in the present paper, characterized by Z = 15 mm, failed under local buckling, differently from thinner structures (Z equal to 4 and 8 mm) which underwent to global buckling phenomena. The video attached at the present work, as support material, shows the different buckling failure modes of isogrid structures with different geometric parameters.
3.2.2 Analysis of the peak load and limiting buckling displacement
The results given by the P-Δh curves were analyzed in terms of the peak load applied during testing and displacement at the onset of buckling. To this purpose, Fig. 10 shows that, irrespective of rib width and cell height, the peak load increases with rib thickness. Furthermore, for a given value of T and Z, the increase in the rib width from 3 to 5 mm leads to a remarkable rise in the Pmax while, irrespective of X and Z values, the increase in the cell height causes a small decrease in the peak load. Finally, independently of Z value, the difference between Pmax of structures with X = 3 mm and X = 5 mm, at same T value, is equal to about 33%.
Figure 11 shows that the displacement at the peak load exhibits a similar behavior to the one experienced by the Pmax (Fig. 10), indicating that the geometric parameters of isogrid structures (X, Z, and T) influence LBD in the same way they affect Pmax, even though the discrepancy between the LBD values for structures with X = 3 mm and X = 5 mm at the same T value, equal to about 23% as the Z value ranges from 4 to 10 mm, increases up to 30% for Z = 15 mm.
The influence of rib width and cell height on the ratio between peak load and limit buckling displacement vs. the rib thickness is shown in Fig. 12. It clearly appears that also the Pmax/LBD ratio increases with Z value even though the difference between the behavior exhibited by the structures with X = 3 mm and those with X = 5 mm strongly decreases as Z = 15 mm. It means that the isogrid structures with X = 3 mm are characterized by load-to-displacement ratios which tend to the ones of the structures with X = 5 mm, notwithstanding the lower Pmax and LBD values with X = 3 mm as compared with those with X = 5 mm. Such behavior can be related to the different growth rates of Pmax and LBD with rib thickness. In particular, while the difference in percentage between the Pmax values at X = 3 mm and X = 5 mm is constant, irrespective of rib thickness, the difference in percentage between the LBD values at X = 3 mm and X = 5 mm is constant as the rib thickness ranges from 4 to 10 mm, but it increases as Z is equal to 15 mm. Such behavior can be attributed to the onset of local buckling at Z = 15 mm which causes a reduction of the load carrying capacity of the structures.
As far as the specific strength is concerned, Fig. 13 shows the effect of rib width and cell height on the peak load-to-weight ratio of isogrid structures as a function of rib thickness. It can be seen that the Pmax/w ratio increases with an almost constant slope with rib thickness as Z value ranges from 4 to 10 mm. Such behavior is consistent with the one showed by the peak load applied during buckling test and showed in Fig. 10. As the rib thickness further increases from 10 to 15 mm, the growth rate of the peak load-to-weight ratio vs. rib thickness strongly decreases. In particular, as X is equal to 5 mm, the growth rate of Pmax/w ratio tends to 0. Since the increase in rib thickness involves an increase in both the load carrying capacity and the weight of isogrid structure, the increase in the specific strength in the region where global buckling occurs is due to the higher effect on Pmax/w ratio of the former than the latter. As Z increases from 10 to 15 mm, very small variations of Pmax/w take place in the local buckling region due to the similar effect on specific strength of Pmax and w of structure.
Figure 14 shows both the peak load-to-weight ratio and the peak load obtained with the different isogrid configurations investigated. The isogrid panels with rib thickness equal to 4 mm exhibit the lowest values of both Pmax and Pmax/w, indicating that in these structures, buckling occurs very early due to their high slenderness. Their load carrying capacity, both in terms of strength and specific strength, is at least five times lower than structures with rib thickness of 8 mm.
As the rib thickness is equal to or higher than 8 mm, Pmax/w shows more uniform values than those of Pmax. It is worth to notice that the geometric parameters leading to the highest strength in terms of Pmax (X = 5 mm; Z = 15 mm; T = 18 mm) are different from the ones providing the highest specific strength in terms of Pmax/w (X = 3 mm; Z = 15 mm T = 18 mm). No significant difference, both in terms of strength and specific strength, can be found among structures with different cell heights. However, irrespective of X and Z values, isogrid structures with a cell height equal to 18 mm show a very slight increase in strength (mean value + 4%) and in specific strength (mean value + 2%) with respect to the ones with a cell height of 25.5 mm.
A significant aspect which engineers must take into account during the design process of stiffened lattice structures concerns the possibility to develop structures characterized by different maximum loads before failure but similar specific strength values. As a matter of fact, Fig. 14 shows that, for each cell thickness investigated, the structures with X = 5 mm and Z = 10 mm, X = 5 mm and Z = 15 mm present very similar values of Pmax/w as compared with those with X = 3 mm and Z = 10 mm, while Pmax shows a marked variation (from about 20 to 46 kN).
The sensitivity of mechanical performances, in terms of peak load and limiting buckling displacement, to the geometric parameters of isogrid structures was also investigated. To this purpose, modeFrontier© by Esteco, a software dedicated to statistical analysis [30], was used. Statistical sensitivity analysis, based on the creation of a DOE (design of experiment), was carried out to define how the outputs of the model change as a function of input variations. The results of the sensitivity analysis are shown in Fig. 15. Rib thickness is the geometric parameter exhibiting the highest effect on both Pmax and LBD, while the cell height results in the lowest contribution. These results are in excellent agreement with those reported by Totaro in [9]. Indeed, it was demonstrated, using an analytical method, that the structure thickness strongly influences both local and global buckling resistances while the contribution of rib width of a lower order of magnitude. It was also showed that the cell height leads to a negligible contribution for both failure modes.
3.3 Optical and scanning electron microscopies
The low magnification optical microscopy of fractured surface of an isogrid after buckling test shows the failure for global buckling which causes cracking of the ribs and delamination (Fig. 16a). The SEM micrograph of the fractured surface (Fig. 16b) that the short carbon fibers dispersed into the polyamide matrix is pulled out. Furthermore, the fractured surface is not homogenous, indicating matrix yielding and debonding between matrix and fibers. This behavior can be attributed to the presence of water molecules into the polyamide which causes ductile fracture of the matrix and physical damage of fiber-matrix interface [21].
4 Conclusion
Isogrid structure is typically realized in aluminum or unidirectional composite materials. The former presents low specific resistance while the latter different manufacturing issues. The 3D printing, owing to the high performances of composite materials and flexibility of manufacturing process, can represent a useful method to replace aluminum and unidirectional composites as used for manufacturing of isogrid structures.
The present work is focused on the manufacturing of high performing composite isogrid structures obtained by means of FDM 3D printing. Polyamide reinforced with 20% in weight of short carbon fibers was used to realize isogrid structures with different rib width, rib thickness, and cell height. Such structures were tested under compressive load in order to evaluate the buckling strength. The main results can be summarized as follows:
-
Mechanical properties of the short fiber reinforced polyamide, in terms of ultimate tensile strength, are similar to those of aluminum alloys of 1XXX and 3XXX series while the elastic modulus is significantly lower. However, the specific strength of the composite material is higher and the elastic modulus is slightly lower than those of aluminum alloys.
-
The load applied to isogrid structures during compression test increases with displacement up to a peak value reached at the onset of buckling.
-
Depending on the values of geometrical parameters, the isogrid structures can undergo to local or global buckling. The former can be attributed to the rib buckling while the latter to the relatively small rib thickness.
-
The peak load strongly increases with the rib thickness and rib width while it undergoes small decrease as cell height increases. The influence of geometric parameters on the displacement at the onset of buckling is very similar to the one on the peak load.
-
The peak load to weight ratio increases with rib thickness up to a value of 10 mm, and then, the growth rate of the ratio strongly decreases.
-
The geometric parameters leading to the highest strength are different to the ones providing the highest specific strength.
-
Local buckling must be avoided because it leads to a decrease in the growth rate of the specific strength.
-
SEM micrograph shows the pull out of the carbon fibers dispersed into the matrix.
To maximize the strength-to-weight ratio of composite isogrid structures, rib thickness and width must be increased. However, there is a limit beyond which local buckling occurs and the specific strength increases slowly. In particular, isogrid structure with a rib width of 3 mm, a rib thickness of 15 mm, and a cell height of 18 mm was characterized by the highest specific strength.
Using 3D printing, it is possible to produce high performing isogrid structures that can be used as a reinforcement to stiffen panels subjected to compressive loads. In addition, as the 3D printing technology of composite is continually growing, it cannot be excluded an implementation of this manufacturing method in the production of reinforcing ribs for aerospace sector in the future. The present study can also pave the way to the wide diffusion of composite 3D printing in industrial sectors not only as a metal replacement method but also as an alternative process for manufacturing traditional composite structures.
Further researcher works will be focused on the investigation of humidity adsorption of polyamide and on the comparison between 3D printed and traditionally produced isogrid structures.
References
Antony A (2017) Effect of RIB orientation in isogrid structures: aerospace applications. 3:319–327
Andrianov IV, Kalamkarov AL, Weichert D (2012) Buckling of fibers in fiber-reinforced composites. Compos B Eng 43:2058–2062. https://doi.org/10.1016/j.compositesb.2012.01.055
Vita A, Castorani V, Germani M (2018) Manufacturing, process simulation and mechanical tests of a thick component produced by compression-RTM process. In: Eccm18 - 18th European conference on composite materials, vol 2018, pp 24–28
Huybrechts SM, Hahn SE, Meink TE (1999) Grid stiffened structures: a survey of fabrication, analysis and design methods. In: ICCM12 - Conference Proceedings
Sorrentino L, Marchetti M, Bellini C, Delfini A, del Sette F (2017) Manufacture of high performance isogrid structure by robotic filament winding. Compos Struct 164:43–50. https://doi.org/10.1016/j.compstruct.2016.12.061
Mack J, Mcgregor O, Mitschang P (2014) Prepreg lay-up technology for manufacturing of lattice structure fuselage sections
Kidane S (2002) Buckling analysis of grid stiffened composite structures. Louisiana State University
S.A. K, J. B, A. K, R.K. G (2008) Isogrid design aspects for cylindrical shell. In: Proceedings of the International Conference on Aerospace Science and Technology. Bangalore, India
Totaro G (2015) Optimal design concepts for flat isogrid and an isogrid lattice panels longitudinally compressed. Compos Struct 129:101–110. https://doi.org/10.1016/j.compstruct.2015.03.067
Shroff S, Acar E, Kassapoglou C (2017) Design, analysis, fabrication, and testing of composite grid-stiffened panels for aircraft structures. Thin-Walled Struct 119:235–246. https://doi.org/10.1016/j.tws.2017.06.006
Parandoush P, Lin D (2017) A review on additive manufacturing of polymer-fiber composites. Compos Struct 182:36–53
Gibson I, Rosen D, Stucker B (2015) Additive manufacturing technologies: 3D printing, rapid prototyping, and direct digital manufacturing, second edition. Addit Manuf Technol 3D Printing, Rapid Prototyping, Direct Digit Manuf Second Ed 1–498. https://doi.org/10.1007/978-1-4939-2113-3
Jiang J, Xu X, Stringer J (2018) Support structures for additive manufacturing: a review. J Manuf Mater Process 2:64. https://doi.org/10.3390/jmmp2040064
Ngo TD, Kashani A, Imbalzano G, Nguyen KTQ, Hui D (2018) Additive manufacturing (3D printing): a review of materials, methods, applications and challenges. Compos B Eng 143:172–196
Hashemi Sanatgar R, Campagne C, Nierstrasz V (2017) Investigation of the adhesion properties of direct 3D printing of polymers and nanocomposites on textiles: effect of FDM printing process parameters. Appl Surf Sci 403:551–563. https://doi.org/10.1016/j.apsusc.2017.01.112
Wang X, Jiang M, Zhou Z, Gou J, Hui D (2017) 3D printing of polymer matrix composites: a review and prospective. Compos B Eng 110:442–458. https://doi.org/10.1016/j.compositesb.2016.11.034
Samykano M, Selvamani SK, Kadirgama K, Ngui WK, Kanagaraj G, Sudhakar K (2019) Mechanical property of FDM printed ABS: influence of printing parameters. Int J Adv Manuf Technol 102:2779–2796. https://doi.org/10.1007/s00170-019-03313-0
Jiang J, Lou J, Hu G (2019) Effect of support on printed properties in fused deposition modelling processes. Virtual Phys Prototyp 14:308–315. https://doi.org/10.1080/17452759.2019.1568835
Jiang J, Hu G, Li X, Xu X, Zheng P, Stringer J (2019) Analysis and prediction of printable bridge length in fused deposition modelling based on back propagation neural network. Virtual Phys Prototyp 14:253–266. https://doi.org/10.1080/17452759.2019.1576010
Fidan I, Imeri A, Gupta A, Hasanov S, Nasirov A, Elliott A, Alifui-Segbaya F, Nanami N (2019) The trends and challenges of fiber reinforced additive manufacturing. Int J Adv Manuf Technol 102:1801–1818. https://doi.org/10.1007/s00170-018-03269-7
Ajinjeru C, Kishore V, Lindahl J, Sudbury Z, Hassen AA, Post B, Love L, Kunc V, Duty C (2018) The influence of dynamic rheological properties on carbon fiber-reinforced polyetherimide for large-scale extrusion-based additive manufacturing. Int J Adv Manuf Technol 99:411–418. https://doi.org/10.1007/s00170-018-2510-z
Nakagawa Y, Ken-ichiro M, Maeno T (2017) 3D printing of carbon fibre-reinforced plastic parts. Int J Adv Manuf Technol 91:2811–2817. https://doi.org/10.1007/s00170-016-9891-7
Saroia J, Wang Y, Wei Q, Lei M, Li X, Guo Y, Zhang K (2020) A review on 3D printed matrix polymer composites: its potential and future challenges. Int J Adv Manuf Technol 106:1695–1721
Güemes A, Del Olmo E, Dorte M, Fernandez-Lopez A (2012) Structural testing and simulation of composite isogrid structures for aerospace applications. In: ECCM15
Li M, Lai C, Zheng Q, Han B, Wu H, Fan H (2019) Design and mechanical properties of hierarchical isogrid structures validated by 3D printing technique. Mater Des 168:107664. https://doi.org/10.1016/j.matdes.2019.107664
Forcellese A, di Pompeo V, Simoncini M, Vita A (2020) Manufacturing of isogrid composite structures by 3D printing. In: Procedia Manufacturing. Elsevier, pp 1096–1100
Strobl G (2007) The physics of polymers: concepts for understanding their structures and behavior. Springer Berlin Heidelberg
Bernasconi A, Rossin D, Armanni C (2007) Analysis of the effect of mechanical recycling upon tensile strength of a short glass fibre reinforced polyamide 6,6. Eng Fract Mech 74:627–641. https://doi.org/10.1016/j.engfracmech.2006.10.002
Wang D, Abdalla MM (2015) Global and local buckling analysis of grid-stiffened composite panels. Compos Struct 119:767–776. https://doi.org/10.1016/j.compstruct.2014.09.050
Castorani V, Vita A, Mandolini M, Germani M (2017) A CAD-based method for multi-objectives optimization of mechanical products. Comput Aided Des Appl 14:14–571. https://doi.org/10.1080/16864360.2016.1274528
Acknowledgments
The authors acknowledge Roboze s.p.a. for the materials.
Funding
Open access funding provided by Università Politecnica delle Marche within the CRUI-CARE Agreement. This research was funded by POR FESR Abruzzo 2014/2020, Linea di Azione 1.1.1 and 1.1.4, Avviso Pubblico per “Sostegno a progetti di Ricerca Industriale, Sviluppo Sperimentale e Innovazione delle PMI nelle aree di specializzazione S3” (CUP: C37H18000070007).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
(MP4 60449 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Forcellese, A., Simoncini, M., Vita, A. et al. 3D printing and testing of composite isogrid structures. Int J Adv Manuf Technol 109, 1881–1893 (2020). https://doi.org/10.1007/s00170-020-05770-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-020-05770-4