1 Introduction

Quality inspection (QI) is an inherent part of the production process [1, 2]. The goal of QI is to check whether the properties of products meet requirements. Along with the development of measurement systems, vision systems and information technologies, a greater integration of QI within the production process has been observed [3, 4]. Integration allows for the recognition of non-conformances that arise during production, on the spot and without delay. In many manufacturing processes, however, QI is still carried out as a separate operation with the use of traditional measuring instruments and with a significant human contribution. This method of conducting QI generates additional costs; therefore, it seems advisable to determine its efficiency [5,6,7].

In this paper, there is a proposal to incorporate the value added by QI into the production process as a criterion for assessing its efficiency. The value added means the difference between quality costs (CQ) incurred within the production process with QI, and those incurred without it. Quality is to be considered here as the sum of the cost of inspection and the costs of non-conformance. The costs of non-conformance include both defective products rejected or those repaired in the process and defective products detected by the end user.

Quality inspection efficiency defined in this way is determined by many factors, but above all by the inspection system’s ability to recognize correctly whether the requirements are met. An inspection system consists of measurement equipment, procedures, environment and the people carrying out the measurements and analysing the data. Costs related to inspection performance and inspection maintenance depend on the point at which the inspection takes place within the production process, its scope and the measurement or assessment methods used [8,9,10].

In relation to the separate stages of the production process, the QI may take place [2, 3]

  • before the process stage starts:

    • input inspection (e.g. inspection of materials, parts, and semi-finished products)

    • inspection of the “first step” (the process can only begin once the first step is considered acceptable)

  • within the process stage (also “process control”)

  • after completion of a process stage:

    • before handing over the products to the next stage

    • before sending the products to an external recipient (acceptance inspection)

The scope of the inspection may include [2]

  • all the parts produced—100% control

  • only some of the items produced—through sampling (the scope of the inspection is planned according to statistical rules)

Data needed to assess whether the products meet requirements can be obtained [3]

  • from measurements, with the use of measuring instruments and the presentation of measurement results in quantitative in the form of numerical values

  • by observation (e.g. visually) and comparison with a standard, and the issuing of a quality rating, for example, as a “conforming product” or “non-conforming product”

Due to the impact on the inspected object, the inspection may be [3]

  • non-destructive (e.g. a dimensional inspection, an X-ray examination, ultrasonic measurement, and visual inspection)

  • destructive (e.g. strength tests)

The inspection parameters listed above form an inspection plan [9]. Its determination should consider the capability of the production process, the capability of the inspection system and the consequences of incorrect inspection, expressed as costs.

The production process capability refers to the requirements specified in the product specifications. Its simplest measure is the percentage of non-conforming products (p) [9]. The value p > 0 indicates that some products do not meet all the requirements and must be repaired, reworked or rejected (i.e. scrapped). More advanced measures of quality effectiveness are indicators of the process capability: Cp and Cpk [2].

Inspection system capability can be determined by type I and type II errors [11, 12]. The type I error is the recognition of a good product as non-conforming, while type II is the reverse. Such errors are particularly frequent in visual inspections, during which measuring instruments are replaced by human senses, which are, by nature, subjective.

It is commonly believed by companies that type II errors are particularly serious as their effects are felt by the customer. This can lead to significant losses associated with the loss of customer trust, and loss of prestige. However, type I errors also contribute to additional and unnecessary costs associated with the need to rework products, which are de facto good, in order to “repair” them.

2 Related work

Determining the effectiveness of quality inspection in production processes is of interest to many researchers.

In the 1970s, Hurst (1973) published the results of studies aimed at developing a method for planning the point of application of a quality inspection within a multistage manufacturing process [13]. Hurst adopted the binomial distribution of the probability of non-conformances occurring in the manufacturing process. However, the cost model proposed did not take into account quality inspection system capability.

Research by Ballou and Pazer (1982) focused on analysing the impact of quality inspection capability on manufacturing costs [14]. Included in the cost model were the cost of inspection, fractions of conforming and non-conforming products, and type I and type II inspection errors. The model proposed was intended to support decisions made concerning the use of quality inspection at a given stage of the manufacturing process. The model was used to verify a process consisting of 3 operations and for 9 different levels of inspection effectiveness. In a series of experiments, it was found that inspection errors had a significant impact on total manufacturing costs. It transpired that type I errors (rejection of conforming units) had a greater impact on the cost of producing a product than type II errors.

Garcia-Diaz et al. (1984) developed a model of quality costs, within which inspection costs, repair costs and a penalty for accepting non-conforming products as conforming were included as variables [15].

Porteus (1996) considered planning QI in terms of achieving an optimal production schedule. The Porteus model made it possible to determine the optimal size of the production batch at a given level of the production process capability and at the assumed risk of not meeting customer requirements [16]. Three scenarios of actions leading to an increase in the effectiveness of QI were considered in the model: (1) increasing the quality capacity of the process, (2) reducing the size of the production batches (division of the order into small production batches, which aids the discovery of quality problems) and (3) application of the first and the second approach together (a hybrid approach). Chand modified the Porteus model introducing into it assumptions related to the probability distribution of costs for so called “bad quality”. In his considerations, he emphasized, like Porteus, the advantages of producing in small batches, the associated learning effect on employees, and consequently an increase in the level of quality [17].

A model allowing an assessment of the efficiency of QI in multistage processes was proposed by Raz and Kaspi [8]. In assessing the quality costs, the following were taken into account: the level of quality inspection capability, the level of non-conformance in the process and the cost of repairing non-conforming products. The model implementation used an integer nonlinear programming approach which, as the authors emphasized, was quite difficult to implement in industrial practice. Alternatively, a method using a dominance relationship was developed, using heuristics. This made it possible to obtain a solution that was not optimal, but achievable. Raz and Bricker (1991) also used a heuristic method to determine a QI procedure that minimized the expected total cost per unit [18]. It was emphasized that the model gave an approximate rather than optimal solution.

Villalobos and Foster (1991) developed a cost model that allowed the planning of quality inspection online [19]. The model included the cost of manufacturing and of scrap and repair. It was dedicated to a specific manufacturing process.

A stochastic model that used dynamic programming to indicate the level of production costs depending on different quality inspection strategies was developed by Fine (1989) [20]. A model taking into account the cost of inspection was also presented by Ng and Hui (1996) [21].

The costs of production, type and form of production, and inspection strategies were considered in the model by Clark and Tannock (1999) [22]. For the calculations, a software model was used which included manufacturing equipment, manufacturing schedule, and quality inspection strategies. This was used to optimize the production process in terms of the costs of quality.

Finkelstein et al. (2005) proposed a model addressing the minimization of the expected total costs of inspection, deficiencies and repairs [23]. The model was based on a dynamic programming algorithm that had a low computational complexity. This supported the analysis of cost sensitivity for various scenarios of inspection plans.

Chiadamrond (2003) developed an empirical model of quality costs as a function of two main components: traditional prevention and assessment costs, and loss of opportunity costs [24].

Duffuaa, Khan and Elshafei devised models for quality inspection planning based on the evaluation of multiple attributes [25, 26]. One of them focused on determining the frequency of inspections with regard to minimizing the total cost of production. Another could be used to determine the number of inspection cycles with a view to minimizing inspection costs.

Anily and Grosfeld-Nir (2006) and Wang and Meng (2009) also addressed the problem of minimizing the costs of the entire manufacturing process by properly planning QI [27, 28]. Theoretical models were developed in which the desirability of using QI and its frequency depended on the size of the production batch, the level of control errors and the expected total cost. Vaghefi and Sarhangian (2009) extended the proposed approach to type II errors in the assessment and applied the model to a multistage production system [29]. The model developed by the researchers made it possible to indicate the optimal frequency of QI at the indicated inspection points thanks to selected process parameters, such as quality level, batch size and inspection effectiveness.

Toteva and Vasileva (2013) considered the problem of quality inspection planning within manufacturing processes with respect to inspection cost and capability [30]. Their approach made it possible to indicate the purposefulness of quality inspection implementation as well as its place and scope. The rules used to decide on the QI strategy were a simple relationship between the loss caused by a defect and the cost of inspection throughout the process. This rule did not take into account the type of costs and the place where the error occurred, or the likelihood of its detection and removal.

Farooq et al. (2017) analysed the quality costs incurred in four scenarios of QI application in the production process: scenario A—double stage acceptance sampling strategy, scenario B—single stage acceptance sampling strategy, scenario C—single stage revised sampling strategy and scenario D—no inspection [31]. The proposed model allowed for the selection of the optimal control scenario.

Data resulting from the aforementioned research is presented in a systematic form in Table 1.

Table 1 Summary of the selected research (own research)
Full size table

Based on the descriptions of the studies presented and their summaries, it can be concluded that the studies mainly concerned multistage production processes. The aims of the research were, for example, to discover the optimal production schedule, to minimize manufacturing costs or, more specifically, to minimize quality costs. Various mathematical models were tested. In some of the studies, operational research methods were used, and model variables were treated as determined or assumed to be stochastic. The variables considered were mostly manufacturing capability and inspection capability, among them type I and type II errors, type of production, costs of inspection, and so on.

The models presented in the discussed works may be useful in determining the quality inspection parameters, thereby making it possible to achieve the demanded inspection effectiveness and thus minimize quality costs. However, most of the models used complicated mathematical apparatus available only to advanced mathematicians. These models are difficult to understand for the practitioners responsible for planning inspections at shop floor level. No model comprehensively considered all the categories of costs related to non-conformances, e.g. costs resulting from complaints.

The aim of this paper is to develop a model for calculating quality costs which is general enough to be valid in relation to the multistage production process while, at the same time, has a mathematical form which is understandable for those who wish to apply the resulting dependencies for inspection planning and optimization. The innovation of the presented approach also consists in using added value for assessing the effectiveness of inspection. Added value is understood as the difference between the quality costs of the manufacturing process with, and without, an inspection.

3 Model of quality costs in a multistage manufacturing process

3.1 Aim and general assumptions

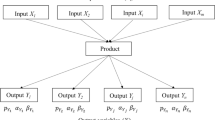
The goal of this paper is to develop a model of quality costs that can be used when planning quality inspection (QI) parameters in a manufacturing process (MP) consisting of a sequence of N separate manufacturing process stages (MPS) within which, parts, subassemblies or products, hereby referred to as items, are processed.

It is assumed that at the nth MPS a product characteristic X (e.g. dimension, roughness, hardness) is shaped. In the QI carried out after the nth MPS, there is a check to discover whether the requirements related to X are met. If these requirements are not met, this means a non-conformance or failure [9]. The non-conformance found in an item therefore renders the item non-conforming.

Once it has passed through the nth MPS, an item can be (Fig. 1)

  • conforming (item_C), or

  • non-conforming (item_N)

Fig. 1
figure 1

Scheme of multistage manufacturing process with inspection

Full size image

In turn, having passed through the nth QI, an item is classified as:

  • conforming (item_C)

  • non-conforming (item_N), with the distinction of

    • non-conforming but repairable (item_NR)

    • non-conforming, being non-repairable (defective items) and to be scrapped (item_NS).

Items inspected and classified as items_C are transferred to the next MPS, and items classified as items_NR are, before transferring, repaired or reworked, while items_NS are scrapped (Fig. 1).Those Items_N not detected during the inspection carried out after the nth MPS may be detected during the inspection carried out at the next MPS, and repaired or scrapped immediately after detection.

If an item_N is not detected until the end of the entire process, it may be detected by the final user. In this case, three scenarios are possible:

  • non-conformance does not affect the possibility of using the item as intended and is not noticed by the user

  • non-conformance affects the possibility of using the item, is detected by the user and is repaired at the cost of the manufacturer

  • non-conformance affects the possibility of using the item and is detected by the user, and the item is scrapped and replaced at the cost of the manufacturer

3.2 Capability of the manufacturing process and inspection system

It is assumed that the manufacturing process capability related to product characteristic X is expressed by the fraction of items meeting the requirements. After passing through the nth MPS, an item belongs to one of the following three fractions (i.e. fractions after manufacturing):

  • fmn(1)

  • fmn(r)

  • fmn(s)

with

  • 1—item_N

  • r—item_NR

  • s—item_NS

Note that the sum fmn(r) + fmn(s) is the equivalent of p (percentage non-conforming), and

$$ {fm}_n(r)+{fm}_n(s)=1-{fm}_n $$

The capability of the inspection system is defined in a similar way. It is assumed that after passing the nth QI, an item from a given production fraction (one of three fmn(1), fmn(r) or fmn(s)) may qualify for one of three inspection fractions fi (fractions of items after the inspection):

  1. 1.

    from fraction fmn(1) as

    • fin(11)

    • fin(1r)

    • fin(1s)

  2. 2.

    from fraction fmn(r) as

    • fin(rr)

    • fin(r1)

    • fin(rs)

  3. 3.

    from fraction fmn(s) as

    • fin(ss)

    • fin(s1)

    • fin(sr)

where, in the first position of the conformance status, it is the result of the manufacturing process, and the second is assigned during the inspection. For example, fraction f(1,r) contains items_C, but qualified in the inspection as items_NR.

The sum of inspection fractions coming from a given production fraction equals 1, e.g.

$$ {fi}_n(11)+{fi}_n(1r)+{fi}_n(1s)=1 $$

This means that if in the nth MPS process the number of L items is processed, the number l of items_C, recognized in the inspection as items_NR, is

$$ l\left(1,r\right)=L\cdotp {fm}_n(1)\ {fi}_n(1r) $$

It should also be emphasized that in reference to the criterion of inspection effectiveness, two groups of fractions may be distinguished:

  • items with a correctly recognized state: fin(11), fin(ss) and fin(rr). Their sum is a measure of the effectiveness of the inspection

  • items with an incorrectly recognized state, among them

    • items_C classified as fin(1r) and fin(1s)—type I-error

    • items_N classified as items-C as fin(r1), fin(s1)—type II error

    • items with an incorrectly recognized non-conformance status—fin(rs) and fin(sr)

The possibility of detecting an item_N manufactured in the nth MPS in the following MPSs or by the user (customer) is defined by the variables pdr or pds. These variables have the meaning of probability and the range of variation is <0. 1>. Depending on whether it concerns an item_NR or item_NS and on the point at which the item is detected, the following variables are distinguished:

$$ {pdr_n}^{n+k},{pds_n}^{n+k},{pdr_n}^u,{pds_n}^u $$

where the indices mean

  • r—item_NR

  • s—item_NS

  • n—number of MPS at which the item_N was manufactured

  • n + k—the number of MPS at which the item_N was detected

  • u—item_N detected by the user (customer).

It was assumed that

$$ {\sum}_{n+1}^f{pdr}_n^{n+k}\le 1;\kern0.5em {\sum}_{n+k=n}^f{pds}_n^{n+k}\kern0.5em \le 1;\kern1em {pdr}_n^u\le 1,\kern1em {pds}_n^u\le \kern0.5em 1, $$

where f = N—number of the last MPS in the manufacturing process.

3.3 Costs of manufacturing and costs of quality

Manufacturing, inspections and the repair or scrapping of defective items all incur costs. If these costs relate to non-conforming items, they are referred to as costs of non-conformance (costs of poor quality and failure costs). The basis for their calculation is unit costs, relating to each item and the nth MPS. The following unit costs are distinguished:

  • CMPn—unit costs of manufacturing (e.g. costs of machining, forming and welding of one conforming item)

  • CQIn—unit costs of inspection

  • CRMn—unit costs of the repair of an item_NR

  • CSMn—unit cost of scrapping an item_NS (i.e. costs incurred manufacturing one unit till the moment of its scrapping)

  • CRUu—unit costs of the repair of an item_NR following a complaint by the user

  • CSUu—unit cost of scrapping an item_NR following a complaint by the user

In order to simplify the quality cost calculations, the above defined unit costs are expressed in relation to the total unit costs of manufacturing one item within the whole manufacturing process (CM) that equals 1:

$$ \mathrm{CMP}=\sum \limits_{n=1}^N{\mathrm{CMP}}_n=1 $$

If, for example, CMP2 = 0.2, this means that the manufacturing unit cost at the second MPS equals 0.2 of the total manufacturing costs of one item. Similarly, if, for example, CQI2 = 0.1, then the unit inspection costs at the 2nd MPS, equal 0.1 of the total unit costs of manufacturing. In turn, the CSUu = 5 means that the cost of the end user scrapping the item_NR is 5 times higher than the manufacturing cost of one item.

Manufacturing and inspection costs incurred per unit of the product throughout the manufacturing process can be easily calculated or determined at the planning phase.

3.4 Calculation of non-conformance costs

Calculating the costs of non-conformance occurring at the nth MPS and incurred in reference to one item within the whole manufacturing process must take the stochastic character of their arising into account. Therefore, only the expected and average cost is calculated based on manufacturing process capability (expressed by the fraction fm), the inspection system capability (expressed by the fraction fi) and the possibility of detecting the item_Ns at the MPS following the nth MPS where the non-conformance appeared, or after finishing the process, i.e. it is detected by the customer (expressed by the variables pds and pdr). For example, the expected average unit cost for the repair of item_NR equals

$$ {\mathrm{CRM}}_n=\left[{fm}_n(r)\cdotp {fi}_n(rr)+{fm}_n(1)\cdotp {fi}_n(1r)+{fm}_n(s)\cdotp {fi}_n(sr)\right]\cdotp {\mathrm{CRM}}_n $$

Similarly expected, average unit costs are defined, such as

  • the scrapping of item_NS before being sent to the user (CSM)

  • the repair of item_NR following a complaint by the user (CRU)

  • the scrapping and replacement of item_NS following a complaint by the user (CSU)

Table 2 presents the scheme for assigning variables defined in Sects. 3.2 and 3.3 to the manufacturing process consisting of N MPSs (the last stage in the process is numbered as final—f). It was assumed that characteristic X is shaped at the nth MPS. The column marked n contains variables assigned to the end user of the manufactured product.

Table 2 Assignment of variables to MPSs
Full size table

The formulas for their calculation are also shown in the Fig. 2. Each formula (from 1 to 8) corresponds to one source of non-conformance costs.

Fig. 2
figure 2

Model for calculating non-conformance costs

Full size image

The sources of the specified non-conformance costs are as follows:

  • (1–3): costs incurred producing an item_NS at MPSs 1 to n. This item is scrapped after the process inspection,

  • (4): costs incurred repairing the non-repairable item_NS and costs incurred for its production at MPSs 1 to n. The item is eventually scrapped (repair is not effective),

  • (5)–(6): costs to repair an item_NR. After repair, this item is returned to the process as a conforming item,

  • (7.1): cost of repairing an item_NR, not detected in the inspection immediately after nth MPS,

  • (8.1): cost incurred producing an item_NS, which was not detected in the inspection immediately after the nth MPS,

  • (7.2): the cost of complaints relating to an item_NR,

  • (8.2): the cost of complaints relating to an item_NS.

3.5 Quality inspection efficiency

As a measure of quality inspection efficiency EQI (efficiency of quality inspection), the ratio of value added created by an inspection (VAI) to the total manufacturing costs (CMP) was adopted:

$$ \mathrm{EQI}=\frac{\mathrm{VAI}}{\mathrm{CMP}} $$

Here value added means the difference between the quality costs of the manufacturing process without an inspection and those with an inspection:

$$ \mathrm{VAI}={\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}}-{\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}={\mathrm{CN}}_{\mathrm{no}\_\mathrm{inspection}}\hbox{--} \kern0.5em \left(\mathrm{CQI}+{\mathrm{CN}}_{\mathrm{with}\_\mathrm{inspection}}\right). $$

Since, according to the assumptions made, total manufacturing costs CMP = 1, the quality inspection efficiency equals the value added created by an inspection:

$$ \mathrm{EQI}=\mathrm{VAI} $$

Depending on whether the quality inspection is applied after the nth MPS, the quality costs as a reference in determining the value added are calculated in one of three ways. In each of them, the quality costs include various groups of non-conformance costs.

  1. 1.

    After the nth MPS quality inspection (nth QI) is carried out.

Quality costs, CQwith_inspection, are the sum of the costs of the quality inspection (CQIn) and of all the non-conformance costs (CN) from the sources (1–8 on the Fig. 2).

  1. 2.

    After the nth MPS quality inspection (nth QI) is carried out, however, non-conforming items manufactured at nth MPS may be detected in the next stages of the MPS (n + 1, and n + 2).

Since all the items after the nth MPS, belonging to the fraction fmn(s), can be assigned a state (s1), which means, that f(r1) = f(s1) = 1, and fmn(rr) = fmn(rs) = fmn(ss) = fmn(sr) = 0, the costs of non-conformance created by the sources 1–6 are zero. The costs of the quality inspection CQIn are also zero.

Eventually, the quality costs (Qno_inspection_A) are the sum of the non-conformance costs calculated according to Eqs. 7.1, 7.2, 8.1 and 8.2 (Fig. 2).

  1. 3.

    Inspection is not carried out during the whole MPS.

In this case: f(r1) = f(s1) = 1; fmn(rr) = fmn(rs) = fmn(ss) = fmn(sr) = 0; also, \( {pdr}_n^u \) = \( {pds}_n^u \) = 0. Consequently, the costs of quality CQno_inspection_B are calculated only from Eqs. 7.2 and 8.2 (Fig. 2).

3.6 Procedure for calculating and analysing quality inspection efficiency

The procedure for calculating and analysing the quality inspection efficiency is presented below:

  • Phase 1. Specifying the input data

    1. a)

      Analysis of the manufacturing process and the defined quality requirements.

    2. b)

      Indication of the characteristics X (group of characteristics) to be analysed by the effectiveness of the inspection.

    3. c)

      Estimation of the manufacturing process capability at the stage n in which the X characteristic is shaped. Process capability is expressed by the fractions fmn(1), fmn(r) and fmn(s). This estimation may be based on a database of the process capability or the results of tests carried out.

    4. d)

      Estimation of the capability of the existing or planned QI for the characteristic X. This is expressed as fractions fin(11), fin(rr) and fin(ss) and the others defined in Chapter 2. Estimation can be done with the use of databases holding the results of the MSA analysis, expert knowledge or the results of specially conducted tests.

    5. e)

      Determining the possibility of detecting and repairing the non-conformance of the characteristic X not detected immediately after the stage at which it arose, at subsequent stages; pdr and pds (on a scale from 0 to 1). The source for this data may be expert knowledge.

    6. f)

      Determination of unit manufacturing costs (CMPn), costs of inspection (CQIn) and repair (CRMn) at subsequent stages of the process. To determine these costs, calculations carried out in the planning department may be used.

    7. g)

      Determination of unit costs of customer complaints (CRUu, CSUu), for instance, based on complaint reports.

  • Phase 2. Calculation of expected average costs of quality (CQ)

  • Phase 3. Calculation of quality inspection efficiency (EQI = VAI)

  • Phase 4. Discussion

In the discussion, two possible cases are considered:

  1. a)

    EQI > 0,

$$ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}<{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_A}\ \mathrm{and}\ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}<{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_B} $$

In this case, the quality inspection creates value added; its implementation is justified.

  1. b)

    EQI > 0,

$$ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}>{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_A}\ \mathrm{and}\ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}\mathrm{and}<{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_B} $$

or

$$ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}>{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_A}\ \mathrm{and}\ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}>{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_B} $$

Meeting one of these conditions means that the quality inspection performed after the nth MPS creates losses. The inspection should be abandoned or measures leading to its improvement should be taken.

4 Model application

4.1 Case study

An application of the developed quality cost model to determine the effectiveness of quality control in a multistage manufacturing process is presented below, using the example of the process of machining a part. The machined part is a constituent element of surgical scissors. The machining process consists of five stages:

  1. 1.

    Face turning and rough turning

  2. 2.

    Precision turning

  3. 3.

    Grinding

  4. 4.

    Superfinishing

  5. 5.

    Marking

Two critical characteristics were specified for the machined part: X1—deviation in the thickness, and X2—roughness of one of the surfaces. These two characteristics determine the quality of the complete surgical tool, primarily the cooperation of its individual parts. The fulfilment of the quality requirements based on these two characteristics is primarily influenced by the second process stage (2nd MPS). After this operation, 100% inspection of both characteristics is carried out. If non-conformance relating to X1 or X2 is not detected after the 2nd MPS, it is possible to detect it at subsequent stages (in self-control or during a post-operative inspection).

Managers responsible for the process would wish to know whether an inspection placed at this stage, considering its efficiency and other factors presented in Tables 3 and 4, is effective, i.e. whether it adds value to the entire manufacturing process.

Table 3 Assignment of MPS variables to MPSs—characteristic X1
Full size table
Table 4 Assignment of MPS variables to MPSs—characteristic X2
Full size table

All the data needed to perform the analysis, i.e. data on the MP capability, the possibility to detect and repair non-conforming items at the 2nd MPS and the following stages, data on the unit cost of production (CMPn), the inspection (CQIn) and repair costs following complaints (CRU and CSU) are presented in Tables 3 and 4. These data were obtained with the use of the hints described in Sect. 3.6.

Since the measurement of the thickness deviation (X1) is more reliable than the measurement of surface roughness (X2), and the process capability in reference to the roughness is higher than in reference to the geometric accuracy, the fractions fmn(1) and fin(11) are greater for X1 than for the deviation X2. Control of the thickness deviation itself is carried out by simple measuring instruments and does not take much time. The roughness measurement requires a special device and consumes more time. Therefore, the CQIn factor for X1 is lower than for X2. The probability of detecting non-compliance in terms of roughness in the operations following MP2 is zero.

For the data specified in Tables 3 and 4, the values for the quality costs presented in the Table 5 were obtained.

Table 5 Quality costs calculated for data according to Tables 3 and 4
Full size table

Many constructive conclusions can be drawn from the results obtained. It can be seen that, in the case of the thickness deviation (X1 characteristic):

$$ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}<{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_}A\ \mathrm{and}\ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}<{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_B} $$

This means that an inspection carried out after the nth MPS is justified. It adds value to the manufacturing process:

$$ \mathrm{VAI}={\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}}-{\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}\_A}=0.208\hbox{--} 0.125=0.083 $$

QI carried out after the nth MOS also gives added value because

$$ \mathrm{VAI}={\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_B}-{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_A}=0.375\hbox{--} 0.208=0.167 $$

Analysing the individual components of the non-conformance costs, it can be seen that QI makes it possible primarily to avoid the costs of non-conformance related to customer complaints (components 7.1 and 7.2).

Regarding the X2 characteristic, surface roughness, QI does not add value to the process because

$$ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}>{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_A}\ \mathrm{and}\ {\mathrm{CQ}}_{\mathrm{with}\_\mathrm{inspection}}>{\mathrm{CQ}}_{\mathrm{no}\_\mathrm{inspection}\_B} $$

This means that the quality inspection of the characteristic X performed after the nth MPS creates losses; the inspection should be abandoned or measures leading to its improvement should be taken.

The main reason for the unprofitability of this inspection is the high cost of running it. This means that efforts should be focused on reducing the cost of the inspection or increasing the quality capability of the machining process. To determine what is more profitable, a more detailed cost analysis is needed.

5 Discussion

With the use of the proposed model of quality costs, it is possible to undertake systematic optimization activities to increase manufacturing process efficiency, particularly inspection efficiency. Before taking such action, it is advisable to recognize the sensitivity of the model in order to adjust its parameters.

An example follows which is based on the case study considered in the previous chapter. It is assumed that, based on knowledge of the process, the possibility of any improvement refers primarily to the manufacturing process capability, inspection system capability and the costs of complaints. Of the many possible relationships between these factors and quality costs, some were selected for illustrative purposes only. They are presented in Figs. 3, 4, 5 and 6. On their bases, several practical conclusions can be formulated.

Fig. 3
figure 3

Dependence of costs of non-conformance on inspection system capability (fm(1) = 0.95, CRU = 5, others as in Table 3)

Full size image
Fig. 4
figure 4

Dependence of costs of non-conformance on manufacturing process capability (fi(11) = 0.95, CRU = 5, others as in Table 3)

Full size image
Fig. 5
figure 5

Dependence of costs of non-conformance on unit costs of repair (fm(1) = 0.95, fi(11) = 0.95, others as in Table 3)

Full size image
Fig. 6
figure 6

Dependence of costs of non-conformance on process capability for various inspection system capability (CRU = 5, others as in Table 3)

Full size image

It can be concluded, for example, that within a certain range of variables, i.e. fm(1) and fi(11), it is reasonable to abandon the QI after the 2nd MPS operation and switch to inspection in the operations following it (in Fig. 3, for fi(11) < 0.85). In a special case, even complete abandonment of the inspection is more beneficial than the use of a post-n inspection (in Fig. 5, for fm(1) > 0.98). The limit values obviously depend on the other parameters of the model, primarily on the relationship between the inspection, manufacture and repair costs.

Figure 5 illustrates the rapid increase in quality costs together with the increased costs of warranty repairs. Figure 6 indicates in turn the influence of type I error on these costs.

The depicted relationships may be helpful when deciding in which direction to take actions towards improvement. Comparing Figs. 3 and 6, it can be concluded, for example, that for the data given in the example, a reduction in quality costs by 0.05 units may be obtained by

  1. 1.

    increasing the process capability from 0.95 to 0.98

  2. 2.

    or, increasing the capability of the inspection system from 0.95 to 0.99

Of course, many technical and organizational factors, as well as those related to people, decide the area to which improvement activities should be directed. However, information on the scale of the challenge in each area may be extremely beneficial.

6 Conclusion

The quality cost model developed makes it possible to determine the effectiveness of the inspection plan used in a multistage manufacturing process. It allows a comprehensive analysis to be carried out, and offers support for managers in optimizing the conditions for conducting the process, and in particular, the inspection itself.

The quality cost model includes all the categories of costs related to non-conformances, among them costs resulting from complaints. For assessing effectiveness of the quality inspection, the added value was used. The added value is the difference between the quality costs of the production process with or without inspection.

The model is general enough to be valid in relation to the multistage production process, and simultaneously has a mathematical form that is easy to understand for practitioners who wish to apply it on a shop floor.

The critical element of the model is the determination of its parameters presented in Table 2. Most of the parameters can be estimated based on standard quality analysis and measurement system tests carried out within companies. However, some of them, for example, the probability of detecting non-conforming units outside the place of their origin, require certain assumptions. One can rely here on knowledge of the process, the competence of employees, etc.

The considerations presented in this article refer to discrete manufacturing processes, such as the manufacture of machine components and the assembly of equipment. However, it should be emphasized that the results and conclusions may be transferred to any manufacturing process, including continuous manufacturing.

The presented model does not consider the stochastic nature of some of its variables, especially the capability of the manufacturing process and the capability of the inspection system. The model is based on the expected values of these variables, not including their distribution, which is sufficient for practical applications. However, further work will be carried out in this direction in the future.