1 Introduction

It is difficult to experimentally measure important phenomena during metal cutting, due to the extreme conditions occurring during the machining process which are localised within small volume of tool material. The historically most common material used is cemented carbide and it is well known that it can handle such extreme thermo-mechanical loads. It is not given that alternative tooling materials like polycrystalline cubic boron nitride (pcBN) are able to cope with such conditions. A direct measurement of these loads is often impossible, hence, in recent years, the finite element modelling technique has become an important numerical tool for simulating the machining process. Constitutive models describing the material flow behaviour as a function of strain hardening, strain rate hardening, and thermal softening are required in order to capture the plasticity behaviour of the workpiece, during the conditions encountered in the machining process [22]. Cemented carbide is the most common material for tooling in metal cutting [20]. Its main constituents, tungsten and cobalt, are classified as critical raw materials [1], and thus a search for alternative tooling, like pcBN, is of industrial importance.

In this paper, the coupled Eulerian–Lagrangian (CEL) method in Abaqus/Explicit v6.14-2 is used to model 3D orthogonal cutting of Inconel 718 workpiece with a pcBN tool. The tool was modelled with a Lagrangian formulation and the workpiece by a Eulerian formulation. This will ensure that issues with mesh distortion will be avoided and in addition no chip separation must be introduced. The focus of this paper is to examine dynamic loads acting on the tool during the periodic chip serration and to evaluate its effects on the induced mechanical and thermal fields in the tool.

This paper has shown the impact the combination of mechanical and thermal load has on the stress concentrations developed in the cutting tool consisting of pcBN material, during a machining process.

2 Experimental investigation

2.1 Mechanical experimental investigation

2.1.1 Static

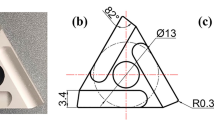
Machining tests were done on SMT 500 CNC lathe. Tubular workpiece (see Fig. 1) was pre-machined out of a solid bar of Inconel 718 that was provided by Siemens Industrial Turbomachinery AB. Supplied Inconel 718 in aged condition has hardness of HRC 45.1 and has fine (ASTM number 8) grain size, as seen in Fig. 2. Wall thickness of the tube was b = 2.41 mm. Orthogonal machining operation was performed at the fixed cutting speed of vc = 250 m/min and feed of f = 0.15 mm/rev. Machining was done with CBN170 tool grade (SECO Tools) of DNGN110308 geometry. To achieve orthogonal machining conditions, CDJNL3225P11 toolholder was milled to modify the tool angles to the major cutting edge angle κ = 90° and inclination angle λ = 0°. Dimensions of the tool-chip contact zone and notch formation were observed with SEM LEO 1560. Static cutting forces were measured with the Kistler 9129AA dynamometer at sampling rate of 100 Hz. Chips were collected, mounted, polished, and etched.

Fig. 1
figure 1

Setup of the experimental static force measurements for orthogonal cutting tests

Full size image
Fig. 2
figure 2

Backscatter SEM image of aged Inconel 718

Full size image

2.1.2 Dynamic and FFT analysis

A special cutting tool, equipped with built-in strain gauge sensors connected in three electrical bridges and allowing the deformation of toolholder in three mutually perpendicular directions due to the influence of cutting forces to be measured [2]. Inconel 718 tube was re-machined to the wall thickness of b = 1.9 mm in order to fit the length of CBN cutting edge of the insert. The signals from the sensors were acquired by CompactDAQ NI-9223 with a sampling rate of 1 MHz, amplified and recorded on the computer. The acceleration of the cutting tool during its engagement has also been experimentally studied in order to cross-validate the signal from the tool dynamometer. Registration of vibration signals in two orthogonal directions was carried out with Bruel & Kjr accelerometers of type 8309 within the frequency range up to 60 kHz.

2.2 Thermal experimental investigation

2.2.1 Cutting process temperature

Tool temperature distribution was measured using a near-infrared charge coupled device sensor technique (IR-CCD). The method is described in details in previous investigation by one of the authors [16]. In the present study, an IR-CCD measurement device was employed and this consisted of a 1024(H)*582(V) array of silicon-based CCD sensors cooled with a double stage Peltier air cooling system to improve the signal/noise ratio. The use of a new 113-mm fixed focal optical lens permitted to reduce the size of the observation area to 2.5(H)*2.5(V) mm. This enabled to achieve a spatial resolution of about 4.5 µm and facilitated the observation of small areas such as the cutting zone. Temperature measurements were restricted to a dry environment in the temperature range of 400–1100 ∘C. This limit was fixed by the spectral response of the Si-based CCD sensors (270–1050 nm wavelength interval) and the IR transmitting black glass filter (830 nm) reducing the NIR wavelength range to 830–1050 nm. A menu-guided control software enabled the adjustment of integration/exposure time that was chosen in the range of 2–16 ms in the present study. The thermal images were acquired in a sequence at a rate of 15 frame per s. A schematic view of the set up can be seen in Fig. 3.

Fig. 3
figure 3

Schematic view of thermal measurements for orthogonal cutting tests

Full size image

2.2.2 Young’s modulus temperature dependence of pcBN

Temperature dependence of Young’s modulus E(T) for CBN170 samples was measured with a pulse-echo technique on a custom-built [29, 30] ultrasonic (10–30 MHz range) equipment illustrated in Fig. 4.

Fig. 4
figure 4

Schematic of customised ultrasonic setup for the determination of Young’s modulus temperature dependence

Full size image

Quartz cylindrical buffer was used to enable ultrasonic wave speed measurement at elevated temperature. Piezo transducer was attached to the bottom of the quartz buffer which was maintained at T = 290 K by a cooling unit, while the sample was glued to the top part of the buffer and was continuously heated by the heater. Three samples with diameter of 6.35 mm and thickness of 3.18 mm were studied. Initially, the procedure involved the determination of longitudinal (vl) and transverse (vt) speeds and sample density (ρ) at T = 300 K. Subsequently, evolution of longitudinal (vl) speed value during the heating cycle was registered. The upper limit of the temperature interval depends on the reliability of the high-temperature glue for transmission of ultrasonic waves. The practical measurement interval was T = 290–630 K for the case in hand. Temperature dependence of Young’s modulus E(T) is based on the obtained vl(T) data according to Eq. 1.

$$ E(T)=\rho v_{l}(T)^{2}\frac{3a^{2}-4}{a^{2}(a^{2}-1)} $$
(1)

Influence of heating on the ratio a = vl/vt = 1.58, Poisson ratio (η = 0.166), and thermal expansion was not accounted for due to their negligible effects [28].

Figure 5 illustrates a typical temperature dependence of Young’s modulus for a CBN170 sample. A solid line 1 on the graph represents experimental E(T) data obtained for the registered vl(T), while dashed line 2 reflects the results of approximation by the exponential Wachtman’s equation (2) [6, 27] within the given temperature range of T = 290–630 K and its extrapolation up to T = 1100 K.

$$ \begin{array}{@{}rcl@{}} E(T)&=&E_{0}-CT\exp\left( \frac{-T_{0}}{T}\right)\\ &=&628.6-0.2054T\exp\left( \frac{-1632.9}{T}\right) \end{array} $$
(2)
Fig. 5
figure 5

Temperature dependent Young’s modulus of CBN170: 1 – experimental; 2 – approximation of experimental curve 1 by exponential function, see Eq. 2 and extrapolation to T = 1100 K

Full size image

Analysis of the data reveals that the largest deviation of approximation line 2 does not deviate from experimental line 1 by more than 0.35%, and the largest expected error for Young’s modulus at T = 1100 K should not exceed ± 2.5–2.8%. Other cBN-based materials were also shown to follow Wachtman’s equation for temperature dependence of Young’s modulus where 27% lower value is found for thin cBN coating [10] and 4% lower for thick ones [12].

3 Numerical modelling

The numerical modelling approach consists of a combination of two finite element (FE) simulations. First, a thermal steady state analysis of the cutting tool was performed in Abaqus/Standard. After that, a metal cutting simulation was conducted in Abaqus/Explicit with the CEL technique. The flow chart in Fig. 6 shows the simulation approach used in the paper.

Fig. 6
figure 6

Flow chart of the simulation approach used in this paper

Full size image

3.1 Thermo-mechanical behaviour

Metal cutting is a complex process where large strains and extreme strain rates occur, and high temperatures are generated by dissipation of the plastic work and by frictional heating. This has to be captured by the flow stress model of the workpiece material. In this paper, the Johnson–Cook plasticity model is used, developed by Johnson and Cook in [13]. This plasticity model has been frequently employed for FE simulations of machining, for example by [5, 11, 14, 17, 21]. The Johnson–Cook model is not valid while studying cryogenic machining, since the temperature level is lower than 𝜃0, as described in [23]. This is not the case in study, since it is an investigation of dry machining and a bulk temperature of the workpiece at 𝜃0. The Johnson–Cook constitutive law is presented in Eq. 3

$$ \bar{\sigma}=(A+B\bar{\varepsilon}^{n})(1+C\ln\dot{\bar{\varepsilon}}^{*})(1-\theta^{*m}) $$
(3)

where \(\bar {\sigma }\) is the equivalent stress, \(\bar {\varepsilon }\) is the equivalent plastic strain, \(\dot {\bar {\varepsilon }}^{*}=\dot {\bar {\varepsilon }}/\dot {\bar {\varepsilon }}_{0}\) is the dimensionless plastic strain rate, \(\dot {\bar {\varepsilon }}\) is the equivalent plastic strain rate, \(\dot {\bar {\varepsilon }}_{0}\) is the reference strain rate, A is the initial yield stress, B is the hardening modulus, C is the strain rate dependency coefficient, n is the strain hardening exponent, m is the thermal softening coefficient. The homologous temperature 𝜃∗ is defined as 𝜃∗ = (𝜃 − 𝜃0)/(𝜃m − 𝜃0) where 𝜃 is the process temperature, 𝜃m is the melting temperature, and 𝜃0 is the reference temperature of the workpiece. The workpiece was considered as Inconel 718, and the cutting tool was modelled as CBN170 tool material grade. The Johnson–Cook parameters used for the workpiece are specified in Table 1. The considered thermo-mechanical properties both for workpiece and cutting tool are presented in Table 2. The temperature-dependent Young’s modulus of CBN 170 was modelled with the numerical expression given in Table 2, which has been determined experimentally as described in Section 2.2. Thermal properties of CBN170 were measured in the temperature range of 25 to 1100 ∘C with light flash apparatus Netzsch LFA 467HT HyperFlash and is presented in Table 3.

Table 1 Johnson–Cook parameters to model the plasticity behaviour of Inconel 718 [25]
Full size table
Table 2 Physical properties of Inconel 718 [3, 4, 25] and CBN170 tool grade
Full size table
Table 3 Temperature dependence of thermal conductivity and specific heat capacity in CBN170 tool grade [4]
Full size table

The chip formation and the segmentation were modelled by damage initiation based on the Johnson–Cook damage model and material softening by stiffness degradation as described in [4].

The friction model used is a combined sliding and sticking formulation, where an upper boundary controls when sticking friction is active, this upper boundary is set to the shear strength of the workpiece material. The sliding zone is modelled with Coulomb friction and the friction coefficient is set to 0.57, which has been adopted from [15]. The combined fiction model used in this present study is presented in Eq. 4.

$$ \tau_{f}=\min\left( \mu\sigma_{n},\tau_{y}\right) $$
(4)

where τf is the frictional stress, μ is the fiction coefficient, σn is the normal stress, and τy is the shear strength of the workpiece, which is defined as \(\tau _{y}={\sigma _{y}}/{\sqrt {3}}\) where σy is the uniaxial yield stress. The heat transfer coefficient at the contact interface between the workpiece and cutting tool is set to 1000 kW/(m2 ⋅K) adopted from [19, 26]

3.2 Metal cutting FE model

The metal cutting simulation was performed with a CEL technique in Abaqus/Explicit. This finite element model consists of two parts—the cutting tool with a Lagrangian formulation and an Euler space with a Eulerian formulation. The Euler space part had an element edge length of 7.5 µm in the xy-plane and an element edge length of 30 µm in the z-direction. The Euler space had the element type EC3D8RT, which is an 8-node thermally coupled linear Eulerian brick element. The Euler space part consisted of a total of 1,675,667 elements. The cutting tool had an element edge length of 5 µm at the cutting interface and the size of the elements at Region C’ according to Fig. 7 was set to 0.5 mm. The cutting tool contained a total of 516,356 elements of the element type C3D4T, which is a 4-node linear Lagrangian tetrahedron thermo-mechanical element.

Fig. 7
figure 7

The initial configuration of the CEL FE model and the mechanical boundary conditions applied to both the Euler space and the tool

Full size image

The cutting tool had an edge radius rβ = 15 µm and a nose radius rε = 0.8 mm; the nose radius was not a part of the cutting depth in order to get a 3D orthogonal cutting condition. A rake angle γ = − 6°, clearance angle α = 6°, and the major cutting edge angle κ = 90°. A wall thickness b = 1 mm and a theoretical chip thickness of h1 = 0.15 mm were simulated. The Eulerian space was initially filled with workpiece material according to the dark grey area in Fig. 7, and the rest of the Eulerian space was considered as a void region. Figure 7 shows the initial configuration of the CEL model with visualised mechanical boundary conditions. Regions A’ and B’ were velocities constrained as vx = vy = 0 and vz = −vc = − 250 m/min. Region C’ was considered to be fixed in all displacement degrees of freedom, i.e., u = 0.

3.3 Initial temperature field in the cutting tool

As can be seen in [4], the thermal steady state condition of the chip formation process, and most importantly in the cutting tool, is reached much later than the steady state condition of the mechanical part in the chip formation process. To achieve a thermal steady state condition at the chip/tool contact area and inside the tool body, the cutting tool was preheated. This was executed in Abaqus/Standard where a thermal steady state analysis was performed in order to calculate the initial temperature field in the cutting tool.

The cutting tool was subjected to boundary conditions according to Fig. 8. The rectangle on the rake face of the tool, i.e., the 1000 ∘C region was 1.0 mm in the x-direction and 0.3 mm in the y-direction, this was an estimate of the maximum contact length lr, which was based on information from [9], also seen in Fig. 17. The boundary condition of 1000 ∘C is selected based on experimental data (see Fig. 13). This rectangle is located where the contact interaction between the tool and the chip develops in the metal cutting simulation. The temperature field achieved in this Abaqus/Standard simulation was then used as an initial condition in the cutting tool for the machining simulation performed in Abaqus/Explicit with the CEL technique.

Fig. 8
figure 8

Thermal boundary conditions for the steady state analysis of the cutting tool

Full size image

4 Results

In this section, the experimental and numerical results are presented. The segmented chip formation from the FE model is shown in Fig. 9. Where the flow stress degradation in the workpiece generated by the damage model is visualised.

Fig. 9
figure 9

Serrated chip formation of Inconel 718 with h1 = 0.15 mm

Full size image

4.1 Cutting forces

In Table 4, the experimental and numerical values for both the cutting force Fc and feed force Ff are presented, as well as the dynamic response in the cutting forces due to the segmented chip formation. The experimental values for the static force measurements are performed as described in Section 2.1.1 and the dynamic according to Section 2.1.2. The static cutting forces have been divided by 2.41 and the dynamic by 1.9 in order to compensate for the differences in wall thickness. In Fig. 10, the cutting forces as a function of time is shown for both the numerical and the dynamic experimental values.

Table 4 Primary cutting force and feed force, for both static and dynamic from FEM and experimental values
Full size table
Fig. 10
figure 10

Primary cutting force and feed force as a function of time for (dynamic) experimental (a) and FEM (b) cases

Full size image

4.2 Chip formation

In Fig. 11, the fast Fourier transform (FFT) power spectrum for both the experimental and numerical cutting forces is visualised; it can be seen that the numerical model under predicts the segmentation frequency (fs) of the machining process. In the studied case, FEM yields fs 20.8 kHz while the experimentally measured value accounts to 28.2 kHz. In Fig. 12a, a micrograph of the chip cross section for the chip formation developed during the experimental investigation is presented, and in Fig. 12b, chip formation process for the numerical model is displayed. From this information, the peak and valley data for the chip formation is extracted and summarised in Table 5 for both the experimental and numerical results. In Table 5, it can be seen that the peak value is very closely captured by FE simulation, but for the valley a larger deviation is observed. The reason for these differences of experimental and numerical values connected to the chip formation is most likely related to the numerical modelling of the stiffness degradation in the workpiece material.

Fig. 11
figure 11

Normalised FFT power spectrum for (dynamic) experimental (a) and FEM (b) cases

Full size image
Fig. 12
figure 12

a Optical image of the chip cross section. b Chip formation of the FEM simulation

Full size image
Table 5 Peak and valley chip thickness over 7 last segments from FEM and experimental data are a result of 30–40 measurements
Full size table

4.3 Thermal load

4.3.1 Experimental

Figure 13 shows the temperature distribution on the tool-chip interface and in the tool itself. It can be seen that the highest registered temperature is at 950 ∘C. Such temperature field is taken from the side face of the tool (see Fig. 3); therefore, the steady state temperature at the midplane of the orthogonal cutting interaction should be higher. As shown in [7, 24], the temperature at the midplane of the chip/tool interaction can be underestimated by 10–30% or even higher. As a consequence the boundary condition for the contact area of the tool is set to 1000 ∘C (see Fig 8) in the initial temperature distribution simulation performed in Abaqus/Standard, as described in Section 3.3.

Fig. 13
figure 13

Experimental measured temperature distribution at the cutting interface

Full size image

4.3.2 Numerical

In Fig. 14, the initial temperature field in the cutting tool, given by the Abaqus/Standard simulation is displayed. Figure 15 visualises the temperature distribution in the cutting tool at time 33.0 ms of the Abaqus/Explicit simulation. It can be seen that the maximum temperature in the cutting tool has moved up on the rake face of the tool, compared to the evenly distributed initial temperature at the contact interface in Fig. 14. Figure 16 shows the temperature at the midpoint of the interaction area between the tool and the workpiece as a function of time, this location is indicated by a symbol “+” in Figs. 14 and 15. In Fig. 16, it can be seen that a steady state behaviour for the temperature at the contact interface is achieved within the simulation time in the Abaqus/Explicit model. It also shows that the average value increases up to 1140 ∘C and fluctuates within 1090 ∘C and 1200 ∘C during a segmentation cycle. Temperature data were also registered for a region outside the direct contact area—the region where notch formation is often observed. The location of such temperature control point is made to coincide with a position of observed highest principle stress as seen in Fig. 18.

Fig. 14
figure 14

The initial temperature field in the tool, given by the steady state simulation in Abaqus/Standard

Full size image
Fig. 15
figure 15

Temperature field in tool at time 33.0 ms which is at mean temperature at (steady state), as can be seen in Fig. 16

Full size image
Fig. 16
figure 16

Temperature for a node at middle cross section at the contact interaction

Full size image

4.4 Mechanical loads

CBN170 belongs to a pcBN class of brittle materials that are not prone to plastic deformation. Therefore, an elastic deformation case is computationally studied, where tool material’s response to the loading case is controlled by its Young’s modulus and its variation with the temperature (see Section 2.2). During the experimental investigation when machining a tubular workpiece, as described in Section 2.2, the cutting tool developed a significant notch wear, as seen in Fig. 17. The principal stress field developed in the tool of the FE simulation at time 17.4 ms is displayed in Fig. 18. It can be seen that three zones are subjected to a high concentration of principal stress, i.e., at the rake and in the zones where notch wear is developed in the experimental investigation. In Fig. 19, the principal stress of the notch and rake region is shown as a function of time. This figure clearly shows that the notch region is subjected to a fluctuation of principle stress from 300 to 450 MPa within a single segmentation cycle, after a steady state chip formation process is achieved. In the rake face region, the variation of the principal stress is more profound ranging from 0 to 350 MPa principal stress; this is probably connected to the variation of contact length at the rake face, due to the serrated chip formation.

Fig. 17
figure 17

Notch wear obtained from the experimental investigation

Full size image
Fig. 18
figure 18

Principal stress σ1 distribution in the tool at time 17.4 ms of the simulation

Full size image
Fig. 19
figure 19

Simulated principal stress σ1 as a function of time, for both the notch and rake face region

Full size image

5 Discussion

The results from this paper show that the CEL formulation is an efficient approach to use for examination of mechanical and thermal loads acting on a cutting tool in a 3D simulation case. The model is validated by comparison with experimental results of static and dynamic cutting forces, chip formation, and thermal load. Both the cutting forces and thermal loads obtained from the numerical simulations shows reasonable agreement with the experimental results. The numerical model presented in this study can accurately simulate the principal stress developed in the notch wear region of the tool. The reason for this is most likely due to the implemented temperature-dependent Young’s modulus of pcBN tool materials that was measured experimentally at elevated temperature. As can be seen in previous studies such as [4, 18], the stress concentration in the notch region is not as profound when a constant Young’s modulus is assumed.

This study demonstrates the ability of FE simulations to investigate how the combination of the periodic mechanical and thermal load affects the material response in the cutting tool. It is the combination of mechanical and thermal load on the cutting tool that gives rise to wear and fracture of the tool material.

In addition to this discussion, it is also very important to realise that temperature and partly the pressure can drastically increase chemical reactions between the workpiece and cutting tool which leads to the deterioration of the cutting tool material. This chemical reaction will generally give rise to a geometry change of the cutting tool that results in stress concentrations especially interacting with the maximal principal stress, as experimentally confirmed in the study [8]. These problems are outside of the scope of this paper. But the mechanical and thermal loads presented here can be of value, when studying these phenomena.

6 Conclusions

This paper has elucidated the impact the combination of mechanical and thermal load has on the stress concentrations developed in the cutting tool material, during a machining process. The following conclusions can be drawn from this study:

  • A comprehensive verification of the presented FE simulation has been performed by comparison with experimental results.

  • The numerical model predicts the temperature of between 1100–1200 ∘C at the centre of the cutting interface, which correlates well with the experimental determined temperature (taken from the side of the tool).

  • With a temperature-dependent Young’s modulus of pcBN, the numerical model is able to predict the principal stress concentrations that is a key component behind developed notch wear during a machining process.

  • The numerical model predicts that the maximal principal stresses (450 MPa) occur at the notch region of the tool. This is in agreement with the notch wear observed experimentally (seen in Fig. 17).

  • A feasible and time-effective FE approach that achieves thermal steady state in the interaction area between workpiece and tool is developed that operates with experimentally measured contact and thermal phenomena.