1 Introduction

Molecular dynamics (MD) simulations of nanocutting of solids received much attention in recent years. In so-called “ultra-high precision machining” processes, the controlled removal of surface layers in the range of tens of nanomilliliters or even nanomilliliters is attempted [1,2,3]. Such nanocutting processes can well be studied by the method of MD simulation, and this approach has provided relevant results both for metals and for ceramics. Thus, for crystalline metals, several studies showed that dislocation formation, reactions, and migration constitute the dominant deformation processes; here, both elemental metals of fcc, bcc, and hcp structure [4,5,6,7,8,9] as well as alloys, compounds, and bulk metallic glasses [10, 11] have been examined. For ceramics, SiC was studied [12,13,14] intensely; but also, elemental Si was investigated repeatedly [3, 9, 15,16,17] as a prototypical example of a brittle material, even if it is not a ceramic in the strict sense of the word. Several studies found that, in the nanoscale, these materials behave in a ductile way; this phenomenon was termed the “brittle-ductile transition” since seemingly brittle materials change their behavior and show ductile features [18,19,20].

While most studies focus on single-phase and single-crystalline materials, simulations of composite materials are more rare. Deng et al. [21] studied experimentally nanolayered laminated composites of Al and SiC and found that such composites exhibit much higher modulus and hardness than the pure Al layer.

A simpler scenario is the cutting of polycrystals. Liu et al. [22] studied scratching in a bi-crystal Ni film containing a Σ5 twist grain boundary; they find that the interface may absorb plastic deformation and allow grain boundary slip, thus decreasing the friction during scratch.

Recently, the machining of Al/Si composites was treated by MD simulation [23,24,25,26,27], since available interatomic interaction potentials [28] are able to describe basic mechanic, plastic, and thermodynamic aspects of these composites sufficiently well. Here, the processes of nanoindentation and surface scratching of composites were investigated. It was found that the composite does not respond as an “average” material; but that in particular, the different hardness of its components influences the response in a complex way, such that Si tends to expand onto the Al side of an interface. In addition, dislocation mobility is enhanced if dislocation glide on the interface is possible. Such investigations are of interest in particular also because of relevant applications of Al/Si composites such as for lightweight engine components [29,30,31].

In the present paper, we study nanocutting of Al/Si bilayer systems. Due to their different hardness, but also due to the different deformation mechanism—dislocation vs. transformation plasticity—the two materials Al and Si react very differently on the applied load. While dislocations cannot penetrate the Al/Si interface, we show that the loading pressure induces twinning in the Al substrate. In addition, we demonstrate material mixing at the interface under machining as well as crack formation in special cases.

2 Simulation method

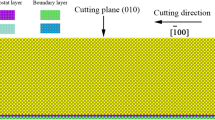
A schematic diagram of the simulation model is shown in Fig. 1. The workpiece consists of a bilayer system, in which the top part has a thickness t, which is varied in this study between t = 32.4 and 81.0 Å. We study both Al top layers over a Si substrate and Si top layers over an Al substrate. We choose a cartesian coordinate system, in which the surface is in the x–y-plane, and z points out of the surface in normal direction; x is the cutting direction. The system size extends 846, 97, and 433 Å in x-, y-, and z-directions, respectively; the total number of atoms amounts to around 1.8 × 106, depending slightly on the system. Periodic boundary conditions were applied in the y-direction, while two fixed layers prevent the workpiece from performing a translational or rotational rigid body motion during the cutting process. Another four atom layers are thermostatted at a low temperature, < 1 K, to keep the system at low temperature. This low temperature eases the detection of lattice defects [32, 33].

Fig. 1
figure 1

Setup of the simulation system. t denotes the thickness of the top layer, which varies between 32.4 and 81.0 Å; d is the cutting depth, which is fixed at d = R for all simulations. We consider both Al and Si as top layer materials above a substrate

Full size image

Al has an fcc structure with a lattice constant of 4.05 Å, while Si has a cubic diamond structure with lattice constant of 5.40 Å. We focus here on a Si (001) ∥ Al (001) interface geometry, where the Al[110] direction (x-direction) is parallel to Si[100]. This choice is motivated by the mobility of dislocations: (i) In Al, dislocations move along the [110] direction, in a quasi-two-dimensional geometry, simplifying the description, since they do not cross the periodic boundaries in y-direction [8]. (ii) Si is misaligned with Al in order to suppress the passage of dislocations through the interface [23]. The system is relaxed by first applying an energy minimization algorithm; then the system is heated to 300 K and cooled back during 140 ps until the temperature has dropped below 1 mK. The temperature dependence of machining has been investigated by MD simulation previously both for metals [34, 35] and for Si [36]; in both cases, no qualitative changes in the plastic behavior occur below 300 K, and the quantitative effects are minor. The reason for these small changes lies in the high machining velocities applied in simulation, which prevent the occurrence of thermally activated processes, such as dislocation cross slip in metals. This lack of thermal dependence justifies our use of small machining temperatures.

The Al–Al interactions have been modeled using the embedded-atom model potential of Mendelev et al. [37], while the Si–Si interactions are based on a modifcation of the Stillinger–Weber potential [38]. The interaction between the Al and Si atoms has been developed by Saidi et al. [28].

As cutting tool, we use a smooth cylindrical surface, which interacts with the atoms of the workpiece via a purely repulsive potential [39],

$$ V(r) = \left\{ \begin{array}{ll} k(R-r)^{3}, & r<R, \\ 0, & r\ge R . \end{array} \right. $$
(1)

Here, R denotes the tool radius, and r is the distance of a substrate atom to the tool axis. The tool radius is fixed to R = 61.16 Å, while the indenter stiffness k has been set to k = 10 eVÅ− 3 [39, 40].

The center of the tool is placed in the surface plane of the substrate (see Fig. 1). We fix the cutting depth to d = R for all simulations presented here; since the top layer thickness t varies between values t < d and t > d, we analyze cuts only in the overlayer and also such that cut through the lower layer. The tool moves with a constant velocity of v = 20 m/s; the total cutting length is 200 Å.

The open-source code LAMMPS [41] is used to carry out the simulations. Dislocations are identified using the crystal analysis tool (CAT) [42,43,44]. The atomistic configurations are analyzed by common neighbor analysis and visualized using the free software OVITO [45].

3 Results

We start by an analysis of the cutting of a pure Al crystal, Section 3.1, and a pure Si crystal, Section 3.2. These elementary systems, and here in particular the metal, are well understood, and may therefore serve as a starting and reference point of our analysis of the Al top system, Section 3.3, and of the Si top system, Section 3.4. Finally, the balance of forces during cutting (Section 3.5) and the chip morphology (Section 3.6) are addressed.

3.1 Pure Al

The deformations occurring in a pure Al workpiece and the resulting defects are displayed in Fig. 2. Deformation is governed by dislocation and twinning plasticity. We first describe the dislocation generation.

Fig. 2
figure 2

Side view of the defects generated in a pure Al crystal at a cutting length of 200 Å. a Atoms are colored according to their local lattice structure—gray: fcc; blue: hcp; red: other. hcp planes identify planar defects in fcc Al, such as stacking fault planes. Red lines in the chip identify grain boundaries separating grains formed in the chip during the cutting process. The inset shows a zoom into the twinned region. Cyan lines highlight the grain orientation. Arrows point at twin boundaries. The gray circle highlights a stacking fault plane. b Zoom into the defect zone below the machined surface showing the variety of dislocations generated. These are colored according to their Burgers vector (plotted in green) – blue: \(\boldsymbol {b} = \frac {1}{6} \langle 1 1 2\rangle \) Shockley partial; light blue: \(\frac {1}{3} \langle 1 1 1\rangle \) Frank partial; red: 〈100〉 perfect; purple: \( \frac {1}{6} \langle 1 1 0\rangle \) partial. In addition, defect atoms are colored as gold for coherent twin boundaries and red for intrinsic stacking faults. Gray lines indicate unidentified defects, such as the workpiece surface

Full size image

The dislocations generated—with the exception of those in the heavily disturbed cutting zone—have their dislocations lines aligned in the y-direction, perpendicular to the plotted plane in Fig. 2; this applies in particular to the family of dislocations emitted in \([1 1 \bar {2}]\) and \([ \bar {1} \bar {1} \bar {2}]\) direction. This alignment of dislocation lines gives the process a quasi two-dimensional nature. These emitted dislocations are mostly \(\boldsymbol {b}= \frac {1}{6} \langle 112 \rangle \) Shockley partials, as can be best seen in the zoom provided in Fig. 2b. This feature has already been demonstrated in a previous study of Al cutting in the same cutting direction [8]. In addition, in the cutting zone, a dense dislocation network consisting of a variety of dislocation types with Burgers vectors \(\boldsymbol {b}= \frac {1}{2} \langle 110 \rangle \), \(\frac {1}{6} \langle 112 \rangle \), \( \frac {1}{6} \langle 110 \rangle \), \(\frac {1}{3} \langle 001 \rangle \), and \(\frac {1}{3} \langle 111 \rangle \) has been created. Here, due to dislocation reactions, the dislocation lines do not follow the y-direction; in other words, this central deformation zone cannot be described in a two-dimensional geometry. Another heavily deformed region is the chip. Here, two grain boundaries have formed due to the strong dislocation reactions. This finding is in agreement with previous work on cutting of Al [8] where the formation of one grain boundary—for a shorter cutting length—has been described in detail.

In addition to dislocation plasticity, extensive twinning is observed. This finding is in agreement with a series of papers by Yamakov et al. [46,47,48] who showed that twinning plays an important role in the deformation of Al in the nanoscale—in contrast to coarse-grained Al, where deformation is governed by dislocation plasticity. As Fig. 2 demonstrates, we find both parallel twin {111} planes as well as wedge-like twin structures. The zoom in Fig. 2b shows these structures in detail. The lowest wedge-like structure has an intrinsic stacking fault plane at its front. By the insertion of \(\frac {1}{6} \langle 112 \rangle \) dislocations into the twin boundaries—see zoom provided in Fig. 2b—kinks are introduced in the twin boundary. Thus, by successive incorporation of such dislocations, the kink structures widen.

We conclude that the deformation induced by cutting of Al is based on both dislocation and twinning plasticity. Families of dislocations are ejected in \([1 1 \bar {2}]\) and \([\bar {1} \bar {1} \bar {2}]\) direction. The central cutting zone is filled with a dense dislocation network. Twin planes are created that shear the material in the rear of the cutting event.

3.2 Pure Si

Figure 3 shows the damage created in Si during cutting. Under nanomachining, Si behaves in a ductile way and no cracks are formed. Rather the material amorphizes under the deformation. Such a deformation-induced phase transformation has indeed been found already in previous studies, in particular under nanoindentation of Si [19, 49, 50]. The amorphous phase is retained both below the machined surface and in the forming chip. The chip is amorphous with several crystalline grains included.

Fig. 3
figure 3

Side view of the defects generated in a pure Si crystal at a cutting length of 200 Å. Atoms are colored according to their local lattice structure—green: cubic diamond; yellow: first neighbor of a cubic diamond atom; purple: amorphous. Yellow atoms are surface or interface atoms, or—if isolated—highlight a dislocation core

Full size image

In addition, some dislocation activity is observed. Dislocations nucleate with Burger vectors \(\boldsymbol {b}= \frac {1}{2} \langle 110 \rangle \) (see Fig. 3), and leave the cutting zone towards the workpiece interior. This is in agreement with the study of Goel et al. [51] who cut polycrystalline Si and observed some partial dislocations with Burgers vector \(\frac {1}{4} \langle 111 \rangle \) and perfect dislocations with Burgers vector \(\frac {1}{2} \langle 110 \rangle \) in several grains below the machined surface.

It is important to notice that in the case of pure Si, we observe amorphization and dislocation activity, but no crack formation. This is due to the cutting geometry, and in particular to the rake angle—in our case, the rake angle measured at the height of the substrate surface is zero—and the cutting depth adopted (in our case d = R). When increasing the rake angle, the plastic deformation takes place only by amorphization, as shown in the study by Goel et al. [3]. It is known that upon increasing the cutting depth, cracks start forming in the cutting zone [18, 52]. Besides for pure silicon, crack formation was also demonstrated for silicon carbide [13].

3.3 Al top

In the case of an Al layer on top of Si, the size of the overlayer thickness t—relative to the cutting depth d—is important. When the layer thickness is t ≥ d (Fig. 4), no deformations are found in the Si substrate. The pressure produced by the moving tool is not sufficient to induce Si amorphization. The machining process operates entirely within the Al top layer; not even dislocations are nucleated in Si. The interface is not affected by the machining process. The deformation in Al proceeds differently from that in a pure Al substrate (Fig. 2), since the hard Si backing does not allow any deformation on the left-hand side of the workpiece, i.e., close to the surface where the cutting process started. Rather all removed material goes into the chip, which is broader than in the pure Al case, and shows no sub-grain formation. No twinning activity is possible in the overlayer. Any dislocations produced in the Al overlayer are absorbed by the interface, since the interface orientation does not allow for dislocation penetration.

Fig. 4
figure 4

Side view of a Si substrate covered by a thick Al layer of thickness t = 81.00 Å at a cutting length of 200 Å. Atoms are colored according to their local lattice structure: green: cubic diamond Si; yellow: first neighbors of a cubic diamond Si atom; purple: amorphous Si; gray: fcc Al; blue: hcp Al; red: other Al

Full size image

In the case that the Al top layer is thinner than the cutting depth, t < d, the machined Si surface amorphizes (see Fig. 5). In addition, dislocations with Burger vectors \(\boldsymbol {b}= \frac {1}{2} \langle 110 \rangle \) are ejected into the substrate interior as in the case of pure Si (Fig. 3b). Al is almost completely removed from the machined surface, while some Si is mixed into the chip at its top part.

Fig. 5
figure 5

Side view of a Si substrate covered by a thin Al layer of thickness t = 32.40 Å at a cutting length of 200 Å. Atoms are colored according to their local lattice structure as in Fig. 4

Full size image

In both cases, the machined surface shows relatively little deformation, as compared to the case of the pure Al substrate. While for thick Al top layers, both the interface and the Si substrate stay defect-free, for thin Al top layers, the deformation mechanisms in the Si substrate are analogous to those found in pure Si, viz. amorphization, and dislocation emission.

We conclude that due to its hardness, Si substrates suffer no deformation if covered by an Al top layer. Only if the cover is so thin that the tool immediately cuts through Si, Si is deformed. Its deformation is then dominated by amorphization, as for a pure Si substrate.

3.4 Si top

In Section 3.2, we reported results of cutting brittle Si. In this section, we discuss what happens if we put ductile Al under Si.

The damage in the Si top layer is characterized by pure amorphization; Fig. 6 gives an example. This case exemplifies the situation that the film thickness equals the cutting depth, t = d. Note that the Al–Si bonds are strong so that the Al top layer is not peeled off the surface. Rather, by the thrust force exerted during the machining, the top layer is pushed down into the Al substrate; since Al is softer than Si, this is easily possible. So, rather than peeling off the Al layer, Si flows under the indenter. In the remaining layer below the machined surface as well as in the formed chip, some crystalline grains may survive. However, no dislocation plasticity is found in the top layer, since the material is too thin to allow for extensive dislocation formation.

Fig. 6
figure 6

Side view of an Al substrate covered by a Si layer of thickness t = 61.16 Å at a cutting length of 200 Å. Atoms are colored according to their local lattice structure as in Fig. 4

Full size image

The defects formed in the Al substrate are more complex. The case shown in Fig. 6 has been obtained for a film thickness which equals the cutting depth, t = d. No dislocation plasticity is observed in Al; however, extensive twinning takes place. Note that now – in contrast to the machining of pure Al, Fig. 2—two families of twin boundaries are created; besides (111), we have also \((\bar {1}\bar {1}1)\) twin planes. As Si flows under the indenter, a wavy Al/Si interface is created; such wavy interfaces are well-known in unsteady plastic flows during cutting [53, 54]. Depending on the slope of this interface, (111) and \((\bar {1}\bar {1}1)\) twin planes are generated. When these twin planes intersect, substantial strains are created which lead to cracking in the Al substrate.

We note that crack formation was reported previously even in defect-free brittle materials; thus, Cai et al. [55] reported crack formation in the cutting zone of Si and Xiao et al. [13] in SiC. However, in our case, we show crack formation in ductile Al, which is a result of the intersecting twin structures created. We found 5 GPa maximum shear stresses before crack formation and relaxation after crack formation.

We study the influence of the thickness of the Si top layer on the damage created in the Al substrate in Fig. 7. This figure focuses on the defects formed in the Al substrate; hence, the Si cover layer has been omitted. Besides the case discussed above in Fig. 6, t = d—now contained in Fig. 7b—the cases of a thick top layer (Fig. 7a) and of a thin top layer (Fig. 7c) are displayed. Clearly, in all cases, twinning constitutes the dominant deformation mode in Al. Dislocations are mostly absent in Al, and only a few \(\boldsymbol {b}= \frac {1}{6} \langle 112 \rangle \) dislocations have been created. The left-hand side of the workpiece—that is, close to the surface where the cutting started—is strongly deformed by the twinning process. Note that the amount of twinning—but not of the deformation—is strongly reduced in the case of a thin Si top layer (Fig. 7c).

Fig. 7
figure 7

Side view of an Al substrate covered by a Si layer of thickness at = 81.00 Å, bt = 61.16 Å, ct = 37.80 Å at a cutting length of 200 Å. The Si top layer is left out for clarity. Top: only defective Al atoms are shown highlighting the twin boundaries (gold). Defects are displayed as in Fig. 2b. Bottom: different shades of blue and red differentiate Al grains separated by twin boundaries (gold). Black vertical lines indicate the initial position of the left boundary of the workpiece. Cyan lines highlight the grain orientation. Other defects are displayed as in Fig. 2b

Full size image

It thus appears that the case of t = d (Fig. 7b), is special in that only here intersecting families of twinning boundaries are created. As mentioned above, this is caused by the non-monotonic surface profile, which is only visible in this case.

We conclude that the deformation in Al substrates below a Si cover is dominated by twinning. When multiple twin boundaries are created and intersect, cracks are formed in Al.

3.5 Forces and friction coefficient

During cutting, the thrust force, Ft, acts in z-direction and is required to hold the tool at its prescribed depth while the cutting force, Fc, acts in x-direction and measures the resistance of the workpiece against cutting (see Fig. 1).

Figure 8 displays the forces when cutting pure Al as well as a representative case of cutting an Al substrate covered by a Si top layer. In both cases, the time evolution of the forces is quite analogous. During the first 10–20 Å, the forces increase without fluctuations; this indicates the elastic regime. Also later, the forces increase until a cutting distance of 60 Å is reached, and a steady state builds up. Large fluctuations are observed which are due to the formation of dislocations and twinning boundaries in the material. The connection of load drops with the generation of lattice defects during machining has been repeatedly documented in the past by MD simulations [33, 34, 56, 57]. The cutting force is always larger than the thrust force; this constitutes the standard situation when cutting ductile metals [8].

Fig. 8
figure 8

Evolution of the cutting force, Fc, and thrust force, Ft, with cutting length in a pure Al and in b an Al substrate covered by a thin Si layer, t = 32.4 Å

Full size image

The cases of cutting pure Si and a Si substrate covered by an Al overlayer are displayed in Fig. 9. Again, the cutting forces reach a sort of steady state towards the end of the simulation; however, at around 60 Å, a maximum in the forces has occurred. This maximum is connected to the increased pressure that has to be exerted on the Si phase to induce amorphization. For Si, the thrust forces are now larger than for Al; they increase beyond the cutting force and increase—in particular for the bilayer system—during the machining process. Indeed, in the bilayer system, Si does not amorphize any more and strong forces are needed to continue the cutting process. The cutting of ductile Al requires less (cutting) force than the harder and more brittle Si; this explains why the cutting force decreases when ductile Al is put over the Si substrate.

Fig. 9
figure 9

Evolution of the cutting forces, Fc, and thrust forces, Ft, with cutting length in a pure Si and in b a Si substrate covered by a thin Al layer, t = 32.4 Å

Full size image

In order to discuss the influence of overlayer film thickness on the thrust and cutting forces quantitatively, we plot in Fig. 10 the average values of the forces, calculated for the last 140 Å of cutting, where at least the cutting forces form a steady state. Pure Si requires higher cutting and thrust forces than pure Al, in agreement with the higher hardness of Si. The relative values of thrust and cutting force for these two systems were already discussed above.

Fig. 10
figure 10

Average cutting forces, Fc, and thrust forces, Ft, for a Si substrates with Al top layers and b Al substrates with Si top layers

Full size image

Interestingly, in Si, the thrust force is larger than the cutting force, in contrast to the case of metals [8]. This result for Si has been observed previously [19]. We argue that it is caused by the almost complete lack of dislocation plasticity in Si; cutting proceeds by the amorphization of the material which requires sufficiently high pressures—and hence thrust forces—to take place.

Both thrust and cutting forces increase monotonically when putting a Si top layer on Al, and almost reach the values of pure Si for large layer thicknesses, t ≫ d. Analogously, an Al top layer on Si lets the thrust force decrease until for large thicknesses of the top layer, values close to those of a pure Al substrate are reached. Here, however, the cutting force is almost independent of the Al layer thickness, and always assumes values similar to those of pure Al and below those of pure Si. This demonstrates that the Al top layer allows for small cutting forces to cut the Si substrate; this is caused by the relative ease to deform the Al top layer.

The forces allow us to calculate the friction coefficient,

$$ \mu=\frac{F_c}{F_t}, $$
(2)

shown in Fig. 11. As discussed above, a Si substrate with an Al overlayer has particularly low friction coefficients; these are caused by the low values of the cutting force and the high values of the thrust force in this case. In contrast, a Si overlayer does not much reduce the high friction coefficient necessary for cutting Al.

Fig. 11
figure 11

Average friction coefficients for a Si substrates with Al top layers and b Al substrates with Si top layers

Full size image

3.6 Chip formation and material mixing

The formation of the chip during cutting is an issue of prime interest, and here in particular the chip morphology is relevant. For the case of metal substrates, it has been reported by Alhafez et al. [8] that the formation of the chip strongly depends on the crystallography of the workpiece and the type and glide of dislocations activated.

For pure Al, the chip morphology is dominated by the formation of subgrains. This process of grain refinement leads to the formation of a “segmented chip.” Such chip segmentation is commonly encountered in the macroscopic cutting of metals [58, 59]; there, however, it may have more complex causes, in particular shear localization leading to shear bands [60]. The chip formed in a pure Al substrate showed 2 subgrains (see Fig. 2a); we note that for the identical cutting system—the Al(001) surface cut in the [110] direction—for a smaller cutting length of 100 Å, only one grain boundary was formed [8]. This demonstrates that the process of subgrain formation continues if the cutting length is increased.

For the Al overlayer systems, no subgrain formation could be observed (see Figs. 4 and 5). Here, evidently, the complex network of dislocations that is necessary to build up the grain boundaries cannot be generated, since the top layer is too thin. We conclude that in Al, chip segmentation, and hence polycrystallinity are strongly influenced by the thickness of the Al top layer.

Figure 12 summarizes the chip morphologies found in the case of Si overlayers; the chip formed in pure Si is displayed in Fig. 3. We observe that the chips are amorphous but contain several embedded crystalline grains. The amount of crystallinity increases for smaller Si thicknesses.

Fig. 12
figure 12

Side view of the chips formed after cutting an Al substrate covered by a Si layer of thickness t at a cutting length of 200 Å. Atoms are colored according to their local lattice structure as in Fig. 4

Full size image

In previous work on Si cutting [3], it was found that for a single-crystalline substrate, the chip was completely amorphous. The complete amorphization is presumably caused by the different tool geometry; Goel et al. [3] used a wedge-like tool with a negative rake angle that exerts a higher pressure on the leading part of the substrate. But also in that study, for polycrystalline Si substrates, the chip was found to contain Si crystallites.

In our case, the Si layer is always a single crystal; however, the fraction of amorphization varies with the layer thickness. In the case of thin overlayers (t < d), all Si is removed from the machined surface and put into the chip. Since pressures are not so high in such a system (cf. Fig. 10b), amorphization does not occur and the chip remains crystalline to a high degree. Conversely, when large pressures are needed for cutting—at high Si thicknesses—the degree of amorphization is high. The case of pure Si (Fig. 3) is an exception, since here pressures are high, but still crystalline grains are found in the chip. A closer inspection of the dynamics of chip formation shows that as the chip is formed in front of the moving tool, it is constantly rotating in counter–clockwise orientation; fragments of crystalline material thus are torn out of the substrate and inserted into the chip. This process does not occur for smaller Si overlayer thickness.

For small overlayer thickness, mechanical mixing of the top layer and the substrate may occur. Figure 13 gives an example of such a process for the case of an Al substrate covered by a Si layer of thickness t = 32.4 Å. Mixing of Al atoms into the chip and of Si atoms into the machined surface are clearly visible. We only observed such mixing processes if Si had been transformed into the amorphous phase. The high pressures that were present then were also sufficient to achieve the mechanical mixing. We note that also in the inverted system—a Si substrate covered by a thin (t = 32.4 Å) Al layer—mechanical mixing of Si atoms into the Al chip and of Al atoms into the machined Si surface was observed (see Fig. 5). Here again, huge thrust forces were at work (see Fig. 10), and created the necessary high pressures.

Fig. 13
figure 13

Side view of an Al substrate covered by a thin Si layer of thickness t = 32.4 Å at a cutting length of 200 Å. Atoms are colored according to their local lattice structure as in Fig. 4. Arrows point at regions where Al and Si atoms were mixed

Full size image

4 Summary

In this paper, the method of MD simulation has been used to study the cutting of an Al/Si bilayer system. The following conclusions can be drawn:

  1. 1.

    The deformation mechanisms of pure Al and pure Si substrates are quite different: dislocation and twinning plasticity in the case of the metal, and amorphization (and some dislocation activity) in the case of Si.

  2. 2.

    The occurrence of twinning as a major deformation mechanism in cutting of Al does not appear to have been described before. However, this finding is in agreement with previous work on deformation mechanisms of Al in the nanoscale [46,47,48].

  3. 3.

    Cutting of Al and Si shows strongly different trends since in Al the cutting force is larger than the thrust force, while in Si it is vice versa, in agreement with previous findings [19]. When putting an Al top layer on a Si substrate, the thrust force is reduced; the opposite effect is observed if a Si top layer is put on an Al substrate.

  4. 4.

    Covering an Al substrate with a thin Si top layer has the detrimental effect that the hard Si requires high pressures for cutting; as a consequence, twinning planes with intersecting directions are generated that ultimately lead to cracks in the ductile Al substrate.

  5. 5.

    Due to its hardness, Si substrates suffer no deformation under cutting if covered by an Al top layer. Only if the cover is so thin that the tool cuts through both Al and Si, Si is deformed. Its deformation is then dominated by amorphization, as for a pure Si substrate.

  6. 6.

    The crystallinity of the Si chip is strongly changed if a (soft) Al substrate is put under the Si top layer. With decreasing thickness of the Si top layer, the Si chip retains a higher degree of crystallinity as the thrust force needed for cutting strongly decreases with decreasing thickness of the Si top layer.

  7. 7.

    Mechanical mixing of the two materials is observed in the cutting zone for thin bilayer systems.

In nanoscale deformation, Si does not behave brittle but deforms in a ductile mode [51]. Nevertheless, its plasticity is strongly different from that of metals: while metal plasticity is dominated by dislocation (and—under the high pressures below a Si substrate—also by twinning) activity, phase transformations—here to the amorphous phase—dominate the behavior of Si. The combination of these two materials to a layered system therefore leads to unexpected behavior. In future research, it appears interesting to widen these studies to polycrystalline bilayered materials, since then the interaction of the deformation processes with grain boundaries may further enrich the morphologies of the structures obtained.