Abstract
It is a well-established fact that when equidistant tool paths are used for 2.5D milling operations tool load varies based on the functions of path curvature. This phenomenon makes the optimal selection of cutting parameters more difficult, and the local load peaks are also detrimental to machining stability and tool life. Numerous publications address possible solutions to eliminate the problems caused by varied cutting parameters. The best solution for this is to keep the cutter engagement at a constant value. Nowadays, several methods are available to generate tool paths which are able to maintain constant cutter engagement, but the widespread use of such solutions is significantly hindered, because in this scenario complex calculations are required. This article offers a solution to this problem by presenting a new non-equidistant offsetting method for ensuring a constant cutter engagement angle. The algorithm developed for this purpose is based on simple geometrical equations and allows for its widespread use just like pixel-based methods. Concerning this new solution, computation needs and uniform tool load are verified by simulation and through experiments. The experiments have shown favourable results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Despite the spread of additive technologies, conventional metal cutting methods are still in use in metal processing [1]. Metal cutting processes could generally be divided into two phases: rough cutting and smoothing. Generally speaking, approximately half of the total metal cutting time is invested in rough cutting [2], and for this reason, a significant number of experimental projects deals with this field. This interest is supported by the fact that the main strategic goal in metal cutting is to improve quality [3] and productivity [4]. Therefore, this article deals with rough milling tool path planning and its further improvement.
The selection of the right tool path is of key importance for efficient manufacturing [5]. During rough cut, it is generally the constant Z level strategy that is in use. The Z level strategy is so widespread that it is also used in the case of free-form rough cutting [6]. In the scope of this, conventional 2.5D rough cutting processes have two basic planning strategies: the direction-parallel and the contour-parallel strategies [7]. In the case of the direction-parallel strategy, tool paths are constituted by straight lines running parallel to one another. As opposed to this, in the contour-parallel strategy, tool paths consist of curves which are equidistant to the contour. These equidistant curves are machined by offsetting the contour. This method requires more extensive calculations, but in the case of complex geometries, this solution could be more advantageous, as it provides shorter tool paths as well as fewer tool entries and exit points compared to the direction-parallel strategy [8]. Besides basic strategies, there are also more complex solutions, which appeared as new developments and are related to computer-aided process planning (CAPP) [9]. In the case of pocket machining, it is generally spiral-like strategies that are in use [10]. These are advantageous in the case of high-speed machining because the path generated with the help of this strategy does not contain corners or sharp changes of direction [11]. The common point of the above-mentioned solutions is that they are all based on geometry, which means that they concentrate only on removing the machining allowance. Thus, their common deficiency is that they do not take into consideration the pertaining technological criteria [12]; therefore, the tool load during cutting may heavily fluctuate [13].
For defining the relationship of the tool and the workpiece, the most effective parameter is the cutter engagement angle (θ) [14], which can be defined as the angle situated towards the centre of the arc length of the tool in contact. The referent values could be determined by using the equation below:
where rtool is the tool radius and ae the radial immersion.
In the case of straight milling, stepover (s) is identical to radial immersion (ae = s), which means that the stepover directly determines the engagement. During milling at arcs and corners, these values differ from each other. This phenomenon is represented in Fig. 1.
When radial immersion changes, chip thickness also changes, which directly influences the applied cutting force [15]. If a constant stepover tool path is in use, the engagement angle will decrease at convex curvatures (θ1 < θ2) and will increase at concave curvatures. Cutting force shows a similar tendency [16]. In the case of concave corners, manifold increases may be observed. However, in the case of difficult-to-machine materials, even a minor increase in engagement can be dangerous [17]. For this reason, controlling the cutter engagement is essential because it is an important input parameter for models describing the cutting force [18, 19].
One solution to compensate for the change of engagement is to control the feed rate. Several experiments were made in this field with a view to keeping the value of the material removal rate constant [20,21,22,23]; nevertheless, some of the associated problems have remained unsolved. On the one hand, the applied machine tool, when operating at slower and higher speeds, should be capable of reaching the desired speed within short periods of time [24], and, on the other hand, it must also be borne in mind that high engagements, which are sometimes used, may cause chatter and a thermal shock [25]. Furthermore, it is very difficult to identify and forecast the impact of changes in cutting parameters [26]. Phrased briefly, controlling the feed rate alone is not adequate in this process. Thus, in order to reach an efficient solution, modifications in the shape of the tool path are necessary [27].
Based on the above explanation and considerations, the following could be established: keeping the engagement angle at a constant value is a necessary condition for achieving the desired tool path [28]. A further advantage of a minor fluctuation in the cutting force is that the risk of minor tool breakage and chatter is reduced [29], and concurrently with this tool life is increased [14]. At the same time, concerns about fluctuations of tool deflection causing inaccuracies can thus be ignored [30]. Therefore, for efficient machining, a stable cutting process is a must [31].
First, in order to keep engagement constant, Iwabe et al. [32] suggested a solution which controls engagement by inserting additional arcs at concave corners. Later Kim et al. [33] also developed a similar strategy. But these additional short connecting-purpose movements resulted in sharp direction changes and small radius arcs, which increased the time period during which the path could be covered. Another approach to the same problem is the application of trochoidal-shaped tool paths [34], which constitute an extremely good solution for ensuring desired smoothness through tool path control [35]. But the disadvantage of this solution is that it contains lots of connecting movements. There are other solutions which also try to ensure acceptable cutting parameters by combining the contour-parallel strategy with the trochoidal strategy [36, 37]. Nowadays, modern CAM systems already contain specialised cycles which combine the morphing spiral-like strategy with the trochoidal strategy [38]. These solutions are expedient in the case of complex geometries, but the formation of simpler pockets may involve unnecessarily huge connecting movements of the tool path. As stated above, the solution to overcome the above problems could be to develop advanced and upgraded contour-parallel-type tool path experiments, which are likely to provide a further step in solving these problems. This study focuses on this issue.
There are several methods to calculate cutter engagement. Determining the cutter engagement is possible basically in two different ways: by applying either the geometrical method or the numerical method [28]. The former one operates appropriately only in the case of simple geometries. A very simple contour geometry is a straight line. In the case of a straight contour, the engagement angle could be determined by using a simple circular equation (see Eq. 1). A more difficult task is to determine the engagement angle if the contour is an arc: but Kramer—using a cosine equation—derived the relevant geometrical functions [39]. Later, proper connections to generally used basic engagement angle events were also developed, where the curvature and straight lines meet under some predefined circumstances [40,41,42,43]. But for general cases, it is not possible to provide explicit functions. Furthermore, in the case of arbitrarily shaped contours, only pixel-based [44] and polygon-mesh [45] solutions could be used.
Thus, there are different direct calculation methods to determine the engagement of an already existing tool path. But, in the scope of planning, a tool path ensuring constant engagement requires an indirect method that determines the tool path shape based on the engagement in question. This could basically be achieved in two different ways: using geometrical algorithms or using pixel-based algorithms. The introduction and description of these alternatives will first discuss geometrical solutions.
Yan et al. [46] developed an uneven offset technique for the removal of the remaining material. They did not concentrate on engagement control but concentrated on the elimination of material remaining at the corners. In the case of tool paths ensuring constant engagement, such a tool path-generating algorithm for complex geometry was first developed by Stori and Wright [47]. Their method was termed constant engagement offsetting. With the help of this technique, it became possible to produce spiral-like tool paths ensuring tool path smoothness. It constitutes an important step that the development of engagement does not happen in a ceiling-limited controlled way but is continuously kept constant at a given value. At the same time, this solution worked only for simple pocket geometries. Later Ibaraki et al. [48] worked out an algorithm which was also good for more complex geometrical shapes. Through experiments, Uddin et al. proved that this strategy ensures more appropriate dimensionally accurate machining as compared to tool paths generated through conventional uniform offsets. This finding supports the notion that, due to constant engagement, cutting force variation will decrease, and so will the impact of flexible shape change [49]. All the above-mentioned solutions construct the tool path in small sections, analyse the relations and construct the tool and workpiece engagement from point to point. This scenario offers quick calculations but could be used only for constant conditions. Another drawback of these solutions is that they cannot be used for generating strategies for tool entry.
For a pixel-based solution, a good example is provided by the algorithm developed by Dumitrache et al. [50]. With the help of a model-based technique, the workpiece and the tool can be represented by bitmap images. After analysis with the help of simple Boolean operations, the relation between the workpiece and tool pixels could be defined. Thus, by way of building the tool path section by section, it is possible to decide in which direction the tool will move on condition the engagement is kept at a fixed value. The determination of the movement direction may happen in three different ways: (1) trying different directions using different angles, (2) using a non-linear equation solver, (3) determining the intersection point of the tool and workpiece boundary. The authors opted for the last solution, which is similar to the solutions that operate through analysing the connecting relations of the contour but offer a very general application. This way transition sections, including tool entry and exit, could be handled easily. The disadvantage of this pixel-based solution is that it requires great amounts of calculations compared to geometry-based solutions.
Based on the above considerations, the goal of this article is to combine the advantages of the above two solutions: quick operation and general use, including complex geometry and the handling of transition sections. In order to achieve this, FACEOM (fast constant engagement offsetting method) has been developed to function as a new method.
1.1 New method of generating tool paths for general planar contours
The task this study has set as an objective can be defined as follows. Given are the tools for the radius rtool, the desired cutter engagement θ and a planar parametric curve c(t), which delineate the boundaries of the workpiece. Based on this, the parametric curve p(t) should be determined, through which the engagement assumes the given value while the tool centre is being moved.
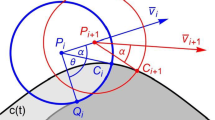
To solve this planar task, the tool is considered as a circular plate with a radius rtool. This is shown in Fig. 2, where the current position of the tool is P. In the first step, we find the intersection point of the tool outline and the contour. If there are more intersection points, we look for the one with the greatest parameter t. This point C rotating around point P by angle θ will provide point Q, where (assuming climb milling) the tool edge should exit the material so that the engagement assumes the given value. It is visible that feed direction (v¯) is perpendicular to the vector originating from the centre of the tool and pointing in the direction of the exit point of the tool \( \left(\overset{\rightharpoonup }{\mathrm{PQ}}\right) \). Based on this, it is easy to determine which direction the tool path tangent from point P should be directed. In order to determine this, vector \( \left(\overset{\rightharpoonup }{\mathrm{PC}}\right) \) should be rotated around point P by an angle of α = 90∘ − θ.
Using a vector field solution method that yielded the desired feed direction at different points of surface, Kumazawa et al. [51] developed a 3D surface finishing tool path. The above-described approach could be extended to all P points situated within the distance rtool as measured from the contour. Thus, as a resolution to this problem, a vector field can be established, which will provide a bulk of possible solutions. The vector field established this way is shown in Fig. 3.
Using green and black streamlines, Fig. 3 shows the vector chart field, which indicates the appropriate directions of the tool at certain points, in case a 60° engagement is to be maintained during metal cutting (the tool diameter is 10 mm). In general, the workpiece contour does not contain such concave arc radiuses which are smaller than rtool − s, and does not contain loops which exhibit narrow areas smaller than the tool diameter. If all of these conditions are satisfied, all the streamlines converge to a stable path. This stable path is marked in black, which is the vector field’s separatrix. Thus, stationary points and periodic orbits will not be included among the streamlines. This situation is shown in Fig. 3.
Unfortunately, the above vector field cannot be filled directly to constitute V(x, y) = (u(x, y), v(x, y)) because the contour has also been given as a parametric vector equation.
Given this, the task to solve is to determine the separatrix in this vector field. This, however, is very difficult to achieve by way of using differential geometry. All in all, the investigation of the vector field provides a solid basis for offering potential solutions to this question, as it shows that irrespective of the starting point of tool path calculation, tool path calculations will always lead to a continual solution.
In order to solve this issue, it is necessary to reconsider the same problem using a geometrical approach. To do this, the situation in Fig. 2 is further analysed. In the scope of this, let us suppose that this figure indicates an adequate status corresponding to ti. With reference to parameter ti, the values of point Pi and the first derivative v¯1 are known. Based on this, parameters for the next status corresponding to ti + 1 can be determined (see Fig. 4).
Therefore, this task is similar to a boundary value problem in the field of differential equations. In analogy with the Euler method, this problem could easily be solved in a numerical way, as described in the following simple steps:
Forward EULER algorithm:
-
Step 1: Take a step along v¯1 from point Pi with increment size h, thereby obtaining Pi + 1⋅
-
Step 2: Determine the intersection point of the circle with a centre Pi + 1 with radius rtool and curve c(t) (if there are several of such points, then determine the point corresponding to the largest t parameter), thereby obtaining Ci + 1⋅
-
Step 3: Rotate vector \( \left(\overset{\rightharpoonup }{{\mathrm{P}}_{\mathrm{i}+1}{\mathrm{C}}_{\mathrm{i}+1}}\right) \) around Pi + 1 by α = 90∘ − θ, thereby obtaining vector \( \overline{{\mathrm{v}}_{\mathrm{i}+1}} \).
-
Step 4: Increase step index(i = i + 1).
-
Step 5: If the end of the contour is not reached, go back to step 1.
This method is capable of building up the required tool path using tiny straight lines, as the tool path p(t) to be determined can be reconstructed using a series of points {Pj}j = 0, … i..
The main disadvantage of this calculation method is that in step 2 one circle and one parametrically given curve intersection point must be determined every time, which requires further calculations for the purpose of numerical operations. In order to avoid the calculation difficulties described above, in the scope of the present study, a new algorithm has been developed, which provides better calculation efficiency. In what follows, the relevant details of this new algorithm are provided.
2 Method
2.1 Goals and requirements
When developing this new method, the main criterion was that the algorithm should be capable of generating tool paths exhibiting constant engagement during machining for general contour curves. In addition to this, as opposed to the currently available geometrical methods, which derive the contour path on the basis of connecting relations established by way of tracing the contours, another requirement concerning the new algorithm was that the method should contain exclusively simple geometrical operations and should appropriately be used in the case of statuses other than only stable operation ones, and should be capable of calculating the tool path for the transition sections.
2.2 Input data
The following data are required for the efficient operation of the algorithm: the desired cutter engagement (θ), the tool radius rtool, the contour curve (parametrical vector equation c(t) defined on interval [tmin, tmax]), the starting parameter (t0), the angle between the tool path and the contour at the starting point (β), and the step size used in the case of the numerical solution method (Δt).
2.3 Initialising
In the initialising step, step index (i = 0) is set to zero, and the variable is fixed at the starting value (ti = t0). It is expedient to select the variable in relation to the contour starting point (t0 = tmin). Then, based on Fig. 5, the contour path starting point parameters could be determined. Point C0 = c(t0) could be obtained using a simple substitution. The following equation could also be deduced: ω = β + θ + 90∘. After this, tangent vector \( \overline{c\hbox{'}}\left({t}_0\right) \) is rotated around point C0 by ω. Then, through establishing the distance rtool from C0 along the rotated vector, point P0 is obtained. After that, knowing P0, C0, and \( {\overline{\mathrm{v}}}_0 \), point Q0 can be determined as described below.
2.4 Calculation methods
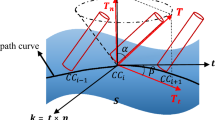
In the initialising step, on the basis of predefined starting points, the tool path can be constructed step by step through connecting tiny straight segments. This scheme contains the following steps of implementation (cf. Fig. 4):
Fast constant engagement offsetting method (FACEOM):
-
Step 1: Substitute parameter ti + Δt in the equation that specifies the contour c(t), thereby obtaining Ci + 1.
-
Step 2: Determine the intersection point of the half-line from point Pi along vector \( {\overline{\mathrm{v}}}_{\mathrm{i}} \) and the circle with a centre point Ci + 1 and radius rtool (if there are more points, then take the point corresponding to the largest t parameter), thereby obtaining Pi + 1
-
Step 3: Rotate vector \( \overset{\rightharpoonup }{{\mathrm{P}}_{1+1}{\mathrm{C}}_{1+1}} \) around point Pi + 1 by α = 90∘ − θ, thereby obtaining vector \( \overline{v_{1+1}}. \)
-
Step 4: Increase parameter (ti = ti + Δt) and step index (i = i + 1).
-
Step 5: If the end of the contour (ti ≤ tmax) is not reached, go back to step 1.
As compared to the simple Euler method, the novelty of the above method is that the determination of the next point does not take place directly based on point Pi. Instead, at first, intersection point C is determined, and from this, the tool path can be established working backwards. Thanks to this, in the scope of step 2, it is not necessary to calculate the intersection point of a parametrical curve and a circle: only the intersection point of a straight half-line and a circle must be determined. In fact, the determination of this intersection point can be considered a trivial task. Owing to this, the newly developed numerical method is more advantageous as far as its effectiveness is concerned.
The steps of this algorithm are to be repeated. Afterward, calculated points {Pj}j = 0, … i.could be projected onto the tool path curve. If the points are determined at an appropriate density, a linear spline can be selected to join the points. This means the points could be used directly as a polyline. During the experiments conducted in the scope of this paper, this method was selected. Of course, higher cubic spline could also be used if requirements regarding the mathematical continuity of the path were stricter (for example in the case of high-speed machining).
2.5 Overview of the algorithm
The operation of the algorithm is portrayed in a block diagram in Fig. 6
3 Results
In this section, the practical application of the above-described method is demonstrated through three examples. In the scope of the next examples, a uniform cutter engagement of 60° has been used. In the figure, blue lines show the boundaries of the workpiece, black lines represent the tool path with constant engagement and the newly generated contours, respectively. In addition, using red lines, a pertaining constant 25% stepover tool path is also indicated for reference.
First, simple contour elements were joined to investigate the operation of the algorithm. Figure 7a shows the tool path generated for a right-angled convex corner. It is seen that the breaking point in the contour did not affect the algorithm; thus, it is sufficient for the curves to contain geometric continuity G0, and it is not necessary for them to be continuously differentiable. This example also shows that the constant engagement tool path removes more material than the constant stepover tool path, because it does not allow the engagement to sink below a given value. This ensures better productivity in the case of rough cutting operations.
Figure 7b also shows a right-angled corner machining, but this time with a concave arc. It is important to note that an internal curvature is not possible to be fully machined at the corner because the tool cannot reach the material. However, rounding with a radius rtool − s is possible in order to assure an acceptable geometry. It is also obvious that, compared to the previous case of machining, the constant engagement now leaves more uncut material in the corner. However, in the case of conventional constant stepover tool path operation, it must be borne in mind that cutting force may occasionally jump, which generates vibration or may lead to tool breakage.
Experiments have been executed using arbitrarily shaped curves, too. Figure 8 shows a parametrically determined sine wave-shaped contour. The algorithm, in this case, operated impeccably. It is to be noted that there is not too much difference between strategies in the case of small curvature sections, because the arcs at these sections are close to straight lines. However, in the case of big curvature sections, the difference between these strategies was significant. The direction of the difference depended on the curvature of the contour and suited to the nature of the curvature depending on whether it was concave or convex. Actually, all these fit in with the previously described examples.
The previous examples demonstrated in what way it was possible to move the cutting tool to the end of the contour curve in a single depth of cut in a manner that the engagement remains constant while observing the goal of decreasing the amount of excess material. This process can be repeated again and again without any alterations only as long as the aim of the process is to reduce the amount of allowance material, which means that the very end of the geometry is not yet reached. Furthermore, it was also examined whether the algorithm could be used successively several times up until the end of workpiece boundaries are reached while the contour curve is recalculated step by step in relation to the end geometry. To test this, a trochoidal tool path was generated for the purpose of machining a straight slot. In the scope of this experiment, a widely used cycloid-shaped trochoidal tool path strategy was adopted as a reference point (see Fig. 9a). This solution also has the peculiarity that, when selecting the shape of path, arising technological parameters are not considered.
As constant engagement is possible only on condition, the middle section of the slot is secured; a roll-in section at the start and a roll-out section at the end were added. In addition to the tool path points, tool exit points were also registered. These points have been marked as Q in Fig. 2, and have been determined by a 90° rotation of the feed direction. These points determine the newly generated contour, for which the path is generated in the next phase. Technically, this could be solved easily in such a way that a spline curve will be projected to the Q points obtained during the last phase, which thereby ensures the parametrical equation in the next phase. As Fig. 9b has already proved, the algorithm with this addition is capable of handling the changes in the boundaries of the workpiece over time. Compared to the conventional strategy, it can be established that despite the same number of loops, through the use of the new trochoidal strategy, the path length has become significantly shorter. This improvement totalled 20%.
The above-mentioned examples prove that the algorithm exhibits a robust operation and could be used for complex tasks. Experiments were also executed for the sine wave shaped curve and for the trochoidal tool path cutting activities. The results of these experiments are found and are discussed in Section 3.2. Nevertheless, before giving an account of this, it is important to discuss issues of accuracy and calculation need, because these parameters are extremely important from the perspective of practical application.
3.1 Accuracy and computational cost
A comparative test was performed to determine the effectiveness of the newly developed FACEOM algorithm. For this purpose, the contour seen in Fig. 8 was used. Three different methods have been examined: the pixel-based method, the Euler method-based algorithm, and the FACEOM algorithm. As all algorithms, in a step-by-step manner, set the tool path approximating the actual path using short straight line segments, it was investigated—in the case of different numerical step sizes—to what extent the time required for the calculations changed, and what the biggest difference, as compared to the nominal value of the engagement, was.
The test was conducted using Wolfram Mathematica version 11 numerical equation solver functions, which enabled the measurement of the necessary CPU time (the CPU type used in the scope of the experiment was Intel Core i3-3220 3.30 GHz). For checking the engagement, a self-developed discrete model-based simulator has been used [13]. The results can be seen in Fig. 10
It is obvious that using the pixel-based algorithm the time required for computation was manifold that of the time required to reach the precision of the geometrical-based algorithm. In line with our expectations, concerning geometrical-based algorithms FACEOM proved to be the most efficient solution. If the tolerable inaccuracy is defined as 1%, then useful pure computational time was ~9 s in the case of the pixel-based algorithm, ~0.45 s in the case of the Euler method and only ~0.17 s in the case of FACEOM. If tolerable accuracy is higher, the FACEOM’s effectiveness proves even more favourable compared to the other methods. However, in the case of rough cutting, this result has only theoretical significance. In the case of rough cutting, as far as practice is concerned, it is not justifiable to increase the time unnecessarily by increasing accuracy-related requirements.
On the other hand, in the scope of the present paper, the issue of the correct step size selection has not been addressed. In order to keep the numerical method stable, it is necessary to apply small steps of the proper size. If done otherwise, the calculation method may get jammed at sections of curves. In fact, it is not possible to provide a generally acceptable step size, because step size heavily depends on the parametrisation of the contour curve. Nevertheless, based on these experiments, it was possible to make suggestions on the maximum increment of step size permissible in the case of contours (see Fig. 11).
Based on the diagram, it is possible to provide estimations as to the fix values of step size. Accordingly, in the case of engagement 60%, if the maximum step on the contour was 2.5% of the tool diameter, the resulting inaccuracy will not exceed 1%.
In case the stability of the algorithm or the achieved accuracy is not satisfactory, the reduction of the step size offers a solution. A further development of the algorithm may consist of the introduction of an adaptive step, which can achieve numerical stability by further reducing computational time.
3.2 Cutting experiments
During cutting experiments, a piezoelectric force measuring device was used to measure the force acting on the workpiece. During evaluation, a Gauss filter was used for signal processing. After filtering the data, the resultant cutting force was observed. In addition, concerning each tool rotation, the pertinent maximum values were included in a diagram. Table 1 contains the experimental conditions used during cutting tests.
Apart from cutting experiments, simulations trials were also made, where the temporal development of the following was observed: engagement angle (θ), material removal rate (MRR), and maximum chip thickness (hex). The figures below show related simulation values.
During the first cutting experiment, a sine wave-shaped contour was machined using two different strategies and the same feed rate (see Fig. 8). The results are summarised in Fig. 12. As it was explained in the theoretical introduction, in the case of the constant stepover tool paths through the convex curves, the tool load was lower; but through concave curves, the tool load was higher. The reasons for this will become clear upon examining the simulation results: the engagement, the material removal rate and the maximum chip thickness follow the same trend. However, in the case of constant engagement tool paths, these indicators remain stable, thus cutting force also remains steady up until the very end of the process. It could be stated that the maximum cutting force is 19% lower compared to the data obtained during the use of the conventional strategy. This difference itself is enormous, and in this example, the contour arc radius did not even approximate the tool radius, at which point the same trend shows a tendency of marked increase. Other experiments were also executed on this contour using different engagement. It was observed that a decrease in the engagement causes an even more drastic difference. While the difference between the force maximums in the case of engagement 90° was only 8%, in the case of engagement 30°, the same value was 38%. Considering that in the case of high-speed machining usually low engagement was used, the application of constant engagement tool paths in the scope of this technology is highly recommendable.
The same experiment was also executed for the purpose of examining the behaviour of trochoidal tool paths. The width of the machined slot was 15 mm, its length was 20 mm. The basis of comparison was the conventional cycloid tool path: in the scope of this experiment, it was important that the constant engagement trochoidal tool path should be composed of the same number of loops, and that in the case of both strategies the machining time should be the same. In order to ensure the desired number of cycloid loops in all periods, 1/8 of the tool diameter was used as the trochoidal step (w = 0.125Dtool). For the comparison of machining time, modification of the feed was also necessary. Section 3 showed that in the case of the conventional strategy the tool path was 20% longer. This longer path was balanced by increasing the feed rate by 30% (from 477 to 620 mm/min). In the case of both machining strategies, an increased speed (3000 mm/min)was used at connecting sections. The tool path constructed along the above-detailed considerations is shown in Fig. 9.
This experiment also justified that the newly developed algorithm efficiently functions, which is demonstrated by the data included in Fig. 13. In the left-hand section of the diagram, the entire process of machining the slot can be seen; in the right-hand section only the last two periods are shown. Force measuring showed that the value of force maximum was 17% lower. This is due not only to the applied lower feed rate but also to the lower engagement value. It is worth mentioning that the force diagram is similar to a square wave signal, which means that the algorithm continuously operates in the most efficient zone, as opposed to the conventional tool path, which exhibits prolonged entry and exit phases. At the same time, the connecting sections have also become shorter; thus, the algorithm seems to yield a better tool path in all respects.
In the magnified part of the figure below, it is observable that in the case of improved tool paths there were peaks in the value of force and in the engagement angle at the roll-in and roll-out sections. Except for this, the newly developed method could provide a better result. Considering the cutting force, the referent value might be as high as 24% as opposed to than 17%. With respect to these transitional sections, optimal planning can further improve efficiency.
As a summary, it can be stated that the experiments clearly justify that the newly developed algorithm generates more efficient tool paths than conventional methods. The limits of the application of the method can be defined by way of formulating two contour requirements: the contour cannot contain concave curves where the curvature is less than, rtool − s, and it cannot contain loops which have narrow open sections smaller than the tool diameter. However, this does not mean a significant limitation, because this may arise only in the case of extreme situations during rough cutting. On the other hand, if this does happen, the problem can easily be solved by reducing the engagement in the vicinity of critical zones.
4 Summary
When developing the FACEOM, the goal was to find an easy and fast way of ensuring efficient rough cutting tool paths in an attempt to replace complex calculations. This research project was prompted by the motivation that even if tool paths with constant engagement offer undeniable advantages, the calculation time related to their operation can still be reduced. As a consequence, reductions in calculation times could be the key to the more widespread use of this technology. As compared to other currently used methods, the development of FACEOM constitutes one step in this direction.
Upon the evaluation of the algorithm, the following could be stated a conclusion:
-
Through simple geometrical steps, the algorithm can produce tool paths for arbitrarily shaped contour curves, while ensuring constant engagement during machining.
-
As opposed to the available geometrical methods, the algorithm can be used in the case of diverse machining conditions, not exclusively in the case of constant machining conditions: the algorithm also operates in the case of transition sections by way of creating suitable tool paths.
-
Similarly to the pixel-based method, this method contains generally applicable comparable characteristics, and—just like the geometrical method—it is also simple and quick to use.
-
In the scope of experiments, it was proved that tool load, in the case of tool paths with constant engagement, remains steady up until the end of the process, which allows for maximum productivity.
-
The new type of trochoidal tool path successfully demonstrated that the newly developed algorithm can also be used for complex tasks, and showed that it is capable of improving efficiency as compared to other widely used solutions.
In other words, it can be stated that the goals of the present paper described in the introduction have been realised completely and successfully.
As a future goal, it is our intention to further develop the algorithm. Our objective is to solve the following shortcomings: the tool path should be generated not exclusively based on the current contour status of the workpiece; and the shape and location of the reaming material should be managed through intelligent solutions. Coupled with the fast operation of the algorithm, remedying these shortcomings may result in a major technological improvement. Such a technological improvement would lie in the potential of adjusting the engagement angle by way of using a function rather than a constant parameter.
Abbreviations
- a e :
-
Effective radial immersion [mm]
- a p :
-
Axial depth of cut [mm]
- c(t):
-
Parametric representation of workpiece contour [{mm, mm}]
- fz :
-
Feed per tooth [mm]
- hex :
-
Maximum chip thickness [mm]
- i, j :
-
Step index [−]
- n :
-
Spindle speed [1/min]
- p(t):
-
Parametric representation of tool path [{mm, mm}]
- r tool :
-
Tool radius [mm]
- s :
-
Stepover [mm]
- t :
-
Free parameter of curve equations [−]
- v¯:
-
Feed vector [{mm, mm}]
- v c :
-
Cutting speed [m/min]
- v f :
-
Feed rate [mm/min]
- w :
-
Trochoidal step [mm]
- z :
-
Number of teeth [−]
- C :
-
Entry point of the cutting edge [{mm, mm}]
- D tool :
-
Tool diameter [mm]
- MRR:
-
Material removal rate [mm3/min]
- P :
-
Tool path point [{mm, mm}]
- Q :
-
Exit point of cutting edge [{mm, mm}]
- V(x, y):
-
Vector field [{mm, mm}, {mm, mm}]
- a, β :
-
Angle parameters [∘]
- Δs:
-
Step size [−]
- θ :
-
Cutter engagement angle [∘]
References
Comak A, Altintas Y (2017) Mechanics of turn-milling operations. Int J Mach Tools Manuf 121:2–9
Abdullah H, Ramli R, Wahab DA (2017) Tool path length optimisation of contour parallel milling based on modified ant colony optimisation. Int J Adv Manuf Technol 92(1–4):1263–1276
Korosec M, Kopaz J (2007) Neural network based selection of optimal tool - path in free form surface machining. J Autom Mob Robot Intell Syst 1(4):41–50
Car Z, Mikac T, and Veza I (2006) Utilization of GA for optimization of tool path on a 2D surface, vol. 6th International workshop on emergent synthesis, pp. 231–236
Póka G, Mátyási G, Németh I (2016) Burr minimisation in face milling with optimised tool path. Procedia CIRP 57:653–657
Chen L, Li Y, Tang K (2018) Variable-depth multi-pass tool path generation on mesh surfaces. Int J Adv Manuf Technol 95(5–8):2169–2183
Held M and de Lorenzo S (2017) On the generation of spiral-like paths within planar shapes. J. Comput Des Eng
Xu K, Li Y, Xiang B (2018) Image processing-based contour parallel tool path optimization for arbitrary pocket shape. Int J Adv Manuf Technol:1–15
Kuric I, Legutko S (2001) Chosen aspects of modern CAPP systems. Comput Methods Sci Technol 7:65–74
Held M, Spielberger C (2009) A smooth spiral tool path for high speed machining of 2D pockets. Comput Aided Des 41(7):539–550
Zhou B, Zhao J, Li L, Xia R (2016) A smooth double spiral tool path generation and linking method for high-speed machining of multiply-connected pockets. Precis Eng 46:48–64
Patel DD, Lalwani DI (2017) Quantitative comparison of pocket geometry and pocket decomposition to obtain improved spiral tool path: a novel approach. J Manuf Sci Eng 139(3):031020–031020–10
Jacso A, Szalay T, Jauregui JC, Resendiz JR (2018) A discrete simulation-based algorithm for the technological investigation of 2.5D milling operations. Proc. Inst. Mech. Eng. Part C, J Mech Eng Sci:78–90
Shixiong W, Zhiyang L, Chengyong W, Suyang L, Wei M (2018) Tool wear of corner continuous milling in deep machining of hardened steel pocket. Int J Adv Manuf Technol:1–19
Biró I, Szalay T (2017) Extension of empirical specific cutting force model for the process of fine chip-removing milling. Int J Adv Manuf Technol 88(9–12):2735–2743
Chan KW, Choy HS (2002) Machining tactics for interior corners of pockets. Int J Adv Manuf Technol 20(10):741–748
Agic A, Eynian M, Hägglund S, Ståhl J-E, Beno T (2017) Influence of radial depth of cut on entry conditions and dynamics in face milling application. J Superhard Mater 39(4):259–270
Altintas Y (2012) Manufacturing automation: metal cutting mechanics, machine tool vibrations, and CNC design, 2nd edn. Cambridge University Press, Cambridge
Cheng K (ed) (2009) Machining dynamics: fundamentals, applications and practices. Springer-Verlag, London
Farouki R, Manjunathaiah J, Nicholas D, Yuan G-F, Jee S (1998) Variable-feedrate CNC interpolators for constant material removal rates along Pythagorean-hodograph curves. Comput Aided Des 30(8):631–640
Wei Z, Wang M, Han X (2010) Cutting forces prediction in generalized pocket machining. Int J Adv Manuf Technol 50(5–8):449–458
Zuperl U, Cus F, Reibenschuh M (2012) Modeling and adaptive force control of milling by using artificial techniques. J Intell Manuf 23(5):1805–1815
Zhang Z, Luo M, Zhang D, Wu B (2018) A force-measuring-based approach for feed rate optimization considering the stochasticity of machining allowance. Int J Adv Manuf Technol:1–12
Pateloup V, Duc E, Ray P (2004) Corner optimization for pocket machining. Int J Mach Tools Manuf 44(12–13):1343–1353
Xu J, Sun Y, Zhang X (2012) A mapping-based spiral cutting strategy for pocket machining. Int J Adv Manuf Technol 67(9–12):2489–2500
Borsos B, Csorgo A, Hidas A, Kotnyek B, Szabo A, Kossa A, Stepan G (2017) Two-dimensional finite element analysis of turning processes. Period Polytech Mech Eng 61(1):44–54
Desai KA, Rao PVM (2016) Machining of curved geometries with constant engagement tool paths. Proc Inst Mech Eng Part B J Eng Manuf 230(1):53–65
Guerrero-Villar F, Dorado-Vicente R, Romero-Carrillo P, López-García R, Mercado-Colmenero J (2015) Computation of instantaneous cutter engagement in 2.5D pocket machining. Procedia Eng 132:464–471
Wang C, Zhang X, Cao H, Chen X, Xiang J (2018) Milling stability prediction and adaptive chatter suppression considering helix angle and bending. Int J Adv Manuf Technol 95(9–12):3665–3677
Nghiep TN, Sarhan AAD, and Aoyama H Analysis of tool deflection errors in precision CNC end milling 0f aerospace aluminum 6061-T6 alloy. Measurement
Pérez-Canales D, Álvarez-Ramírez J, Jáuregui-Correa JC, Vela-Martínez L, Herrera-Ruiz G (2011) Identification of dynamic instabilities in machining process using the approximate entropy method. Int J Mach Tools Manuf 51(6):556–564
Hiroyasu IWABE, Yoshiya FUJII, Katsumasa SAITO, Takeshi KISHINAMI (1989) Study on corner cut by end mill. Journal of the Japan Society for Precision Engineering 55(5):841–846
Kim H-C, Lee S-G, Yang M-Y (2006) An optimized contour parallel tool path for 2D milling with flat endmill. Int J Adv Manuf Technol 31(5–6):567–573
Niaki FA, Pleta A, Mears L (2018) Trochoidal milling: investigation of a new approach on uncut chip thickness modeling and cutting force simulation in an alternative path planning strategy. Int J Adv Manuf Technol 97(1–4):641–656
Elber G, Cohen E, Drake S (2005) MATHSM: medial axis transform toward high speed machining of pockets. Comput Aided Des 37(2):241–250
Ibaraki S, Yamaji I, Matsubara A (2010) On the removal of critical cutting regions by trochoidal grooving. Precis Eng 34(3):467–473
Shixiong W, Bin L, Wei M, and Chengyong W Trochoidal machining for the high-speed milling of pockets, J Mater Process Technol
Jacso A, Szalay T (2018) Analysing and optimizing 2.5D circular pocket machining strategies. Lect Notes Mech Eng 201519:355–364
Kramer TR (1992) Pocket milling with tool engagement detection. J Manuf Syst 11(2):114–123
Adesta EYT, Hamidon R, Riza M, Alrashidi RFFA, Alazemi AFFS (2018) Investigation of tool engagement and cutting performance in machining a pocket. IOP Conf Ser Mater Sci Eng 290(1):012066
Gupta SK, Saini SK, Spranklin BW, Yao Z (2005) Geometric algorithms for computing cutter engagement functions in 2.5D milling operations. Comput Aided Des 37(14):1469–1480
Han X, Tang L (2015) Precise prediction of forces in milling circular corners. Int J Mach Tools Manuf 88:184–193
Wu S, Ma W, Bai H, Wang C, Song Y (2017) Engagement angle modeling for multiple-circle continuous machining and its application in the pocket machining. Chin J Mech Eng 30(2):256–271
Wang H, Jang P, Stori JA (2005) A metric-based approach to two-dimensional (2D) tool-path optimization for high-speed machining. J Manuf Sci Eng 127(1):33–48
Gong X and Feng H-Y Cutter-workpiece engagement determination for general milling using triangle mesh modeling, J Comput Des Eng
Yan S, Shuilai W, Shuiguang T (2000) Uneven offset method of NC tool path generation for free-form pocket machining. Comput Ind 43(1):97–103
Stori JA, Wright PK (2000) Constant engagement tool path generation for convex geometries. J Manuf Syst 19(3):172–184
Ibaraki S, Ikeda D, Yamaji I, Matsubara A, Kakino Y, and Nishida S (2004) Constant engagement tool path generation for two-dimensional end milling, vol. 2004 Japan-USA Symposium on Flexible Automation Japan
Uddin MS, Ibaraki S, Matsubara A, Nishida S, Kakino Y (2006) Constant engagement tool path generation to enhance machining accuracy in end milling. JSME Int J Ser C Mech Syst Mach Elem Manuf 49(1):43–49
Dumitrache A, Borangiu T (2012) IMS10-image-based milling toolpaths with tool engagement control for complex geometry. Eng Appl Artif Intell 25(6):1161–1172
Kumazawa GH, Feng H-Y, Barakchi Fard MJ (2015) Preferred feed direction field: a new tool path generation method for efficient sculptured surface machining. Comput Aided Des 67(68):1–12
Acknowledgements
Open access funding provided by Budapest University of Technology and Economics (BME). The research reported in this paper was developed as a part of the Higher Education Excellence Program of Hungary’s Ministry of Human Capacities in the framework of Budapest University of Technology and Economics’ research area ‘Artificial Intelligence’ (BME FIKP-MI).
Funding
Research work for this paper was partly supported by the European Commission through project H2020 EPIC under grant no. 739592. The results introduced in this paper have been applied in the scope of project no. ED_18-22018-0006, which project was implemented with support provided by the National Research, Development and Innovation Fund of Hungary, and was financed in the scope of (publicly funded) funding schemes according to Section 13(2) of the Act on Scientific Research, Development and Innovation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jacso, A., Matyasi, G. & Szalay, T. The fast constant engagement offsetting method for generating milling tool paths. Int J Adv Manuf Technol 103, 4293–4305 (2019). https://doi.org/10.1007/s00170-019-03834-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-019-03834-8