Force-field instability in surface grinding

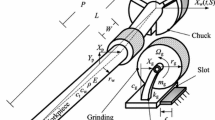
Abstract

In this paper, a particular kind of non-regenerative instability in surface grinding is studied. Clear evidences have been collected suggesting that vibrations can occur suddenly even during the first grinding pass, just after wheel dressing. These circumstances exclude workpiece and wheel surface regeneration as instability origin, whereas both surfaces have to be considered initially smooth. On these bases, the stability of the dynamic system constituted by an oscillating ideal wheel (namely without waviness on the surface) immerged in a positional and velocity-dependent process force field has been studied, demonstrating that, under particular conditions, the force field generates an unstable behaviour. The instability occurrence is strictly related to the oscillation direction of the wheel centre, according to the mode shape associated to the dominant resonance, with respect to the direction of the grinding force (identified by the ratio between its tangential and normal components). The analysis leads to the identification of a simple necessary condition for instability occurrence. The analytical results are confirmed by time-domain grinding simulations and compared with experimental evidences.

Appendix 1

Let the inequality Δq _c < 0 be considered, namely

$$ \left(\operatorname{sgn}\Omega \mathrm{a}\kern0.2em { \cos}^2\alpha -\operatorname{sgn}\Omega \sqrt{a{D}_{\mathrm{w}}} \sin \alpha \cos \alpha - a\mu \cos \alpha \sin \alpha +\mu \sqrt{a{D}_{\mathrm{w}}}\kern0.1em { \sin}^2\alpha \right)\kern-0.4em <\kern-0.2em 0 $$

(23)

Dividing both members by cos² α and posing t = tan α with $-\frac{\pi }{2}<\alpha <\frac{\pi }{2}$, it yields

$$ \mu \sqrt{\frac{D_{\mathrm{w}}}{a}}{t}^2-\left(\operatorname{sgn}\Omega \cdot \sqrt{\frac{D_{\mathrm{w}}}{a}}+\mu \right)t+\operatorname{sgn}\Omega <0 $$

(24)

whose boundary solution is

$$ {t}_{1,2}=\frac{\left(\operatorname{sgn}\Omega \cdot \sqrt{\frac{D_{\mathrm{w}}}{a}}+\mu \right)\pm \sqrt{{\left(\operatorname{sgn}\Omega \cdot \sqrt{\frac{D_{\mathrm{w}}}{a}}+\mu \right)}^2-4\mu \sqrt{\frac{D_{\mathrm{w}}}{a}}\operatorname{sgn}\Omega}}{2\mu \sqrt{\frac{D_{\mathrm{w}}}{a}}} $$

(25)

(both cases sgn Ω = 1 and sgn Ω = −1 must be taken into account). Stating that

$$ {D}_{\mathrm{w}}>>a\Rightarrow \sqrt{\frac{D_{\mathrm{w}}}{a}}>>1, $$

(26)

the discriminant of the parabola represented by the first term of the (Eq. 24) is always positive. As the coefficient of t² is always positive as well, the parabola has the vertex belonging to the negative half-plane and a positive concavity; therefore, the negative values are internal to the interval comprised between the solutions t_1,2. Going back to the original variable α, inequality solution becomes

$$ \left\{\begin{array}{l}\alpha >{ \tan}^{-1}\left(\frac{\left(\operatorname{sgn}\Omega \cdot \sqrt{\frac{D_{\mathrm{w}}}{a}}+\mu \right)-\sqrt{{\left(\operatorname{sgn}\Omega \cdot \sqrt{\frac{D_{\mathrm{w}}}{a}}+\mu \right)}^2-4\mu \sqrt{\frac{D_{\mathrm{w}}}{a}}\operatorname{sgn}\Omega}}{2\mu \sqrt{\frac{D_w}{a}}}\right)\kern0.5em \mathrm{and}\ \\ {}\alpha <{ \tan}^{-1}\left(\frac{\left(\operatorname{sgn}\Omega \cdot \sqrt{\frac{D_{\mathrm{w}}}{a}}+\mu \right)+\sqrt{{\left(\operatorname{sgn}\Omega \cdot \sqrt{\frac{D_{\mathrm{w}}}{a}}+\mu \right)}^2-4\mu \sqrt{\frac{D_{\mathrm{w}}}{a}}\operatorname{sgn}\Omega}}{2\mu \sqrt{\frac{D_{\mathrm{w}}}{a}}}.\right)\end{array}\right. $$

(27)

Condition (26) leads to the following approximation:

$$ {t}_1\approx 0;\kern1.25em {t}_2\approx \mu $$

(28)

Thus, (27) becomes

$$ \begin{array}{ll}\alpha \in \left[0,{ \tan}^{-1}\frac{1}{\mu}\right]\kern0.5em \mathrm{for}\kern0.75em \mathrm{sgn}\kern.2em \Omega =1;\hfill & \alpha \in \left[-{ \tan}^{-1}\frac{1}{\mu },0\right]\ \mathrm{for}\kern0.75em \mathrm{sgn}\kern.2em \Omega =-1\hfill \end{array}. $$

(29)

Finally, the minimum of the first member of (24) can be easily computed by equating to zero its first derivative. It yields

$$ \begin{array}{ll}\ {\alpha}_{\min }={ \tan}^{-1}\left(\frac{1}{2\mu}\right)\kern0.5em \mathrm{for}\kern0.5em \mathrm{sgn}\kern.2em \Omega =1;\hfill & {\alpha}_{\min }=-{ \tan}^{-1}\left(\frac{1}{2\mu}\right)\kern0.5em \mathrm{for}\kern0.5em \mathrm{sgn}\kern.2em \Omega =-1\hfill \end{array}. $$

(30)