Spatial Cournot competition in two intersecting circular markets

Abstract

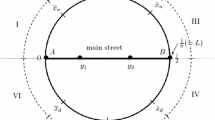
This paper analyzes the location equilibrium in two intersecting circular markets where two identical firms engage in Cournot competition. It is shown that each of the two intersection points occupied by one of the firms is the unique fully symmetric location equilibrium and also the social optimum, which is neither maximal nor minimal differentiation. The intuition of our result is that by each firm locating at each of the intersection points, firms can minimize their transport costs and partially avoid competition, compared with both locating at one of the intersection points. Our finding coincides with the real-world phenomenon that transport hubs may attract the presence of more firms.

Appendices

Appendices

1.1 Appendix 1: The proof that $[x_1,y_2]=[0,0]$ is not an equilibrium

Given $x_1=0$, $y_2\in [0,\delta ]$, and $\delta$ is small, we can show that it is profitable for firm 2 to deviate from $y_2=0$. The domestic market for both firms can be divided into six segments ([0, s], [s, 1 / 2], $[1/2,y_2+1/2]$, $[y_2+1/2,1-s]$, $[1-s,1-y_2]$, $[1-y_2,1]$), and the nondomestic market can also be divided into six segments ($[0,y_2]$, $[y_2,s]$, [s, 1 / 2], $[1/2,y_2+1/2]$, $[y_2+1/2,1-s]$, $[1-s,1]$) as shown in Fig. 9. The profits for firm 1 and firm 2 at a location point x on market X are

$$\begin{aligned}&\pi _1^X=\left( a-b(q_1^X+q_2^X)-t|x-x_1|\right) q_1^X, \end{aligned}$$

(24)

$$\begin{aligned}&\pi _2^X=\left( a-b(q_1^X+q_2^X)-t\left( \min \{|s-y_2|+|x-s|, |(1-s)-y_2|+|x-(1-s)|\}\right) \right) q_2^X. \end{aligned}$$

(25)

Solving $\partial \pi _1^X/\partial q_1^X=0$ and $\partial \pi _2^X/\partial q_2^X=0$ simultaneously yields $q_1^X$ and $q_2^X$. The profits for firm 1 and firm 2 at a location y on market Y are

$$\begin{aligned}&\pi _1^Y=\pi _2^X=\left( a-b(q_1^Y+q_2^Y)-t\left( \min \{|s-x_1|+|y-s|, |(1-s)-x_1|+|y-(1-s)|\}\right) \right) q_1^X. \\&\pi _2^Y=\left( a-b\left( q_1^Y+q_2^Y\right) -t|y-y_2|\right) q_2^Y. \end{aligned}$$

Solving $\partial \pi _1^Y/\partial q_1^Y=0$ and $\partial \pi _2^Y/\partial q_2^Y=0$ simultaneously yields $q_1^Y$ and $q_2^Y$.

Fig. 9

The case when $x_1=0$, $y_2\in [0,\delta ]$, $0\le \delta \le s$

After some calculations, given $x_1=0$, the total profit for firm 2 is

$$\begin{aligned} \Pi _2& = \int _0^s\pi _2^X(x)\hbox {d}x + \int _s^{1/2}\pi _2^X(x)\hbox {d}x + \int _{1/2}^{1/2+y_2} \pi _2^X(x)\hbox {d}x + \int _{1/2+y_2}^{1-s}\pi _2^X(x)\hbox {d}x \\&\quad +\, \int _{1-s}^{1-y_2}\pi _2^X(x)\hbox {d}x + \int _{1-y_2}^1\pi _2^X(x)\hbox {d}x +\int _0^{y_2}\pi _2^Y(y)\hbox {d}y + \int _{y_2}^s\pi _2^Y(y)\hbox {d}y \\&\quad +\, \int _s^{1/2}\pi _2^Y(y)\hbox {d}y + \int _{1/2}^{y_2+1/2}\pi _2^Y(y)\hbox {d}y +\int _{y_2+1/2}^{1-s}\pi _2^Y(y)\hbox {d}y + \int _{1-s}^1\pi _2^Y(y)\hbox {d}y \\& = \int _0^s\frac{(a-4ts+2ty_2+3s)^2}{9b}\hbox {d}x +\int _s^{1/2}\frac{(a-tx+2ty_2)^2}{9b}\hbox {d}x \\&\quad +\, \int _{1/2}^{y_2+1/2}\frac{(a-3tx+2ty_2+t)^2}{9b}\hbox {d}x +\int _{y_2+1/2}^{1-s}\frac{(a-t-2ty_2+tx)^2}{9b}\hbox {d}x \\&\quad +\, \int _{1-s}^{1-y_2}\frac{(a-4ts+3t-2ty_2-3tx)^2}{9b}\hbox {d}x +\int _{1-y_2}^1\frac{(a-4ts+2ty_2-t+tx)^2}{9b}\hbox {d}x \\&\quad +\, \int _0^{y_2}\frac{(a-2ty_2+ty+2ts)^2}{9b}\hbox {d}y +\int _{y_2}^s\frac{(a-3ty+2ty_2+2ts)^2}{9b}\hbox {d}y \\&\quad +\, \int _s^{1/2}\frac{(a-ty+2ty_2)^2}{9b}\hbox {d}y +\int _{1/2}^{y_2+1/2}\frac{(a-ty+2ty_2)^2}{9b}\hbox {d}y \\&\quad +\, \int _{y_2+1/2}^{1-s}\frac{(a-t+ty-2ty_2)^2}{9b}\hbox {d}y +\int _{1-s}^1\frac{(a-3t+ty-2ty_2+2ts)^2}{9b}\hbox {d}y \\& = \frac{8t^2y_2^3+6(3t-24ts+10a)ty_2^2+t^2(88s^3+1) +6a(2a-t-4ts^2)}{54b}{,} \end{aligned}$$

since

$$\begin{aligned} \frac{\partial \Pi _2}{\partial y_2}=\frac{2ty_2(10a-24ts+2ty_2+3t)}{9b}, \end{aligned}$$

which is monotonically increasing in $y_2$, because $a>2t$ and $s\le 1/4$. In other words, given $x_1=0$, firm 2 will choose $y_2=\delta$ when $y_2\in [0,\delta ]$. Therefore, $[x_1,y_2]=[0,0]$ cannot be an equilibrium.

1.2 Appendix 2: The proof that $[x_1,y_2]=[1/2,1/2]$ is not an equilibrium

Given $x_1=1/2$, $y_2\in [1/2-\delta ,1/2]$, and $\delta$ is small, we can show that it is profitable for firm 2 to deviate from $y_2=1/2$. The domestic market for both firms can be divided into six segments, and the nondomestic market can also be divided into six segments for further calculations as shown in Fig. 10. The profits for firm 1 and firm 2 at a location point x on market X are the same as Eqs. (24) and (25).

Fig. 10

The case when $x_1=1/2$ and $y_2\in [1/2-\delta ,1/2]$, $0\le \delta \le s$

After some calculations and given $x_1=1/2$, the total profit of firm 2 is

$$\begin{aligned} \Pi _2& = \int _0^s\pi _2^X(x)\hbox {d}x + \int _s^{1/2}\pi _2^X(x)\hbox {d}x +\int _{1/2}^{1-y_2}\pi _2^X(x)\hbox {d}x + \int _{1-y_2}^{1-s}\pi _2^X(x)\hbox {d}x \\&\quad +\, \int _{1-s}^{y_2+1/2}\pi _2^X(x)\hbox {d}x + \int _{y_2+1/2}^2\pi _2^X(x)\hbox {d}x + \int _0^s\pi _2^Y(y)\hbox {d}y + \int _s^{y_2}\pi _2^Y(y)\hbox {d}y \\&\quad +\, \int _{y_2}^{1/2}\pi _2^Y(y)\hbox {d}y + \int _{1/2}^{1-s}\pi _2^Y(y)\hbox {d}y + \int _{1-s}^{y_2+1/2}\pi _2^Y(y)\hbox {d}y + \int _{y_2+1/2}^1\pi _2^Y(y)\hbox {d}y \\& = \int _0^s\frac{(a-2ty+t/2+tx)^2}{9b}\hbox {d}x + \int _s^{1/2} \frac{(a-2ty_2+4ts+t/2-3tx)^2}{9b}\hbox {d}x \\&\quad +\, \int _{1/2}^{1-y_2}\frac{(a-2ty_2+4ts-tx-t/2)^2}{9b}\hbox {d}x + \int _{1-y_2}^{1-s}\frac{(a-9t/2+4ts+2ty_2+3tx)^2}{9b}\hbox {d}x \\&\quad +\, \int _{1-s}^{y_2+1/2}\frac{(a-tx+2ty_2-t/2)^2}{9b}\hbox {d}x + \int _{y_2+1/2}^1\frac{(a-2ty_2+3tx-5t/2)^2}{9b}\hbox {d}x \\&\quad +\, \int _0^s\frac{(a-2ty_2+ty+t/2)^2}{9b}\hbox {d}y + \int _s^{y_2} \frac{(a-2ty_2+3ty-2ts+t/2)^2}{9b}\hbox {d}y \\&\quad +\, \int _{y_2}^{1/2}\frac{(a-ty+2ty_2-2ts+t/2)^2}{9b}\hbox {d}y +\int _{1/2}^{1-s}\frac{(a-3ty+2ty_2+3t/2-2ts)^2}{9b}\hbox {d}y \\&\quad +\, \int _{1-s}^{y_2+1/2}\frac{(a-ty+2ty_2-t/2)^2}{9b}\hbox {d}y +\int _{y_2+1/2}^1\frac{(a+ty-2ty_2-t/2)^2}{9b}\hbox {d}y \\& = \frac{24a^2+6at-t^2-16t^2y_2^3+12(10a-7t+24ts) ty_2^2+24(4t-5a-12ts)ty_2}{108b} \\&\quad +\,\frac{24(11t-2a)ts^2+12(4a-5t)ts-176t^2s^3}{108b}. \end{aligned}$$

Since

$$\begin{aligned} \frac{\partial \Pi _2}{\partial y_2}=\frac{2t(2y_2-1)(5a-4t+t(12s-y_2))}{9b} <0, \quad \forall \; y_2\in \left[ \frac{1}{2}-\delta ,\frac{1}{2}\right] . \end{aligned}$$

In other words, given $x_1=1/2$, firm 2 will choose $y_2=1/2-\delta$ when $y_2\in [1/2-\delta ,1/2]$. Therefore, $[x_1,y_2]=[1/2,1/2]$ cannot be an equilibrium.

1.3 Appendix 3: The proof that $[x_1,y_2]=[1/4,3/4]$ is not an equilibrium

Given $x_1=1/4$ and $y_2\in [3/4,1-s]$, we can show that it is profitable for firm 2 to deviate from $y_2=3/4$. The X market can be divided into six segments ([0, s], [s, 1 / 4], $[1/4,1/2-s]$, $[1/2-s,3/4]$, $[3/4,1-s]$, $[1-s,1]$), and the Y market can also be divided into six segments ([0, s], $[s,y_2-1/2]$, $[y_2-1/2,s+1/2]$, $[s+1/2,y_2]$, $[y_2,1-s]$, $[1-s,1]$) as shown in Fig. 11. The profits for firm 1 and firm 2 at a location point x on market X are

$$\begin{aligned}&\pi _1^X=\left( a-b(q_1^X+q_2^X)-t|x-x_1|\right) q_1^X, \end{aligned}$$

(26)

$$\begin{aligned}&\pi _2^X=\left( a-b(q_1^X+q_2^X)-t\left( \min \{|s-y_2|+|x-s|,|(1-s) -y_2|+|x-(1-s)|\}\right) \right) q_2^X. \end{aligned}$$

(27)

Solving $\partial \pi _1^X/\partial q_1^X=0$ and $\partial \pi _2^X/\partial q_2^X=0$ simultaneously yields $q_1^X$ and $q_2^X$. The profits for firm 1 and firm 2 at a location y on market Y are

$$\begin{aligned}&\pi _1^Y=\pi _2^X=\left( a-b(q_1^Y+q_2^Y)-t\left( \min \{|s-x_1|+|y-s| ,|(1-s)-x_1|+|y-(1-s)|\}\right) \right) q_1^X. \end{aligned}$$

(28)

$$\begin{aligned}&\pi _2^Y=\left( a-b\left( q_1^Y+q_2^Y\right) -t|y-y_2|\right) q_2^Y. \end{aligned}$$

(29)

Solving $\partial \pi _1^Y/\partial q_1^Y=0$ and $\partial \pi _2^Y/\partial q_2^Y=0$ simultaneously yields $q_1^Y$ and $q_2^Y$.

Fig. 11

Two cases when $x_1=1/4$ and $y_2\in [3/4,1-s]$

After some calculations, given $x_1=1/4$, the total profit for firm 2 is

$$\begin{aligned} \Pi _2& = \int _0^s\pi _2^X(x)\hbox {d}x + \int _s^{1/4}\pi _2^X(x)\hbox {d}x + \int _{1/4}^{1/2-s}\pi _2^X(x)\hbox {d}x + \int _{1/2-s}^{3/4}\pi _2^X(x)\hbox {d}x \\&\quad +\, \int _{3/4}^{1-s}\pi _2^X(x)\hbox {d}x + \int _{1-s}^1\pi _2^X(x)\hbox {d}x + \int _0^{s}\pi _2^Y(y)\hbox {d}y + \int _{s}^{y_2-1/2}\pi _2^Y(y)\hbox {d}y \\&\quad +\, \int _{y_2-1/2}^{s+1/2}\pi _2^Y(y)\hbox {d}y + \int _{s+1/2}^{y_2} \pi _2^Y(y)\hbox {d}y + \int _{y_2}^{1-s}\pi _2^Y(y)\hbox {d}y + \int _{1-s}^1\pi _2^Y(y)\hbox {d}y \\& = \int _0^s \frac{(-2t+2ty_2+a+tx_1-3tx)^2}{9b}\hbox {d}x + \int _s^{1/4} \frac{(-2t+2ty_2+a+tx_1-3tx)^2}{9b}\hbox {d}x \\&\quad +\, \int _{1/4}^{1/2-s}\frac{(-2t+2ty_2+a-tx-tx_1)^2}{9b}\hbox {d}x + \int _{1/2-s}^{3/4}\frac{(-4t+4ts+2ty_2+a+3tx-tx_1)^2}{9b}\hbox {d}x \\&\quad +\, \int _{3/4}^{1-s}\frac{(-3t+4ts+2ty_2+a+tx+tx_1)^2}{9b}\hbox {d}x + \int _{1-s}^1\frac{(t+2ty_2+a-3tx+tx_1)^2}{9b}\hbox {d}x \\&\quad +\, \int _0^{s}\frac{(a-2t+2ty_2-3ty+tx_1)^2}{9b}\hbox {d}y + \int _{s}^{y_2-1/2}\frac{(a-2t+2ty_2-ty-2ts+tx_1)^2}{9b}\hbox {d}y \\&\quad +\, \int _{y_2-1/2}^{s+1/2}\frac{(a-2ty_2+3ty-2ts+tx_1)^2}{9b}\hbox {d}y + \int _{s+1/2}^{y_2}\frac{(a-2ty_2+ty+t+tx_1)^2}{9b}\hbox {d}y \\&\quad +\, \int _{y_2}^{1-s}\frac{(a-3ty+2ty_2+t+tx_1)^2}{9b}\hbox {d}y + \int _{1-s}^1\frac{(a-3ty+2ty_2+t+tx_1)^2}{9b}\hbox {d}y \\& = \frac{8t^2y_2^3}{27b} + \frac{(-384t^2s-96t^2)y_2^2}{432b} + \frac{(192ta+384t^2s^2-240t^2+960t^2s)y_2}{432b}. \end{aligned}$$

$$\begin{aligned} \frac{\partial \Pi _2}{\partial y_2} =\frac{t(-4ty_2+8ty_2^2-5t+4a+20ts-16ty_2s+8ts^2)}{9b}, \end{aligned}$$

which is monotonically increasing in $y_2$, since $\frac{\partial ^2\Pi _2}{\partial y_2^2} =\frac{4t^2(4y_2-4s-1)}{9b}>0$ by the assumptions $s\le 1/4$ and $y_2\ge 3/4$. Given $\left. \frac{\partial \Pi _2}{\partial y_2}\right| _{y_2=\frac{3}{4}}=\frac{t(8a-7t+16ts(1+s))}{18b}>0$, firm 2 will choose $y_2=1-s$ when $y_2\in [3/4,1-s]$. Therefore, $[x_1,y_2]=[1/4,3/4]$ cannot be an equilibrium.

1.4 Appendix 4: The proof that $[x_1,y_2]=[s,s]$ is not an equilibrium

Given $x_1=s$ and $y_2\in [s,s+\delta ]$, where $\delta$ is not large, we can show that firm 2 will choose $y_2^*=s$. Similarly, given $x_1=s$ and $y_2\in [0,s]$, we can also show that firm 2 will choose $y_2^*=s$. Given $x_1=s$ and $y_2=s$, we have $\Pi _2 =\frac{t^2+12a^2-6ta}{54b}$. Comparing this with the profit of firm 2 in Proposition 1, we have $\Pi _2(x_1=s,y_2=1-s) -\Pi _2(x_1=s,y_2=s)=\frac{16t^2s^2(3-8s)}{27b}>0$. Therefore, each firm locating at each of the intersecting points dominates the local solutions [s, s] or $[1-s,1-s]$ that both firms agglomerate at one intersecting point.