Abstract
This paper explores a linear and circular model with spatial Cournot competition. It is shown that agglomeration of firms at the center of the main street is the equilibrium when the demand density on the main street (linear market) is high, and there exists a unique separated location equilibrium when the density is moderate. Moreover, the socially desirable interior locations are more dispersed than the equilibrium ones. Finally, extensions on tax policies, nonlinear demand, non-uniform distribution, and others are also discussed.





Similar content being viewed by others
Notes
Ebina et al. (2011) consider a unit-length circular market with a caveat at point 0. An extra cost of amount \(\beta \in [0,1]\) is incurred when transporting across this point. If \(\beta \) is large and no firm transports across this point, then the market corresponds to a linear market. They showed that the location pattern in Pal (1998) only emerges when \(\beta =0\).
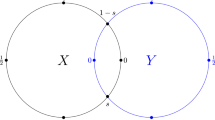
The “linear” segment and the “circular” segment are conceptual in this model, as a curved main street can still be represented as the linear segment under the condition that there is no fork road along this segment, except the two endpoints connected with a closed fork road with a \(\pi \) times longer than the linear segment.
Note that locations on the main street are dominant strategies for firms when \(\theta \) is not small, rather than the locations on the beltway. Intuitively, Pal (1998) has proved that in a pure circular market, firms locate at the two ends of a diameter in equilibrium. When there exists a main street connecting to the circular market, the main street diameter is superior to those of any other diameters. That is, firms will not choose to locate at the non-main street points. In fact, \(\theta \) is allowed to be less than one in our model, allowing for a country such as Australia where there is a difficult-to-traverse or less inhabited area in the middle. A threshold value for \(\theta \) is required to avoid both firms locating in the circular market. If \(\theta \) is sufficiently small, then any pair of endpoints along diameters is equilibrium locations a la Pal (1998). For instance, \((x_1=1/4,x_2=3/4)\) is (is not) an equilibrium when \(\theta <(>)\frac{2t\pi }{4\pi a+2t-t\pi }\le \frac{2\pi }{7\pi +10}\approx 0.1964\). Another justification is that real cities may enact business-residential zoning regulations, where only the main street is allowed to set up stores.
In fact, detailed analysis shows that firms will never choose locations outside the main street [0, L], because the centripetal force of the main street induces firms to move closer to the center. If \(\theta \rightarrow 0\), firms locate approaching [0, L] when we restrict locations on the main street. For locations \(y_1\le 0\) and \(y_2 \ge L\), dominant strategies for both firms are \(y_1=0\) and \(y_2=L\). Intuitively, moving to outside the main street will increase transport costs without any increase in demand.
This assumption of inverse demand functions implies that the demand density on the main street is \(\theta \) times higher than the density on the circular market, given equal prices.
Since \(\hat{x}_u\) and \(\hat{x}_d\) (\(\overline{x}_u\) and \(\overline{x}_d\)) are indifferent points for firm 1 (firm 2) either by clockwise shipping or by anti-clockwise shipping, we divide the market into six segments to ensure the shipping direction for each firm is unique in each interval, and thus, the quantities in each point can be determined.
In a mixed duopoly framework such as Matsushima and Matsumura (2003, 2006), there is one private firm competing with a welfare-maximizing public firm. If our model is replaced with mixed duopoly firms, it is expected that the equilibrium locations will become much closer to the socially optimal locations than in the current model. The intuition is that the distortion will be partially offset by this state-owned firm.
We sincerely thank three anonymous referees for pointing out some of these extensions.
We are grateful to one of the referees for pointing this out.
References
Anderson SP, Neven D (1991) Cournot competition yields spatial agglomeration. Int Econ Rev 32:793–808
Benassi C (2014) Dispersion equilibria in spatial Cournot competition. Ann Reg Sci 52:611–625
Chamorro-Rivas JM (2000) Spatial dispersion in Cournot competition. SpanEconRev 2:145–152
Colombo S (2015a) A model of three cities: the locations of two firms with different types of competition. International regional science review, forthcoming
Colombo S (2015b) Location choices with a non-linear demand function. Papers in regional science, forthcoming
Ebina T, Matsumura T, Shimizu D (2011) Spatial Cournot equilibria in a quasi-linear city. Pap Reg Sci 90:613–628
Gupta B, Lai FC, Pal D, Sarkar J, Yu CM (2004) Where to locate in a circular city? Int J Ind Organ 22:759–782
Hamilton J, Thisse JF, Weskamp A (1989) Bertrand vs. Cournot in a model of location choice. Reg Sci Urban Econ 19:87–102
Hwang H, Mai CC (1990) Effects of spatial price discrimination on output, welfare, and location. Am Econ Rev 80:567–575
Lambertini L (1997) Optimal fiscal regime in a spatial duopoly. J Urban Econ 41:407–420
Matsumura T, Matsushima N (2012) Spatial Cournot competition and transportation costs in a circular city. Ann Reg Sci 48:33–44
Matsumura T, Shimizu D (2005) Spatial Cournot competition and economic welfare: a note. Reg Sci Urban Econ 35:658–670
Matsushima N (2001) Cournot competition and spatial agglomeration revisited. Econ Lett 73:175–177
Matsushima N, Matsumura T (2003) Mixed oligopoly and spatial agglomeration. Can J Econ 36:62–87
Matsushima N, Matsumura T (2006) Mixed oligopoly, foreign firms, and location choice. Reg Sci Urban Econ 36:753–772
Pal D (1998) Does Cournot competition yield spatial agglomeration? Econ Lett 60:49–53
Pal D, Sarkar J (2002) Spatial competition among multi-store firms. Int J Ind Organ 20:163–190
Shimizu D (2002) Product differentiation in spatial Cournot markets. Econ Lett 76:317–322
Yu CM, Lai FC (2003) Cournot competition in spatial markets: some further results. Pap Reg Sci 82:569–580
Acknowledgments
We thank the Editor, and three anonymous referees for their valuable comments. All remaining errors are ours.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Proposition 1
Solving \(\partial R_1/\partial y_1=0\) and \(\partial R_2/\partial y_2=0\) yields two equilibrium location pairs. The first one is the agglomeration solution at the center of the main street such that \((y_1^*,y_2^*)=(\frac{1}{2\pi },\frac{1}{2\pi })\). The second one is a separated solution such that \((y_1^*,y_2^*)=(\frac{2\pi \theta a-4\pi a-2\pi t-t\theta +6t}{4(2+\theta )t\pi },\frac{4\pi a-2\pi \theta a+2\pi t+5t\theta +2t}{4(2+\theta )t\pi })\). We divide our proof into three cases for the validity of solutions.
-
1.
Since the first-order conditions \(\partial R_1/\partial y_1=\partial R_2/\partial y_2=0\) at \(y_1=y_2=L/2\), we should check the second-order conditions for the agglomeration solution:
$$\begin{aligned} \frac{\partial ^2 R_1}{\partial y_1^2}=\frac{\partial ^2 R_2}{\partial y_2^2}=\frac{-4t(2t-4\pi a-\pi t-2t\theta +2\pi \theta a)}{9\pi b}<0. \end{aligned}$$The above condition implies that \(\theta >\frac{4\pi a+\pi t-2t}{2(\pi a-t)}\equiv \theta _A^{{\textit{SOC}}}\) is required for \(\partial ^2 R_1/\partial y_1^2<0\) and \(\partial ^2 R_2/\partial y_2^2<0\). Moreover, the stability condition in location space \(\frac{\partial ^2 R_1}{\partial y_1^2}\cdot \frac{\partial ^2 R_2}{\partial y_2^2} -\frac{\partial ^2 R_1}{\partial y_1\partial y_2}\cdot \frac{\partial ^2 R_2}{\partial y_1\partial y_2} =\frac{16t^2(\theta -2)(2\pi a-t)((\theta -2)2\pi a-t(2\pi +3\theta -2))}{81b^2\pi ^2}\ge 0\), which implies \(\theta \ge \theta _A^*\), because \(\theta _A^{SOC}>2\) and \(\theta _A^*>2\).
-
2.
From the second solution, \((y_1^*=0,y_2^*=L)\) at the separate solution requires a boundary condition \(\theta \le \theta _\mathrm{Pal}^*=\frac{2(2\pi a+\pi t-3t)}{2\pi a-t}\).
-
3.
Plugging the separate locations into the second-order conditions yields \(\partial ^2R_1/\partial y_1^2=\partial ^2R^2/\partial y_2^2\) \(=-\frac{4(\pi +\theta )t^2}{9b\pi }<0\). In other words, the separate equilibrium locations always satisfy the second-order condition. However, \(y_1^*<L/2\) (or the same condition \(y_1^*<y_2^*\)) is required for this solution, which implies \(\theta <\theta _A^*=\frac{2(2\pi a+\pi t-t)}{2\pi a-3t}\). Moreover, the stability condition \(\frac{\partial ^2 R_1}{\partial y_1^2}\cdot \frac{\partial ^2 R_2}{\partial y_2^2} -\frac{\partial ^2 R_1}{\partial y_1\partial y_2}\cdot \frac{\partial ^2 R_2}{\partial y_1\partial y_2} =\frac{-16t^2(\theta -2)(2\pi a-t)((\theta -2)2\pi a-t(2\pi +3\theta -2))}{81b^2\pi ^2}\ge 0\) is satisfied here for \(\theta \le \theta _A^*\).
Therefore, we have proved Proposition 1. \(\square \)
1.2 Proof of Proposition 2
The interior solutions are valid when \(\theta _\mathrm{Pal}^*<\theta <\theta _A^*\). Differentiating \(y_1^*\) with respect to \(\theta \), a, and t yields
which proves Proposition 2. \(\square \)
1.3 Proof of Proposition 3
-
1.
Solving \(y_1^S=\frac{1}{2\pi }\) for \(\theta \) yields \(\theta =\frac{8\pi a+7\pi t-4t}{4\pi a-9t}=\theta _A^\mathrm{SW}\).
-
2.
Solving \(y_1^o=0\) for \(\theta \) yields \(\theta =\frac{8\pi a+7\pi t-18t}{2(2\pi a-t)}\).
-
3.
From the condition \(y_1^o>0\), the interior solution is valid when \(\theta _\mathrm{Pal}^\mathrm{SW}<\theta <\theta _A^\mathrm{SW}\).
\(\square \)
1.4 Proof of Proposition 4
-
1.
Solving \(\partial R_1/\partial y_1=0\) and \(\partial R_2/\partial y_2=0\) simultaneously yields two solutions: \((y_1^*,y_2^*)=(\frac{1}{2\pi },\frac{1}{2\pi })\) and \((y_1^*,y_2^*)=(\frac{2\theta \pi a-\theta t-3\pi t}{4\theta \pi t},L-y_1^*)\). The agglomeration solution is valid only when the second-order conditions \(\partial ^2 R_1/\partial y_1^2=\partial ^2 R_2/\partial y_2^2=\frac{-8t(\theta (\pi a-t)-\pi t)}{9\pi b}<0\), which leads to the condition \(\theta >\frac{\pi t}{\pi a-t}\). Furthermore, the stability condition implies \(\theta \ge \frac{3\pi t}{2\pi a-3t}\), which is greater than \(\frac{\pi t}{\pi a-t}\). Therefore, \(\theta \ge \frac{3\pi t}{2\pi a-3t}\) leads to the agglomeration solution.
-
2.
The dispersed solution is valid by the assumption \(a\ge 2t(1+\frac{1}{\pi })\). The second-order conditions for this solution are always valid since \(\partial ^2 R_1/\partial y_1^2=\partial ^2 R_2/\partial y_2^2=-\frac{4t^2(\pi +\theta )}{9\pi b}<0\). The endpoint solution \((y_1^*,y_2^*)=(0,L)\) is valid when this dispersed solution satisfies the corner solution, which implies \(\theta \le \frac{3\pi t}{2\pi a-t}\).
-
3.
The interior solution \(0<y_1^*<\frac{L}{2}\) implies the condition \(\frac{3\pi t}{2\pi a-t}<\theta <\frac{3\pi t}{2\pi a-3t}\). Finally, \(\partial y_1^*/\partial \theta =\frac{3}{4\theta ^2}>0\), \(\partial y_1^*/\partial a=\frac{1}{2t}>0\), \(\partial y_1^*/\partial t=-\frac{a}{2t^2}<0\) for the interior solution. \(\square \)