The fluidic pinball with symmetric forcing displays steady, periodic, quasi-periodic, and chaotic dynamics

Abstract

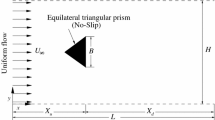
We numerically investigate the fluidic pinball under symmetric forcing and find seven flow regimes under different rotation speeds. The fluidic pinball consists of three rotatable cylinders placed at the vertices of an equilateral triangle pointing upstream in a uniform oncoming flow. The starting point is the unforced asymmetric periodic vortex shedding at Reynolds number Re = 100 based on the cylinder diameter. The flow is symmetrically actuated by rotating the two rear cylinders at constant speed |b| up to three times the oncoming velocity in both directions. Counterclockwise (b > 0) and clockwise (b < 0) rotation of the bottom cylinder correspond to boat tailing and base bleeding, respectively. A total of seven distinct flow regimes are observed, including a steady flow, three symmetric/asymmetric periodic types of shedding, two symmetric/asymmetric quasi-periodic behaviors, and a chaotic dynamics. The vortex shedding features multiple coupled oscillator modes, including in-phase, anti-phase, and out-of-phase synchronization and non-synchronization. These shedding regimes are analyzed employing the temporal evolution of the aerodynamic forces and a dynamical mode decomposition of the wake flow. The kaleidoscope of unforced and forced dynamics promotes the fluidic pinball as a challenging modeling and control benchmark.

Graphic abstract

Appendices

Transient and post-transient dynamics

In this work, we start numerical simulations from a steady solution with $\text {Re}=100$ and activate the actuation after $t=5$. This symmetric solution is one of three unstable steady solutions obtained by solving the steady Navier–Stokes equations [20]. As shown in Fig. 14, the unforced flow takes a long time to reach a stable post-transient regime, starting from the steady solution with a tiny initial perturbation. Before that, the transient flow successively undergoes the destabilization around the steady solution and the transition from the steady solution to the attracting set, associated with the nonlinear saturation of the instability of the system.

Fig. 14

Transient and post-transient dynamics of the unforced fluidic pinball at $\text {Re}=100$, illustrated by the temporal evolution of the resultant lift coefficient and representative snapshots. It has been divided into four regimes: (I) the steady solution, (II) the destabilization around the steady solution, (III) the transition from the steady solution to the attracting set, and (IV) the post-transient regime

Proper orthogonal decomposition

The flow is equidistantly sampled with a time interval $\Delta t$, yielding M velocity field snapshots $\varvec{u}^m (\varvec{x}):= \varvec{u}(\varvec{x}, t^m)$ at $t^m = m \Delta t, m = 1, \ldots , M$. The velocity field is decomposed into a base flow $\varvec{u}_0$ and the fluctuating contribution $\varvec{v}^m$,

$$\begin{aligned} \varvec{u}^m = \varvec{u}_0 + \varvec{v}^m, \end{aligned}$$

(B1)

where the base flow is defined as the time-averaged field in this work:

$$\begin{aligned} \varvec{u}_0 = \frac{1}{M} \sum _{m=1}^{M} \varvec{u}^m. \end{aligned}$$

(B2)

The inner product of two velocity fields $\varvec{v}$, $\varvec{w}$ in the observation domain $\Omega$ reads

$$\begin{aligned} \left( \varvec{v}, \varvec{w}\right) _\Omega = \int _\Omega d\varvec{x}\, \varvec{v}(\varvec{x}) \cdot \varvec{w}(\varvec{x}) . \end{aligned}$$

(B3)

The POD modes are computed with the snapshot method, i.e. require the correlation matrix $\textbf{C}$ of the fluctuating contribution. The elements of $\textbf{C}$ read

$$\begin{aligned} C^{mn} = \frac{1}{M} (\varvec{v}^m, \varvec{v}^n)_\Omega , \quad m,n = 1, \ldots , M. \end{aligned}$$

(B4)

The spectral decomposition of the positive semi-definite matrix $\textbf{C}$ yields non-negative eigenvalues $\lambda _i$, $i=1,\ldots ,M$ and orthogonal eigenvectors $\varvec{e}_i$,

$$\begin{aligned} \textbf{C} \varvec{e}_i = \lambda _i \varvec{e}_i, \quad i = 1, \ldots , M. \end{aligned}$$

(B5)

The ith normalized eigenvector has M components $\varvec{e}_i = \left[ e^1_i, e^2_i, \cdots , e^M_i\right] ^\intercal$. The ith POD mode is a linear combination of the fluctuations,

$$\begin{aligned} \varvec{u}_i = \frac{1}{\sqrt{M \lambda _i}} \sum _{m=1}^{M} e^m_i \varvec{v}^m, \end{aligned}$$

(B6)

and the corresponding temporal coefficients are rescaled eigenvectors of the correlation matrix,

$$\begin{aligned} a_i^m = {\sqrt{M \lambda _i}} \, e_i^m. \end{aligned}$$

(B7)

In the end, the fluctuating contribution is represented as the sum of spatial modes weighted by temporal coefficients. These modes are ranked according to their energetic contribution. A low-dimensional approximation $\varvec{\tilde{v}}^m$ of the fluctuating part $\varvec{{v}}^m$ reads

$$\begin{aligned} \varvec{\tilde{v}}^m = \sum _{i=1}^{N} a_i^m\, \varvec{u}_i, \end{aligned}$$

(B8)

where $N \le M$ is the selected number of leading POD modes.

The POD modes compress the velocity snapshots to N dimensions and minimize the representation error. As in Eqs. (B1) and (B8), the POD modes and the corresponding temporal coefficients allow for the linear reconstruction [70] of the flow field at any instant.

Dynamic mode decomposition

The state snapshot matrices $\textbf{Y}$ and $\textbf{Y}^\prime$ read,

$$\begin{aligned} \textbf{Y}= & {} \left[ \varvec{a}^1, \varvec{a}^2, \cdots , \varvec{a}^{M-1} \right] , \end{aligned}$$

(C9a)

$$\begin{aligned} \textbf{Y}^\prime= & {} \left[ \varvec{a}^2, \varvec{a}^3, \cdots , \varvec{a}^{M} \right] , \end{aligned}$$

(C9b)

where the snapshot matrices are of size $N \times (M-1)$.

We assume that the time step $\Delta t$ is small enough for a linear discrete dynamics where $\varvec{a}^{m+1}$ can be obtained from the current state $\varvec{a}^m$ by a full-state mapping matrix $\textbf{A} \in \mathcal {R}^{N \times N}$,

$$\begin{aligned} \varvec{a}^{m+1} = \textbf{A} \> \varvec{a}^m. \end{aligned}$$

(C10)

We also assume that the matrix $\textbf{A}$ does not change with increasing time. The latter assumption is legitimate for the considered post-transient regimes where DMD approximates a Fourier analysis. Such time-invariant linear dynamics are clearly invalid for transients from steady to unsteady solutions [65].

Equation (C10) implies for Eq. (C9)

$$\begin{aligned} \textbf{Y}^\prime = \left[ \textbf{A} \varvec{a}^1, \textbf{A} \varvec{a}^2, \cdots , \textbf{A} \varvec{a}^{M}\right] = \textbf{A} \textbf{Y}. \end{aligned}$$

(C11)

When the time step is small enough, the system can satisfy this linear approximation.

We can optionally find a low-rank $r < M-1$ projection of the full-state $\textbf{A}$ by singular value decomposition,

$$\begin{aligned} \textbf{Y} = \textbf{U} \varvec{\Sigma } \textbf{V}^\intercal , \end{aligned}$$

(C12)

where $\textbf{U}$ and $\textbf{V}$ are square unitary matrices of sizes $N \times N$ and $(M-1) \times (M-1)$, the superscript ‘$\intercal$’ indicates the transpose, and $\varvec{\Sigma }$ is an $N \times (M-1)$ rectangular diagonal matrix. For the low-rank projection, we keep the first r columns of $\textbf{U}$ and $\textbf{V}$ and the first $r \times r$ elements in $\varvec{\Sigma }$, then the approximated matrix $\widetilde{\textbf{A}}$ of the full-state $\textbf{A}$ is

$$\begin{aligned} \widetilde{\textbf{A}} = \textbf{U}^\intercal \textbf{A} \textbf{U}, \end{aligned}$$

(C13)

which can be seen as the least-squares fit or minimum-norm solution of $\textbf{A}$ for $\textbf{Y}^\prime = \textbf{A} \textbf{Y}$,

$$\begin{aligned} \mathop {\text {min}}\limits _{\widetilde{\textbf{A}}} \Vert \textbf{Y}^\prime - \textbf{U} \widetilde{\textbf{A}} \varvec{\Sigma } \textbf{V}^\intercal \Vert _2 , \end{aligned}$$

(C14)

then, $\widetilde{\textbf{A}}$ can be written as,

$$\begin{aligned} \widetilde{\textbf{A}} = \textbf{U}^\intercal \textbf{Y}^\prime \textbf{V} \Sigma ^{-1}. \end{aligned}$$

(C15)

The eigenvalues $\varvec{\Lambda }$ and eigenvectors $\textbf{W}$ are obtained by eigendecomposition of $\widetilde{\textbf{A}}$:

$$\begin{aligned} \widetilde{\textbf{A}} \textbf{W} = \textbf{W} \varvec{\Lambda }. \end{aligned}$$

(C16)

The diagonal elements of $\varvec{\Lambda }$ are Ritz eigenvalues $\mu _j$, $j = 1, \ldots , r$. The $\mu _j$ are used to calculate the growth rate $\sigma _j = \textrm{Re} (\ln \mu _j / \Delta t)$ and the oscillating frequency $\omega _j = \textrm{Im} (\ln \mu _j / \Delta t)$. The DMD modes are the columns of the matrix $\varvec{\Phi }$ of size $N \times r$, which can be computed by,

$$\begin{aligned} \varvec{\Phi } = \textbf{Y}^\prime \textbf{V} \varvec{\Sigma }^{-1} \textbf{W}. \end{aligned}$$

(C17)

Finally, the spatial velocity field of DMD modes is reconstructed following Eq. (B8), by using the DMD mode as the temporal coefficients of the leading N POD spatial modes $u_i$, which reads

$$\begin{aligned} \varvec{u}^\textrm{DMD}_j = \sum _{i=1}^{N} {\Phi }_{i, j}\, \varvec{u}_i . \end{aligned}$$

(C18)

Figure 15 depicts the eigenvalues obtained from the DMD analysis for varying values of b in the range $\left[ -3, 2\right]$. The real and imaginary parts of the eigenvalues are represented along the horizontal and vertical axes, respectively. The eigenvalues corresponding to the vortex-shedding frequency are marked with red dots. Notably, for the chaotic and quasi-periodic cases, the eigenvalues corresponding to the base-bleeding jet frequency are marked with blue dots.

Fig. 15

Eigenvalues for varying $b \in \left[ -3, 2\right]$, with (a) $\sim$ (l) similar to Fig. 5. The real and imaginary parts of the eigenvalues are shown along the horizontal and vertical axes, respectively. The red points represent eigenvalues related to the vortex shedding, and the blue points correspond to the base-bleeding jet eigenvalues. The corresponding modes are plotted in Figs. 11, 12 and 13 (colour figure online)

As illustrated in Fig. 5, the power spectral density (PSD) curves of the lift coefficient exhibit a harmonic series of peaks. The dominant peak and the lowest peak align with the vortex-shedding frequency and the base-bleeding jet frequency, respectively. Further insight into the eigenvalue distribution is presented in Fig. 15, where the real and imaginary parts of the eigenvalues are plotted. The points falling outside the unit circle have positive growth rates, indicating divergence and instability. The points falling inside have negative growth rates, indicating convergence and stability, and the points on the circle have zero growth rates, indicating stability. Most of the points lie very close to the unit circle in the spectrums. The eigenvalues associated with the characteristic frequencies are marked with red points on the unit circle, calculated as $\omega _j=2\pi f_j$. Each frequency is represented by two points on the DMD modal eigenvalue distribution, sharing the same real part and opposite imaginary parts. The eigenvalues of the extracted modes cluster around the unit circle, indicating their stability. In particular, for a higher rotation speed $\left| b \right|$, more points fall within the unit circle, signifying faster convergence to a stable state.