Fluid flow past a freely moving body in a straight or distorted channel

Abstract

The focus here is on a thin solid body passing through a channel flow and interacting with the flow. Unsteady two-dimensional interactive properties from modelling, analysis and computation are presented along with comparisons. These include the effects of a finite dilation or constriction, as the body travels through, and the effects of a continuing expansion of the vessel. Finite-time clashing of the body with the channel walls is investigated as well as the means to avoid clashing. Sustained oscillations are found to be possible. Wake properties behind the body are obtained, and broad agreement in trends between full-system and reduced-system responses is found for increased body mass.

Graphical abstract

1 Introduction

This paper addresses the interactive effects associated with a thin body that is free to move in the flow of the surrounding fluid within a channel. The background for the present work mainly concerns industrial and biomedical applications such as in problems on firing of bullet-like bodies in a defence context and the entry of objects into engine intakes in an aerodynamic safety context [1,2,3], the travel of solids within vessels of major networks in the human body, the transport of blood clots, and embolisation procedures in stroke treatment in a biomedical context [4,5,6]. Another possible practical use of the current research is in development of a body-transport approach to trace any weaknesses in an arterial wall or other containing wall. The internal transient movement of the body through an artery makes a weak part of an artery wall change shape (due to the weak part being more elastic) and hence show up in a clinical scan. Practical interests also exist in industry, biomedical, environmental and engineering problems with constrictions and branchings especially in respect to the medical aspect in terms of flow blockage and disease initiation. An example is in predicting where a thrombus becomes stuck in an artery, or where a loose shard entering an aircraft engine intake eventually hits the engine walls and can cause damage there.

A number of studies have addressed fluid-body interaction by means of direct simulations and, in a few cases, experiments [7,8,9,10,11,12,13,14,15]. Our concern is more on the analytical side. The present study of the body and fluid flow inside a channel is based on [16, 17]. The body considered here is relatively thin and free to move along a channel in which fluid is travelling. The channel has an indentation (constriction or dilation) which is either of prescribed shape or is due to wall flexibility. In [16] interactions between a finite number of infinitesimally thin moving bodies or grains and the surrounding fluid within a straight-walled channel are analysed in detail together with the instability about the uniform state. The grains there are straight and free to move in a nearly parallel configuration in quasi-inviscid fluid, the combined motion being assumed to be planar. Smith et al. [17] considers a single body having thickness or camber (or both) interacting with the flow in a straight-walled channel. Another aspect of theoretical investigation on collisions, bouncing and skimming, e.g. shallow-water skipping in fluid-body or fluid-fluid impacts, is given in [18,19,20]. Moreover, most of the research in this area has been for two spatial dimensions ($x,\, y$, say) and time (t) but a recent work [21] has included three spatial dimensions (thus $x,\, y, \,z$ as well as time t). The current contribution has almost the same interaction structure as in [17] with the new piece here being on the unsteady interactions between a body and the fluid flow past it, inside an indented (constricted or dilated) channel. The indentation is either a given shape or an unknown shape due to flexibility involving the combined effect of the fluid pressure in the respective gap and the external pressure. The present investigation involves numerical and analytical studies as well as comparisons between the two.

Clashes are significant events. The typical clash occurs either near the leading edge of the body as in [16] or near the mid-body region as in [17]. The majority of the cases are found to yield a solid–solid clash within a finite scaled time as in [17]: see also the reviews in [22, 23]. The effects of an indentation in the containing channel and of flexibility in the wall of the channel on this phenomenon are to be investigated. Clashes within a viscous fluid are also examined in recent work [24,25,26,27]. We focus however on a basic nonlinear problem assuming in effect oncoming plug flow in the undisturbed part of the channel; strictly this corresponds to the local fluid being already in motion prior to the body travelling through it. See Fig. 1. Our aim is to understand and provide predictions for configurations such as that in the figure, as well as tackling major analytical issues and the possibility of some continued oscillations arising between the freely moving body and the surrounding fluid flow. Again, recent analytical work [28,29,30] implies that significant body oscillations may occur within a fluid-body interaction under certain conditions such as for a front-heavy body; we intend to study this possibility here.

The layout of the paper is as follows: Section 2 describes the motion of a thin heavy body with or without camber passing through, and interacting with, the fluid in a straight channel. This is followed by Sect. 3 which describes an analysis-based reduced system obtained for increased mass and moment of inertia and gives comparisons with the full solutions of the previous section. Oscillations are also discussed. Detailed wake effects are examined in Sect. 4. The influences of distortions in the channel walls are addressed in Sect. 5, while Sect. 6 presents final discussion points and conclusions.

Fig. 1

a Sketch in non-dimensional form of a body moving with axial velocity B through a fixed channel (with an indentation shown); the overtaking fluid has uniform velocity $1 + B$. Here, undisturbed channel width $H_0 = 1$. b As in (a) but in the reference frame wherein the body is fixed: so the indentation moves upstream in relative terms if $B > 0$ but downstream if $B < 0$. (The case $B = -1$ corresponds to the body travelling into fluid at rest.)

2 The straight configuration: numerical solutions

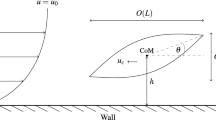
The concern in this section is with a single body which is thin but with, in general, nonzero thickness or camber (or both) and moving through fluid in a straight-walled channel as drawn in Fig. 2. With a subscript ${\mathcal {D}}$ denoting a dimensional quantity, the nondimensionalisation applied is based on the channel width $L_{\mathcal {D}}$, oncoming fluid flow velocity $U_{\mathcal {D}}$, pressure $p_{\mathcal {D}}$ and fluid density $\rho _{{\mathcal {D}}{\mathcal {F}}}$, while the body length is $L_{\mathcal {D}}/{\mathcal {E}}$ say with ${\mathcal {E}}$ being small. The interactions between body and fluid assume that the fluid is in effect inviscid and incompressible and the entire motion with unknown velocity components $U_{\mathcal {D}} (u, {\mathcal {E}}v)$ takes place in a two-dimensional $L_{\mathcal {D}} (x / {\mathcal {E}}, y)$ plane. The body is taken to have its angles of inclination during motion being of the same small order, ${\mathcal {E}}$, as those of the containing channel. The angle $\theta$ shown in figure 2 is scaled such that the real angle is ${\mathcal {E}} \theta$, yielding typical slopes $\tan ({\mathcal {E}} \theta ) \sim \sin ({\mathcal {E}} \theta ) \sim {\mathcal {E}} \theta$, a property which is used in the formulation below.

Fig. 2

The body having both thickness and camber at a general position and orientation in the flow, with fluid-filled gaps 1, 2. Here, h is y-position of the body centre of mass (CoM) measured from the lower wall; also $f_1=0, \, f_2 = 1$. The chord line, being the straight line through the leading and trailing edges, makes a small angle $\theta$ with the x-axis. The incident velocity $u_0 = 1$

The main objective is to examine a model for nonlinear interactions with a single body (occupying $0 \le x \le 1$) of uniform density $\rho _{{\mathcal {D}}{\mathcal {B}}}$ contained within side walls. Two-way nonlinear interaction takes place simply because the fluid dynamical forces lead to body movement which in turn affects the fluid motion. The background governing equations for the fluid are the continuity and Navier–Stokes equations and for the body are those of rigid body motion. The flow equations, given the above assumptions on thinness and the absence of incident vorticity, become the thin-layer system

$$\begin{aligned} H_{nt} + (H_n u_n)_x = 0 \quad \text{ and } \quad u_{nt} + u_n u_{nx} = - p_{nx}, \end{aligned}$$

(2.1)

for $n=1, \,2$. Here, $H_n$ are the unknown thicknesses of the two fluid-filled gaps between the body surface and the walls, whereas $u_n$ and $p_n$ represent the corresponding unknown velocities and pressures in each region. The incident velocity is $u_0 = 1$ and the scaled pressure is zero upstream of the leading edge, without loss of generality. The system here applies for $0 \le x \le 1$ as, due to the drag force being relatively small, the axial velocity of the thin body is constant; this constant is zero in the current frame of reference. The body occupies the region

$$\begin{aligned} f^-(x,\, t)< y <f^+(x,\, t), \quad x \in [0, \,1], \end{aligned}$$

(2.2)

where $y = f^\pm (x, \, t)$ are the curves of the upper $(+)$ and lower $(-)$ surfaces of the body as it moves. At the leading and trailing edges, for closure,

$$\begin{aligned} f^-(0,\, t) = f^+(0,\, t) \quad \text{ and } \quad f^-(1,\, t) = f^+(1,\, t). \end{aligned}$$

(2.3)

The overall mass-conservation balance requires

$$\begin{aligned} \sum _{i=1}^2 u_i(1\text{- },\,t) H_i(1\text{- },\,t) = 1, \end{aligned}$$

(2.4)

by virtue of the incident conditions ahead of the body. Here, in more explicit form, the values

$$\begin{aligned} H_1&= h(t) + F_1(x) + (x-a) \theta (t) , \end{aligned}$$

(2.5a)

$$\begin{aligned} H_2&= 1 - h(t) - F_2(x) - (x-a) \theta (t) \end{aligned}$$

(2.5b)

are the thicknesses of the regions of fluid flow between the lower wall of the channel and the lower surface of the body, and between the upper wall of the channel and upper surface of the body, respectively. Thus, $f^+ = F_2(x) + h(t) +(x - a) \theta (t)$ and $f^- = F_1(x) + h(t) + (x - a) \theta (t)$. We allow the body to have arbitrary shape, with underbody and overbody shapes (when not moving) given by $y = F_1(x) = C(x) - T(x)/2$ and $y = F_2(x) = C(x) + T(x)/2$ with C(x) and T(x) being camber and thickness of the body, in turn. Note that C(x) can be negative or positive. The condition at the body’s trailing edge is in effect the Kutta condition requiring the flow to be smooth and this imposes on the fluid flow the constraint

$$\begin{aligned} p_1(1\text{- }, \, t) = p_2(1\text{- },\, t) = \pi _e(t) \end{aligned}$$

(2.6)

as another boundary condition, with the pressure value $\pi _e(t)$ being an unknown function of t. In order for the Kutta condition on $p_n(1\text{- }, \,t )$ to be enforced at the trailing edge (TE), the interactive system requires the existence of a short Euler region of quasi-steady flow surrounding the leading edge (LE), in consequence of which we have

$$\begin{aligned} p_n(0+, \, t) + \frac{1}{2} u_n^2(0+, \, t) = \frac{1}{2} \end{aligned}$$

(2.7)

from the Bernoulli theorem. The Kutta condition applies as each region of fluid flows enter into the common wake, requiring the pressures across the two gap regions to be equal there, whereas the velocities are unequal generally, thus allowing vortex sheets into the common wake. The fluid dynamical part of the interactive motion has thus been described.

To determine the body motion equations, we neglect gravity and we should also note that the main force driving the body motion is the pressure force due to the fluid flow. Thus,

$$\begin{aligned} M h_{tt} = \int _0^1 (p_1 - p_2) \,dx, \quad I \theta _{tt} = \int _0^1 (x-a) (p_1 - p_2) \,dx = \tau . \end{aligned}$$

(2.8)

Here, $\tau$ is the torque applied on the body by the fluid flow, while $\theta _{tt}$ and $h_{tt}$ represent the angular acceleration and linear acceleration in the positive y-direction, respectively. Also M and I represent the scaled non-dimensional mass and moment of inertia of the body, respectively, with I being at most M/4 for physical sense, while a($=1/2$ in this section) is the x-position of the centre of mass. Here, $M, \,I, \,u_0$ and $F_1(X), \,F_2(x)$ are treated as given, and we intend to solve for the behaviour of the body, i.e. h and $\theta$ as functions of time.

Numerical solutions of the dynamic fluid-body interaction were derived using the method detailed in [16, 17, 31] among others. Figure 3 shows numerical evolutions of the system (2.1)–(2.8) for the body’s leading and trailing edge positions and $\theta , \, {{\dot{\theta }}}$ for increasing M and I values in a straight channel. The body has a sinusoidal nonzero thickness. The initial conditions are $(h, \, h_t, \,\theta , \, \theta _t) = (0.5, \,0, \, 0.1, \,0)$. The early motion is dominated by a linear increase in $\theta$. The figure suggests that the resulting lift-induced migration to the wall and angular acceleration affect the flow more slowly for heavier bodies. The impact time was found as $2.3832, \; 3.0278, \; 3.4330$ for $M=2, \; 6, \; 10$, respectively. We now present an analysis for the effect of the enhanced mass and moment of inertia and of the centre of mass position on the fluid and body motions.

Fig. 3

a Body leading edge (LE) and trailing edge (TE) positions for $M=2, \;6,\;10, \;I=M/5$ and thickness $T(x) = 0.4 \sin (\pi x)$, camber $C(x) = 0$, b angle $\theta$, angular velocity ${{\dot{\theta }}}$

3 Analysis for the straight case

The computational results of the previous section point to some relevant new analysis in the present section concerning successively the effects of enhanced mass, reduced ratio of moment of inertia to mass and positional variation of the centre of mass.

First however, given that uniform flow with zero pressure variation constitutes an exact solution of the interaction system for the case of an aligned flat plate in the middle of the channel, small perturbations from the uniform state are of interest. These take the form

$$\begin{aligned} (H, u, p) = \left( \dfrac{1}{2}, \,1, \,0\right) + O(\delta ), \end{aligned}$$

(3.1a)

with $\delta \ll 1$. Substitution [16, 23] into the full system leaves at leading order linearised equations and conditions for the $O(\delta )$ perturbations in (3.1a). When the body thickness is negligible, the time-dependence becomes exponential, proportional to exp(Qt) say. Thus, (2.1) then yields, at order $\delta$, the ordinary differential equation

$$\begin{aligned} Q \ H_n^+ + \frac{d}{dx} H_n^+ + \frac{d}{dx} u_n^+ = 0, \end{aligned}$$

while (2.8) gives the integral constraints

$$\begin{aligned} Q^2 M \ h^+= & {} \int _0^1 (p_1^+ - p_2^+) \ dx, \\ Q^2 I \ \theta ^+= & {} \int _0^1 (x-a) \ (p_1^+ - p_2^+) \ dx, \end{aligned}$$

where $(H_n^+, u_n^+) \exp (Qt)$ are the $O(\delta )$ perturbations in (3.1a). Similar working applies for the other quantities with superscripts $`+'$ and for the linearised versions of (2.4)–(2.7). We are led to an eigenvalue equation for the constant Q, namely

$$\begin{aligned}{} & {} Q^2 \ \bigg \{ (3M+1) \bigg ( I+\dfrac{1}{180} \bigg ) Q^3 + \bigg ( 3MI \ + \ \dfrac{M}{10} \nonumber \\{} & {} \quad + \ 4I \ + \ \dfrac{1}{20} \bigg ) Q^2 - \bigg ( \dfrac{M}{2} - 6I - \dfrac{1}{5} \bigg ) Q + \bigg (\dfrac{1}{3} - M \bigg ) \bigg \} = 0. \end{aligned}$$

(3.1b)

The main concern here is in the cubic form inside the curly brackets, rather than the presence of two zero-Q roots (from the $Q^2$ factor outside) which are associated with uniform translation. Plots in [23] of the cubic form in the left-hand side of (3.1b) establish that for any $M > 1/3$, there is a single eigenvalue with a positive real part, due to the signs of the terms in (3.1b). The fact that this eigenvalue is O(1) indicates the modelled interaction exhibits instability but only over the time scale of the complete interaction, not over shorter or longer time scales. See [16, 23]. In addition, there is much current interest in the response for large $M, \ I$ values with $M, \ I$ remaining comparable. Here, (3.1b) shows that the relevant Q root then tends to zero, with

$$\begin{aligned} Q \sim (3 I)^{-1/2} \quad \text{ for } \quad M \sim I \gg 1. \end{aligned}$$

(3.1c)

The finding (3.1c) suggests three features, specifically that the evolution slows down as $M, \ I$ are increased, which makes sense physically, that the typical time scale increases like $M^{1/2}$ and that the variation of $\theta$ may come to dominate. These analytical features combine with the computations above to guide the following analysis.

3.1 Behaviour for large mass

If the mass M is large and the moment of inertia I is comparable with M, then the typical time scale t increases, as implied by Q becoming small in the linear result (3.1c). In the nonlinear regime, the time scale can be seen to grow like $M^{1/2}$ in view of the mass-acceleration-force balance in (2.8), given that when h is of order unity the velocity and pressure responses are likely to be also of order unity, which requires $M/t^2$ to be O(1). Similar reasoning applies to the rotation motion balance. Hence, $t = M^{1/2} t^*$ say, with $t^*$ of order unity, and taking the initial conditions to involve no substantial velocities $dh/dt, \, d \theta /dt$ (e.g. for a body starting from rest) we have the expansion

$$\begin{aligned} (h, \theta , \ u, \ p) = (h^*, \theta ^*, u^*, p^*) + \dots \end{aligned}$$

(3.2)

with the scale of x and the body surface shapes remaining typically of O(1). The velocities $dh/dt, \ d \theta /dt$ just mentioned are of order $M ^{-1/2}$ and hence small. It follows that the fluid flow part of the whole interaction becomes quasi-steady; at leading order the governing equations of the flow remain as in (2.1) but with the time derivatives omitted and with asterisks inserted as per (3.2). Therefore, the flows in the two gaps for $n=1, \,2$ are described by

$$\begin{aligned} u_n^*H_n^*&= d_n^*(t^*) = \frac{ {{H_n}^*}_{TE} }{ H_0} , \end{aligned}$$

(3.3a)

$$\begin{aligned} p_n^*&= \frac{1}{2} \left\{ \frac{1}{H_0^2} - \frac{ {d_n^*}^2 }{ {{H_n}^*}^2 } \right\} , \end{aligned}$$

(3.3b)

from the quasi-steady mass conservation and Bernoulli property. Here, the functions $d_n^*(t^*)$ depend only on the scaled time $t^*$ as in (3.3a), the subscript TE denotes evaluation at the trailing edge $x = 1$ and, to clarify, the gap widths are $H_1^*(x, t^*) = f ^- - f_1, \, H_2^*(x, t^*) = f_2 - f^+$ while in the present context $H_0 = 1, \, f_1 =0, \, f_2 = 1$. Thus,

$$\begin{aligned} H_1^*(x, t^*) = F_1(x) + h^*(t^*) + (x - a) \theta ^*(t^*), \quad H_2^*(x, t^*) = 1 - F_2(x) - h^*(t^*) - (x - a) \theta ^*(t^*).\qquad \end{aligned}$$

(3.3c)

The reduced system here then comprises (3.3a)–(3.3c) combined with the body motion part of the interaction in the form

$$\begin{aligned} \frac{ d^2 h^*}{ {dt^*}^2 }&= \int _0^1 (p_1^*- p_2^*) \,dx , \end{aligned}$$

(3.3d)

$$\begin{aligned} I^*\frac{ d^2 \theta ^*}{ {dt^*}^2 }&= \int _0^1 (x - a) (p_1^*- p_2^*) \, dx . \end{aligned}$$

(3.3e)

Here, $I^*$ denotes the I/M body ratio of the moment of inertia relative to the mass.

Solutions of the reduced system (3.3a)–(3.3e) are presented in Fig. 4. (Here and in certain other figures below, the dots typically indicate every 50th data point, for clarity of presentation.) Comparisons with the full numerical results prove to be useful and are also included in that figure. In Fig. 4, numerical results are shown for the evolutions of $h, \ \theta$ obtained from the full and the reduced systems for a flat-plate body. The agreement is evident in terms of the trends of the evolution curves as $M, \ I$ increase.

Fig. 4

Evolutions of $h, \ \theta$ from the full system (with unsteady fluid and body motion) for M of $16, \ {36, \ 256}$ and from the reduced system (steady fluid flow), plotted against scaled time $t^*= M^{- 1/2} t$. This is for a flat-plate body in a straight channel, with $I = M/5$ throughout. Dots indicate every 50th data point

3.2 Small ratio of moment of inertia to mass

Here, we suppose additionally that the ratio $I^*$ is small. Then, because of the balances of contributions in (3.3e), the time scale $t^*$ decreases accordingly such that $t^*= {I^*}^{1/2} t^{**}$ say with $t^{**}$ being of O(1). This assumes the two gap pressures remain characteristically of order unity, from reasoning as in Sect. 3.1. So the controlling Eqs. (3.3d) and (3.3e) become

$$\begin{aligned} \frac{ d^2 h^*}{ {dt^{**}}^2 }&= 0 , \end{aligned}$$

(3.4a)

$$\begin{aligned} \frac{ d^2 \theta ^*}{ {dt^{**}}^2 }&= \int _0^1 (x - a) (p_1^*- p_2^*) dx , \end{aligned}$$

(3.4b)

to leading order. The first equation gives simply

$$\begin{aligned} h^*(t^{**}) = h^*(0) + t^{**} \frac{dh^*}{dt^{**} } (0) \end{aligned}$$

(3.5)

explicitly and so, on use of (3.3b) for the pressures, we are left with the single equation

$$\begin{aligned} \frac{ d^2 \theta ^*}{ {dt^{**}}^2 } = \frac{1}{2} \int _0^1 (x - a) \left\{ \frac{{H_2^*(1, \, t^{**})}^2 }{ {H_2^*(x, \, t^{**})}^2 } - \frac{{H_1^*(1, \, t^{**})}^2 }{ {H_1^*(x, \, t^{**})}^2 } \right\} dx \end{aligned}$$

(3.6)

which acts as an integro-differential equation for the scaled angle $\theta ^*(t^{**})$. In (3.6), the terms $H_n^*(x, \, t^{**})$ are given by (3.3c) with $t^*$ replaced by $t^{**}$ but with $h^*$ prescribed by the known form (3.5) as well as the body shapes $F_1(x), \, F_2(x)$ being known.

In the basic case of a flat-plate body $F_1(x), \, F_2(x)$ are zero. If in addition the initial velocity $dh^*/ dt^{**}(0)$ is zero then, with the constant $h^*(0)$ written as $\beta$ for convenience, the terms inside the integral on the right-hand side of (3.6) simplify somewhat since

$$\begin{aligned} H_1^*(x, t^{**}) = \beta + (x - a) \theta ^*(t^{**}), \quad H_2^*(x, t^{**}) = 1 - \beta - (x - a) \theta ^*(t^{**}). \end{aligned}$$

(3.7)

The integral, which can be worked out analytically [32], is somewhat unwieldy, and as an alternative a straightforward numerical treatment can be applied to the reduced form (3.3a)–(3.3e). The solutions of interest which are shown in Fig. 5 highlight that impact with one of the walls can still occur in this regime but also the beginnings of oscillations of $\theta ^*$ with respect to time $t^{**}$ are seen under certain conditions. The solutions for $h, \ \theta$ in Fig. 5 hint at the possibility of oscillatory solutions, in the sense that when the centre of mass is moved forward on the body an undulation appears in the results and this acts to delay the impact with the channel wall.

Fig. 5

Solutions of the reduced form (3.3a)–(3.3e) for $h, \ \theta$ vs $t^*$ when the centre of mass location $x = a$ is varied from 0.5 to 0.1. Here, $I^*(= I / M) = 0.2$ Vertical lines indicate a wall-body clash

3.3 Oscillations

The intriguing property of oscillations arising comes to the fore especially when the centre of mass ‘a’ is varied. A linearised analysis (given below) first shows this and indicates a critical value of $a = a_c = 1/3$ for the switch to oscillatory behaviour, as follows. The linearised analysis corresponds to the scaled angle $\theta ^*$ in (3.6) being assumed to be small, with the constants $\beta ,\ a$ remaining of O(1) in general. Hence in view of (3.7), the following expansions are implied,

$$\begin{aligned} \theta ^*(t^{**})&= \epsilon {{\bar{\theta }}} (t^{**}) + \dots , \end{aligned}$$

(3.8a)

$$\begin{aligned} H_1^*(x, t^{**})&= \beta + \epsilon (x - a) {{\bar{\theta }}} (t^{**}) + \dots , \end{aligned}$$

(3.8b)

$$\begin{aligned} H_2^*(x, t^{**})&= 1 - \beta - \epsilon (x - a) {{\bar{\theta }}} (t^{**}) + \dots , \end{aligned}$$

(3.8c)

where $\epsilon \ll 1$ is a measure of the size of $\theta ^*$, leaving ${{\bar{\theta }}} (t^{**})$ of order unity. Substitution into (3.6) leads to the linear equation

$$\begin{aligned} \frac{d^2 {{\bar{\theta }}} }{{dt^{**}}^2} = \frac{ {{\bar{\theta }}} }{ ( \beta (1 - \beta ))} \int _0^1 (x - a) (x - 1) dx, \end{aligned}$$

(3.9a)

from which the form

$$\begin{aligned} \frac{d^2 {{\bar{\theta }}}}{{dt^{**}}^2} = \frac{1}{2} \bigg (a - \frac{1}{3} \bigg ) \frac{{{\bar{\theta }}} }{(\beta (1 - \beta ) )} \end{aligned}$$

(3.9b)

is obtained. Here, (3.9b) confirms the critical value as $a_c = 1/3$. If $a > a_c$, then the small disturbance grows exponentially in $t^{**}$, whereas if $a < a_c$ then small oscillations are predicted: the frequency of such oscillations increases when the body is placed close to either wall where the value of $\beta$ is near zero or unity. (This is a matter taken further in Sect. 6.) Nonlinear solutions then support the finding. See Figs. 6 and 7. Figure 6 shows the response over the $t^{**}$ time scale with h remaining at its initial value of 0.5 throughout and $\theta$ gradually increasing, in Fig. 6a, such that the flat-plate body clashes with the upper and lower walls almost simultaneously at a $t^{**}$ value of about 4.5, in Fig. 6b; the leading edge impacts on the lower wall and the trailing edge on the upper. The impact is indicated by the vertical line in Fig. 6a. In Fig. 7, the centre of mass is at $x = 0.1$ instead of the usual value 0.5 and this is seen, in Fig. 7a, to lead to oscillations. The largest oscillation which is for an initial $\theta$ equal to 0.55 displays the effects of nonlinearity through a movement of the peak and trough locations in particular, with the body’s trailing edge almost but not quite hitting the walls as the oscillations continue.

Fig. 6

a Evolutions $h, \ \theta$ plotted against scaled time $t^{**}$ as discussed in Sect. 3. b Body positions at times $t^{**} = 0, \ 2, \ 4$

The analysis appears to be in keeping with the numerical solutions of (3.3a)–(3.3e). The analytical oscillatory response is also consistent with the earlier numerical work on the full system, particularly when I is large but significantly less than M.

Fig. 7

Oscillatory interactions. a Angle $\theta$ vs $t^{**}$ for initial conditions $\theta (0) = 0.1, \ 0.4, \ 0.55$ in the case $a = 0.1$. b Evolution of body positions for the 0.55 initial condition

4 Wake behaviour

The wake behind the body arises because the velocity components $u_1,\ u_2$ of the body-scale flow studied in Sect. 2 are unequal in general at the trailing edge. This is shown by taking the integral of (2.1) with respect to x from the leading edge to the trailing edge, together with the Euler and Kutta conditions on pressure in (2.6), (2.7). Spatial and temporal evolution must therefore take place in the wake to restore uniform flow far downstream. The argument here is similar to that in Sect. 2. In the wake, where $x > 1$, the absence of a solid body implies that the pressures $p_1, \ p_2$ must be equal but the dividing streamline, which marks the interface between fluid that has come from above the body in $0<x<1$ and fluid from below the body, is unknown in advance.

The relevant flow system to be solved in the wake $x>1$ is thus

$$\begin{aligned} \frac{\partial H_n}{\partial t} + \frac{\partial (H_n u_n)}{\partial x}&= 0, \end{aligned}$$

(4.1a)

$$\begin{aligned} \frac{\partial u_n}{\partial t} + u_n \frac{\partial u_n}{\partial x}&= - \frac{\partial p_n}{\partial x}, \end{aligned}$$

(4.1b)

together with the pressure equality

$$\begin{aligned} p_1 = p_2 \end{aligned}$$

(4.1c)

and

$$\begin{aligned} H_1 + H_2 = 1. \end{aligned}$$

(4.1d)

Here, (4.1d) represents the feature that the thicknesses $H_1$ of the lower fluid flow and $H_2$ of the upper fluid flow must add up to unity, which is the overall width of the straight channel. The initial conditions are typically that

$$\begin{aligned} H_1 = H_2 = \dfrac{1}{2}, \quad p_1 = p_2 = 0, \quad u_1 = u_2 = 1 \quad \text{ at } \text{ time } \quad t = 0, \end{aligned}$$

(4.2a)

while the boundary conditions at the start of the wake, i.e. at $x = 1 +$, are

$$\begin{aligned} (H_1, \ H_2, \ u_1, \ u_2, \ p_1, \ p_2) (1 +, \ t) = (H_1,\ H_2, \ u_1, \ u_2,\ p_1, \ p_2) (1-, \ t), \end{aligned}$$

(4.2b)

for all $t > 0$. The form (4.2b) matches with the fluid /body interaction properties considered in Sects. 2, 3 at the trailing edge of the body, with the Kutta condition assuring that $p_1, \ p_2$ are equal there and so the pressure can be continuous. It is notable that in the limit of large $M, \ I$ there is no wake effect to leading order because the flow contribution is then quasi-steady and so the Kutta condition on pressure leads to $u_1, \ u_2$ being equal in that case.

Fig. 8

Lower and upper layer widths $H_1$ and $H_2$ until time $t = 2$. Here, $M=10, \ I = 2$. a The lower layer width $H_1$ for $x \in [1, \ {3.4}]$. b The lower upper width $H_2$

The system was solved numerically by means of an adjustment of the method described in [16, 17, 31]. In addition a linearised analytical solution appropriate for small perturbations from the state (4.2a) is described in [31]: see also the analysis in (3.1a)–(3.1c). Analysis along the lines to be discussed in the following section also applies in the wake part of the present interaction. Tests on the accuracy of the numerical work are given in [31].

The results are presented in Figs. 8, 9, 10 and 11. Figures 8, 9 and 10 are for a thick body in $0<x<1$ with initial conditions $(0.5, \ 0, \ 0, \ 0.1)$ for $(h, \ dh/dt. \ \theta , \ d \theta / dt)$. Here, Fig. 8 shows the lower and upper widths $H_1, \ H_2$, while Fig. 9 presents the velocities $u_1, \ u_2$ and Fig. 10 the pressure solution $p_1 = p_2$. The incident conditions (4.2b) at $x = 1$ in Fig. 8a, b indicate that $H_1$ there decreases with time whereas $H_2$ increases, in line with (4.1d). This temporal decay and growth in $H_1, \ H_2$ is arrested at larger x values however and replaced by growth and decay, respectively, ahead of a travelling front, while downstream of that front the quantities given by the initial conditions in (4.2a) remain undisturbed. Similar phenomena appear in Figs. 9a, b and 10. In all cases, the existence of a travelling front is clear in the wake, the front speed being approximately unity as would be expected. Figure 11 exhibits the combined body-flow and wake-flow properties in terms of $u_1, \ u_2$ plotted against x between the body leading edge $x=0$ and the wake position $x=3.4$, for a range of times t as shown. In this interaction an impact of the body with the lower wall of the channel occurs at a time of about 3.4. Again the travelling front is apparent in the wake.

Fig. 9

Velocities $u_1$ and $u_2$ in the wake region until time $t = 2$. Here, $M=10,\ I = 2$. a Velocity in the lower wake layer $u_1$ for $x \in [1, \ {3.4}]$. b Velocity in the upper wake layer $u_2$. The initial conditions are as in Fig. 8

5 Body motion through dilated or constricted channels

We consider here the effects of a continued dilation (expansion) of the channel width, in Sect. 5.1, followed by a study of finite dilation or constriction in Sect. 5.2.

Fig. 10

Pressure p solutions in the wake region until time $t = 2$

5.1 Channel expansions

In the configuration studied in this section, the lower wall is moving upstream, i.e. leftward, from right to left, with constant speed, relative to the body. Certain analytical features are worth describing first since they influence the coupling between the flow ahead of the body and that around the body in the fluid-body interplay.

Upstream of the body the wall eventually becomes distorted from its original straight form after a finite time, $t = t_0$ say. Since no body is present, there the relevant governing equations are

$$\begin{aligned} H_t + (uH)_x&= 0, \end{aligned}$$

(5.1a)

$$\begin{aligned} u_t + u u_x&= - p_x , \end{aligned}$$

(5.1b)

for $x < 0$ (ahead of the body) but $x > x_0(t)$ (the position where wall distortion begins). Here, (5.1a, 5.1b) applies across the whole channel. Let us assume that the incident velocity and channel thickness $u_0, \ H_0$ are maintained as constant in the straight channel far upstream. We suppose also that the lower wall is prescribed as $y = f_L(x, \ t)$, which holds for $x > x_0(t)$, when $x_0(t) < 0$. Upstream of $x = x_0(t)$ the channel remains straight. The upper wall is at $y=1$ say. (In the body frame, we repeat, the body’s leading edge remains at $x=0$ and the trailing edge remains at $x=1$.) Ahead of the leading edge, for $x_0(t)< x < 0$, we have (5.1a) with the gap width being $H = 1 - f_L(x,t)$. Hence, $(uH)_x = \partial f_L/ \partial t$ and integration in x then gives

$$\begin{aligned} u H (x, \ t) = u_0 H_0 + \int _{x_0(t)}^x \ \bigg ( \dfrac{\partial f_L}{\partial t} \bigg ) \ dx, \end{aligned}$$

(5.2a)

and in particular at the onset of the leading edge

$$\begin{aligned} u H (0,\ t) = u_0 H_0 + \int _{x_0(t)}^0 \ \bigg ( \dfrac{\partial f_L}{\partial t} \bigg ) \ dx. \end{aligned}$$

(5.2b)

On the other hand, where the body is present, i.e. for $0< x < 1$, we have the two kinematic balances $H_{1t} + (u_1 H_1)_x = 0$ and $H_{2t} + (u_2 H_2)_x = 0$ from Sect. 2. Integrating these two equations from $x=0$ to $x=1$ and adding the results gives us

$$\begin{aligned} \bigg ( \dfrac{d}{dt} \bigg ) \int _0^1 (H_1 + H_2) \ dx + (u_1 H_1+u_2 H_2)(1,\ t) = (u_1 H_1 + u_2 H_2)(0,\ t). \end{aligned}$$

(5.2c)

Then using the fact that $H_1 = 1 - f_+ (x) - h(t) - (x - a) \ \theta (t)$ and $H_2$ is given by a similar formula, we find from (5.2c) that

$$\begin{aligned} (u_1 H_1 + u_2 H_2 )(0,\ t) = - \int _0^1 \bigg ( \dfrac{\partial f_L}{\partial t} \bigg ) \ dx + (u_1 H_1 + u_2 H_2) (1,\ t). \end{aligned}$$

(5.2d)

However, the Euler region surrounding the leading edge contains quasi-steady flow and hence mass conservation in that region simply tells us that the left-hand side of (5.2b) is equal to the left-hand side of (5.2d). Therefore, from the right-hand sides, we have

$$\begin{aligned} (u_1 H_1 + u_2 H_2) (1,\ t) = u_0 H_0 + \int _{x_0(t)}^1 \bigg ( \dfrac{\partial f_L}{\partial t} \bigg ) \ dx. \end{aligned}$$

(5.2e)

This is the main mass-conservation requirement. Using the result

$$\begin{aligned} u_1 = \bigg [c_1 - {h'} \ (x - {a}) - \dfrac{1}{2} \ \theta ' \ (x - {a})^2 + \int _{x_0(t)}^x \bigg ( \dfrac{\partial f_L}{\partial t} \bigg ) \ dx \bigg ]/[{h} + \theta (x - {a}) - f_L] \end{aligned}$$

(5.2f)

(where $c_1 (t)$ is an unknown function of integration, while we recall a is the position of the centre of mass) and a similar result for $u_2$, we then substitute these into (5.2e). We are led to the mass-conservation requirement

$$\begin{aligned} c_1(t) + c_2(t) = 1, \end{aligned}$$

(5.3)

Fig. 11

Velocities for a body of profile $T(x) = 0.4 \sin (\pi x), \ C(x) = 0$, with $M = 10, \ I = 2$, approaching impact with the lower wall at the scaled time of t about 3.4. (Solutions are presented from time $t=0$ to $t=3.3$). a The velocity $u_1$ in gap 1 for $0<x<3.4$ (body and wake regions) and approaching the clash. b The upper layer velocity $u_2$. (The evolution in $u_1$ is sufficiently small over the whole time interval in the body region where $0<x<1$)

which acts as a generalisation of the mass condition (2.4). It is notable that the integral in (5.2f) has $x_0(t)$ as its lower limit; this leads to (5.3). In addition the momentum balance (5.1b) gives, on integration, the form

$$\begin{aligned} p + \dfrac{1}{2} u^2 = \dfrac{1}{2} - \int _{x_0(t)}^x u_t \ dx \end{aligned}$$

(5.4)

for the pressure head. Hence, in particular, we obtain the result

$$\begin{aligned} \left( p + \dfrac{1}{2} u^2 \right) (0-, \ t) = \frac{1}{2} + M^{- \frac{1}{2}} \left( 1 + M^{- \frac{1}{2}} \right) \mu x_0 \ / \ (1 + \mu x_0), \end{aligned}$$

(5.5)

holding at the leading edge for the specific case addressed in the results shown in Fig. 12. Here, $x_0(t) = 1 - M^{- 1/2} t$ $= 1 - t^*$, (5.5) holds for $t > M^{1/2}$ and $\mu$ is a constant. Figure 12 shows $h, \ \theta$ against $t^*$ for the expanding channel, in Fig. 12a, where the wall which is moving upstream relative to the body has shape $f_L = \mu (x - 1 + t^*)$ for $x > 1 - t^*$, with $\mu = - 1$ in this example. Here, Fig. 12b gives the evolving body positions as seen in the laboratory frame. We note that $h, \ \theta$ can be shown to grow in the form $O(t^*) + O(\ln t^*)$ at large $t^*$ values within the expanding channel; the dependence on the centre of mass location a is implicit in the $O(t^*)$ term but explicit in the $O(\ln t^*)$ contribution.

Fig. 12

For an expanding channel. Solutions of the reduced system (3.3a)–(3.3e) with $I = M / 5 \ (I^*= 0.2)$ for a flat-plate body with centre of mass location $a = 0.5$. a $h, \ \theta$ vs time $t^*$. b Body positions in the channel at times $0, \ 1, \ 2$

Most significant for the fluid-body interaction are the channel width at the leading edge at any time t and the initial conditions at zero time on the velocities $u_1, \ u_2$. Both the channel width and the initial conditions are built in to the solution procedure, as is (5.3) to preserve total mass. By contrast, (5.5) does not affect the body-scale solution significantly. This is due to the property that an arbitrary function of t can be added to each of the pressures $p_1, \ p_2$ without altering the interactive flow equations and, additionally, the fluid-body interaction itself involves only the pressure difference $p_1 - p_2$, as seen in (2.8), thereby cancelling out the arbitrary function just described.

Computational solutions for the fluid-body interaction are presented in Fig. 12. These are for the case of large $M, \ I$ as described in Sect. 3 but now with channel expansion, such that in the laboratory frame the body is moving into a spatially expanding channel. The lower channel wall is given in the body frame by

$$\begin{aligned} f_L(x, \ t) = \mu (x + t^*- 1) \quad \text{ for } \quad x > x_0(t^*), \ \text{ zero } \text{ otherwise }, \end{aligned}$$

(5.6)

where $\mu = - 1$ and $x_0 = 1 - t^*$. The upstream effect in (5.5) is small since M is large, while the initial conditions here correspond to a symmetric start at time zero [see also (3.1a)] and the channel width at the leading edge increases as $1 - \mu (t^*- 1)$, that is, as $t^*$, for times $t^*> 1$. The figure shows the evolution of $h, \ \theta$ as well as the body and wall positions, with no impacts taking place in this example. It can be shown that for large times $t^*$, the accelerations continue to reduce as the time scale increases and in effect the pressure approaches a stagnation value as the channel continues to expand.

Fig. 13

In a constricted channel. Here again the ratio $I / M = 0.2$. a $h, \ \theta$ solutions plotted against time $t = 4t^*(= M^{1/2} t^*$) from full system at $M = 16$ (dotted curves) and from reduced system (labelled Limit). b The positions of the body at times $t^*= 0, \ 0.2, \ 0.4$ prior to impact, according to the reduced system. Comparisons for other M values are described in the text

5.2 Finite dilation or constriction

The channel here is straight-walled except for the occurrence of a finite indentation or bump over which the moving body travels, such that in the present moving frame (the body frame) the indentation appears to enter the region of interest in the rightward direction with constant speed less than unity: in terms of Fig. 1 the constant B is negative in this case.

Considerations and analysis essentially identical with those in (5.1)–(5.5) again apply ahead of the body here. This is relevant from the initial time because of the rightward motion of the lower wall in the present case. On the other hand, the finite distortion, whether a dilation or a constriction, remains fixed in the laboratory frame in which the channel is stationary and we can expect the flow there to be steady at leading order, implying that in our body coordinates the effect upstream of the body depends only on $(x - \lambda t)$. Here, $\lambda$ is a given positive constant. Mass flux uH is conserved then, from the kinematic condition (5.1a), while the momentum balance (5.1b) now becomes

$$\begin{aligned} (u -\lambda ) \ u_x = - p_x, \end{aligned}$$

(5.7)

which can be integrated readily as in Sect. 3 to yield the variation of the pressure head $(p + 1/2 \ u^2)$. Following this, however, the same comments as in Sect. 5.1, on the pressure difference and on the significance of the channel width at the body’s leading edge and the initial conditions, still hold in the current scenario.

The results shown in Fig. 13 are for the full problem [of (2.1)–(2.8)] with an M value of 16, for a finite constriction, with $\mu = - 6,$ together with a comparison with the result from the reduced problem [of (3.3a)–(3.3e)] where $M,\ I$ are taken as asymptotically large. In the latter regime, the wall-velocity factor $\lambda$ is small and the upstream effect corresponding to (5.5) is negligible at leading order over the current time scales. As previously, the solution of the reduced problem is observed to capture the qualitative trend of the full solution; see also the next paragraph. In more detail, the results in Fig. 13 are specifically for a lower wall which produces a constriction, moving downstream relative to the body, with Fig. 13a showing $h, \ \theta$ and a comparison with the full-system results which suggests qualitative agreement. In contrast, Fig. 13b is presented in the laboratory frame and depicts the body evolution at three successive times. The position of the body at time $t^*= 0.2$ is altered only a little from that at time $t^*= 0$, with the leading edge seen to move upstream of its original position with hardly any body rotation, but by the time $t^*= 0.4$ the rotation has increased. The effective squeezing of fluid locally accompanied by a lowered pressure means that the body thereby approaches the constriction and then impacts upon it soon afterwards, at a $t^*$ value of about 0.5 according to the calculation.

The comparison in Fig. 13 for M of 16 indicates that the approximate impact time predicted by the reduced system is $t = 1.98$, whereas that from the full system is $t = 2.89$. The ratio is thus 0.685. With I kept at the value M/5, the corresponding times for M of 64 are found to be 3.96 and 4.95, respectively, giving a ratio of 0.80, while for M of 256 we find 7.92 and 9.10 in turn and hence a ratio of 0.87. The trend, namely $0.685, \ 0.80, \ 0.87$, is encouraging as far as the approach to the limiting value of unity for the ratio at asymptotically large $M, \ I$ is concerned.

6 Discussion and conclusions

The study has sought increased understanding of the free movement of a slender body in a surrounding fluid flow within a channel. This is with two-way interaction being considerable between the fluid motion and the body motion and with fully unsteady evolution being active for both motions in general. The work has addressed numerical aspects for a thin or thick object inside a channel with straight walls and the corresponding analytical features for comparatively large values of the scaled mass and moment of inertia. The latter lead to a significantly reduced system. Oscillations coupling the body and the fluid motions have been found, including some particularly interesting ones which occur for relatively small values of the moment of inertia. Wake responses and the influences of non-straight walls associated with finite dilation and constriction or with continued expansion of the channel have also been investigated.

The main findings from the present modelling, analysis and computations, along with comparisons, are felt to be the following. First is the finite-time clashing of the body with the channel walls, which is a quite common phenomenon here, but there are means to avoid such clashing. The impact or clashing of the body when it does occur on a stationary or a moving wall is as in [16] if at the leading edge of the body or [17] in terms of a mid-body clash. However, a continuing expansion of the vessel is found to readily lead to the avoidance of such an impact. The second main finding concerns sustained oscillations. These are found to be possible as mentioned earlier and their occurrence can be supported clearly in analytical form. They arise especially for a front-loaded body. Third, wake properties behind the body show a distinct travelling front downstream. The fourth finding is concerned with the body flow through a dilated or constricted channel, which generates substantial nonlinear effects upstream of the body, whether the body travels leftwards towards the oncoming fluid flow or rightwards with the oncoming flow. Fifth is the broad agreement seen in the solution trends between full-system and reduced-system responses as the body mass and moment of inertia increase.

An interesting issue arises if the body lies near one of the walls. Suppose that the whole body is close to the lower wall (see Fig. 2), whether the wall is straight or otherwise; this is the case of a thin flat plate if the wall is straight. To leading order, the flow in the thin gap, of small thickness of order $\delta$ say, dominates the fluid-body interaction and gives a boundary-layer type of response as in [27] within region 1 of Fig. 2, the pressure $p_1$ being of order unity and satisfying the Kutta condition. Here, region 1 refers to the gap where the fluid velocity has subscript unity and region 2 to the other gap above the body. This boundary layer implies that the height h and angle $\theta$ are known to leading order, with $O(\delta )$ relative corrections. (As a significant point here, the present argument supports the boundary layer analyses of [23, 27, 29, 34] in the sense that only the underbody pressure affects the body motion to leading order in the boundary layer case and also the fluid flow is quasi-steady if the scaled mass is relatively large.) At issue next is the question of how the solution in region 2 is determined. This appears to be by means of a linearised system in that region, which involves an $O(\delta )$ perturbation from the uniform incident stream and a corresponding pressure $p_2$ of order $\delta$. The boundary condition on the top surface of the body now acts at zero y in effect. Combined with the no-penetration condition at the top wall, it indicates a behaviour similar to that studied in a single channel (Sect. 5). The pressure $p_2$ can be found thereby and has a nonzero value generally at the trailing edge: this value provides a small corrective feedback to the pressure in the region 1. A similar reasoning applies to the wake of the near-wall body, a wake which is concentrated near the lower wall to leading order and is governed by the inviscid Burgers’ equation, that is, by (4.1b) for $u_1(x,\ t)$ in $x > 1$ but with zero pressure $p_1$ in order to match with the majority of the flow at every wake station.

Potential future work has much of interest. It would be valuable to add in the influence of viscosity, for example as in [24,25,26], to admit three-dimensional interactions [21], and to include more than one body [33]. Similarly, the modelling of a flexible elastic wall or flexible body in the channel could be of great concern, not least because of the possible application to the tracing of vessel weaknesses described in the Introduction. We would also like to highlight the effects of reduced mass and moment of inertia, specifically in the eigenvalue Eq. (3.1b). The reduction leads to one real negative root for Q along with two complex conjugates and corresponds directly to demanding that the right-hand sides of the body motion balances (2.8) be zero. Thus, the pressures have to adjust to make the lift and moment integrals remain zero throughout the evolution. In this mass reduction case, the time derivatives of the fluid flow stay significant, in contrast with the mass enhancement case of Sect. 3 where the time derivatives of the body movements dominate the interaction. Work in [34] considers the mass reduction case in a boundary-layer context for an ice particle in water; it would be interesting to continue this case for the present internal flow configuration.