Abstract
The control of complex systems is of critical importance in many branches of science, engineering, and industry, many of which are governed by nonlinear partial differential equations. Controlling an unsteady fluid flow is particularly important, as flow control is a key enabler for technologies in energy (e.g., wind, tidal, and combustion), transportation (e.g., planes, trains, and automobiles), security (e.g., tracking airborne contamination), and health (e.g., artificial hearts and artificial respiration). However, the high-dimensional, nonlinear, and multi-scale dynamics make real-time feedback control infeasible. Fortunately, these high-dimensional systems exhibit dominant, low-dimensional patterns of activity that can be exploited for effective control in the sense that knowledge of the entire state of a system is not required. Advances in machine learning have the potential to revolutionize flow control given its ability to extract principled, low-rank feature spaces characterizing such complex systems. We present a novel deep learning model predictive control framework that exploits low-rank features of the flow in order to achieve considerable improvements to control performance. Instead of predicting the entire fluid state, we use a recurrent neural network (RNN) to accurately predict the control relevant quantities of the system, which are then embedded into an MPC framework to construct a feedback loop. In order to lower the data requirements and to improve the prediction accuracy and thus the control performance, incoming sensor data are used to update the RNN online. The results are validated using varying fluid flow examples of increasing complexity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The robust and high-performance control of fluid flows presents an engineering grand challenge, with the potential to enable advanced technologies in domains as diverse as transportation, energy, security, and medicine. In many of these areas, the flows—described by the three-dimensional Navier–Stokes equations—are turbulent or exhibit chaotic dynamical behavior in the relevant regimes. As a consequence, the control of fluid flows is challenging due to the confluence of strong nonlinearity, high-dimensionality, and multi-scale physics, thus typically leading to an intractable optimization problem. However, recent advances in machine learning (ML) are revolutionizing computational approaches for these traditionally intractable optimizations by providing principled approaches to feature extraction methods with improved optimization algorithms. We develop a deep learning model predictive control framework that leverages ML methods to achieve robust control performance in a complex fluid system without recourse to the governing equations, and with access to only a few physically realizable sensors. This sensor-based, data-driven learning architecture is critically important for practical implementation in control-based engineering applications.
Model predictive control (MPC) [10, 23] is among the most versatile and widely used model-based control approaches, which involves an online optimization of the control strategy over a predictive receding horizon. Generally, improved models result in better control performance [43], although the online iterative optimization requires relatively inexpensive models [28, 46]. The challenge of MPC for controlling fluid flows is centered on the high-dimensional nature of spatiotemporal flow fields. Fortunately, these systems often exhibit dominant patterns of low-dimensional activity. Indeed, it is observed that flying insects, birds, and bats are able to harness these dominant patterns to execute exceptional control performance. Thus, there is a vibrant field in reduced-order models [4] that balance accuracy and efficiency to capture essential physical mechanisms, while discarding distracting features.
A very prominent approach in model reduction for nonlinear systems is the proper orthogonal decomposition (POD) [38], where the dynamical system is projected onto a lower-dimensional subspace of modes representing dominant flow structures that are constructed from simulation data. Over the past years, many control frameworks based on POD have been proposed for fluid flows, see, e.g., [7, 13, 25, 34, 36, 44]. However, POD and related methods face difficulties when the system exhibits chaotic behavior, as the dynamics cannot be restricted to low-dimensional subspaces in that case.
In the recent past, data-driven methods have provided an increasingly successful alternative for model reduction in nonlinear systems. Among machine learning algorithms, deep learning [11, 21, 22] has seen unprecedented success in a variety of modeling tasks across industrial, technological, and scientific disciplines. It is no surprise that deep learning has been rapidly integrated into several leading control architectures, including MPC and reinforcement learning. Deep reinforcement learning [27, 35] has been widely used to learn games [27, 37], and more recently for physical systems, for example to learn flight controllers [17, 41] or the collective motion of fish [42]. A combination of the representational power of deep neural networks with the flexible optimization framework of MPC, called DeepMPC, is also a promising strategy. There exist various approaches for using data-driven surrogate models for MPC (e.g., based on the Koopman operator [15, 16, 20, 31,32,33]), and DeepMPC has considerable potential [3, 24, 30]. The ability of DeepMPC to control the laminar flow past a circular cylinder was recently demonstrated in [30]; the flow considered in this work is nearly linear and may be well approximated using more standard linear modeling and control techniques. However, this study provides an important proof of concept. In this work, we extend DeepMPC for flow control in two key directions: (1) We apply this architecture to control significantly more complex flows that exhibit broadband phenomena; and (2) we develop our architecture to work with only a few physically realizable sensors, as opposed to earlier studies that involve the assumption of full flow field measurements. There is a significant gap between academic flow control examples and industrially relevant configurations. The present work takes a step toward complexity and importantly develops a data-driven, sensor-based architecture that is likely to scale to harder problems. More importantly, one rarely has access to the full flow field, and instead control must be performed with very few measurements [26]. Biological systems, such as flying insects, provide proof by existence that it is possible to enact extremely robust control with limited flow measurements [29]. In this work, we design our learning approach to leverage time histories of limited sensors (i.e., measurable body forces), providing a more direct connection to engineering applications. In order to improve the prediction accuracy and thus the control performance, incoming sensor data— which needs to be collected with a relatively high frequency within the MPC framework—is used to perform batch-wise online learning. Finally, we provide a physical interpretation for the learned control strategy, which we connect to the underlying symmetries of the dynamical system.
2 Model predictive control of complex systems
Our main task is to control a complex nonlinear system in real time. We do this by using the well-known MPC paradigm, in which an open-loop optimal control problem is solved in each time step using a model of the system dynamics:
Here, \(f(y)=z\) is the observation of the time (and potentially space) dependent system state y that has to follow a reference trajectory \(z^{\mathrm{ref}}\), and \(\alpha \) and \(\beta \) are regularization parameters penalizing the control input as well as its variation. The time-T map \(\Phi \) of the system dynamics describes how the system state evolves over one time step given the current state and control input. Problem (1) is then solved repeatedly over a fixed prediction horizon N and the first entry is applied to the real system. As the initial condition in the next time step, the real system state is used such that a feedback behavior is achieved. Note that \(u_{-1}\) is the control input that was applied to the system in the previous time step. The scheme is visualized in Fig. 1, where the MPC controller based on the full system dynamics is shown in green.
MPC has successfully been applied to a very large number of problems. However, a major challenge is the real-time requirement, i.e., (1) has to be solved within the sample time \(\Delta t = t_{i+1} - t_i\). In order to achieve this, linearizations are often used. Since even these can be too expensive to solve for large systems, we will here use a surrogate model which does not model the entire system state but only the control relevant quantities. In a flow control problem, these can be the lift and drag coefficients of a wing, for instance. Such an approach has successfully been used in combination with surrogate models based on dynamic mode decomposition [33] or clustering [31]. We thus aim at directly approximating the dynamics \(\overline{\Phi }\) for the observable \(z=f(y)\) and replacing the constraint in Problem (1) by a surrogate model. Following Takens embedding theory [39], we will use delay coordinates, an approach which has been successfully applied to many systems [8]. Therefore, we define
where d is the number of delays. Given a history of states z and controls u, the reduced dynamics \(\overline{\Phi }\) then yield the state at the next time instant. This allows us to replace Problem (1) by the following surrogate problem:
The resulting MPC controller is visualized in Fig. 1 in orange.
Remark 1
Note that another advantage of modeling only the quantities relevant to the control part is that we depend much less strongly on the scales of the flow field (i.e., grid size and time step), as integral quantities such as body forces may evolve on their own (and possibly somewhat slower) time scale.
2.1 Related work
The main challenge in flow control—the construction of fast yet accurate models—has been addressed by many researchers in various ways. We here give a short overview of alternative methods (mostly related to the cylinder flow) and relate them to our approach.
From a control-theoretical standpoint, the best way to compute a control law is via the exact model, i.e., the full Navier–Stokes equations. Using such a model in combination with an adjoint approach, a significant drag reduction could be achieved for the cylinder flow in [12] for Reynolds numbers up to 1000. However, this approach is too expensive for real-time control. To this end, several alternatives have been proposed, the most intuitive and well known being linearization around a desired operating point, cf. [18] for an overview. As a popular alternative, proper orthogonal decomposition (POD) [38] has emerged over the past decades, where the full state is projected onto a low-dimensional subspace spanned by orthogonal POD modes which are determined from snapshots of the full system. The resulting Galerkin models have successfully been used for control of the cylinder wake, see, e.g., [7, 13]. Balanced truncation POD models can be obtained for linear [44] or linearized systems [36]. In order to ensure convergence to an optimal control input, the POD model can be updated regularly within a trust-region framework [6]. Alternative approaches that are similar in spirit are moment matching [1] and linear–quadratic–Gaussian (LQG) balanced truncation [5].
The above-mentioned methods have as their main drawback that they quickly become prohibitively expensive with increasing Reynolds number. This is due to the fact that linearizations are less efficient or that the dynamics no longer live in low-dimensional subspaces that can be spanned by a few POD modes. Furthermore, all approaches require knowledge of the entire velocity (and potentially pressure) field, at least for the model construction. Both issues can be avoided when not considering the entire velocity field but only sensor data, which results in purely data-driven models or feedback laws. Several machine learning-based approaches have been presented in this context, for instance cluster-based surrogate models (cf. [31], where the drag of an airplane wing was reduced), feedback control laws constructed by genetic programming [45], or reinforcement learning controllers [35]. These approaches are often significantly faster, rendering real-time control feasible. The approach presented in the following falls into this category as well.
3 DeepMPC: model predictive control with a deep recurrent neural network
In order to solve (2), the surrogate model \(\overline{\Phi }\) for the control relevant system dynamics is required. For this purpose, we will use a deep RNN architecture which is implemented in TensorFlow [2]. Once the model is trained and can predict the dynamics of z (at least over the prediction horizon), the model can be incorporated into the MPC loop.
3.1 Design of the RNN
As previously mentioned, the surrogate model is approximated using a deep neural network similar to [3]. Each cell of the RNN predicts the system state for one time step. In order to capture the system dynamics using few observations only, we use the delay coordinates introduced above. Consequently, each RNN cell takes as input a sequence of past observations \(\hat{z}_i\) as well as corresponding control inputs \(\hat{u}_i\). The RNN consists of an encoder and a decoder (cf. Fig. 2a), where the decoder performs the actual prediction task and consists of N cells—one for each time step in the prediction horizon. This means that a single decoder cell computes \(\hat{z}_{i+1} = \overline{\Phi }(\hat{z}_i, \hat{u}_i)\). The state information \(\hat{z}_{i+1}\) is then forwarded to the next cell to compute the consecutive time step. In order to take long-term dynamics into account, an additional latent state \(l_{k+1}\) is computed based on past state information and forwarded from one cell to another. To properly compute this state for the first decoder cell, an encoder with M cells, whose cells only predict this latent state, is prepended to the decoder. As the encoder cell only predicts the latent state, it is a reduced version of the decoder cell which additionally contains elements for predicting the current and future dynamics, cf. Fig. 2a, b.
More precisely, the decoder cells are divided into three functional parts capturing different parts of the dynamics, i.e., long term (which is equivalent to an encoder cell) and current dynamics as well as the influence of the control inputs (see Fig. 2b). Therefore, the input \((\hat{z}_k,\hat{u}_k)\) of each cell k is divided into three parts, two time series \(z_{k-2b+1,\dots ,k-b}\) and \(z_{k-b+1,\dots ,k}\) of the observable with the corresponding control inputs \(u_{k-2b,\dots ,k-b-1}\), and \(u_{k-b,\dots ,k-1}\) and a separate sequence of control inputs \(u_{k-b+1,\dots ,k}\). The input length b is thus related to the delay via \(d=2b\). In summary, the inputs \((\hat{z}_k,\hat{u}_k) = (z_{k-2b,\dots ,k},u_{k-2b,\dots ,k})\) are required.
As shown in Fig. 2b, the encoder and decoder consist of different smaller sub-units, represented by gray boxes. Each of the gray boxes represents a fully connected neural network. The encoder cell consists of three parts, \(h_{l,\mathrm{past}}\), \(h_{l,\mathrm{current}}\) and \(h_{\mathrm{latent}}\). In \(h_{l,\mathrm{past}}\) and \(h_{l,\mathrm{current}}\) latent variables for the last \(k-2{b+1},\dots ,k-{b}\) and \(k-{b+1},\dots ,k\) time steps are computed, respectively. The current latent state \(l_{k+1}\) can be computed based on the information given by \(h_{l,\mathrm{past}}\), \(h_{l,\mathrm{current}}\) and the latent variable of the last RNN cell \(l_k\). In a decoder cell, the future state \(z_{k+1}\) is additionally computed. Therefore, the latent state \(l_{k+1}\) is used as an input for \(h_{\mathrm{past}}\), and the results of \(h_{\mathrm{past}}\), \(h_{\mathrm{current}}\) and \(h_{\mathrm{future}}\) are used to calculate the predicted state \(z_{k+1}\) and thus, \(\hat{z}_{k+1}\). The corresponding equations can be found in Appendix A.
The RNN-based MPC problem (2) is solved using a gradient-based optimization algorithm—in our case a BFGS method. The required gradient information with respect to the control inputs can be calculated using standard backpropagation through time. This is represented by the red arrows in Fig. 2b. Since the RNN model requires temporal information from at least \(M + 2{b}\) time steps (M encoder cells and input sequence of length 2b) to predict future states, there is an initialization phase in the MPC framework during which the control input is fixed to 0.
3.2 Training of the RNN
The RNN is trained offline with time series data \(\left( (z_0,u_0),\ldots ,(z_n,u_n)\right) \). For the data collection, the system is actuated with uniformly distributed random yet continuously varying inputs. In order to overcome difficulties with exploding and vanishing gradients as well as problems with the effect of nonlinearities when iterating from one time step to another, we use the three-stage approach for learning as proposed in [24] and used in [3]. First, a conditional restricted Boltzmann machine is used to compute good initial parameters for the RNN according to the work by [40]. In the second stage, only the model for a single time step is trained as this is faster and more stable than directly training the entire network, i.e., the model for the entire prediction horizon. In the final stage, another training phase is performed, this time for the complete RNN with N decoder cells, improving and making the predictions more robust for the system state over N time steps. Both the individual RNN cell and the entire network were trained using the ADAM optimizer [19].
3.3 Online training of the RNN
During system operation, we obtain incoming sensor data in each iteration, i.e., with a relatively high frequency. In order to improve the prediction accuracy and thus the control performance of the model, these data are used to perform batch-wise online learning. To this end, we begin with a model which was trained in the offline phase as previously described. We then collect data over a fixed time interval such that we can update the RNN via batch-wise training using the ADAM optimizer.
To control the influence of the newly acquired data on the model—i.e., to avoid overfitting while yielding improved performance—it is important to select the training parameters accordingly, in particular the batch size and the learning rate. In our experiments, we have observed that the same initial learning rate and the same batch size as in the offline training phase are typically a good choice. However, the optimal choice of those parameters highly depends on the initial training data and the data collected during the control process.
4 Results
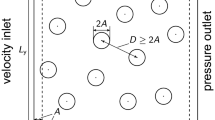
In order to study the performance of the proposed MPC framework, four flow control problems of increasing complexity are considered. Instead of a real physical system, we here use a numerical simulation of the full model as our plant. In all four cases, the flow around one or multiple cylinders (cf. Fig. 3) is governed by the incompressible 2D Navier–Stokes equations with fluid entering from the left at a constant velocity \(y_{\mathrm{in}}\). The Reynolds number \(\mathrm{Re}= y_{\mathrm{in}} / \nu D\) (based on the kinetic viscosity \(\nu \) and the cylinder diameter D) ranges from 100 to 200, i.e., we are in the laminar regime. The full system is solved using a finite volume discretization and the open-source solver OpenFOAM, cf. [14]. The control relevant quantities are the lift and drag forces (i.e., the forces in \(x_2\) and \(x_1\) direction) acting on the cylinders. These consist of both friction and pressure forces which can be computed from the system state (or easily measured in the case of a real system). The system can be controlled by rotating the cylinders, i.e., the control variables are the angular velocities.
4.1 One cylinder
The first example is the flow around a single cylinder, cf. Fig. 3a, which was also studied in [30]. At \(\mathrm{Re}=100\), the uncontrolled system possesses a periodic solution, the so called von Kármán vortex street. On the cylinder surface, the fluid and the cylinder velocity are identical (no-slip condition) such that the flow can be steered by rotating the cylinder. The control relevant quantities are the forces acting on the cylinder—the lift \(C_\mathrm{l}\) and drag \(C_\mathrm{d}\). We thus set \(z = (C_\mathrm{l}, C_\mathrm{d})\), and the aim is to control the cylinder such that the lift follows a given trajectory, e.g., a piecewise constant lift.
In order to create training data, a time series of the lift and the drag is computed from a time series of the full system state with a random control sequence. To avoid high input frequencies, a random rotation between \(u=-2\) and \(u=2\) is selected according to an equal distribution every \(0.5\,\text {s}\). The intermediate control inputs are then computed using a spline interpolation on the grid of the time-T map, where \(\Delta t = 0.1\,\text {s}\). For the RNN training, a time series with 110,000 data points is used which corresponds to a duration of 11,000 s. The concrete parameters for the RNN can be found in Appendix B.
Remark 2
In the first experiments, we use abundant measurement data in order to rule out this source of insecurity. The chosen amount significantly exceeds the amount that is required for a good performance, as we will see below. Considering the uncontrolled system, the fluidic time scale is in the range of seconds, and even in the actuated situation, a much smaller amount of data is sufficient, in particular in combination with the stochastic gradient descent optimization which selects random subsets of the data set in each iteration.
In a first step, the quality of the RNN prediction is evaluated on the basis of an exemplary control input sequence. As one can see in Fig. 4a, the prediction is very accurate over several time steps for many combinations of observations z and control inputs u. There are only small regions where the predictions deviate stronger from the real lift and drag.
System with one cylinder at \(\mathrm{Re}= 100\). a Results for the prediction by the RNN for a given control input sequence. The prediction for the next 5 time steps for lift and drag (at each \(t_i\)) is shown in brightening red or blue tones. b Results of the control task. The aim is to force the lift to \(+1\), 0 and \(-1\) for \(20\,\text {s}\), respectively (color figure online)
The good prediction quality enables us to use the RNN in the MPC framework, where the aim is to force the lift to \(+1\), 0 and \(-1\) for \(20\,\text {s}\), respectively. This results in the following realization of (2):
The parameter \(\beta \) is set to 0.01 in order to avoid too rapid variations of the input. Furthermore, the control is bounded by the minimum and maximum control input of the training data (i.e., \(\pm 2\)). We solve the optimization problem (3) using a BFGS method and with a prediction horizon of length \(N=5\), as our experiments have shown that this is a good compromise between accuracy and computing effort. As visualized in Fig. 4b, the DeepMPC scheme leads to a good performance. Due to the periodic fluctuation of the uncontrolled system, a periodic control is expected to suppress this behavior which is what we observe.
4.2 Fluidic pinball
In the second example, we control the flow around three cylinders in a triangular arrangement, as shown in Fig. 3b. This configuration is known as the fluidic pinball, see [9] for a detailed study. The control task is to make the lift of the three cylinders (\(C_{\mathrm{l},1}\), \(C_{\mathrm{l},2}\) and \(C_{\mathrm{l},3}\)) follow given trajectories by rotating the rear cylinders while the cylinder in the front is fixed. We thus want to approximate the system dynamics of the forces acting on all three cylinders, i.e., \(z=(C_{\mathrm{l},1},C_{\mathrm{l},2},C_{\mathrm{l},3},C_{\mathrm{d},1},C_{\mathrm{d},2},C_{\mathrm{d},3})\). Similar to the single cylinder case, the system possesses a periodic solution at \(\mathrm{Re} = 100\). When increasing the Reynolds number, the system dynamics become chaotic [9] and the control task is much more challenging. We thus additionally study the chaotic cases \(\mathrm{Re}=140\) and \(\mathrm{Re} = 200\). The behavior of the observables of the uncontrolled flow for the three cases is presented in Fig. 5. Interestingly, the flow is non-symmetric in all cases. At \(\mathrm{Re}=100\), for instance, the amplitudes of the oscillations of \(C_{\mathrm{l},2}\) and \(C_{\mathrm{l},3}\) are different, and which one is larger depends on the initial condition.
As we now have two inputs and three reference trajectories, we obtain the following realization of problem (2):
where the value of \(\beta \) is set to 0.1. For \(\mathrm{Re} = 100\), the prediction horizon is again \(N=5\). Since the dynamics are more complex for \( \mathrm{Re} = 140\) and \(\mathrm{Re} = 200\), the prediction horizon has to be larger and we experimentally found \(N=10\) to be an appropriate choice. The average number of iterations as well as the number of function and gradient evaluations for the MPC optimization are shown in Table 1 for the three considered cases.
For all three Reynolds numbers, the training data are computed by simulating the system with random yet smoothly varying control inputs as before, i.e., uniformly distributed random values between \(u=-2\) and \(u=2\) for each cylinder independently every \(0.5\,\text {s}\). Due to the significantly smaller time step of the finite volume solver for the fluidic pinball, the control is interpolated on a finer grid with step size \(0.005\,\text {s}\). Since the control input has to be fixed over one lag time due to the discrete-time mapping via the RNN, the mean over one lag time (i.e., over 20 data points) is taken for u. Time series with 150,000, 200,000 and 800,000 data points are used for \(\mathrm{Re}=100\), \(\mathrm{Re}=140\) and \(\mathrm{Re}=200\), respectively. As already mentioned in Remark 2, the chosen amount of data exceeds the maximum that is required. We will address this below. The concrete parameters for the RNN can be found in Appendix B.
At \(\mathrm{Re} = 100\), where the dynamics are periodic, the control is quite effective, almost comparable to the single cylinder case, cf. Fig. 6a. In particular, the lift at the bottom cylinder is controlled quite well. The fact that the two lift coefficients cannot be controlled equally well is not surprising as the uncontrolled case is also asymmetric, cf. Fig. 5.
In comparison, the error \(e_{\mathrm{mean}}\) for the mildly chaotic case \(\mathrm{Re}=140\) (Fig. 6b) is approximately one order of magnitude larger. The reference is still tracked, but larger deviations are observed. However, since the system is chaotic, this is to be expected. It is more difficult to obtain an accurate prediction and—more importantly—the system is more difficult to control, see also [32].
In order to improve the controller performance, we incorporate system knowledge, i.e., we exploit the symmetry along the horizontal axis. Numerical simulations suggest that this symmetry results in two metastable regions in the observation space and that the system changes only occasionally from one region to the other, analogous to the Lorenz attractor [8]. Therefore, we symmetrize (and double) the training data as follows:
This step is not necessary at \(\mathrm{Re}=100\), since the collected data are already nearly symmetric. Nevertheless, the amount of training data can be doubled by exploiting the symmetry, and therefore, the simulation time to generate the training data can be reduced.
In Fig. 6c, the results for \(\mathrm{Re}=140\) with symmetric training data are shown. In this example, the tracking error is reduced by nearly \(50\%\). In particular, the second lift is well controlled. This indicates that it is advisable to incorporate known physical features such as symmetries in the data assimilation process. However, we still observe that the existence of two metastable regions results in a better control performance for one of the cylinders, depending on the initial condition.
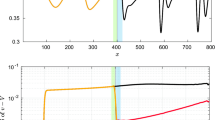
For the final example, the Reynolds number is increased to \(\mathrm{Re} = 200\) in order to further increase the complexity of the dynamics, and symmetric data are used again. Due to the higher Reynolds number, switching between the two metastable regions occurs much more frequently, and the use of symmetric data yields less improvement. The results are presented in Fig. 6d, and we see that even though tracking is achieved, the oscillations around the desired state are larger. In Fig. 7a, the mean and the maximal error for the three Reynolds numbers are shown. Since the system dynamics become more complex with increasing Reynolds number, both the prediction by the RNN and the control task itself become more difficult and the tracking error increases.
In order to study the robustness of the training process as well as the influence of the amount of training data on the tracking error, 5 identical experiments for \(\mathrm{Re}=200\) have been performed for different amounts of training data (\(10\%\), \(50\%\) and \(100\%\) of the symmetrized data points), respectively, see Fig. 7b. We observe no trend with respect to the amount of training data, in particular considering that the standard deviation is approximately 0.03 for the average and 0.15 for the maximal error. Figure 8 shows a comparison between two solutions using RNNs trained with \(100\%\) and \(10\%\) of the data, respectively. Although the solution trained with less data appears to behave less regularly, its performance is on average almost as good as the solution trained with \(100\%\) of the data. In conclusion, shorter time series already cover a sufficiently large part of the dynamics and are thus sufficient to train the model. In order to further improve the performance, the size of the RNN as well as the length of the training process would very likely have to be increased significantly and also, much smaller lag times would be required.
4.3 Online learning
Since we want to avoid a further increase in computational effort and data collection, we instead use small amounts of data sampled in the relevant parts of the observation space, i.e., close to the desired state. To this end, we perform online updates using the incoming sensor data. In our final experiment, we study how the control performance can be improved by performing batch-wise online updates of the RNN using the incoming data as described in Sect. 3.3. In the feedback loop, a new data point is collected from the real system at each time step. Our strategy is to collect new data over \(25\,\text {s}\) for each update. By exploiting the symmetry, we obtain a batch size of 500 points within each interval that is used for further training of the RNN. In the right plot of Fig. 9, we compare the tracking error over several intervals, and we see that it can be decreased very efficiently within a few iterations by using online learning (see also Fig. 6a for a comparison). Besides reducing the tracking error, the control cost \(\left| \left| u \right| \right| _2\) decreases, which further demonstrates the importance of using the correct training data. Significant improvements of both the tracking performance as well as the controller efficiency are obtained very quickly with comparably few measurements.
5 Conclusion and further work
We present a deep learning MPC framework for feedback control of complex systems. Our proposed sensor-based, data-driven learning architecture achieves robust control performance in a complex fluid system without recourse to the governing equations, and with access to only a few physically realizable sensors. In order to handle the real-time constraints, a surrogate model is built exclusively for control relevant and easily accessible quantities (i.e., sensor data). This way, the dimension of the RNN-based surrogate model is several orders of magnitude smaller compared to a model of the full system state. On the one hand, this enables applicability in a realistic setting since we do not rely on knowledge of the entire state. On the other hand, it allows us to address systems of higher complexity, i.e., it is a sensor-based and scalable architecture. The approach shows very good performance for high-dimensional systems of varying complexity, including chaotic behavior. To avoid prohibitively large training data sets and long training phases, an online update strategy using sensor data is applied. This way, excellent performance can be achieved for \(\mathrm{Re}=100\). For future work, it will be important to further improve and robustify the online updating process, in particular for chaotic systems. Furthermore, it is of great interest to further decrease the training data requirements by designing RNN structures specifically tailored to control problems.
Deep learning MPC is a critically important architecture for real-world engineering applications where only limited sensors are available to enact control authority. Therefore, in the context of real-world applications it would be of significant interest how the framework reacts to noisy sensor data. Since neural networks can in general work well with noisy data, we expect that DeepMPC gives a good noise-robustness. Furthermore, it should be investigated what happens if the Reynolds number changes slightly from the one used to train the RNN.
References
Ahmad, M.I., Benner, P., Goyal, P., Heiland, J.: Moment-matching based model reduction for Navier–Stokes type quadratic-bilinear descriptor systems. ZAMM J. Appl. Math. Mech. 97(10), 1252–1267 (2017)
Abadi et al., M.: Tensorflow: A system for large-scale machine learning. In: 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), pp. 265–283 (2016)
Baumeister, T., Brunton, S.L., Kutz, J.N.: Deep learning and model predictive control for self-tuning mode-locked lasers. J. Opt. Soc. Am. B 35(3), 617–626 (2018)
Benner, P., Gugercin, S., Willcox, K.: A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 57(4), 483–531 (2015)
Benner, P., Heiland, J.: Lqg-balanced truncation low-order controller for stabilization of laminar flows. In: King, R. (ed.) Active Flow and Combustion Control 2014, pp. 365–379. Springer International Publishing, Cham (2015)
Bergmann, M., Cordier, L.: Optimal control of the cylinder wake in the laminar regime by trust-region methods and POD reduced-order models. J. Comput. Phys. 227(16), 7813–7840 (2008)
Bergmann, M., Cordier, L., Brancher, J.P.: Optimal rotary control of the cylinder wake using proper orthogonal decomposition reduced-order model. Phys. Fluids 17, 1–21 (2005)
Brunton, S.L., Brunton, B.W., Proctor, J.L., Kaiser, E., Kutz, J.N.: Chaos as an intermittently forced linear system. Nat. Commun. 8, 19 (2017)
Deng, N., Noack, B.R., Morzyński, M., Pastur, L.R.: Low-order model for successive bifurcations of the fluidic pinball. J. Fluid Mech. 884, A37-1–A37-41 (2019)
Garcia, C.E., Prett, D.M., Morari, M.: Model predictive control: theory and practice—a survey. Automatica 25(3), 335–348 (1989)
Goodfellow, I., Bengio, Y., Courville, A.: Deep Learning. MIT Press, Cambridge (2016)
He, J.W., Glowinski, R., Metcalfe, R., Nordlander, A., Periaux, J.: Active control and drag optimization for flow past a circular cylinder: I. Oscillatory cylinder rotation. J. Comput. Phys. 163(1), 83–117 (2000)
Hinze, M., Volkwein, S.: Proper orthogonal decomposition surrogate models for nonlinear dynamical systems: error estimates and suboptimal control. In: Benner, P., Sorensen, D.C., Mehrmann, V. (eds.) Reduction of Large-Scale Systems, vol. 45, pp. 261–306. Springer, Berlin Heidelberg (2005)
Jasak, H., Jemcov, A., Tukovic, Z.: OpenFOAM : A C++ library for complex physics simulations. In: International Workshop on Coupled Methods in Numerical Dynamics pp. 1–20 (2007)
Kaiser, E., Kutz, J.N., Brunton, S.L.: Data-Driven Discovery of Koopman Eigenfunctions for Control. arXiv:1707.0114 (2017)
Kaiser, E., Kutz, J.N., Brunton, S.L.: Sparse identification of nonlinear dynamics for model predictive control in the low-data limit. Proc. R. Soc. A Math. Phys. Eng. Sci. 474(2219), 20180335 (2018)
Kim, H.J., Jordan, M.I., Sastry, S., Ng, A.Y.: Autonomous helicopter flight via reinforcement learning. In: Advances in Neural Information Processing Systems, pp. 799–806 (2004)
Kim, J., Bewley, T.R.: A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39(1), 383–417 (2007)
Kingma, D.P., Ba, J.: Adam: A Method for Stochastic Optimization. arXiv:1412.6980 (2014)
Korda, M., Mezić, I.: Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 93, 149–160 (2018)
Krizhevsky, A., Sutskever, I., Hinton, G.E.: ImageNet classification with deep convolutional neural networks. In: Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems 25, pp. 1097–1105. Curran Associates, Inc. (2012). http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
LeCun, Y., Bengio, Y., Hinton, G.: Deep learning. Nature 521(7553), 436–444 (2015)
Lee, J.H.: Model predictive control: review of the three decades of development. Int. J. Control Autom. Syst. 9(3), 415–424 (2011)
Lenz, I., Knepper, R.A., Saxena, A.: DeepMPC: Learning deep latent features for model predictive control. In: Robotics: Science and Systems. Rome, Italy (2015)
Lorenzi, S., Cammi, A., Luzzi, L., Rozza, G.: POD–Galerkin method for finite volume approximation of Navier–Stokes and RANS equations. Comput. Methods Appl. Mech. Eng. 311, 151–179 (2016)
Manohar, K., Brunton, B.W., Kutz, J.N., Brunton, S.L.: Data-driven sparse sensor placement. IEEE Control Syst. Mag. 38(3), 63–86 (2018)
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A.A., Veness, J., Bellemare, M.G., Graves, A., Riedmiller, M., Fidjeland, A.K., Ostrovski, G., Petersen, S., Beattie, C., Sadik, A., Antonoglou, I., King, H., Kumaran, D., Wierstra, D., Legg, S., Hassabis, D.: Human-level control through deep reinforcement learning. Nature 518(7540), 529–533 (2015)
Mohanty, S.: Artificial neural network based system identification and model predictive control of a flotation column. J. Process Control 19(6), 991–999 (2009)
Mohren, T.L., Daniel, T.L., Brunton, S.L., Brunton, B.W.: Neural-inspired sensors enable sparse, efficient classification of spatiotemporal data. Proc. Natl. Acad. Sci. 115(42), 10564–10569 (2018)
Morton, J., Jameson, A., Kochenderfer, M.J., Witherden, F.: Deep dynamical modeling and control of unsteady fluid flows. In: Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 31, pp. 9258–9268. Curran Associates Inc., New York (2018)
Nair, A.G., Yeh, C.A., Kaiser, E., Noack, B.R., Brunton, S.L., Taira, K.: Cluster-based feedback control of turbulent post-stall separated flows. J. Fluid Mech. 875, 345–375 (2019)
Peitz, S.: Controlling Nonlinear PDEs Using Low-Dimensional Bilinear Approximations Obtained From Data. arXiv:1801.06419 (2018)
Peitz, S., Klus, S.: Koopman operator-based model reduction for switched-system control of PDEs. Automatica 106, 184–191 (2019)
Peitz, S., Ober-Blöbaum, S., Dellnitz, M.: Multiobjective optimal control methods for the Navier–Stokes equations using reduced order modeling. Acta Appl. Math. 161(1), 171–199 (2019)
Rabault, J., Kuchta, M., Jensen, A., Réglade, U., Cerardi, N.: Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 865, 281–302 (2019)
Rowley, C.W.: Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurc. Chaos 15(3), 997–1013 (2005)
Silver, D., Huang, A., Maddison, C.J., Guez, A., Sifre, L., van den Driessche, G., Schrittwieser, J., Antonoglou, I., Panneershelvam, V., Lanctot, M., Dieleman, S., Grewe, D., Nham, J., Kalchbrenner, N., Sutskever, I., Lillicrap, T., Leach, M., Kavukcuoglu, K., Graepel, T., Hassabis, D.: Mastering the game of go with deep neural networks and tree search. Nature 529(7587), 484–489 (2016)
Sirovich, L.: Turbulence and the dynamics of coherent structures part I: coherent structures. Q. Appl. Math. 45(3), 561–571 (1987)
Takens, F.: Detecting strange attractors in turbulence. In: Dynamical Systems and Turbulence, Warwick, Vol. 1980, pp. 366–381. Springer (1981)
Taylor, G.W., Hinton, G.E., Roweis, S.T.: Modeling human motion using binary latent variables. In: Schölkopf, B., Platt, J.C., Hoffman, T. (eds.) Advances in Neural Information Processing Systems 19, pp. 1345–1352. MIT Press, Cambridge (2007)
Tedrake, R., Jackowski, Z., Cory, R., Roberts, J.W., Hoburg, W.: Learning to fly like a bird. In: 14th International symposium on robotics research. Lucerne, Switzerland (2009)
Verma, S., Novati, G., Koumoutsakos, P.: Efficient collective swimming by harnessing vortices through deep reinforcement learning. PNAS 115(23), 5849–5854 (2018)
Weisberg Andersen, H., Kümmel, M.: Evaluating estimation of gain directionality. J. Process Control 2(2), 67–86 (1992)
Willcox, K., Peraire, J.: Balanced model reduction via the proper orthogonal decomposition. AIAA J. 40(11), 2323–2330 (2002)
Wu, Z., Fan, D., Zhou, Y., Li, R., Noack, B.R.: Jet mixing optimization using machine learning control. Exp. Fluids 59(8), 131 (2018)
Xi, Y.G., Li, D.W., Lin, S.: Model predictive control—status and challenges. Acta Autom. Sin. 39(3), 222–236 (2013)
Acknowledgements
Open Access funding provided by Projekt DEAL. KB acknowledges support by the German Federal Ministry of Education and Research (BMBF) within the project “Information-based optimization of surgery schedules (IBOSS)”. The calculations were performed on resources provided by the Paderborn Center for Parallel Computing (PC\(^2\)). SLB acknowledges support from the Army Research Office (ARO W911NF-19-1-0045).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Maziar S. Hemati.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Equations of a single RNN cell
As described in Sect. 3.1, the kth RNN cell takes as input \((\hat{z}_k, \hat{u}_k) = (z,u)_{k-2b,\dots ,k}\). This input is divided into three smaller sequences: \(x_{\mathrm{past}} = (z_{k-2b+1,\dots ,k-b}, u_{k-2b,k-b-1})\), \(x_{\mathrm{current}} = (z_{k-b+1,\dots ,k}, u_{k-b,k-1})\), \(u_{\mathrm{future}} = u_{k-b+1,k}\).
Input: \((\hat{z}_k, \hat{u}_k) \rightarrow x_{\mathrm{past}}, x_{\mathrm{current}}, u_{\mathrm{future}}\)
The equations for the encoder resp. the long term part of the decoder are given by
where \(\circ \) is the element-wise multiplication of vectors and relu computes the rectified linear, i.e., \(\max (0,x)\) for each element in x. The weights and the biases are the variables which are optimized during the training process and have the following dimensions:
where \(N_l\) is the size of the latent state \(l_k\) and \(N_h\) the size of the hidden layers. \(N_l\) and \(N_h\) can be chosen appropriately depending on the problem, cf. Appendix B for the concrete values as used in our experiments. \(N_x\) is determined by the delay \(d = 2b\), the number of observables \(n_o\) and the number of control inputs \(n_u\) as \(N_x = b (n_o + n_u)\). For the fluidic pinball, we observe the lift and drag at the three cylinders, and we can adapt the angular velocity of the two rear cylinders. Therefore, we have \(n_o = 6\) and \(n_u = 2\).
In order to predict the future state, the decoder consists of three additional parts. The equations are given by
where
with \(N_u = b n_u\). The final output \(z_{k+1}\) is computed via a linear layer:
where \(W_{\mathrm{out}} \in \mathbb {R}^{N_h \times N_{\mathrm{out}}}\) and \(b_{\mathrm{out}} \in \mathbb {R}^{N_{\mathrm{out}}}\) with \(N_{\mathrm{out}} = n_o\).
Parameter choice for the RNN
The structure of the RNN is defined by the number of neurons in the hidden layers, i.e., by \(N_h\) and \(N_l\), the number of encoder cells M and the chosen delay \(d =2b\). We performed different experiments to find appropriate values, and in Table 2 we summarize our final choices.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bieker, K., Peitz, S., Brunton, S.L. et al. Deep model predictive flow control with limited sensor data and online learning. Theor. Comput. Fluid Dyn. 34, 577–591 (2020). https://doi.org/10.1007/s00162-020-00520-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00162-020-00520-4