Skip to main content
SpringerLink
Log in

A compressed-sensing approach for closed-loop optimal control of nonlinear systems

  • Original Article
  • Published:
Theoretical and Computational Fluid Dynamics Aims and scope Submit manuscript

Abstract

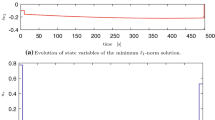
We present a method that seeks to combine the properties of optimal control with the robust character of closed-loop control. The method relies on the availability of a reduced model of the system to be controlled, in order to express the control problem in a low-dimensional space where the system-state-dependent optimal control law is subsequently approximated in a preprocessing stage. A polynomial expansion is used for the approximation, enabling fast update of the optimal control law each time a new observation of the system state is made available. It results in a real-time compatible, efficient (optimal-like), and robust control strategy. A compressed-sensing approach is proposed to efficiently construct the approximate control law, exploiting the compressible character of the optimal control law in the retained approximation basis. The method is demonstrated for the control of the flow around a cylinder and is shown to perform as well as the much more costly receding-horizon optimal control approach, where the exact optimal control problem is actually recomputed, even in the presence of large aleatoric perturbations. Potential and remaining issues toward application to larger dimensional reduced systems are also discussed, and some directions for improvement are suggested.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abramowitz M., Stegun I.: Handbook of mathematical functions. Dover, NY (1970)

    Google Scholar 

  2. Åkervik E., Hœpffner J., Ehrenstein U., Henningson D.S.: Optimal growth, model reduction and control in a separated boundary layer flow using global eigenmodes. J. Fluid Mech. 579, 305–314 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  3. Becker, S, Bobin, J, Candès, E.: NESTA: a fast and accurate first-order method for sparse recovery. Caltech Institute of Technology, Tech. Rep. (2009)

  4. Benner P., Jing-Rebecca L., Pentzl T.: Numerical solution of large-scale Lyapunov equation, Riccati equations, and linear-quadratic optimal control problems. Num. Lin. Alg. Appl. 15, 755–777 (2008)

    Article  MATH  Google Scholar 

  5. Candès E.J., Tao T.: Near-optimal signal recovery from random projections: universal encoding strategies. IEEE Trans. Inform. Theory. 52, 5406–5425 (2006)

    Article  MathSciNet  Google Scholar 

  6. Candès E.J., Romberg J., Tao T.: Stable signal recovery from incomplete measurements. Comm. Pure Appl. Math. 59, 1207–1223 (2005)

    Article  Google Scholar 

  7. Candès E.J., Romberg J.: Quantitative robust uncertainty principles and optimally sparse decompositions. Found. Comput. Math. 6(2), 227–254 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  8. Clenshaw C., Curtis A.: A method for numerical integration on a automatic computer. Numer. Math. 2, 197–205 (1960)

    Article  MATH  MathSciNet  Google Scholar 

  9. Donoho D.L.: Compressed sensing. IEEE Trans. Inform. Theory. 52(4), 1289–1306 (2006)

    Article  MathSciNet  Google Scholar 

  10. Efron B., Hastie T., Johnstone I., Tibshirani R.: Least Angle Regression. Ann. Phys. 32, 407–499 (2004)

    MATH  MathSciNet  Google Scholar 

  11. Gerstner T., Griebel M.: Numerical integration using sparse grids. Numer. Algorithm 18, 209–232 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  12. Gilbert J.C., Lemaréchal C.: Some numerical experiments with variable-storage quasi-Newton algorithms. Math. Program. 45, 407–435 (1989)

    Article  MATH  Google Scholar 

  13. Iollo A., Lanteri S., Désidéri J.-A.: Stability properties of POD-Galerkin approximations for the compressible Navier-Stokes equations. Theor. Comput. Fluid Dyn. 13, 377–396 (2000)

    Article  MATH  Google Scholar 

  14. Iooss G., Joseph D.D.: Elementary stability and bifurcation theory. 2nd edn. Springer, Berlin (1990)

    Book  MATH  Google Scholar 

  15. Kim J., Bewley T.R.: A Linear Systems Approach to Flow Control. Ann. Rev. Fluid Mech. 39, 383–417 (2007)

    Article  MathSciNet  Google Scholar 

  16. Laub A.J.: A Schur method for solving algebraic Riccati equations. IEEE Trans. Auto. Control. 24, 913–921 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  17. LeMaître O., Scanlan R.H., Knio O.M.: Estimation of the flutter derivatives of an NACA airfoil by means of Navier-Stokes simulation. J. Fluid Struct. 17(1), 1–28 (2003)

    Article  Google Scholar 

  18. Le Maître O., Mathelin L.: Equation-free model reduction for complex dynamical systems. Int. J. Numer. Meth. Fluid. 63(2), 163–184 (2009)

    Google Scholar 

  19. Lewis F., Syrmos V.: Optimal control. 2nd edn. Wiley, New York (1995)

    Google Scholar 

  20. Lumley, J.L.: The structure of inhomogeneous turbulent flows. In: Iaglom, A.M., Tatarski, V.I. (eds.) Atmospheric Turbulence and Radio Wave Propagation, 221–227 (1967)

  21. Lumley, J.L.: Coherent structures in turbulence. In: Meyer, R.E. (ed.) Transition Turbul. 315–342 (1981)

  22. Mathelin, L, Gallivan, K.: A compressed sensing approach for partial differential equations with random input data. Comm. in Comput. Phys., submitted (2010)

  23. Mathelin L., Le Maître O.: Robust control of uncertain cylinder wake flows based on robust reduced order models. Comput. Fluid. 38, 1168–1182 (2009)

    Article  Google Scholar 

  24. Morris, K, Navasca, C.: Solution of Algebraic Riccati Equations Arising in Control of Partial Differential Equations. In: Zolesio J.P., Cagnol J. (eds.) Control and Boundary Analysis. Lecture Notes in Pure Appl. Math., vol. 240. CRC Press, Boca Raton (2005)

  25. Nobile F., Tempone R., Webster C.G.: An anisotropic sparse grid stochastic collocation method for partial differential equations with random input data. SIAM J. Num. Anal. 46, 2411–2442 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  26. Novak E., Ritter K.: High-dimensional integration of smooth functions over cubes. Numer. Math. 75, 79–97 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  27. Novak E., Ritter K.: Simple cubature formulas with high polynomial exactness. Constr. Approx. 15, 499–522 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  28. Petras K.: On the Smolyak cubature error for analytic functions. Adv. Comput. Math. 12, 71–93 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  29. Petras K.: Fast calculation in the Smolyak algorithm. Numer. Algorithm. 26, 93–109 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  30. Rugh W.J., Shamma J.S.: Research on gain scheduling. Automatica. 36, 1401–1425 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  31. Sirovitch L.: Turbulence and the dynamics of coherent structures part i: Coherent structures. Quart. Appl. Math. 45(3), 561–571 (1987)

    MathSciNet  Google Scholar 

  32. Smolyak S.A.: Quadrature and interpolation formulas for tensor products of certain classes of functions. Dokl. Akad. Nauk. SSSR 4, 240–243 (1963)

    Google Scholar 

  33. Takens F.: Detecting strange attractors in turbulence. Lect. Notes Math. 898, 366–381 (1981)

    Article  MathSciNet  Google Scholar 

  34. Van den Berg E., Friedlander M.P.: Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 31(2), 890–912 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  35. Wright S.J.: Primal-Dual Interior-Point Methods. SIAM Publications, Philadelphia, PA (1997)

    Book  MATH  Google Scholar 

  36. Zibulevsky M., Elad M.: L1-L2 optimization in signal and image processing. IEEE Signal Proc. Mag. 27(3), 76–88 (2010)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. LIMSI-CNRS, BP 133, Orsay, 91403, France

    Lionel Mathelin, Luc Pastur & Olivier Le Maître

  2. University Paris-Sud 11, Orsay cedex, 91405, France

    Luc Pastur

Authors
  1. Lionel Mathelin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luc Pastur
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Olivier Le Maître
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lionel Mathelin.

Additional information

Communicated by Knio.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mathelin, L., Pastur, L. & Le Maître, O. A compressed-sensing approach for closed-loop optimal control of nonlinear systems. Theor. Comput. Fluid Dyn. 26, 319–337 (2012). https://doi.org/10.1007/s00162-011-0235-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00162-011-0235-9

Keywords

Search

Navigation