Dynamic large strain formulation for nematic liquid crystal elastomers

Abstract

Liquid crystal elastomers (LCEs) are a class of materials which exhibit an anisotropic behavior in their nematic state due to the main orientation of their rod-like molecules called mesogens. The reorientation of mesogens leads to the well-known actuation properties of LCEs, i.e. exceptionally large deformations as a consequence of particular external stimuli, such as temperature increase. Another key feature of nematic LCEs is the capability to undergo deformation by constant stresses while being stretched in a direction perpendicular to the orientation of mesogens. During this plateau stage, the mesogens rotate towards the stretching direction. Such characteristic is defined as semisoft elastic response of nematic LCEs. We aim at modeling the semisoft behavior in a dynamic finite element method based on a variational-based mixed finite element formulation. The reorientation process of the rigid mesogens relative to the continuum rotation is introduced by micropolar drilling degrees of freedom. Responsible for the above-mentioned characteristics is an appropriate free energy function. Starting from an isothermal free energy function based on the small strain theory, we aim to widen it into the framework of large strains by identifying tensor invariants. In this work, we analyze the isothermal influence of the tensor invariants on the mechanical response of the finite element formulation and show that its space-time discretization preserves mechanical balance laws in the discrete setting.

1 Introduction

Liquid crystal elastomers (LCEs) are a class of materials, which is capable of remarkable deformations and actuation properties as a consequence of particular external stimuli, such as temperature change or electric fields. These charachteristics are due to the reorientation of the mesogens, i.e. the rodlike molecules which are linked to the backbone chains of the elastomer. The continuum theories included the main direction of the mesogens as a nematic director unit vector [1]. Another main feature of nematic LCEs is the experimentally observed semisoft elastic behavior of LCEs. The stress–strain plot of a stretched specimen, whose nematic director lies orthogonally to the direction of stretch, is characterized by a plateau of constant stress [2] due to the reorientation of the nematic director. Verwey et al. [3] distinguished between the ideal soft-elastic and semisoft elastic response: by the former, the rotation of the mesogens is achieved at a stress equal to zero [4, 5], whereas by the latter, the reorientation of the mesogens is accompanied by a slight increase of the stress, which was described by Urayama et al. [6] as quasi-plateau and it is preceded and followed by another stage without reorientation of the mesogens, i.e. the hard regime [3]. Both ideal softness and semi-softness were observed in experiments [1, 7]. The main reason for deviation from ideal softness lies in the thermomechanical history of the specimen [1]: if crosslinking occurred in the isotropic phase, the specimen will behave as ideally soft, whereas crosslinking occurred in the nematic phase leads to a semisoft response. A particular aspect which causes the diverting from ideal softness is the finite extensibility of polymer chains [8]: concerning this issue, Mao et al. [8] corrected the trace formula of Warner and Terentjev [1] by a variational approach starting from the Bogoliubov–Feynman inequality. Furthermore, if the specimen is stretched orthogonal to the original orientation of the nematic director, the reorientation of the mesogens is observed experimentally with the arise of a striped pattern in the elastomer [9]. In two adjacent stripes, the mesogens rotate in opposite directions [3]. Among the other remarkable properties, nematic elastomers also exhibit excellent damping properties by virtue of their softness [10], therefore the investigation on models which couple the exceptional features of nematic LCEs with dynamics is essential. A recent contribution to this topic was given by Wang et al. [11], who considered the additive split of the deformation gradient into the elastic and viscous part, and subsumed the latter under the internal variables, along with the deformation gradient, the nematic director and its gradient. In this way, they separated the dissipations due to the rotations of the mesogens and to the inherent viscoelasticity of the elastomer and compared their model with experimental results of Martin Linares et al. [12] in terms of rate-dependency. Liang and Li [13] explored the tunability of metamaterials by exploiting the semisoft elasticity of nematic LCEs. Semisoft elasticity was modeled by adding a term depending on fluctuations in the ordering of the nematic LCE to the trace formula of Warner and Terentjev [1, 14]. They performed simulations by changing the shape and size of pores and ligaments in the metamaterial, as well as by considering several anisotropy fluctuations parameters and ratios between step lenghts. Selingen et al. [15] modeled the elastodynamics starting from the Hamiltonian of the system [16] and widening it into finite strains by considering the Green–Lagrange strain tensor; the authors were able to mimic complex motions, such as peristalsis and crawling of an earthworm made of nematic elastomer. Mbanga et al. [17] used the same approach and focused on the semisoft elasticity and the rise of the striped pattern in monodomain nematic elastomers. Zhang et al. [18] considered distinct dissipations for the symmetric part of the spatial velocity gradient and the objective rate of the director, in order to model semisoftness in LCEs by the free energy of Verney and Warner [14] at different loading rates.

In the present work, we describe the numerical framework for reproducing semisoft elasticity of nematic LCEs. Firstly, the continuum model is taken from the work of Concas and Groß [19] and improved with the mesogen rotation mapping $\varvec{\beta }$ as further independent variable, which is also included in the strain energy function along with the previous continuum rotation mapping $\varvec{\alpha }$; secondly, the mesogen rotation mapping $\varvec{\beta }$ is defined by describing the reorientation of mesogens as dissipative process with subsequent application of the Coleman–Noll procedure to the other internal variables in the Clausius–Planck inequality; afterwards, the dissipation related to the reorientation of the nematic director is included as a functional in the principle of virtual power and the weak forms and corresponding momentum and moment of momentum balances are obtained. Finally, virtual experiments involving stretched films of nemating elastomers prove the preservation of balance laws, as well as the capability of our approach in reproducing semisoftness (Table 1).

Table 1 List of symbols

2 The finite element formulation

2.1 Continuum model

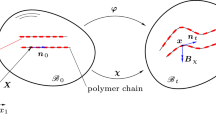
The LCE material is considered as a continuum body with two distinct mappings [20], i.e. the orientation mapping $\varvec{\chi }$ between the nematic director $\varvec{n}_0$ in the reference configuration $\mathscr {B}_{0}$ at time $t=0$ and the nematic director $\varvec{n}_t$ in the current configuration $\mathscr {B}_{t}$ and the deformation mapping $\varvec{\varphi }$, which maps a position vector $\varvec{X}\in \mathscr {B}_{0}$ to a position vector $\varvec{x}\in \mathscr {B}_{t}$. The continuum configuration was depicted by Concas and Groß [19]. In order to formulate the free energy density, we introduce the deformation gradient $\varvec{F}$, the right and left Cauchy–Green strain tensors, $\varvec{C}=\varvec{F}^{T}\varvec{F}$ and $\varvec{B}=\varvec{F}\varvec{F}^{T}$, respectively. The velocity vector $\varvec{\textrm{v}}\left( \varvec{X},t\right) :=\dot{\varvec{\varphi }}\left( \varvec{X},t\right) =\dot{\varvec{x}}$, the linear momentum vector $\varvec{\textrm{p}}:=\rho _0 \varvec{\textrm{v}}$ relating to the deformation mapping $\varvec{\varphi }$ are considered as variables along with the orientational velocity vector $\varvec{\textrm{v}}_{\chi }\left( \varvec{X},t\right) :=\dot{\varvec{\chi }}\left( \varvec{X},t\right) =\dot{\varvec{n}}_t$ and the orientational momentum vector $\varvec{\textrm{p}}_{\chi }:=\rho _0 l _{\chi }^{2} \varvec{\textrm{v}}_{\chi }$ for the orientation mapping $\varvec{\chi }$ [19]. In contrast to the work of Concas and Groß [19], in this work rotations of the nematic director have been separated from rotations occuring in the bulk elastomer. The distinction is made according to De Gennes [21], who introduced distinct rotations for the nematic director and the solids as two additive terms of the energy density. The first term consists in the squared Euclidean norm of cross product between the difference of both rotations $\left( \varvec{\alpha }-\varvec{\beta }\right)$ with the nematic director in the current configuration $\varvec{n}_t$; the second term is the scalar contraction of both indices of the deformation tensor with the nematic director and the aforesaid cross product. Since both parts of this rotational free energy are dependent on the relative rotations of the nematic director with respect to rotation occurring in the solids, the free energy is invariant for simultaneous rotations of the nematic director and of the solid. Warner and Terentjev [1] added two further cubic parts to the free energy of De Gennes. The second-order deformation tensor is defined within the linear elasticity limit [1]. Motivated by Groß et al. [22], we define the continuum rotation $\varvec{\alpha }$, which maps a material point described by the position vector $\varvec{X}\in \mathscr {B}_{0}$ to its three-dimensional rotation $\varvec{\gamma }=\varvec{\alpha }\left( \varvec{X}\right)$ in the current configuration $\mathscr {B}_{t}$. Analogously, the mesogen rotation $\varvec{\beta }$ maps $\varvec{X}\in \mathscr {B}_{0}$ to its absolute three-dimensional rotation $\varvec{\omega }=\varvec{\beta }\left( \varvec{X}\right)$ in the current configuration $\mathscr {B}_{t}$. Since the mesogens are embedded in the bulk elastomer, the mesogen rotation mapping $\varvec{\beta }$ refers to the material point $\varvec{X}$ in the reference configuration $\mathscr {B}_{0}$. The micropolar rotations are shown in Fig. 1, inspired by the representation of Warner and Terentjev [1]. Whereas the mesogen rotation mapping $\varvec{\beta }$ relates to the absolute rotation of the nematic director, the continuum rotation mapping $\varvec{\alpha }$ is directly linked to rotations of line elements [23] in the current configuration $\mathscr {B}_{t}$. The continuum rotation mapping $\varvec{\alpha }$ is described through its time derivative as the axial vector of the spatial velocity gradient

Fig. 1

Illustration of the rotation mappings $\varvec{\alpha }=\alpha \left( \varvec{X}\right) \varvec{e}_{3}$ and $\varvec{\beta }=\beta \left( \varvec{X}\right) \varvec{e}_{3}$ in case of a two-dimensional motion: the nematic director $\varvec{n}_0$ and a line element $\textrm{d}\varvec{X}$ in the reference configuration $\mathscr {B}_{0}$ (left), the nematic director $\varvec{n}_t$ and the line element $\textrm{d}\varvec{x}$ in the current configuration $\mathscr {B}_{t}$ with the respective absolute rotations $\varvec{\beta }=\varvec{\beta }\left( \varvec{X}\right)$ and $\varvec{\alpha }=\varvec{\alpha }\left( \varvec{X}\right)$ (right)

$$\begin{aligned} \dot{\varvec{\alpha }}=-\frac{1}{2}\varvec{\epsilon }:\dot{\varvec{F}}\varvec{F}^{-1}\,. \end{aligned}$$

(1)

The motion of the nematic director is outlined as a rigid-body rotation [24], in which the time derivative of the nematic director in the current configuration, that corresponds to the time derivative of the orientational mapping, is given by the cross product between the relative rotation of the director with respect to the solid and the orientational mapping

$$\begin{aligned} \dot{\varvec{\chi }}= \left( \dot{\varvec{\alpha }}-\dot{\varvec{\beta }}\right) \times \varvec{\chi }\,. \end{aligned}$$

(2)

By applying the principle of virtual power, Eqs. (1–2) are constraints, which have to be included into the functionals through scalar contraction with the corresponding Lagrange multipliers, i.e. the stress vector $\varvec{w}_{\tau }$

$$\begin{aligned} \varvec{w}_{\tau }=\varvec{\tau }_{\text {skw}}^{T}: \varvec{\epsilon } \end{aligned}$$

(3)

as double axial vector of the skew-symmetric Kirchhoff stress tensor $\varvec{\tau }_{\text {skw}}$ for the constraint of Eq. (1) and the reorientation stress vector $\varvec{\tau }_{\chi }$ for the constraint of Eq. (2) [19]. Both rotation mappings appear in the strain energy density

$$\begin{aligned}{} & {} \psi =\psi _e + \psi _i + \psi _r. \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \psi _e = c_1 \left( \varvec{I}: \varvec{C}-3-2 \log \left( J\right) \right) +\dfrac{\lambda }{2}\left( \left[ \log \left( J\right) \right] ^2+{\left( J-1\right) }^2\right) +c_3 \varvec{n}_{0}\cdot \varvec{C}\varvec{n}_{0}, \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \psi _i = c_3 \left( \varvec{I}: \left( \varvec{n}_t\otimes \varvec{n}_t\right) -1\right) + c_{9}\Vert \varvec{F}^T \varvec{n}_t\Vert ^2 +c_{10}\left( \varvec{n}_{0}\cdot \varvec{F}^T \varvec{n}_t\right) ^2, \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \psi _r = \dfrac{c_{11}}{2} {\textrm{tr}[\varvec{B}\varvec{W}_{\alpha -\beta }\left( \varvec{n}_t\otimes \varvec{n}_t\right) \varvec{W}_{\alpha -\beta }]}+\dfrac{c_{12}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_t\right] ^{2}. \end{aligned}$$

(7)

By defining three types of the strain energy density, we follow the approach of Anderson et al. [20]. The elastic strain energy density in Eq. (5) consists in the sum between the Neo-Hookean model and the double contraction of the right Cauchy–Green strain tensor with the dyad of the nematic director in the reference configuration $\varvec{n}_0$. In contrast with the work of Concas and Groß [19], the translational interactive energy density in Eq. (6) contains a further term with $c_3$ as prefactor, in order to fulfill the stress-free reference configuration [25], which is discussed in more detail in the Appendix A of this work. In Eqs. (5–6), the trace formula of Warner and Terentjev [1] appears as sum of invariants, i.e. the first term with prefactor $c_1$ and the last term with prefactor $c_3$ of Eq. (5), along with the last two terms of Eq. (6) with prefactors $c_9$ and $c_{10}$. This representation of the trace formula was also used by other authors, e.g. Anderson et al. [20]. By this notation of the trace formula, we assumed that the ratio r between lengths of step is the same in the reference and current configuration [19]. The remaining terms in Eq. (5) belong to the Neo-Hookean model and to the penalty functions for enforcing incompressibility with the second Lamé constant $\lambda$ as penalty term. We define Eq. (7) as rotational interactive energy density, which includes two terms depending on the relative rotation $\left( \varvec{\alpha }-\varvec{\beta }\right)$: the first one is another representation of one of the cubic relative energy density terms described by Warner and Terentjev [1], in which the prefactor $D_{22}$ and the small strain tensor have been replaced with the constant value $c_{11}$ and the left Cauchy–Green strain tensor, respectively; the second term is the already-mentioned squared Euclidean norm of De Gennes [21] with the constant $c_{12}$ instead of $D_1$ as prefactor. Such term penalizes relative rotation of the nematic director with respect to the bulk elastomer [1]. Among all the strain energy density terms described by De Gennes [21] and Warner and Terentjev [1], only the terms of Eq. (7) have been taken for the large strain formulation, since the strain energy density must be invariant by sign changes of all variables $\varvec{\chi }$, $\varvec{\alpha }$ and $\varvec{\beta }$. For instance, the strain energy density term of De Gennes [21] with $D_2$ as prefactor is a quadratic form of $\varvec{n}_t$, and hence it is invariant for positive and negative $\varvec{n}_t$, but not for positive or negative $\left( \varvec{\alpha }-\varvec{\beta }\right)$. The cubic term with the prefactor $D_{33}$, that were described by Warner and Terentjev [1], is discussed in Sect. 3. All terms of the rotational interactive energy density are invariant according to Zheng [26]. $\varvec{W}_{\alpha -\beta }$ is the skew-symmetric tensor associated with the cross product between the relative rotation and the nematic director.¹ Since $\varvec{W}_{\alpha -\beta }$ is a skew-symmetric tensor, the dot product $\varvec{W}_{\alpha -\beta }\left( \varvec{n}_t\otimes \varvec{n}_t\right) \varvec{W}_{\alpha -\beta }$ is a symmetric second-order tensor and its double contraction with the left Cauchy–Green strain tensor $\varvec{B}$ is invariant. This term allows the mutual influence between deformations occurring in the bulk elastomer, which are represented by $\varvec{B}$, and the reorientation of the nematic director induced by the relative rotation.

It is worth mentioning that the introduction of the mesogen rotation mapping $\varvec{\beta }$ is necessary for simulating the semisoft elastic behavior by using the present dynamic numerical framework, which includes the constraints of Eqs. (1–2) on the continuum rotation mapping $\varvec{\alpha }$ and the nematic director, respectively. The relative rotation $(\varvec{\alpha }-\varvec{\beta })$ of the nematic director with respect to the bulk elastomer was described by Warner and Terentjev [1] as a suitable physical variable for the free energy density function. If rotations of the nematic director is driven only by rotations occurring in the bulk elastomer, e.g. as in the work of Concas and Groß [19], our dynamic numerical framework cannot reproduce the rotation of the nematic directors towards the stretching direction. The values of the prefactors $\lambda$, $c_1$, $c_3$, $c_9$, $c_{10}$, as well as the reasoning concerning the usage of the same ratio r for the reference and current configuration, are described and explained in the work of Concas and Groß [19] and references therein. The newly added prefactors $c_{11}=-0.05\mu$ and $c_{12}=0.05\mu$ of the aforesaid invariants have been evaluated from preliminary simulations for the purpose of ensuring numerical stability. The invariance of the free energies in Eqs. (5–7) for rotations of the reference and the current configuration is proved in the Appendix B of this work.

2.2 Reorientation of the nematic director

The time evolution of the mesogen rotation mapping $\varvec{\beta }$ is described as a dissipative process. By following the same approach of Oates and Wang [27], the isothermal Clausius-Planck inequality reads

$$\begin{aligned} \mathcal {D}^{\textrm{int}}:=\varvec{N}:\dot{\varvec{F}}+\varvec{\eta }\cdot \dot{\varvec{\chi }}-\dot{\psi }\ge 0\,, \end{aligned}$$

(8)

where $\varvec{N}$ is a generalized first Piola–Kirchhoff stress tensor, since it includes any stress work-conjugated to the deformation gradient $\varvec{F}$. The vector $\varvec{\eta }$ is a conservative internal micro-stress vector [27]. According to Eqs. (4–7), the free energy density is a function of the deformation gradient, the nematic director $\varvec{n}_t$, i.e. the relating orientation mapping $\varvec{\chi }$, and both rotation mappings $\varvec{\alpha }$ and $\varvec{\beta }$. In contrast to the work of Wang et al. [11], we introduce here both independent rotations $\varvec{\alpha }$ and $\varvec{\beta }$ as internal variables, we also leave out the gradient of the nematic director and neglect viscoelastic effects on the bulk elastomer. The time derivative of the free energy density $\dot{\psi }$ is

$$\begin{aligned} \dot{\psi }=\dfrac{\partial \psi }{\partial \varvec{F}}:\dot{\varvec{F}}+\dfrac{\partial \psi }{\partial \varvec{\chi }}\cdot \dot{\varvec{\chi }}+\dfrac{\partial \psi }{\partial \varvec{\alpha }}\cdot \dot{\varvec{\alpha }}+\dfrac{\partial \psi }{\partial \varvec{\beta }}\cdot \dot{\varvec{\beta }}\,. \end{aligned}$$

(9)

By inserting Eq. (9) in Eq. (8), we obtain the new Clausius-Planck inequality as

$$\begin{aligned} \mathcal {D}^{\textrm{int}}:=\left( \varvec{N}-\dfrac{\partial \psi }{\partial \varvec{F}}\right) :\dot{\varvec{F}}+\varvec{\eta }\cdot \dot{\varvec{\chi }}-\dfrac{\partial \psi }{\partial \varvec{\chi }}\cdot \dot{\varvec{\chi }}-\dfrac{\partial \psi }{\partial \varvec{\alpha }}\cdot \dot{\varvec{\alpha }}-\dfrac{\partial \psi }{\partial \varvec{\beta }}\cdot \dot{\varvec{\beta }}\ge 0\,. \end{aligned}$$

(10)

In Eq. (1), the rate of the continuum rotation of the solid $\varvec{\alpha }$ depends on the axial vector of the spatial velocity gradient, and its contribution can thus be inserted² into the definition of the generalized first Piola–Kirchhoff stress tensor by applying the Coleman–Noll procedure

$$\begin{aligned} \varvec{N}:=\dfrac{\partial \psi }{\partial \varvec{F}}-\dfrac{1}{2}\dfrac{\partial \psi }{\partial \varvec{\alpha }}\cdot \varvec{\epsilon }\cdot \varvec{F}^{-T}\,. \end{aligned}$$

(11)

The definition of the conservative micro-stress vector $\varvec{\eta }$

$$\begin{aligned} \varvec{\eta }=\dfrac{\partial \psi }{\partial \varvec{\chi }} \end{aligned}$$

(12)

is also obtained through the Coleman–Noll procedure. Hence, the internal dissipation is

$$\begin{aligned} \mathcal {D}^{\textrm{int}}:=-\dfrac{\partial \psi }{\partial \varvec{\beta }}\cdot \dot{\varvec{\beta }}\ge 0. \end{aligned}$$

(13)

We impose on the internal dissipation to have a specific formulation

$$\begin{aligned} \mathcal {D}^{\textrm{int}}\overset{!}{=}\varvec{\Sigma }_{\beta }\cdot \dot{\varvec{\beta }}\qquad \text {with}\qquad \varvec{\Sigma }_{\beta }=V_{\beta }\dot{\varvec{\beta }}\,, \end{aligned}$$

(14)

where $\varvec{\Sigma }_{\beta }$ and $V_{\beta }$ denote the rotational non-equilibrium stress and the rotational viscosity parameter, respectively [28]. We consider a simple linear form for $\varvec{\Sigma }_{\beta }$, but a tensorial form of the viscosity might be chosen as well and possibly investigated in a future work. Our approach is different from the one followed by Zhang et al. [18], who set to zero most of the viscosity coefficients and obtained a liquid-crystal-related dissipation term depending only on the Jaumann rate of the nematic director. Our approach is comparable to the one of Garikipati et al. [29], who dealt with remodeling of biological tissue. Since the rotation of the collagen fibrils has to overcome the resistance offered by the surrounding gel, their relative rotation with respect to the gel is considered as dissipative process. Analogously, the relative rotation of the mesogens with respect to the bulk elastomer corresponds to an energy cost. In the work of Garikipati et al. [29], the dissipation is modeled as square of the Euclidean norm of the angular velocity of the fibrils similar to Eq. (14).

2.3 Variational-based weak formulation

In order to formulate the weak forms, we apply the principle of virtual power as in the work of Concas and Groß [19]. We start from the total energy balance, as described by Groß et al. [30], in which the sum of the functionals of the time rates of the kinetic energy, the external energy and internal energy is equal to zero. The sum of the virtual energy rates, which is integrated over any time step $\mathscr {T}_{n}:=\left[ t_{n},t_{n+1}\right]$ is

$$\begin{aligned}&\displaystyle \int ^{t_{n+1}}_{t_n}\left[ \delta _{*}\dot{\mathcal {T}}\left( \dot{\varvec{\varphi }},\dot{\varvec{\textrm{v}}},\dot{\varvec{\textrm{p}}}\right) +\delta _{*}\dot{\mathcal {T}}_{n}\left( \dot{\varvec{\chi }},\dot{\varvec{\textrm{v}}}_{\chi },\dot{\varvec{\textrm{p}}}_{\chi }\right) +\delta _{*}\dot{\Pi }^{\text {ext}}\left( \dot{\varvec{\varphi }},\varvec{R}\right) +\delta _{*}\dot{\Pi }^{\text {ext}}_n\left( \dot{\varvec{\chi }}\right) \right. \nonumber \\&\quad +\left. \delta _{*}\dot{\Pi }^{\text {int}}\left( \dot{\varvec{\varphi }},\dot{\varvec{\chi }},\dot{\varvec{\alpha }},\dot{\varvec{\beta }},\varvec{\tau }_{\chi },\varvec{w}_{\tau }\right) \right] \,\textrm{d}t:=0\,. \end{aligned}$$

(15)

Distinct kinetic energies and external energies for the deformation mapping $\varvec{\varphi }$ and the orientation mapping $\varvec{\chi }$ are considered [20]. The deformational and orientational kinetic powers and the corresponding variations, i.e. the Gateaux derivatives with respect to the variables $\dot{\varvec{\varphi }}$, $\dot{\varvec{\textrm{v}}}$, $\dot{\varvec{\textrm{p}}}$, $\dot{\varvec{\chi }}$, $\dot{\varvec{\textrm{v}}}_{\chi }$ and $\dot{\varvec{\textrm{p}}}_{\chi }$ are

$$\begin{aligned} \dot{\mathcal {T}}\left( \dot{\varvec{\varphi }},\dot{\varvec{\textrm{v}}},\dot{\varvec{\textrm{p}}}\right)&:=\displaystyle \int _{\mathscr {B}_{0}}\dot{\varvec{\textrm{v}}}\cdot \rho _0 \varvec{\textrm{v}}\,\textrm{d}V- \displaystyle \int _{\mathscr {B}_{0}}\dot{\varvec{\textrm{p}}}\cdot \left[ \varvec{\textrm{v}}-\dot{\varvec{\varphi }}\right] \,\textrm{d}V-\displaystyle \int _{\mathscr {B}_{0}}\varvec{\textrm{p}}\cdot \left[ \dot{\varvec{\textrm{v}}}-\ddot{\varvec{\varphi }}\right] \,\textrm{d}V\,, \end{aligned}$$

(16)

$$\begin{aligned} \dot{\mathcal {T}}_{n}\left( \dot{\varvec{\chi }},\dot{\varvec{\textrm{v}}}_{\chi },\dot{\varvec{\textrm{p}}}_{\chi }\right)&:=\displaystyle \int _{\mathscr {B}_{0}}\dot{\varvec{\textrm{v}}}_{\chi }\cdot \left[ \rho _0 l _{\chi }^2\right] \varvec{\textrm{v}}_{\chi }\,\textrm{d}V-\displaystyle \int _{\mathscr {B}_{0}}\dot{\varvec{\textrm{p}}}_{\chi }\cdot \left[ \varvec{\textrm{v}}_{\chi }-\dot{\varvec{\chi }}\right] \,\textrm{d}V\nonumber \nonumber \\&\quad -\displaystyle \int _{\mathscr {B}_{0}}\varvec{\textrm{p}}_{\chi }\cdot \left[ \dot{\varvec{\textrm{v}}}_{\chi }-\ddot{\varvec{\chi }}\right] \,\textrm{d}V\,, \end{aligned}$$

(17)

$$\begin{aligned} \delta _{*}\dot{\mathcal {T}}\left( \dot{\varvec{\varphi }},\dot{\varvec{\textrm{v}}},\dot{\varvec{\textrm{p}}}\right)&:=\displaystyle \int _{\mathscr {B}_{0}}\dot{\varvec{\textrm{p}}}\cdot \delta _{*}\dot{\varvec{\varphi }}\,\textrm{d}V+\displaystyle \int _{\mathscr {B}_{0}}\left( \rho _0 \varvec{\textrm{v}}-\varvec{\textrm{p}}\right) \cdot \delta _{*}\dot{\varvec{\textrm{v}}}\,\textrm{d}V\nonumber \nonumber \\&\quad -\displaystyle \int _{\mathscr {B}_{0}}\left[ \varvec{\textrm{v}}-\dot{\varvec{\varphi }}\right] \cdot \delta _{*}\dot{\varvec{\textrm{p}}}\,\textrm{d}V\,, \end{aligned}$$

(18)

$$\begin{aligned} \delta _{*}\dot{\mathcal {T}}_{n}\left( \dot{\varvec{\chi }},\dot{\varvec{\textrm{v}}}_{\chi },\dot{\varvec{\textrm{p}}}_{\chi }\right)&:=\displaystyle \int _{\mathscr {B}_{0}}\dot{\varvec{\textrm{p}}}_{\chi }\cdot \delta _{*}\dot{\varvec{\chi }}\,\textrm{d}V+\displaystyle \int _{\mathscr {B}_{0}}\left( \rho _0 l _{\chi }^2 \varvec{\textrm{v}}_{\chi }-\varvec{\textrm{p}}_{\chi }\right) \cdot \delta _{*}\dot{\varvec{\textrm{v}}}_{\chi }\,\textrm{d}V\nonumber \nonumber \\&\quad -\displaystyle \int _{\mathscr {B}_{0}}\left[ \varvec{\textrm{v}}_{\chi }-\dot{\varvec{\chi }}\right] \cdot \delta _{*}\dot{\varvec{\textrm{p}}}_{\chi }\,\textrm{d}V\,, \end{aligned}$$

(19)

respectively. The second and third terms of Eq. (16) relate to the definitions $\varvec{\textrm{v}}=\dot{\varvec{\varphi }}$, $\dot{\varvec{\textrm{v}}}=\ddot{\varvec{\varphi }}$ for the deformational velocity and its time rate. Analogously, the second and third terms of Eq. (17) refer to the identities $\varvec{\textrm{v}}_{\chi }=\dot{\varvec{\chi }}$, $\dot{\varvec{\textrm{v}}}_{\chi }=\ddot{\varvec{\chi }}$ for the orientational velocity field and its time rate. The first term of Eq. (17) depends on the square of the radius of gyration $l _{\chi }$, whose description can be found in our previous work [19] and references therein. Kinetic energies and their variations are identical to those of the work of Concas and Groß [19], as well as the external deformational power and its variation with respect to the variables $\dot{\varvec{\varphi }}$ and $\varvec{R}$

$$\begin{aligned} \dot{\Pi }^{\text {ext}}\left( \dot{\varvec{\varphi }},\varvec{R}\right)&:=-\displaystyle \int _{\mathscr {B}_{0}}\rho _0 \varvec{B}_{\varphi }\cdot \dot{\varvec{\varphi }}\,\textrm{d}V-\displaystyle \int _{\partial _{T}\mathscr {B}_{0}}\varvec{T}\cdot \dot{\varvec{\varphi }}\,\textrm{d}A\nonumber \\&\quad -\displaystyle \int _{\partial _{\varphi }\mathscr {B}_{0}}\varvec{R}\cdot \left( \dot{\varvec{\varphi }}-\dot{\bar{\varvec{\varphi }}}\right) \,\textrm{d}A \end{aligned}$$

(20)

$$\begin{aligned} \delta _{*}\dot{\Pi }^{\text {ext}}\left( \dot{\varvec{\varphi }},\varvec{R}\right)&:=-\displaystyle \int _{\mathscr {B}_{0}}\rho _0 \varvec{B}_{\varphi }\cdot \delta _{*}\dot{\varvec{\varphi }}\,\textrm{d}V-\displaystyle \int _{\partial _{T}\mathscr {B}_{0}}\varvec{T}\cdot \delta _{*}\dot{\varvec{\varphi }}\,\textrm{d}A- \displaystyle \int _{\partial _{\varphi }\mathscr {B}_{0}}\varvec{R}\cdot \delta _{*}\dot{\varvec{\varphi }}\,\textrm{d}A\nonumber \\&\quad -\displaystyle \int _{\partial _{\varphi }\mathscr {B}_{0}}\delta _{*}\varvec{R}\cdot \left[ \dot{\varvec{\varphi }}-\dot{\bar{\varvec{\varphi }}}\right] \,\textrm{d}A\,, \end{aligned}$$

(21)

where $\dot{\bar{\varvec{\varphi }}}$ is the prescribed velocity on the Dirichlet boundary $\partial _{\varphi }\mathscr {B}_{0}$ and $\varvec{R}$ is the reaction force vector, i.e. the Lagrange multiplier for the constraint $\dot{\varvec{\varphi }}=\dot{\bar{\varvec{\varphi }}}$ [19]. The functional of the dissipation is included into the external orientational power

$$\begin{aligned} \dot{\Pi }^{\text {ext}}_n\left( \dot{\varvec{\chi }},\dot{\varvec{\beta }}\right)&:=-\displaystyle \int _{\mathscr {B}_{0}}\rho _0 \varvec{B}_{\chi }\cdot \dot{\varvec{\chi }}\,\textrm{d}V-\displaystyle \int _{\partial _{W}\mathscr {B}_{0}}\varvec{W}\cdot \dot{\varvec{\chi }}\,\textrm{d}A+\displaystyle \int _{\mathscr {B}_{0}}\varvec{\Sigma }_{\beta }\cdot \dot{\varvec{\beta }}\,\textrm{d}V\,, \end{aligned}$$

(22)

$$\begin{aligned} \delta _{*}\dot{\Pi }^{\text {ext}}_n\left( \dot{\varvec{\chi }},\dot{\varvec{\beta }}\right)&:=-\displaystyle \int _{\mathscr {B}_{0}}\rho _0 \varvec{B}_{\chi }\cdot \delta _{*}\dot{\varvec{\chi }}\,\textrm{d}V-\displaystyle \int _{\partial _{W}\mathscr {B}_{0}}\varvec{W}\cdot \delta _{*}\dot{\varvec{\chi }}\,\textrm{d}A\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\varvec{\Sigma }_{\beta }\cdot \delta _{*}\dot{\varvec{\beta }}\,\textrm{d}V\,. \end{aligned}$$

(23)

The internal power contains both contributions of the deformational and orientational mapping and the constraints of Eqs. (1–2)

$$\begin{aligned} \dot{\Pi }^{\text {int}}\left( \dot{\varvec{\varphi }},\dot{\varvec{\chi }},\dot{\varvec{\alpha }},\dot{\varvec{\beta }},\varvec{\tau }_{\chi },\varvec{w}_{\tau }\right)&:=\displaystyle \int _{\mathscr {B}_{0}}\left[ \frac{\partial \psi }{\partial \varvec{F}}:\dot{\varvec{F}}+\frac{\partial \psi }{\partial \varvec{\chi }}\cdot \dot{\varvec{\chi }}+\frac{\partial \psi }{\partial \varvec{\alpha }}\cdot \dot{\varvec{\alpha }}+\frac{\partial \psi }{\partial \varvec{\beta }}\cdot \dot{\varvec{\beta }}\right] \,\textrm{d}V\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\varvec{\tau }_{\chi } \cdot \left[ \dot{\varvec{\chi }}- \left( \dot{\varvec{\alpha }}\times \varvec{\chi }\right) +\left( \dot{\varvec{\beta }}\times \varvec{\chi }\right) \right] \,\textrm{d}V\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\varvec{w}_{\tau } \cdot \left[ \frac{1}{2}\varvec{\epsilon }:\dot{\varvec{F}}\varvec{F}^{-1}+\dot{\varvec{\alpha }}\right] \,\textrm{d}V. \end{aligned}$$

(24)

The corresponding virtual internal power reads

$$\begin{aligned} \delta _{*}\mathcal {P}^{\text {int}}&:=\displaystyle \int _{\mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{F}}:\dfrac{\partial \varvec{F}}{\partial \varvec{\varphi }}\cdot \delta _{*}\dot{\varvec{\varphi }}\,\textrm{d}V+\displaystyle \int _{\mathscr {B}_{0}}\dfrac{1}{2}\varvec{w}_{\tau }\cdot \varvec{\epsilon }\cdot \varvec{F}^{-t}:\dfrac{\partial \varvec{F}}{\partial \varvec{\varphi }}\cdot \delta _{*}\dot{\varvec{\varphi }}\,\textrm{d}V\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{\chi }}\cdot \delta _{*}\dot{\varvec{\chi }}\,\textrm{d}V+\displaystyle \int _{\mathscr {B}_{0}}\varvec{\tau }_{\chi }\cdot \delta _{*}\dot{\varvec{\chi }}\,\textrm{d}V\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{\alpha }}\cdot \delta _{*}\dot{\varvec{\alpha }}-\displaystyle \int _{\mathscr {B}_{0}}\delta _{*}\dot{\varvec{\alpha }}\cdot \left( \varvec{\chi }\times \varvec{\tau }_{\chi } \right) \,\textrm{d}V\nonumber +\displaystyle \int _{\mathscr {B}_{0}}\varvec{w}_{\tau } \cdot \delta _{*}\dot{\varvec{\alpha }}\,\textrm{d}V\,\textrm{d}V\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{\beta }}\cdot \delta _{*}\dot{\varvec{\beta }}\,\textrm{d}V+\displaystyle \int _{\mathscr {B}_{0}}\delta _{*}\dot{\varvec{\beta }}\cdot \left( \varvec{\chi }\times \varvec{\tau }_{\chi } \right) \,\textrm{d}V\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\delta _{*}\varvec{\tau }_{\chi }\cdot \left[ \dot{\varvec{\chi }}- \left( \dot{\varvec{\alpha }}\times \varvec{\chi }\right) +\left( \dot{\varvec{\beta }}\times \varvec{\chi }\right) \right] \,\textrm{d}V\nonumber \\&\quad +\displaystyle \int _{\mathscr {B}_{0}}\delta _{*}\varvec{w}_{\tau }\cdot \left[ \frac{1}{2}\varvec{\epsilon }:\dot{\varvec{F}}\varvec{F}^{-1}+\dot{\varvec{\alpha }}\right] \,\textrm{d}V, \end{aligned}$$

(25)

where $\mathcal {P}^{\text {int}}$ is an abbreviation for $\dot{\Pi }^{\text {int}}\left( \dot{\varvec{\varphi }},\dot{\varvec{\chi }},\dot{\varvec{\alpha }},\dot{\varvec{\beta }},\varvec{\tau }_{\chi },\varvec{w}_{\tau }\right)$. We point out that the functional of the dissipation is included into the external power, because it is a non-conservative process. The choice to include the internal dissipation into Eq. (22) is in line with the procedure of Groß et al. [28]. By considering Eq. (15), the variations with respect to all variables are gathered in order to obtain the weak forms. Summarizing the integrals contracted with the variation $\delta _{*}\dot{\varvec{\varphi }}$ yields to the weak balance of linear momentum

$$\begin{aligned}&\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\delta _{*}\dot{\varvec{\varphi }}\cdot \left[ \dot{\varvec{\text {p}}}-\rho _0 \varvec{B}_{\varphi }\right] \,\text {d}V\,\text {d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\dfrac{1}{2}\varvec{w}_{\tau }\cdot \varvec{\epsilon }\cdot \varvec{F}^{-T}:\dfrac{\partial \varvec{F}}{\partial \varvec{\varphi }}\cdot \delta _{*}\dot{\varvec{\varphi }}\,\text {d}V\,\text {d}t\nonumber \\ {}&\quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{F}}:\dfrac{\partial \varvec{F}}{\partial \varvec{\varphi }}\cdot \delta _{*}\dot{\varvec{\varphi }}\,\text {d}V\,\text {d}t-\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{T}\mathscr {B}_{0}}\delta _{*}\dot{\varvec{\varphi }}\cdot \varvec{T}\,\text {d}A\,\text {d}t\,\nonumber \\ {}&\quad -\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{\varphi }\mathscr {B}_{0}}\delta _{*}\dot{\varvec{\varphi }}\cdot \varvec{R}\,\text {d}A\,\text {d}t=0\,, \end{aligned}$$

(26)

as well as the weak balance of orientational momentum for the variation $\delta _{*}\dot{\varvec{\chi }}$

$$\begin{aligned}&\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\delta _{*}\dot{\varvec{\chi }}\cdot \left[ \dot{\varvec{\textrm{p}}}_{\chi }-\rho _0 \varvec{\gamma }\right] \,\textrm{d}V\,\textrm{d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{\chi }}\cdot \delta _{*}\dot{\varvec{\chi }}\,\textrm{d}V\,\textrm{d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\delta _{*}\dot{\varvec{\chi }}\cdot \varvec{\tau }_{\chi }\,\textrm{d}V\,\textrm{d}t\nonumber \\&\quad -\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{W}\mathscr {B}_{0}}\delta _{*}\dot{\varvec{\chi }}\cdot \varvec{W}\,\textrm{d}A\,\textrm{d}t=0\,, \end{aligned}$$

(27)

the weak balances of the orientation rates for the variation $\delta _{*}\varvec{\tau }_{\chi }$

$$\begin{aligned} \displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\delta _{*}\varvec{\tau }_{\chi }\cdot \left[ \dot{\varvec{\chi }}-\left( \dot{\varvec{\alpha }}\times \varvec{\chi }\right) +\left( \dot{\varvec{\beta }}\times \varvec{\chi }\right) \right] \,\textrm{d}V\,\textrm{d}t=0, \end{aligned}$$

(28)

the weak continuum rotation equation for the variation $\delta _{*}\varvec{w}_{\tau }$

$$\begin{aligned} \displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\delta _{*}\varvec{w}_{\tau }\cdot \left[ \dot{\varvec{\alpha }}+\dfrac{1}{2}\varvec{\epsilon }:\dot{\varvec{F}}\varvec{F}^{-1}\right] \,\textrm{d}V\,\textrm{d}t=0 \end{aligned}$$

(29)

and finally the weak balances of the reorientation stress $\varvec{\tau }_{\chi }$

$$\begin{aligned}&\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\delta _{*}\dot{\varvec{\alpha }}\cdot \left[ \varvec{w}_{\tau }-\left( \varvec{\chi }\times \varvec{\tau }_{\chi }\right) +\frac{\partial \psi }{\partial \varvec{\alpha }}\right] \,\textrm{d}V\,\textrm{d}t=0, \end{aligned}$$

(30)

$$\begin{aligned}&\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\delta _{*}\dot{\varvec{\beta }}\cdot \left[ \left( \varvec{\chi }\times \varvec{\tau }_{\chi }\right) +\frac{\partial \psi }{\partial \varvec{\beta }}+\varvec{\Sigma }_{\beta }\right] \,\textrm{d}V\,\textrm{d}t=0 \end{aligned}$$

(31)

for the variations $\delta _{*}\dot{\varvec{\alpha }}$ and $\delta _{*}\dot{\varvec{\beta }}$. The weak forms for the other variations $\delta _{*}\dot{\varvec{\textrm{p}}}$, $\delta _{*}\dot{\varvec{\textrm{v}}}$ and $\delta _{*}\varvec{R}$ are shown in the work of Groß et al. [30] in their discrete form and weak forms for $\delta _{*}\dot{\varvec{\textrm{p}}}_{\chi }$ and $\delta _{*}\dot{\varvec{\textrm{v}}}_{\chi }$ can be deduced in the same way. The reorientation stress is determined by the weak forms in Eq. (30–31) and is thereby dependent on the skew-symmetric Kirchhoff stress tensor and on the rotational non-equilibrium stress. By this procedure, the rotational non-equilibrium stress $\varvec{\Sigma }_{\beta }$ has a direct influence on the reorientation rate $\dot{\varvec{\chi }}$ by driving the Lagrange multiplier $\varvec{\tau }_{\chi }$.

2.4 Balance laws

The balance laws are obtained from the weak equations in Eqs. (25–31) replacing the test functions, i.e. the variations with another function, since the test function may assume any value except 0. For instance, by replacing the variation $\delta _{*}\dot{\varvec{\varphi }}$ of Eq. (26) with the arbitrary constant vector $\varvec{c}$ in the weak balance of the linear momentum in Eq. (26), the following linear momentum balance is obtained

$$\begin{aligned} \varvec{L}\left( t_{n+1}\right) -\varvec{L}\left( t_{n}\right)&=\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\rho _0\varvec{B}_{\varphi }\,\textrm{d}V\,\textrm{d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{T}\mathscr {B}_{0}}\varvec{T}\,\textrm{d}A\,\textrm{d}t\nonumber \\&\quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{\varphi }\mathscr {B}_{0}}\varvec{R}\,\textrm{d}A\,\textrm{d}t. \end{aligned}$$

(32)

Analogously, by replacing the test function $\delta _{*}\dot{\varvec{\chi }}$ with the arbitrary constant vector $\varvec{c}$ in the weak balance of the orientational momentum in Eq. (27), the orientational momentum balance reads

$$\begin{aligned} \varvec{L}_n\left( t_{n+1}\right) -\varvec{L}_n\left( t_{n}\right)&=\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\rho _0 \varvec{B}_{\chi }\,\textrm{d}V\,\textrm{d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{W}\mathscr {B}_{0}}\varvec{W}\,\textrm{d}A\,\textrm{d}t\nonumber \\&-\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left[ \varvec{\tau }_{\chi }+\frac{\partial \psi }{\partial \varvec{\chi }}\right] \,\textrm{d}V\,\textrm{d}t\,. \end{aligned}$$

(33)

In order to formulate the balance of the moment of linear momentum, the test functions are set to $\delta _{*}\dot{\varvec{\varphi }}=\varvec{c} \times \varvec{\varphi }$, $\delta _{*}\dot{\varvec{\alpha }}=\varvec{c}$ and $\delta _{*}\dot{\varvec{\beta }}=\varvec{c}$ and inserted in the Eq. (26), Eqs. (30) and (31), respectively. Afterwards, Eqs.  (30–31) are inserted in Eq. (26) that gives back the following balance of the moment of linear momentum

$$\begin{aligned} \varvec{J}\left( t_{n+1}\right) -\varvec{J}\left( t_{n}\right)= & {} -\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left( \varvec{F} \times \dfrac{\partial \psi }{\partial \varvec{F}}\right) \,\textrm{d}V\,\textrm{d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left[ \varvec{\varphi }\times \rho _0\varvec{B}_{\varphi }\right] \,\textrm{d}V\,\textrm{d}t\nonumber \\{} & {} \quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{T}\mathscr {B}_{0}}\left[ \varvec{\varphi }\times \varvec{T}\right] \,\textrm{d}A\,\textrm{d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{\varphi }\mathscr {B}_{0}}\left[ \varvec{\varphi }\times \varvec{R}\right] \,\textrm{d}A\,\textrm{d}t\nonumber \\{} & {} \quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{\alpha }}\,\textrm{d}V\,\textrm{d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\frac{\partial \psi }{\partial \varvec{\beta }}\,\textrm{d}V\,\textrm{d}t\nonumber \\{} & {} \quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\varvec{\Sigma }_{\beta }\,\textrm{d}V\,\textrm{d}t. \end{aligned}$$

(34)

Inserting the test function $\delta _{*}\dot{\varvec{\chi }}=\varvec{c}\times \varvec{\chi }$ in Eq. (27) yields the balance of the moment of orientational momentum

$$\begin{aligned} \varvec{J}_{\chi }\left( t_{n+1}\right) -\varvec{J}_{\chi }\left( t_{n}\right)&=-\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left( \varvec{\chi }\times \dfrac{\partial \psi }{\partial \varvec{\chi }}\right) \,\textrm{d}V\,\textrm{d}t-\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left( \varvec{\chi }\times \varvec{\tau }_{\chi }\right) \,\textrm{d}V\,\textrm{d}t\nonumber \\&\quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left[ \varvec{\chi }\times \rho _0 \varvec{B}_{\chi }\right] \,\textrm{d}V\,\textrm{d}t\nonumber \\&\quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{W}\mathscr {B}_{0}}\left[ \varvec{\chi }\times \varvec{W}\right] \,\textrm{d}A\,\textrm{d}t \end{aligned}$$

(35)

By summing up Eqs. (34–35) the following balance is obtained

$$\begin{aligned}&\varvec{J}\left( t_{n+1}\right) -\varvec{J}\left( t_{n}\right) +\varvec{J}_{n}\left( t_{n+1}\right) -\varvec{J}_{n}\left( t_{n}\right) =-\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left( \varvec{F} \times \dfrac{\partial \psi }{\partial \varvec{F}}\right) \,\text {d}V\,\text {d}t\nonumber \\ {}&\quad -\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left( \varvec{\chi }\times \dfrac{\partial \psi }{\partial \varvec{\chi }}\right) \,\text {d}V\,\text {d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\varvec{\Sigma }_{\beta }\,\text {d}V\,\text {d}t-\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left( \varvec{\chi }\times \varvec{\tau }_{\chi }\right) \,\text {d}V\,\text {d}t\nonumber \\ {}&\quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left[ \varvec{\chi }\times \rho _0 \varvec{B}_{\chi }\right] \,\text {d}V\,\text {d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{W}\mathscr {B}_{0}}\left[ \varvec{\chi }\times \varvec{W}\right] \,\text {d}A\,\text {d}t\nonumber \\ {}&\quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \mathscr {B}_{0}}\left[ \varvec{\varphi }\times \rho _0\varvec{B}_{\varphi }\right] \,\text {d}V\,\text {d}t+\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{T}\mathscr {B}_{0}}\left[ \varvec{\varphi }\times \varvec{T}\right] \,\text {d}A\,\text {d}t\nonumber \\ {}&\quad +\displaystyle \int \!\!\!\int \limits _{\mathscr {T}_{n}\times \partial _{\varphi }\mathscr {B}_{0}}\left[ \varvec{\varphi }\times \varvec{R}\right] \,\text {d}A\,\text {d}t\,. \end{aligned}$$

(36)

The terms with the partial derivative of the free energy with respect to $\varvec{\alpha }$ and $\varvec{\beta }$ have been canceled in Eq. (36), since the following identity

$$\begin{aligned} \frac{\partial \psi }{\partial \varvec{\alpha }}=-\frac{\partial \psi }{\partial \varvec{\beta }} \end{aligned}$$

(37)

is valid and it will be discussed in the Appendix A, whereas the identity

$$\begin{aligned} \varvec{F} \times \dfrac{\partial \psi }{\partial \varvec{F}}=-\varvec{\chi }\times \dfrac{\partial \psi }{\partial \varvec{\chi }} \end{aligned}$$

(38)

is not satisfied for any invariant of Eq. (7).

In order to ensure stability and accuracy of our numerical framework, the weak forms and all the balance laws have to be fulfilled for each time step, hence Eqs. (27–31) and Eqs. (32–36) are represented as a double integral over the time domain $\mathscr {T}_{n}:=\left[ t_{n},t_{n+1}\right]$ and the space domain (either volume or boundary).

2.5 Space and time discretization

Consistently with the work of Concas and Groß [19], different fields of variables are considered: the time rate variables $\dot{\varvec{\phi }}\in \left\{ \dot{\varvec{\varphi }},\,\dot{\varvec{\alpha }},\,\dot{\varvec{\beta }},\,\dot{\varvec{\chi }},\,\dot{\varvec{\textrm{p}}},\,\dot{\varvec{\textrm{v}}},\,\dot{\varvec{\textrm{p}}}_{\chi },\,\dot{\varvec{\textrm{v}}}_{\chi }\right\}$ are discretized in space and time as follows

$$\begin{aligned} {\dot{\varvec{\phi }}}^{e} = \dfrac{1}{h_n}\sum ^{k+1}_{I=1}M'_{I}\left( \xi _{J}\right) \sum ^{\mathrm {n_{n}}}_{A=1} N_{A}\left( \zeta _{B}\right) {\varvec{\phi }}^{eA}_{I}\,; \end{aligned}$$

(39)

whereas the stress variables and variations ${\varvec{\varepsilon }}\in \big \{\varvec{\tau }_{\chi },\,\varvec{w}_{\tau },\,\varvec{R},\,\delta _{*}\dot{\varvec{\varphi }},\,\delta _{*}\dot{\varvec{\alpha }},\,\delta _{*}\dot{\varvec{\beta }},\,\delta _{*}\dot{\varvec{\chi }},\,\delta _{*}\varvec{\tau }_{\chi },\,\delta _{*}\varvec{w}_{\tau },\,\delta _{*}\varvec{R},\,\delta _{*}\dot{\varvec{\textrm{p}}},\,\delta _{*}\dot{\varvec{\textrm{v}}},\,\delta _{*}\dot{\varvec{\textrm{p}}}_{\chi },\,\delta _{*}\dot{\varvec{\textrm{v}}}_{\chi }\big \}$ are discretized as

$$\begin{aligned} {\varvec{\varepsilon }}^{e} = \sum ^{k}_{I=1}\tilde{M}_{I}\left( \xi _{J}\right) \sum ^{\mathrm {n_{n}}}_{A=1} N_{A}\left( \zeta _{B}\right) {\varvec{\varepsilon }}^{eA}_{I}\,, \end{aligned}$$

(40)

where ${\varvec{\phi }}^{eA}_{I}$ and ${\varvec{\varepsilon }}^{eA}_{I}$ are the spatial and temporal nodal values of each variable fields and $N_{A}\left( \zeta _{B}\right)$ is the spatial shape function with the Gauss points $\zeta _B$ with $B=1,..,n_{n}$. According to the continuous Galerkin method, different temporal shape functions $M'_{I}\left( \xi _{J}\right)$ and $\tilde{M}_{I}\left( \xi _{J}\right)$ are used for the time rate fields and the fields including stress variables and variations [31]. $M'_{I}\left( \xi _{J}\right)$ and $\tilde{M}_{I}\left( \xi _{J}\right)$ are Lagrange polynomials of degree k and $k-1$, respectively. $\xi _J$ denotes the temporal Gauss points with $J=1,...,k$ for $M'_{I}\left( \xi _{J}\right)$ and $J=1,...,k-1$ for $\tilde{M}_{I}\left( \xi _{J}\right)$. Consistently again with Concas and Groß [19], the fields $\varvec{\phi }\in \left\{ \varvec{\varphi },\,\varvec{\alpha },\,\varvec{\beta },\,\varvec{\chi },\,\varvec{\textrm{p}},\,\varvec{\textrm{v}},\,\varvec{\textrm{p}}_{\chi },\,\varvec{\textrm{v}}_{\chi }\right\}$ without time derivative are discretized in space and time as follows

$$\begin{aligned} {\varvec{\phi }}^{e} = \sum ^{k+1}_{I=1}M_{I}\left( \xi _{J}\right) \sum ^{\mathrm {n_{n}}}_{A=1} N_{A}\left( \zeta _{B}\right) {\varvec{\phi }}^{eA}_{I} \end{aligned}$$

(41)

The temporal shape functions $M_{I}\left( \xi _{J}\right)$ and $\tilde{M}_{I}\left( \xi _{J}\right)$ can be found in the work of Groß et al. [30]. The temporal shape function $M'_{I}\left( \xi _{J}\right)$ is the derivative of the shape function $M_{I}\left( \xi _{J}\right)$ with respect to the normalized time $\alpha$ [30]

$$\begin{aligned} \alpha :=\dfrac{t-t_{n}}{h_n} \end{aligned}$$

(42)

where $h_n:=t_{n+1}-t_{n}$ is the time step size. Further details relating to the space and time discretizations are reported by Concas and Groß [19] and references therein.

3 Numerical results

We aim to validate our model by simulating the stretch on both ends of a LCE film. Since the stretching direction is perpendicular to the nematic director in the reference configuration, the semisoft elastic response is observed. In all simulations, we used the density $\rho _0 = 1760$ kg/m$^{3}$, the Young’s modulus $E=0.914$ MPa and the Poisson’s ratio is $\nu =0.493$ [32]. The radius of gyration and the ratio between step lengths are set to $l _{\chi }=28\cdot 10^{-10}$ m [1] and $r=1.88$ [33] for the temperature of 60 $^{\circ }$C, respectively. As in the work of Concas and Groß [19], we describe a numerical framework, which takes into account only isothermal processes. The system of weak equations is solved by using UMFPACK [34]. The value of the rotational viscosity parameter is set to $V_{\beta }=200$ Pa s based on preliminary numerical tests. We implemented the model described in the Sects. 2.1–2.2 and the relating numerical framework in our in-house dynamic finite element software. All numerical experiments are performed within a time span of 0.1 s [32] with the time step size of 0.005 s. The scope of this work is to provide a numerical framework for semisoftness of nematic LCEs, hence we do not take into account any rate effect and our outcomes, such as stress–strain curves of stretched specimens, can be compared with experimental or numerical results from the literature only qualitatively. Concerning the space-time discretization, we have considered a degree $k=2$ for the Lagrangian polynomials of the temporal shape functions and a hexahedral element with eight nodes [19]. We use the same convergence criteria as Concas and Groß [19], but in this work we used a tolerance of $10^{-5}$ in order to deal with possible instabilies of the mesh that are due to the nematic directors rotating in opposite directions. In our virtual experiments, we consider a thin film ($0.0125\times 0.125\times 0.0005$ m) stretched in the x-direction and whose nematic directors are oriented in the $y-$direction in the reference configuration. The geometry and the boundary conditions are shown in Fig. 2. The only one boundary condition is the prescribed speed $\dot{\bar{\varvec{\varphi }}}=0.4$ m/s, which acts simultaneously on both ends of the geometry. Dirichlet boundary conditions are imposed in our numerical framework through the Lagrange multiplier $\varvec{R}$, i.e. the reaction force vector. We avoid to use any other Dirichlet boundary conditions, which may influence $\varvec{R}$. The variable $\varvec{R}$ determines engineering stresses in our stress–strain plots. Since no further boundary conditions are applied at the ends of the specimen, a dogbone shape for avoiding the influence of the clamps on the specimen is not needed. The geometry has a length to width ratio of 10 in order to increase the length of the plateau stage [1] and the corresponding mesh has 10000 linear hexahedral elements. Exploiting the symmetries of the geometry, as in the work of Conti et al. [4], would need a fewer number of elements and thereby reduce the computational burden, but in that case symmetry boundary conditions for the orientation mapping should be implemented, which is beyond the scope of this work. Moreover, asymmetrical deformations or rotations of the specimen can be detected only by modeling the whole geometry. In Fig. 3, the engineering stress—engineering strain curves are plotted for three different interactive energy densities: in the first case, the rotational interactive energy density is zero, i.e. $c_{11}=c_{12}=0$; in the second case, only the first term $\psi ^{c_{11}}$ of the rotational interactive energy density in Eq. (7) is considered (with $c_{12}=0$) and in the third case, only the second term $\psi ^{c_{12}}$ is regarded ($c_{11}=0$). Keeping both prefactors $c_{11}\ne 0$ and $c_{12}\ne 0$ leads to numerical instabilities, hence both terms of the rotational interactive energy density must be analyzed separately. The engineering stresses is given by the average of the reaction force $\varvec{R}$ nodal values on the right end of the specimen and dividing it by its cross-sectional area in the reference configuration. The reaction force has only a component in the x-direction, since the prescribed Dirichlet boundary condition $\dot{\varvec{\varphi }}=\dot{\bar{\varvec{\varphi }}}$ acts parallel to the x-direction. According to our preliminary analysis, trends are the same if nodes on the left end of the specimen were considered, instead of the right end, except with a few negligible deviations during the quasi-plateau stage. All curves in Fig. 3 exhibit the same drop of the engineering stresses between the linear elastic stage and the quasi-plateau stage. All trends are qualitatively comparable to the numerical simulations of Wang et al. [11], especially in terms of the pronounced drop in the engineering stresses, but not quantitatively due to e.g. the different strain rates. Therefore, it may be deduced that the semisoft elastic response is guided mainly by the dissipation rather than by the invariants of the rotational interactive energy density. Nonetheless, the trend of the quasi-plateau stage is steeper if $c_{11}=c_{12}=0$ and at least one of the invariants in $\psi ^{c_{11}}$ or $\psi ^{c_{12}}$ is thus needed for reducing the steepness of the plateau. A common feature of all curves is a pronounced saw-tooth-like trend in the linear elastic stage, which might be due to fluctuations in the nodal values of the reaction force $\varvec{R}$, since nematic directors do not rotate at all during this stage.

Fig. 2

Stretch ($\dot{\bar{\varvec{\varphi }}}=0.4$ m/s) of nematic LCE film with a length to width ratio of 10. The nematic directors are depicted as black arrows every 60 nodes in the front side of the geometry

Fig. 3

Engineering stresses—engineering strain curve for three different interactive energy density: without any rotational interactive energy density, with only the rotational energy density $\psi ^{c_{11}}$ and the rotational energy density $\psi ^{c_{12}}$

Fig. 4

Engineering stress—engineering strain curve (a) for the simulation of a nematic LCE without rotational interactive energy density ($c_{11}=c_{12}=0$) under stretch. The images show the nematic directors and the distribution of the reorientational stress vector on the LCE film for five different stages (b–f) of the virtual experiment

Fig. 5

Linear momentum and moment of momentum (a), orientational momentum and moment of orientational momentum (b), normalized errors of the linear momentum balance and of the moment of linear momentum balance (c), normalized errors of the orientational momentum balance and of the moment of orientational momentum balance (d) over time for the LCE film under stretch without rotational interactive energy density ($c_{11}=c_{12}=0$). In all of the plots, the left y-axis refers to the momenta and the right y-axis to the moments of momentum

Fig. 6

Engineering stress—engineering strain curve (a) for the simulation of a nematic LCE with rotational interactive energy density $\psi ^{c_{11}}$ ($c_{12}=0$) under stretch. The images show the nematic directors and the distribution of the reorientational stress vector on the LCE film for five different stages (b–f) of the virtual experiment

Fig. 7

Linear momentum and moment of momentum (a), orientational momentum and moment of orientational momentum (b), normalized errors of the linear momentum balance and of the moment of linear momentum balance (c), normalized errors of the orientational momentum balance and of the moment of orientational momentum balance (d) over time for the LCE film under stretch with only the rotational interactive energy density $\psi ^{c_{11}}$ ($c_{12}=0$). In all of the plots, the left y-axis refers to the momenta and the right y-axis to the moments of momentum

Fig. 8

Engineering stress—engineering strain curve (a) for the simulation of a nematic LCE with rotational interactive energy density $\psi ^{c_{12}}$ ($c_{11}=0$) under stretch. The images show the nematic directors and the distribution of the reorientational stress vector on the LCE film for five different stages (b–f) of the virtual experiment

Fig. 9

Linear momentum and moment of momentum (a), orientational momentum and moment of orientational momentum (b), normalized errors of the linear momentum balance and of the moment of linear momentum balance (c), normalized errors of the orientational momentum balance and of the moment of orientational momentum balance (d) over time for the LCE film under stretch with only the rotational interactive energy density $\psi ^{c_{12}}$ ($c_{11}=0$). In all of the plots, the left y-axis refers to the momenta and the right y-axis to the moments of momentum

In Fig. 4a, the engineering stress–strain curve is shown for the virtual experiment, in which the rotational interactive strain energy is set to zero. Figure 4b–f shows the specimen with the nematic directors and the distribution of the magnitude of the reorientation stress vector $\varvec{\tau }_{\chi }$ for five different steps: the first step (b) during the linear elastic stage; the stages (c) and (d) at the peak of the engineering stress and at its drop, respectively; the fourth (e) and the fifth (f) step during the quasi-plateau stage. The nematic directors are shown only on the front surface of the specimen every 60 nodes for the sake of clarity. The orientation of the nematic director is strongly related to the trend of the engineering stress: in the stage (b) nematic directors keep their orientation of the reference configuration and begin to rotate once the peak of stress (c) is reached. The beginning of the rotation can be noticed in the upper corners of the specimen in Fig. 4c. The sudden decrease of the engineering stress is achieved due to the pronounced rotation of the nematic directors in some areas of the specimen. By approaching either the right end or the left end of the specimen in Fig. 4d, nematic directors which are rotating in opposite directions are noticeable and the domains can be compared with the microstructure of Conti et al. [4]. Inhomogenities in the rotation of the nematic directors are accompanied by an increase in the magnitude of the reorientation stress vector $\varvec{\tau }_{\chi }$ and by distortions of elements, which make the usage of a mesh with 10000 elements unavoidable. In Fig. 4e, rotations of the nematic directors continue up to the stage (f), in which all nematic directors are mainly horizontal and no further reorientation occurs.

Figure 5 shows the trends of the momenta, angular momenta and relating normalized errors for the simulation of the LCE film under stretch with $c_{11}=c_{12}=0$. In Fig. 5a the linear momentum is given by Eq. (32) and since all the volume loads and surface loads are zero, it depends only on the reaction force $\varvec{R}$, whereas the moment of linear momentum is also dependent on the first Piola–Kirchhoff stress tensor and the rotational non-equilibrium stress (see Eq. (34)). The x-component of the linear momentum is zero up to the time step, where the stress drop from the peak begins, after which the linear momentum assumes an oscillating trend. The sudden decrease of the engineering stress leads to changes in the trends of the components of the moment of linear momentum, the orientational momentum and the moment of orientational momentum (see also Fig. 5b). Figure 5c, d shows the normalized errors, i.e. the difference between left- and right-hand sides of Eqs. (32–35) divided by the tolerance $10^{-5}$ for the linear momentum, the moment of linear momentum, the orientational momentum and the moment of orientational momentum, respectively. The normalized errors are well below 1, hence our numerical framework preserves all balances of the momentum and the angular momentum.

Figures 6 and 8 show the stress–strain curve and the specimen with the nematic directors and the distribution of the magnitude of the reorientation stress vectors $\varvec{\tau }_{\chi }$ for a rotational interactive energy density equal to $\psi ^{c_{11}}$ and $\psi ^{c_{12}}$, respectively. The distribution of $\varvec{\tau }_{\chi }$ is consistent with the case of the rotational interactive energy density equal to zero, with a higher magnitude of $\varvec{\tau }_{\chi }$ for nodes of adjacent elements, in which the nematic director rotates in opposite directions. However, the complete rotation of the directors is not achieved in the Fig. 6e, as in the middle of the specimen some nematic directors do not rotate at all and are still oriented in the $y-$direction. Furthermore, the specimen shows a cusp-like contour in the middle due to the presence of nematic directors with opposite orientations in adjacent elements. A cusp-like deformation also occurs by lower stretches for the cases in which the rotational interactive energy density is zero or equal to $\psi ^{c_{12}}$, although the relating images of the specimen are not depicted in Figs. 4 and 8. It may thus be deduced that $\psi ^{c_{11}}$ leads to a slower reorientation, which would be completed if a longer time span were analyzed. The coupling between deformations in the bulk elastomer and reorientation of the nematic director is strengthened if only $\psi ^{c_{11}}$ is taken into account as rotational interactive strain energy density, since the left Cauchy–Green strain tensor $\varvec{B}$ is double contracted with the dyad of the vector $\left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_t$. Based on our preliminary investigation, the reorientation of the nematic director might be even more restrained if another strain energy density described by Warner and Terentjev [1] with the prefactor $D_{33}$ is considered. This further part of the free energy density consists in the product of two scalar: the first scalar is the invariant of $\psi ^{c_{12}}$, i.e. the square of the Euclidean norm of the vector $\left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_t$ (see also the second term of Eq. 7); the second scalar is given by the double contraction of the strain tensor with the dyad of the nematic director in the current configuration. In this case, the prefactor $D_{33}$ must also be replaced in order to ensure numerical stability in the large strain regime. However, in order to achieve the complete reorientation of the nematic directors as in e.g Fig. 4e, a longer time span must be observed and hence the widening of the free energy density of Warner and Terentjev [1] to the large strain regime might be the subject of a future work. In Figs. 7 and 9 linear and orientational momenta, the moments of linear momentum and orientational momentum are shown along with the relating normalized errors. The drop of the reaction force and thus of the engineering stress causes the increase in the absolute value of the momenta from the zero value. By comparing Figs. 7a, b with 9a, b, trends over time are different for the linear momentum, the moment of linear momentum and the moment of orientational momentum, but the peak in the trend of the $y-$component of the orientational momentum occurs for all the invariants of Eq. (7) and also if the rotational interactive energy density is zero. The peak arises in correspondence of the drop of the engineering stress and begin of the quasi-plateau stage. All the normalized errors, which are depicted in Figs. 7c, d with 9c, d, are below 1, therefore the momenta and moments of momentum are preserved.

4 Conclusion

In this work, our dynamic numerical framework for reproducing semisoft elasticity in nematic LCEs has been described. We have started from the approach of Concas and Groß [19] and have included separate variables [21] as rotation mappings $\varvec{\beta }$ and $\varvec{\alpha }$ in order to distinguish between rotations of the nematic director and rotations occuring into the bulk elastomer, respectively. We have considered terms of the free energies of Warner and Terentjev [1] and De Gennes [21], which are defined for small strains and are invariants with respects to the above-mentioned variables. We have adapted these terms in order to make them suitable for simulations in the large strain regime and thus include them in our dynamic numerical framework: we have replaced the small strain tensor, which was double contracted with the dyad of the vector $\left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_t$ [1], with the left Cauchy–Green strain tensor $\varvec{B}$ and we have also applied prefactors $c_{11}$ and $c_{12}$, that are dependent only on the shear modulus $\mu$. We have defined the evolution of the mesogen rotation mapping $\varvec{\beta }$ as dissipative process. Based on the results discussed in this work, our numerical framework, which is based on the principle of virtual power, is able to reproduce semisoftness of nematic LCEs in the dynamic regime and to preserve mechanical balance laws. Furthermore, the usage of the energy densities of Warner and Terentjev [1] and De Gennes [21] improves the steepness of the quasi-plateau stage. In our simulations, we observed the arise of adjacent domains, where nematic directors rotate in opposite directions and the boundaries between domains are marked by a higher magnitude of the reorientation stress vector $\varvec{\tau }_{\chi }$. This feature can be enhanced in a future work for modeling the striped pattern occuring in nematic LCE under stretch. The model must be also improved under the aspect of the plateau length, since the described results show a fast rotation of the nematic director during the considered time span. A possible way to deal with the reduced length of the plateau stage might involve the free energy density of Warner and Terentjev [1] with $D_{33}$ as prefactor. In a future work, we also aim to extend our dynamic numerical framework to modelling fundamental features of nematic LCEs, such as their actuation response to light as a consequence of the isotropic-nematic transition, which was recently modelled by Brighenti and Cosma [35] by using a staggered scheme.

Appendices

Appendix A

The conditions for the stress-free reference configuration [25] have to be fulfilled not only for the free energy of Eqs. (5–7) and the first Piola–Kirchhoff stress tensor, but also for the stresses, that are work-conjugated to the other variables $\varvec{\chi }$, $\varvec{\alpha }$ and $\varvec{\beta }$, i.e.

$$\begin{aligned} \psi =0,\quad \frac{\partial \psi }{\partial \varvec{F}}=\varvec{0},\quad \frac{\partial \psi }{\partial \varvec{\chi }}=\varvec{0},\quad \frac{\partial \psi }{\partial \varvec{\alpha }}=\varvec{0},\quad \frac{\partial \psi }{\partial \varvec{\beta }}=\varvec{0} \end{aligned}$$

(A1)

must be valid in the reference configuration with

$$\begin{aligned} \varvec{F}=\varvec{I},\quad \varvec{n}_t=\varvec{n}_0,\quad \varvec{\alpha }=\varvec{\beta }\,. \end{aligned}$$

(A2)

The stress-free reference configuration is checked as first for Eq. (6) along with the last term of Eq. (5). The sum of the other terms in Eq. (5) is the Neo-Hookean model, for which the conditions for the stress-free reference configuration can be easily demonstrated. In order to check whether the reference configuration is stress-free, Eq. (A2) is inserted in the above-mentioned part of the energy density and in the following stresses, which are work conjugated to $\varvec{F}$

$$\begin{aligned} \dfrac{\partial \psi }{\partial \varvec{F}}=2c_3\varvec{F}\left( \varvec{n}_0\otimes \varvec{n}_0\right) +2c_9\left( {\varvec{n}_t}\otimes {\varvec{n}_t}\right) \varvec{F}+2c_{10}\left( \varvec{n}_0\varvec{F}^{T}\varvec{n}_t\right) \left( \varvec{n}_t\otimes \varvec{n}_0\right) \end{aligned}$$

(A3)

and $\varvec{\chi }$

$$\begin{aligned} \dfrac{\partial \psi }{\partial \varvec{\chi }}=2c_3\varvec{n}_t+2c_9\varvec{B}\varvec{n}_t+2c_{10}\left( \varvec{n}_0\varvec{F}^{T}\varvec{n}_t\right) \left( \varvec{F}\varvec{n}_0\right) \end{aligned}$$

(A4)

respectively. The free energy densities in Eqs. (5–6) are independent of the variables $\varvec{\alpha }$ and $\varvec{\beta }$ and the relating work conjugated stresses are thus zero. Replacing the prefactors $c_3$, $c_9$ and $c_{10}$ with their functions³ and using another representation for $\Vert \varvec{F}^T \varvec{n}_t\Vert ^2$⁴ yields

$$\begin{aligned} \psi&=\dfrac{\mu }{2}\left( r-1\right) \left[ \varvec{n}_0\cdot \varvec{n}_0+ \varvec{n}_0\cdot \varvec{n}_0-1\right] + \dfrac{\mu }{2}\left( \dfrac{1}{r}-1\right) \varvec{n}_0\cdot \varvec{n}_0\nonumber \\&\quad +\dfrac{\mu }{2}\left( 2-\dfrac{1}{r}-r\right) \left( \varvec{n}_{0}\cdot \varvec{n}_0\right) ^2=0 \end{aligned}$$

(A5)

for the free energy density,

$$\begin{aligned} \dfrac{\partial \psi }{\partial \varvec{F}}&=2\dfrac{\mu }{2}\left( r-1\right) \left( \varvec{n}_0\otimes \varvec{n}_0\right) +2\dfrac{\mu }{2}\left( \dfrac{1}{r}-1\right) \left( \varvec{n}_0\otimes \varvec{n}_0\right) \nonumber \\&\quad +2\dfrac{\mu }{2}\left( 2-\dfrac{1}{r}-r\right) \varvec{n}_0\cdot \varvec{n}_0\left( \varvec{n}_0\otimes \varvec{n}_0\right) ={\varvec{0}} \end{aligned}$$

(A6)

for the first Piola–Kirchhoff stress tensor and

$$\begin{aligned} \dfrac{\partial \psi }{\partial \varvec{\chi }}&=2\dfrac{\mu }{2}\left( r-1\right) \varvec{n}_0+2\dfrac{\mu }{2}\left( \dfrac{1}{r}-1\right) \varvec{n}_0+2\dfrac{\mu }{2}\left( 2-\dfrac{1}{r}-r\right) \left( \varvec{n}_0\cdot \varvec{n}_0\right) \varvec{n}_0=\varvec{0} \end{aligned}$$

(A7)

for the stress vector, which is work conjugated to $\varvec{\chi }$. The rotational interactive energy density of Eq. (7) is also dependent on $\varvec{\alpha }$ and $\varvec{\beta }$, therefore the relating work conjugated stress vectors are

$$\begin{aligned} \dfrac{\partial \psi ^{c_{11}}}{\partial \varvec{\alpha }}=c_{11}\left( \varvec{\mathcal {\epsilon }}\cdot \varvec{n}_t\right) \varvec{B}\left[ \left( \varvec{\mathcal {\epsilon }}\cdot \varvec{\beta }\right) -\left( \varvec{\mathcal {\epsilon }}\cdot \varvec{\alpha }\right) \right] \varvec{n}_t \end{aligned}$$

(A8)

and

$$\begin{aligned} \dfrac{\partial \psi ^{c_{11}}}{\partial \varvec{\beta }}=c_{11}\left( \varvec{\mathcal {\epsilon }}\cdot \varvec{n}_t\right) \varvec{B}\left[ \left( \varvec{\mathcal {\epsilon }}\cdot \varvec{\alpha }\right) -\left( \varvec{\mathcal {\epsilon }}\cdot \varvec{\beta }\right) \right] \varvec{n}_t\,. \end{aligned}$$

(A9)

for the energy density $\psi ^{c_{11}}$ with $c_{11}$ as prefactor and

$$\begin{aligned} \dfrac{\partial \psi ^{c_{12}}}{\partial \varvec{\alpha }}=-c_{12}\left( \varvec{\mathcal {\epsilon }}\cdot \varvec{n}_t\right) \left( \varvec{\mathcal {\epsilon }}\cdot \varvec{n}_t\right) \left( \varvec{\alpha }-\varvec{\beta }\right) \end{aligned}$$

(A10)

and

$$\begin{aligned} \dfrac{\partial \psi ^{c_{12}}}{\partial \varvec{\beta }}=-c_{12}\left( \varvec{\mathcal {\epsilon }}\cdot \varvec{n}_t\right) \left( \varvec{\mathcal {\epsilon }}\cdot \varvec{n}_t\right) \left( \varvec{\beta }-\varvec{\alpha }\right) \,. \end{aligned}$$

(A11)

for the energy density $\psi ^{c_{12}}$ with $c_{12}$ as prefactor. The work conjugated to $\varvec{\chi }$ are

$$\begin{aligned}&\dfrac{\partial \psi ^{c_{11}}}{\partial \varvec{\chi }}=c_{11}\varvec{W}_{\alpha -\beta }\varvec{B}\varvec{W}_{\alpha -\beta }\varvec{n}_t\,. \end{aligned}$$

(A12)

$$\begin{aligned}&\dfrac{\partial \psi ^{c_{12}}}{\partial \varvec{\chi }}=-c_{12}\varvec{W}_{\alpha -\beta }\varvec{W}_{\alpha -\beta }\varvec{n}_t\,. \end{aligned}$$

(A13)

The first Piola–Kirchhoff stress is

$$\begin{aligned} \dfrac{\partial \psi ^{c_{11}}}{\partial \varvec{F}}=c_{11}\varvec{W}_{\alpha -\beta }\left( \varvec{n}_t\otimes \varvec{n}_t\right) \varvec{W}_{\alpha -\beta }\varvec{F} \end{aligned}$$

(A14)

for $\psi ^{c_{11}}$. $\psi ^{c_{12}}$ is independent of $\varvec{F}$ and its work conjugated stress is thus zero. Since $\varvec{\alpha }=\varvec{\beta }$ (see Eq. (A2)) is valid in the reference configuration, and all of the rotational interactive energy densities in Eq. (7) and of the stresses in Eqs. (A8–A14) are dependent on the skew-symmetric second-order tensor $\varvec{W}_{\alpha -\beta }$ or its other representation $\left[ \left( \varvec{\mathcal {\epsilon }}\cdot \varvec{\beta }\right) -\left( \varvec{\mathcal {\epsilon }}\cdot \varvec{\alpha }\right) \right]$, the condition for the stress-free reference configuration is satisfied. Furthermore, due to the invariants of the rotational interactive free energy densities of Eq. (7), in which the continuum rotation mapping $\varvec{\alpha }$ appears always with the mesogen rotation $\varvec{\beta }$ as a difference of both variables, the identity in Eq. (37) is also satisfied.

Appendix B

In nematic LCEs, the free energy densities in Eqs. (5–7) must be invariant for rotations in the reference configurations $\mathscr {B}_{0}$ and the current configuration $\mathscr {B}_{t}$ [36]. In order to proof their invariance, we follow the approach of Steinmann [37] and introduce a second-order orthogonal tensor⁵$\varvec{Q}$ for indicating a rotation of the reference configurations $\mathscr {B}_{0}$, which transforms the initial nematic director $\varvec{n}_0$ and the deformation gradient $\varvec{F}$ as follows

$$\begin{aligned}{} & {} \varvec{n}_{0\,*}=\varvec{Q}^{T}\varvec{n}_0 \end{aligned}$$

(B1)

$$\begin{aligned}{} & {} \varvec{F}_{*}=\varvec{F} \varvec{Q}. \end{aligned}$$

(B2)

Vectors and tensors with the symbol ’$*$’ as subscript denote the transformed terms for rotations occurring on the reference configuration $\mathscr {B}_{0}$. On the other hand, terms with the superscript ’$*$’ are transformed for rotations of the current configuration $\mathscr {B}_{t}$, e.g. the nematic director $\varvec{n}_t$ transforms as

$$\begin{aligned} \varvec{n}_{t}^{*}=\varvec{Q} \varvec{n}_t \end{aligned}$$

(B3)

and the deformation gradient $\varvec{F}$ as

$$\begin{aligned} \varvec{F}^{*}=\varvec{Q}\varvec{F} \,. \end{aligned}$$

(B4)

using the same orthogonal second-order tensor $\varvec{Q}$. In order to check the invariance of the free energy densities of Eqs. (5–7), one must take into account that the initial nematic director $\varvec{n}_0$ and the right Cauchy–Green strain tensor $\varvec{C}$ are inherently invariant for rotations of the current configuration, whereas the current nematic director $\varvec{n}_t$ and the left Cauchy–Green strain tensor $\varvec{B}$ are inherently invariant for rotations of the reference configuration. Being equal to zero in the undeformed state, the relative rotation vector $\left( \varvec{\alpha }- \varvec{\beta }\right)$ is inherently invariant in the reference configuration and must be affected only by rotations of the current configuration [38] as

$$\begin{aligned} \left( \varvec{\alpha }-\varvec{\beta }\right) ^{*}=\varvec{Q} \left( \varvec{\alpha }-\varvec{\beta }\right) \,. \end{aligned}$$

(B5)

The terms of Eq. (5) involving J result to be invariant for rotations of both reference and current configurations⁶ [24]. By writing the rotational energy density $\psi ^{c_{11}}$ as

$$\begin{aligned} \psi ^{c_{11}}=\dfrac{c_{11}}{2} {\textrm{tr}[\varvec{B}\varvec{W}_{\alpha -\beta }\left( \varvec{n}_t\otimes \varvec{n}_t\right) \varvec{W}_{\alpha -\beta }]}= -\dfrac{c_{11}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{\chi }\right] \varvec{B}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{\chi }\right] \,, \end{aligned}$$

(B6)

the transformed free energy density for rotations of the reference configuration is

$$\begin{aligned} \psi _{*}&= c_1 \left( \varvec{I} : \varvec{C}_{*}-3-2 \log \left( J_{*}\right) \right) +\dfrac{\lambda }{2}\left( \left[ \log \left( J_{*}\right) \right] ^2+{\left( J_{*}-1\right) }^2\right) \nonumber \\&\quad +c_3 \varvec{n}_{0\,*}\cdot \varvec{C}_{*}\varvec{n}_{0\,*}+ c_3 \left( \varvec{I} : \left( \varvec{n}_{t\,*}\otimes \varvec{n}_{t\,*}\right) -1\right) \nonumber \\&\quad + c_{9}\varvec{n}_{t\,*}\cdot \varvec{B}_{*}\varvec{n}_{t\,*} +c_{10}\left( \varvec{n}_{0\,*}\cdot \varvec{F}^{T}_{*} \varvec{n}_{t\,*}\right) ^2\nonumber \\&\quad -\dfrac{c_{11}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) _{*}\times \varvec{n}_{t\,*}\right] \varvec{B}_{*}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) _{*}\times \varvec{n}_{t\,*}\right] +\dfrac{c_{12}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) _{*}\times \varvec{n}_{t\,*}\right] ^{2}\nonumber \\&= c_1 \left( \left( \varvec{Q}\varvec{Q}^{T}\right) : \varvec{C}-3-2 \log \left( J\right) \right) +\dfrac{\lambda }{2}\left( \left[ \log \left( J\right) \right] ^2+{\left( J-1\right) }^2\right) \nonumber \\&\quad +c_3 \varvec{n}_{0}\cdot \varvec{Q}\varvec{Q}^{T}\varvec{C}\varvec{Q}\varvec{Q}^{T}\varvec{n}_{0}+ c_3 \left( \varvec{I} : \left( \varvec{n}_{t}\otimes \varvec{n}_{t}\right) -1\right) \nonumber \\&\quad + c_{9}\varvec{n}_{t}\cdot \varvec{B}\varvec{n}_{t}+c_{10}\left( \varvec{n}_{0}\cdot \varvec{Q}\varvec{Q}^{T}\varvec{F}^{T} \varvec{n}_{t}\right) ^2\nonumber \\&\quad -\dfrac{c_{11}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] \varvec{B}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] +\dfrac{c_{12}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] ^{2}, \end{aligned}$$

(B7)

in which we consider the following identity

$$\begin{aligned} \varvec{I} : \left( \varvec{Q}^{T}\varvec{C}\varvec{Q}\right) =\left( \varvec{Q}\varvec{Q}^{T}\right) : \varvec{C}\,, \end{aligned}$$

(B8)

is identical as the sum of Eqs. (5–7). The transformed free energy density for rotations of the current configuration

$$\begin{aligned} \psi ^{*}&= c_1 \left( \varvec{I} : \varvec{C}^{*}-3-2 \log \left( J^{*}\right) \right) +\dfrac{\lambda }{2}\left( \left[ \log \left( J^{*}\right) \right] ^2+{\left( J^{*}-1\right) }^2\right) \nonumber \\&\quad +c_3 \varvec{n}^{*}_{0}\cdot \varvec{C}^{*}\varvec{n}^{*}_{0}+ c_3 \left( \varvec{I} : \left( \varvec{n}^{*}_{t}\otimes \varvec{n}^{*}_{t}\right) -1\right) \nonumber \\&\quad + c_{9}\varvec{n}^{*}_{t}\cdot \varvec{B}^{*}\varvec{n}^{*}_{t} +c_{10}\left( \varvec{n}^{*}_{0}\cdot \varvec{F}^{*\,T} \varvec{n}^{*}_{t}\right) ^2\nonumber \\&\quad +\dfrac{c_{11}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) ^{*}\times \varvec{n}^{*}_{t}\right] \varvec{B}^{*}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) ^{*}\times \varvec{n}^{*}_{t}\right] +\dfrac{c_{12}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) ^{*}\times \varvec{n}^{*}_{t}\right] ^{2}\nonumber \\&= c_1 \left( \varvec{I} : \varvec{C}-3-2 \log \left( J\right) \right) +\dfrac{\lambda }{2}\left( \left[ \log \left( J\right) \right] ^2+{\left( J-1\right) }^2\right) \nonumber \\&\quad +c_3 \varvec{n}_{0}\cdot \varvec{C}\varvec{n}_{0}+ c_3 \left( \left( \varvec{Q}^{T}\varvec{Q}\right) : \left( \varvec{n}_{t}\otimes \varvec{n}_{t}\right) -1\right) \nonumber \\&\quad + c_{9}\varvec{n}_{t}\cdot \varvec{Q}^{T}\varvec{Q}\varvec{B}\varvec{Q}^{T}\varvec{Q}\varvec{n}_{t} +c_{10}\left( \varvec{n}_{0}\cdot \varvec{F}^{T} \varvec{Q}^{T}\varvec{Q}\varvec{n}_{t}\right) ^2\nonumber \\&\quad +\dfrac{c_{11}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] \cdot \varvec{Q}^{T}\varvec{Q}\varvec{B}\varvec{Q}^{T}\varvec{Q}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] \nonumber \\&\quad +\dfrac{c_{12}}{2}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] \cdot \varvec{Q}^{T}\varvec{Q}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] \,, \end{aligned}$$

(B9)

with the identities [38]

$$\begin{aligned} \varvec{Q}\left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{Q}\varvec{n}_{t}=\varvec{Q}\left[ \left( \varvec{\alpha }-\varvec{\beta }\right) \times \varvec{n}_{t}\right] \end{aligned}$$

(B10)

and

$$\begin{aligned} \varvec{I} : \left( \varvec{Q}\varvec{n}_{t}\otimes \varvec{Q}\varvec{n}_{t}\right) =\left( \varvec{Q}^{T}\varvec{Q}\right) : \left( \varvec{n}_{t}\otimes \varvec{n}_{t}\right) \,, \end{aligned}$$

(B11)

is also identical as the sum of Eqs. (5–7). Hence, the invariance is fulfilled for rotations of both the reference and current configurations.