1 Introduction

The problem of collisions in plasmas has been widely studied since the first decades of the last century, starting with Landau’s pioneering work in 1936 [9]. The binary collisions between charged particles in plasma physics are caused by the long-range Coulomb interactions and have been modeled through different operators, with different physical characteristics and mathematical structures [9, 10, 20]. Coulombic interactions in the absence of wave-particle resonance are well described by the Landau integral operator [9], which is a nonlinear, integro-differential, Fokker–Planck type operator that satisfies the H-theorem for entropy growth [7].

It is generally believed that in a weakly collisional plasma, such as the solar wind, collisions are too weak to produce any significant effect on the plasma dynamics. However, in order to consider particle heating and the consequent entropy growth, the collisional approach appears to be necessary [11, 14, 16]. In fact, because of the H-theorem, thermalization is uniquely due to collisions, which produce heating in general thermodynamic sense.

The main difficulty of a kinetic approach is that the numerical solution of the (FPL) equation requires a huge computational cost. A possible strategy is that of replacing the Landau collisional operator with the Dougherty operator which is a nonlinear differential operator of the Fokker–Planck type which requires a significantly lighter computational effort [5]. A comparison between the Landau and the Dougherty collision operator can be found in [16,17,18].

In this paper, we propose to adopt the alternative approach used by Grad in gas dynamics [6], which approximates the kinetic model by a 13-moment system, with closure relations based on the Maximum Entropy Principle (MEP) [13]. This principle has been successfully used in other fields of physics and applied mathematics such as radiative fluid dynamics [12] and charge and energy transport in semiconductors [1,2,3, 15]. The main advantage of this approach is that its solution requires a much lower computational cost with respect to the numerical approximation of the kinetic equation, notwithstanding the use of the Landau operator.

The main objective of this paper is to derive the general moment system from the FPL equation coupled with the Maxwell equations and to underline a general procedure for obtaining closure relations for the extra moments and the moments of the collisional operator by applying the Maximum Entropy Principle. Furthermore, we specialize the above scheme to the 13-moment system, and in this case, we explicitly compute the closure relations. To test the validity of the model, we analytically solve the case of the relaxation towards equilibrium of a homogeneous plasma with a temperature anisotropy [16] and compare the results with those given by the special solution to the kinetic equation proposed by Kogan [8].

The paper is organized as follows: In Sect. 2, we introduce the FPL equation coupled with the Maxwell equations and we find the evolution equations for moments of electron distribution function f with weight functions which are tensorial products of the microscopic velocity. In Sect. 3, we define the internal moments, since their evolution equations are more suitable to be closed on the basis of the MEP. In Sect. 4, we consider the case of 13 moments, which have an immediate physical meaning, by explicitly computing the closure relations for the extra–fluxes and the production terms by expanding the MEP distribution function at the first order in anisotropy. Finally, in Sect. 5, we exploit a numerical test to check up to what extent the small anisotropy approximation gives good results, comparing them with those given by the Kogan solution [8], in the case of the relaxation towards equilibrium of a homogeneous plasma with a temperature anisotropy.

2 The Fokker–Planck–Landau equation and the moments equations

From a kinetic point of view, the dynamics of electrons in a plasma is described by means of their distribution function \(f({\textbf{x}},{\textbf{v}},t)\). This function represents the density of electrons at time t in an elementary volume \(\text {d}{\textbf{x}}\text {d}{\textbf{v}}\), around position \({\textbf{x}}\) and velocity \({\textbf{v}}\). The distribution f satisfies the Fokker–Planck–Landau (FPL) transport equation coupled with the self-consistent Maxwell equations:

$$\begin{aligned}{} & {} \frac{\partial f}{\partial t}+v_i\frac{\partial f}{\partial x_i}+\frac{q}{m}\Bigg [E_i +(\textbf{v}\wedge \textbf{B})_i\Bigg ]\frac{\partial f}{\partial v_i} =\mathcal {C}[f], \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \quad \mathcal {C}[f]:= \frac{\partial }{\partial v_i}\!\int _{\mathbb {R}^3}U_{ij}(\textbf{v}-\textbf{v}')\!\left[ f'\frac{\partial f}{\partial v_j}-f\frac{\partial f'}{\partial v'_j}\right] \!\textrm{d}\textbf{v}'\!, \quad U_{ij}(\textbf{w})=U_0|\textbf{w}|^{-3}(|\textbf{w}|^2\delta _{ij}-w_iw_j), \nonumber \\{} & {} -\epsilon \Delta \phi = q n:= q\int _{\mathbb {R}^3} f\,\textrm{d} \textbf{v}, E_i=-\frac{\partial \phi }{\partial x_i}. \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \nabla \cdot \textbf{B}=0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \nabla \wedge \textbf{E}+\frac{\partial }{\partial t}\textbf{B}=0, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \nabla \wedge \textbf{B}-\epsilon \mu \frac{\partial }{\partial t}\textbf{E}=q\mu \textbf{u}:=(q\mu /n)\int _{\mathbb {R}^3} \textbf{v f}\,\textrm{d}\textbf{v}. \end{aligned}$$
(5)

Here, the Einstein convention about the sum over repeated indices is adopted, q is the charge of the carriers (with sign), \({\textbf{v}}\) is the carrier velocity, \({\textbf{E}}\) is the electric field, \(\phi \) is the electric potential, \({\textbf{B}}\) is the magnetic field, \(\epsilon \) is the dielectric constant, \(\mu \) is the permeability, n is the carrier number density (concentration) and \({\textbf{u}}\) is the charge average velocity. The operator \({{\mathcal {C}}}[f]\) gives the time rate of change of f due to collisions, the prime denotes evaluation at \({\textbf{v}}'\), as in \(f'=f({\textbf{x}},{\textbf{v}}',t)\). Thus, (1) is a nonlinear integro-differential equation in seven independent variables.

An important property of the collision operator \({\mathcal {C}}[f]\) is the existence of physically relevant collisional invariants:

$$\begin{aligned} \int _{{\mathbb {R}}^3}\psi \,{{\mathcal {C}}}[f]\,\textrm{d}{\textbf{v}}=0, \quad \psi =1, v_i, \frac{1}{2} v_kv_k. \end{aligned}$$
(6)

This property implies conservation of the carrier number density, the average momentum and the average energy.

Another property of \({\mathcal {C}}[f]\) is the existence of an H-theorem, which can be stated in the following form:

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}^3}\log f/y\,{{\mathcal {C}}}[f]\textrm{d}{\textbf{v}} \ge 0, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} {{\mathcal {C}}}[f]=0 \; \iff \; f=\frac{m ^{\frac{3}{2}} n}{(2\pi k_B T)^{3/2}}\exp \left( -\frac{|{\textbf{v}}-{\textbf{u}}|^2}{2k_B T}\right) , \end{aligned}$$
(8)

with T the temperature, m the particle mass and \(y=2\left( \frac{m}{2\pi \hbar }\right) ^3\). This property establishes the existence of an entropy, i.e., \(h(f)=- \int _{{\mathbb {R}}^3} {f}(\log {f/y}-1) \text {d}{\textbf{v}}\), and of equilibrium distributions, i.e., shifted Maxwellians, of the system.

Macroscopic models can be obtained from the FPL equation by introducing moments of the distribution function which correspond to suitable choices of weight functions. One of the most common choices is that of taking tensor products of the microscopic velocity as weight functions, which gives the following moments

$$\begin{aligned} M_{i_1i_2\cdots i_k}:=\int _{{\mathbb {R}}^3} v_{i_1}v_{i_2}\cdots v_{i_k}\, f \,\textrm{d}{\textbf{v}},\,\,k=0,1,2,\dots . \end{aligned}$$
(9)

The first few moments have an immediate physical interpretation, that is, M is the number density, \(m\,M_i\) is the momentum density, \(\frac{1}{2}\,m\,M_{ii}\) is the energy density, \(m\,M_{ij}\) is the momentum flux, and \(\frac{1}{2}\,m\,M_{ijj}\) is the energy flux. The evolution equations for these moments can be easily obtained by multiplying equation (1) by \(v_{i_1}v_{i_2}\cdots v_{i_k}\) and integrating over \({\mathbb {R}}^3\), with a suitable vanishing condition for f as \(|{\textbf{v}}|\rightarrow \infty \). So doing, one gets

$$\begin{aligned}{} & {} \frac{\partial }{\partial t}M_{i_1i_2\cdots i_k} +\frac{\partial }{\partial x_r}M_{ri_1i_2\cdots i_k}= C_{i_1i_2\cdots i_k} +\frac{q}{m} k\bigg (E_{(i_1}M_{i_2\cdots i_k)}+B_{k}\epsilon _{jk(i_1}M_{i_2\cdots i_{k-1}) j}\bigg ), \end{aligned}$$
(10)

with \(k\ge 0\) and

$$\begin{aligned} C_{i_1i_2\cdots i_k}:=\int _{{\mathbb {R}}^3}v_{i_1}v_{i_2}\cdots v_{i_k} \,{{\mathcal {C}}}[f]\,\textrm{d}{\textbf{v}} \end{aligned}$$

production terms, and \(\epsilon _{ijk}\) the three-dimensional Levi–Civita symbol. Parentheses in suffices in (10) denote symmetrization with respect to the indices enclosed by them. In this way, there are only four independent variables, but the system is infinite. One needs to truncate the system at a finite order N, but the resulting system is not closed, since there appear extra variables which are the production terms and the flux \(M_{r i_1 i_2\dots i_N}\).

Constitutive equations are needed for these extra variables, which can be obtained by exploiting the MEP.

3 Internal moments and the Maximum Entropy Principle closure

For the system of the moments with \(0\le k\le N\), the MEP states that the closure relations for the extra moments and for the moments of \({\mathcal {C}}[f]\) can be evaluated by using the distribution function which maximizes the entropy under the constraint that the leading moments (9) are preserved [13]. Since, as has been proved in [19], the entropy does not depend on the mean velocity \(u_i=\frac{M_i}{M}\), it is convenient to introduce the so-called internal or non-convective moments which are defined as follows:

$$\begin{aligned} {\hat{M}}_{i_1i_2\cdots i_r}:=\int _{{\mathbb {R}}^3} fc_{i_1}c_{i_2}\cdots c_{i_r}\,\textrm{d}{\textbf{c}}, \end{aligned}$$

where \(c_i=v_i-u_i\) is the random component of the velocity.

Also in this case, the first moments have a particular interpretation, that is \({\hat{M}}=M\), \({\hat{M}}_i=0\), \(m{\hat{M}}_{ii}=2 n {\textsf{e}}=3p\), with \({\textsf{e}}\) the specific internal energy and p the pressure, \(m{\hat{M}}_{ij}=P_{ij}\), with \(P_{ij}\) the pressure tensor, and \(m{\hat{M}}_{ijj}=2q_i\) with \(q_i\) the heat flux.

It can be shown [19] that the internal moments are related to the old ones through the relation

$$\begin{aligned} {\textbf{M}}={\textbf{X}}({\textbf{u}})\hat{{\textbf{M}}} \end{aligned}$$
(11)

where \({\textbf{M}}=\left( \begin{array}{c} M\\ M_{i_1}\\ \vdots \\ M_{i_1\dots i_N} \end{array} \right) \) is the vector of all the moments taken into account, and \(\hat{{\textbf{M}}}\) is the vector of the corresponding internal moments, with \({\hat{M}}_{i_1}=0\), while \({\textbf{X}}({\textbf{u}})\) is the following matrix:

$$\begin{aligned} \left( \begin{array}{cccccc} 1 &{} 0 &{} \ldots &{} 0 &{}\dots &{} 0 \\ u_{i_1} &{} \delta _{i_1}^{j_1} &{} 0 &{} \ldots &{} \dots &{} 0 \\ u_{i_1}u_{i_2} &{} 2\delta _{(i_1}^{j_1}u_{i_2)} &{} \delta _{i_1}^{j_1}\delta _{i_2}^{j_2} &{} 0 &{} \dots &{}0\\ u_{i_1}u_{i_2}u_{i_3} &{} 3\delta _{(i_1}^{j_1}u_{i_2}u_{i_3)} &{}\dots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ u_{i_1} u_{i_2}\dots u_{i_n} &{}\left( \genfrac{}{}{0.0pt}{}{n}{1}\right) \delta _{(i_1}^{j_1}u_{i_2}\dots u_{i_n)} &{} \dots &{} \dots &{}\dots &{}\dots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ u_{i_1}u_{i_2}\dots u_{i_N} &{} \left( \genfrac{}{}{0.0pt}{}{N}{1}\right) \delta _{(i_1}^{j_1}u_{i_2}\dots u_{i_N)} &{} \dots &{} \left( \genfrac{}{}{0.0pt}{}{N}{3}\right) \delta _{(i_1}^{j_1}\delta _{i_2}^{j_2}\delta _{i_3}^{j_3}u_{i_4}\dots u_{i_N)} &{} \dots &{} \delta _{i_1}^{j_1}\delta _{i_2}^{j_2}\dots \delta _{i_N}^{j_N} \end{array} \right) , \end{aligned}$$

where the bottom indices are column indices and the upper ones are row indices. The above-written relation can be retrieved directly from the definitions of \(M_{i_1\dots i_k}\) and \({\hat{M}}_{i_1\dots i_k}\). However (11) relates all tensorial state quantities to their evaluation in the local rest frame, if the evolution evolution equations of these quantities are Galilean invariant [19], as is the case for the moments of the distribution function.

The evolution equations for the internal moments can be obtained by substituting (11) into (10), which gives

$$\begin{aligned}{} & {} \frac{\partial }{\partial t} {\hat{M}}_{i_1\dots i_k}+\frac{\partial }{\partial x_i}\left( {\hat{M}}_{i_1\dots i_k}u_i+{\hat{M}}_{i i_1\dots i_k}\right) \nonumber \\{} & {} \quad +k{\hat{M}}_{\bigg (i_1\dots i_{k-1}}\frac{\partial }{\partial t}u_{i_k\bigg )} +k\bigg (u_i{\hat{M}}_{\big (i_1\dots i_{k-1}} +{\hat{M}}_{i(i_1\dots i_{k-1}}\bigg )\frac{\partial }{\partial x_i}u_{i_k)} \nonumber \\{} & {} \quad -\frac{q}{m}k\Big ( E_{\big (i_k}{\hat{M}}_{i_1\dots i_{k-1}\big )}+B_{k}\epsilon _{jk\big (i_1}{\hat{M}}_{i_2\cdots i_{k-1}\big ) j}\Big )={\hat{C}}_{i_1i_2\dots i_k} \end{aligned}$$
(12)

where \({\textbf{C}}={\textbf{X}}({\textbf{u}})\hat{{\textbf{C}}}\), with obvious meaning of \({{\textbf{C}}}\) and \(\hat{{\textbf{C}}}\).

At this point, in order to obtain the necessary constitutive relations, the first step is to find the extremum of the entropy density

$$\begin{aligned} h=-k_B\int _{{\mathbb {R}}^3} {f}(\log (f/y)-1) \,\textrm{d}{\textbf{c}}, \end{aligned}$$

under the constraints

$$\begin{aligned} {\hat{M}}_{i_1\dots i_{k}}=\int _{{\mathbb {R}}^3}c_{i_1}\dots c_{i_k}f \,\textrm{d}{\textbf{c}},\quad k=0,\dots ,N. \end{aligned}$$
(13)

The solution is given by

$$\begin{aligned}{} & {} f_{\textrm{ME}}=y\exp (-{\chi }), \quad \text {with}\quad {\chi }=\sum _{k=0}^{N} {\hat{\lambda }}_{i_1\cdots i_k}c_{i_1}\cdots c_{i_k}. \end{aligned}$$
(14)

The physical interpretation of the Lagrange multipliers \(\hat{\varvec{\lambda }}\) follows from the generalized Gibbs relation

$$\begin{aligned} \textrm{d}h(f_{\textrm{ME}})=k_B\sum _{k=0}^{N}{\hat{\lambda }}_{i_1\cdots i_k}\,\textrm{d}{\hat{M}}_{i_1\cdots i_k}, \end{aligned}$$

which holds as a consequence of the MEP [13].

Inserting (14) into the constraints (13) and solving the resulting equations with respect to the Lagrange multipliers, in principle it is possible to express the ME distribution as function of the moments \(\hat{{\textbf{M}}}\). Eventually, substituting the so obtained \(f_{\textrm{ME}}\) into the integrals defining the extra variables, the needed constitutive relations could be found. Actually, in general, inversion can be done only numerically; however if the system is not too far from local equilibrium that it is slightly anisotropic, the ME distribution (14) can be expanded around the local equilibrium values of the Lagrange multipliers, so simplifying the inversion. At the first order, the expanded \(f_{\textrm{ME}}\) is strictly related to the Grad distribution which is widely used in extended thermodynamics. In the next section, we will present this procedure in the particular case when thirteen moments are used, the moments with an immediate physical interpretation.

4 The 13-moment model

In this section, we will explicitly write the moment system, including the closure relations, when the first thirteen moments with an immediate physical interpretation are taken as state variables. We recall that these moments are as follows: \(n={\hat{M}}\), \(u_i\), \(P_{ij}=m{\hat{M}}_{ij}\), and \(q_{i}=\frac{1}{2} m{\hat{M}}_{ikk}\), which respectively correspond to the weight functions \(\{1, v_i, m c_ic_j, \frac{1}{2}m c^2c_i\}\), with \(c^2={\textbf{c}}\cdot {\textbf{c}}\). The corresponding moment system, written in a conservative form, can be easily retrieved from (12) and reads

$$\begin{aligned}{} & {} \frac{\partial n}{\partial t}+\frac{\partial }{\partial x_r}\left( nu_r\right) =0, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( m n u_i\right) +\frac{\partial }{\partial x_r}\left( m n u_iu_r+P_{ri}\right) =q n\Big ( E_i+\epsilon _{ijk}u_jB_k\Big ), \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( m n u_iu_j+P_{ij}\right) +\frac{\partial }{\partial x_r}\left( m n u_iu_ju_r+P_{ij}u_r+P_{ri}u_j+P_{rj}u_i+m{\hat{M}}_{rij}\right) \nonumber \\ {}{} & {} \quad =m{\hat{C}}_{ij}+\frac{q}{m}\left[ E_i m n u_j+E_j m n u_i+B_k\epsilon _{lk(i}\left( n m u_{j)}u_l+P_{j)l} \right) \right] , \qquad \left( {\hat{C}}_{kk}=0\right) \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( \frac{1}{2} mnu^2 u_i+ n{\textsf{e}} u_i+P_{ik}u_k+q_{i}\right) +\frac{\partial }{\partial x_r}\left( \frac{1}{2} mn u^2 u_iu_r+n{\textsf{e}} u_iu_r \right. \nonumber \\{} & {} \qquad \left. +P_{ik}u_ku_r+P_{rk}u_iu_k+\frac{1}{2} P_{ri}u^2+q_{i}u_r+q_{r}u_i+m{\hat{M}}_{rik}u_k+\frac{1}{2}m{\hat{M}}_{rikk}\right) \nonumber \\{} & {} \quad =m{\hat{C}}_{ik}u_k\!+\!\frac{1}{2}m{\hat{C}}_{ikk}\!+\!\frac{q}{m}\left\{ E_i \left( \frac{1}{2} m n u^2+n{\textsf{e}}\right) \!+\!E_k (m n u_iu_k+P_{ik})+B_r\Big [2\epsilon _{lrj}\Big (\frac{1}{2} m{\hat{M}}_{ijl}\right. \nonumber \\{} & {} \qquad \left. + 3 u_{(j}P_{il)}+\frac{1}{2}m u_{i}u_{j}u_{l}\Big )+\epsilon _{lri}\Big (q_l+2u_{j}P_{jl} +u_l n{\textsf{e}} +\frac{1}{2}m u^2u_l\Big )\Big ]\right\} . \end{aligned}$$
(18)

Closure relations are needed for the extra-fluxes \({\hat{M}}_{rij}\), \({\hat{M}}_{rikk}\) and the collision terms \({\hat{C}}_{ij}\), \({\hat{C}}_{ikk}\):

$$\begin{aligned}{} & {} {\hat{M}}_{rij}=\int _{{\mathbb {R}}^3}c_{r}c_{i}c_{j}f_{\textrm{ME}}\,\textrm{d}{\textbf{c}},\nonumber \\{} & {} \quad {\hat{M}}_{rikk}=\int _{{\mathbb {R}}^3}c_{r}c_{i}c_{k}c_{k}f_{\textrm{ME}}\,\textrm{d}{\textbf{c}}, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \quad {\hat{C}}_{ij}=\int _{{\mathbb {R}}^3}c_{i}c_{j} \,{{\mathcal {C}}}[f_{\textrm{ME}}]\,\textrm{d}{\textbf{c}},\nonumber \\{} & {} \quad {\hat{C}}_{ikk}=\int _{{\mathbb {R}}^3}c_{i}c_{k}c_{k} \,{{\mathcal {C}}}[f_{\textrm{ME}}]\,\textrm{d}{\textbf{c}}. \end{aligned}$$
(20)

Here, the Maximum Entropy distribution function \(f_{\textrm{ME}}\) is given by:

$$\begin{aligned}{} & {} f_{\textrm{ME}}=y\exp \left( -\hat{\lambda }^{n}-\hat{\lambda }^{u}_{i}c_{i}-\hat{\lambda }^{P}_{ij}mc_{i}c_{j}-\hat{\lambda }^{q}_{i}\,\frac{1}{2} mc^2c_{i}\right) , \end{aligned}$$
(21)

and the Lagrangian multipliers can be obtained by inverting the constraints

$$\begin{aligned}{} & {} \int _{{\mathbb {R}}^3}f_{\textrm{ME}}\,\textrm{d}{\textbf{c}}=n,\nonumber \\{} & {} \quad \int _{{\mathbb {R}}^3}c_{i}f_{\textrm{ME}}\,\textrm{d}{\textbf{c}}=0, \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \quad m\int _{{\mathbb {R}}^3}c_{i}c_{j}f_{\textrm{ME}}\,\textrm{d}{\textbf{c}}=P_{ij},\nonumber \\{} & {} \quad \frac{1}{2} m\int _{{\mathbb {R}}^3}c^2 c_{i}f_{\textrm{ME}}\,\textrm{d}{\textbf{c}}=q_{i}. \end{aligned}$$
(23)

The resulting 13-moment system (15)–(18) is a symmetrizable hyperbolic system, coupled with a Poisson equation.

4.1 Inversion of the constraint relations

In order to invert the constraints, we consider the trace-free part of the tensor \(P_{ij}\), defined as \(P_{\langle ij \rangle }=P_{ij}-\frac{1}{3} P_{kk}\delta _{ij}\) and, recalling that \(P_{kk}=2n{\textsf{e}}\), we write \(P_{\langle ij \rangle }=P_{ij}-\frac{2}{3} n{\textsf{e}}\delta _{ij}\). We notice that \(P_{\langle ij \rangle }\) and \(n{\textsf{e}}\) are the moments associated to the weights \(mc_{\langle i}c_{i \rangle }\) and \(m\frac{1}{2} c^2\). Then, the Maximum Entropy distribution function becomes

$$\begin{aligned}{} & {} f_{\textrm{ME}}=y\exp \left( -\hat{\lambda }^{n}-\hat{\lambda }^{\textsf{e}}\frac{1}{2} m c^2 -\hat{\lambda }^{u}_{i}c_{i} -\hat{\lambda }^{P}_{\langle ij \rangle }mc_{\langle i}c_{j \rangle } -\hat{\lambda }^{q}_{i}\,\frac{1}{2} mc^2c_{i}\right) , \end{aligned}$$
(24)

with \(\hat{\lambda }^{\textsf{e}}=\frac{2}{3} \hat{\lambda }^{P}_{kk}\). We introduce a distinction between isotropic moments, n, \(n{\textsf{e}}\), and anisotropic moments, \(u_i\), \(P_{\langle ij \rangle }\), \(q_i\), by assuming small anisotropic Lagrange multipliers, \(\hat{\lambda }^{u}_{i}\), \(\hat{\lambda }^{P}_{\langle ij \rangle }\), \(\hat{\lambda }^{q}_{i}\). Then, at first order in anisotropy, the ME function reads

$$\begin{aligned} f_{\textrm{ME}}=f_{\textrm{ME}}^{(0)}({\textbf{c}})\big [1-f_{\textrm{ME}}^{(1)}({\textbf{c}})\big ], \end{aligned}$$
(25)

with

$$\begin{aligned} f_{\textrm{ME}}^{(0)}=y e^{-\hat{\lambda }^n-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2},\quad f_{\textrm{ME}}^{(1)}=\hat{\lambda }^u_i c_i+m\hat{\lambda }^P_{\langle ij \rangle }c_ic_j+ \frac{1}{2}m\hat{\lambda }^q_{i}c^2c_i. \end{aligned}$$

Substituting the \(f_{\textrm{ME}}\) (25) into the constraint relations, it is immediate to obtain the following system

$$\begin{aligned}{} & {} n=y e^{-\hat{\lambda }^n}\int _{{\mathbb {R}}^3}e^{-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2} \,\textrm{d}{\textbf{c}}, \quad n {\textsf{e}} =y e^{-\hat{\lambda }^n}\frac{1}{2}m\int _{{\mathbb {R}}^3}c^2e^{-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2} \,\textrm{d}{\textbf{c}}, \\{} & {} \quad 0=-y e^{-\hat{\lambda }^n}\Bigg [\hat{\lambda }^u_j\int _{{\mathbb {R}}^3}c_jc_i e^{-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2}\,\textrm{d}{\textbf{c}} +\frac{1}{2}m\hat{\lambda }^q_j\int _{{\mathbb {R}}^3}c_jc_ic^2 e^{-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2}\,\textrm{d}{\textbf{c}}\Bigg ], \\{} & {} \quad q_i=-\frac{1}{2}m y e^{-\hat{\lambda }^n}\Bigg [\hat{\lambda }^u_j\int _{{\mathbb {R}}^3}c_jc_i c^2e^{-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2}\,\textrm{d}{\textbf{c}} +\frac{1}{2}m\hat{\lambda }^q_j\int _{{\mathbb {R}}^3}c_jc_i c^4 e^{-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2}\,\textrm{d}{\textbf{c}}\Bigg ], \\{} & {} \quad P_{\langle ij \rangle }=-m^2ye^{-\hat{\lambda }^n} \hat{\lambda }^P_{\langle kl \rangle }\int _{{\mathbb {R}}^3}c_{\langle i}c_{j\rangle } c_{\langle k}c_{l \rangle } \,e^{-\frac{1}{2}m\hat{\lambda }^{{\textsf{e}}} c^2}\,\textrm{d}{\textbf{c}}. \end{aligned}$$

Defining \(n_i:=c_i/c\) and recalling the two properties

$$\begin{aligned} \int _{S^2}n_{i_1}\dots n_{i_k}\,\textrm{d}\Omega = \left\{ \begin{array}{ll} 0 &{} \text {if }k\text { is odd},\\ \frac{4\pi }{k+1}\delta _{(i_1 i_2}\dots \delta _{i_{k-1} i_k)} &{} \text {if}\,\,k\text { is even}, \end{array} \right. \\ \int _0^\infty x^n e^{-x^2}\,\textrm{d}x=\frac{1}{2}\Gamma \Big (\frac{n+1}{2}\Big )= \left\{ \begin{array}{ll} \frac{1}{2}\big (\frac{n-1}{2}\big )! &{} \text {if}\,\,n\text { is odd},\\[1ex] \frac{\sqrt{\pi }}{2^{n/2+1}}(n-1)!! &{} \text {if}\,\,n\text { is even}, \end{array}\right. \end{aligned}$$

where \(S^2\) is the unit sphere of \({\mathbb {R}}^3\), \(d\Omega \) is the element of the solid angle and \(\Gamma \) is the Gamma function; it is possible to solve the previous system with respect to the Lagrange multipliers to get

$$\begin{aligned} \hat{\lambda }^n= & {} \log {\Big [\frac{y}{n}\Big (\frac{4\pi {\textsf{e}}}{3 m}\Big )^{3/2}\Big ]},\quad \hat{\lambda }^{\textsf{e}}=\frac{3}{2{\textsf{e}}},\\ \hat{\lambda }^{u}_i= & {} \frac{9\, m}{4 \,n{\textsf{e}}^2}q_i,\quad \hat{\lambda }^{q}_i=-\frac{27\, m}{20\, n{\textsf{e}}^3}q_i,\quad \hat{\lambda }^{P}_{\langle ij \rangle }=-\frac{9}{8\,n{\textsf{e}}^2}P_{\langle ij \rangle }. \end{aligned}$$

These results are typical of the first-order approximation of extended thermodynamics of monatomic gases. It is well-known in the literature that this causes a reduction of the hyperbolicity region of the system, which improves if the second order approximation is used [4]. As said, the hypothesis of small anisotropy could be removed by numerically inverting the constraints which would require additional computational effort. We plan to do this in a future paper.

4.2 Closure for the extra-fluxes and the collision terms

Having analytically solved the constraints under the small anisotropy assumption, one can find the constitutive relations by inserting the approximate expression

$$\begin{aligned} f_{\textrm{ME}}\approx n\Big (\frac{3m}{4\pi {\textsf{e}}}\Big )^{\frac{3}{2}}\exp {\Big (-\frac{3m}{4{\textsf{e}}}c^2\Big )}\Big [1-\Big (\frac{9m}{4n{\textsf{e}}^2} -\frac{27m^2}{40n{\textsf{e}}^3 }c^2\Big ) c_i q_i+\frac{9m}{8n{\textsf{e}}^2}P_{\langle ij \rangle }c_ic_j \Big ] \end{aligned}$$
(26)

into the integral expressions of the extra variables.

For the extra-fluxes, one easily obtains

$$\begin{aligned} {\hat{M}}_{ijk}= & {} \frac{6}{5 m}\delta _{(ij}q_{k)}=\frac{2}{5 m}(\delta _{ij}q_{k}+\delta _{ki}q_{j}+\delta _{kj}q_{i}),\\ {\hat{M}}_{ijkk}= & {} \frac{20n{\textsf{e}}^2}{9 m^2}\delta _{ij}+\frac{14{\textsf{e}}}{3 m^2} P_{\langle ij \rangle }. \end{aligned}$$

The calculation of the production terms is more involved, due to the expression of the collision operator. We first notice that the kernel of the collision operator satisfies the following

Property 1

$$\begin{aligned} U_{ij}({\textbf{w}})w_i=U_{ij}({\textbf{w}})w_j=0. \end{aligned}$$

Moreover, at the first order, we have

$$\begin{aligned}{} & {} f_{\textrm{ME}}({\textbf{c}}')\frac{\partial f_{\textrm{ME}}({\textbf{c}})}{\partial c_k}\!\approx \! -f_{\textrm{ME}}^{(0)}({\textbf{c}}') f_{\textrm{ME}}^{(0)}({\textbf{c}}) \Bigg \{\!\Big [1\!-\!f_{\textrm{ME}}^{(1)}({\textbf{c}}')\!-\!f_{\textrm{ME}}^{(1)}({\textbf{c}})\Big ] {\hat{\lambda }}^{{\textsf{e}}}m c_k\!+\!\frac{\partial f^{(1)}_{\textrm{ME}}({\textbf{c}})}{\partial c_k}\!\Bigg \},\qquad \end{aligned}$$
(27)

with

$$\begin{aligned} \frac{\partial f^{(1)}_{\textrm{ME}}({\textbf{c}})}{\partial c_k}={\hat{\lambda }}^{{\textsf{u}}}_k+2m{\hat{\lambda }}^{P}_{\langle jk \rangle }c_j+\frac{1}{2}m{\hat{\lambda }}^{{\textsf{q}}}_i \big (c^2\delta _{ik}+2c_k c_i\big ). \end{aligned}$$

Indicating by \(\psi ({\textbf{c}})\) a generic weight function, the corresponding production term is

$$\begin{aligned} {\hat{C}}_{\psi }= & {} \iint \psi ({\textbf{c}})\frac{\partial }{\partial c_l} U_{lk} \Big [f_{\textrm{ME}}({\textbf{c}}')\frac{\partial f_{\textrm{ME}}({\textbf{c}})}{\partial c_k}- f_{\textrm{ME}}({\textbf{c}})\frac{\partial f_{\textrm{ME}}({\textbf{c}}')}{\partial c'_k}\Big ]\,\textrm{d}{\textbf{c}} \,\textrm{d} {\textbf{c}}'\\= & {} -\frac{1}{2}\iint U_{lk}\Bigg (f_{\textrm{ME}}({\textbf{c}}')\frac{\partial f_{\textrm{ME}}({\textbf{c}})}{\partial c_k}- f_{\textrm{ME}}({\textbf{c}})\frac{\partial f_{\textrm{ME}}({\textbf{c}}')}{\partial c'_k}\Bigg ) \Bigg (\frac{\partial \psi ({\textbf{c}})}{\partial c_l}-\frac{\partial \psi ({\textbf{c}}')}{\partial c'_l}\Bigg ) \,\textrm{d}{\textbf{c}} \,\textrm{d} {\textbf{c}}', \end{aligned}$$

where we have exploited the behaviour at infinity of \(f_{\text {M}E}\) and changed the role of \({\textbf{c}}\) and \({\textbf{c}}'\) for one half of the integral. Using Property 1 and (27), one has

$$\begin{aligned} U_{kl}({\textbf{c}}-{\textbf{c}}')\, \Bigg (f_{\textrm{ME}}({\textbf{c}}')\frac{\partial f_{\textrm{ME}}({\textbf{c}})}{\partial c_k}- f_{\textrm{ME}}({\textbf{c}})\frac{\partial f_{\textrm{ME}}({\textbf{c}}')}{\partial c'_k}\Bigg ) \approx -f_{\textrm{ME}}^{(0)}({\textbf{c}}') f_{\textrm{ME}}^{(0)}({\textbf{c}}) U_{lk} \Bigg \{\frac{\partial f^{(1)}_{\textrm{ME}}({\textbf{c}})}{\partial c_k}-\frac{\partial f^{(1)}_{\textrm{ME}}({\textbf{c}}')}{\partial c'_k}\Bigg \}. \end{aligned}$$

As a consequence the generic production term can be written as follows:

$$\begin{aligned} {\hat{C}}_{\psi }= & {} \frac{1}{2}\iint f_{\textrm{ME}}^{(0)}({\textbf{c}}') f_{\textrm{ME}}^{(0)}({\textbf{c}}) U_{lk}({\textbf{c}}-{\textbf{c}}')\Bigg (\frac{\partial \psi ({\textbf{c}})}{\partial c_l}-\frac{\partial \psi ({\textbf{c}}')}{\partial c'_l}\Bigg )\\{} & {} \times \big \{ 2m{\hat{\lambda }}^{P}_{\langle jk\rangle }(c_j-c'_j) +\frac{1}{2}m{\hat{\lambda }}^{{\textsf{q}}}_j \big [(c^2-c'^2)\delta _{jk}+2(c_k c_j-c'_kc'_j)\big ] \big \} \,\textrm{d}{\textbf{c}} \,\textrm{d} {\textbf{c}}'. \end{aligned}$$

This expression can be further simplified, if we distinguish between \(\psi ({\textbf{c}})\) being an even or an odd function. In fact, indicating the even and odd functions by \(\psi _e\) and \(\psi _o\), respectively, we have

$$\begin{aligned} {\hat{C}}_{\psi _e}= & {} m \,\lambda ^{P}_{\langle jk\rangle }\iint f_{\textrm{ME}}^{(0)}({\textbf{c}}') f_{\textrm{ME}}^{(0)}({\textbf{c}}) U_{lk}({\textbf{c}}-{\textbf{c}}')\Bigg (\frac{\partial \psi _e({\textbf{c}})}{\partial c_l}-\frac{\partial \psi _e({\textbf{c}}')}{\partial c'_l}\Bigg ) (c_j-c'_j)\,\textrm{d}{\textbf{c}} \,\textrm{d} {\textbf{c}}',\\ {\hat{C}}_{\psi _o}= & {} \frac{m}{4}\,\lambda ^{{\textsf{q}}}_{j}\iint f_{\textrm{ME}}^{(0)}({\textbf{c}}') f_{\textrm{ME}}^{(0)}({\textbf{c}}) U_{lk}({\textbf{c}}-{\textbf{c}}')\Bigg (\frac{\partial \psi _o({\textbf{c}})}{\partial c_l}-\frac{\partial \psi _o({\textbf{c}}')}{\partial c'_l}\Bigg ) \\ {}{} & {} \times \big [(c^2-c'^2)\delta _{jk} +2(c_k c_j-c'_kc'_j)\big ] \,\textrm{d}{\textbf{c}} \,\textrm{d} {\textbf{c}}'. \end{aligned}$$

In the thirteen moment model, the production terms to compute are as follows: C, \(C_i\), \({\hat{C}}_{ij}\), and \({\hat{C}}_{ill}\). It is immediate to see that the first two vanish together with \({{\hat{C}}}_{ll}\), the latter as consequence of Property 1. This is consistent with the conservation of number of particles, momentum and energy in the collisions between particles. Therefore, the collision terms which remain to be computed are \({\hat{C}}_{\langle ij \rangle }\) and \({\hat{C}}_{ill}\), the first involves an even function, \({c}_{\langle i}c_{j\rangle }\), the second an odd one, \(c_ic_lc_l\). After some algebra and making the substitution \({\textbf{c}}''={\textbf{c}}-{\textbf{c}}'\), one finds

$$\begin{aligned} {\hat{C}}_{ij}= & {} 2mU_0\hat{\lambda }^P_{\langle kl \rangle }\iint \!\!\!\iint f^{(0)}_{\textrm{ME}}({\textbf{c}}''+{\textbf{c}}')f^{(0)}_{\textrm{ME}}({\textbf{c}}') c''^3 c'^2\Big \{\delta _{k(i} n''_{j)} -n''_i n''_j n''_k\Big \} n_l''\,\textrm{d}\Omega ''\,\textrm{d}\Omega '\,\textrm{d}c'' \,\textrm{d}c',\\ {\hat{C}}_{ill}= & {} \frac{m}{4}U_0\hat{\lambda }^q_{k}\iint \!\!\!\iint f^{(0)}_{\textrm{ME}}({\textbf{c}}''+{\textbf{c}}')f^{(0)}_{\textrm{ME}}({\textbf{c}}')c''^3c'^2\Big \{ \big ( c''+2 c'{\textbf{n}}'\cdot {\textbf{n}}''\big )^2\delta _{ik}\\{} & {} -\big [ c''^2 +8 c' c'' {\textbf{n}}'\cdot {\textbf{n}}''+16\big ({\textbf{n}}'\cdot {\textbf{n}}'' \big )^2 c'^2-4 c'^2\big ]n''_i n''_k\\{} & {} +4 c' \big ( c''+2 c'{\textbf{n}}'\cdot {\textbf{n}}''\big ) n'_{(i}n''_{k)} \Big \} \,\textrm{d}\Omega ''\,\textrm{d}\Omega '\,\textrm{d}c''\,\textrm{d} c', \end{aligned}$$

where \(c'=|{\textbf{c}}'|\), \(c''=|{\textbf{c}}''|\). If in the integration with respect to \({\textbf{c}}'\) one uses as reference frame one which has the z-axis parallel to \({\textbf{n}}''\), the above-written integrals can be explicitly computed to get

$$\begin{aligned} {\hat{C}}_{ij}= & {} -\frac{3}{5} n U_0\left( \frac{6m}{\pi {\textsf{e}}^3} \right) ^{\frac{1}{2}} P_{\langle ij \rangle }, \end{aligned}$$
(28)
$$\begin{aligned} {\hat{C}}_{ikk}= & {} -\frac{4}{5} n U_0 \left( \frac{6m}{\pi {\textsf{e}}^3}\right) ^{\frac{1}{2}} q_{i}. \end{aligned}$$
(29)

As can be seen, after lengthy and cumbersome computations, the closure relations have very simple explicit expressions.

The final system is the following:

$$\begin{aligned}{} & {} \frac{\partial n}{\partial t}+\frac{\partial }{\partial x_r}\left( nu_r\right) =0, \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( {m} n u_i\right) +\frac{\partial }{\partial x_r}\left( {m} n u_iu_r+\frac{2}{3} n{\textsf{e}}\delta _{ri}+P_{\langle ri \rangle }\right) =q n \Big ( E_i+\epsilon _{ijk}u_jB_k\Big ) \end{aligned}$$
(31)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( {m} n u_iu_j+\frac{2}{3} n{\textsf{e}}\delta _{ij}+P_{\langle ij \rangle }\right) +\frac{\partial }{\partial x_r}\left( {m} n u_iu_ju_r +\frac{2}{3} n{\textsf{e}}(u_r\delta _{ij}+u_j\delta _{ri}+u_i\delta _{rj}) \right. \nonumber \\ {}{} & {} \qquad \left. +P_{\langle ij \rangle }u_r+P_{\langle ri \rangle }u_j+P_{\langle rj \rangle }u_i +\frac{2}{5}(q_{j}\delta _{ri}+q_{i}\delta _{rj}+q_{r}\delta _{ij})\right) \nonumber \nonumber \\{} & {} \qquad =-\frac{3}{5} n U_0\left( \frac{6m^3}{\pi {\textsf{e}}^3} \right) ^{\frac{1}{2}} P_{\langle ij \rangle }+ \frac{q}{m}\left[ E_i m n u_j+E_j m n u_i+B_k\epsilon _{lk(i}\left( n m u_{j)}u_l+P_{\langle j)l\rangle } \right) \right] , \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( \frac{1}{2} {m}nu^2 u_i+ \frac{5}{3} n{\textsf{e}} u_i+P_{\langle ik \rangle }u_k+q_{i}\right) +\frac{\partial }{\partial x_r}\left( \frac{1}{2} {m}n u^2 u_iu_r+\frac{7}{3} n{\textsf{e}} u_iu_r +\frac{1}{3} n{\textsf{e}}u^2\delta _{ri} \right. \nonumber \\{} & {} \qquad +P_{\langle ik \rangle }u_ku_r+P_{\langle rk \rangle }u_ku_i+\frac{1}{2}P_{\langle ri \rangle }u^2 +\frac{7}{5}(q_{i}u_r+q_{r}u_i)+\frac{2}{5}q_{k}u_k\delta _{ri} \nonumber \\{} & {} \qquad \left. +\frac{10}{9m}n{\textsf{e}}^2\delta _{ri}+\frac{7}{3 m}{\textsf{e}}\, P_{\langle ri \rangle }\right) =-\frac{2}{5} n U_0\left( \frac{6m^3}{\pi {\textsf{e}}^3} \right) ^{\frac{1}{2}} \left( \frac{3}{2} P_{\langle ik \rangle }u_k+ q_{i}\right) \nonumber \\{} & {} \qquad +\frac{q}{m}\left\{ E_i \left( \frac{1}{2} {m} n u^2+\frac{5}{3} n{\textsf{e}}\right) +E_k ({m} n u_iu_k+P_{\langle ik \rangle })+B_r\Big [2\epsilon _{lrj}\Big (3 u_{(j}P_{\langle il \rangle )}\right. \nonumber \\{} & {} \qquad \left. +\frac{1}{2}m u_{i}u_{j}u_{l}\Big )+\epsilon _{lri}\Big (q_l+2u_{j}P_{\langle jl\rangle } +\frac{7}{3}u_l n{\textsf{e}} +\frac{1}{2}m u^2u_l\Big )\Big ]\right\} . \end{aligned}$$
(33)

Equation (32) can be replaced by the equations

$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( \frac{1}{2} {m} n u^2+n{\textsf{e}}\right) +\frac{\partial }{\partial x_r}\left( \frac{1}{2}{m} n u^2u_r +\frac{5}{3} n{\textsf{e}}u_r +P_{\langle rk \rangle }u_k +q_{r}\right) =\frac{q}{m}\Big [ E_k m n u_k\nonumber \\{} & {} \quad +B_k\epsilon _{lkj}\left( n m u_{j}u_l+P_{\langle j l\rangle } \right) \Big ], \end{aligned}$$
(34)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( {m} n u_{\langle i}u_{j \rangle }+P_{\langle ij \rangle }\right) +\frac{\partial }{\partial x_r}\left( {m} n u_{\langle i}u_{j \rangle }u_r +\frac{2}{3} n{\textsf{e}}(u_{j}\delta _{ir}+u_{i}\delta _{jr}-\frac{2}{3} u_{r}\delta _{ij})+P_{\langle ij \rangle }u_r \right. \nonumber \\{} & {} \quad \left. +P_{\langle ri \rangle }u_j+P_{\langle rj \rangle }u_i-\frac{2}{3} P_{\langle rk \rangle }u_k\delta _{ij} +\frac{2}{5}(q_{j}\delta _{ri}+q_{i}\delta _{rj}-\frac{2}{3} q_{r}\delta _{ij})\right) =-\frac{3}{5} n U_0\left( \frac{6m^3}{\pi {\textsf{e}}^3} \right) ^{\frac{1}{2}} P_{\langle ij \rangle } \nonumber \\{} & {} \quad + \frac{q}{m}\left[ m n\left( E_i u_j+E_j u_i-\frac{2}{3}E_ku_k\delta _{ij}\right) +B_k\epsilon _{lk(\langle i}\left( n m u_{j\rangle )}u_l +P_{\langle j\rangle )l\rangle } \right) \right] , \end{aligned}$$
(35)

where \(a_{\langle i}b_{j\rangle }=a_ib_j-\frac{1}{3} {\textbf{a}}\cdot {\textbf{b}}\,\delta _{ij},\quad \forall {\textbf{a}}, {\textbf{b}}\).

5 A numerical test

From now on, time is scaled to the inverse plasma frequency \(\omega _p\), lengths to the Debye length \(\lambda _D\) and velocities to the thermal speed \(v_{\textrm{th}}\), the electron density \(n=1\), and all other physical quantities will be scaled using these characteristic parameters. In this section, we exploit a numerical test to check to what extent the small anisotropy approximation gives good results, by a comparison with the results obtained by the kinetic model [8], in the case of the relaxation towards equilibrium of a homogeneous field-free plasma with a temperature anisotropy. Therefore, at a microscopic level, the electron state can be described by a bi-Maxwellian distribution function:

$$\begin{aligned} f(c_x,c_y,c_z)=\frac{1}{(2\pi )^{3/2}T_\perp \sqrt{T_{||}}}\exp {\Bigg [-\Bigg (\frac{c_1^2+c_2^2}{2T_\perp }-\frac{c_3^2}{2T_{||}}\Bigg )\Bigg ]}. \end{aligned}$$
(36)

Here, the subscript || indicates the z direction, while x and y are the perpendicular (\(\perp \)) directions. Let us define the temperature anisotropy, at time t, as \(A(t) = T_\perp (t)/T_{||}(t)\), with \(A_0=A(0)\). By assuming that the distribution function remains a bi-Maxwellian during the process of collisional relaxation, and recalling that the total temperature \(T=\frac{2T_\perp +T_{||}}{3}\) remains constant in time, the evolution of the distribution is determined by that of \(T_\perp \).

The evolution equation of \(T_\perp \) was found by Kogan [8] and reads

$$\begin{aligned} \frac{d T_\perp }{dt} = -\nu _K ( T_{\perp } -T_{||}), \end{aligned}$$
(37)

\(\nu _K\) being a thermalization frequency given by:

$$\begin{aligned} \nu _K =\frac{U_0}{\pi ^{1/2} T_{||}^{3/2}} \frac{ ({\tilde{A}} + 3) \varphi ({\tilde{A}})-3}{{\tilde{A}}^2}, \end{aligned}$$

where \({\tilde{A}}:=A-1:=T_\perp /T_{||}-1\) and

$$\begin{aligned} \varphi (x) = \left\{ \begin{array}{c} \tan ^{-1}(\sqrt{x})/\sqrt{x}, \,\, x > 0, \\ 1, \,\, x = 0,\\ \tanh ^{-1}(\sqrt{x})/\sqrt{x},\,\,x<0. \end{array}\right. \end{aligned}$$

The solution of (37) can be determined numerically.

To obtain the corresponding evolution equation for \(T_\perp \) given by the model presented in this paper, first of all we have to expand the bi-Maxwellian in small anisotropy, which gives

$$\begin{aligned}{} & {} f(c_1,c_2,c_3)\approx \bigg (\frac{2T_{||}+T_\perp }{6\pi T_{||}T_\perp }\bigg )\exp {\bigg (-\frac{1}{6}\frac{2T_{||}+T_\perp }{ T_{||} T_\perp }|\textbf{c}|^2\bigg )}\\{} & {} \quad \times \left\{ \begin{array}{c} \bigg [1-\frac{1}{6}\frac{T_{\perp }-T_{||}}{T T_{\perp }}\Big (c_1^2+c_2^2-2c_3^2\Big )\bigg ], \,\,\textrm{if} \,\,T_\perp \ge T_{||}\\[2ex] \bigg [1-\frac{1}{6}\frac{T_{||}-T_{\perp }}{ T T_{||}}\Big (c_1^2+c_2^2-2c_3^2\Big )\bigg ], \,\,\textrm{otherwise}, \end{array} \right. \end{aligned}$$

where \(\frac{2T_{||}+T_\perp }{ T_{||}T_\perp }\) is the trace of the inverse temperature tensor, and the expansion is made with respect to \(\frac{T_\perp -T_{||}}{ T_\perp }\) if \(T_\perp \ge T_{||}\) and to \(\frac{T_{||}-T_\perp }{ T_{||}}\) otherwise. After that, comparing this expansion with the MEP distribution (26), taken with \({\textbf{q}}=0\) and \(P_{<11>}=P_{<22>}\), we find

$$\begin{aligned} P_{<11>}= \left\{ \begin{array}{ll} T\frac{T_\perp -T}{T_\perp }, &{}\,\,\textrm{if} \,\,T_\perp \ge T_{||}\\ T\frac{T_\perp -T}{3T-2T_\perp },&{}\,\,\textrm{otherwise}. \end{array} \right. \end{aligned}$$
(38)

Now, we have to write the moments system in the case where no spatial dependence and no fields are present. The resulting system is as follows:

$$\begin{aligned}{} & {} \frac{\partial n}{\partial t} =0, \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( n u_i\right) =0, \end{aligned}$$
(40)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( \frac{1}{2} n u^2+n{\textsf{e}}\right) =0, \end{aligned}$$
(41)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( n u_{\langle i}u_{j \rangle }+P_{\langle ij \rangle }\right) =-\frac{3}{5} n U_0\left( \frac{6}{\pi {\textsf{e}}^3} \right) ^{\frac{1}{2}} P_{\langle ij \rangle }, \end{aligned}$$
(42)
$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( \frac{1}{2} nu^2 u_i+ \frac{5}{3} n{\textsf{e}} u_i+P_{\langle ik \rangle }u_k+q_{i}\right) =-\frac{2}{5} n U_0\left( \frac{6m^3}{\pi {\textsf{e}}^3} \right) ^{\frac{1}{2}} \left( \frac{3}{2} P_{\langle ik \rangle }u_k+ q_{i}\right) . \end{aligned}$$
(43)

We get that n is constant, as well as \({\textbf{u}}\) and \({\textsf{e}}\). If the velocity and the heat flux are posed equal to zero, we remain with the equation:

$$\begin{aligned}{} & {} \frac{\partial P_{\langle ij \rangle }}{\partial t} =-\nu _\textrm{ME} P_{\langle ij \rangle }, \end{aligned}$$
(44)

where

$$\begin{aligned} \nu _\textrm{ME}=\frac{3}{5} n U_0\left( \frac{6}{\pi {\textsf{e}}^3} \right) ^{\frac{1}{2}}. \end{aligned}$$

Therefore, by solving this equation and using (38), we find

$$\begin{aligned} T_\perp =\left\{ \begin{array}{ll} T/(T-P_{11}^{(0)}\exp (-\nu _\textrm{ME}t)),&{} \quad \textrm{if}\,\,T_{\perp }\ge T_{||},\\ (3 P_{11}^{(0)}\exp {(-\nu _\textrm{ME}t)+T)}/(2P_{11}^{(0)}\exp (-\nu _\textrm{ME}t)+T),&{}\quad \textrm{otherwise}, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} P_{<11>}^{(0)}= \left\{ \begin{array}{ll} T\frac{T_\perp ^{(0)}-T}{T_\perp ^{(0)}}, &{}\,\,\textrm{if} \,\,T_\perp \ge T_{||}\\ T\frac{T_\perp ^{(0)}-T}{3T-2T_\perp ^{(0)}},&{}\,\,\textrm{otherwise}. \end{array} \right. \end{aligned}$$

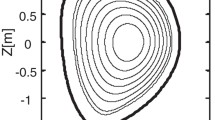
In Figs. 1 and 2 and in the left side of Fig. 3, we compare the results for the two models, in the cases \(A_0=0.03,0.9,1.5, 15,\) 30. We can see that, for \(A_0>1\), the results of the macroscopic (ME) model are in excellent agreement with the kinetic ones, with a maximum relative error which is equal to around 1% for \(A_0=30\), see Fig. 4. Worse are the results for \(A_0<1\) with a maximum relative error which rapidly increases from around 3.4% for \(A_0=0.5\) to around 47% for \(A_0=0.03\), see Fig. 4.

Fig. 1
figure 1

\(T_\perp \) as a function of time, for \(A_0=0.03\) (left) and \(A_0=0.9\) (right)

Full size image
Fig. 2
figure 2

\(T_\perp \) as a function of time, for \(A_0=1.5\) (left) and \(A_0=15\) (right)

Full size image
Fig. 3
figure 3

Left: \(T_\perp \) as a function of time, for \(A_0=30\). Right: Relative error of the ME model with respect to the kinetic one

Full size image
Fig. 4
figure 4

Maximum relative error of the macroscopic model with respect to the kinetic one, for various values of \(A_0\)

Full size image

This different behaviour can be explained by looking at the trend of the right-hand side of \(\frac{\text {d} T_\perp }{\text {d}t}\) as a function of \(T_\perp \) for the two models, which is shown in the left side of Fig. 5. As can be seen, the two production functions are much nearer for \(T_\perp >T\). It can be noticed that the ME model works well beyond the limit of small anisotropy, which, in the present case, is related to the smallness of the trace-free part of the inverse temperature tensor which is proportional to \(\frac{T_\perp -T_{||}}{T_\perp T_{||}}\). In fact, as can be seen in the right side of Fig. 5, the neighbourhood of \(T_\perp =T\) where \(\frac{|T_\perp -T_{||}|}{T_\perp T_{||}}\) is small is much narrower than that where the results of the ME model are in good agreement with those of the kinetic model.

Fig. 5
figure 5

Left: Right–hand side of \(\frac{\text {d} T_\perp }{\text {d}t}\) as a function of \(T_\perp /T\). Right: Trend of \(\frac{|T_\perp -T_{||}|}{T_\perp T_{||}}\)

Full size image

6 Conclusions

In this paper, we have described a general procedure to obtain a physics-based closure to the moment equations derived from the FPL transport equation for plasmas, with an arbitrary number of moments. In particular, we have explicitly written the 13-moment model for the intrinsic moments and we have tested it in the case of a homogeneous field-free plasma with an anisotropic temperature, obtaining results which are in good agreement with those given by the FPL equation. This agreement gives hints that the proposed macroscopic model, which requires a significantly lighter computational effort with respect to the kinetic model, makes self-consistent simulations of plasmas in presence of collisions affordable, even in the three-dimensional space geometry. This will be the object of a future paper.