Unsteady ballistic heat transport in a 1D harmonic crystal due to a source on an isotopic defect

Abstract

In the paper we apply asymptotic technique based on the method of stationary phase and obtain the approximate analytical description of thermal motions caused by a source on an isotopic defect of an arbitrary mass in a 1D harmonic crystal. It is well known that localized oscillation is possible in this system in the case of a light defect. We consider the unsteady heat propagation and obtain formulae, which provide continualization (everywhere excepting a neighbourhood of a defect) and asymptotic uncoupling of the thermal motion into the sum of the slow and fast components. The slow motion is related to ballistic heat transport, whereas the fast motion is energy oscillation related to transformation of the kinetic energy into the potential one and in the opposite direction. To obtain the propagating component of the fast and slow motions we estimate the exact solution in the integral form at a moving point of observation. We demonstrate that the propagating parts of the slow and the fast motions are “anti-localized” near the defect. The physical meaning of the anti-localization is a tendency for the unsteady propagating wave-field to avoid a neighbourhood of a defect. The effect of anti-localization increases with the absolute value of the difference between the alternated mass and the mass of a regular particle, and, therefore, more energy concentrates just behind the leading wave-front of the propagating component. The obtained solution is valid in a wide range of a spatial co-ordinate (i.e. a particle number), everywhere excepting a neighbourhood of the leading wave-front.

Appendices

Non-dimensionalization

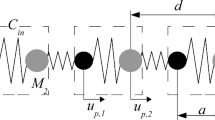
The equations of motion for the system under consideration are

$$\begin{aligned} \tilde{m}_n\frac{\mathrm d^2 {\tilde{u}}_n}{\mathrm d\tilde{t}^2} -\tilde{C}(\tilde{u}_{n+1}-2\tilde{u}_n+\tilde{u}_{n-1})= \delta _n \tilde{p}\big (\tilde{t}\big ). \end{aligned}$$

(A.1)

Here $n \in \mathbb {Z}$, $\tilde{t}$ is the time, $\tilde{u}_n(\tilde{t})$ is the displacement of the particle with a number n, $\tilde{m}_n$ is the mass of a particle with number n:

$$\begin{aligned} \tilde{m}_n=\tilde{M}+\delta _n(\tilde{m}-\tilde{M}), \end{aligned}$$

(A.2)

$\tilde{C}$ is the bond stiffness. The dimensionless equations of motion (3.1) can be obtained by introducing the following dimensionless quantities:

$$\begin{aligned} u_n=\frac{\tilde{u}_n}{\tilde{A}};\quad t=\omega \tilde{t};\quad p=\frac{\tilde{p}}{\tilde{C}\tilde{A}},\quad m=m_0=\frac{\tilde{m}}{\tilde{M}}. \end{aligned}$$

(A.3)

Here $\tilde{A}$ is the lattice constant (the distance between neighbouring particles); $\omega {\mathop {=}\limits ^{\text{ def }}}\sqrt{{\tilde{C}}/{\tilde{M}}}$.

The Erdélyi lemma

Theorem 1

Let $a>0,\ \alpha \ge 1,\ \beta >0$, $f(\varOmega )\in C^\infty$, $f^{(n)}(a)=0\ \forall n.$ Then

$$\begin{aligned}{} & {} \int _0^a\varOmega ^{\beta -1}f(\varOmega )\,\mathrm e^{\mathrm it\varOmega ^\alpha }\,\mathrm d\varOmega \sim \sum _{k=0}^\infty c_k t^{-\frac{k+\beta }{\alpha }},\quad t\rightarrow \infty ; \end{aligned}$$

(B.1)

$$\begin{aligned}{} & {} c_k=\frac{f^{(k)}(0)}{k!\alpha }\, \varGamma \left( \frac{k+\beta }{\alpha }\right) \mathrm e^{\frac{\mathrm i\pi (k+\beta )}{2\alpha }}. \end{aligned}$$

(B.2)

The proof can be found in [58, 59].

In Sect. 7 we sometimes apply Erdélyi lemma to integrals, where $\beta =1$, $0<\alpha <1$. The corresponding asymptotics can be obtained by taking $\varOmega ^\alpha$ as the new integration variable, and applying the Erdélyi lemma to the obtained integral.

The trapped energy ratio

According to Eq. (3.17) the initial kinetic energy, as well as the total energy of the chain for all t, is $\mathcal E$. On the other hand, according to (3.14), (3.19)

$$\begin{aligned} \langle K_n\rangle = \frac{1}{2}{\mathcal E}\mathcal T_n. \end{aligned}$$

(C.1)

One has

$$\begin{aligned} \frac{\sum _{n=-\infty }^{\infty }\langle K_n(t)\rangle }{\mathcal E} = \frac{\sum _{n=-\infty }^{\infty }\mathcal T_n(t)}{2}. \end{aligned}$$

(C.2)

Considering the energy trapped near the defect as $t\rightarrow \infty$, we substitute into Eq. (C.2) $\mathcal T_n=\mathcal T_n^\textrm{stop}\simeq 2mm_n({v}_n^\textrm{stop})^2$:

$$\begin{aligned} \frac{\sum _{n=-\infty }^{\infty }\langle K_n(t)\rangle }{\mathcal E} =m\sum _{n=-\infty }^{\infty } m_n({v}_n^\textrm{stop})^2=m^2(v_0^\textrm{stop})^2+2m\sum _{n=1}^\infty ({v}_n^\textrm{stop})^2. \end{aligned}$$

(C.3)

Using Eq. (10.9) to calculate the right-hand side of (C.3) at $t=\frac{\pi k}{\varOmega _0}$, $k\in \mathbb Z$, $k\rightarrow \infty$ (when the trapped kinetic energy equals the trapped total energy), we obtain the ratio R of the trapped total energy to the total energy of the chain. Due to (10.9) on has

$$\begin{aligned} ({v}^\textrm{stop}_n)^2\Big |_{t=\frac{\pi k}{\varOmega _0}} = \frac{4(1-m)^2m^{2(|n|-1)}}{(2-m)^{2(|n|+1)}} . \end{aligned}$$

(C.4)

Calculating the sum of the geometric series in the right-hand side of Eq. (C.3), one, finally, gets

$$\begin{aligned} R=\frac{4(1-m)^2}{m(2-m)^2}\left( m +\frac{2q}{1-q}\right) =1-\frac{m}{2-m}. \end{aligned}$$

(C.5)

Here

$$\begin{aligned} q=\frac{m^2}{(2-m)^2} \end{aligned}$$

(C.6)

is a common ratio for the geometric series.

The plot of the trapped total energy R versus m is presented in Fig. 7. For $m\rightarrow +0$ all energy is trapped near the defect, for $m\rightarrow 1-0$ all energy is radiated away from the defect.

Formula (C.5) was previously obtained in [41].

Fig. 7

The trapped total energy ratio R versus m