Geometrical investigation of cooling channels with two alternated isothermal blocks under forced convective turbulent flow

Abstract

The present work performs a numerical analysis of the geometrical investigation of a two-dimensional channel with two alternated isothermal rectangular blocks subjected to turbulent forced convective flows. Constructal Design associated with Exhaustive Search is used to investigate the influence of the geometry of the isothermal blocks over the performance of the cooling convective flows in a multi-objective viewpoint, i.e., considering the pressure drop and heat transfer rate. The time-averaged equations of continuity, momentum, and energy conservation are solved with the finite volume method. The k–$\omega$ shear stress transport model is used for the closure of turbulence. The effect of the two proposed degrees of freedom, the height/length ratio of the two blocks ($H_{1}/L_{1}$ and $H_{2}/L_{2})$, is analyzed in relation to the proposed objectives. Regarding the thermal purpose, the geometry with the highest insertion into the channel led to the best performance, while the opposite configuration led to the best fluid dynamic performance. This behavior was similar to that previously found in the literature for forced convective laminar flows. For a multi-objective perspective, the use of technique for order preference by similarity to ideal solution indicated that asymmetric blocks led to the best multi-objective performance when both performance indicators had the same weight.

1 Introduction

The process of technological evolution in all areas of engineering provides many advances for society, but it also generates problems. One is the need to remove the heat generated by many systems (e.g., machines, equipment, plants, electronic packages, gas turbine, and nuclear reactors) inherent to their functioning. One important alternative for cooling heat generation systems is the use of channel or microchannel heat sinks. Therefore, it is highly important to understand the factors that contribute to their thermal and fluid dynamic performance, like thermal conductivity, thermal resistance, fluid properties, the design of the channels, flow rate, transition from laminar to turbulence and heat flux, among others [1,2,3].

To mitigate the heat dissipation problem through channels, micro-channels, and other flows with heat transfer, designers and engineers have been proposing some strategies. Examples are seen in the use of nanofluids [4,5,6], the association of magnetic fields, chemical reaction, and radiative heat transfer with convective flows [7], the use of porous surfaces [8], the addition of micro- and nanoparticles to modify the channel surface [9], the insertion of nanostructures like nanowires and carbon nanotubes [10], and two-phase boiling flow [11, 12]. One of the most used alternatives to minimize the effects of high magnitudes of heat dissipation has been the study of the geometric configuration of heat sink channels. The geometric optimization of these channels requires not only the thermal analysis but also the fluid dynamic one, mainly for the situations where the overall performance of the system and the power supplied to drive the fluid flow are essential aspects. In this sense, a multi-objective approach is recommended to study cooling channels to predict the designs that improve the fluid dynamic and thermal performance separately and/or simultaneously [13, 15].

Considering the complexity of the physical problem of turbulent cooling channel flows and the requirement to remove a large amount of heat from real devices, the investigation of the influence of many different arrangements, shapes, geometries, flow conditions, and working fluids over the comprehension of flow behavior and performance of cooling channels is still an important subject. Therefore, many studies about convective flows around obstacles, fins, blocks, deflectors, and bluff bodies (such as circular, rectangular, and triangular) in channels, mini-channels, and micro-channels have been performed [4, 16,17,18,19]. Fan and Luo [20] reviewed the applications of microchannels heat exchangers and their design optimization. They also reviewed the literature on channels and microchannels heat exchangers design with the application of the Fractal technique and the Constructal Theory. Afterward, Naqiuddin et al. [1] reviewed the progress in the design of microchannels for high flux applications. They presented the main types and structures of microchannel geometries, like straight and wavy channels, pin-fins, oblique fins, baffles, ribs, and dimples. They also emphasized the importance of numerical tools in the study of microchannels geometry. Ismael [18] studied a channel numerically with two alternated baffles, separated by a flexible wall segment, subjected to forced convection. It was found that the flexible wall segment had almost any effect on the thermal-hydraulic performance of a non-baffled channel. In contrast, a baffled channel produced an eddy between the two baffles, thus a considerable effect over the heat transfer and fluid dynamic. For high Reynolds numbers and high values of the downstream baffle height, two additional eddies formed along the exit length of the channel, reducing the fluid dynamic performance. Later, Adhikari et al. [21] investigated experimentally and numerically the geometry of parallel rectangular fins in a channel subject to a forced convective flow at low Reynolds numbers. In addition, a different number of fins, fin spacing, and channel length were analyzed. They found that the heat transfer rate decreases linearly with the increase in channel length but remains constant with increasing the number of fins. The importance of design in turbulent flows has also been demonstrated in other conditions, such as for the improvement of hydro-acoustic characteristics of fluid flows [22], in the thermal behavior and performance of forced convective curved channel flows [23] and in the investigation of the influence of riblets over the statistics of turbulence in forced convective rectangular channels [24].

The Constructal Design method is used in this work to perform the geometric investigation, defining the search space as a function of constraints and degrees of freedom. The exhaustive search is used for optimization, defining the form that the search space is investigated [25]. Constructal Design is the method used to demonstrate how the design in any finite-size flow system is governed by a physical principle named Constructal Law of Design and Evolution. Constructal Law states that for a finite-size flow system to persist in time (to live), its configuration must freely evolve to facilitate the access of the internal currents that flow in the thermodynamic system [26,27,28]. Engineering has been a prolific field to demonstrate the applicability of Constructal Law. Several recommendations of design have been reached for renewable energy conversion devices [29, 30], resin infusion manufacturing processes [31], and even solid mechanics [32, 33].

Despite the several signs of progress in the areas mentioned above, the heat transfer area is of particular interest since several observations reached in this field are used to improve the comprehension of the influence of design in other engineering areas and design in nature. Important applications of Constructal Design in heat transfer have been noticed in the study of cavities of different shapes intruded into heat-generated walls [25], cavities with heated elements inside [34], and external flows subjected to convection heat transfer [35, 36]. Concerning the convective flows in channels, Adewumi et al. [37] investigated the influence of placement of fins, the number of rows of pins and dimensions of the channel on the thermal performance of the system subjected to natural convective flows. Afterward, Feijó et al. [17] evaluated the design of two alternated rectangular blocks mounted on the inferior and superior surfaces of the channel subjected to laminar forced convective flows ($\textrm{Re}_{\textrm{H}} = 100$ and $\textrm{Pr} = 0.71$). In this work, it was sought the minimization of pressure drop and maximization of heat transfer rate. In general, results indicated that the highest insertion of the blocks led to the best thermal performance, while the lowest insertion was the best for the fluid dynamic performance. The multi-objective analysis demonstrated that asymmetric configuration led to the best behavior. Teixeira et al. [38] investigated a similar case studied in the work of Feijó et al. [17]. However, it was investigated the domain subjected to mixed convective flows for three different Reynolds and Grashof numbers (nine Richardson numbers) and the distance between the rectangular blocks over the thermal performance of the problem. Other shapes for the mounted blocks have been the object of investigation, e.g., Moreira et al. [19] evaluated the influence of trapezoidal blocks mounted in channels subjected to forced convective flows of water ($\textrm{Pr} = 6.99$) for two different Reynolds numbers ($\hbox {Re}_{\textrm{H}} =60$ and 160). It was observed that the heat transfer rate was strongly affected by the length/height ratios of the trapezoidal blocks. Razera et al. [15] investigated the insertion of semi-elliptical blocks in the channel for forced convective and laminar flows. Three different Reynolds numbers were simulated ($\textrm{Re}_{\textrm{H}} =10$, 50, and 100), and airflow is considered as working fluid ($\hbox {Pr}=0.72$). The purpose was to maximize the heat transfer rate and minimize the pressure drop. The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method was employed to tackle the multi-objective analysis. Results proved the applicability of Constructal Design in this kind of problem. Into the multi-objective framework, scenarios with different weights of importance of fluid dynamic and thermal performance and their effects on the designs that conducted to the best performances were proposed. It is also important to mention the contributions of the application of Constructal Design for geometric investigation of channels for cooling of heat-generating bodies [39].

The present study proposes the application of the Constructal Design for the geometric investigation of a channel with two rectangular heated blocks subjected to forced convective turbulent flows of water, which to the best of authors’ knowledge was not previously investigated in the literature. It is worth mentioning that the main contribution here is not concerned with the influence of the design on the statistical behavior of turbulent channel flows with forced convection heat transfer but with the influence of design over the performance of turbulent flows. More precisely, it analyzed the effect of the height/length ratios of the upstream and downstream blocks ($H_{1}/L_{1}$ and $H_{2}/L_{2})$ over the heat transfer rate between the heated blocks and the cooling flow and pressure drop in the channel. All studied cases considered constant magnitudes of Reynolds and Prandtl numbers ($\textrm{Re}_{D} =76,000$ and Pr = 0.88). The time-averaged equations of continuity, momentum and energy conservation are solved numerically with the Finite Volume Method (FVM), by means of the ANSYS FLUENT commercial code [40,41,42]. For closure of turbulence, the k – $\omega$ SST model is used [43, 44].

2 Mathematical modeling

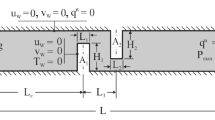
Consider a two-dimensional channel containing two rectangular blocks (Fig. 1), bathed by an incompressible, turbulent, steady, and forced convective flow. The fluid enters the channel on its left side with prescribed velocity and temperature equal $u_{\textrm{in}} = 0.5$ m/s and $T_{\infty } =500$ K, respectively. It exits through the right side, where a gauge pressure condition of $p_{\textrm{g}}=0$ atm (compared with operating pressure) is imposed. The two blocks, as well as their surrounding region (in red in Fig. 1), are at a constant temperature of $T_{\textrm{w}} =526$ K. It is considered that the other surfaces of the channel are thermally insulated. The walls of the channel and blocks have a non-slip and impermeability condition ($u = v =0$ m/s). Also, the fluid flow in the channel has an operating pressure of 4.5 MPa, and the gravitational forces can be disregarded. In addition to the boundary conditions already mentioned, it is considered that the initial conditions are: the fluid flow at rest ($u = v = 0$ m/s) and the entering temperature ($T = T_{\textrm{in}})$. A turbulence intensity of $I={\sqrt{{2k} /3} } / {\bar{{u}}} =4$%, and the channel height as the length scale are considered at the inlet of the channel for turbulent parameters.

Fig. 1

Illustration of the Computational Domain of the channel with alternated rectangular blocks

The channel has dimensions of $D =20$ mm, $L =250$ mm, $L_\textrm{in} =100$ mm, $L_\textrm{out} =54$ mm, $L_\textrm{ocu} = 96$ mm, $L_{c1} = L_{c2} =24$ mm and $L_{3} =48$ mm (see Fig. 1). For all cases, it is considered a Reynolds number of $\textrm{Re}_{D} =$ ($\rho u_\textrm{in}D)/\mu = 76.600$. The working fluid is water, with a Prandtl number of $\textrm{Pr} = \upsilon /\lambda =0.88$, representing the liquid water at the operating pressure and inlet temperature used in the present simulations. The thermal conditions studied here are defined since there are some important applications in heat exchangers, turbines, and others where high pressures and temperatures characterize the fluid flow. Moreover, the conditions used here allow the future comparison with a similar problem subjected to boiling convection heat transfer, which is in progress by the authors. Here, $\rho$ is the fluid density (kg/m$^{3}$), $u_\textrm{in}$ is the velocity at the channel inlet (m/s), $\mu$ is the dynamic viscosity of the fluid (N.s/m$^{2}$), $\upsilon$ is the kinematic viscosity of the fluid (m$^{2}$/s), and $\lambda$ is the thermal diffusivity of the fluid (m$^{2}$/s).

The Constructal Design method is applied to define search space and performance indicators [26, 27]. However, it is not an optimization method. Therefore, the exhaustive search technique is used here to optimize the search space of geometries defined with the Constructal Design.

The problem is subject to three constraints: the channel area (A), the occupation area for each block ($A_{1})$, which is the same for both blocks in the present investigation, and the cross-sectional area of the rectangular blocks ($A_{2})$ also the same for both blocks. These areas are, respectively, given by:

$$\begin{aligned} A= & {} DL \end{aligned}$$

(1)

$$\begin{aligned} A_{1}= & {} D\left( {L_{c1} +{L_{3} } / 2} \right) =D\left( {L_{c2} +{L_{3} } / 2} \right) \end{aligned}$$

(2)

$$\begin{aligned} A_{2}= & {} H_{1} L_{1} =H_{2} L_{2} \end{aligned}$$

(3)

The ratios between the cross-sectional area of each block over their occupation area ($A_{2}/A_{1})$ are called $\phi _{1}$ and $\phi _{2}$, and, in this study, these ratios are considered constant $\phi _{1} = \phi _{2} =0.2$, i.e., each block occupies 20% of its occupation area. The objectives of the geometric evaluation are to maximize the heat transfer from the blocks to the surrounding flow and to minimize the pressure difference between the inlet and outlet of the channel. For this purpose, two degrees of freedom are defined: the ratio between the height and the length of each block: $H_{1}/L_{1}$ and $H_{2}/L_{2}$. The distance between the upstream and downstream blocks ($L_{3})$ is also a degree of freedom, but in the present study, it is maintained constant.

Fig. 2

Flowchart with the main steps of application of Constructal Design and Exhaustive Search for the geometrical optimization studied in the present problem

Fig. 3

Diagram with the studied cases investigated in the present work with Constructal Design and Exhaustive Search

Figure 2 illustrates a flowchart with the main steps of application of the Constructal Design method for the present problem. The Constructal Design defines the flow system, constraints, degrees of freedom, and performance indicators (which indicates how the system facilitates the access of the internal currents), as can be seen in Steps 1 to 5. For geometrical optimization, the Exhaustive Search method, which consists of investigating of all geometrical possibilities of search space defined with Constructal Design, is employed [27, 31]. The optimization description can be noticed in Steps 6b to 9b. Figure 3 shows in detail the diagram of simulations performed in the present work and illustrated in Step 6b of Fig. 2. In total, 144 simulations were performed. First, the geometry is optimized by varying the ratio $H_{1}/L_{1}$, keeping $H_{2}/L_{2}$ fixed. The maximum value found for the heat transfer rate is called the rate once maximized, $q_{1,{\textrm{max}}}$, and the corresponding $H_{1}/L_{1}$ is called the rate once thermally optimized ($H_{1}/L_{1})_{\textrm{o,T}}$. Since this is a multi-objective problem, it can obtain different values for the ($H_{1}/L_{1})_{{\textrm{o}}}$, one for the thermal problem and another for the fluid dynamic problem. For this reason, it is also found a minimum value for the pressure difference between the inlet and outlet of the channel, $\Delta P_{1,{\textrm{min}}}$, corresponding to ($H_{1}/L_{1})_{\textrm{o,F}}$. In a second step, the process is repeated for other values of $H_{2}/L_{2}$. Among all simulated cases, the maximum heat transfer rate is the twice maximized rate, $q_{2,{\textrm{max}}}$, and the smallest pressure difference is the twice minimized, $\Delta P_{2,{\textrm{min}}}$. Regarding the optimal geometries, in this step, $H_{2}/L_{2}$ is also once optimized for the thermal objective and once optimized for the fluid dynamic objective, ($H_{2}/L_{2})_{\textrm{o,T}}$ and ($H_{2}/L_{2})_{\textrm{o,F}}$. Likewise, the twice optimized ratios ($H_{1}/L_{1})_{\textrm{oo,T}}$ and ($H_{1}/L_{1})_{\textrm{oo,F}},$ are obtained. Subsequently, the geometric evaluation is carried out, considering the multi-objective (thermal and fluid dynamics, simultaneously). In the end, the optimal multi-objective geometry is reached: ($H_{1}/L_{1})_{{\textrm{oo}}}$ and ($H_{2}/L_{2})_{{\textrm{o}}}$. The third degree of freedom ($L_{3})$ is kept constant for all simulations in the present study.

The present work employs the multi-criteria analytical decision method Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [45, 46] to conduct the multi-objective analysis. This method is based on the definition of criteria and alternatives and the principle that the alternative chosen in a multi-criteria problem with several alternatives must be the one with the smallest Euclidean distance to the ideal positive solution and the greatest distance to the negative solution. The TOPSIS method assesses a decision matrix comprising m alternatives and n criteria (or attributes), like matrix D in the following example:

where Alt$_{i}$ is the ith alternative to be considered and $x_{ij}$ is the numerical value of the ith alternative with respect to the jth criterion.

The criteria are considered as “benefit” or “cost,” depending on their effect on the ideal solution. It is also possible to define different weights for each criterion according to their importance. After the decision matrix D with m alternatives and n criteria is defined, the TOPSIS method is carried out with the following steps:

1$^{{\varvec{st}}}$ step: Normalization of decision matrix D: Matrix D is normalized using the following equation for each element of the matrix:

$$\begin{aligned} r_{i,j} =\frac{x_{i,j} }{\sqrt{\sum \limits _{i=1}^m {x_{i,j}^{2} } } } \end{aligned}$$

(4)

2$^{{\varvec{nd}}}$ step: Construction of the weighted normalized decision matrix: Each element of the matrix $r_{ij}$ is multiplied by a weight $w_{j}$ corresponding to a criterion j, generating a matrix V:

$$\begin{aligned} V_{i,j} =r_{i,j} \cdot w_{j} \end{aligned}$$

(5)

where $\sum \limits _{j=1}^n w_{j} =1$.

3$^{{\varvec{rd}}}$ step: Determination of the positive and negative ideal solutions: The positive ideal solution is given by:

$$\begin{aligned} A^{*}=\left\{ {V_{1}^{*} ,\ldots ,V_{n}^{*} } \right\} =\left. {\left. {\left\{ {\left( {\left. {\mathop {{\max }}\limits _{i} V_{i,j} } \right| j\in J} \right) } \right. ,\left( {\left. {\mathop {{\min }}\limits _{i} V_{i,j} } \right| j\in J^{'}} \right) } \right| i=1,2,\ldots ,m} \right\} \end{aligned}$$

(6)

and the negative ideal solution is given by:

$$\begin{aligned} A^{-}=\left\{ {V_{1}^{-} ,\ldots ,V_{n}^{-} } \right\} =\left. {\left. {\left\{ {\left( {\left. {\mathop {{\min }}\limits _{i} V_{i,j} } \right| j\in J} \right) } \right. ,\left( {\left. {\mathop {{\max }}\limits _{i} V_{i,j} } \right| j\in J^{'}} \right) } \right| i=1,2,\ldots ,m} \right\} \end{aligned}$$

(7)

where $J=\left\{ j=1,\, 2,\, \ldots ,\, n\vert j \right\}$ is associated with the benefit criterion and $J^{'}=\left\{ j=1,\, 2,\, \ldots ,\, n\vert j \right\}$ is associated with the cost criterion.

4$^{{\varvec{th}}}$ step: Calculate the distances between each alternative and the ideal solutions: The distance from an alternative ito the positive ideal solution is:

$$\begin{aligned} D_{i}^{*} =\sqrt{\sum \limits _{j=1}^m {(V_{i,j} -V_{j}^{*} )^{2}} } \quad ,\,\;i=1,2,\ldots ,m \end{aligned}$$

(8)

and the distance to the negative ideal solution is:

$$\begin{aligned} D_{i}^{-} =\sqrt{\sum \limits _{j=1}^m {(V_{i,j} -V_{j}^{-} )^{2}} } \quad ,\,\;i=1,2,\ldots ,m \end{aligned}$$

(9)

5$^{{\varvec{th}}}$ step: Calculate the relative proximity between each alternative and the ideal solution:

$$\begin{aligned} C_{i} =\frac{D_{i}^{-} }{(D_{i}^{-} +D_{i}^{*} )}\quad ,\,\;i=1,2,\ldots ,m \end{aligned}$$

(10)

6$^{{\varvec{th}}}$ step: Order the alternatives according to the values obtained from $C_{i}$. The closer to 1 the value of $C_{i}$, the higher the alternative should be ranked.

In the present study, the thermal and the fluid dynamic objectives have weights called $w_\textrm{T}$ and $w_\textrm{F}$.

For each geometric configuration, solving the incompressible, turbulent, forced convective flows in the two-dimensional domain at the steady state is necessary. For modeling this problem, it is required to solve the time-averaged equations of continuity, momentum in x and y directions, and energy conservation, which are, respectively, given by [47, 48]:

$$\begin{aligned}{} & {} \frac{\partial \bar{{u}}}{\partial x}+\frac{\partial \bar{{v}}}{\partial y}=0 \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \bar{{u}}\frac{\partial \bar{{u}}}{\partial x}+\bar{{v}}\frac{\partial \bar{{u}}}{\partial y}=-\frac{1}{\rho }\frac{\partial \bar{{p}}}{\partial x}+\left( {\upsilon +\upsilon _{t} } \right) \left( {\frac{\partial ^{2}\bar{{u}}}{\partial x^{2}}+\frac{\partial ^{2}\bar{{u}}}{\partial y^{2}}} \right) \end{aligned}$$

(12)

$$\begin{aligned}{} & {} \bar{{u}}\frac{\partial \bar{{v}}}{\partial x}+\bar{{v}}\frac{\partial \bar{{v}}}{\partial y}=-\frac{1}{\rho }\frac{\partial \bar{{p}}}{\partial y}+\left( {\upsilon +\upsilon _{t} } \right) \left( {\frac{\partial ^{2}\bar{{v}}}{\partial x^{2}}+\frac{\partial ^{2}\bar{{v}}}{\partial y^{2}}} \right) \end{aligned}$$

(13)

$$\begin{aligned}{} & {} \bar{{u}}\frac{\partial \bar{{T}}}{\partial x}+\bar{{v}}\frac{\partial \bar{{T}}}{\partial y}=\left( {\lambda +\lambda _{t} } \right) \left( {\frac{\partial ^{2}\bar{{T}}}{\partial x^{2}}+\frac{\partial ^{2}\bar{{T}}}{\partial y^{2}}} \right) \end{aligned}$$

(14)

where u and v are, respectively, the flow velocities (m/s) in the x and y directions, p is the pressure (Pa), $\upsilon$ is the fluid kinematic viscosity (kg/(m$\cdot$s)), $\upsilon _{t}$ is the turbulent kinematic viscosity (kg/(m$\cdot$s)), T is the temperature (K), $\lambda$ is the thermal diffusivity (m$^{2}$/s), $\lambda _{t}$ is the turbulent thermal diffusivity (m$^{2}$/s), and the overbar (–) represents the time-averaged operator.

The present study applied the k–$\omega$ SST model for turbulence [43, 44]. This model is a kind of mixture of the traditional k–$\omega$ [48] and k–$\varepsilon$ [49] models and differs in the modification of the turbulent viscosity formulation, using the modeling of k–$\omega$ in the near wall region and the k–$\varepsilon$ in the free stream region of turbulent flow. It is worth mentioning that the $k-\omega$ leads to more adequate solutions in the near wall region (anisotropic flow condition) without the need to use wall functions since a more refined mesh in comparison with k–$\varepsilon$ model is used. On the opposite, the k–$\varepsilon$ model is better adjusted for isotropic conditions, as those regions in the center regions of channel flow. Therefore, in the present work, the use of the combination of the two models is recommended for adequate prediction in the whole domain.

The turbulent kinematic viscosity ($\upsilon _{t})$ and turbulent diffusivity ($\lambda _{t})$ are given by:

$$\begin{aligned} \upsilon _{t}= & {} \frac{a_{1} k}{\max \left( {a_{1} \omega ,SF_{2} } \right) } \end{aligned}$$

(15)

$$\begin{aligned} \lambda _{t}= & {} \frac{\upsilon _{t} }{\Pr _{t} } \end{aligned}$$

(16)

where $a_{1}$ is a constant ($a_{1} =0.31$), k is the turbulent kinetic energy (m$^{2}$/s$^{2}$), $\omega$ is the specific turbulence dissipation rate (1/s) and S is the invariant measure of the strain rate (1/s), and $\textrm{Pr}_{t}$ is the turbulent Prandtl number ($\textrm{Pr}_{t} =1.0$).

The turbulent kinetic energy (k) and specific turbulence dissipation rate ($\omega )$ are defined by two transport equations given by:

$$\begin{aligned}{} & {} \frac{\partial k}{\partial t}+\frac{\partial \left( {\bar{{u}}_{i} k} \right) }{\partial x_{i} }=\tilde{{P}}_{k} -\frac{k^{3/2}}{L_\textrm{T} }+\frac{\partial }{\partial x_{i} }\left[ {\left( {\mu +\sigma _{k} \mu _{t} } \right) \frac{\partial k}{\partial x_{i} }} \right] \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \frac{\partial \omega }{\partial t}+\frac{\partial \left( {\bar{{u}}_{i} \omega } \right) }{\partial x_{i} }=\frac{\alpha }{\mu _{t} }\tilde{{P}}_{k} -\beta \omega ^{2}+\frac{\partial }{\partial x_{i} }\left[ {\left( {\mu +\sigma _{\omega } \mu _{t} } \right) \frac{\partial \omega }{\partial x_{i} }} \right] +2\left( {1-F_{1} } \right) \frac{\sigma _{\omega 2} }{\omega }\frac{\partial k}{\partial x_{i} }\frac{\partial \omega }{\partial x_{i} } \end{aligned}$$

(18)

where $\tilde{{P}}_{k}$ is a function that prevents the turbulence generation in stagnation regions, i represents the spatial coordinate ($i =1$ and 2 represents the coordinates x and y, respectively), $\beta =0.09$, $\sigma _{k} =0.85$, $\sigma _{w} =0.5$, $\sigma _{2} =0.44$, $\sigma _{\textrm{k2}} =$1, $\sigma _{\textrm{w2}} =0.856$ are ad hoc constants used in by Menter [43, 44]. $F_{1}$ and $F_{2}$ are blending functions between variables, defined by:

$$\begin{aligned}{} & {} F_{1} =tanh \left\{ {\left\{ {min \left[ {max \left( {\frac{k^{1/2}}{\beta ^{*}\omega y},\frac{500\upsilon }{y^{2}\omega }} \right) ,\frac{4\rho \sigma _{\omega 2} k}{CD_{k\omega } y^{2}}} \right] } \right\} ^{4}} \right\} \end{aligned}$$

(19)

$$\begin{aligned}{} & {} F_{2} =tanh \left\{ {\left[ {max \left( {\frac{2k^{1/2}}{\beta ^{*}\omega y},\frac{500\upsilon }{y^{2}\omega }} \right) } \right] ^{2}} \right\} \end{aligned}$$

(20)

where $\beta ^{*}$ is a constant equal to 0.09 and y is the distance to the nearest wall (m).

The function ${\tilde{P}}_{k}$ is defined by:

$$\begin{aligned} \tilde{{P}}_{k} =min \left( {P_{k} ,10\cdot \beta ^{*}\rho k\omega } \right) \end{aligned}$$

(21)

where $P_{k}$ is given by:

$$\begin{aligned} P_{k} =\mu _{t} \frac{\partial \bar{{u}}_{i} }{\partial x_{j} }\left( {\frac{\partial \bar{{u}}_{i} }{\partial x_{j} }+\frac{\partial \bar{{u}}_{j} }{\partial x_{i} }} \right) \end{aligned}$$

(22)

3 Numerical modeling

The present study employed the ANSYS FLUENT software to perform the numerical simulations [42]. The software uses the FVM to solve Eqs. (11)–(21) for each geometric configuration [40, 41]. For the pressure-velocity coupling scheme, the SIMPLE method is used. In addition, second-order spatial discretization for momentum, energy, turbulent kinetic energy, and specific turbulence dissipation rate are used. For pressure, body force weighted is applied. The simulations are carried out in a steady state regime, converging when the residuals are lower than $1.0 \times 10^{-6}$.

Table 1 Mesh independence study performed for the channel with two blocks with $H_{1}/L_{1} = H_{2}/L_{2} =1.55$

Fig. 4

Mesh with triangular and quadrilateral finite volumes employed in the present study

It is considered a discretization composed of triangular and quadrilateral finite volumes. A mesh independency study is conducted to define the spatial discretization used in the present study. The case with the most complex geometry is chosen for this purpose ($H_{1}/L_{1} =1.55$ and $H_{2}/L_{2} =1.55$), assuming similar characteristics of discretization for the other cases. The mesh size is considered independent when the relative deviation of the heat transfer rate between two successive meshes is less than 0.1% or in absolute terms ($R = |(q^{j}- q^{j+1})/q^{j}| < 1.0 \times 10^{-3})$. This magnitude of R is achieved for a mesh with 60.463 volumes and 0.41 mm of maximum dimension mesh size, as presented in Table 1. It can be seen in Fig. 4 that the mesh employed in this study has extra refinement closer to the walls in order to properly capture the velocity, pressure, and temperature in the turbulent boundary layer. In this sense, it is considered a mesh refined enough in the near-wall regions so the parameter $y^{+} \quad \le$ 0.75 is achieved. The $y^{+}$ is defined as follows [43, 44, 48]:

$$\begin{aligned} y^{+}=\frac{y\sqrt{{\tau _{w} } / \rho } }{\upsilon }=\frac{yu_{\tau } }{\upsilon } \end{aligned}$$

(23)

where y is the normal distance to the wall (m), $\tau _{w}$ is the surface tension in the wall (N/m$^{2}$), and $u_{\tau }$ is the friction velocity (m/s).

The present case study is composed of two main flow bases: a parietal flow due to the fluid flow in the channel surfaces and a free shear flow caused by the boundary layer generated by the interaction between the flow and the isothermal blocks. Then, to validate the present computational method in the two different conditions of flow basis, two different case studies are investigated here: forced convective turbulent flow in a duct channel and forced turbulent convective flow over a bluff body.

For validation of the first case study, an additional simulation is performed for a forced convective turbulent flow in a two-dimensional domain (axisymmetric domain). The same Reynolds and Prandtl numbers applied to define the cases of geometrical investigation are used here. Moreover, the channel has a diameter of 20 mm and a length of 0.4 m, and the peripheral wall has a heat flux of $10~ \hbox {kW/m}^{2}$. The results for spatial averaged Nusselt number in fluid dynamics and thermally developed region of the forced convective flow obtained in the numerical simulation are compared with the results described in three experimental correlations of Dittus and Boelter [50], Sieder and Tate [51], and Gnielinski [52], which are defined, respectively, by:

$$\begin{aligned}{} & {} {\overline{\textrm{Nu}_{D} }} =0.023\textrm{Re}_{D}^{4 /5} Pr^{0.4} \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \overline{\textrm{Nu}_{D} } =0.027\textrm{Re}_{D}^{4/5} Pr^{1/3}\left( {\mu /{\mu _{s} }} \right) ^{0.14} \end{aligned}$$

(25)

$$\begin{aligned}{} & {} {\overline{\textrm{Nu}_{D}}} =\frac{\left( {f/8} \right) \left( {\textrm{Re}_{D} -1000} \right) Pr }{1+12.7\left( {f/8} \right) ^{1/2}\left( {Pr ^{2/3}-1} \right) } \end{aligned}$$

(26)

where $\mu$ is the dynamic viscosity at the inlet temperature (kg/m$\cdot$s), $\mu _{s}$ is the dynamic viscosity at the temperature of the wall, and f is the friction factor, being a function of $\textrm{Re}_{D}$.

Table 2 compares the results between the local Nusselt Number obtained at the wall in the present study simulation and the Nusselt Number given by experimental correlations. It can be seen that, regardless of the correlation used for comparison, the Nusselt Number is within 2.1% and, therefore, the numerical model employed is considered validated to simulate forced turbulent convective flows in channels.

Table 2 Comparison of the Nusselt number in a tube obtained with the present numerical model and experimental correlations of literature

For the free shear flows, it is reproduced in the present work the investigation performed in the study of Teixeira et al. [36], which verified and validated the simulation of forced convective turbulent flows over a square bluff body. More precisely, in that work, the results of the local Nusselt number in the body were compared with other results predicted numerically and experimentally in the literature [53, 54]. The results also proved the capability of the present method for predicting free shear turbulent flows. Table 3 shows the mean Nusselt number obtained with the present work and those predicted in Refs. [53, 54]. More details and comparisons with other works can be seen in the work of Teixeira et al. [36].

Table 3 Comparison of the mean Nusselt number in a bluff body in a forced convective flow with $\textrm{Re}_{D} =22{,}000$ and Pr $=0.71$

It is also important to mention that the transient and steady solutions used in the present model were compared for the grid independence study case and the results of the Nusselt number for steady and unsteady solutions are in close agreement, justifying the use of steady solutions in the present work.

4 Results and discussions

The results obtained in the present study simulations are presented below in a three-step analysis. First, a thermal analysis is conducted to show the influence of the geometry of the blocks over the thermal performance indicator (maximization of the heat transfer rate) and to obtain the optimal thermal geometry that corresponds to the highest heat transfer rate found in all cases simulated. Secondly, a fluid dynamics analysis is conducted in a similar form to that performed for the thermal purpose, now considering the fluid dynamics objective (minimization of the pressure drop along the channel) and determining the optimal fluid dynamic geometry that corresponds to the lowest pressure drop found. Then, the final analysis is a multi-objective analysis, where thermal and fluid dynamics objectives are considered simultaneously to determine the optimal multi-objective geometries, i.e., those that satisfy both objectives in the best possible way compared to the other geometries.

4.1 Thermal analysis

Figure 5 shows the effect of $H_{1}/L_{1}$ over the heat transfer rate (q) for different values of $H_{2}/L_{2}$. As expected, the increase in $H_{1}/L_{1}$ and $H_{2}/L_{2}$ generates the highest heat transfer rates (q), i.e., the highest intrusion led to the best thermal performance. This behavior can be associated with the increase in interaction between the heated blocks and the cooler flow, as well as with the augmentation of momentum of the flow in the region of the blocks due to the definition of the problem where momentum is imposed at the channel inlet. A similar effect of $H_{1}/L_{1}$ over q was previously noticed in the work of Feijó et al. [17] for laminar forced convective flows in channels with two alternated blocks mounted on the channel surfaces. An almost linear increase in the heat transfer rate with the intrusion of the blocks in the spanwise direction of the flow is also observed.

Fig. 5

Effect of $H_{1}/L_{1}$ over the heat transfer rate (q) for different magnitudes of $H_{2}/L_{2}$

Compared with the previous analysis for laminar flows studied in Feijó et al. [17], the augmentation of q with $H_{1}/L_{1}$ behavior is slightly different. In the previous work, an augmentation of rate of increase in q with $H_{1}/L_{1}$ is noticed for the superior ratios of $H_{1}/L_{1}$ investigated. This difference can be associated with the restriction imposed on the height of the blocks in the present investigation, which is restricted to D/2. This additional restriction was not imposed in the study of laminar flows. The behavior observed for turbulent and laminar flows is strongly similar for a similar range of magnitudes of $H_{1}/L_{1}$ and $H_{2}/L_{2}$ studied. It is also important to mention that differences of nearly 60% were obtained when the best and worst shapes were compared, showing the relevance of design investigation for this kind of problem.

The best results in Fig. 5 are compiled and presented in Fig. 6 to obtain the second optimization level. More precisely, Fig. 6 shows the effect of the ratio $H_{2}/L_{2}$ over the once maximized heat transfer rate, $q_{1,{\textrm{max}}}$, and the corresponding optimal ratio of $H_{1}/L_{1}$, ($H_{1}/L_{1})_{\textrm{o,T}}$. Figure 6 shows that apart from the range of 0.065 $<H_{2}/L_{2}< 0.2$, the maximum heat transfer increases with the increase in $H_{2}/L_{2}$. Also, the once thermally optimized ratio ($H_{1}/L_{1})_{\textrm{o,T}}$ is constant for each $H_{2}/L_{2}$ and equal to its highest possible value assumed here, i.e., ($H_{1}/L_{1})_{\textrm{o,T}} =1.55.$ Results also indicated that the difference of performance between the second optimized configuration, ($H_{2}/L_{2})_{\textrm{o,T}} =$ ($H_{1}/L_{1})_{\textrm{oo,T}} =1.55$, and the worst among the once optimized shapes, $H_{2}/L_{2} =0.2$ and ($H_{1}/L_{1})_{\textrm{o,T}} =1.55$, is about 12%. Therefore, even in the second level of optimization, an important improvement in performance of the system is achieved showing the importance of rationalizing the design in this kind of problem. Compared with the laminar case studied in Feijó et al. [17], the effect of $H_{2}/L_{2}$ over $q_{1,{\textrm{max}}}$ obtained here for turbulent flows is similar to that predicted for the laminar flows. In general, results indicated that the mean effect of the intrusion of the rectangular blocks over the thermal performance is not significantly affected by the regime (laminar or turbulent) of forced convective flow.

Fig. 6

Effect of $H_{2}/L_{2}$ over the once maximized heat transfer rate $(q)_{1,max}$ and corresponding optimal ratio of $H_{1}/L_{1},\, (H_{1}/L_{1})_{{o,T}}$

In order to illustrate the effect of the geometry of the blocks on the thermal performance, Fig. 7 shows the thermal field for the blocks with the highest and lowest insertion in the channel. More precisely, Fig. 7a shows the thermal field for the best configuration obtained with ($H_{1}/L_{1})_{\textrm{oo,T}} =1.55$ and ($H_{2}/L_{2})_{\textrm{o,T}} =1.55$, and Fig. 7b illustrates the thermal field for the case with $H_{1}/L_{1} =$ $H_{2}/L_{2} =0.0625.$ In Fig. 7a, it is possible to observe that the highest intrusion of the blocks has an important role since it allows a strong interaction between the heated blocks and the fluid flow. Moreover, the momentum in the region of the blocks is intensified, leading to an augmentation of heat transfer between the heated portion of the channel and blocks and the fresh current of flow. Figure 7b shows that the interaction between the blocks and the fluid flow is strongly restricted for the case with the lowest intrusion. It is also important to mention that, due to the condition of no-slip and impermeability imposed on the walls, the blocks are subjected to low magnitudes of momentum of the fluid flow in the channel. Consequently, a strong difference in heat transfer rate is noticed for the two investigated cases, with the optimal configuration leading to a twice maximized heat transfer rate of $q_{2,{\textrm{max}}} =83$,195.89 W.

Fig. 7

Thermal field (K) obtained for two extreme conditions of insertion of the blocks in the channel: a $(H_1/L_1)_{oo,T} = (H_{2}/L_{2})_{o,T} = 1.55$; b $H_{1}/L_{1} = H_{2}/L_{2} = 0.0625$

In order to illustrate the influence of blocks configuration on the local conditions of heat transfer, Fig. 8 shows the comparison between the optimal thermal geometry and the worst thermal geometry for the local surface Nusselt number along the heated blocks inserted in the channel. It can be seen that the optimal geometry has higher magnitudes of Nusselt number across the walls, especially in the frontal face of the blocks (0.003 m $\le p \le$ 0.01 m). It can also be observed strong peaks of Nusselt number in the region near the corner blocks ($x\sim 0.01$ m in the upper and lower walls of the optimal case) related to the incidence of the fresh fluid over the left surface of the blocks. These peaks are highly smoothed for the configuration with the lowest intrusion of the blocks in the spanwise direction of the turbulent flow. Results also show that the blocks with lower intrusion have a higher magnitude of Nusselt number for $p \ge$ 0.017 m than the optimal shape. Despite that, this performance is not enough to compensate for the highest peaks of the Nusselt number caused by the strong insertion of the heated blocks.

Fig. 8

Surface Nusselt number along the heated region of the wall for $(H_{1}/L_{1})_{oo,T} = (H_{2}/L_{2})_{o,T} = 1.55$ and for $H_{1}/L_{1} = H_{2}/L_{2} = 0.0625$

4.2 Fluid dynamics analysis

From the results obtained for the pressure difference between the inlet and outlet of the channel, it is possible to analyze the problem from a fluid dynamic point of view and determine which geometries perform better in this regard. The effect of $H_{1}/L_{1}$ over the pressure drop along the channel ($\varDelta P)$ for different values $H_{2}/L_{2}$ can be seen in Fig. 9. As expected, the lowest values of$H_{1}/L_{1}$ and $H_{2}/L_{2}$ provide the best fluid dynamic results. The increase in these ratios also increases the pressure drop. Results also demonstrated that the geometric investigation led to significant improvement in the fluid dynamic performance of the problem, with the twice optimized configuration, ($H_{2}/L_{2})_{\textrm{o,F}} =$ ($H_{1}/L_{1})_{\textrm{oo,F}} =0.0625$, leading to a twice minimized pressure drop, $\Delta P_{2,{\textrm{min}}}$ nearly 50% inferior to that reached for the worst configuration, i.e., $H_{2}/L_{2} = H_{1}/L_{1} =1.55.$ Compared with the cases of laminar flows studied in Feijó et al. [14], a similar tendency in the effect of $H_{1}/L_{1}$ over $\Delta P$ for the different magnitudes of $H_{2}/L_{2}$ is observed.

Similarly to the investigation performed for the thermal purpose, the best results obtained in Fig. 9 are compiled and presented in Fig. 10. Therefore, Fig. 10 illustrates the effect of the ratio $H_{2}/L_{2}$ over the once minimized pressure drop $\Delta P_{1,{\textrm{min}}}$ and the corresponding optimal ratio of $H_{1}/L_{1}$, ($H_{1}/L_{1})_{\textrm{o,F}}$. Results demonstrated that for each $H_{2}/L_{2}$, the optimal value of $H_{1}/L_{1}$ is constant and equal to the lowest possible value, ($H_{1}/L_{1})_{\textrm{o,F}} =0.0625.$ Moreover, the magnitude of $\Delta P_{1,{\textrm{min}}}$ decreases for the lowest magnitudes of the ratio $H_{2}/L_{2}$. In the second optimization level, the best shape led to an improvement of almost 30% compared to the worst once optimized shape. Results demonstrated that the fluid dynamic performance could be strongly affected by the configuration of the blocks mounted in the channel. The optimal shapes and the effect of degrees of freedom over fluid dynamic and thermal performance obtained here for turbulent flows and those predicted in Feijó et al. [17] for laminar flows led to similar behavior. In this sense, for the present conditions, the change in flow regime does not lead to significant differences in the prediction of the design when the performance indicators are analyzed individually. Only the magnitudes of heat transfer rate and pressure drop are affected.

Fig. 9

Effect of $H_{1}/L_{1}$ over the pressure drop ($\varDelta P$) for different magnitudes of $H_{2}/L_{2}$

Fig. 10

Effect of $H_{2}/L_{2}$ over the pressure drop once minimized $\varDelta P_{\textrm{1,min}}$ and the corresponding optimal ratio of $H_{1}/L_{1},\, (H_{1}/L_{1})_{o,F}$

In order to investigate the influence of the geometric configurations of the blocks over the fluid dynamic behavior of turbulent channel flows investigated here, Figs. 11 and 12 illustrate the velocity and pressure fields for the optimal configuration, ($H_{2}/L_{2})_{\textrm{o,F}} =$ ($H_{1}/L_{1})_{\textrm{oo,F}} =0.0625$, and the worst one, $H_{1}/L_{1} =$ $H_{2}/L_{2} =1.55.$ Results of Fig. 11a, b demonstrated that the velocity field is only slightly affected for the case with the lowest intrusion of the blocks in the channel. Moreover, the pressure drop shows a uniform distribution between the inlet and exit of the channel. It had a twice minimized pressure drop of $\mathrm {\Delta }P_{2,{\textrm{min}}} =1$,972.99 Pa. For the case with the highest intrusion, Fig. 12, results demonstrated a strong augmentation of the magnitude of velocity fields in the region between the blocks, Fig. 12a, which is suitable for heat exchange between the blocks and the cooler stream of the flow. However, the intrusion of the blocks generates a step variation of pressure between the regions upstream and downstream of the blocks, as can be seen in Fig. 12b. In general, it can be observed that the optimal geometry has a much more stable velocity profile along the channel and that the pressure has a much smoother transition compared to the worst fluid dynamic geometry. Figure 13 illustrates the pressure drop along the channel measured in the centerline of the channel for the optimal and the worst fluid dynamic geometries. A strong variation of pressure can be observed for the case with $H_{1}/L_{1} = H_{2}/L_{2} =1.55$ in the region 0.10 m $\le x \le$ 0.20 m, which is a region affected by the presence of the alternated blocks.

Fig. 11

Velocity (m/s) (a) and pressure (Pa) (b) fields for $(H_{1}/L_{1})_{oo,F} = 0.0625$ and $(H_{2}/L_{2})_{o,F} = 0.0625$

Fig. 12

Velocity (m/s) (a) and pressure (Pa) (b) fields for $H_{1}/L_{1} = 1.55$ and $H_{2}/L_{2} = 1.55$

Fig. 13

Area-weighted average pressure (Pa) along the channel length

4.3 Multi-objective analysis

In the present study, the multi-objective analysis is conducted using the TOPSIS multi-criteria method. For each of the combinations of weights $w_\textrm{T}\,$ and $w_\textrm{F}$ analyzed, the parameter $C_{i}$ of all simulated geometries is calculated, the relative proximity to the ideal solution, and the closer this value is to 1.0, the closer the geometry is to the ideal solution. Through $C_{i}$ it is possible to compare how suitable the geometries, the possible alternatives, are relative to the proposed multi-objective (established by the weights $w_\textrm{T}$ and $w_\textrm{F})$ and thus, define the optimal geometry from this point of view. In the present work, three combinations of weights were considered: $w_\textrm{T}=w_\textrm{F}=0.5$, $w_\textrm{T} =0.9$ and $w_\textrm{F}=0.1$ and $w_\textrm{T}=0.1$ and $w_\textrm{F}=0.9.$ It is important to note that the value of $C_{i}$ depends on the combination of weights, so it is not possible to compare the multi-objective performance of geometries (either the same or different) in which combinations of different weights have been used.

Fig. 14

Effect of $H_{1}/L_{1}$ over the relative proximity to the ideal solution $(C_{i})$ for different magnitudes of $H_{2}/L_{2}$ and for $w_\textrm{T}=0.5$ and $w_\textrm{F}=0.5$

Figure 14 demonstrates the effect of $H_{1}/L_{1}$ on $C_{i}$ for different $H_{2}/L_{2}$ considering $\, w_\textrm{T}=w_\textrm{F}=0.5$. It is possible to observe that from $H_{1}/L_{1}=0.0625$ to approximately $H_{1}/L_{1}=0.9$, the multi-objective performance of all geometries increases with the increase in $H_{1}/L_{1}$ and that the geometries with the lowest values of $H_{2}/L_{2}$ are closer to the ideal. It is also noticed only a slight difference in $C_{i}$ for geometries with $H_{2}/L_{2}$ between 0.0625 and 0.3. As $H_{1}/L_{1}$ increases above 0.9, this performance difference increases. Around $H_{1}/L_{1}=$ 1.3, it is observed that the geometries reach a point of maximum proximity to the ideal solution and, from this value, their performance starts to decrease, which is an important difference in the effect of $H_{1}/L_{1}$ over the performance when compared with the thermal and fluid dynamic performances analyzed in isolated form. Figures 15 and 16 show the effect of $H_{1}/L_{1}$ on $C_{i}$ for different $H_{2}/L_{2}$, now considering $w_\textrm{T} =$ 0.9 and $w_\textrm{F}=0.1$ (Fig. 15) and $w_\textrm{T}=0.1$ and $w_\textrm{F}=0.9$ (Fig. 16). It is possible to see that the effect of the geometries on $C_{i}$ is very close to those obtained in the thermal (Fig. 5) and fluid dynamics (Fig. 9) analysis, but with slight differences due to the multi-objective consideration. The results of Figs. 15 and 16 also demonstrate that when $w_\textrm{T}$ increases to values near unity ($w_\textrm{T} \sim 1.0$), the effect of $H_{1}/L_{1}$ over $C_{i}$ tends to the effect of $H_{1}/L_{1}$ over q, while a similar behavior is noticed for the fluid dynamic purpose when $w_\textrm{F}$ tends to unity ($w_\textrm{F}\sim 1.0$), remembering that the decrease in pressure drop is the purpose in the fluid dynamics analysis.

Fig. 15

Effect of $H_{1}/L_{1}$ over the relative proximity to the ideal solution $(C_{i})$ for different magnitudes of $H_{2}/L_{2}$ and for $w_\textrm{T}=0.9$ and $w_\textrm{F}=0.1$

Fig. 16

Effect of $H_{1}/L_{1}$ over the relative proximity to the ideal solution $(C_{i})$ for different magnitudes of $H_{2}/L_{2}$ and for $w_\textrm{T}=0.1$ and $w_\textrm{F}=0.9$

Fig. 17

Effect of $H_{2}/L_{2}$ over the relative proximity to the ideal solution $(C_{i})$

The effect of $H_{2}/L_{2}$ over ($C_{i})_{1,{\textrm{max}}\, }$ is shown in Fig. 17 for the different weights considered. As shown in Fig. 14, for $w_\textrm{T}=w_\textrm{F}=0.5$ the geometries with the lowest values of $H_{2}/L_{2}$ presented the results with the greatest relative proximity to the ideal solution. It is possible to notice an almost linear decrease in ($C_{i})_{1,{\textrm{max}}\, }$ with the increase in $H_{2}/L_{2}$. The behavior of ($C_{i})_{1,{\textrm{max}}}$ was also decreasing with increasing $H_{2}/L_{2}$ to $w_\textrm{T}=0.1$ and $w_\textrm{F}=0.9$ while an increase in ($C_{i})_{1,{\textrm{max}}\, }$ was observed with increasing $H_{2}/L_{2}$ for $w_\textrm{T}=0.9$ and $w_\textrm{F}=0.1$. It is also notable that for $w_\textrm{T}=0.1$ and $w_\textrm{F}=0.9$ there is a greater variation of ($C_{i})_{1,{\textrm{max}}\, }$ with $H_{2}/L_{2}$ than for $w_\textrm{T} =0.9$ and $w_\textrm{F}=0.1$. Figure 18 demonstrates the effect of $H_{2}/L_{2}$ over the respective optimal geometries of $H_{1}/L_{1}$, ($H_{1}/L_{1})_{{\textrm{o}}}$. It is noticed that when $w_\textrm{T} = w_\textrm{F} =0.5$, high magnitudes of the once optimized ratio of $H_{1}/L_{1}$, ($H_{1}/L_{1})_{{\textrm{o}}}$, are reached for the lowest magnitudes of $H_{2}/L_{2}$ (where the highest magnitudes of $C_{i}$ are reached). In this sense, for the multi-objective investigation with $w_\textrm{T} = w_\textrm{F} =0.5$, highly asymmetric configurations of upstream and downstream blocks are obtained. For the other weights, the effect of $H_{2}/L_{2}$ over ($H_{1}/L_{1})_{{\textrm{o}}}$ was similar to that reached when the thermal and fluid dynamic performances were investigated in isolated form. A slight difference for the lowest magnitudes of $H_{2}/L_{2}$ when $w_\textrm{T} =0.1$ and $w_\textrm{F} =0.9$ is noticed. More precisely, it is seen an increase in the magnitude of ($H_{1}/L_{1})_{{\textrm{o}}}$ with the decrease in $H_{2}/L_{2}$ when $H_{2}/L_{2} \quad \le$ 0.3, which is not noticed when a similar investigation is performed for the fluid dynamic performance, see Fig. 10.

Fig. 18

Effect of $H_{2}/L_{2}$ over the corresponding optimal ratio of $H_{1}/L_{1}$, $(H_{1}/L_{1})_{o}$

Fig. 19

Temperature (K) (a), velocity (m/s) (b) and pressure (Pa) (c) fields for $(H_{1}/L_{1})_{\textrm{oo}} = 1.4$ and $(H_{2}/L_{2})_{\textrm{o}} = 0.0625$

Fig. 20

Temperature (K) (a), velocity (m/s) (b) and pressure (Pa) (c) fields for $H_{1}/L_{1} = 0.0625$ and $H_{2}/L_{2} = 1.55$

Figure 19 presents the temperature, velocity, and pressure fields of the optimal multi-objective geometry obtained in the present study with $L_{3}/L_\textrm{ocu}=0.5$ and for $w_\textrm{T}=w_\textrm{F}=0.5$. This geometry is ($H_{1}/L_{1})_{{\textrm{oo}}\, }=1.4$ and ($H_{2}/L_{2})_{{\textrm{o}}}=0.0625$, a geometry where the blocks are asymmetric, with the first block having a height close to the established maximum height (but smaller than this) and the second fin having the lowest possible height within the established for this study. For the sake of comparison, the worst multi-objective geometry (for $w_\textrm{T}=w_\textrm{F}=0.5)$ was $H_{1}/L_{1}=0.0625$ and $H_{2}/L_{2}=1.55$, and their fields can be seen in Fig. 20, a geometry where each of the two blocks had a geometry practically opposite to that observed in the optimal geometry. It is possible to observe in Fig. 19 that the optimal multi-objective geometry is capable of generating a considerable heat exchange, equal to $q_{2,{\textrm{max}}\, }=71$,497.26 W. At the same time, it can also avoid a very large pressure gradient, as observed in the worst fluid dynamic geometry in Fig. 12. The optimal multi-objective geometry obtained a pressure drop equal to $\mathrm {\Delta }P_{2,{\textrm{min}}\, }=2$,545.08 Pa. Table 4 presents the values obtained for the optimal geometries and their respective rates of twice maximized heat transfer rate and twice minimized pressure drop for the different weight combinations considered in the present work. It is noteworthy to observe that the optimal geometry for $w_\textrm{T}=w_\textrm{F}=0.5$ led to a thermal performance nearly 13% inferior to the best configuration for $w_\textrm{T} =0.9$ and $w_\textrm{F} =0.1$ and 49% superior to the best configuration with $w_\textrm{T} =0.1$ and $w_\textrm{F} =0.9.$ Concerning the fluid dynamic performance, the optimal configuration for $w_\textrm{T} = w_\textrm{F} =0.5$ has a performance nearly 30% and 26% superior and inferior, respectively, than the optimal configurations reached for $w_\textrm{T} =0.9$ and $w_\textrm{F} =0.1$ and $w_\textrm{T} =0.1$ and $w_\textrm{F} =0.9.$

Table 4 Optimal multi-objective geometries for each $w_\textrm{T}$ and $w_\textrm{F}$ and corresponding twice maximized heat transfer rates, ($q)_{{\textrm{oo}}}$, and twice minimized pressure drops, ($\Delta P)_{{\textrm{oo}}}$

5 Conclusions

In the present numerical study, the Constructal Design method and Exhaustive Search were applied in the geometric evaluation of a channel with two heated blocks subjected to turbulent forced convective flows, which to the best of authors’ knowledge, has not been investigated in the literature. The Finite Volume Method (FVM) was used to numerically solve the time-averaged equations of continuity, momentum, energy conservation, and additional transport equations [40,41,42]. For closure of turbulence, the k – $\omega$ SST model was employed [43, 44]. Concerning the geometrical investigation, the objectives were to maximize the heat transfer from the blocks to the surrounding flow and to minimize the pressure drop between the inlet and outlet of the channel, analyzing the various geometry arrangements of the two blocks. Two degrees of freedom were defined: the ratio between the height and the length of each block: $H_{1}/L_{1}$ and $H_{2}/L_{2}$. Also, three geometrical constraints were defined: the channel area (A), the area of occupation of each block ($A_{1}$, equal for the two blocks), and the area of the blocks ($A_{2}$, also the same for the two blocks). The problem was analyzed from thermal, fluid dynamic, and multi-objective perspectives using the TOPSIS method [45, 46]. For the present investigation, an amount of 144 cases were simulated.

From the results obtained, it was possible to observe that the optimal geometries for the thermal and fluid dynamic objectives were those in which the ratios of the two blocks had the highest and lowest values, respectively. These results are within expectations and in accordance with the Reynolds analogy. The optimal thermal geometry was ($H_{1}/L_{1})_{{\textrm{oo,T}}} =1.55$ and ($H_{2}/L_{2})_{\textrm{o,T}} =1.55$ and generated a maximum heat transfer rate of $q_{2,{\textrm{max}}} =83$,195.89 W. This configuration led to a thermal performance nearly 60% superior to the worst configuration. Concerning the optimal fluid dynamic geometry, it was achieved for the lowest intrusion of the blocks in the channel, i.e., ($H_{1}/L_{1})_{\textrm{oo,F}} =0.0625$ and ($H_{2}/L_{2})_{\textrm{o,F}} =0.0625$, and had a minimum pressure drop of ${\Delta }P_{2,{\textrm{min}}} =1$,972.99 Pa, which is almost 50% lower than the worst configuration. When the results obtained for turbulent flows were compared with previous results of Feijó et al. [17] for similar cases under laminar forced convective flows, the effect of the ratios $H_{1}/L_{1}$ and $H_{2}/L_{2}$ over the thermal and fluid dynamic performance had similar behavior. In other words, the change of flow regime was not significant to influence the achievement of optimal configurations for the investigation of performance parameters in individual form.

The multi-objective analysis considering weights of $w_\textrm{T}=w_\textrm{F}=0.5$ led to the optimal geometry with an asymmetry between the blocks, equal to ($H_{1}/L_{1})_{{\textrm{oo}}}=1.4$ and ($H_{2}/L_{2})_{{\textrm{o}}}=0.0625.$ This result showed that, when considering the multi-objective, the geometry of the blocks is forced to adapt to meet the two proposed objectives better. The increase in the height of the first block proved to be positive in the multi-objective, from $H_{1}/L_{1}=0.0625$ to a point close to $H_{1}/L_{1}=1.4$, with a slight decrease in performance ($C_{i})$ after this point. About $H_{2}/L_{2}$, the lowest values showed a better performance. The results obtained considering the other two weight combinations ($w_\textrm{T} =0.9$ and $w_\textrm{F}=0.1$; $w_\textrm{T}=0.1$ and $w_\textrm{F}=0.9)$ were very close to those obtained in the thermal and fluid dynamics analyses, respectively. However, it was possible to observe the influence exerted by the geometry over the ideal solution when considering a small fraction of another objective instead of the purely thermal and fluid dynamic analysis. In general, results showed that, when the multi-objective is taken into account, the best configurations assumed asymmetric configurations, contrarily to what was noticed for thermal and fluid dynamic performances when these performance indicators were analyzed in isolated form. In other words, the design can be strongly affected when the flow system is subjected to multi-objective purposes. Moreover, for the multi-objective investigation, the best configurations and the effect of geometry were affected by the flow regime (laminar or turbulent), which can be noticed when the present results were compared with previous results of Feijó et al. [17] for laminar flow in similar conditions.

For future works, the effect of the geometrical configuration of blocks over the fluid dynamic and thermal performance of boiling convective flow in channels is recommended to investigate the influence of phase change flow on the design and performance of cooling convective channel flows.