1 Introduction

The simulation of large plastic deformations, as they occur many technical applications like metal forming, has been the subject of intensive research activities since the middle of the last century. In the beginning, the question of an appropriate introduction of plastic variables has been a particular issue for which different solutions have been suggested and debated. The problem behind this has always been the transformation of the elastic law by which the current stresses can be determined within some particular elastic range . Since the elastic range in the strain space is rather small compared to the plastic deformations, it is customary to use a linear Hooke’s law with an (isotropic or anisotropic) stiffness tetrad and a so-called elastic strain variable with respect to an unloaded configuration, for which evolution laws are required.

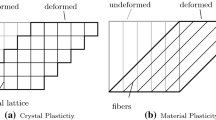
In the case of single crystals, this problem has been fully understood quite early. The introduction of the isoclinic configuration in [10] combined with Schmid’s law and slip system mechanisms gives a clear picture of the current elastic behavior and its governing anisotropy. Mathematically speaking, for single crystals the elastic law remains isomorphic, whatever the plastic deformations are. This isomorphy concept has been suggested in [2, 3], and it is applicable in many other cases too, but surely not in all, as we will see in the sequel.

In most applications, we do not deal with single crystals but with polycrystals. In such cases, crystal plasticity still helps us to understand the local behavior on the microscale. For practical applications, however, a macromodel is needed. And on the macroscale the behavior of polycrystals is completely different from its single-crystal constituents.

The influence of the plastic deformation on the elastic constants has already been experimentally proven in [18]. In his famous experiments, Weerts has demonstrated that due to plastic deformations the elastic stiffnesses are essentially altered. This is, as we know now, due to the evolution of the crystallographic texture. Since then, many attempts have been made to properly describe this texture evolution and its influence on the elastic behavior, see [4,5,6] and [19]—a rather demanding task which will probably never be solved exactly.

A completely different situation is given in the case of fiber-reinforced materials where both the fibers and the matrix material are jointly deformed. In this case, the anisotropy directions of the material presented by the fiber directions are deformed together with the material, at least in the average, a reason to call this effect material plasticity. The concept of material plasticity was initially introduced in [7] for the case of twinning where a similar effect can be observed. This is in contrast to the lattice structure of a crystal, where the crystal axes do not deform like material line elements. Needless to say that the concept of isomorphic elastic ranges is not applicable in such cases of material plasticity.

One way to approach this problem is based on the introduction of structural tensors, see [1, 8, 12]. These tensors contain the information of the current direction of the fibers and determine the transformation of the stiffness tensor. One can use isotropic tensor function representations, which leads to sets of scalar invariants. Unfortunately, the physical interpretation of them cannot be easily given, which complicates the identification of their evolution equations.

Another approach dealing with material plasticity based on different transformations of the stiffness tetrad and the stress-free placement is shown in [16]. So two evolution equations are needed instead of just one flow rule, which are again difficult to be identified.

In the present paper, we will introduce a novel method to describe the stiffness of a fiber-reinforced material by using a superposition of transversely isotropic stiffnesses for each fiber. The five elastic constants of each transversely isotropic law are calibrated for each fiber in the initial configuration. In order to calculate the stiffness tensor after the plastic deformation, we rotate the direction of the transversal axis in the same way as a material line element and again superimpose them. So after having identified the elastic behavior in the initial placement, it can be easily transformed into the current placement by the use of just one plastic variable. This is the usual plastic deformation tensor which is up-dated by a flow rule.

This method is compared with other, more simple ones to up-date the elastic stiffness during plastic deformations, namely with

  1. 1.

    A constant (initial) one;

  2. 2.

    The push-forward of the initial one by the plastic deformation;

  3. 3.

    The forward rotation of the initial one by the rotational part of the plastic deformation.

In order to compare the efficiency and exactness of these four methods, we will apply them to different sample materials with one, two, and three fiber reinforcements under typical test deformations.

Due to the lack of appropriate experimental results, we use a numerical laboratory in the form of finite element calculations of a representative volume element. We submit this RVE to different test deformations and determine the elasticity tensors before and after the deformation by averaging over the local stress field resulting from the FE calculations.

The Frobenius norm of the difference between the numerically determined elasticity tensor and the one calculated by one of these three methods can be used as a measure of the precision of each of these methods. This comparison gives us a tool to judge upon the different methods and give a recommendation as a compromise between precision and invested work.

Before we start with this program, we will briefly introduce some useful tensor notations.

2 Notations

We denote scalars (reals) by italic letters like a, vectors by bold small letters like \(\varvec{v}\), and N-th-order tensors by \(\overset{\scriptscriptstyle \langle N \rangle }{\mathbb {K}}\). As an exception, second-order tensors or dyads are written as usual by bold capital letters like \(\varvec{A}\). The dyad product of two vectors is denoted as \(\varvec{a} \otimes \varvec{b}\).

The application of a second-order tensor \(\varvec{A}\) on a vector \(\varvec{v}\) is written as \(\varvec{A}\varvec{v}\) (single contraction). The application of a fourth-order tensor \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\) on a second-order tensor \(\varvec{A}\) is written as \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}: \varvec{A}\) (double contraction). The Frobenius norm of a fourth-order tensor \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\) is noted as \(\Vert \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\Vert \).

Although we prefer a direct tensor notation, we have to use an index notation in some cases. We will then always refer to an orthonormal vector basis and use the summation convention like, e.g., for a fourth-order tensor

$$\begin{aligned} \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}= K^{ijkl} \varvec{e}_i \otimes \varvec{e}_j \otimes \varvec{e}_k \otimes \varvec{e}_l \ . \end{aligned}$$

The Rayleigh product of a second-order tensor \(\varvec{A}\) and an N-th-order tensor \(\overset{\scriptscriptstyle \langle N \rangle }{\mathbb {K}}\) is defined by:

$$\begin{aligned} \varvec{A} * \overset{\scriptscriptstyle \langle N \rangle }{\mathbb {K}} = K^{i_1 i_2 \dots i_N} \varvec{A}\varvec{e}_{i_1} \otimes \varvec{A}\varvec{e}_{i_2} \otimes \dots \otimes \varvec{A}\varvec{e}_{i_N} \ . \end{aligned}$$

Particularly, if \(\varvec{A}\) is orthogonal, this application can be interpreted as a rotation of the tensor\(\overset{\scriptscriptstyle \langle N \rangle }{\mathbb {K}}\).

3 Elastic laws

In the elastoplastic constitutive theory, it is assumed that the stresses at each instant can be determined by the current elastic law. If the elastic deformations are small although the plastic ones can be arbitrarily large, it is justified to use a linear elastic law of the form

$$\begin{aligned} \varvec{T} = \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}: \varvec{E} \ . \end{aligned}$$
(1)

Such laws are known from finite elasticity as St.-Venant-Kirchhoff laws with \(\varvec{T}\) being the second Piola–Kirchhoff stress tensor, \(\varvec{E}\) Green’s deformation tensor, and \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\) the fourth order elasticity tensor or stiffness tetrad. Note that this form is only valid if the reference placement is stress-free or unloaded, so that it depends on the previous plastic deformation. If both \(\varvec{E}\) and the rotations are small, as we assume further on, it can be taken as the linear deformation tensor, and \(\varvec{T}\) can be also interpreted as Cauchy’s stress tensor.

The main open problem when using this form is the determination of the stiffness tetrad \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\) since it evolves during the plastic deformation in a non-trivial way. The rest of this paper is dedicated to the challenging task to model this evolution.

However, before we do so, we will investigate its general properties. First we will limit our considerations to elastic laws which are also hyperelastic, thus imposing the major symmetry on \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\). If \(K^{ijkl}\) are the components of it w.r.t. some orthonormal vector basis, the

  • (major) symmetry is \(K^{ijkl} = K^{klij}\).

By the symmetry of the stress and of the deformation tensors, we can also assume the

  • Left subsymmetry \(K^{ijkl} = K^{jikl}\),

  • Right subsymmetry \(K^{ijkl} = K^{ijlk}\).

In what follows we will always impose these symmetries to all stiffness tetrads, which have therefore in general 21 independent components.

The usual way to further reduce the number of independent components is by using material symmetries. In our cases dealing with solids, we can limit our considerations to orthogonal transformations. We thus call an orthogonal tensors \(\varvec{Q}\) a symmetry transformation of a particular elastic stiffness \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\), if

$$\begin{aligned} \varvec{Q} * \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}= \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\end{aligned}$$

by using the Rayleigh product introduced in the previous section. Since the order of the tetrad is even, it does not matter here whether we allow for all orthogonal tensors or just the proper ones.

All symmetry transformations of a particular \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}\) form a group under composition, namely the symmetry group of the elastic law. The following table contains all discrete groups for linear elastic solids, see Table 1. Additionally, the continuous isotropic and transversely isotropic symmetry groups must be considered.

Table 1 Generators of the discrete symmetry groups, see [15]. The diagonal is given by \(\varvec{d} =\nicefrac {\left( \varvec{e}_1 + \varvec{e}_2 + \varvec{e}_3\right) }{\sqrt{3}}\). Here \(\varvec{Q}_{\varvec{a}}^\varphi \) denotes a rotation around the axis \(\varvec{a}\) by the angle \(\varphi \)
Full size table

In the literature, e.g., [11], useful Voigt representations for all tetrads with one of the discrete or continuous symmetry groups can be found. One must keep in mind, however, that these representations hold only w.r.t. particular vector bases, which we will call canonical bases.

4 Four different models

In this section, we will describe four different methods to transform the elastic stiffness due to large plastic deformations. We will always refer to the elastic law in the original form, cf. (1), with the following interpretation. The reference placement will always be the one obtained after the plastic deformation upon unloading. \(\varvec{T}\) is the current Cauchy stress tensor after a superimposed elastic deformation described by the linear deformation tensors \(\varvec{E}\), which must be small to remain in the current elastic range. In the following, the subscript “p” is added to the stiffness to emphasize the effort of modeling the evolution of it under plastic deformations.

For this purpose, we will next describe four alternative methods.

Method 1

We assume that the stiffness is not effected by the plastic deformation, so that the current one \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p}\) is always equal to the initial one, i.e.,

$$\begin{aligned} \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p} = \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_0 \ . \end{aligned}$$

Method 2

We assume that the current elastic stiffness is the push-forward of the initial one by the plastic part of the deformation \(\varvec{F}_\text {p}\) resulting from the concept of a multiplicative decomposition of the deformation gradient, i.e.,

$$\begin{aligned} \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p} = \varvec{F}_\text {p} * \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_0 \ . \end{aligned}$$

This is essentially the concept of elastic isomorphy, see [2, 3].

Method 3

We decompose \(\varvec{F}_\text {p}\) into its symmetric and positive definite part and its orthogonal part \(\varvec{R}_\text {p}\) from the polar decomposition. The latter one stands for the mean rotation of the line elements.

We use only this rotation for the push-forward of the stiffness, i.e.,

$$\begin{aligned} \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p} = \varvec{R}_\text {p} * \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_0 \ . \end{aligned}$$

Thus, this method is rather similar to the previous one, but needs the polar decomposition at each step.

Method 4

This last and most sophisticated method aims to model the stiffness of a fiber-reinforced material as a superposition of transversely isotropic ones. We will introduce this methods in two steps.

The first one deals with the stiffness in the initial configuration.

Let us start with a unidirectionally reinforced material in the initial configuration. Its resulting stiffness is either exactly transversely isotropic or can be at least approximated by it. With respect to an orthonormal basis with \(\varvec{e}_3\) directing in the fiber direction, it has the following normalized Voigt representation

$$\begin{aligned} \begin{pmatrix} K_{1111} &{} K_{1122} &{} K_{1133} &{} 0 &{} 0 &{} 0 \\ &{} K_{1111} &{} K_{1133} &{} 0 &{} 0 &{} 0 \\ &{} &{} K_{3333} &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} 2 K_{2323} &{} 0 &{} 0 \\ &{} &{} &{} &{} 2 K_{2323} &{} 0 \\ \text {sym.} &{} &{} &{} &{} &{} K_{1111} - K_{1122} \end{pmatrix} \end{aligned}$$

with five independent constants.

If the material has N fiber directions \(\varvec{d}_i\), we approximate the initial stiffness by a superposition of N transversely isotropic laws as

$$\begin{aligned} \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_0 = \sum _{i=1}^{N} w_i \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_{0i} \end{aligned}$$
(2)

with \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_{0i}\) being the stiffness of the i-th individual fiber with the symmetry axis \(\varvec{d}_i\). The weights \(w_i\) may be used to account for material differences in a particular fiber direction, e.g., a different number or size of fibers. However, since the materials discussed here have the same number of fibers in each fiber direction, we choose \(w_i = 1\) for all i.

If the fibers are different in geometry and/or material, we have to identify all of these stiffnesses individually, which results in 5N independent constants. If they are equal and just have different directions, we can transform the first one into the others by an appropriate rotation \(\varvec{Q}_{1i}\), i.e.,

$$\begin{aligned} \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_{0i} = \varvec{Q}_{1i} * \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_{01} \end{aligned}$$

before superimposing them. In this case, we have to identify only five constants in total. Generally one has to note that this approximation by as the above weighted sum (2) does not imply a micro-macro approach. It is performed exclusively on the macro-scale. So we do not identify each transversely isotropic stiffness separately, but only as the above resulting sum. Principally this results in the optimization problem of minimizing the difference

$$\begin{aligned} d(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {exp}, \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p}):= \frac{\Vert \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {exp} - \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p} \Vert }{\Vert \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {exp} \Vert }\ \end{aligned}$$
(3)

between the measured stiffness and \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_0\) by an appropriate choice of the remaining elastic constants. Such a procedure of material identification is standard in elasticity and will be therefore not further explained in the present context. For the following examples, this step could be performed without problems.

In a second step, we transform the initial stiffness into the current one, i.e., after a finite plastic deformation \(\varvec{F}_\text {p}\). This is done individually for each fiber after the following algorithm.

If the fiber index is i and \(\varvec{d}_i\) is a vector in the direction of this fiber in the initial configuration, then under the deformation, this direction will be turned into the direction of the vector \(\varvec{F}_\text {p}\varvec{d}_i\). Now let \(\varvec{R}_{\text {p}i}\) be an orthogonal tensor which rotates the direction \(\varvec{d}_i\) into the direction of \(\varvec{F}_\text {p}\varvec{d}_i\). Since this orthogonal tensor is not unique, we use the one that minimizes the rotation angle. We use this rotation to approximate the entire current stiffness as the superposition of the rotated individual stiffnesses of the fibers, i.e.,

$$\begin{aligned} \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p} = \sum _{i = 1}^{N} \varvec{R}_{\text {p}i} * \overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_{0i} \ . \end{aligned}$$

Note that this rotation is different from \(\varvec{R}_{\text {p}i}\) of method 3. Here, no spectral decomposition of \(\varvec{F}_\text {p}\) is involved. Thus, for this transformation only the initial stiffnesses and \(\varvec{F}_\text {p}\) are needed, but no additional parameter identification has to be performed. So each updating process of \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p}\) consists only of simple algebraic operations.

Before we apply these four methods for some typical test deformations, we need to furnish our numerical laboratory to perform such tests.

5 Representative volume element

In order to compare these four methods with experimental results, we use the numerical laboratory as described below. This choice has at least two reasons. First of all, it is not easy and rather time-consuming and costly to perform such experiments in reality. Second, in our numerical laboratory we are much more flexible in the choice of such experiments as we were in a real laboratory. Moreover, we can study the behavior in each detail with any desired preciseness.

Our numerical laboratory mainly consists of a representative volume element (RVE) made of a (fictitious) material with an ideal internal structure as close as possible to realistic composites. Our RVE is a cuboid of finite elements submitted to periodic boundary conditions, see [9]. It contains one, two, or three perpendicular fibers with either circular or quadratic cross section, see Fig. 1.

Fig. 1
figure 1

Representative volume elements of the uni-, bi-, and tridirectional material

Full size image

For simplicity, it is assumed that both the fibers and matrix are made out of homogeneous isotropic elastoplastic materials with linear hardening as pre-implemented in Abaqus, see [13], with a v. Mises yield stress and linear isotropic strain hardening. So the anisotropy of the RVE results exclusively from the fiber arrangement. Furthermore, we assume that all fibers in each of our chosen example materials have the same shape, dimensions, and material parameters. For the unidirectional RVE, the macro-behavior is expected to be transversely isotropic, for the bidirectional one tetragonal, and for the tridirectional one cubic.

In order to make the effect of the fiber structure more visible, we give the fibers a significantly bigger stiffness than the matrix material. The used material constants are given in Table 2.

Table 2 Material parameters used in RVE calculations
Full size table

We can now submit our three RVEs to different deformation processes. These are prescribed by some parameter-dependent deformation gradient \(\varvec{F}(c)\) on the macroscale containing a parameter c which is initially zero and grows up to some final value of one, controlling the magnitude of the deformation.

We perform these tests with the macro-stiffness tensor at different stages of such deformation paths controlled by the parameter c. To do this, we make a small variation of the final macro-deformation in six directions and calculate the according variations of the averaged stresses (macro-stresses). It is important that these variations occur purely elastically, i.e., without further yielding. This can be assured by applying an additional variation \(\delta \varvec{F}\) and \(-\delta \varvec{F}\). If we then compare the stress increments componentwise in both directions, a further plastic deformation would give a much smaller value for the tangent as a purely elastic one and can therefore ruled out. The ratios of the stress variations and the strain variations give 36 macro-stiffness values. The resulting stiffness matrix turns out to be symmetric in all cases due to the hyperelasticity of the materials on the microscale.

The calculated stiffness tetrads can be further compared with those resulting from our four evolution models.

6 Comparison

In order to test and compare the four methods for predicting the elastic stiffnesses, we will determine it in the undeformed state (\(\varvec{F}_\text {p} = \varvec{1}\)) with the stiffness after several large plastic deformations (\(\varvec{F}_\text {p} \ne \varvec{1}\)) for each of the considered composites. However, due to the different fiber arrangements, different deformations are used for different composites.

For the comparison of two stiffness tensors, namely \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {exp}\) resulting from the numerical experiment, and \(\overset{\scriptscriptstyle \langle 4 \rangle }{\mathbb {K}}_\text {p}\) from the model, we use the relative Frobenius norm of the difference of them shown in (3). This distance will be called relative error.

It should be mentioned that one can also determine the distance of a stiffness tetrad to the class of all tetrads with a certain symmetry as well as the closest element to it within this class, see [14] and [17].

6.1 Unidirectionally reinforced material

We choose a unidirectionally reinforced material with fiber direction \(\varvec{e}_3\) under two different deformations. Therefore, we examine two different deformations which change the initial fiber direction, i.e.,

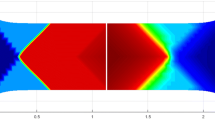
$$\begin{aligned} \varvec{F}_{\text {p,uni}, 1}(c) = \begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} c \\ 0 &{} 0 &{} 1 \end{pmatrix}_{ij} \varvec{e}_i \otimes \varvec{e}_j \quad \text {and} \quad \varvec{F}_{\text {p,uni}, 2}(c) = \begin{pmatrix} 1 &{} 0 &{} c \\ 0 &{} 1 &{} c \\ 0 &{} 0 &{} 1 \end{pmatrix}_{ij} \varvec{e}_i \otimes \varvec{e}_j \ . \end{aligned}$$

The control parameter c starts at zero in the reference placement and is gradually increased to the final value one in the final placement. Both are a simple shear test in different planes. Figure 2 shows RVEs of the unidirectionally reinforced material in an undeformed and deformed state. One can observe that the fibers (green) are deformed together with the matrix material (blue), but also inhomogeneities occur, mainly in the soft phase (matrix).

Fig. 2
figure 2

Undeformed (left) and deformed (right) representative volume element of the unidirectionally reinforced material. The right RVE was deformed using \(\varvec{F}_{\text {p,uni}, 1}(1)\)

Full size image
Fig. 3
figure 3

Unidirectionally reinforced material while being plastically deformed with \(\varvec{F}_{\text {p, uni}, 1}(c)\) (left) and \(\varvec{F}_{\text {p, uni}, 2}(c)\) (right)

Full size image

The results of the different methods of taking the stiffness change into account are shown in Fig. 3. As indicated by the dashed graph in Fig. 3 (left), considering Method 1 for calculations in the deformed state would yield a relative error of nearly 45 %. The situation is improved by using Method 3. Applying this method yields a relative error of approximately 22 % for the maximum applied shear parameter \(c = 1\).

The best result is gained by using Method 4. This approach yields relative errors below 5 % throughout the whole range of the shear parameter.

These relative errors are shown in Fig. 3 (right) for the same composite using the second deformation \(\varvec{F}_{\text {p,uni}, 2}(c)\). The overall behavior of the composite is similar to the previously discussed case. However, the relative errors in all cases are slightly higher than in the case using \(\varvec{F}_{\text {p,uni}, 1}(c)\). Nonetheless, Method 4 shows the best behavior and delivers a maximal relative error of approximately 6 %.

6.2 Bidirectionally reinforced material

We now come to the material reinforced in two initially orthogonal directions as shown in Fig. 1.

Initially, the fiber directions of the bidirectionally reinforced material are taken as \(\varvec{e}_1\) and \(\varvec{e}_2\). The deformations

$$\begin{aligned} \varvec{F}_{\text {p,bi}, 1}(c) = \begin{pmatrix} 1 &{} c &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix}_{ij} \varvec{e}_i \otimes \varvec{e}_j \quad \text {and} \quad \varvec{F}_{\text {p,bi}, 2}(c) = \begin{pmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ c &{} c &{} 1 \end{pmatrix}_{ij} \varvec{e}_i \otimes \varvec{e}_j \ . \end{aligned}$$
(4)

are chosen in order to ensure a change of the initial fiber direction. Figure 4 shows RVEs of the bidirectionally reinforced material in an undeformed and deformed state.

Fig. 4
figure 4

Undeformed (left) and deformed (right) representative volume element of the bidirectionally reinforced material. The right RVE was deformed using \(\varvec{F}_{\text {p,bi}, 1}(1)\)

Full size image
Fig. 5
figure 5

Bidirectionally reinforced material while being plastically deformed with \(\varvec{F}_{\text {p,bi}, 1}(c)\) (left) and \(\varvec{F}_{\text {p,bi}, 2}(c)\) (right)

Full size image

Comparing the undeformed stiffness with the stiffnesses calculated using Method 1, a maximal difference of approximately 18 % for \(c = 1\) is achieved, see Fig. 5 (left). As seen in the unidirectional case, using Method 2 does not improve the ability to portrait the materials’ behavior during the deformation. On the contrary, using this approach yields worse results than using the undeformed stiffness in an deformed state. Furthermore, Method 3 is not useful in this case. Even though a small improvement can be seen, the difference between this approach and the undeformed stiffness is miniscule throughout the whole range of deformations under consideration. Solely the approach using the transversely isotropic stiffnesses shows a significant improvement over using the undeformed stiffness in a deformed state. The difference between the stiffness calculated using this approach to the stiffness obtained from finite element calculations is less than 4 % for the largest deformation examined.

The results achieved when using the deformation \(\varvec{F}_{\text {p,bi}, 2}(c)\), see Fig. 5 (right), show a different behavior. The maximal deviation from the undeformed state in this case is roughly 24 %. Transforming the stiffness using the deformation gradient itself (Method 2) does not improve the ability to mimic the behavior of the deformed composite. However, transforming the undeformed stiffness using the rotational part of the deformation gradient (Method 3) reduces the error to less than 15 %. Nonetheless, Method 4 provides the best result by far. The deviation from the finite element results stays below 3 % in the whole range of the deformation parameter c.

6.3 Tridirectionally reinforced material

In the initial state, the fibers in the tridirectionally reinforced material are oriented in the direction of \(\varvec{e}_1\), \(\varvec{e}_2\), and \(\varvec{e}_3\), see Fig. 1. A tridirectionally reinforced material differs significantly from the previously discussed composites. The expected symmetry class of such a composite is the cubic class since all fibers are the same in geometry and material parameters. This symmetry class is closest to the isotropic class. It is therefore reasonable to assume that the maximal achievable deviation from the undeformed state due to deformation is comparably smaller than for the previously discussed composites. When using the deformation \(\varvec{F}_{\text {p,tri}, 1}(c) = \varvec{F}_{\text {p,bi}, 1}(c)\), this can be observed in Fig. 6.

Fig. 6
figure 6

Tridirectionally reinforced material during plastical deformation with \(\varvec{F}_{\text {p,tri}, 1}(c)\).

Full size image

The maximal deviation achieved is roughly 16 %. Similar to the bidirectional case using \(\varvec{F}_{\text {p,bi}, 1}(c)\), Method 3 does not yield an improvement. Furthermore, Method 4 does neither convince in this case. This is due to several factors.

Firstly, as mentioned before, the expected deviation from the undeformed state is already small. This limits the range (and the need) for improvement. Secondly, the inner structure of the tridirectionally reinforced material promotes the interaction of the fibers under the deformation regardless of the specific deformation, see Fig. 7. This causes mutual fiber wrapping that influences the stiffness of the deformed materials. None of our four methods accounts for this phenomenon.

Fig. 7
figure 7

Interaction of the fibers in the tridirectionally reinforced material. It can be observed that the fibers start to bend around one another due to the interaction between them. The deformation shown in the figure is \(\varvec{F}_{\text {p,tri}, 1}(1)\)

Full size image

Besides this deformation, other deformations have been investigated in the context of tridirectionally reinforced materials. However, the obtained results show essentially the same behavior and do not provide further insight. This is due to the fact that there is no deformation which changes at least one of the three fiber directions and simultaneously does not cause the fibers to bend around each other. The aforementioned phenomenon therefore persists independent of the investigated deformation.

7 Resumẽ

The effect of finite plastic deformations on the stress–strain dependence within the elastic ranges and, in particular, on the elastic stiffness, cannot be neglected in the case of material plasticity. Particularly, for fiber-reinforced composites one has to take into account a change of the material symmetry of it during yielding. As an example, a reinforced material with two initially orthogonal fiber directions will behave tetragonally. However, if the direction of the fibers is inclined due to plastic deformations, this tetragonality will vanish toward another classes of (lower) symmetry.

In the present paper, four different methods to model the evolution of Hooke’s law under finite plastic deformations are presented and compared in their efficiency to describe this evolution. These methods do not only differ in the amount of work to identify and implement them in an FEM code, but also in their capability to describe this effect. While the first three methods are widely spread in the literature, to the best of our knowledge only the fourth method has been created here for these particular applications.

After applying and comparing these methods for different materials under different conditions, the ansatz with a superposition of transversely isotropic stiffnesses clearly shows the best results in case of uni- and bidirectionally reinforced material. At the same time, one can state as a fact that the results are more convincing the more anisotropy is initially shown by the structure. In these examples, some specifications have been made, which are, however, not necessary for the applicability of this method. First of all, it applies to any number of fiber bundles, and not only to one, two, or three. Also, the form, volume fraction, material properties, etc. of these bundles do not have to be identical. And, of course, their mutual angles need not be orthogonal, as we assumed in our examples. Only for random fiber distributions, this method is not applicable.

Another advantage of this method is its rather limited work effort, which is of orders smaller than that of other homogenization methods like the unit cell approach. The elastic identification has to be made only once for the undeformed material. The only internal variable needed for the update of the stiffness is the plastic deformation \(\varvec{F}_{\text {p}}\). No other internal variable has to be introduced; no other evolution equation for it is needed. And its update is a pure algebraic operation, which can be easily performed for each deformation step at each integration point.

Naturally, this method does not give an exact formula for the evolution of the stiffness tensor, but only an approximation. However, this might be a good compromise between precision and computational expense, as it is just needed for engineering purposes.