1 Introduction

It is well known that classical elasticity theory is not valid at small scales and leads to unphysical singularities at small scales. For instance, the (classical) stress and elastic strain fields of screw and edge dislocations possess a 1/r-singularity (see, e.g., [12, 34, 39]). On the other hand, generalized continuum theories such as strain gradient elasticity and nonlocal elasticity are continuum theories valid at small scales (see, e.g., [8, 29, 31]). In particular, Mindlin [36] (see also [37]) developed the theory of first strain gradient elasticity which is a powerful theory. In first strain gradient elasticity, the elastic energy density depends on the gradient of the elastic strain tensor in addition to the elastic strain tensor. Due to the strain gradients, strain gradient elasticity possesses a weak nonlocality important for the mathematical modeling of crystals in the framework of generalized continua. Isotropic first strain gradient elasticity theory contains two Lamé constants and five strain gradient parameters leading to two characteristic lengths.

Toupin and Grazis [47] and Mindlin [38] (see also [13]) showed that first strain gradient elasticity, which is sometimes called gradient elasticity of grade-2, can be considered as the continuum version of a lattice theory with up to second-neighbor interactions (nearest and next-nearest neighbor interactions). Therefore, a second nearest neighbor interatomic potential should be used for the computation of material parameters in first strain gradient elasticity. Nowadays, it has been understood that strain gradient elasticity is a straightforward continuum theory for mechanics at small scales. Using ab initio density functional theory (DFT) calculations, Shodja et al. [45] showed that the two characteristic lengths of Mindlin’s isotropic strain gradient elasticity theory are in the order of \(\sim 10^{-10}\) m (Ångström) for several fcc and bcc materials. The size of the characteristic lengths gives the information where the weak nonlocality of strain gradient elasticity is dominant. Therefore, the weak nonlocality is dominant in strain gradient elasticity at the Ångström-scale. All material parameters of first strain gradient elasticity can be computed using interatomic potentials [1, 31, 43]. In particular, the atomistic representation of the constitutive tensors in first strain gradient elasticity has been given by Admal et al. [1].

Let us note that in the early days of gradient elasticity, several trials (e.g., [16, 44]) to find non-singular fields produced by dislocations were not successful, leading only to additional singularities in the dislocation fields. More than three decades later, Altan and Aifantis [3] have derived a simplified version of Mindlin’s first strain gradient elasticity. Using such a simplified first strain gradient elasticity with only one characteristic length scale parameter, Gutkin and Aifantis [9, 10] found, for the first time, non-singular elastic strain fields of screw and edge dislocations. Lazar and Maugin [19] (see also [20, 27]) have shown how non-singular stress and strain fields of screw and edge dislocations can be computed in simplified first strain gradient elasticity. Such simplified first strain gradient elasticity is a particular version of Mindlin’s first strain gradient elasticity where the double stress tensor can be expressed in terms of the gradient of the Cauchy stress tensor (see, e.g., [19, 26]). An important mathematical property of strain gradient elasticity is that it provides a mathematical regularization based on partial differential equations (PDEs) of higher order where the characteristic length scale parameter plays the role of the regularization parameter. Using an incompatible version of Mindlin’s first strain gradient elasticity, non-singular and smooth displacement fields of screw and edge dislocations have been recently given by Delfani and Tavakol [4] and Delfani et al. [5], respectively. All non-singular dislocation fields including elastic strain, stress, and displacement fields of screw and edge dislocations have been derived by Lazar [30] in the framework of incompatible first strain gradient elasticity of Mindlin type.

The main disadvantage of simplified first strain gradient elasticity is that it possesses only one characteristic length scale in addition to the two Lamé constants in contrast to Mindlin’s first strain gradient elasticity which possesses two characteristic length scales for the isotropic case. As a consequence, the elastic shear strain (deviatoric part of the elastic strain tensor) and elastic dilatation (spherical part of the elastic strain tensor) have the same characteristic length scale, which is to some degree unphysical because shear strain and dilatation are the two irreducible pieces of the elastic strain tensor or the two eigen-modes (see [27]). To be more physical, at least every eigen-mode or every Lamé constant should have its own independent characteristic length scale. On the other hand, Mindlin’s first strain gradient elasticity with its five gradient-elastic constants is sometimes too complicated and sophisticated for applications. For that reason, we want to derive the reduced strain gradient elasticity model with two characteristic length scale parameters in addition to the two Lamé constants. The reduced strain gradient elasticity model is a robust gradient model similar to the simplified strain gradient model but includes the main properties of Mindlin’s strain gradient elasticity like two characteristic length scales. Moreover, the reduced strain gradient elasticity model is the bridge between simplified strain gradient elasticity and Mindlin’s first strain gradient elasticity.

The paper is organized as follows. In Sect. 2, we present the reduced strain gradient elasticity model with two characteristic lengths as a particular version of the incompatible strain gradient elasticity of Mindlin type with a reduced number of material parameters. We give the expressions for the three-dimensional and two-dimensional Green tensors together with their decomposition into longitudinal and transverse parts. For aluminum, the material parameters including the characteristic lengths have been computed based on a second nearest neighbor modified embedded-atom method (2NN MEAM) interatomic potential. Exact analytical solutions of screw and edge dislocations are given in Sects. 3.1 and 3.2, respectively. In Sect. 3.3, the limit to simplified strain gradient elasticity is shown and performed. Moreover, the comparison of the dislocation fields in reduced strain gradient elasticity, Mindlin’s strain gradient elasticity and simplified strain gradient elasticity is given and similarities and differences are pointed out. Conclusions are given in Sect. 4.

2 Incompatible strain gradient elasticity

In this section, we develop the reduced strain gradient elasticity model in the framework of incompatible strain gradient elasticity of Mindlin type. First, we present the basics of incompatible strain gradient elasticity of Mindlin type. In the second part, the reduced strain gradient elasticity model is derived and presented.

2.1 Mindlin’s first strain gradient elasticity

In Mindlin’s theory of first strain gradient elasticity [36, 37] (see also [28]), the strain energy density for an isotropic materials is given by

$$\begin{aligned} {\mathcal {W}}(\varvec{e},\varvec{\nabla }\varvec{e}) =\frac{1}{2}\, {\mathbb {C}}_{ijkl}e_{ij}e_{kl}+\frac{1}{2}\, {\mathbb {D}}_{ijmkln}\partial _m e_{ij} \partial _n e_{kl}\, . \end{aligned}$$
(1)

The isotropic constitutive tensor of rank four reads as

$$\begin{aligned} {\mathbb {C}}_{ijkl}=\lambda \, \delta _{ij}\delta _{kl} +\mu \big (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}\big ), \end{aligned}$$
(2)

where \(\lambda \) and \(\mu \) are the Lamé moduli (elastic constants) and \(\delta _{ij}\) is the Kronecker symbol. The isotropic constitutive tensor of rank six reads as

$$\begin{aligned} {\mathbb {D}}_{ijmkln}&= \frac{a_1}{2}\big (\delta _{ij}\delta _{km}\delta _{ln} +\delta _{ij}\delta _{kn}\delta _{lm} +\delta _{kl}\delta _{im}\delta _{jn} +\delta _{kl}\delta _{in}\delta _{jm}\big ) +2a_2\, \delta _{ij}\delta _{kl}\delta _{mn}\nonumber \\&\quad +\frac{a_3}{2}\big (\delta _{jk}\delta _{im}\delta _{ln} +\delta _{ik}\delta _{jm}\delta _{ln} +\delta _{il}\delta _{jm}\delta _{kn} +\delta _{jl}\delta _{im}\delta _{kn}\big ) +a_4\big (\delta _{il}\delta _{jk}+\delta _{ik}\delta _{jl}\big )\delta _{mn}\nonumber \\&\quad +\frac{a_5}{2}\big (\delta _{jk}\delta _{in}\delta _{lm} +\delta _{ik}\delta _{jn}\delta _{lm} +\delta _{jl}\delta _{km}\delta _{in} +\delta _{il}\delta _{km}\delta _{jn}\big ) , \end{aligned}$$
(3)

where \(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\) are the five strain gradient parameters (gradient-elastic constants) in Mindlin’s isotropic first strain gradient elasticity theory [36] (see also [28, 31, 37]). The incompatible elastic strain tensor \(e_{ij}\) reads as

$$\begin{aligned} e_{ij}=\frac{1}{2}\left( \beta _{ij}+\beta _{ji}\right) \, , \end{aligned}$$
(4)

which is given by the symmetric part of the incompatible elastic distortion tensor

$$\begin{aligned} \beta _{ij}=\partial _j u_{i}-\beta ^{\mathrm {P}}_{ij}. \end{aligned}$$
(5)

The incompatible elastic distortion tensor (5) is nothing but the gradient of the displacement vector \(u_i\) minus the plastic distortion (or eigendistortion) tensor \(\beta ^{\mathrm {P}}_{ij}\). Note that we use the following abbreviation for the partial derivative: \(\partial _j=\partial /\partial x_j\).

In dislocation theory, the dislocation density tensor is defined in terms of the incompatible plastic distortion tensor (see, e.g., [15, 25])

$$\begin{aligned} \alpha _{ij}=-\epsilon _{jkl}\partial _k\beta _{il}^{\mathrm {P}}\end{aligned}$$
(6)

and may also be expressed in terms of the incompatible elastic distortion tensor

$$\begin{aligned} \alpha _{ij}=\epsilon _{jkl}\partial _k\beta _{il} , \end{aligned}$$
(7)

where \(\epsilon _{jkl}\) indicates the Levi-Civita tensor. Moreover, the dislocation density tensor satisfies the Bianchi identity of dislocations

$$\begin{aligned} \partial _j\alpha _{ij}=0, \end{aligned}$$
(8)

which means that dislocations cannot end inside the body.

The Cauchy stress tensor \(\sigma _{ij}\) and the double stress tensor \(\tau _{ijm}\) are defined by

$$\begin{aligned} \sigma _{ij}&=\frac{\partial {\mathcal {W}}}{\partial e_{ij}} ={\mathbb {C}}_{ijkl}e_{kl}\, , \end{aligned}$$
(9)
$$\begin{aligned} \tau _{ijm}&=\frac{\partial {\mathcal {W}}}{\partial (\partial _m e_{ij})} = {\mathbb {D}}_{ijmkln} \partial _n e_{kl}. \end{aligned}$$
(10)

Using Eqs. (2) and (3), the Cauchy stress tensor reads as

$$\begin{aligned} \sigma _{ij}=\lambda \, \delta _{ij} e_{ll}+2 \mu \, e_{ij} \end{aligned}$$
(11)

and the double stress tensor reads as

$$\begin{aligned} \tau _{ijm}&=\frac{a_1}{2} \big (\delta _{im}\partial _j e_{ll}+\delta _{jm} \partial _i e_{ll}+2\delta _{ij} \partial _l e_{lm}\big ) +2 a_2 \delta _{ij} \partial _m e_{ll}\nonumber \\&\quad +a_3\big (\delta _{im}\partial _l e_{jl}+\delta _{jm}\partial _l e_{il}\big ) +2 a_4 \partial _m e_{ij} +a_5 \big (\partial _i e_{jm}+\partial _j e_{im}\big ). \end{aligned}$$
(12)

In presence of body forces, the (static) Lagrangian density of strain gradient elasticity is given by

$$\begin{aligned} {\mathcal {L}}&=-{\mathcal {W}}-{\mathcal {V}}, \end{aligned}$$
(13)

where \({\mathcal {W}}\) is given in Eq. (1) and \({\mathcal {V}}\) is the potential of body forces given by

$$\begin{aligned} {\mathcal {V}}=-u_i f_i. \end{aligned}$$
(14)

Here \(f_i\) denotes the body force density vector. The static (force) equilibrium condition is given by the Euler–Lagrange equation of strain gradient elasticity (see, e.g., [2, 35])

$$\begin{aligned} \frac{\delta {\mathcal {L}}}{\delta u_i}\equiv \frac{\partial {\mathcal {L}}}{\partial u_i} -\partial _j\, \frac{\partial {\mathcal {L}}}{\partial (\partial _j u_i)} +\partial _m \partial _j\, \frac{\partial {\mathcal {L}}}{\partial (\partial _m \partial _j u_i)}=0. \end{aligned}$$
(15)

In terms of the Cauchy stress and double stress tensors, the equation of equilibrium (15) takes the following form [36]

$$\begin{aligned} \partial _j\big (\sigma _{ij}-\partial _m\tau _{ijm}\big )=-f_i, \end{aligned}$$
(16)

which has the physical meaning of the force equilibrium condition. Moreover, the total or effective stress tensor \({\widehat{\sigma }}_{ij}\) can be defined as a variational derivative

$$\begin{aligned} {\widehat{\sigma }}_{ij}:=\frac{\delta {\mathcal {W}}}{\delta e_{ij}} =\frac{\partial {\mathcal {W}}}{\partial e_{ij}} -\partial _k\, \frac{\partial {\mathcal {W}}}{\partial (\partial _k e_{ij})}. \end{aligned}$$
(17)

Using Eqs. (9) and (10), it reads as (see also [22, 28, 35, 47])

$$\begin{aligned} {\widehat{\sigma }}_{ij}=\sigma _{ij}-\partial _m\tau _{ijm} \end{aligned}$$
(18)

and Eq. (16) reduces to the simple form

$$\begin{aligned} \partial _j {\widehat{\sigma }}_{ij}=-f_i. \end{aligned}$$
(19)

Using Eqs. (11) and (12), the total or effective stress tensor (18) reduces to

$$\begin{aligned} {\widehat{\sigma }}_{ij}&= 2 \mu \, e_{ij} +\lambda \, \delta _{ij} e_{ll} -a_1 \big (\partial _i\partial _j e_{ll}+\partial _k\partial _l \delta _{ij} e_{kl}\big ) -2 a_2 \delta _{ij} \Delta e_{ll} \nonumber \\&\quad -(a_3+a_5)\big (\partial _i\partial _l e_{jl}+\partial _j\partial _l e_{il}\big ) -2 a_4 \Delta e_{ij}, \end{aligned}$$
(20)

where \(\Delta \) denotes the Laplace operator. If we substitute the total stress tensor (20) into Eq. (19), then the displacement equation of equilibrium is given by

$$\begin{aligned} L^{\text {M}}_{ik} u_k=\mu \big [1-\ell _2^2\Delta \big ]\big (\partial _l \beta ^{\mathrm {P}}_{il}+\partial _l \beta ^{\mathrm {P}}_{li}\big ) +\big [\lambda -(a_1+2a_2)\Delta \big ] \partial _i \beta ^{\mathrm {P}}_{ll} -(a_1+a_3+a_5) \partial _i \partial _k\partial _l \beta ^{\mathrm {P}}_{kl} -f_i, \end{aligned}$$
(21)

where \(L^{\text {M}}_{ik}\) denotes the tensorial linear partial differential operator of fourth order, appearing in Mindlin’s first strain gradient elasticity, and is called the Mindlin operator. The isotropic Mindlin operator reads as

$$\begin{aligned} L_{ik}^\text {M}&= (\lambda +2\mu )\big [1-\ell _1^2\Delta \big ]\partial _i\partial _k +\mu \big [1-\ell _2^2\Delta \big ](\delta _{ik}\Delta -\partial _i\partial _k). \end{aligned}$$
(22)

Note that \(L_{ik}^\text {M}=L_{ki}^\text {M}\). The two characteristic lengths in Mindlin’s strain gradient elasticity, defined in terms of the five gradient-elastic constants and the two Lamé constants, are defined by

$$\begin{aligned} \ell _1^2&=\frac{2(a_1+a_2+a_3+a_4+a_5)}{\lambda +2\mu }, \end{aligned}$$
(23)
$$\begin{aligned} \ell _2^2&=\frac{a_3+2a_4+a_5}{2\mu }. \end{aligned}$$
(24)

Using the longitudinal and transverse sound speeds

$$\begin{aligned} c^2_{\mathrm {L}}=\frac{\lambda +2\mu }{\rho },\qquad c^2_{\mathrm {T}}=\frac{\mu }{\rho }, \end{aligned}$$
(25)

where \(\rho \) denotes the mass density, the Mindlin operator (22) can be decomposed into a longitudinal part and a transverse part and can be rewritten as

$$\begin{aligned} L_{ik}^\text {M}&= \rho c^2_{\mathrm {L}}\big [1-\ell _{\mathrm {L}}^2\Delta \big ]\partial _i\partial _k + \rho c^2_{\mathrm {T}}\big [1-\ell _{\mathrm {T}}^2\Delta \big ](\delta _{ik}\Delta -\partial _i\partial _k), \end{aligned}$$
(26)

namely

$$\begin{aligned} L_{ik}^\text {M}&=L_{ik}^\text {M,L}+L_{ik}^\text {M,T} \end{aligned}$$
(27)

with

$$\begin{aligned} L_{ik}^\text {M,L}&=\rho c^2_{\mathrm {L}}\big [1-\ell _{\mathrm {L}}^2\Delta \big ]\partial _i\partial _k \end{aligned}$$
(28)
$$\begin{aligned} L_{ik}^\text {M,T}&=\rho c^2_{\mathrm {T}}\big [1-\ell _{\mathrm {T}}^2\Delta \big ](\delta _{ik}\Delta -\partial _i\partial _k) \end{aligned}$$
(29)

and the conditions for the longitudinal and transverse parts

$$\begin{aligned} \epsilon _{lji}\partial _j L_{ik}^\text {M,L}&=0 \end{aligned}$$
(30)
$$\begin{aligned} \partial _i L_{ik}^\text {M,T}&=0 . \end{aligned}$$
(31)

It can be seen in Eq. (26) that every sound velocity has its own characteristic length. Therefore, the characteristic length \(\ell _1\) has the physical meaning of characteristic longitudinal length \(\ell _{\mathrm {L}}\) and the characteristic length \(\ell _2\) has the physical meaning of characteristic transverse length \(\ell _{\mathrm {T}}\):

$$\begin{aligned} \ell _1=\ell _{\mathrm {L}},\qquad \ell _2=\ell _{\mathrm {T}}. \end{aligned}$$
(32)

2.2 Reduced strain gradient elasticity model with two characteristic lengths

The reduced strain gradient elasticity model with two characteristic lengths is obtained from Mindlin’s isotropic first strain gradient elasticity if we assume to every Lamé constant \(\lambda \) and \(\mu \) an independent length \(\ell _\lambda \) and \(\ell _\mu \), which we may call the characteristic lengths of the Lamé constants, via

$$\begin{aligned} a_1=0,\quad a_2=\frac{\lambda \, \ell _\lambda ^2}{2},\quad a_3=0,\quad a_4=\mu \, \ell _\mu ^2,\quad a_5=0 . \end{aligned}$$
(33)

On the one hand, the reduced strain gradient elasticity model is a particular case of Mindlin’s first strain gradient elasticity theory. On the other hand, it is a generalization of the simplified first strain gradient elasticity model to include two different characteristic length scale parameters.

Using the relations in(33), the constitutive tensor of rank six, Eq. (3), reduces to

$$\begin{aligned}&{\mathbb {D}}_{ijmkln}=\lambda \, \ell _\lambda ^2\, \delta _{ij}\delta _{kl}\delta _{mn} +\mu \, \ell _\mu ^2 \big (\delta _{il}\delta _{jk}+\delta _{ik}\delta _{jl}\big )\delta _{mn} \end{aligned}$$
(34)

and the double stress tensor (12) becomes

$$\begin{aligned} \tau _{ijm}&=\lambda \, \ell ^2_\lambda \delta _{ij} \partial _m e_{ll}+2 \mu \, \ell _\mu ^2 \partial _m e_{ij} . \end{aligned}$$
(35)

It is worth noting that the double stress tensor (35) is nothing but the gradient of the Cauchy stress tensor (11) with an independent length scale for every Lamé constant. The double stress tensor (35) is much simpler than the expression of the double stress tensor (12) in Mindlin’s strain gradient elasticity. Substituting the constitutive tensors (2) and (34) into Eq. (1), the elastic strain energy density reduces to

$$\begin{aligned} {\mathcal {W}}(\varvec{e},\varvec{\nabla }\varvec{e}) =\frac{1}{2} \,\lambda \, e_{ii}e_{jj}+\mu \, e_{ij}e_{ij} +\frac{1}{2}\,\lambda \,\ell _\lambda ^2 \, \partial _k e_{ii}\partial _k e_{jj}+\mu \, \ell _\mu ^2\, \partial _k e_{ij} \partial _k e_{ij} . \end{aligned}$$
(36)

By means of Eqs. (11) and (35), the total or effective stress tensor (20) simplifies to

$$\begin{aligned} {\widehat{\sigma }}_{ij}&= 2 \mu \big [1-\ell _\mu ^2\Delta \big ] e_{ij} +\lambda \big [1-\ell _\lambda ^2\Delta \big ] \delta _{ij} e_{ll} , \end{aligned}$$
(37)

where it can be seen that every elastic constant possesses its own Helmholtz operator. For the total stress tensor (37) with two independent characteristic length scales, the equation of equilibrium (19) gives in the framework reduced strain gradient elasticity the corresponding displacement equation of equilibrium

$$\begin{aligned} \mu \big [1-\ell _\mu ^2\Delta \big ] \big (\Delta u_i + \partial _i\partial _k u_k\big ) +\lambda \big [1-\ell _\lambda ^2\Delta \big ] \partial _i\partial _k u_k&= \mu \big [1-\ell _\mu ^2\Delta \big ]\partial _l \big (\beta ^{\mathrm {P}}_{il}+ \beta ^{\mathrm {P}}_{li}\big ) \nonumber \\&\quad +\lambda \big [1-\ell _\lambda ^2\Delta \big ] \partial _i \beta ^{\mathrm {P}}_{ll}-f_i . \end{aligned}$$
(38)

However, sometimes this representation in terms of length scales of the Lamé constants \(\ell _\lambda \) and \(\ell _\mu \) is not very suitable for the investigation of specific gradient phenomena. Consequently, we use a more suitable representation in terms of longitudinal and transverse length scales \(\ell _1\) and \(\ell _2\). Therefore, the following representation is used

$$\begin{aligned} a_1=0,\quad a_2=\frac{(\lambda +2\mu )\, \ell _1^2}{2}-\mu \, \ell _2^2,\quad a_3=0,\quad a_4=\mu \, \ell _2^2,\quad a_5=0 \end{aligned}$$
(39)

and the relations between the length scales (\(\ell _\lambda \), \(\lambda _\mu \)) and the longitudinal and transverse length scales (\(\ell _1\), \(\ell _2\)) read

$$\begin{aligned} \ell ^2_\mu =\ell ^2_2,\qquad \ell ^2_\lambda =\frac{\lambda +2\mu }{\lambda }\, \ell _1^2-\frac{2\mu }{\lambda }\, \ell _2^2\ \end{aligned}$$
(40)

and

$$\begin{aligned} \ell ^2_1=\frac{\lambda \ell _\lambda ^2+2\mu \ell _\mu ^2}{\lambda +2\mu } . \end{aligned}$$
(41)

Substituting Eq. (40) into Eq. (36), the elastic strain energy density can be written as

$$\begin{aligned} {\mathcal {W}}(\varvec{e},\varvec{\nabla }\varvec{e})&=\frac{1}{2} \,(\lambda +2\mu )\, e_{ii}e_{jj}+\mu \, (e_{ij}e_{ij}- e_{ii}e_{jj}) \nonumber \\&\quad +\frac{1}{2}\,(\lambda +2\mu ) \,\ell _1^2 \, \partial _k e_{ii}\partial _k e_{jj} +\mu \, \ell _2^2\, \big (\partial _k e_{ij} \partial _k e_{ij}-\partial _k e_{ii}\partial _k e_{jj}\big ) . \end{aligned}$$
(42)

Then the constitutive tensor of rank six, Eq. (34), reduces to

$$\begin{aligned}&{\mathbb {D}}_{ijmkln}=(\lambda +2\mu ) \ell _1^2\, \delta _{ij}\delta _{kl}\delta _{mn} +\mu \, \ell _2^2 \big (\delta _{il}\delta _{jk}+\delta _{ik}\delta _{jl}-2\delta _{ij}\delta _{kl}\big )\delta _{mn} \end{aligned}$$
(43)

and the double stress tensor (34) becomes

$$\begin{aligned} \tau _{ijm}= (\lambda +2\mu ) \ell _1^2 \delta _{ij} \partial _m e_{ll} +2 \mu \ell _2^2 \partial _m \big ( e_{ij}-\delta _{ij} e_{ll} \big ) . \end{aligned}$$
(44)

Moreover, the Cauchy stress tensor (11) can be written in the form

$$\begin{aligned} \sigma _{ij}=(\lambda +2\mu )\, \delta _{ij} e_{ll}+2 \mu \, (e_{ij} -\delta _{ij} e_{ll}) \end{aligned}$$
(45)

and the total or effective stress tensor (37) reduces to

$$\begin{aligned} {\widehat{\sigma }}_{ij}&= (\lambda +2\mu ) \big [1-\ell _1^2\Delta \big ] \delta _{ij} e_{ll} +2 \mu \big [1-\ell _2^2\Delta \big ] \big ( e_{ij}-\delta _{ij} e_{ll} \big ). \end{aligned}$$
(46)

Substituting the total stress tensor (46) into the equation of equilibrium (19), the displacement equation of equilibrium is obtained as

$$\begin{aligned} (\lambda +2\mu ) \big [1-\ell _1^2\Delta \big ] \partial _i\partial _k u_k +\mu \big [1-\ell _2^2\big ] \big (\Delta u_i - \partial _i\partial _k u_k\big )&= (\lambda +2\mu ) \big [1-\ell _1^2\Delta \big ] \partial _i \beta ^{\mathrm {P}}_{ll} \nonumber \\&\quad +\mu \big [1-\ell _2^2\Delta \big ] \big (\partial _l \beta ^{\mathrm {P}}_{il}+ \partial _l \beta ^{\mathrm {P}}_{li}-2 \partial _i \beta ^{\mathrm {P}}_{ll}\big ) -f_i , \end{aligned}$$
(47)

which can be written in terms of the Mindlin operator (22)

$$\begin{aligned} L^\text {M}_{ik} u_k = (\lambda +2\mu ) \big [1-\ell _1^2\Delta \big ] \partial _i \beta ^{\mathrm {P}}_{ll} +\mu \big [1-\ell _2^2\Delta \big ] \big (\partial _l \beta ^{\mathrm {P}}_{il}+ \partial _l \beta ^{\mathrm {P}}_{li}-2 \partial _i \beta ^{\mathrm {P}}_{ll}\big ) -f_i \end{aligned}$$
(48)

or in terms of longitudinal and transverse length scales and longitudinal and transverse speeds of sound

$$\begin{aligned} c_{\mathrm {L}}^2 \big [1-\ell _{\mathrm {L}}^2\Delta \big ] \partial _i\partial _k u_k +c_{\mathrm {T}}^2 \big [1-\ell _{\mathrm {T}}^2\Delta \big ] \big (\Delta u_i - \partial _i\partial _k u_k\big )&= c_{\mathrm {L}}^2 \big [1-\ell _{\mathrm {L}}^2\Delta \big ] \partial _i \beta ^{\mathrm {P}}_{ll}\nonumber \\&\quad +c_{\mathrm {T}}^2 \big [1-\ell _{\mathrm {T}}^2\Delta \big ]\big (\partial _l \beta ^{\mathrm {P}}_{il}+ \partial _l \beta ^{\mathrm {P}}_{li}-2 \partial _i \beta ^{\mathrm {P}}_{ll}\big ) -f_i /\rho . \end{aligned}$$
(49)

It is important to note that the left-hand side of the displacement equation of equilibrium in Mindlin’s strain gradient elasticity (21) and in reduced strain gradient elasticity (48) is formally given by the same type of differential operator, namely the Mindlin operator \(L^\text {M}_{ik}\), whereas the right-hand side of the displacement equation of equilibrium is much simpler in reduced strain gradient elasticity than in Mindlin’s strain gradient elasticity. In contrast to the right hand side of Eq. (21), the right hand side of Eq. (48) is given in terms of longitudinal and transverse Helmholtz operators. For the compatible case, where the plastic distortion is zero, both equations (21) and  (48) reduce to the same partial differential equation, namely

$$\begin{aligned} L^\text {M}_{ik} u_k=-f_i . \end{aligned}$$
(50)

Moreover, for both Eqs. (21) and (48), the particular solutions can be given by the convolution of the inhomogeneous parts and the Green tensor of the Mindlin operator, which is given in the next section.

2.3 Green tensor of the Mindlin operator

The Green tensor of the isotropic Mindlin operator (22), being the fundamental solution, is defined by (see, e.g., [28])

$$\begin{aligned} L^{\text {M}}_{ik}G^{\text {M}}_{kj}(\varvec{R}) =-\delta _{ij} \delta (\varvec{R}), \end{aligned}$$
(51)

where \(\delta (.)\) denotes the Dirac delta function. Note that the Green tensor is a symmetric tensor: \(G^{\text {M}}_{kj}=G^{\text {M}}_{jk}\).

The three-dimensional Green tensor of the Mindlin operator (22) reads as (see [14, 28, 44])

$$\begin{aligned} G^{\text {M}}_{ij}(\varvec{R})= \frac{1}{8\pi }\, \Big [ \frac{1}{\lambda +2\mu }\, \partial _i\partial _j A(R,\ell _1) +\frac{1}{\mu } \big (\delta _{ij}\Delta -\partial _i\partial _j\big ) A(R,\ell _2)\Big ] \end{aligned}$$
(52)

with the two scalar auxiliary functions

$$\begin{aligned} A(R,\ell _1)&=R+\frac{2\ell _1^2}{R}\, \Big (1-\text {e}^{-R/\ell _1}\Big ), \end{aligned}$$
(53)
$$\begin{aligned} A(R,\ell _2)&=R+\frac{2\ell _2^2}{R}\, \Big (1-\text {e}^{-R/\ell _2}\Big ), \end{aligned}$$
(54)

where \(i,j=x,y,z\) and \(\varvec{R}\in \mathbb R^3\).

The two-dimensional Green tensor of the plane strain problem in Mindlin’s strain gradient elasticity reads as (see [14, 28, 44])

$$\begin{aligned} G^{\text {M}}_{ij}(\varvec{R})= \frac{1}{8\pi }\, \Big [ \frac{1}{\lambda +2\mu }\, \partial _i\partial _j A(R,\ell _1) + \frac{1}{\mu } \big (\delta _{ij}\Delta -\partial _i\partial _j\big ) A(R,\ell _2)\Big ] \end{aligned}$$
(55)

with the two scalar auxiliary functions

$$\begin{aligned} A(R,\ell _1)&=-\Big (R^2\ln R -R^2+4\ell _1^2\, \big [\ln R+K_0\big (R/\ell _1\big )\big ]\Big ), \end{aligned}$$
(56)
$$\begin{aligned} A(R,\ell _2)&=-\Big (R^2\ln R -R^2+4\ell _2^2\, \big [\ln R+K_0\big (R/\ell _2\big )\big ]\Big ) , \end{aligned}$$
(57)

where \(i,j=x,y\) and \(\varvec{R}\in \mathbb R^2\). Here \(K_n\) is the modified Bessel function of the second kind of order n.

In general, the Green tensor of the Mindlin operator can be decomposed into longitudinal and transverse pieces according to

$$\begin{aligned} G^{\text {M}}_{ij}(\varvec{R})=G^{\text {M}, {\mathrm {L}}}_{ij}(\varvec{R})+G^{\text {M}, {\mathrm {T}}}_{ij}(\varvec{R}) , \end{aligned}$$
(58)

where the longitudinal and transverse Green tensors are given by

$$\begin{aligned} G^{\text {M}, {\mathrm {L}}}_{ij}(\varvec{R})&= \frac{1}{8\pi \rho c_{\mathrm {L}}^2}\, \partial _i\partial _j A(R,\ell _{\mathrm {L}}) , \end{aligned}$$
(59)
$$\begin{aligned} G^{\text {M}, {\mathrm {T}}}_{ij}(\varvec{R})&= \frac{1}{8\pi \rho c_{\mathrm {T}}^2}\, \big (\delta _{ij}\Delta -\partial _i\partial _j\big ) A(R,\ell _{\mathrm {T}}) \end{aligned}$$
(60)

with the conditions to be longitudinal and transverse

$$\begin{aligned} \epsilon _{lkj} \partial _k G^{\text {M}, {\mathrm {L}}}_{ij}(\varvec{R})&=0 \end{aligned}$$
(61)
$$\begin{aligned} \partial _j G^{\text {M}, {\mathrm {T}}}_{ij}(\varvec{R})&=0 . \end{aligned}$$
(62)

For the anti-plane strain problem, the Mindlin operator (22) reduces to the two-dimensional Laplace–Helmholtz operator depending only on the length \(\ell _2\)

$$\begin{aligned} L_{zz}^\text {M}&=\mu \big [1-\ell _2^2\Delta \big ] \Delta . \end{aligned}$$
(63)

The corresponding Green function of anti-pane strain is defined by (see, e.g., [28])

$$\begin{aligned} L^{\text {M}}_{zz}G^{\text {M}}_{zz}(\varvec{R}) =-\delta (\varvec{R}) \end{aligned}$$
(64)

and reads as (see [28])

$$\begin{aligned} G^{\text {M}}_{zz}(\varvec{R})=-&\frac{1}{2\pi \mu }\, \big [\ln R+K_0\big (R/\ell _2\big )\big ]. \end{aligned}$$
(65)

Moreover, the two-dimensional Green function of the Helmholtz operator is needed in problems of straight dislocations and is defined by

$$\begin{aligned} L_I G^{L_I}=\delta (\varvec{R}) , \qquad I=1,2 \end{aligned}$$
(66)

and reads as

$$\begin{aligned} G^{L_I}=\frac{1}{2\pi \ell _I^2}\, K_0(R/\ell _I), \end{aligned}$$
(67)

where the isotropic scalar Helmholtz operator (differential operator of second order) reads

$$\begin{aligned} L_I=1-\ell _I^2\Delta , \qquad \ell _I>0. \end{aligned}$$
(68)

Sometimes in the mathematical literature, the differential operator (68) is called modified Helmholtz operator [48] or metaharmonic operator [40].

2.4 Material parameters

In Mindlin’s first strain gradient elasticity theory, the elastic constants and the gradient-elastic constants are characteristic material parameters which can be computed from interatomic potentials (see, e.g., [1, 43]) or via ab DFT calculations (see, e.g., [46]). For some important cubic materials such as Al, Cu, Fe and W, the 3 elastic constants and 11 gradient-elastic constants have been computed using the second nearest neighbor modified embedded-atom-method (2NN MEAM) interatomic potential given by Lee et al.[32] (see  [1, 31, 33, 43]). Although W and Al are nearly isotropic concerning the elastic constants because they satisfy the isotropy condition for the constitutive tensor of rank 4, \({\mathbb {C}}_{ijkl}\), the 11 gradient-elastic constants of W and Al do not satisfy any of the 6 isotropy conditions for the constitutive tensor of rank 6, \({\mathbb {D}}_{ijmkln}\), as shown in [31]. Based on the Hermann theorem, the rank 6 of the constitutive tensor \({\mathbb {D}}_{ijmkln}\) is too high for a crystal possessing a cubic symmetry to be isotropic [31]. Therefore, an average of the gradient-elastic constants of cubic materials is necessary to get isotropic gradient-elastic constants. Lazar et al.[31] proposed and used a Voigt-type average of the sixth-rank constitutive tensor \({\mathbb {D}}_{ijmkln}\) for the computation of the 5 isotropic gradient-elastic constants (\(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\)) of Al and W.

For the numerical analysis of the dislocation fields produced by screw and edge dislocations we choose aluminum (Al) and we use the corresponding Lamé moduli (\(\mu \), \(\lambda \)) and the 5 gradient-elastic constants (\(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\)) given in [31]. The Lamé constants, gradient-elastic constants, characteristic lengths, and the Poisson ratio of aluminum, which have been computed from the 2NN MEAM interatomic potential [31], are given in Table 1. The 2 characteristic lengths are given in terms the 2 Lamé moduli (\(\mu \), \(\lambda \)) and the 5 gradient-elastic constants (\(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\)) by Eqs. (23) and (24).

Even for the so-called simplified first strain gradient elasticity theory possessing only 1 characteristic length for isotropic and cubic materials, the characteristic length can be computed directly from the fourth-rank constitutive tensor \({\mathbb {C}}_{ijkl}\) and the sixth-rank constitutive tensor \({\mathbb {D}}_{ijmkln}\) by means of a projection method [42] leading to the formula for the characteristic length:

$$\begin{aligned} \ell ^2=\frac{1}{18}\,{\mathbb {C}}^{-1}_{ijkl} {\mathbb {D}}_{ijmklm} \end{aligned}$$
(69)

with the inverse tensor of elastic constants for an isotropic material

$$\begin{aligned} {\mathbb {C}}^{-1}_{ijkl}= \frac{1}{4\mu }\Big ( \delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}-\frac{2\lambda }{3\lambda +2\mu }\, \delta _{ij}\delta _{kl}\Big ). \end{aligned}$$
(70)

If we substitute Eqs. (3) and (70) into Eq. (69), then we obtain the following formula for the characteristic length in terms of the 2 Lamé moduli (\(\mu \), \(\lambda \)) and the 5 gradient-elastic constants (\(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\))

$$\begin{aligned} \ell ^2= \frac{2 \mu (a_1 + 3 a_2) +(5 \lambda + 4 \mu ) (a_3 + 3 a_4 + a_5)}{6 \mu (3 \lambda + 2 \mu )}. \end{aligned}$$
(71)

Eq. (71) gives an atomistic determination of the characteristic length \(\ell \) of simplified first strain gradient elasticity from the numerical values of the elastic and gradient elastic constants computed from interatomic potentials or via ab initio DFT. Using the elastic and gradient-elastic constants of Al given in Table 1, the characteristic length \(\ell \) is computed using Eq. (71) and reported in Table 1. It can be seen that for aluminum the length \(\ell \) of simplified strain gradient elasticity is a slightly smaller than the 2 characteristic lengths of Mindlin’s strain gradient elasticity theory but in the same size-range.

Table 1 Lamé moduli, gradient-elastic constants, characteristic lengths, equilibrium lattice parameter, and Poisson ratio for aluminum (Al) computed from 2NN MEAM interatomic potential [31]
Full size table

The size of the characteristic lengths tells us where (weak) nonlocality in gradient theories is dominant. As it can be seen in Table 1, nonlocality is dominant in strain gradient elasticity theory at the Ångström-scale, where classical elasticity theory breaks down and leads to unphysical singularities. In other words, the Ångström-scale is the scale of nonlocality in strain gradient elasticity. Strain gradient elasticity becomes relevant at small distances in materials such as crystals. It seems that nonlocality is a fundamental property of nature at small scales. Therefore, strain gradient elasticity is a straightforward continuum theory valid at small scales like the Ångström-scale leading to a straightforward non-singular dislocation theory with non-singular dislocation fields in the dislocation core region as it will be shown in the next section.

3 Application of reduced strain gradient elasticity to straight dislocations

In this section, we investigate the anti-plane strain and plane strain problems of screw and edge dislocations, respectively, in the framework of incompatible reduced strain gradient elasticity for vanishing body force density \(f_i=0\). For the numerical study of the dislocation fields, the elastic constants and the characteristic length scales of aluminum given in Table 1 are used.

3.1 Screw dislocation

The screw dislocation is located at the position \((x,y)=(0,0)\) with Burgers vector \(b_z\) and the dislocation line in the z-direction of a Cartesian coordinate system. For a screw dislocation, Eq. (48) simplifies to

$$\begin{aligned} L^{\text {M}}_{zz} u_z&=\mu L_2 \partial _y \beta _{zy}^{{\mathrm {P}}} \end{aligned}$$
(72)

with

$$\begin{aligned} L_2 \beta _{zy}^{{\mathrm {P}}}&=\beta _{zy}^{{\mathrm {P}},0}\ \end{aligned}$$
(73)

and

$$\begin{aligned} L^{\text {M}}_{zz} u_z&=\mu \partial _y \beta _{zy}^{{\mathrm {P}},0} . \end{aligned}$$
(74)

The classical plastic distortion of a screw dislocation given by deWit [6] (see also [39]) reads

$$\begin{aligned} \beta _{zy}^{{\mathrm {P}},0} =b_z \delta (y) H(-x)=b_z \delta (y)\int _x^{\infty } \delta (X)\,{\mathrm {d}}X, \end{aligned}$$
(75)

which possesses a discontinuity at \(y=0\) for \(x<0\). Here H(.) denotes the Heaviside step function.

By substituting Eq. (75) into Eq. (73) and using the Green function (67), the plastic distortion is calculated as

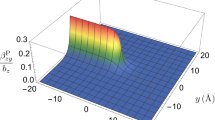
$$\begin{aligned} \beta _{zy}^{{\mathrm {P}}}&=G^{L_2}*\beta _{zy}^{{\mathrm {P}},0}=\frac{b_z}{2\pi \ell _2^2}\int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell _2\big )\, {\mathrm {d}}X, \end{aligned}$$
(76)

which is non-singular, smooth and finite as it can be seen in Fig. 1. The symbol \(*\) denotes spatial convolution.

Fig. 1
figure 1

Plastic distortion \(\beta ^{\mathrm {P}}_{zy}\) of a screw dislocation near the dislocation line

Full size image

The dislocation density of a screw dislocation is obtained as

$$\begin{aligned} \alpha _{zz}&=-\partial _x \beta _{zy}^{{\mathrm {P}}}=\frac{b_z}{2\pi \ell _2^2}\, K_0\big (r/\ell _2\big ), \end{aligned}$$
(77)

where \(r=\sqrt{x^2+y^2}\). The dislocation density (77) is plotted in Fig. 2 and gives the shape and size of the dislocation core of a screw dislocation.

Fig. 2
figure 2

Contour plot of the dislocation density of a screw dislocation \(\alpha _{zz}\) (normalized by the Burgers vector \(b_z\))

Full size image

Using the dislocation density (77), the effective Burgers vector \(b_z(r)\) of a screw dislocation is defined by (see, e.g., [7, 17, 18, 23])

$$\begin{aligned} b_z(r) = \int ^{2\pi }_0\int ^r_0 \alpha _{zz}(r')\,r'\,{\mathrm {d}}r' {\mathrm {d}}\phi = b_z\bigg [1-\frac{r}{\ell _2}\, K_1\big (r/\ell _2\big )\bigg ] . \end{aligned}$$
(78)

The effective Burgers vector differs appreciably from the classical Burgers vector \(b_z\), which is constant, in the region from \(r=0\) up to \(r\simeq 6\ell _2\). Thus, it is suggestive to take \(r_{\text {c}}\simeq 6 \, \ell _2\) as the dislocation core radius. Outside this dislocation core region, the effective Burgers vector reaches its constant value \(b_z\). Accordingly, the gradient solution approaches the classical one outside the dislocation core region. Using the values given in Table 1, the dislocation core radius reads for aluminum: \(r_{\text {c}}\simeq 1.875\, a =7.594\,\)Å. The effective Burgers vector (78) is plotted in Fig. 3.

Fig. 3
figure 3

Effective Burgers vector \(b_z(r)\) of a screw dislocation (normalized by the Burgers vector \(b_z\))

Full size image

If we substitute Eq. (75) into Eq. (74) and use the Green function (65), the displacement field \(u_z\) is calculated as

$$\begin{aligned} u_{z}&=-\mu \, \partial _y G^{\text {M}}_{zz}*\beta _{zy}^{{\mathrm {P}},0}\nonumber \\&=-\frac{b_z}{2\pi } \partial _y \int _x^{\infty } \Big [ \ln \sqrt{X^2+y^2} +K_0\big (\sqrt{X^2+y^2}/\ell _2\big ) \Big ]\, {\mathrm {d}}X\nonumber \\&=\frac{b_z}{2\pi } \bigg (\arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y) +\partial _y \int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell _2\big ) \, {\mathrm {d}}X \bigg ), \end{aligned}$$
(79)

where the first part in Eq. (79) is the angle \(\varphi \) with range (\(-\pi \), \(\pi \)] and discontinuity of \(2\pi \) across the negative x-axis (see also [6, 41])

$$\begin{aligned} \varphi =\arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y). \end{aligned}$$
(80)

The displacement field (79) is plotted in Fig. 4. The displacement field (79) is non-singular and has a smooth form due to the superposition of the classical jump discontinuity (first term) and the gradient term (second term).

Fig. 4
figure 4

Displacement field \(u_z\) of a screw dislocation near the dislocation line

Full size image
Fig. 5
figure 5

Elastic distortion components of a screw dislocation near the dislocation line: a \(\beta _{zx}\) and b \(\beta _{zy}\)

Full size image

The two non-vanishing components of the elastic distortion are calculated as

$$\begin{aligned} \beta _{zx}&=\mu b_z\partial _y G^\text {M}_{zz}=-\frac{b_z}{2\pi }\,\frac{y}{r^2}\bigg [1-\frac{r}{\ell _2}\, K_1(r/\ell _2 )\bigg ], \end{aligned}$$
(81)
$$\begin{aligned} \beta _{zy}&=-\mu b_z\partial _x G^\text {M}_{zz}=\frac{b_z}{2\pi }\,\frac{x}{r^2}\bigg [1-\frac{r}{\ell _2}\, K_1(r/\ell _2 )\bigg ]. \end{aligned}$$
(82)

The two components of the elastic distortion tensor, Eqs. (81) and (82), are plotted in Fig. 5a, b. It can be seen that they are non-singular. The corresponding two non-vanishing components of the non-singular stress tensor simply read

$$\begin{aligned} \sigma _{zx}&=-\frac{\mu b_z}{2\pi }\,\frac{y}{r^2}\bigg [1-\frac{r}{\ell _2}\, K_1(r/\ell _2 )\bigg ]\, , \end{aligned}$$
(83)
$$\begin{aligned} \sigma _{zy}&=\frac{\mu b_z}{2\pi }\,\frac{x}{r^2}\bigg [1-\frac{r}{\ell _2}\, K_1(r/\ell _2 )\bigg ]\, . \end{aligned}$$
(84)

All the dislocation fields obtained in reduced strain gradient elasticity are in agreement with the dislocation fields obtained in Mindlin’s strain gradient elasticity (see [4, 30]).

3.2 Edge dislocation

The edge dislocation of glide-mode is located at the position \((x,y)=(0,0)\) with Burgers vector \(b_x\). The dislocation line coincides with the z-axis of a Cartesian coordinate system. For an edge dislocation of glide-mode with Burgers vector \(b_x\), Eq. (48) reduces to

$$\begin{aligned} L^{\text {M}}_{ik} u_k&=\mu L_2 \partial _l \big (\beta _{il}^{{\mathrm {P}}}+\beta _{li}^{{\mathrm {P}}}\big ) \end{aligned}$$
(85)

with

$$\begin{aligned} L_2 \beta _{ij}^{{\mathrm {P}}}&=\beta _{ij}^{{\mathrm {P}},0}, \qquad i\ne j \end{aligned}$$
(86)

and

$$\begin{aligned} L^{\text {M}}_{ik} u_k&=\mu \partial _l \big (\beta _{il}^{{\mathrm {P}},0}+\beta _{li}^{{\mathrm {P}},0}\big ) . \end{aligned}$$
(87)

The classical plastic distortion of an edge dislocation of glide-mode given by deWit [6] (see also [39]) reads

$$\begin{aligned} \beta _{xy}^{{\mathrm {P}},0} =b_x \delta (y) H(-x)=b_x \delta (y)\int _x^{\infty } \delta (X)\,{\mathrm {d}}X. \end{aligned}$$
(88)

Substituting Eq. (88) into Eq. (86), the plastic distortion of an edge dislocation is calculated as

$$\begin{aligned} \beta ^{\mathrm {P}}_{xy}&=G^{L_2}*\beta ^{{\mathrm {P}},0}_{xy} =\frac{b_x}{2\pi \ell _2^2}\int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell _2\big )\, {\mathrm {d}}X \end{aligned}$$
(89)

and the corresponding dislocation density is obtained as

$$\begin{aligned} \alpha _{xz}&=-\partial _x\beta ^{\mathrm {P}}_{xy}=\frac{b_x}{2\pi \ell _2^2}\, K_0\big (r/\ell _2\big ). \end{aligned}$$
(90)

The plastic distortion (89) is non-singular and finite as it can be seen in Fig. 6. The dislocation density (90) is plotted in Fig. 7 and gives the shape and size of the dislocation core of the edge dislocation. Note that in reduced strain gradient elasticity, the plastic distortion (89) and dislocation density (90) of an edge dislocation have the same form as the corresponding fields (76) and (77) of a screw dislocation. The dislocation cores of screw and edge dislocations possess a cylindrical symmetry (see Figs. (2) and (7)) and have the same shape and size in the reduced strain gradient elasticity model.

Fig. 6
figure 6

Plastic distortion \(\beta ^{\mathrm {P}}_{xy}\) of an edge dislocation near the dislocation line

Full size image
Fig. 7
figure 7

Contour plot of the dislocation density of an edge dislocation \(\alpha _{xz}\) (normalized by the Burgers vector \(b_x\))

Full size image

Using the dislocation density (90), the effective Burgers vector \(b_x(r)\) of an edge dislocation is given by

$$\begin{aligned} b_x(r) = \int ^{2\pi }_0\int ^r_0 \alpha _{xz}(r')\,r'\,{\mathrm {d}}r' {\mathrm {d}}\phi = b_x\bigg [1-\frac{r}{\ell _2}\, K_1\big (r/\ell _2\big )\bigg ] . \end{aligned}$$
(91)

This effective Burgers vector differs appreciably from the classical Burgers vector \(b_x\), which is constant, in the region from \(r=0\) up to \(r\simeq 6\ell _2\). Note that the effective Burgers vector (91) of an edge dislocation has the same form as the effective Burgers vector (78) of a screw dislocation. The effective Burgers vector (91) is plotted in Fig. 8.

Fig. 8
figure 8

Effective Burgers vector \(b_x(r)\) of an edge dislocation (normalized by the Burgers vector \(b_x\))

Full size image

The solution of Eq. (87) provides the displacement field of the edge dislocation in the following form

$$\begin{aligned} u_{x}&=\mu \Big ( G_{xy}^\text {M}*\alpha _{xz}^{0}-\partial _y G_{xx}^\text {M}*\beta _{xy}^{{\mathrm {P}},0}\Big ) , \end{aligned}$$
(92)
$$\begin{aligned} u_{y}&=\mu \Big ( G_{yy}^\text {M}*\alpha _{xz}^{0}-\partial _y G_{yx}^\text {M}*\beta _{xy}^{{\mathrm {P}},0}\Big ) , \end{aligned}$$
(93)

where \(\alpha _{xz}^{0}=-\partial _x \beta _{xy}^{{\mathrm {P}},0}=b_x \delta (x)\delta (y)\) is the classical dislocation density of an edge dislocation. Substituting the classical plastic distortion and the Green tensor (55) into Eqs. (92) and (93), a straightforward calculation gives

$$\begin{aligned} u_x&=\frac{b_x}{2\pi } \bigg [ \arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y) +\partial _y \int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell _2\big ) \, {\mathrm {d}}X\nonumber \\&\quad +\frac{xy}{r^2} \bigg (1-\frac{4\ell _2^2}{r^2}+2K_2(r/\ell _2)\bigg ) -\frac{1-2\nu }{2(1-\nu )}\, \frac{xy}{r^2} \bigg (1-\frac{4\ell _1^2}{r^2}+2K_2(r/\ell _1)\bigg ) \bigg ], \end{aligned}$$
(94)
$$\begin{aligned} u_{y}&=-\frac{b_x}{4\pi } \bigg [\frac{1-2\nu }{1-\nu } \bigg \{\ln r+K_0(r/\ell _1) -\frac{x^2-y^2}{r^2} \bigg (1-\frac{4\ell _1^2}{r^2}+2K_2(r/\ell _1)\bigg ) \bigg \} \nonumber \\&\quad +\frac{x^2-y^2}{r^2} \bigg (1-\frac{4\ell _2^2}{r^2}+2K_2(r/\ell _2)\bigg ) \bigg ], \end{aligned}$$
(95)

where \(\nu \) is the Poisson ratio. The displacement fields (94) and (95) are plotted in Fig. 9a, b, respectively. Note that the displacement fields (94) and (95) are non-singular and smooth functions. The displacement fields (94) and (95) obtained in reduced strain gradient elasticity are in agreement with the displacement fields obtained in Mindlin’s strain gradient elasticity (see [5, 30]).

Fig. 9
figure 9

Displacement fields of an edge dislocation near the dislocation line: a \(u_x\) and b \(u_y\)

Full size image

If we substitute the displacement fields (92) and (93) and the plastic distortion (89) into Eq. (5), a straightforward calculation gives the four non-vanishing components of the incompatible elastic distortion tensor

$$\begin{aligned} \beta _{xx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )+\frac{2x^2}{r^2}-2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \}\nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) -\frac{2x^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(96)
$$\begin{aligned} \beta _{yy}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )-\frac{2x^2}{r^2}+2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \}\nonumber \\&\quad -(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(97)
$$\begin{aligned} \beta _{xy}&=\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(3-2\nu )-\frac{2y^2}{r^2}-2(1-\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) +\frac{x^2+3y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \}\nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(98)
$$\begin{aligned} \beta _{yx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(1-2\nu )+\frac{2y^2}{r^2}+2(1-\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \}\nonumber \\&\quad -(1-2\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ] . \end{aligned}$$
(99)

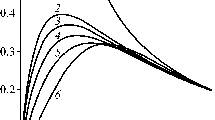
The components of the elastic distortion tensor, Eqs. (96)–(99), are plotted in Figs. 10a–d and 11a–d. It can be seen that they are non-singular and zero at the dislocation line. The elastic distortion components (96), (97) and (99) obtained in reduced strain gradient elasticity are in full agreement with the corresponding ones obtained in Mindlin’s strain gradient elasticity (see [30]). Only the elastic distortion component (98) is slightly different because it depends only on 2 lengths scales (\(\ell _1\), \(\ell _2\)), whereas in Mindlin’s strain gradient elasticity the component \(\beta _{xy}\) depends on 3 lengths scales (\(\ell _1\), \(\ell _2\), \(\ell _4\)) (see [30]). In the dislocation core region, the component \(\beta _{xy}\) obtained in the reduced strain gradient elasticity model is higher than the component \(\beta _{xy}\) in Mindlin’s strain gradient elasticity (see Fig. 11c). Using the values of the material parameters given in Table 1, the additional length in Mindlin’s first strain gradient elasticity is computed as \(\ell _4=1.4405\) Å (see also [30]).

Fig. 10
figure 10

Elastic distortion components of an edge dislocation near the dislocation line: a \(\beta _{xx}\), b \(\beta _{yy}\), c \(\beta _{xy}\) and d \(\beta _{yx}\)

Full size image
Fig. 11
figure 11

Plots of the elastic distortion components of an edge dislocation in reduced strain gradient elasticity (RSGE), simplified strain gradient elasticity (SSGE), and classical elasticity (Classical): a \(\beta _{xx}/b_x\), b \(\beta _{yy}/b_x\), c \(\beta _{xy}/b_x\), and d \(\beta _{yx}/b_x\)

Full size image

The trace of the elastic distortion tensor gives the elastic dilatation which reads as

$$\begin{aligned} \beta _{ll}&=-\frac{b_x(1-2\nu )}{2\pi (1-\nu )}\, \frac{y}{r^2}\bigg [1-\frac{r}{\ell _1}\, K_1(r/\ell _1 )\bigg ], \end{aligned}$$
(100)

depending on the longitudinal length \(\ell _1\). The skew-symmetric part of the elastic distortion tensor gives the elastic rotation which reads as

$$\begin{aligned} \omega _{xy}&=\frac{b_x}{2\pi }\, \frac{x}{r^2}\bigg [1-\frac{r}{\ell _2}\, K_1(r/\ell _2)\bigg ], \end{aligned}$$
(101)

depending on the transverse length \(\ell _2\).

Substituting the symmetric part of the elastic distortion tensor given in Eqs. (96)–(99) and the elastic dilatation (100) into the Hooke law (11), the non-vanishing components of the Cauchy stress tensor of an edge dislocation are calculated as

$$\begin{aligned} \sigma _{xx}&=-\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^2} \bigg [\frac{3x^2+y^2}{r^2}-\frac{2\nu r}{\ell _1}\,K_1(r/\ell _1) \nonumber \\&\quad -2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \}\nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) -\frac{2x^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(102)
$$\begin{aligned} \sigma _{yy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^2} \bigg [\frac{x^2-y^2}{r^2}+\frac{2\nu r}{\ell _1}\,K_1(r/\ell _1)\nonumber \\&\quad -2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ] , \end{aligned}$$
(103)
$$\begin{aligned} \sigma _{xy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{x}{r^2} \bigg [\frac{x^2-y^2}{r^2} \nonumber \\&\quad -2(1-\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) +\frac{2y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(104)
$$\begin{aligned} \sigma _{zz}&= -\frac{\mu \nu b_x}{\pi (1-\nu )}\, \frac{y}{r^2}\bigg [1-\frac{r}{\ell _1}\, K_1(r/\ell _1 )\bigg ]. \end{aligned}$$
(105)

The components of the Cauchy stress tensor, Eqs. (102)–(105), are plotted in Figs. 12a–d and 13a–d. It can be seen that they are non-singular. At the dislocation line, the stress is zero. The stress components (102), (103) and (105) obtained in reduced strain gradient elasticity are in full agreement with the corresponding stress components obtained in Mindlin’s strain gradient elasticity (see [30]). Only the stress component (104) is slightly different because it depends only on 2 lengths scales, whereas in Mindlin’s strain gradient elasticity the component \(\sigma _{xy}\) depends on 3 lengths scales (see [30]). In the dislocation core region, the component \(\sigma _{xy}\) obtained in the reduced strain gradient elasticity model is higher than the component \(\sigma _{xy}\) in Mindlin’s strain gradient elasticity (see Fig. 13c).

Fig. 12
figure 12

Cauchy stress components of an edge dislocation near the dislocation line: a \(\sigma _{xx}\), b \(\sigma _{yy}\), c \(\sigma _{xy}\) and d \(\sigma _{zz}\)

Full size image
Fig. 13
figure 13

Plots of the Cauchy stress components of an edge dislocation in reduced strain gradient elasticity (RSGE), simplified strain gradient elasticity (SSGE), and classical elasticity (Classical): a \(\sigma _{xx}/b_x\), b \(\sigma _{yy}/b_x\), c \(\sigma _{xy}/b_x\), and d \(\sigma _{zz}/b_x\)

Full size image

3.3 Limit to simplified strain gradient elasticity

In this section, we carry out the limit from reduced strain gradient elasticity to simplified strain gradient elasticity for the fields of screw and edge dislocations. Since reduced strain gradient elasticity is a generalization of simplified strain gradient elasticity, the dislocation fields of the simplified strain gradient elasticity model must be recovered from the dislocation fields of the reduced strain gradient elasticity model. The limit towards simplified strain gradient elasticity reads [19, 28]

$$\begin{aligned} a_1=0,\quad a_2=\frac{\lambda \ell ^2}{2},\quad a_3=0,\quad a_4=\mu \ell ^2,\quad a_5=0 \end{aligned}$$
(106)

and

$$\begin{aligned} \ell _1=\ell _2=\ell . \end{aligned}$$
(107)

For a screw dislocation, the limit reads \(\ell _2=\ell \) in Eqs. (76), (77), (79), (81) and (82) which leads to known results in the literature (see, e.g., [9, 11, 19, 24, 30]). Therefore, the dislocation fields of a screw dislocation in reduced strain gradient elasticity are in agreement with the dislocation fields of a screw dislocation in simplified strain gradient elasticity.

For an edge dislocation, the plastic distortion (89) and the dislocation density (90) reduce to formulas known in simplified strain gradient elasticity (see, e.g., [21, 24, 30]). The displacement fields (92) and (93) simplify to

$$\begin{aligned} u_x&=\frac{b_x}{4\pi (1-\nu )} \bigg [ 2(1-\nu )\bigg ( \arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y) +\partial _y \int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell \big ) \, {\mathrm {d}}X \bigg ) \nonumber \\&\quad \quad +\frac{xy}{r^2} \bigg (1-\frac{4\ell ^2}{r^2}+2K_2(r/\ell )\bigg ) \bigg ] , \end{aligned}$$
(108)
$$\begin{aligned} u_{y}&=-\frac{b_x}{4\pi (1-\nu )} \bigg [ (1-2\nu ) \Big (\ln r+K_0(r/\ell )\Big ) +\frac{x^2-y^2}{2r^2} \bigg (1-\frac{4\ell ^2}{r^2}+2K_2(r/\ell )\bigg ) \bigg ]. \end{aligned}$$
(109)

Equation (108) is in agreement with the displacement field given in [5, 21, 30]. Equation (109) agrees with the expression given in [5, 10, 21, 30].

The incompatible elastic distortion fields (96)–(99) reduce to

$$\begin{aligned} \beta _{xx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )+\frac{2x^2}{r^2} -\frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2(y^2-\nu r^2)}{\ell r }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(110)
$$\begin{aligned} \beta _{yy}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )-\frac{2x^2}{r^2} +\frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2(x^2-\nu r^2)}{\ell r}\,K_1(r/\ell )\bigg ] \, , \end{aligned}$$
(111)
$$\begin{aligned} \beta _{xy}&=\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(3-2\nu )-\frac{2y^2}{r^2} -\frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2\big (y^2+(1-\nu ) r^2\big )}{\ell r}\,K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(112)
$$\begin{aligned} \beta _{yx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(1-2\nu )+\frac{2y^2}{r^2} +\frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2\big (x^2-\nu r^2\big )}{\ell r}\,K_1(r/\ell ) \bigg ] , \end{aligned}$$
(113)

which agree with the formulas given in [21, 24, 30]. The elastic distortion (96)–(99) obtained in reduced strain gradient elasticity, the elastic distortion (110)–(113) obtained in simplified strain gradient elasticity and the classical elastic distortion are plotted in Fig. 11 using the values of the length scales given in Table 1. It can be seen that for these values of the length scales, the elastic distortion in reduced strain gradient elasticity and the elastic distortion in simplified strain gradient elasticity are in good agreement even in the dislocation core region. Only the extremum values of the elastic distortion in the dislocation core region are slightly higher in simplified strain gradient elasticity than in reduced strain gradient elasticity for the used values of the length scales.

The stress fields (102)–(105) simplify to

$$\begin{aligned} \sigma _{xx}&=-\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^4} \bigg [(3x^2+y^2) -(3x^2-y^2) \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2y^2r}{\ell }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(114)
$$\begin{aligned} \sigma _{yy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^4} \bigg [(x^2-y^2) -(3x^2-y^2) \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) +\frac{2x^2 r}{\ell }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(115)
$$\begin{aligned} \sigma _{xy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{x}{r^4} \bigg [(x^2-y^2) -(x^2-3y^2) \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2y^2 r}{\ell }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(116)
$$\begin{aligned} \sigma _{zz}&= -\frac{\mu \nu b_x}{\pi (1-\nu )}\, \frac{y}{r^2}\bigg [1-\frac{r}{\ell }\, K_1(r/\ell )\bigg ], \end{aligned}$$
(117)

which agree with the formulas given in [11, 19, 30]. The stress fields (102)–(105) obtained in reduced strain gradient elasticity, the stress fields (114)–(117) obtained in simplified strain gradient elasticity and the classical stress fields are plotted in Fig. 11 using the values of the length scales given in Table 1. It can be seen that for these values of the length scales, the stresses in reduced strain gradient elasticity and the stresses in simplified strain gradient elasticity are in good agreement even in the dislocation core region. The extremum values of the stress fields in the dislocation core region are slightly higher in simplified strain gradient elasticity than in reduced strain gradient elasticity for the used values of the length scales.

4 Conclusions

The reduced strain gradient elasticity model is developed in this paper. Reduced strain gradient elasticity is a strain gradient elasticity model involving two internal characteristic lengths in addition to the two Lamé parameters. It allows to eliminate elastic singularities and discontinuities and to interpret elastic size effects. Reduced strain gradient elasticity is a gradient model at a level of simplicity and complexity between simplified strain gradient elasticity and Mindlin’s strain gradient elasticity. One advantage of reduced strain gradient elasticity is the fact that is possesses two internal characteristic lengths like Mindlin’s strain gradient elasticity but less gradient-elastic constants than the five in Mindlin’s gradient theory leading to simpler expressions for the total stress and double stress tensors. The reduced strain gradient elasticity model is the appropriate model if two length scales are needed but the full Mindlin strain gradient elasticity theory is too sophisticated for applications. Thus, reduced strain gradient elasticity theory contains most features of the full Mindlin strain gradient elasticity theory and can be used for many important applications at the Ångström-scale, but also as effective (gradient) theory with two independent length scales. Therefore, the reduced strain gradient elasticity model is a particular case of Mindlin’s first strain gradient elasticity theory, and is a generalization of the simplified first strain gradient elasticity model to include two different characteristic length scale parameters.

In order to show the main advantages of the reduced strain gradient elasticity model, it has been employed to investigate straight dislocations. Exact analytical solutions for the displacement fields, elastic distortions, Cauchy stresses, plastic distortions and dislocation densities of screw and edge dislocations have been derived which demonstrate the elimination of any singularity from elastic and plastic fields at the dislocation line, except the dislocation density field possessing a logarithmic singularity at the dislocation line. The dislocation fields of a screw dislocation only depend on the characteristic transverse length \(\ell _2\), whereas the dislocation fields of an edge dislocation depend on the characteristic longitudinal lengths \(\ell _1\) and the characteristic transverse length \(\ell _2\). The most important length scale for the characteristic dislocation profiles of the displacement, plastic distortion and dislocation density fields of screw and edge dislocations is the transverse length \(\ell _2\). The dependence of the dislocation fields on the characteristic length scale parameters \(\ell _1\) and \(\ell _2\) is as follows.

The fields of a screw dislocation only depend on the characteristic transverse length \(\ell _2\) in the following way:

  • displacement field: \(u_z=u_z(\varvec{r}, \ell _2)\)

  • plastic distortion: \(\beta ^{\mathrm {P}}_{zy}=\beta ^{\mathrm {P}}_{zy}(\varvec{r}, \ell _2)\)

  • dislocation density: \(\alpha _{zz}=\alpha _{zz}(\varvec{r}, \ell _2)\)

  • incompatible elastic distortion: \(\beta _{ij}=\beta _{ij}(\varvec{r}, \ell _2)\)

  • Cauchy stress: \(\sigma _{ij}=\sigma _{ij}(\varvec{r}, \ell _2)\).

The fields of an edge dislocation depend on the characteristic longitudinal length \(\ell _1\) and the characteristic transverse length \(\ell _2\) in the following way:

  • displacement field: \(u_i=u_i(\varvec{r}, \ell _1, \ell _2)\)

  • plastic distortion: \(\beta ^{\mathrm {P}}_{xy}=\beta ^{\mathrm {P}}_{xy}(\varvec{r}, \ell _2)\)

  • dislocation density: \(\alpha _{xz}=\alpha _{xz}(\varvec{r}, \ell _2)\)

  • incompatible elastic distortion: \(\beta _{ij}=\beta _{ij}(\varvec{r}, \ell _1, \ell _2)\)

  • Cauchy stress: \(\sigma _{ij}=\sigma _{ij}(\varvec{r}, \ell _1, \ell _2)\).

It is important to note that the main feature of the obtained solutions of screw and edge dislocations is the absence of any singularity in the displacement, elastic distortion, plastic distortion and stress fields due to the regularization in the framework of gradient elasticity.