1 Introduction

In 1948, Pennes [1] presented an equation of heat transfer in human tissue, which included the effects of blood flow on tissue temperature. This equation, known as the ‘traditional’ or ‘classic’ or ‘Pennes’ bioheat equation [2], has the following form

$$\begin{aligned} c\rho \frac{\partial T(\mathbf {x},t)}{\partial t}=\varvec{\nabla }\left[ {{\lambda }\varvec{\nabla }T(\mathbf {x},t)} \right] +Q(\mathbf {x},t) \end{aligned}$$
(1)

where c, \(\rho \), \(\lambda \) are the specific heat, density and thermal conductivity of tissue, respectively, T denotes the temperature, x, t are the geometrical coordinates and time. The source term Q(x, t) is as follows

$$\begin{aligned} Q(\mathbf {x},t)=w_{\mathrm {b}} c_{\mathrm {b}} \left[ {T_{\mathrm {b}} -T(\mathbf {x},t)} \right] +Q_{\mathrm {m}} \end{aligned}$$
(2)

where \( w_{\mathrm {b}} \) is the blood perfusion rate, \(c_{\mathrm {b}}\) is the specific heat of blood, \(T_{\mathrm {b}}\) is the arterial blood temperature, and \( Q_{\mathrm {m}}\) is the metabolic heat source.

Pennes checked the validity of this approximation by comparing temperatures predicted by his equation with experimentally measured temperatures in the human forearm.

It should be noted that the Pennes equation is in fact the Fourier one in which the source components related to perfusion and metabolism are introduced. The Pennes equation (like the Fourier equation) is based on the Fourier law

$$\begin{aligned} {\mathbf{q}}\,(\mathbf {x},\,\,t)=-\,{\lambda }\,\varvec{\nabla }\,T(\mathbf {x},\,t) \end{aligned}$$
(3)

where q(x, t) is the heat flux and \(\nabla T \)(x, t) is the temperature gradient.

Another model of the bioheat transfer is based on the Cattaneo–Vernotte equation [3, 4]. This model takes into account the nonhomogeneous inner structure of biological tissues, which causes that the thermal wave propagates through the medium with a finite velocity. The heat flux delay relative to the temperature gradient is introduced

$$\begin{aligned} {\mathbf{q}}\,(\mathbf {x},\,\,t+{\tau }_{q} )=-\,{\lambda }\,\varvec{\nabla }\,T(\mathbf {x},\,t) \end{aligned}$$
(4)

where \(\tau _{q}= a\)/\(C^{2}\) is the relaxation time, \(a = \lambda \)/(\(c\rho )\) is the thermal diffusivity of tissue, C is the velocity of thermal wave in the medium.

Taking into account the first-order Taylor expansion for q

$$\begin{aligned} {\mathbf{q}}\,(\mathbf {x},\,\,t)+{\tau }_{q} \frac{\partial {\mathbf{q}}\,(\mathbf {x},\,\,t)}{\partial t}=-\,{\lambda }\,\varvec{\nabla }\,T(\mathbf {x},\,t) \end{aligned}$$
(5)

one obtains the Cattaneo–Vernotte equation in the form

$$\begin{aligned} c\rho \left[ {\frac{\partial T(\mathbf {x},t)}{\partial t}+{\tau }_{q} \frac{\partial ^{2}T(\mathbf {x},t)}{\partial t^{2}}} \right] =\varvec{\nabla }\left[ {{\lambda }\varvec{\nabla }T(\mathbf {x},t)} \right] +Q(\mathbf {x},t)+{\tau }_{q} \frac{\partial Q(\mathbf {x},t)}{\partial t} \end{aligned}$$
(6)

Experimentally determined values of \(\tau _{q}\) can be found, among others, in [5, 6], but they are questioned by some researchers, e.g., [7]. Mitra et al. [5] reported that relaxation time \(\tau _{q}\) in processed meat could be as large as 16 s. Kaminski [6] reported that \(\tau _{q}\) ranges from 10 to 50 s in his experiment with materials with inhomogeneous inner structures. Roetzel et al. [8] in a similar experiment estimated the value of this parameter at 1.77 s.

The next model of bioheat transfer is based on the following relationship [9, 10]

$$\begin{aligned} {\mathbf{q}}\,(\mathbf {x},\,\,t+{\tau }_{q} )=-\,{\lambda }\,\varvec{\nabla }\,T(\mathbf {x},\,t+{\tau }_{T} ) \end{aligned}$$
(7)

where \(\tau _{T}\) is the thermalization time.

Taking into account the first-order Taylor expansions for q and T

$$\begin{aligned} {\mathbf{q}}\,(\mathbf {x},\,\,t)+{\tau }_{q} \frac{\partial {\mathbf{q}}\,(\mathbf {x},\,\,t)}{\partial t}=-\,{\lambda }\,\varvec{\nabla }\,T(\mathbf {x},\,t) -{\tau }_{q} \frac{\partial \left[ {{\lambda }\varvec{\nabla }\,T(\mathbf {x},\,t)} \right] }{\partial t} \end{aligned}$$
(8)

one obtains the following form of bioheat transfer equation

$$\begin{aligned} c\rho \left[ {\frac{\partial T(\mathbf {x},t)}{\partial t}+{\tau }_{q} \frac{\partial ^{2}T(\mathbf {x},t)}{\partial t^{2}}} \right] =\varvec{\nabla }\left[ {{\lambda }\varvec{\nabla }T(\mathbf {x},t)} \right] +{\tau }_{T} \frac{\partial \left[ {{\lambda }\varvec{\nabla }T(\mathbf {x},t)} \right] }{\partial t}+{\tau }_{q} \frac{\partial Q(\mathbf {x},t)}{\partial t} \end{aligned}$$
(9)

Equation (9) is called dual-phase lag equation (DPLE) in which \(\tau _{q}\) is the phase lag in establishing the heat flux and associated conduction through the medium, and \(\tau _{T}\) is the phase lag in establishing the temperature gradient across the medium during which conduction occurs through its small-scale structures [9].

It is also worth mentioning the model based on the theory of porous media proposed by Zhang [11]

$$\begin{aligned} C\left( {\frac{\partial T(\mathbf {x},t)}{\partial ~ t}+\tau _{q} \frac{\partial ^{2}T(\mathbf {x},t)}{\partial t^{2}}} \right)= & {} \varvec{\nabla }\left[ {\Lambda \varvec{\nabla } T(\mathbf {x},t)} \right] +\tau _{T} \frac{\partial }{\partial ~ t}\left[ {\varvec{\nabla }\left( {\Lambda \varvec{\nabla }T(\mathbf {x},t)} \right) } \right] \nonumber \\&+\, G\left[ {T_{\mathrm {b}} -T(\mathbf {x},t)} \right] +{\varepsilon }Q_{\mathrm {b}} +\left( {1-{\varepsilon }} \right) Q_{\mathrm {m}} \nonumber \\&+\frac{\tau _{q} ~ C}{\left( {1-{\varepsilon }} \right) \rho c}\left[ {{\varepsilon }\frac{\partial Q_{\mathrm {b}} }{\partial ~ t}+\left( {1-{\varepsilon }} \right) \frac{\partial Q_{\mathrm {m}} }{\partial ~ t}} \right] \end{aligned}$$
(10)

where

$$\begin{aligned} \Lambda =\left( {1-{\varepsilon }} \right) {\lambda }+{\varepsilon } ~ {\lambda }_{\mathrm {b}} \end{aligned}$$
(11)

and

$$\begin{aligned} C=\left( {1-{\varepsilon }} \right) \rho c+ ~ ~ {\varepsilon }\,\rho _{\mathrm {b}} c_{\mathrm {b}} \end{aligned}$$
(12)

are the effective thermal conductivity and effective heat capacity, respectively (subscript b denotes blood sub-domain), \(Q_{\mathrm {m}}\) and \(Q_{\mathrm {b}}\) are the metabolic heat sources in the tissue and blood sub-domain, respectively, G is the coupling factor, and \(\varepsilon \) denotes the porosity (the ratio of blood volume to the total volume).

The phase lags for heat flux and temperature gradient and the coupling factor are defined as [11]

$$\begin{aligned} {\tau }_{q} =\frac{{\varepsilon }\left( {1-{\varepsilon }} \right) \rho c \rho _{\mathrm {b}} c_{\mathrm {b}} }{G C} \end{aligned}$$
(13)

and

$$\begin{aligned} {\tau }_{T} =\frac{{\varepsilon }\left( {1-{\varepsilon }} \right) ~ ~ \rho _{\mathrm {b}} c_{\mathrm {b}} {\lambda }}{G \Lambda } \end{aligned}$$
(14)

while

$$\begin{aligned} G=A\alpha +w_{\mathrm {b}} \,c_{\mathrm {b}} \end{aligned}$$
(15)

where A [\(\hbox {m}^{2}\)/\(\hbox {m}^{3}\)] is the volumetric heat transfer area between tissue and blood, \(\alpha \) is the heat transfer coefficient, and \( w_{\mathrm {b}}\) is the blood perfusion rate.

As can be observed, the phase-lag times are expressed in terms of the properties of blood and tissue, the interphase convective heat transfer coefficient \(\alpha \) and the blood perfusion rate \(w_{\mathrm {b}}\). These parameters are closely related to the porosity, and larger porosity values determine larger values of these parameters. Zhang [11] computed and argued that reasonable relaxation time \(\tau _{q} \) and thermalization time \(\tau _{T}\) should range from 0.464 to 6.825 s.

As can be seen, the key parameters in the non-Pennes bioheat equations are the delay times \(\tau _{q} \) and \(\tau _{T}\). Experimental studies show that delay times vary widely and are different for different types of biological tissues. The purpose of the research is to estimate the temperature changes in heated tissues due to perturbation in time delays. To achieve this, sensitivity analysis methods can be used [12,13,14,15]. In the direct approach of sensitivity analysis, the basic problem described by the dual-phase lag equation and appropriate boundary-initial conditions is differentiated with respect to the parameter under consideration. Next, these both problems are solved using (in the case considered) the numerical methods. Finally, based on the solutions obtained, the impact of changes in individual parameters on the tissue temperature distribution is assessed. In this way one can analyze the influence of the parameters appearing in the mathematical model on the final form of problem solution; in other words, which of these parameters are more or less important.

2 Formulation of the problem

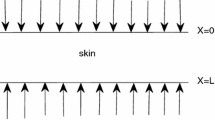
Axisymmetric tissue region heated by an external heat flux, as shown in Fig. 1, is considered. To describe the temperature field in the tissue dual-phase lag equation (9) for constant thermophysical parameters is applied

$$\begin{aligned}&(r,z)\in \Omega :\;\quad c \rho \,\left[ {\frac{\partial \,T(r,z,\,\,t)}{\partial \,t}+{\tau }_{q} \frac{\partial ^{2}\,T(r,z,\,\,t)}{\partial \,t^{2}}} \right] \nonumber \\&\quad ={\lambda }\varvec{\nabla }^{2}\,T(r,z,\,\,t) + \lambda \tau _{T} \frac{\partial \left[ {\varvec{\nabla }^{2}\,T(r,z,\,\,t)} \right] \,}{\partial \,t}+Q\,(r,z,t)+{\tau }_{q} \frac{\partial \,Q ~ ~ (r,z,\,\,t)}{\partial \,t} \end{aligned}$$
(16)

where

$$\begin{aligned} \varvec{\nabla }^{2}T(r,z,t)= & {} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T(r,z,t)}{\partial r}} \right) +\frac{\partial ^{2}T(r,z,t)}{\partial z^{2}} \nonumber \\= & {} \frac{1}{r}\frac{\partial T(r,z,t)}{\partial r}+\frac{\partial ^{2}T(r,z,t)}{\partial r^{2}}+\frac{\partial ^{2}T(r,z,t)}{\partial z^{2}} \end{aligned}$$
(17)

Introducing Eq. (2) into Eq. (16) one obtains

$$\begin{aligned}&\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \frac{\partial \,T(r,z,\,\,t)}{\partial \,t}+{\tau }_{q} c \rho \,\frac{\partial ^{2}\,T(r,z,\,\,t)}{\partial \,t^{2}}\nonumber \\&\quad ={\lambda }\varvec{\nabla }^{2}\,T(r,z,\,\,t) +{\lambda \tau }_{T} \frac{\partial \left[ {\varvec{\nabla }^{2}\,T(r,z,\,\,t)} \right] \,}{\partial \,t}+w_{\mathrm {b}} c_{\mathrm {b}} \left[ {T_{\mathrm {b}} -T(r,z,t)} \right] +Q_{\mathrm {m}} \end{aligned}$$
(18)

On the fragment of the tissue surface \(\Gamma _{1}\): \(r \le r_{D}\), \(z = 0\) (Fig. 1), for \(t \le t_{\mathrm {e}}\), where \(t_{\mathrm {e}}\) is the exposure time, the Neumann condition is assumed [16]

$$\begin{aligned} q_{\mathrm {b}} (r,0,t)=q_{0} \frac{t}{t{ }_{\mathrm {e}}}\left( {1-\frac{t}{t{ }_{\mathrm {e}}}} \right) \exp \left( {-\frac{r^{2}}{r_{D}^{2} }} \right) \end{aligned}$$
(19)

where \(q_{0}\) is a constant value. For \(t > t_{\mathrm {e}}\) : \(q_{\mathrm {b}}\) \((r, 0, t) = 0\). On the remaining surfaces \(\Gamma _{2}\) of the domain, the no-flux condition is accepted.

It should be noted that the dual-phase lag model requires the adequate transformation of boundary conditions which appear in the typical macroheat conduction models. In the case considered one has [17]

$$\begin{aligned} -{\lambda }\left[ {{\mathbf{n}}\cdot \varvec{\nabla }T\left( {r,\,\,z,\,\,t} \right) +\tau _{T} \frac{\partial \left[ {{\mathbf{n}}\cdot \varvec{\nabla }T\left( {r,\,\,z,\,\,t} \right) } \right] }{\partial t}} \right] =q_{\mathrm {b}} (r,z,t)+{\tau }_{q} \frac{\partial q_{\mathrm {b}} (r,z,t)}{\partial t} \end{aligned}$$
(20)

where n is the normal outward vector.

The initial conditions are also given (c.f. Eq. (2))

$$\begin{aligned} t=0:\quad T\left( {r,z,\,0} \right) =T_{p} ,\quad \left. {\frac{\partial \,T\left( {r,z,\;0} \right) }{\partial \,t}} \right| _{\,t\,=\,0} =\frac{1}{c\rho }Q\,(r,z,0)=\frac{1}{c\rho }\left[ {w_{\mathrm {b}} c_{\mathrm {b}} \left( {T_{\mathrm {b}} -T_{p} } \right) +Q_{\mathrm {m}} } \right] \end{aligned}$$
(21)

where \(T_{p}\) is a constant initial temperature.

Fig. 1
figure 1

Domain considered

Full size image

3 Sensitivity analysis

To estimate the changes of tissue temperature due to relaxation and thermalization times, the direct approach of sensitivity analysis is applied [12, 15]. This approach is related to the differentiation of governing equations with respect to the parameter considered.

Thus, the differentiation of Eq. (18) with respect to the relaxation time \(\tau _{q} \) gives (the arguments of the T function are omitted here)

$$\begin{aligned}&w_{\mathrm {b}} c_{\mathrm {b}} \frac{\partial \,T}{\partial \,t}+\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \frac{\partial \,^{2}T}{\partial \,{\tau }_{q} \partial \,t}+c \rho \,\frac{\partial ^{2}\,T}{\partial \,t^{2}}+{\tau }_{q} c \rho \,\frac{\partial ^{3}\,T}{\partial \,{\tau }_{q} \partial \,t^{2}} \nonumber \\&\quad ={\lambda }\frac{\partial \,\left( {\varvec{\nabla }^{2}\,T} \right) }{\partial \,{\tau }_{q} }+{\lambda \tau }_{T} \frac{\partial ^{2}\left( {\varvec{\nabla }^{2}\,T} \right) \,}{\partial \,{\tau }_{q} \partial \,t}-w_{\mathrm {b}} c_{\mathrm {b}} \frac{\partial \,T}{\partial \,{\tau }_{q} } \end{aligned}$$
(22)

Using the Schwartz theorem one can obtain

$$\begin{aligned} \left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \frac{\partial \,^{2}U}{\partial \,t}+{\tau }_{q} c \rho \,\frac{\partial ^{2}\,U}{\partial \,t^{2}}={\lambda }\varvec{\nabla }^{2}\,U+{\lambda \tau }_{T} \frac{\partial \left( {\varvec{\nabla }^{2}\,U} \right) \,}{\partial \,t}-w_{\mathrm {b}} c_{\mathrm {b} } U-w_{\mathrm {b}} c_{\mathrm {b}} \frac{\partial \,T}{\partial \,t}-c \rho \,\frac{\partial ^{2}\,T}{\partial \,t^{2}} \end{aligned}$$
(23)

where \(U = \partial T\)/\(\partial \tau _{q}\) is the sensitivity function.

Boundary condition (20) and initial condition (21) are also differentiated

$$\begin{aligned} {-\lambda \left[ {{\mathbf{n}}\cdot \varvec{\nabla }U+\tau _{T} \frac{\partial \left( {{\mathbf{n}}\cdot \varvec{\nabla }U} \right) }{\partial t}} \right] =\frac{\partial q_{\mathrm {b}} }{\partial t}} \end{aligned}$$
(24)

and

$$\begin{aligned} t=0:\quad U=0,\quad \left. {\frac{\partial \,U}{\partial \,t}} \right| _{\,t\,=\,0} =0 \end{aligned}$$
(25)

In a similar manner, an additional problem related to the sensitivity function with respect to the thermalization time \(\tau _{T}\) can be obtained

$$\begin{aligned} \left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \frac{\partial \,W}{\partial \,t}+{\tau }_{q} c \rho \,\frac{\partial ^{2}\,W}{\partial \,t^{2}}={\lambda }\varvec{\nabla }^{2}\,W+{\lambda }\frac{\partial \left( {\varvec{\nabla }^{2}\,T} \right) \,}{\partial \,t}+{\lambda \tau }_{T} \frac{\partial \left( {\varvec{\nabla }^{2}\,W} \right) \,}{\partial \,t}-w_{\mathrm {b}} c_{\mathrm {b}} W \end{aligned}$$
(26)

and

$$\begin{aligned} -\lambda \left[ {{\mathbf{n}}\cdot \varvec{\nabla }W+\tau _{T} \frac{\partial \left( {{\mathbf{n}}\cdot \varvec{\nabla }W} \right) }{\partial t}} \right] =\lambda \frac{\partial \left( {{\mathbf{n}}\cdot \varvec{\nabla }T} \right) }{\partial t} \end{aligned}$$
(27)

while

$$\begin{aligned} t=0:\quad W=0,\quad \left. {\frac{\partial \,W}{\partial \,t}} \right| _{\,t\,=\,0} =0 \end{aligned}$$
(28)

where \(W = \partial T\)/\(\partial \tau _{T}\) .

4 Method of solution

The formulated problem is solved using the implicit scheme of the finite difference method. The temperature for time \(t^{\, f} = f \Delta t\) (\(f \ge 2\)) is denoted as \(T^{f} = T(r\), z, \(f \Delta t)\), where \(\Delta t\) is the constant time step. The uniform spatial grid of dimensions \(n \times n\) with a constant grid step h, the same in both directions, is introduced. For the node i, j the temperature is denoted as \(T_{i,j}^{f} =\left( {i h,j h,f\Delta t} \right) \), where \(i = 0, 1, \ldots n\), \(j = 0, 1, \ldots , n\). From initial conditions (21) it follows that \(T_{i,j}^{0} =T_{p} ,\,\;T_{i,j}^{ ~ 1} =T_{p} +\Delta t\left[ {w_{\mathrm {b}} c_{\mathrm {b}} \left( {T_{\mathrm {b}} -T_{p} } \right) +Q_{\mathrm {m}} } \right] /(c\rho )\), \({i }= 1, 2,\ldots , n - 1\), \(j = 1, 2, \ldots , n - 1\).

The following approximate form of Eq. (18) is proposed

$$\begin{aligned}&\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \frac{T_{\,i,j}^{f} -T_{\,i,j}^{f-1} }{\Delta t}+{\tau }_{q} c \rho \,\frac{T_{ ~ i,j}^{f} -2T_{i,j}^{f-1} +T_{ ~ i,j}^{f-2} }{\left( {\Delta t} \right) ^{2}}={\lambda }\left( {\varvec{\nabla }^{2}\,T} \right) ^{f} \nonumber \\&\quad +\frac{{\lambda \tau }_{T} }{\Delta t}\left[ {\left( {\varvec{\nabla }^{2}\,T} \right) ^{f}-\left( {\varvec{\nabla }^{2}\,T} \right) ^{f-1}} \right] +w_{\mathrm {b}} c_{\mathrm {b}} \left( {T_{\mathrm {b}} -T_{i,j}^{f} } \right) +Q_{\mathrm {m}} \end{aligned}$$
(29)

or

$$\begin{aligned}&\frac{\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \Delta t+{\tau }_{q} c \rho +w_{\mathrm {b}} c_{\mathrm {b}} \left( {\Delta t} \right) ^{2}}{\left( {\Delta t} \right) ^{2}}T_{\,i,j}^{f} -\frac{\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \Delta t+2{\tau }_{q} c \rho }{\left( {\Delta t} \right) ^{2}}T_{\,i,j}^{f-1} +\frac{{\tau }_{q} c \rho }{\left( {\Delta t} \right) ^{2}}T_{\,i,j}^{f-2} \nonumber \\&\quad =\frac{{\lambda }\left( {\Delta t+{\tau }_{T} } \right) }{\Delta t}\left( {\varvec{\nabla }^{2}\,T} \right) ^{f}-\frac{{\lambda \tau }_{T} }{\Delta t}\left( {\varvec{\nabla }^{2}\,T} \right) ^{f-1}+w_{\mathrm {b}} c_{\mathrm {b}} T_{\mathrm {b}} +Q_{\mathrm {m}} \end{aligned}$$
(30)

where (c.f. Eq. (17))

$$\begin{aligned} \left( {\varvec{\nabla }^{2}T} \right) _{i,j}^{l} = \frac{1}{r_{i,j} }\frac{T_{i,j+1}^{l} -T_{i,j-1}^{l} }{2h}+\frac{T_{i,j-1}^{l} -2T_{i,j}^{l} +T_{i,j+1}^{l} }{h^{2}}+\frac{T_{i-1,j}^{l} -2T_{i,j}^{l} +T_{i+1,j}^{l} }{h^{2}} \end{aligned}$$
(31)

while \(l = f\) or \(l = f\) – 1.

Introducing (31) into (30) one has

$$\begin{aligned} T_{\,i,j}^{f}= & {} \frac{A_{2} }{A_{1} }\left[ {\left( {1-\frac{h}{2r_{i,j} ~ }} \right) T_{i,j-1}^{f} +\left( {1+\frac{h}{2r_{i,j} ~ }} \right) T_{i,j+1}^{f} +T_{i-1,j}^{f} +T_{i+1,j}^{f} } \right] \nonumber \\&-\frac{{\lambda \tau }_{T} }{A_{1} \Delta t}\left( {\frac{1}{r_{i,j} }\frac{T_{i,j+1}^{f-1} -T_{i,j-1}^{f-1} }{2h}+\frac{T_{i,j-1}^{f-1} -2T_{i,j}^{f-1} +T_{i,j+1}^{f-1} }{h^{2}}+\frac{T_{i-1,j}^{f-1} -2T_{i,j}^{f-1} +T_{i+1,j}^{f-1} }{h^{2}}} \right) \nonumber \\&+\frac{\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \Delta t+2{\tau }_{q} c \rho }{A_{1} \left( {\Delta t} \right) ^{2}}T_{\,i,j}^{f-1} -\frac{{\tau }_{q} c \rho }{A_{1} \left( {\Delta t} \right) ^{2}}T_{\,i,j}^{f-2} +\frac{w_{\mathrm {b}} c_{\mathrm {b}} T_{\mathrm {b}} +Q_{\mathrm {m}} }{A_{1} } \end{aligned}$$
(32)

where

$$\begin{aligned} A_{2}= & {} \frac{{\lambda }\left( {\Delta t+{\tau }_{T} } \right) }{h^{2}\Delta t} \nonumber \\ A_{1}= & {} \frac{\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \Delta t+{\tau }_{q} c \rho +w_{\mathrm {b}} c_{\mathrm {b}} \left( {\Delta t} \right) ^{2}}{\left( {\Delta t} \right) ^{2}}+4A_{2} \end{aligned}$$
(33)

Boundary condition (20) is written in the form

$$\begin{aligned} -\lambda ~ \,{\mathbf{n}}\cdot \left( {\varvec{\nabla }T} \right) _{0,j}^{f} -\frac{\lambda \tau _{T} }{\Delta t}\left[ {{\mathbf{n}}\cdot \left( {\varvec{\nabla }T} \right) _{0,j}^{f} -{\mathbf{n}}\cdot \left( {\varvec{\nabla }T} \right) _{0,j}^{f-1} } \right] =q_{\mathrm {b}0,j}^{f} +\tau _{q} \left( {\frac{\partial q_{\mathrm {b}} }{\partial t}} \right) _{0,j}^{f} \end{aligned}$$
(34)

where

$$\begin{aligned} {{\mathbf{n}}\cdot \left( {\varvec{\nabla }T} \right) _{0,j}^{f} =\frac{T_{1,j}^{f} -T_{0,j}^{f} }{h},\quad {\mathbf{n}}\cdot \left( {\varvec{\nabla }T} \right) _{0,j}^{f-1} =\frac{T_{1,j}^{f-1} -T_{0,j}^{f-1} }{h}} \end{aligned}$$
(35)

After mathematical manipulations one has

$$\begin{aligned} {T_{0,j}^{f} =T_{1,j}^{f} -\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {T_{1,j}^{f-1} -T_{0,j}^{f-1} } \right) } +\frac{h\Delta t}{{\lambda }\left( {\Delta t+{\tau }_{T} } \right) }\left[ {q_{\mathrm {b}\,0,j}^{f} +{\tau }_{q} \left( {\frac{\partial q_{\mathrm {b}} }{\partial t}} \right) _{0,j}^{f} } \right] \end{aligned}$$
(36)

On the remaining surfaces (the no-flux boundary condition) the temperatures are calculated using the equations

$$\begin{aligned}&{T_{n,j}^{f} =T_{n-1,j}^{f} +\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {T_{n,j}^{f-1} -T_{n-1,j}^{f-1} } \right) } \end{aligned}$$
(37)
$$\begin{aligned}&{T_{i,0}^{f} =T_{i,1}^{f} -\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {T_{i,1}^{f-1} -T_{i,0}^{f-1} } \right) } \end{aligned}$$
(38)
$$\begin{aligned}&{T_{i,n}^{f} =T_{i,n-1}^{f} +\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {T_{i,n}^{f-1} -T_{i,n-1}^{f-1} } \right) } \end{aligned}$$
(39)

The system of Eqs. (32), (36)–(39) for transition \(t^{{f}^{-1}}\rightarrow t^{f}\) is solved using the iterative method. The iteration process is continued until the condition \(\left| {\left( {T_{i,j}^{f} } \right) ^{k}-\left( {T_{i,j}^{f} } \right) ^{k-1}} \right| \le {\delta }\) for each node has been fulfilled, where k is the number of iteration. It should be noted that the presented algorithm is unconditionally stable [18].

Proceeding in a similar manner, one obtains appropriate difference equations for the sensitivity functions. Thus, the approximation of the additional problem related to the sensitivity function U has the form (c.f. Eqs.  (23), (24), (25))

$$\begin{aligned} U_{\,i,j}^{f}= & {} \frac{A_{2} }{A_{1} }\left[ {\left( {1-\frac{h}{2r_{i,j} ~ }} \right) U_{i,j-1}^{f} +\left( {1+\frac{h}{2r_{i,j} ~ }} \right) U_{i,j+1}^{f} +U_{i-1,j}^{f} +U_{i+1,j}^{f} } \right] \nonumber \\&-\frac{{\lambda \tau }_{T} }{A_{1} \Delta t}\left( {\frac{1}{r_{i,j} }\frac{U_{i,j+1}^{f-1} -U_{i,j-1}^{f-1} }{2h}+\frac{U_{i,j-1}^{f-1} -2U_{i,j}^{f-1} +U_{i,j+1}^{f-1} }{h^{2}}+\frac{U_{i-1,j}^{f-1} -2U_{i,j}^{f-1} +U_{i+1,j}^{f-1} }{h^{2}}} \right) \nonumber \\&+\frac{\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \Delta t+2{\tau }_{q} c \rho }{A_{1} \left( {\Delta t} \right) ^{2}}U_{\,i,j}^{f-1} -\frac{{\tau }_{q} c ~ \rho }{A_{1} \left( {\Delta t} \right) ^{2}}U_{\,i,j}^{f-2} \nonumber \\&-\frac{1}{A_{1} }\left( {w_{\mathrm {b}} c_{\mathrm {b}} \frac{T_{i,j}^{f} -T_{i,j}^{f-1} }{\Delta t}+c \rho \frac{T_{ i,j}^{f} -2T_{i,j}^{f-1} +T_{i,j}^{f-2} }{\left( {\Delta t} \right) ^{2}}} \right) ,\,\;i=1,2,\ldots ,n-1, j=1,2,\ldots ,n-1\nonumber \\ \end{aligned}$$
(40)
$$\begin{aligned}&{U_{0,j}^{f} =U_{1,j}^{f} -\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {U_{1,j}^{f-1} -U_{0,j}^{f-1} } \right) } +\frac{h\Delta t}{{\lambda }\left( {\Delta t+{\tau }_{T} } \right) }\left( {\frac{\partial q_{\mathrm {b}} }{\partial t}} \right) _{0,j}^{f} \end{aligned}$$
(41)
$$\begin{aligned}&{U_{n,j}^{f} =U_{n-1,j}^{f} +\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {U_{n,j}^{f-1} -U_{n-1,j}^{f-1} } \right) } \end{aligned}$$
(42)
$$\begin{aligned}&{U_{i,0}^{f} =U_{i,1}^{f} -\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {U_{i,1}^{f-1} -U_{i,0}^{f-1} } \right) } \end{aligned}$$
(43)
$$\begin{aligned}&{U_{i,n}^{f} =U_{i,n-1}^{f} +\frac{{\tau }_{T} }{\Delta t+{\tau }_{T} }\left( {U_{i,n}^{f-1} -U_{i,n-1}^{f-1} } \right) } \end{aligned}$$
(44)

In turn, the approximation of the additional problem related to the sensitivity function W can be expressed as follows (c.f. Eqs. (26)–(28))

$$\begin{aligned} W_{\,i,j}^{f}= & {} \frac{A_{2} }{A_{1} }\left[ {\left( {1-\frac{h}{2r_{i,j} ~ }} \right) W_{i,j-1}^{f} +\left( {1+\frac{h}{2r_{i,j} ~ }} \right) W_{i,j+1}^{f} +W_{i-1,j}^{f} +W_{i+1,j}^{f} } \right] \nonumber \\&-\frac{{\lambda \tau }_{T} }{A_{1} \Delta t}\left( {\frac{1}{r_{i,j} }\frac{W_{i,j+1}^{f-1} -W_{i,j-1}^{f-1} }{2h}+\frac{W_{i,j-1}^{f-1} -2W_{i,j}^{f-1} +W_{i,j+1}^{f-1} }{h^{2}}+\frac{W_{i-1,j}^{f-1} -2W_{i,j}^{f-1} +W_{i+1,j}^{f-1} }{h^{2}}} \right) \nonumber \\&+\frac{\left( {c \rho +{\tau }_{q} w_{\mathrm {b}} c_{\mathrm {b}} } \right) \Delta t+2{\tau }_{q} c \rho }{A_{1} \left( {\Delta t} \right) ^{2}}W_{\,i,j}^{f-1} -\frac{{\tau }_{q} c ~ \rho }{A_{1} \left( {\Delta t} \right) ^{2}}W_{\,i,j}^{f-2} \nonumber \\&+\frac{{\lambda }}{A_{1} \Delta t}\left( {\frac{1}{r_{i,j} }\frac{T_{i,j+1}^{f} -T_{i,j-1}^{f} }{2h}+\frac{T_{i,j-1}^{f} -2T_{i,j}^{f} +T_{i,j+1}^{f} }{h^{2}}+\frac{T_{i-1,j}^{f} -2T_{i,j}^{f} +T_{i+1,j}^{f} }{h^{2}}} \right) \nonumber \\&-\frac{{\lambda }}{A_{1} \Delta t}\left( {\frac{1}{r_{i,j} }\frac{T_{i,j+1}^{f-1} -T_{i,j-1}^{f-1} }{2h}+\frac{T_{i,j-1}^{f-1} -2T_{i,j}^{f-1} +T_{i,j+1}^{f-1} }{h^{2}}+\frac{T_{i-1,j}^{f-1} -2T_{i,j}^{f-1} +T_{i+1,j}^{f-1} }{h^{2}}} \right) ,\; \nonumber \\ i= & {} 1,2,\ldots ,n-1,\;j=1,2,\ldots ,n-1 \end{aligned}$$
(45)
$$\begin{aligned} W_{0,j}^{f}= & {} W_{1,j}^{f} -\frac{\tau _{T} }{\Delta t+\tau _{T} }\left( {W_{1,j}^{f-1} -W_{0,j}^{f-1} } \right) +\frac{1}{\Delta t+\tau _{T} }\left( {T_{1,j}^{f} -T_{0,j}^{f} -T_{1,j}^{f-1} +T_{0,j}^{f-1} } \right) \end{aligned}$$
(46)
$$\begin{aligned} W_{n,j}^{f}= & {} W_{n-1,j}^{f} +\frac{\tau _{T} }{\Delta t+\tau _{T} }\left( {W_{n,j}^{f-1} -W_{n-1,j}^{f-1} } \right) -\frac{1}{\Delta t+\tau _{T} }\left( {T_{n,j}^{f} -T_{n-1,j}^{f} -T_{n,j}^{f-1} +T_{n-1,j}^{f-1} } \right) \end{aligned}$$
(47)
$$\begin{aligned} W_{i,0}^{f}= & {} W_{i,1}^{f} -\frac{\tau _{T} }{\Delta t+\tau _{T} }\left( {W_{i,1}^{f-1} -W_{i,0}^{f-1} } \right) +\frac{1}{\Delta t+\tau _{T} }\left( {T_{i,1}^{f} -T_{i,0}^{f} -T_{i,1}^{f-1} +T_{i,0}^{f-1} } \right) \end{aligned}$$
(48)
$$\begin{aligned} W_{i,n}^{f}= & {} W_{i,n-1}^{f} +\frac{\tau _{T} }{\Delta t+\tau _{T} }\left( {W_{i,n}^{f-1} -W_{i,n-1}^{f-1} } \right) -\frac{1}{\Delta t+\tau _{T} }\left( {T_{i,n}^{f} -T_{i,n-1}^{f} -T_{i,n}^{f-1} +T_{i,n-1}^{f-1} } \right) \end{aligned}$$
(49)

5 Results of computations

The cylindrical tissue domain (\(R = 0.02\) m, \(Z = 0.02\) m) at the initial temperature \(T_{p}= 37~^{\circ }\hbox {C}\) is considered. The following values of parameters are assumed: thermal conductivity of tissue \(\lambda = 0.5\) W/(mK), specific heat \(c = 4000\) J/(kg K), density \(\rho = 1000\,\hbox {kg/m}^{3}\), blood perfusion rate \(w_{\mathrm {b}}= 0.53\) kg/(\(\hbox {m}^{3}\) s), specific heat of blood \(\textit{c}_{\mathrm {b}} = 3770\) J/(kg K), arterial blood temperature \( T_{\mathrm {b}} = 37\,^{\circ }\hbox {C}\), metabolic heat source \(\textit{Q}_{m\, }= 250\,\hbox {W/m}^{3}\), relaxation time \(\tau _{q} = 15\) s, thermalization time \(\tau _{T}= 10\) s [20]. For boundary condition (5): \( q_{0}= 15{,}000\,\hbox {W/m}^{2}\), \(r_{D} = R/4\), \(t_{\mathrm {e}} = 100\) s.

The problem is solved under the assumption that the grid step is equal to \(h = 0.0002\) m (\(n = 100\)) and next \(h = 0.0004\) m (\(n =\) 50), while the time step is equal to \(\Delta t = 0.0005\) s. The system of equations resulting from the FDM algorithm is solved with the tolerance \({\updelta }=10^{-12}\). In Fig. 2 the temperature histories at the selected nodes A(0, 0.0004 m), B(0, 0.002 m) and C(0, 0.004 m) from the domain (for two variants of grid steps) are shown. It can be seen that the temperatures are lower with a denser mesh, especially in the most heated node A.

The time step was also changed, and it turned out that for the first mesh (\(h = 0.0002\) m) the differences in the results for time steps \(\Delta t = 0.0005\) s and \(\Delta t = 0.005\) s are very small. Therefore, further computations were performed for \(n = 100\) and \(\Delta t = 0.005\) s.

Fig. 2
figure 2

Temperature history at selected points (dotted lines—\(h = 0.0002\) m, solid lines—\(h = 0.0004\) m)

Full size image

In Fig. 3 the temperature field in the fragment of the domain \(r \le R/2\), \(z \le Z/2\) after 50 s and 100 s is shown. Figures 4 and 5 illustrate the distribution of sensitivity functionsU and W, respectively.

Fig. 3
figure 3

Temperature distribution a \( t = 50\) s b \(t = 100\) s

Full size image
Fig. 4
figure 4

Distribution of function U a \( t = 50\) s b \(t = 100\) s

Full size image
Fig. 5
figure 5

Distribution of function W a \( t = 50\) s b \(t = 100\) s

Full size image

Knowledge of the sensitivity functions allows one, among others, to estimate the changes of temperatures due to the perturbations of the parameters considered. At first, the influence of change of single parameter on the temperature distribution is analyzed and then

$$\begin{aligned} \text{ D}_{{1}} T=U ~ \Delta ~ {\tau } _{q} ,\;\;\text{ D}_{{2}} T=W ~ \Delta ~ {\tau } _{T} \end{aligned}$$
(50)

where \(\Delta \tau _{q}\) and \(\Delta \tau _{T}\) are the assumed perturbations of parameters. It should be noted that the estimate performed here is a linearization and thus only admissible for relatively small \(\Delta \tau _{q}\) and \(\Delta \tau _{T}\).

In Figs. 6 and 7 the changes of temperature at the points A, B and C under the assumption that \(\Delta \tau _{q} = 0.3 \tau _{q}\) and \(\Delta \tau _{T} = 0.3 \tau _{T}\) are shown.

Fig. 6
figure 6

Changes of temperature \(\hbox {D}_{1}T \) at selected points

Full size image
Fig. 7
figure 7

Changes of temperature \(\hbox {D}_{2}T \) at selected points

Full size image

As can be seen, the maximum temperature change is observed at the point A, of course. The maximum of function \(D_{1}T\) at this point corresponds approximately to the maximum value of boundary heat flux (19) for \(t = t_{\mathrm {e}}/2 = 50\) s (Fig. 6). At the cooling stage \(t > 50\) s, the value of the \(D_{1}T\) function decreases reaching a minimum after 115 s and then tends to zero. The temperature changes at the points B and C are similar, with the maximum and minimum values being lower and appearing later.

In the case of the temperature change caused by a perturbation in the thermalization time (Fig. 7), during the heating stage (\(t \le 50\) s), at the point A, the function \(D_{2}T\) tends to a minimum and then reaches its maximum value after 115 s. Temperature changes at the points B and C are similar, but the minimum and maximum values are lower and appear later. It should be noted that the maximum temperature change in the whole domain due to the perturbation of relaxation time \(\tau _{q}\) is less than \(1.67~ ^{\circ }\hbox {C}\), while the temperature change due to the perturbation of thermalization time \(\tau _{T}\) is less than \(1.28^{\circ }\hbox {C}\).

It is also possible to estimate the changes of temperature due to the simultaneous perturbations of two parameters, namely

$$\begin{aligned} \text{ D }T=\sqrt{\left( {U\Delta {\tau }_{q} } \right) ^{2}+\left( {W\Delta {\tau }_{q} } \right) ^{2}} \end{aligned}$$
(51)

In Fig. 8 the courses of function DT at the points A, B and C are shown. As can be seen, the maximum temperature change at the point A is about \(0.95 ~^{\circ } \hbox {C}\).

Fig. 8
figure 8

Courses of function DT at the selected points (\(q_{0}= 15{,}000\,\hbox {W/m}^{2}\), \(t_{\mathrm {e}} = 100\) s)

Full size image

The computations were repeated for \(q_{0}= 30{,}000\,\hbox {W/m}^{2}\), \(t_{\mathrm {e}} = 100\) s and \(q_{0}= 30{,}000\,\hbox {W/m}^{2}\), \(t_{\mathrm {e}} = 50\) s, respectively (c.f. boundary condition (19)). In Figs. 9 and 10 the changes of temperature due to the simultaneous perturbations of relaxation time and thermalization time (Eq. (51)) are presented. As shown in Fig. 9, for larger value of boundary heat flux, the changes in temperature are also larger. For example, the maximum temperature change at the point A is about \(1.9 ~^{\circ } \hbox {C}\). Moreover, for a shorter exposure time (Fig. 10) these differences are even larger and the maximum temperature change at point A is about 2.1 \(^{\circ } \hbox {C}\).

Fig. 9
figure 9

Courses of function DT at the selected points (\(q_{0}= 30{,}000\,\hbox {W/m}^{2}\), \(t_{\mathrm {e}} = 100\) s)

Full size image
Fig. 10
figure 10

Courses of function DT at the selected points (\(q_{0}= 30{,}000\,\hbox {W/m}^{2}\), \(t_{\mathrm {e}} = 50\) s)

Full size image

6 Conclusions

The tissue heating process described by the dual-phase lag equation supplemented with appropriate boundary-initial conditions has been considered. Sensitivity analysis with respect to delay times has been done. To solve the basic problem and additional ones the implicit scheme of the finite difference method has been used.

First, the influence of a single parameter on the changes in tissue temperature was examined. It turned out that slightly larger changes in temperature are observed in the case of disturbed relaxation time than in the case of disturbed thermalization time. Then, the changes in temperature caused by simultaneous perturbation of both parameters were analyzed. These changes depend on the value of the external heat flux and the exposure time. It turned out that the higher the value of the external heat flux and the shorter the exposure time, the larger the temperature changes, the detail can be found in the previous sub-chapter.

It would seem that the temperature changes are relatively small. However, it should be remembered that in artificial hyperthermia treatments, which consists in increasing the temperature of the diseased tissues to 44–\(45 ~^{\circ }\hbox {C}\), the difference of \(2^{\circ }\hbox {C}\) is very significant.