Extended micropolar approach within the framework of 3M theories and variations thereof

Abstract

As part of his groundbreaking work on generalized continuum mechanics, Eringen proposed what he called 3M theories, namely the concept of micromorphic, microstretch, and micropolar materials modeling. The micromorphic approach provides the most general framework for a continuum with translational and (internal) rotational degrees of freedom (DOF), whilst the rotational DOFs of micromorphic and micropolar continua are subjected to more and more constraints. More recently, an “extended” micropolar theory has been presented by one of the authors: Eringen’s 3M theories were children of solid mechanics based on the concept of the indestructible material particle. Extended micropolar theory was formulated both ways for material systems as well as in spatial description, which is useful when describing fluid matter. The latter opens the possibility to model situations and materials with a continuum point that on the microscale consists no longer of the same elementary units during a physical process. The difference culminates in an equation for the microinertia tensor, which is no longer a kinematic identity. Rather it contains a new continuum field, namely an independent production term and, consequently, establishes a new constitutive quantity. This makes it possible to describe processes of structural change, which are difficult if not impossible to be captured within the material particle model. This paper compares the various theories and points out their communalities as well as their differences.

1 The need for more sophisticated continuum approaches

The term Generalized Continuum Theories (GCTs) was coined by Eringen and Maugin, see discussions in [22, 23], in order to emphasize the need for a mathematical framework capable of describing the physical behavior of matter with an inner structure, i.e., internal length scales. Traditional continuum mechanics concepts, such as (linear) elasticity or (visco-) plasticity theory, do not contain internal length scale parameters. They are suitable for many macroscopic engineering constructions. However, if the engineering structures become smaller, or if the considered materials are more sophisticated than traditional polycrystalline metals or ceramics, the inherent inner length scale cannot be ignored in a more realistic modeling of the deformation behavior.

Without going into the mathematical details at this point, the following GCTs should be mentioned: (a) the micromorphic, microstretch and micropolar approaches, essentially developed by the school of Eringen [12,13,14], for which he coined the term 3M theories; (b) the liquid crystal director theory developed by Ericksen and Leslie, see [34, 35, 40]; (c) non-local and, in particular, higher gradient theories [2, 15]. In this review article, we will focus on an in-depth discussion of 3M theories and compare them with the recently presented “Extended” Micropolar Theory (EMT). As we shall see, the latter is based on the concept of spatial description and emphasizes the need for a true balance of the microinertia tensor. The differences of this concept to the 3M theories will be discussed in detail. Moreover, in context with the notion of directors, some comparison will also be made to (b).

More specifically the review is organized as follows. We will first outline the kinematics of the 3M theories and dwell upon some of their deficiencies, in a particular in context with the microstretch formulation. The kinematics of extended micropolar theory will essentially be identical to the corresponding 3M version. In this context, we will also present the concept of directors required to described the internal rotational degree of freedom of the continuum point. This will then be followed by the introduction of all relevant continuum fields of 3M and extended micropolar theory. Here the differences between the 3M and the extended approach will become obvious when we compare the situation for material particles and the (open) Representative Volume Element (RVE) used in spatial description. The following sections are dedicated to the continuum balances of 3M and extended theories. In context with the latter, we will again emphasize the concept of spatial description. Another focus of attention will be the balance for the microinertia tensor.

At this point, it seems justified to state our main theses, which will be supported in what follows:

• 3M theories and EMT both introduce a continuum “point” with an intrinsic substructure. This substructure is used to model more complex materials with additional kinematic degrees of freedom, specifically rotational ones.

• 3M theories use a continuous description for this substructure from the very beginning on, whereas EMT is based on homogenization of properties of discrete elementary particles and then arrives at a continuum formulation. Moreover, there is some precedent work similar to Eringen’s 3M theories, which use a discrete approach, primarily [31] and [36] but also more recently [4, 5, 30, 32, 33] and the references cited therein.

• 3M theories are based on the concept of a material particle, which is a closed indestructible system. They are theories in the spirit of solid mechanics. EMT uses the concept of an open representative volume element containing matter. It is a theory emphasizing the needs of fluid mechanics.

• The rate equation for the microinertia tensor of 3M theories is an identity although in later work, as we shall discuss, efforts have been made by Eringen to complement it by a production term. Eringen explicitly refers to the microinertia and to its rate equation as conserved quantity and conservation law, respectively, and compares it to mass. In contrast to that, microinertia in EMT is definitely not conserved and contains a production term. Hence, it introduces a new constitutive quantity, which can be used to model processes of structural change not covered by 3M theories.

2 Kinematics of 3M theories

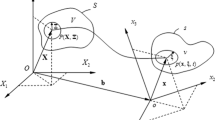
Consider the situation shown in Fig. 1.¹ Eringen considers in [12] a microelement P, which is the continuum point on the macrolevel, with a substructure. For Eringen the continuum point is a material point. Hence, following the concepts established in ordinary continuum mechanics of solids, he considers a micromotion between material subpoints within this material element: He determines the distance vector from the center of mass c to an arbitrary neighboring point $c'$ within the current configuration by the vector $\varvec{\xi }$, and in the reference configuration by the vector $\varvec{\varXi }$, as shown. Both are linked by a mapping $\varvec{\chi }$, the so-called micromotion, as follows:²

$$\begin{aligned} \varvec{\xi }=\varvec{\chi }\cdot \varvec{\varXi }\quad \Leftrightarrow \quad \xi _{k}=\chi _{kM}\varXi _{M}. \end{aligned}$$

(2.1)

hereinafter “$\cdot$” stands for the dot product.

Fig. 1

Micromotion in 3M theory

Therefore, recalling the concepts of ordinary continuum theory, $\varvec{\chi }$ is the equivalent of the deformation gradient tensor $\varvec{F}$ on the microlevel. Eringen refers to it as the microdeformation tensor. $\varvec{\xi }$ is called relative position of microelements within a macroelement (or material point) on the macro- or continuum scale in the current configuration. Its components refer to the Cartesian base $\varvec{i}_k$ of the reference configuration, $\varvec{\xi }=\xi _k\varvec{i}_k$, whereas its counterpart $\varvec{\varXi }$ in the reference configuration is decomposed with respect to a Cartesian base $\varvec{I}_M$ characteristic of the reference placement, so that $\varvec{\varXi }=\varXi _M\varvec{I}_M$. Capital letters are used to characterize this fact. Hence,

$$\begin{aligned} \varvec{\chi }=\chi _{kM}\varvec{i}_k\otimes \varvec{I}_M\quad \mathrm {where}\quad \chi _{kM}=\frac{\partial \xi _k}{\partial \varXi _M}, \end{aligned}$$

(2.2)

which clearly shows that $\varvec{\chi }$ (just like $\varvec{F}$) has one “leg” in the current and the other one in the reference configuration. It also indicates that due to the physical meaning of $\varvec{\xi }$ and $\varvec{\varXi }$, it is a materially based quantity and that the development of 3M theories has its origin in the continuum mechanics of solids. Here “$\otimes$” is the dyadic product.

Another important kinematic quantity in 3M theories is the microgyration tensor [12, p. 24]:

$$\begin{aligned} \varvec{\nu }=\dot{\varvec{\chi }}\cdot \varvec{\chi }^{-1}\quad \Leftrightarrow \quad \nu _{kl} ={\dot{\chi }}_{kM}\chi _{Ml}^{-1}. \end{aligned}$$

(2.3)

It should be emphasized that the dot in this equation stands for a material time derivative in material description (see [18]) of the material field $\varvec{\chi }$:

$$\begin{aligned} \dot{\left( \cdot \right) }\equiv \frac{\mathrm d (\cdot )}{\mathrm dt}=\frac{\partial (\cdot )}{\partial t}+\varvec{v}\cdot \nabla (\cdot ), \end{aligned}$$

(2.4)

where $\varvec{v}$ is the velocity of a material point and the partial derivatives refer to its time and position. Suffice it to say that the partial time derivative is executed at a fixed current position of the material point (the position of its motion or “motion” for short, see [37, p. 6]) and the nabla is w.r.t. that position at a fixed point in time. All the fields $\left( \cdot \right)$ to be differentiated are expressed as functions of the motion of the material point and of time.

Moreover, it is now simple to prove the following equation for the material time derivative in material description of relative position vector between microelements in the current configuration:

$$\begin{aligned} \dot{\varvec{\xi }}=\varvec{\nu }\cdot \varvec{\xi }\quad \Leftrightarrow \quad {\dot{\xi }}_k=\nu _{kl}\xi _l. \end{aligned}$$

(2.5)

Indeed, from (2.1) and (2.3), we have the identities

$$\begin{aligned} \dot{\varvec{\xi }}=\dot{\varvec{\chi }}\cdot \varvec{\varXi }=\left( \dot{\varvec{\chi }}\cdot \varvec{\chi }^{-1}\right) \cdot \left( \varvec{\chi }\cdot \varvec{\varXi }\right) =\varvec{\nu }\cdot \varvec{\xi }. \end{aligned}$$

In general, the micromotion tensor obeys a polar decomposition theorem,

$$\begin{aligned} \varvec{\chi }=\varvec{V}\cdot \varvec{R}, \end{aligned}$$

(2.6)

where $\varvec{V}$ is a stretch tensor and $\varvec{R}$ characterizes a rotation, such that $\varvec{R}\cdot \varvec{R}^\intercal =\varvec{1}=\varvec{R}^\intercal \cdot \varvec{R}$, $\varvec{1}$ is the unit tensor. Then, clearly, $\varvec{\nu }$ does not have the properties expected from a true spin (or angular velocity) tensor: It is not antisymmetric and cannot be mapped onto an axial angular velocity vector, in general.

The situation changes if we switch to microstretch continua, in the case of which the stretch tensor has a special form, namely $\varvec{V}=\alpha \varvec{1}$. The scalar stretch factor $\alpha$ is also a material field, dependent on space and time. Hence, the microgyration tensor becomes in this case:

$$\begin{aligned} \varvec{\nu }=\frac{{\dot{\alpha }}}{\alpha }\varvec{1}+\varvec{\dot{R}}\cdot \varvec{R}^\intercal \equiv \frac{{\dot{\alpha }}}{\alpha }\varvec{1}+\varvec{\omega }\times \varvec{1}, \end{aligned}$$

(2.7)

where $\times$ denotes the cross-product. So the conversion of the entity $\varvec{\dot{R}}\cdot \varvec{R}^\intercal$ to the axial angular velocity vector $\varvec{\omega }$ becomes possible, because it is antisymmetric. We may therefore decompose the microgyration tensor for microstretch materials as follows:

$$\begin{aligned} \varvec{\nu }=\tfrac{1}{3}\nu _0\varvec{1}+\varvec{\omega }\times \varvec{1}\,,\,\,\nu _0={{\,\mathrm{\textsf {Tr}}\,}}\varvec{\nu }=3\nicefrac {{\dot{\alpha }}}{\alpha }\quad \Leftrightarrow \quad \nu _{kl}=\tfrac{1}{3}\nu _0\delta _{kl}-\varepsilon _{klr}\omega _r\,,\,\,\nu _0=\nu _{pp}, \end{aligned}$$

(2.8)

$\epsilon _{ijk}$ being the Levi–Civita symbol and ${{\,\mathrm{\textsf {Tr}}\,}}$ is the trace operator.

It must be pointed out that the derivation of this relation in [12] on pp. 26-27 contains typographical errors. The starting point of the confusion is Eringen’s definition of microstretch materials through the relation

$$\begin{aligned} \varvec{\chi }^{-1}=\frac{1}{j^2}\varvec{\chi }^\intercal \quad \Leftrightarrow \quad \chi ^{-1}_{Ml}=\frac{1}{j^2}\chi _{lM}\,,\,\,j=\det \varvec{\chi }. \end{aligned}$$

(2.9)

Note that if we take the determinant on both sides of the equation, we obtain the obviously incorrect result $\nicefrac {1}{j}=\nicefrac {1}{j^5}$. This definition of a microstretch material is not permissible and should be replaced by the requirement $\varvec{V}=\alpha \varvec{1}$ and the following chain of arguments shown in (2.7). Instead of (2.9) one should use another formula

$$\begin{aligned} \varvec{\chi }^{-1}=\frac{1}{j^{2/3}}\varvec{\chi }^\intercal . \end{aligned}$$

Nevertheless, to pinpoint down further errors, we now briefly outline Eringen’s line of arguments. For the material time derivative of the determinant j, the following relation is noted by him, which is valid for micromorphic materials,

$$\begin{aligned} \frac{\mathrm dj}{\mathrm dt}= \nu _0 j. \end{aligned}$$

(2.10)

This is the analogue to the following relation known from traditional continuum mechanics that involves the deformation gradient $\varvec{F}$ and its determinant $J=\det \varvec{F}$:

$$\begin{aligned} \frac{\mathrm dJ}{\mathrm dt}= \dot{F}_{iK}F^{-1}_{Ki} J. \end{aligned}$$

(2.11)

Moreover, Eringen defines the following tensor $\bar{\varvec{\chi }}$:

$$\begin{aligned} \bar{\varvec{\chi }}=\frac{\varvec{\chi }}{j}, \end{aligned}$$

(2.12)

which due to (2.9) is orthogonal:

$$\begin{aligned} \bar{\varvec{\chi }}\cdot \bar{\varvec{\chi }}^\intercal =\varvec{\chi }\cdot \frac{\varvec{\chi }^\intercal }{j^2}\equiv \varvec{\chi }\cdot \varvec{\chi }^{-1}=\varvec{1}. \end{aligned}$$

(2.13)

Hence, the following chain of equations holds for microstretch materials according to the definition (2.9):

$$\begin{aligned} \varvec{\nu }=\dot{\varvec{\chi }}\cdot \varvec{\chi }^{-1}=\frac{\dot{\varvec{\chi }}}{j} \cdot \frac{\varvec{\chi }^\intercal }{j}=\dot{\bar{\varvec{\chi }}}\cdot \bar{\varvec{\chi }}^\intercal +\bar{\varvec{\chi }}\cdot \bar{\varvec{\chi }}^\intercal \frac{1}{j}\frac{\mathrm dj}{\mathrm dt}\equiv \bar{\varvec{\nu }}+\nu _0\varvec{1}. \end{aligned}$$

(2.14)

The tensor $\bar{\varvec{\nu }}$ is antisymmetric; hence, it can be replaced by an axial vector, $\bar{\varvec{\nu }}=\varvec{\omega }\times \varvec{1}$, and we finally obtain:

$$\begin{aligned} \varvec{\nu }=\nu _0\varvec{1}+\varvec{\omega }\times \varvec{1}. \end{aligned}$$

(2.15)

In comparison with the (correct) result (2.8), we see that a factor $\nicefrac {1}{3}$ is missing. However, it is included in Eringen’s final equation (1.8.32), where he uses the symbol $\nu$ in front of the spherical term of the decomposition of the microgyration tensor.

The transition from microstretch to micropolar materials is simple. Micropolar materials have no stretch tensor, hence $\alpha =1$ or $\nu _0=0$. The microgyration tensor for micropolar materials therefore reads:

$$\begin{aligned} \varvec{\nu }=\varvec{\omega }\times \varvec{1}\quad \Leftrightarrow \quad \nu _{kl}=-\varepsilon _{klr}\omega _r\qquad \mathrm {or} \qquad \varvec{\omega }=-\tfrac{1}{2}\varvec{\nu }_\times \quad \Leftrightarrow \quad \omega _r =-\tfrac{1}{2}\varepsilon _{rkl}\nu _{kl}, \end{aligned}$$

(2.16)

where the Gibbsian cross has been used, $\left( \varvec{a}\otimes \varvec{b}\right) _\times =\varvec{a}\times \varvec{b}$.

In context with the kinematics of 3M media the concept of so-called directors has proven to be quite valuable. In the theory of micropolar media, e.g., [7], they are frequently introduced formally as an orthonormal tripod, $\varvec{d}_k$, $k=1, 2, 3$, used to describe the rigid body rotation of a material particle with additional intrinsic rotational degrees of freedom. This notion needs to be generalized for 3M media. In [12] Eringen uses the microdeformation tensor $\varvec{\chi }$ to define three non-orthonormal director vectors in the current configuration as follows:

$$\begin{aligned} \varvec{d}_M=\varvec{\chi }\cdot \varvec{I}_M\quad \Leftrightarrow \quad \varvec{d}_M=\chi _{kM}\varvec{i}_k. \end{aligned}$$

(2.17)

Note that these directors are not formally introduced quantities. Rather they are physics-based and linked to matter in view of the original relation (2.1). In fact, by comparison of Eqs. (2.1) and (2.17), we conclude that the directors $\varvec{I}_M$, $M=1,2,3$, of the reference configuration are pointing in the direction of three orthogonal, relative position vectors $\varvec{\varXi }_M=\left| \varvec{\varXi }_{{{\underline{M}}}}\right| \varvec{I}_{{{\underline{M}}}}$³ based in the center of mass of the material point (no summation over M here). They form an orthonormal tripod attached to the center of mass. These unit vectors change their length and their orientation w.r.t. each other when moving into the current configuration of the material point to become $\varvec{d}_M$. However, the directors $\varvec{d}_M$ of the current configuration are still attached to the center of mass of the material point. The directors $\varvec{I}_M$ obviously span a unit size microvolume, whereas the current microvolume, v, is given by:

$$\begin{aligned} v=\varvec{d}_1\cdot \left( \varvec{d}_2\times \varvec{d}_3\right) =\varepsilon _{klm}d_{1k}d_{2l}d_{3m}\equiv j\ne 1. \end{aligned}$$

(2.18)

Hence, the microvolume is not conserved for micromorphic materials. Note that for micromorphic materials we have because of (2.10):

$$\begin{aligned} v(t)=v(0)\exp \left( \nu _0t\right) \,,\,\,\nu _0=\nu _{pp}={\dot{\chi }}_{pM} \chi ^{-1}_{Mp}\,,\,\,v(0)=1. \end{aligned}$$

(2.19)

Consequently, the conclusion that the microvolume is not conserved stays valid for microstretch materials. However, for micropolar materials $\nu _0=0$ and therefore their corresponding initial microvolume of unit size is preserved.

Next we investigate the current lengths of the directors (2.17). If we choose $M=1$ as an example, we obtain for micromorphic materials:

$$\begin{aligned} \varvec{d}_1\cdot \varvec{d}_1=d_{1k}d_{1k}\ne 1. \end{aligned}$$

(2.20)

Recall that the length of the corresponding reference director $\varvec{I}_1$ was one. As expected, the length will change because in general there is a complex deformation on the microlevel. In the case of microstretch material, we can be more specific. We consider the time derivative of the square of length of $\varvec{d}_1$, observe Eqs. (2.5) and (2.8) and obtain:

$$\begin{aligned} \dot{\varvec{d}}_1=\tfrac{1}{3}\nu _0\varvec{d}_1+\varvec{\omega }\times \varvec{d}_1\quad \Rightarrow \quad \frac{\mathrm d}{\mathrm dt}\left( \varvec{d}_1\cdot \varvec{d}_1\right) =\tfrac{1}{3}\nu _0\varvec{d}_1\cdot \varvec{d}_1. \end{aligned}$$

(2.21)

Hence,

$$\begin{aligned} l_1(t)=l_1(0)\exp \left( \tfrac{1}{3}\nu _0t\right) \equiv \exp \left( \tfrac{1}{3} \nu _0t\right) \,,\,\,l_1(t)=\left| \varvec{d}_1\right| . \end{aligned}$$

(2.22)

The same relation holds for the lengths $l_{2,3}$ of the two other directors. We shall see shortly that for microstretch materials the directors $\varvec{d}_M$, $M=1,2,3$ are perpendicular to each other. Hence, the volume v(t) spanned by them is simply $v(t)=l_1l_2l_3=\exp (\nu _0t)$, because the length of the directors in the reference configuration is $l_i(0)=1$, and this is consistent with our previous result (2.19).

It was mentioned already that the directors of micromorphic materials are not normal to each other. This can also be shown formally. Consider, for example, $\varvec{\chi }_1$ and $\varvec{\chi }_2$ to find:

$$\begin{aligned} \varvec{d}_1\cdot \varvec{d}_2=d_{1k}d_{2k}\ne 0. \end{aligned}$$

(2.23)

However, the directors of microstretch materials are perpendicular to each other. In other words, they keep the $90^\circ$ angle of the directors of the reference configuration. To show this, we analyze the following time derivative and observe the decomposition (2.8):

$$\begin{aligned} \frac{\mathrm d}{\mathrm dt}\left( \varvec{d}_1\cdot \varvec{d}_2\right) =\tfrac{2}{3}\nu _0\varvec{d}_1\cdot \varvec{d}_{2}. \end{aligned}$$

(2.24)

If we use Eq. (2.22), the following relation for the angle $\beta _{12}$ between the two directors is obtained:

$$\begin{aligned} \frac{\mathrm d}{\mathrm dt}\cos \beta _{12}=\tfrac{1}{3}\nu _0\cos \beta _{12}\quad \Rightarrow \quad \cos \beta _{12}(t)=\cos \beta _{12}(0)\exp \left( \tfrac{1}{3}\nu _0t\right) =0, \end{aligned}$$

(2.25)

because $\cos \beta _{12}(0)=0$. Clearly, micropolar directors also stay perpendicular.

In summary, the directors of micromorphic materials undergo a complex coupled 3D deformation and rotation on the microscale. They do not keep their original microvolume of unit size. The directors of microstretch materials stay perpendicular, their lengths change equally, the microvolume they encompass changes accordingly, and they perform a rigid body rotation. Finally, the directors of micropolar materials do not change their lengths, they keep their original unit microvolume, and they perform a rigid body rotation.

At the end of this section is instructive to establish links to quantities known from ordinary continuum mechanics. For instance, the equivalent of the mapping $\varvec{\chi }$ is the deformation gradient $\varvec{F}$. The microgyration tensor $\varvec{\nu }$ corresponds to the velocity gradient,

$$\begin{aligned} (\nabla \otimes \varvec{v})^\intercal =\dot{\varvec{F}}\cdot \varvec{F}^{-1}\quad \Leftrightarrow \quad \frac{\partial v_k}{\partial x_l}=\dot{F}_{kM}F^{-1}_{Ml}. \end{aligned}$$

(2.26)

In fact, the dimensions of the velocity gradient and the microgyration are the same. Moreover, as a tensor of second rank, the velocity gradient can be decomposed into a symmetric and into an antisymmetric part. The latter can be mapped onto an axial vector, the vorticity. Its corresponding quantity on the microlevel is the angular velocity vector. It is so-to-speak the “vorticity we cannot see.” The symmetric part of the velocity gradient can be decomposed into a spherical and a deviatoric tensor. The spherical part, or explicitly $\nabla \cdot \varvec{v}$, determines the compressibility of the material. The corresponding quantity on the microlevel is $\nu _0$.

3 Kinematics of EMT

In [20], which introduces EMT, the kinematics of a micropolar continuum is first presented in material description. In this context, two sets of orthonormal tripod directors are introduced, one for the current configuration, $\varvec{d}_k$, and one for the reference placement, $\varvec{D}_k$, $k=1,2,3$. These vectors appear formally in order to characterize the intrinsic rotational degree of freedom of the material point. Using the nomenclature of this paper, both are related by the microdeformation tensor $\varvec{\chi }$ according to

$$\begin{aligned} \varvec{d}_k=\varvec{\chi }\cdot \varvec{D}_k. \end{aligned}$$

(3.1)

This formula bears a certain similarity to Eq. (2.17). However, here the microdeformation tensor $\varvec{\chi }$ is an orthogonal tensor $\varvec{\chi }\equiv \varvec{Q}$ with $\varvec{Q}\cdot \varvec{Q}^\intercal =\varvec{1}=\varvec{Q}^\intercal \cdot \varvec{Q}$. Hence, its time derivative can be mapped onto an axial vector, the angular velocity vector $\varvec{\omega }$, by means of the so-called Poisson relation,

$$\begin{aligned} \frac{\mathrm d\varvec{Q}}{\mathrm dt}=\varvec{\omega }\times \varvec{Q}\quad \Leftrightarrow \quad \dot{\varvec{Q}}\cdot \varvec{Q}^\intercal =\varvec{\omega }\times \varvec{1}. \end{aligned}$$

(3.2)

This is in agreement with Eq. (2.16) of the micropolar medium of 3M theory.

Things become more complex when we start looking at micropolar media from the spatial point of view. As we shall learn in Sect. 5, the continuum field $\varvec{\omega }$ is still a kinematic quantity on the continuum level characterizing the intrinsic rotational degree of freedom of the matter passing through an RVE. However, unlike the $\varvec{\omega }$ from (2.8), it is introduced by a homogenization process from the inertial characteristics and the angular velocities of the elementary particles within the RVE at that time, Eq. (5.16). Nevertheless, it is still possible to write down an equation similar to (3.2)$_1$, namely

$$\begin{aligned} \frac{\updelta \varvec{Q}}{\updelta t}=\varvec{\omega }\times \varvec{Q}, \end{aligned}$$

(3.3)

but this time derivative is the material time derivative in spatial description:

$$\begin{aligned} \frac{\updelta (\cdot )}{\updelta t}=\frac{\mathrm d (\cdot )}{\mathrm dt}+(\varvec{v}-\varvec{w})\cdot \nabla (\cdot ). \end{aligned}$$

(3.4)

The symbol $\varvec{w}$ stands for the velocity of the RVE grit, if we allow it to move. The geometric center $\varvec{x}$ of an RVE is also referred to as the “observational point.” Hence, $\varvec{w}$ is its velocity. Note that this is a “mathematical” velocity used for convenience during calculations, for example for active grit manipulations. It is zero if a static grit is used. $\varvec{v}$ is the velocity field vector of the matter passing through an RVE at time t. We will define it in (5.7) and (5.8) in terms of the inertial characteristics and the velocities of the elementary particles within the RVE. The nabla operator is the spatial gradient operation w.r.t. the RVE’s geometrical center $\varvec{x}$. Finally, the operation $\nicefrac {\mathrm d (\cdot )}{\mathrm dt}$ is a total derivative, namely

$$\begin{aligned} \frac{\mathrm d (\cdot )}{\mathrm dt}=\frac{\partial (\cdot )}{\partial t}+\frac{\mathrm d\varvec{x}}{\mathrm dt}\cdot \nabla (\cdot )\equiv \frac{\partial (\cdot )}{\partial t}+\varvec{w}\cdot \nabla (\cdot ). \end{aligned}$$

(3.5)

In contrast to that the material derivative in material description shown in Eq. (2.4) is simply a total time derivative. It should also be pointed out that all fields $(\cdot )$ are in spatial notation, this means they depend of the location of the geometric center $\varvec{x}$ of the RVE and of time t. Consequently, the partial derivative w.r.t. time is at a fixed position $\varvec{x}$ of an RVE. If (3.5) is now inserted into (3.4), we obtain the following relation which regarding the symbols looks the same as Eq. (2.4); however, their meaning is completely different:⁴

$$\begin{aligned} \frac{\updelta (\cdot )}{\updelta t}=\frac{\partial (\cdot )}{\partial t}+\varvec{v}\cdot \nabla (\cdot ). \end{aligned}$$

(3.6)

It is for this reason that the notation ‘$\updelta$’ is used whenever the material derivative in spatial description is meant. It also explains the meaning of the left-hand side of Eq. (3.3). Its interpretation is as follows: Unlike the relation (3.2) for a material particle, it does not define the axial angular momentum vector $\varvec{\omega }$ as a replacement of the combination $\dot{\varvec{Q}}\cdot \varvec{Q}^\intercal$. In spatial description, there is actually a need to use this relation as an additional equation, because in context with constitutive equations this quantity becomes an additional state variable (see [20], Sect. 5 for a discussion). Moreover, the Poisson relation (3.3) is helpful to derive and motivate the balance for the microinertia tensor.

Next we discuss a rational method of how to introduce directors in spatial description. The starting point is the microinertia tensor field $\varvec{j}$ introduced by homogenization of the inertial properties of the particles within the RVE in Eq. (5.11) and (5.12). It is a symmetric tensor of second rank, and as such a system of three orthonormal eigenvectors $\varvec{e}'_i$, $i=1,2,3$ can be found with respect to which the tensor assumes a diagonal form, $\varvec{j}=j'_{11}\varvec{e}'_1\otimes \varvec{e}'_1+j'_{22}\varvec{e}'_2\otimes \varvec{e}'_2+j'_{33}\varvec{e}'_3\otimes \varvec{e}'_3$. These eigenvectors can be used as an orthonormal director tripod, which performs a rigid body rotation:

$$\begin{aligned} \frac{\updelta \varvec{e}'_i}{\updelta t}=\varvec{\omega }\times \varvec{e}'_i. \end{aligned}$$

(3.7)

Note that unlike the directors from Eq. (2.17), if specialized to microstretch materials, they keep their unit length. However, what changes in time are the eigenvalues $j'_{{\underline{i}}\,{\underline{i}}}$.

It is interesting to note that the concepts of a director in the liquid crystal theory proposed by Ericksen and Leslie are closely linked to microinertia as well, even though this is not explicitly said so. On a microlevel, their elementary particles are rigid digits, [8], Sect. 2. Their average orientation is characterized by a so-called director, which is of unit length and capable of rotation. In fact its movement is controlled by a director balance, [21], Section A, which is linked to the intrinsic moment of momentum. Müller makes this more explicit in [25] and explicitly derives this balance from first principles based on an expression for the inertia tensor of a rigid digit. However, it is fair to say that transition from elementary particles to a continuum field by homogenization remains rather sketchy. In [11] Eringen attempts to relate his micropolar theory concept to the director approach of Ericksen and Leslie. In particular he relates the microinertia tensor $\varvec{j}$ to that of a rigid rod, with the director being its main axis. Finally, it is remarkable that Ericksen and Leslie base their fluid theory on the idea of a material particle, which is mentioned many times in the provided references and many others of their work. Their formulation is not truly in spatial description.

4 Continuum fields of 3M theories

Consider the situation shown in Fig. 2. The bubble represents a material particle undergoing a deformation process. In other words, this is the continuum “point” of 3M theories. The particle has a substructure characterized by an intrinsic mass density $\rho '$.

Fig. 2

Microvolume element in 3M theory

The mass of the material point $\mathrm \varDelta m$ is by definition conserved during the motion. It can be used to define the continuum density $\rho (\varvec{x},t)$ in the current configuration by:

$$\begin{aligned} \mathrm \varDelta m=\rho \mathrm \varDelta v=\int \limits _{\mathrm \varDelta v}\rho '\mathrm dv'\quad \Rightarrow \quad \rho (\varvec{x},t)=\frac{1}{\mathrm \varDelta v}\int \limits _{\mathrm \varDelta v}\rho '\mathrm dv'. \end{aligned}$$

(4.1)

The density within the material particle or microelement can be a function of position and time, $\rho '=\rho '(\varvec{x}',t)$.

In order to define the translational velocity $\varvec{v}(\varvec{x},t)$ at the continuum level consider first the location vector $\varvec{x}^{\mathrm c}$ of the center of mass for the material point. By using the symbols of Fig. 2, we find:

$$\begin{aligned} \rho \varvec{x}^{\mathrm c}\mathrm \varDelta v=\int \limits _{\mathrm \varDelta v}\rho '\varvec{x}'\mathrm dv'=\int \limits _{\mathrm \varDelta v}\rho '\left( \varvec{x}^{\mathrm c}+\varvec{\xi }\right) \mathrm dv'\quad \Rightarrow \quad \int \limits _{\mathrm \varDelta v}\rho '\varvec{\xi }\mathrm dv'=\varvec{0}. \end{aligned}$$

(4.2)

This, in fact, is nothing but the definition of the center of mass, such that the first moment of the mass density vanishes.

We now rewrite the expression for the total linear momentum $\mathrm \varDelta \varvec{p}$ contained in the material point:

$$\begin{aligned} \mathrm \varDelta \varvec{p}=\rho \varvec{v}\mathrm \varDelta v=\int \limits _{\mathrm \varDelta v}\rho '{\dot{\varvec{x}}}'\mathrm dv'=\rho \dot{\varvec{x}}^{\mathrm c}\mathrm \varDelta v+\int \limits _{\mathrm \varDelta v}\rho '{\dot{\varvec{\xi }}}\mathrm dv'=\rho \dot{\varvec{x}}^{\mathrm c}\mathrm \varDelta v+\varvec{\nu }\cdot \int \limits _{\mathrm \varDelta v}\rho '\varvec{\xi }\mathrm dv'\equiv \rho \dot{\varvec{x}}^{\mathrm c}\mathrm \varDelta v+\varvec{0}, \end{aligned}$$

(4.3)

where we have made use of (2.5). The dots on the various position or distance related vectors refer to material time derivatives in material description, see Eq. (2.4). Hence, we conclude that in 3M theories the continuum velocity is, in the end by definition, the velocity of the center of mass of the material point carrying a substructure, $\varvec{v}\equiv \dot{\varvec{x}}^{\mathrm c}$.

Following up on the vanishing first moment of intrinsic mass density of (4.2), 3M theories introduce a microinertia tensor $\varvec{i}$ in the current configuration as its non-vanishing second moment ( [12, p. 31]):

$$\begin{aligned} \rho \varvec{i}\mathrm \varDelta v=\int \limits _{\mathrm \varDelta v}\rho '\varvec{\xi }\otimes \varvec{\xi }\mathrm dv'. \end{aligned}$$

(4.4)

However, this expression does not have the mathematical structure of the inertia tensor $\varvec{j}$ commonly known in rigid body mechanics, which should be ( [17, p. 194]):

$$\begin{aligned} \rho \varvec{j}\mathrm \varDelta v=\int \limits _{\mathrm \varDelta v}\rho '\left( \varvec{\xi }\cdot \varvec{\xi }\,\varvec{1}-\varvec{\xi }\otimes \varvec{\xi }\right) \mathrm dv'. \end{aligned}$$

(4.5)

Both quantities are related by

$$\begin{aligned} \varvec{j}=i_0\varvec{1}-\varvec{i}\,,\,\,i_0={{\,\mathrm{\textsf {Tr}}\,}}\varvec{i}\,,\,\,\varvec{i}=\tfrac{1}{2}j_0\varvec{1}-\varvec{j}\,,\,\,j_0={{\,\mathrm{\textsf {Tr}}\,}}\varvec{j}. \end{aligned}$$

(4.6)

The specific kinetic energy K contained in the continuum point is given by:

$$\begin{aligned} \rho K\mathrm \varDelta v=\tfrac{1}{2}\int \limits _{\mathrm \varDelta v}\rho '{\dot{\varvec{x}}}'\cdot {\dot{\varvec{x}}}'\mathrm dv'=\tfrac{1}{2}\int \limits _{\mathrm \varDelta v}\rho '\left( \dot{\varvec{x}}^{\mathrm c}+\dot{\varvec{\xi }}\right) \cdot \left( \dot{\varvec{x}}^{\mathrm c}+\dot{\varvec{\xi }}\right) \mathrm dv'=...=\tfrac{1}{2}\rho \left[ \varvec{v}\cdot \varvec{v}+{{\,\mathrm{\textsf {Tr}}\,}}\left( \varvec{\nu }\cdot \varvec{i}\cdot \varvec{\nu }^\intercal \right) \right] \mathrm \varDelta v. \nonumber \\ \end{aligned}$$

(4.7)

Note that the mixed terms disappear, because the center of mass was chosen as the pole.

The algebraic manipulations are fairly similar to those used in (4.3). We conclude that the specific kinetic energy can be additively decomposed into the kinetic energy associated with the center of mass and a rotational part,

$$\begin{aligned} K=\tfrac{1}{2}\left[ \varvec{v}\cdot \varvec{v}+{{\,\mathrm{\textsf {Tr}}\,}}\left( \varvec{\nu }\cdot \varvec{i}\cdot \varvec{\nu }^\intercal \right) \right] =\tfrac{1}{2}\left( v_iv_i+\nu _{mk}i_{kl}\nu _{ml}\right) , \end{aligned}$$

(4.8)

a result that can be found in similar form also in the mechanics of a rigid body. However, there are two crucial differences. In the case of the rigid body the inertia tensor is, first, of the type shown in (4.5) and, second, the angular velocity vector $\varvec{\omega }$ replaces the microgyration tensor. Indeed, only for micromorphic continua the specific kinetic energy has this complicated structure. Because of the decompositions (2.8) and (2.16) of the microgyration tensor, we obtain by observing the general relations between the two microinertia tensors (4.6) from (4.7) for microstretch continua

$$\begin{aligned} K=\tfrac{1}{2}\left( \varvec{v}\cdot \varvec{v}+\tfrac{1}{2}j_0\nu _0^2+\varvec{\omega }\cdot \varvec{j}\cdot \varvec{\omega }\right) \end{aligned}$$

(4.9)

and (as expected) for micropolar media (with rigid directors)

$$\begin{aligned} K=\tfrac{1}{2}\left( \varvec{v}\cdot \varvec{v}+\varvec{\omega }\cdot \varvec{j}\cdot \varvec{\omega }\right) . \end{aligned}$$

(4.10)

Note that the transition from the specific kinetic energy of the microstretch material to the micropolar one is achieved by putting $\nu _0=0$ and not by $j_0=0$.

Moreover, it is known that the moment of momentum, $\int \rho \varvec{x}\times \varvec{v}\,\mathrm d v$, of a rigid body can be additively decomposed into a moment of momentum part w.r.t. the center of mass and a contribution given by the scalar product of the inertia tensor (w.r.t. the center of mass) and its angular velocity, the so-called spin or moment of momentum intrinsic to the material particle. The temporal change of this scalar product is driven by the applied moments. The spin of 3M materials follows similar laws. For example, its temporal change is characterized by a tensorial quantity called the spin inertia, $\varvec{\sigma }$. It is defined as follows ([12, p. 33]):

$$\begin{aligned} \rho \varvec{\sigma }\mathrm \varDelta v=\int \limits _{\mathrm \varDelta v}\rho '{\ddot{\varvec{\xi }}}'\otimes {\varvec{\xi }}'\mathrm dv'. \end{aligned}$$

(4.11)

This definition allows to explain the notion spin inertia. The term ‘spin’ refers to the intrinsic moment of momentum of the material particle represented by $\dot{\varvec{\xi }}=\varvec{\nu }\cdot \varvec{\xi }$, whereas ‘inertia’ refers to the second derivative in time of $\varvec{\xi }$. By using the same algebraic manipulations as in context with (4.3), this expression can be rewritten as:

$$\begin{aligned} \varvec{\sigma }=\left( \dot{\varvec{\nu }}+\varvec{\nu }\cdot \varvec{\nu }\right) \cdot \varvec{i}\quad \Leftrightarrow \quad \sigma _{kl}=\left( {\dot{\nu }}_{km}+\nu _{kn}\nu _{nm}\right) i_{ml}. \end{aligned}$$

(4.12)

Eringen remarks in a footnote in [12] that (in contrast to rigid body mechanics) the spin inertia tensor is not a time-rate. It just has the unit of specific spin per time, which is $\nicefrac {\mathrm m^2}{\mathrm s^2}$. This statement becomes even clearer if we use the conservation law for the microinertia tensor (which will be discussed in detail around Eq. (6.2)) to rewrite the last equation:

$$\begin{aligned} \varvec{\sigma }=\frac{\mathrm d}{\mathrm dt}\left( \varvec{\nu }\cdot \varvec{i}\right) -\varvec{\nu }\cdot \varvec{i}\cdot \varvec{\nu }^\intercal \quad \Leftrightarrow \quad \sigma _{kl}=\frac{\mathrm d}{\mathrm dt}\left( i_{ml}\nu _{km}\right) -i_{mp}\nu _{lp}\nu _{km}. \end{aligned}$$

(4.13)

These complex general formulae for micromorphic continua simplify if we specialize to the two subgroups of 3M theories. In the case of microstretch materials, a more explicit form can be obtained. We insert the corresponding decomposition for the microgyration tensor shown in Eq. (2.8), observe Eq. (4.6) and find:

$$\begin{aligned} \begin{aligned}&\varvec{\sigma }=-\tfrac{1}{3}\left( {\dot{\nu }}_0+\tfrac{1}{3}\nu _0^2-3\varvec{\omega }\cdot \varvec{\omega }\right) \left( \varvec{j}-\tfrac{1}{2}j_0\varvec{1}\right) -\left( \dot{\varvec{\omega }}+\tfrac{2}{3}\nu _0\varvec{\omega }\right) \times \left( \varvec{j}-\tfrac{1}{2}j_0\varvec{1}\right) -\varvec{\omega }\otimes \varvec{\omega }\cdot \left( \varvec{j}-\tfrac{1}{2}j_0\varvec{1}\right) ,\\&\sigma _{kl}=-\tfrac{1}{3}\left( {\dot{\nu }}_0+\tfrac{1}{3}\nu _0^2-3\omega _p \omega _p\right) \left( j_{kl}-\tfrac{1}{2}j_0\delta _{kl}\right) -\varepsilon _{kmr} \left( {\dot{\omega }}_m+\tfrac{2}{3}\nu _0\omega _m\right) \left( j_{rl}- \tfrac{1}{2}j_0\delta _{rl}\right) \\&-\omega _k\omega _m\left( j_{ml}-\tfrac{1}{2}j_0\delta _{ml}\right) . \end{aligned} \end{aligned}$$

(4.14)

This is not Eringen’s formula (1.10.19) in [12] for the microgyration tensor $\varvec{\sigma }$ of microstretch materials yet.⁵ In order to motivate the latter, we argue as follows. Any tensor second rank can be decomposed additively into a symmetric and an antisymmetric part:

$$\begin{aligned} \begin{aligned}&\varvec{\sigma }=\varvec{\sigma }^{\mathrm s}+\varvec{\sigma }^{\mathrm a}\quad \mathrm {with}\\&\varvec{\sigma }^{\mathrm s}=\tfrac{1}{2}\left( \varvec{\sigma }+\varvec{\sigma }^\intercal \right) \,,\,\,\varvec{\sigma }^{\mathrm a}=\tfrac{1}{2}\left( \varvec{\sigma }-\varvec{\sigma }^\intercal \right) \quad \Leftrightarrow \quad \sigma ^{\mathrm s}_{kl}=\tfrac{1}{2}\left( \sigma _{kl}+\sigma _{lk}\right) \,,\,\,\sigma ^{\mathrm a}_{kl}=\tfrac{1}{2}\left( \sigma _{kl}-\sigma _{lk}\right) . \end{aligned} \end{aligned}$$

(4.15)

Moreover, the antisymmetric part can be mapped onto an axial vector, $\mathring{\varvec{s}}$, such that

$$\begin{aligned} \mathring{\varvec{s}}=-\varvec{\sigma }_\times \equiv -\varvec{\sigma }^{\mathrm a}_\times \Leftrightarrow \varvec{\sigma }^{\mathrm a}=\tfrac{1}{2}\mathring{\varvec{s}}\times \varvec{1}\quad \mathrm {or}\quad \mathring{s}_m=-\varepsilon _{mkl}\sigma ^{}_{kl}\equiv -\varepsilon _{mkl}\sigma ^{\mathrm a}_{kl}\Leftrightarrow \sigma ^{\mathrm a}_{kl}=-\tfrac{1}{2}\varepsilon _{klm}\mathring{s}_m. \end{aligned}$$

(4.16)

This decomposition is now applied to the expression (4.14) for the microgyration tensor of a microstretch material and we find:

$$\begin{aligned} \mathring{\varvec{s}}=-\varvec{\sigma }_\times =\varvec{j}\cdot \dot{\varvec{\omega }}+\tfrac{2}{3}\nu _0\varvec{j}\cdot \varvec{\omega }+\varvec{\omega }\times \varvec{j}\cdot \varvec{\omega }\quad \Leftrightarrow \quad \mathring{s}_q=-\varepsilon _{qkl}\sigma _{kl}=j_{ql}{\dot{\omega }}_l+\tfrac{2}{3} \nu _0j_{ql}\omega _l+\varepsilon _{qkm}j_{ml}\omega _k\omega _l,\nonumber \\ \end{aligned}$$

(4.17)

where $\nu _0={{\,\mathrm{\textsf {Tr}}\,}}\varvec{\nu }=\nu _{pp}$.

This is, in fact, Eringen’s formula (1.10.21)$_2$ for the spin vector. It is also the antisymmetric part of his Eq. (1.10.19). In so far agreement has been reached. The expression for the symmetric part in (1.10.19) still needs some explanation. Before we turn to that, we may say that in the case of microstretch materials the spin inertia vector characterizes the rotational movement of the material particle. Note that the circle on $\varvec{s}$ does not automatically imply a time-rate. It was introduced here merely to remind us that this quantity has the unit of a specific spin per time. However, if the conservation of microinertia for microstretch materials is observed (see the discussion in context with Eq. (6.3)), the last relation can be rewritten as follows:

$$\begin{aligned} \mathring{\varvec{s}}=\frac{\mathrm d}{\mathrm d t}\left( \varvec{j}\cdot \varvec{\omega }\right) \quad \Leftrightarrow \quad \mathring{s}_k=\frac{\mathrm d}{\mathrm d t}\left( j_{kl}\omega _l\right) . \end{aligned}$$

(4.18)

This shows that for microstretch materials the spin inertia vector $\mathring{\varvec{s}}$ can surprisingly be written as the time-rate of the spin vector $\varvec{s}=\varvec{j}\cdot \varvec{\omega }$, hence $\mathring{\varvec{s}}\equiv \dot{\varvec{s}}$. This result will allow us later to establish a vectorial form of the balance of internal moment of momentum for microstretch materials, the spin balance or the intrinsic part of Euler’s second law of motion.

Regarding the symmetric part of Eringen’s equation (1.10.19) for the spin inertia, we now note that $\varvec{\sigma }$, being a tensor of second rank, can also be decomposed into a spherical and a deviatoric part. The spherical part, which is given by one third of the trace, characterizes the motion associated with dilatoric (or volumetric) deformation, whereas the deviator accounts for a shape change. In this spirit, Eringen proposes in [12] the following decomposition of the spin inertia for microstretch materials:

$$\begin{aligned} \varvec{\sigma }=\tfrac{1}{3}\sigma _0\varvec{1}+\tfrac{1}{2}\dot{\varvec{s}}\times \varvec{1}\,,\,\,\sigma _0={{\,\mathrm{\textsf {Tr}}\,}}\varvec{\sigma }\quad \Leftrightarrow \quad \sigma _{kl}=\tfrac{1}{3}\sigma _0\delta _{kl}-\tfrac{1}{2}\varepsilon _{klm}\dot{s}_m\,,\,\,\sigma _0=\sigma _{pp}. \end{aligned}$$

(4.19)

We now compare this with Eqs. (4.15) and (4.16) and conclude that the deviatoric part $\varvec{\sigma }$ must be given by its antisymmetric part. However, the spherical part of $\varvec{\sigma }$ is of course not equal to its symmetric part. In other words, the suggested decomposition (4.19) neglects certain symmetric terms that are still contained in (4.14). All one can say is that the mathematical form of Eq. (4.19) is similar to the one for the microgyration tensor $\varvec{\nu }$ of microstretch materials shown in Eq. (2.8), which was exact.

Nevertheless, if the decomposition (4.19) is accepted and inserted in (4.12), and if the relations (2.8) and (4.6) are observed, the following relations result:

$$\begin{aligned} \begin{aligned}&\dot{\varvec{s}}=\frac{\mathrm d}{\mathrm d t}\left( \varvec{j}\cdot \varvec{\omega }\right) \quad \Leftrightarrow \quad \dot{s}_k=\frac{\mathrm d}{\mathrm d t}\left( j_{kl}\omega _l\right) ,\\&\sigma _0=\tfrac{1}{6}j_0\left( {\dot{\nu }}_0+\tfrac{1}{3}\nu _0^2\right) -\varvec{\omega }\cdot \varvec{j}\cdot \varvec{\omega }\quad \Leftrightarrow \quad \sigma _0=\tfrac{1}{6}j_0 \left( {\dot{\nu }}_0+\tfrac{1}{3}\nu _0^2\right) -j_{kl}\omega _k\omega _l. \end{aligned} \end{aligned}$$

(4.20)

Finally, for micropolar materials there is no spin inertia associated with volume change. Hence,

$$\begin{aligned} \varvec{\sigma }=\tfrac{1}{2}\dot{\varvec{s}}\times \varvec{1}\quad \Leftrightarrow \quad \sigma _{kl}=-\tfrac{1}{2}\varepsilon _{klm}\dot{s}_m. \end{aligned}$$

(4.21)

The first line in (4.20) stays valid for micropolar materials, the second line is irrelevant. However, it is curious to note that the second line in (4.20) does not vanish identically when the transition from microstretch to micropolar is performed by putting $\nu _0=0$.

At the end of this section, a few critical comments regarding the introduction of the microinertia tensor field in Eq. (4.5) are in order. However, in order to appreciate them fully, we start with a discussion of the mass density field which was introduced in 3M theories according to Eq. (4.1). In a Matrioshka manner, Eringen introduces a subcontinuum within the continuum. This avoids answering the question regarding the meaning of the following limit process:⁶

$$\begin{aligned} \rho (\varvec{x},t)=\lim \limits _{\mathrm \varDelta v\rightarrow 0}\frac{\mathrm {\varDelta }m}{\mathrm {\varDelta }v}, \end{aligned}$$

(4.22)

where $\mathrm {\varDelta }m$ is the mass present in a volume $\mathrm {\varDelta }v$ around a true mathematical point. Representative of the continuum mechanics literature we read for example in [1, p. 2]: “The continuum theory regards matter as indefinitely divisible. Thus within the theory, one accepts the idea of an infinitesimal volume of material referred to as a particle in the continuum, and in every neighborhood of a particle there are always infinitely many particles present.” We conclude that Eq. (4.22) and all other fields of continuum theory are an attempt to apply the powerful mathematical tools of calculus to describe real world problems. Nevertheless, it must be possible to test the applicability of a mathematical concept by relating it to quantities that are accessible to experiment, at least in principle. In this spirit we relate the left-hand side of Eq. (4.22) to measurable quantities by

$$\begin{aligned} \rho (\varvec{x},t)=\frac{m}{v}, \end{aligned}$$

(4.23)

where m is the mass within a volume v around a point of space $\varvec{x}$. If we choose v to become smaller and smaller, there will be a range of volumes v where we the ratio given by (4.23) will remain almost constant. However, if we keep decreasing v this constancy will again disappear. Within this range of v, it is reasonable to describe physical properties in terms of continuous fields and to use the mathematical methods of calculus. This is referred to in [20] as weakly size-dependent behavior and it is what we mean when we say that the size of the material particle must be representative.

We now turn to the definition of the microinertia field in Eq. (4.5). Consider first the following equation analogous in form to (4.22):

$$\begin{aligned} \rho \varvec{j}(\varvec{x},t)=\lim \limits _{\mathrm \varDelta v\rightarrow 0}\frac{\mathrm {\varDelta }\varvec{J}^{(\mathrm c)}}{\mathrm {\varDelta }v}, \end{aligned}$$

(4.24)

where

$$\begin{aligned} \varDelta \varvec{J}^{(\mathrm c)}=\int \limits _{\mathrm \varDelta v}\rho '\left( \varvec{\xi }\cdot \varvec{\xi }\,\varvec{1}-\varvec{\xi }\otimes \varvec{\xi }\right) \mathrm dv'\rightarrow J^{\mathrm {axis}}=\mathrm {\varDelta } mr^2 \end{aligned}$$

(4.25)

is the inertia tensor w.r.t. the center of mass of the matter within $\mathrm {\varDelta }v$, r being the radius of gyration w.r.t. the momentary axis of gyration ( [17, p. 192]). By combining both equations and observing Eq. (4.22), we obtain

$$\begin{aligned} \varvec{j}(\varvec{x},t)\sim \lim \limits _{\mathrm \varDelta v\rightarrow 0}r^2\equiv 0, \end{aligned}$$

(4.26)

because the radius of gyration, which is smaller than the characteristic dimensions of $\mathrm \varDelta v$, must inevitably approach zero, if the volume $\mathrm \varDelta v$ goes to zero. Moreover, if in analogy to Eq. (4.23), we define the microinertia field by

$$\begin{aligned} \rho \varvec{j}(\varvec{x},t)=\frac{\varvec{J}^{(\mathrm c)}}{v}\,,\,\, \varvec{J}^{(\mathrm c)}=\int \limits _{ v}\rho '\left( \varvec{\xi }\cdot \varvec{\xi }\,\varvec{1}-\varvec{\xi }\otimes \varvec{\xi }\right) \mathrm dv' \end{aligned}$$

(4.27)

then, unlike in the case of mass density, there will be no constancy of the ratio $\nicefrac {\varvec{J}^{(\mathrm c)}}{v}$ within a range of smaller and smaller volumes v. Rather it will continuously decrease. In [20], this is referred to as strongly size-dependent behavior.

All of this leaves a certain aftertaste in context with the introduction of the microinertia tensor field $\varvec{j}$ in the form (4.5). We shall see that these problems do not occur when we introduce this field in spatial description based on the concept of the averages particle in the next section.

5 Continuum fields of extended micropolar theory

Consider the situation depicted in Fig. 3. In the center of the figure, the open RVE $\mathrm \varDelta v$ is shown. This is the continuum “point” in spatial description. We refer to it as the mesoscale. The continuously distributed matter and the continuum point are shown on the left of the cartoon. This is the viewpoint at the continuum or macroscale. The geometric center of the RVE is characterized by the vector $\varvec{x}$ with respect to the inertial frame spanned by the three Cartesian base unit vectors $\varvec{\mathrm i}_i$. The RVE is filled with $i=1, ..., N(\varvec{x},t)$ elementary particles $\varDelta v_i$ of mass $m_i$ and inertia tensor $\varvec{J}_i$ (w.r.t. their center of mass). All of these elementary particles may be different. Their inertial characteristics refer to what we call the microscale.

Fig. 3

The three scales of extended micropolar theory

In [20], it is said that the elementary particles possess linear velocity vectors $\varvec{v}_i$ and angular velocity vectors $\varvec{\omega }_i$ with respect to the global inertial frame. In fact $\varvec{v}_i$ is nothing else but the velocity of the center of mass of an elementary particle. The angular velocity vector $\varvec{\omega }_i$ is more problematic to explain. If the elementary particle was rigid, then it is well defined and simply characterizes its rigid body motion. However, tacitly it is assumed that the elementary particles are deformable. For instance, it is assumed in the example problems in [20] that they can be inflated and change their volume or that they can be crushed and be divided into smaller pieces. This makes it difficult to understand what the angular velocity vector really is. With a grain of salt we may say that the elementary particles are small enough so that their rotational movement can be captured sufficiently well by discrete velocity vectors $\varvec{\omega }_i$ without the need for a field concept within the elementary particle. Having said that the question arises how to compute the inertia tensor $\varvec{J}_i$ without knowing the density distribution $\rho (\varvec{x}',t)$ within the elementary particle, which, in fact, is given by

$$\begin{aligned} \varvec{J}_i=\int \limits _{v_i}\rho (\varvec{x}',t)\left( \varvec{x}^{\mathrm c}{'}\cdot \varvec{x}^{\mathrm c}{'}\varvec{1}-\varvec{x}^{\mathrm c}{'}\otimes \varvec{x}^{\mathrm c}{'}\right) \,\mathrm d v'\,,\,\,\varvec{x}^{\mathrm c}{'}=\varvec{x}'-\varvec{x}^{\mathrm c}, \end{aligned}$$

(5.1)

where we chose the center of mass c as the pole as mentioned above and $v_i$ is the volume of an elementary particle. It is fair to say that in all papers of the authors where applications of this discrete theory were presented the standard formulae for rigid particles were used whenever it was necessary to write down an explicit equation for the moment of inertia tensor $\varvec{J}_i$.

Fig. 4

Homogenization of discrete properties of matter within an RVE

We now proceed to define all relevant field quantities on the macroscale based on this discrete viewpoint, see Fig. 4. The matter traveling through the RVE will be characterized by average properties. As it is customary in continuum physics, it is then necessary to assume that the RVE contains sufficiently many elementary particles in order to avoid statistical fluctuations. In fact we will perform a homogenization and replace the different particles in the RVE with the same number of “average particles” carrying identical characteristics, such that the total characteristic of the average ensemble equals the one of the original RVE. Clearly, the particle density,

$$\begin{aligned} n(\varvec{x},t)=\frac{N(\varvec{x},t)}{\mathrm \varDelta v}, \end{aligned}$$

(5.2)

is then the same field function for the original RVE and the homogenized replacement, $\mathrm \varDelta v$ being the corresponding volume.

Our first average characteristic is mass. In this spirit the average particle carries the mass

$$\begin{aligned} m(\varvec{x},t)=\frac{1}{N(\varvec{x},t)}\sum \limits _{i=1}^{N(\varvec{x},t)}m_i. \end{aligned}$$

(5.3)

The mass density field $\rho (\varvec{x},t)$ is now introduced as an average characteristic by

$$\begin{aligned} \rho (\varvec{x},t)=m(\varvec{x},t)n(\varvec{x},t). \end{aligned}$$

(5.4)

By combination of these formulae, we obtain a relation for the total mass $\mathrm \varDelta m$ stored in the RVE at time t:

$$\begin{aligned} \mathrm \varDelta m\equiv N(\varvec{x},t)m(\varvec{x},t)=\rho (\varvec{x},t)\mathrm \varDelta v=\sum \limits _{i=1}^{N(\varvec{x},t)}m_i\quad \Rightarrow \quad \rho (\varvec{x},t)=\frac{1}{\mathrm \varDelta v}\sum \limits _{i=1}^{N(\varvec{x},t)}m_i. \end{aligned}$$

(5.5)

This chain of equations has a strong resemblance to Eq. (4.1) for the density field of 3M theories, and it confirms what we expect: The total mass in the original RVE is equal to the total mass of the homogenized volume with average particles. However, note the introduction of the mass density in Eq. (4.1) is based on totally different premises.

In order to define the field for the translational velocity $\varvec{v}(\varvec{x},t)$, we start by averaging the total linear momentum in the RVE,

$$\begin{aligned} \varvec{p}(\varvec{x},t)=\frac{1}{N(\varvec{x},t)}\sum \limits _{i=1}^{N(\varvec{x},t)}m_i\varvec{v}_i. \end{aligned}$$

(5.6)

Consequently, an average velocity would then be

$$\begin{aligned} \varvec{v}(\varvec{x},t)=\frac{\varvec{p}(\varvec{x},t)}{m(\varvec{x},t)}. \end{aligned}$$

(5.7)

By combining the previous equations, we can also write for the total linear momentum $\mathrm \varDelta \varvec{p}$ stored in the RVE:

$$\begin{aligned} \mathrm \varDelta \varvec{p}\equiv N(\varvec{x},t)\varvec{p}(\varvec{x},t)=\rho \varvec{v}\mathrm \varDelta v=\sum \limits _{i=1}^{N(\varvec{x},t)}m_i\varvec{v}_i\quad \Rightarrow \quad \varvec{v}(\varvec{x},t)=\frac{\sum \nolimits _{i=1}^{N(\varvec{x},t)}m_i\varvec{v}_i}{\sum \nolimits _{i=1}^{N(\varvec{x},t)}m_i}. \end{aligned}$$

(5.8)

We conclude that the total linear momentum of the RVE is equal to the total linear momentum of the average ensemble, as it should. Moreover, note the formal resemblance to Eq. (4.3). Indeed, in [20] the vector $\varvec{v}(\varvec{x},t)$ was also referred to as barycentric velocity. This notion is problematic, because the barycentric velocity $\dot{\varvec{x}}^{\mathrm c}$ was originally introduced for a system of N point masses $m_i$ at positions $\varvec{x}_i(t)$ by differentiation of the center of mass vector (hence the term barycentric) with respect to time:

$$\begin{aligned} \varvec{x}^{\mathrm c}(t)=\frac{\sum \nolimits _{i=1}^{N}m_i\varvec{x}_i(t)}{\sum \nolimits _{i=1}^{N}m_i}\quad \Rightarrow \quad \dot{\varvec{x}}^{\mathrm c}(t)=\frac{\sum \nolimits _{i=1}^{N}m_i\dot{\varvec{x}}_i(t)}{\sum \nolimits _{i=1}^{N}m_i}. \end{aligned}$$

(5.9)

In contrast to that, the elementary particles in the RVE are no point masses and their total number is time dependent. (5.8)$_2$ cannot be obtained by differentiation of the current center of mass vector of the RVE with respect to time. We must conclude that (5.8)$_2$ defines the velocity vector at the continuum level based on the assumption that the total linear momentum $\mathrm \varDelta \varvec{p}$ of the RVE can be obtained from elementary momenta $m_i\varvec{v}_i$, whereby the velocities $\varvec{v}_i$ are the velocities of the center of mass of the elementary particles.

We now define the inertia tensor of an average particle by

$$\begin{aligned} \varvec{J}(\varvec{x},t)=\frac{1}{N(\varvec{x},t)}\sum \limits _{i=1}^{N(\varvec{x},t)}\varvec{J}_i. \end{aligned}$$

(5.10)

This allows to introduce a microinertia tensor field for the average particle as:

$$\begin{aligned} \varvec{j}(\varvec{x},t)=\frac{\varvec{J}(\varvec{x},t)}{m(\varvec{x},t)}. \end{aligned}$$

(5.11)

The total microinertia $\mathrm \varDelta \varvec{J}$ contained in the homogenized volume is then:

$$\begin{aligned} \mathrm \varDelta \varvec{J}\equiv N(\varvec{x},t)\varvec{J}(\varvec{x},t)=\rho \varvec{j}\mathrm \varDelta v=\sum \limits _{i=1}^{N(\varvec{x},t)}\varvec{J}_i\quad \Rightarrow \quad \varvec{j}(\varvec{x},t)=\frac{\sum \nolimits _{i=1}^{N(\varvec{x},t)}\varvec{J}_i}{\sum \nolimits _{i=1}^{N(\varvec{x},t)}m_i}, \end{aligned}$$

(5.12)

and it is equal to the total microinertia in the original RVE. Note that this microinertia tensor is very different from the one shown in Eq. (4.5). It is not obtained from an integration process w.r.t. the center of mass of the RVE (which is also constantly changing because the RVE is not material but open) nor by some application of Steiner’s theorem to the discrete elementary particles. It therefore does not suffer from the deficiencies discussed in context with Eqs. (4.26) and (4.27) and it is not strongly size dependent.

Next we define the intrinsic angular momentum of an average particle:

$$\begin{aligned} \varvec{S}=\frac{1}{N(\varvec{x},t)}\sum \limits _{i=1}^{N(\varvec{x},t)}\varvec{J}_i\cdot \varvec{\omega }_i. \end{aligned}$$

(5.13)

The spin vector field of an average particle is then given by

$$\begin{aligned} \varvec{s}(\varvec{x},t)=\frac{\varvec{S}(\varvec{x},t)}{m(\varvec{x},t)}. \end{aligned}$$

(5.14)

Consequently, the following relations for the total intrinsic angular momentum $\mathrm \varDelta \varvec{S}$ of the equivalent ensemble hold:

$$\begin{aligned} \mathrm \varDelta \varvec{S}\equiv N(\varvec{x},t)\varvec{S}(\varvec{x},t)=\rho \varvec{s}\mathrm \varDelta v=\sum \limits _{i=1}^{N(\varvec{x},t)}\varvec{J}_i\cdot \varvec{\omega }_i\quad \Rightarrow \quad \varvec{s}(\varvec{x},t)=\frac{\sum \nolimits _{i=1}^{N(\varvec{x},t)}\varvec{J}_i\cdot \varvec{\omega }_i}{\sum \nolimits _{i=1}^{N(\varvec{x},t)}m_i}. \end{aligned}$$

(5.15)

We conclude that the intrinsic angular momentum of the original RVE and the average ensemble are equal. The caveat regarding the meaning of the angular velocities $\varvec{\omega }_i$ should be observed.

By combination of (5.12) and (5.15), the angular velocity vector $\varvec{\omega }$ at the continuum level is obtained:

$$\begin{aligned} \varvec{s}=\varvec{j}\cdot \varvec{\omega }=\sum \limits _{i=1}^{N(t)}\varvec{J}_i\cdot \varvec{\omega }_i\quad \Rightarrow \quad \varvec{\omega }(\varvec{x},t)=\left( \sum \limits _{i=1}^{N(t)}\varvec{J}_i\right) ^{-1}\sum \limits _{i=1}^{N(t)}\varvec{J}_i\cdot \varvec{\omega }_i. \end{aligned}$$

(5.16)

At this point a remark regarding the kinetic energy contained within the RVE is in order (also see [20], Eqs. (84)ff). Analogously to the previously defined averages is certainly also possible to define a kinetic energy of an average particle according to:

$$\begin{aligned} \varvec{e}_{\mathrm {kin}}=\frac{1}{N(\varvec{x},t)m(\varvec{x},t)}\sum \limits _{i=1}^{N(\varvec{x},t)}\tfrac{1}{2}\left( m_i\varvec{v}_i^2+\varvec{\omega }_i\cdot \varvec{J}_i\cdot \varvec{\omega }_i\right) . \end{aligned}$$

(5.17)

However, this is not identical with the expression ${\mathscr {K}}=\tfrac{1}{2}\left( \varvec{v}^2+\varvec{\omega }\cdot \varvec{j}\cdot \varvec{\omega }\right)$ from [20], in which the averages from Eqs. (5.8), (5.11), and (5.16) are used. The approach suggested in [20] does not put energies first but uses the kinematic quantities of linear and angular velocities instead. A further investigation of the consequences is left to future work.

We now summarize the salient features of the fields introduced in extended micropolar theory and point out the differences to 3M theories:

• The fields of the 3M theories are based on a continuum formulation on the mesolevel. Extended micropolar theory defines its continuum fields from a discrete viewpoint.

• The fields of the 3M theories are based on the concept of an indestructible material point. Extended micropolar theory uses an open RVE instead.

• In particular in 3M theories the microinertia tensor is defined as the (continuous) second moment of the mass distribution at the mesolevel. It suffers from the flaw of being a strongly size dependent quantity.

• The linear velocity and the angular velocity vector at the continuum level of extended micropolar theory are introduced through the amount of linear and (intrinsic) angular momentum stored in the RVE, which are both obtained for a discrete ensemble of elementary particles.

• The velocity of 3M theories at the continuum level is introduced through the linear momentum stored in a material particle in continuous formulation. In contrast to extended micropolar theory it is therefore identical to the barycentric velocity of the material point.

• The kinematics of rotation in 3M theories is, in general, based on a spin inertia tensor, which is defined on a continuous mesoscale. The specific kinetic energy of a material point can be expressed by a sum combining specific translational and rotational kinetic energies. The latter is expressed as a double scalar product between the microgyration and the spin inertia tensors. In the case of microstretch and micropolar theories, it becomes possible to represent (parts of) these tensors by axial vectors.

6 Balances of 3M theories

In general, all the fields appearing in the balances of 3M theories are in material form. Time derivatives are material derivatives in material description, Eq. (2.4). For simplicity we will focus only on the local balances in regular points. More information on global balances and local balances (jump conditions) at singular interfaces can be found in [12], Chapter 2.

The balance of mass has the usual form for all 3M theories:

$$\begin{aligned} \frac{\mathrm d \rho }{\mathrm d t}+\rho \varvec{\nabla }\cdot \varvec{v}=0\quad \Leftrightarrow \quad \frac{\mathrm d \rho }{\mathrm d t}+\rho \frac{\partial v_k}{\partial x_k}=0. \end{aligned}$$

(6.1)

Based on the its definition in Eq. (4.4) and the relation (2.5), the material time derivative of the microinertia tensor $\varvec{i}$ of micromorphic materials can be written as:

$$\begin{aligned} \frac{\mathrm d\varvec{i}}{\mathrm dt}=\varvec{i}\cdot \varvec{\nu }^\intercal +\varvec{\nu }\cdot \varvec{i}\quad \Leftrightarrow \quad \frac{\mathrm di_{kl}}{\mathrm dt}=i_{km}\nu _{lm}+i_{lm}\nu _{km}. \end{aligned}$$

(6.2)

It is a kinematic identity. Eringen refers to this equation as the “local law of conservation of microinertia,” [12, p. 42], and he uses the same terminology for the corresponding equations for micromorphic and micropolar continua (see Eqs. (6.3) and (6.5)). We speculate that he uses the word “conservation” to emphasize that there is no production of microinertia in this equation, just as there is no production of mass, and will soon elaborate on this issue even more.

Indeed, based on the definition in (4.5) and the relations (4.6), (2.8), Eq. (6.2) can be rewritten for microstretch materials to obtain a comparatively simple equation in terms of $\varvec{j}$:

$$\begin{aligned} \frac{\mathrm d\varvec{j}}{\mathrm dt}=\tfrac{2}{3}\nu _0\varvec{j}+\varvec{\omega }\times \varvec{j}-\varvec{j}\times \varvec{\omega }\quad \Leftrightarrow \quad \frac{\mathrm dj_{kl}}{\mathrm dt}=\tfrac{2}{3}\nu _0j_{kl}-\varepsilon _{kpr}j_{lp}\omega _{r}- \varepsilon _{lpr}j_{kp}\omega _{r}. \end{aligned}$$

(6.3)

The following scalar relation is a consequence of the previous equation:

$$\begin{aligned} \frac{\mathrm d j_0}{\mathrm dt}=2\nu _0 j_0\quad \Rightarrow \quad j_0(t)=j_0(0)\exp (2\nu _0t)\quad \Rightarrow \quad j_0(t)=j_0(0)v^2(t), \end{aligned}$$

(6.4)

the latter because of Eq. (2.22).

Note that rewriting Eq. (6.2) in terms of $\varvec{j}$ for general micromorphic materials yields a complicated relation. We may say that $\varvec{i}$ and not $\varvec{j}$ is the more appropriate quantity to be used in a micromorphic theory.

The conservation of microinertia tensor of micropolar materials is now easily obtained from Eq. (6.3) by putting $\nu _0=0$:

$$\begin{aligned} \frac{\mathrm d\varvec{j}}{\mathrm dt}=\varvec{\omega }\times \varvec{j}-\varvec{j}\times \varvec{\omega }\quad \Leftrightarrow \quad \frac{\mathrm dj_{kl}}{\mathrm dt}=-\varepsilon _{kpr}j_{lp}\omega _{r}-\varepsilon _{lpr}j_{kp}\omega _{r}. \end{aligned}$$

(6.5)

We also conclude from Eq. (6.4) that the trace of $\varvec{j}$ is conserved for micropolar materials.

It should be noted that there are extensions of the equations for the temporal development of microinertia in Eringen’s work in terms of production terms. In [12], Eq. (6.2) for micromorphic materials is generalized as follows:

$$\begin{aligned} \frac{\mathrm di_{kl}}{\mathrm dt}=i_{km}\nu _{lm}+i_{lm}\nu _{km}+\frac{1}{\rho }\frac{\partial \mathfrak {M}_{mkl}}{\partial x_m}, \end{aligned}$$

(6.6)

where (following [29])

$$\begin{aligned} {\mathcal {m}}_{klm}^{\mathrm {kin}}=\frac{1}{\rho }\mathfrak {M}_{kmn}\nu _{ln}, \end{aligned}$$

(6.7)

is a kinetic flux contribution to the stress moment tensor (see (6.10)). According to [12] this kinetic term arises “from the internal motions of microelements that contribute to nonsmooth macroscopic fields” but no further details are provided.

Moreover, in [9] and [13, p. 118] Eq. (6.5) for the microinertia of micropolar materials was extended to

$$\begin{aligned} \frac{\mathrm d\varvec{j}}{\mathrm dt}=\varvec{\omega }\times \varvec{j}-\varvec{j}\times \varvec{\omega }+\varvec{\mathrm {f}}\quad \Leftrightarrow \quad \frac{\mathrm dj_{kl}}{\mathrm dt}=-\varepsilon _{kpr}j_{lp}\omega _{r}-\varepsilon _{lpr}j_{kp}\omega _{r}+\mathrm f_{kl}. \end{aligned}$$

(6.8)

The newly introduced quantity $\varvec{\mathrm {f}}$ is a constitutive tensor function of second rank and, among other variable, depends on $\varvec{j}$. It is used to describe suspensions: “Suspended rigid particles in isotropic viscous fluids, from a single continuum viewpoint, are like anisotropic micropolar fluids. The suspended particles, together with fluid sticking to them, will have a microinertia tensor appropriate to their shapes. Thus, anisotropy is controlled by the microinertia tensor $j_{kl}$ which undergoes its evolution according to the balance law governed by $j_{kl}$. In the case of suspensions, motions of suspensions cause nonsmooth macroscopic fields.” In this sense it can be considered as a production of microinertia.

The balance of linear momentum has the commonly known form for all 3M materials:

$$\begin{aligned} \rho \frac{\mathrm d \varvec{v}}{\mathrm d t}=\varvec{\nabla }\cdot {\varvec{t}}+\rho \varvec{f}\quad \Leftrightarrow \quad \rho \frac{\mathrm d v_i}{\mathrm d t}=\frac{\partial t_{ji}}{\partial x_j}+\rho f_i, \end{aligned}$$

(6.9)

where $\varvec{t}$ is the Cauchy stress tensor and $\varvec{f}$ the body force.

The balance equation for the spin inertia tensor of micromorphic materials reads:

$$\begin{aligned} \rho \varvec{\sigma }=\varvec{\nabla }\cdot {\varvec{\mathcalligra {m}}}+\varvec{t}-\varvec{s}+\rho {\varvec{\mathcalligra {l}}}\quad \Leftrightarrow \quad \rho \sigma _{kl}=\frac{\partial {{\mathcalligra {m}}}_{mkl}}{\partial x_m}+t_{kl}-s_{kl}+\rho {{\mathcalligra {l}}}_{kl}, \end{aligned}$$

(6.10)

where $\varvec{{\mathcalligra {m}}}$ is the stress moment tensor of third rank, $\varvec{s}$ is the symmetric, so-called stress average tensor (see [10]), and $\varvec{{\mathcalligra {l}}}$ is the body moment density tensor.

A remark is in order. Because $\varvec{\sigma }$ cannot be written as a material time derivative, it is daring to call (6.10) a balance equation. This will change when we specialize it to microstretch materials. For these, Eringen requires the following decompositions to hold:

$$\begin{aligned} \begin{aligned}&{\varvec{\mathcalligra {m}}}=\tfrac{1}{3}\, {{\,\mathrm{\textsf {Tr}}\,}}{\varvec{\mathcalligra {m}}}\varvec{1}+\tfrac{1}{2}\varvec{\mu }\times \varvec{1}\,,\,\, {{\,\mathrm{\textsf {Tr}}\,}}{\varvec{\mathcalligra {m}}}={{\mathcalligra {m}}}\,{\cdot }{\cdot }\varvec{1} \quad \Leftrightarrow \quad {\mathcalligra {m}}_{klm}=\tfrac{1}{3} {\mathcalligra {m}}_k\delta _{lm}-\tfrac{1}{2}\varepsilon _{lmr} \mu _{kr}\,,\,\,{\mathcalligra {m}}_k={\mathcalligra {m}}_{kpp},\\&\varvec{{\mathcalligra {l}}}=\tfrac{1}{3}l_0\varvec{1}+\tfrac{1}{2}\varvec{m}\times \varvec{1}\,,\,\,l_0={{\,\mathrm{\textsf {Tr}}\,}}{\varvec{{\mathcalligra {l}}}}\quad \Leftrightarrow \quad {\mathcalligra {l}}_{kl}=\tfrac{1}{3}l_0\delta _{kl}-\tfrac{1}{2} \varepsilon _{klr}m_{r}\,,\,\,l_0={\mathcalligra {l}}_{pp}. \end{aligned} \end{aligned}$$

(6.11)

The second-order tensor $\varvec{\mu }$ is called the couple stress tensor and the axial vector $\varvec{m}$ is the body moment couple density vector. Note that these decompositions are in the same way limited as Eq. (4.19) and in our opinion should be considered as useful assumptions. Because of (4.20) Eq. (6.12) is then mapped onto an axial vector balance for the spin vector $\varvec{s}$ and a scalar relation for the traces:

$$\begin{aligned} \begin{aligned}&\frac{\mathrm d\varvec{s}}{\mathrm d t}=\nabla \cdot \varvec{\mu }+\varvec{t}_\times +\rho \, \varvec{m}\quad \Leftrightarrow \quad \frac{\mathrm d s_i}{\mathrm d t}=\frac{\partial \mu _{ji}}{\partial x_j}+\varepsilon _{ijk}t_{jk}+m_i,\\&\sigma _0=t_0-s_0+\rho \, l_0\,,\,\,t_0={{\,\mathrm{\textsf {Tr}}\,}}{\varvec{\varvec{t}}}=t_{pp},\,s_0={{\,\mathrm{\textsf {Tr}}\,}}{\varvec{\varvec{s}}}=s_{pp}. \end{aligned} \end{aligned}$$

(6.12)

Finally, for micropolar materials the scalar relation vanishes identically and the vector relation remains. Also recall that for microstretch materials the part $\varvec{\sigma }^{\mathrm s}-\tfrac{1}{3}\sigma _0\varvec{1}$ in (4.14) remained unaccounted for in the decomposition (4.19). It should be possible to correct this by proposing a suitable form of the stress average tensor $\varvec{s}$ from (6.10), which is symmetric and therefore capable to do so.

The balance of the specific internal energy u reads for micromorphic materials:

$$\begin{aligned} \begin{aligned}&\rho \frac{\mathrm du}{\mathrm d t}=\varvec{t}\,{\cdot }{\cdot }\left( \nabla \otimes \varvec{v}-\varvec{\nu }\right) +\varvec{s}\,{\cdot }{\cdot }\varvec{\nu }+\varvec{\mathcalligra {m}}\,{\cdot } {\cdot }{\cdot }\nabla \otimes \varvec{\nu }-\nabla \cdot \varvec{q}+\rho r\quad \Leftrightarrow \\&\rho \frac{\mathrm du}{\mathrm d t}=t_{kl}\left( \frac{\partial v_l}{\partial x_k}-\nu _{kl}\right) +s_{kl}\nu _{kl}+\varvec{\mathcalligra {m}}_{klm}\frac{\partial \nu _{lm}}{\partial x_k}-\frac{\partial q_k}{\partial x_k}+\rho r, \end{aligned} \end{aligned}$$

(6.13)

where $\varvec{q}$ is the heat flux vector and r the specific radiation supply. It is the consequence of the principle that the total energy of the material body, i.e., the sum of kinetic energy in the form (4.8) and the internal energy, is conserved (see [26]). In order to obtain the formula (6.13) several algebraic manipulations are required after scalar multiplication of the balance of linear momentum (6.9) with $\varvec{v}$ and the balance for the spin inertia tensor (6.10) by $\varvec{\nu }$.

In order to obtain the internal energy balance for microstretch materials, we observe Eqs. (2.8), (6.11)$_1$, and (4.6). Then, we obtain from Eq. (6.13):

$$\begin{aligned} \begin{aligned}&\rho \frac{\mathrm du}{\mathrm d t}=\varvec{t}\,{\cdot }{\cdot }\left( \nabla \otimes \varvec{v}+ \varvec{1}\times \varvec{\omega }\right) +\varvec{\mu }\,{\cdot }{\cdot }\nabla \otimes \varvec{\omega }+\tfrac{1}{3}{{\,\mathrm{\textsf {Tr}}\,}}{\varvec{\mathcalligra {m}}}\cdot \nabla \nu _0+\tfrac{1}{3}\left( s_0-t_0\right) \nu _0- \nabla \cdot \varvec{q}+\rho r\quad \Leftrightarrow \\&\rho \frac{\mathrm du}{\mathrm d t}=t_{kl}\left( \frac{\partial v_l}{\partial x_k}+\varepsilon _{lkr}\omega _r\right) +\mu _{kl}\frac{\partial \omega _{l}}{\partial x_k}+\tfrac{1}{3}\varvec{\mathcalligra {m}}_k\frac{\partial \nu _0}{\partial x_k}+\tfrac{1}{3}\left( s_0-t_0\right) \nu _0-\frac{\partial q_k}{\partial x_k}+\rho r. \end{aligned} \end{aligned}$$

(6.14)

Finally, the balance of internal energy of micropolar materials can be obtained from the previous relation by putting $\nu _0$ equal to zero:

$$\begin{aligned} \begin{aligned}&\rho \frac{\mathrm du}{\mathrm d t}=\varvec{t}\,{\cdot }{\cdot }\left( \nabla \otimes \varvec{v}+\varvec{1} \times \varvec{\omega }\right) +\varvec{\mu }\,{\cdot }{\cdot }\nabla \otimes \varvec{\omega }-\nabla \cdot \varvec{q}+\rho r\quad \Leftrightarrow \\&\rho \frac{\mathrm du}{\mathrm d t}=t_{kl}\left( \frac{\partial v_l}{\partial x_k}+\varepsilon _{lkr}\omega _r\right) +\mu _{kl}\frac{\partial \omega _{l}}{\partial x_k}-\frac{\partial q_k}{\partial x_k}+\rho r. \end{aligned} \end{aligned}$$

(6.15)

7 Balances of extended micropolar theory

Note that all the fields in the following local balances in regular points are written in spatial description. They are functions of the geometric center of the RVE and time. Time derivatives are given in terms of the material time derivative $\nicefrac {\updelta (\cdot )}{\updelta t}$ shown in Eq. (3.4).

The balance of mass takes the form:

$$\begin{aligned} \frac{\updelta \rho }{\updelta t}=-\rho \varvec{\nabla }\cdot \varvec{v}\quad \Leftrightarrow \quad \frac{\updelta \rho }{\updelta t}=-\rho \frac{\partial v_j}{\partial x_j}. \end{aligned}$$

(7.1)

The balance of specific microinertia $\varvec{j}$ as introduced in Eq. (5.11) reads:

$$\begin{aligned} \frac{\updelta \varvec{j}}{\updelta t}=\varvec{\omega }\times \varvec{j}-\varvec{j}\times \varvec{\omega }+\varvec{\chi }^j\quad \Leftrightarrow \quad \frac{\updelta j_{ij}}{\updelta t}=\varepsilon _{irs}\omega _r j_{sj}-\varepsilon _{jrs}j_{ir}\omega _s+\chi ^j_{ij}. \end{aligned}$$

(7.2)

Recall that $\varvec{j}$ is an average characteristic of the matter in the RVE. It can change because of internal structural transformations, which explains the necessity for a production $\varvec{\chi }^j$. This can further be motivated by postulating that the specific microinertia in a co-rotating frame, $\varvec{j}'$ is not conserved:

$$\begin{aligned} \frac{\updelta \varvec{j}'}{\updelta t}=\varvec{\chi ^j}'\,, \end{aligned}$$

(7.3)

such that

$$\begin{aligned} \varvec{j}=\varvec{Q}\cdot \varvec{j}'\cdot \varvec{Q}^\intercal \,,\,\,\varvec{\chi }^j=\varvec{Q}\cdot \varvec{\chi ^j}'\cdot \varvec{Q}^\intercal \,. \end{aligned}$$

(7.4)

Equation (7.3) then follows if the Poisson relation Eq. (3.3) is observed. Also recall the eigenvector relations from Eq. (3.7) in this context. $\varvec{\chi ^j}'$ then describes the temporal change of the eigenvalues $j'_{{\underline{i}}\,{\underline{i}}}$.

The balance of linear momentum assumes the customary form:

$$\begin{aligned} \rho \frac{\updelta \varvec{v}}{\updelta t}=\varvec{\nabla }\cdot \varvec{\sigma }+\rho \varvec{f}\quad \leftrightarrow \quad \rho \frac{\updelta v_i}{\updelta t}=\frac{\partial \sigma _{ji}}{\partial x_j}+\rho f_i\,. \end{aligned}$$

(7.5)

For the balance of spin $\varvec{s}=\varvec{j}\cdot \varvec{\omega }$, we write:

$$\begin{aligned} \rho \cdot \frac{\updelta \varvec{s}}{\updelta t}=\varvec{\nabla }\cdot \varvec{\mu }+\varvec{t}_\times +\rho \varvec{m}+\rho \varvec{\chi }\cdot \varvec{\omega }\quad \Leftrightarrow \quad \rho \cdot \frac{\updelta s_i}{\updelta t}=\frac{\partial \mu _{ji}}{\partial x_j}+\varepsilon _{ijk}t_{jk}+\rho m_i+\rho \chi _{ij}\omega _j. \end{aligned}$$

(7.6)

This relation is a consequence of the balance of total angular momentum from which the balance of moment of momentum (obtained from the balance of linear momentum after vector multiplication by $\varvec{x}$) has been subtracted, see [26] for details.

If the balance of microinertia (7.2) is taken into account, this can be rewritten as:

$$\begin{aligned} \rho \varvec{j}\cdot \frac{\updelta \varvec{\omega }}{\updelta t}=-\varvec{\omega }\times \varvec{j}\cdot \varvec{\omega }+\varvec{\nabla }\cdot \varvec{\mu }+\varvec{t}_\times +\rho \varvec{m}\quad \Leftrightarrow \quad \rho j_{ij}\frac{\updelta \omega _j}{\updelta t}=-\varepsilon _{ijk}\omega _j j_{kl}\omega _l+\frac{\partial \mu _{ji}}{\partial x_j}+\varepsilon _{ijk}t_{jk}+\rho m_i. \nonumber \\ \end{aligned}$$

(7.7)

The advantage of this equation is that the production of microinertia takes no longer part in it.

The balance of internal energy reads:

$$\begin{aligned} \begin{aligned}&\rho \frac{\updelta u}{\updelta t}=\varvec{t}\,{\cdot }{\cdot }\big (\nabla \otimes \varvec{v} +\varvec{1}\times \varvec{\omega }\big )+\varvec{\mu }\,{\cdot }{\cdot }\nabla \otimes \varvec{\omega }-\nabla \cdot \varvec{q}+\rho r\quad \Leftrightarrow \\&\rho \frac{\updelta u}{\updelta t}=t_{kl}\left( \frac{\partial v_l}{\partial x_k}+\varepsilon _{lkr}\omega _r\right) +\mu _{kl}\frac{\partial \omega _{l}}{\partial x_k}-\frac{\partial q_k}{\partial x_k}+\rho r. \end{aligned} \end{aligned}$$

(7.8)

Note that this equation is free of production terms for the microinertia. It is a consequence of the balance of total energy from which the balance of kinetic energy has been subtracted (which both contain production terms).

8 Comparison and discussion of the balances of microinertia

Consider the two balances of microinertia for micropolar materials of 3M theories and EMT, Eqs. (6.8) and (7.2), respectively. Both contain production terms. It was mentioned already that Eringen introduced the production term $\varvec{\mathrm f}$ in micropolar 3M theory in order to study suspensions: The surrounding fluid will attach to essentially rigid particles to which and, consequently, their initial microinertia will change. Eringen assumes in [13, p. 117] that the tensor function $\varvec{\mathrm f}$ depends on the microinertia $\varvec{j}$ and the difference between velocity gradient and the microgyration tensor, $\varvec{a}$

$$\begin{aligned} \varvec{a}=\nabla \otimes \varvec{v}-\varvec{\omega }\times \varvec{1}\quad \Leftrightarrow \quad a_{kl}=\frac{\partial v_l}{\partial x_k}+\varepsilon _{klr}\omega _r. \end{aligned}$$

(8.1)

He then uses representation theorems for isotropic tensor functions to make the dependence explicit. In contrast to this procedure the production of microinertia, $\varvec{\chi }^j$, in the papers on EMT by the authors was introduced by using micromodels. For example, in [20], two homogeneous problems were presented, namely the refinement of spherical elementary particles and the inflation of pressurized particles under the influence of an external pressure. In the first case a negative growth law was used, and for the latter a micromechanical model helped to obtain explicit expressions for the production term. In [24] based on a micromodel with spheres that could undergo thermal expansion equations for the (isotropic) microinertia tensor and the production were motivated. Then, the interrelation of heat propagation (transient thermal gradient between two plates) and the developing angular velocity was studied. The aspect of spatial description and an open RVE was not addressed in these examples.

The necessity for a spatial description and open systems was first examined in [28] where the so-called crusher problem was studied initially in 1D-form: Isotropic matter of irregular but arbitrarily oriented elementary particles (i.e., $\varvec{J}=J_0\varvec{1}$) were transported on a conveyor belt and entered a region of finite length in which the average size of these particles was reduced (crushing). This affects the value of $J_0$. The particles pass and finally leave the region such that $J_0$ continuously decreases. Eventually a position-dependent stationary state is reached in the crusher region. Consequently, this is no longer a homogeneous problem. Nevertheless, it decouples completely from the other fields, such as linear and angular velocity. In fact both are of no importance here.

A further generalization of the crusher problem was presented in [16]. A funnel-shape 2D geometry of the crusher was considered, where arbitrarily shaped and oriented particles were passing through from the top to the bottom under the influence of external pressure and gravity. Consequently, both $\varvec{j}$ and $\varvec{\chi }^j$ are isotropic and only the size of the average particle changes. The balance of momentum had to be solved numerically in combination with the balance of microinertia with a (negative) production term. Moreover, a coupling between both was achieved by assuming that the shear viscosity depends on average elementary particle size, and therefore on microinertia. Moreover, the parameters in the production term depended on the local pressure.

In summary, the microinertia and the production term in all crusher problems are spherical,

$$\begin{aligned} \varvec{j}=j\varvec{1}\,,\,\,\varvec{\chi }^j=\chi ^j\varvec{1}\,,\,\,\chi ^j=-\alpha _0\left( j-j_*\right) , \end{aligned}$$

(8.2)

where $\alpha _0$ is a parameter that can either be a positive constant or depend (linearly) on the trace of the stress tensor (i.e., on the local pressure) and $j_*$ is related to the minimum particle size the crusher works can produce.

A generalization of such a form for $\chi$ was presented in [27]. Here the focus was on dielectric polarization of bipolar matter, such that $\varvec{j}$ would change from an initially isotropic into a transversally isotropic form under the influence of an external electric field $\varvec{E}$. Hence, the production would depend on a vector and on a symmetric tensor second rank, $\varvec{\chi }^j=\varvec{\chi }^j(\varvec{E},\varvec{j})$. Representation theorems were used (as in Eringen’s 3M micropolar theory) to find all possible dependencies.

Following on to that, a detailed study of orientational polarization of dielectric materials was presented in [38] and [39]. The temporal development of the polarization vector, $\varvec{P}=nq{\varvec{\bar{l}}}$, q being the electric charge of an elementary electric dipole, was modeled by computing a homogenized average dipole length, ${\bar{l}}(t)$, from the expression of the deviatoric part of the developing microinertia:

$$\begin{aligned} \varvec{j}(t)^{\mathrm {dev}}=\frac{{\bar{l}}(t)^2}{36}(\varvec{1}-3\varvec{n}\otimes \varvec{n})\,, \end{aligned}$$

(8.3)

which is transversally isotropic, $\varvec{n}$ being the unit direction of the applied electric field. One may say that a deviatoric part of $\varvec{j}$ appears only when there is preferred orientation of particles, which must then also be non-spherical. It reflects the combined effect of shape of particles (on the microscale) and on orientation. The temporal development of the microinertia itself is dictated by the balance (7.2), if a suitable form for the production $\varvec{\chi }^j$ is assumed. Specifically, it was assumed that it consists of two additive parts, one due to the presence of the electric fields forcing the elementary dipoles to align, and another one accounting for thermal movement, i.e., disorientation of the dipoles. The introduction of the average length ${\bar{\varvec{l}}}(t)$ must not be confused with the length of the elementary tripod of microstretch materials from Eq. (2.22), which is of completely different physical origin. EMT is a micropolar theory and the production term of microinertia does not equal a microstretch effect.

Eringen proposed to include the microinertia tensor into a set of arguments in constitutive relations [14]. Let us note that this will also affect material symmetry. In other words, referential microinertia tensors determine the material symmetry together with stiffness parameters. So an anisotropy of elastic micropolar materials could be analyzed considering both symmetries of a strain energy density and referential microinertia tensors as in [6].

9 Conclusion

In this paper, the following was achieved:

• A detailed review of the introduction of the basic fields of 3M theories and EMT as well as the corresponding balances was provided.

• The main difference between the fields of 3M theories and EMT was explained: The fields of 3M theories are based on the concept of a subcontinuum within a material point. EMT fields are introduced by homogenization from the physical properties of discrete microparticles. Specifically the averages of microscopic physical properties within an RVE are determined such that the total physical property within the original RVE and the homogenized replacement stay the same. Their microinertia field suffers has the drawback of being strongly size dependent.

• Some inconsistencies within Eringen’s concept of microstretch continua were pointed out and remedied.

• The balances of microinertia of 3M theories and EMT were listed, derived and compared.