Modularity of the displacement coefficients and complete plate theories in the framework of the consistent-approximation approach

Abstract

Starting from the three-dimensional theory of linear elasticity, we arrive at the exact plate problem by the use of Taylor series expansions. Applying the consistent-approximation approach to this problem leads to hierarchic generic plate theories. Mathematically, these plate theories are systems of partial-differential equations (PDEs), which contain the coefficients of the series expansions of the displacements (displacement coefficients) as variables. With the pseudo-reduction method, the PDE systems can be reduced to one main PDE, which is entirely written in the main variable, and several reduction PDEs, each written in the main variable and several non-main variables. So, after solving the main PDE, the reduction PDEs can be solved by insertion of the main variable. As a great disadvantage of the generic plate theories, there are fewer reduction PDEs than non-main variables so that not all of the latter can be determined independently. Within this paper, a modular structure of the displacement coefficients is found and proved. Based on it, we define so-called complete plate theories which enable us to determine all non-main variables independently. Also, a scheme to assemble Nth-order complete plate theories with equations from the generic plate theories is found. As it turns out, the governing PDEs from the complete plate theories fulfill the local boundary conditions and the local form of the equilibrium equations a priori. Furthermore, these results are compared with those of the classical theories and recently published papers on the consistent-approximation approach.

1 Introduction

The three-dimensional theory of linear elasticity (short: 3D theory) describes the linear-elastic deformation of a three-dimensional body under arbitrary volume and surface loads. The corresponding modeling equations (e.g., kinematic relations) can be derived from basic physical principles [1], thus they are totally accepted within the applied mechanics community. The disadvantage of the 3D theory is the lack of general closed-form solutions. For quasi two-dimensional continua (disc and plate problem) we treat, like in the three-dimensional case, partial differential equations, however, solutions for a variety of problems are available. Because of their attempt to describe a three-dimensional object in lower dimensions, the related theories are inherently approximative.

For plates and discs, the characteristic thickness dimension h is much smaller than the characteristic in-plane dimension a. Plates are classically loaded transversely to their midplanes. In contrast, discs are classically loaded in their midplanes. By assuming at least monoclinic material (with the midplane as symmetry plane), we can treat both problems individually. Within the present paper, we will assume a homogeneous isotropic material and a constant thickness and deal only with the plate problem. For the sake of simplicity, we will also neglect edge-effects and with it all “Reissner-like” variables.¹

Although there have been a lot of contributions in the field of plate theories in the last two centuries, the topic is still subject of ongoing research. This is evidenced by the numerous recent publications [3,4,5,6, 12], dealing predominately with complex material models. The most known theories, the Kirchhoff [11], the Reissner [18], the Mindlin [13] and Reddy’s plate theory [17], are underlying the classical approach, which is based on kinematic a-priori assumptions (ad-hoc assumptions). These classical theories are limited regarding the material model, the applied forces and the achievable accuracy. Because with increasing complexity of the plate theory, it is very difficult to postulate ad-hoc assumptions (e.g., normal hypothesis of the Euler–Bernoulli beam theory). Systematic approaches, alternatively, are derived from the 3D theory with physical and mathematical reasoning. They lead to hierarchical theories, which are free from ad-hoc assumptions and easily extendable toward more accuracy, more complex material models and more complex load cases. Because our aim is to build a sound foundation for plate theories of any load case, material model or accuracy, we further use the branch of systematic approaches for the derivation of our plate theory.

Following that branch, the first variations of the elastic and dual potential have to vanish. After partial integration in the two in-plane directions, the virtual displacement and load distributions in the resulting equations are substituted by their series expansions (e.g., Taylor series) with respect to the thickness coordinate. Applying further the fundamental lemma of the calculus of variations leads to the two-dimensional equilibrium equations and Neumann and Dirichlet conditions at the midplane boundary or the quasi-two-dimensional problem. It has been shown by Schneider et al. [21] that this problem is equivalent to the 3D theory and plates can be loaded in all directions. The quasi-two-dimensional problem can be represented as a system of infinitely many partial differential equations (PDEs) with infinitely many coefficients of the series expansions of the displacement functions (displacement coefficients). For the truncation of this system, we will follow the consistent-approximation approach (or uniform-approximation approach). With this technique, the PDE system is truncated in relation to the power of the dimensionless plate parameter $c =h\text {/}(\sqrt{12}\,a)$ which evolves from the integration of the thickness variable over the thickness. This parameter is used for the truncation because it essentially describes the energetic size of the individual terms of the PDE system. So, a Nth-order generic plate theory contains all terms multiplied by $c^{2n}$, $n \le N$, whereas higher-order terms $n > N$ are neglected (cf. [7, 15]).

Following the publications of Kienzler [7] and Schneider et al. [21], we will make use of the pseudo-reduction method to reduce the PDE system of an Nth-order generic plate theory to one main PDE, which is entirely written in the main variable (displacement coefficient), and several reduction PDEs, each written in the main variable and several non-main variables. Solving the main PDE yields the main variable. Afterward, the reduction PDEs can be solved by insertion of the main variable which gives us the non-main variables. But not all of the latter can be determined independently from each other, since some reduction PDEs eliminate linear combinations of several non-main variables. Kienzler and Schneider [10] have used these degrees of freedom (undetermined variables) to fulfill the local Neumann boundary conditions on the upper and lower face of the plate and the local form of the equilibrium equations (specific local conditions) for the second-order generic plate theory. In a subsequent paper, Kienzler and Kashtalyan [9] confirmed the resulting displacement distribution and additionally found the main PDEs for two still undetermined variables by employing an exact solution of the 3D theory.

Following Kienzler and Schneider [10], we split the displacement coefficients ${{}^{j}}{}{u}_i$ into an infinite series of displacement-coefficient parts ${{}^{j}}{}{u}_i^{n}$ (dcps) of different powers of $c^{2n}$. As a novelty, we will prove up to the second-order generic plate theory that the main and reduction PDEs (reduction equations) written in the dcps remain unchanged over these orders. This unchangeability of the PDEs implies the unchangeability of the dcps within a specific problem. Because the unchangeability of the dcps implies further a modular structure of the displacement coefficients, we call this characteristic the modularity of the displacement coefficients. Based on it, we will assemble PDEs from different orders of the generic plate theories to so-called complete plate theories. The resulting PDE systems allow now to determine all non-main variables independently. A scheme to create the complete plate theories for every order is also given.

Since an exact solution of the 3D theory has to fulfill the local boundary conditions and the local form of the equilibrium equations, a plate theory can be assessed by checking whether or not the reduction equations satisfy them. As it turns out, the reduction equations of the PDE systems of the complete plate theories indeed satisfy the specific local conditions within their respective order of approximation. This result is remarkable, because it is, to the authors best knowledge, the first time the specific local conditions are fulfilled a priori by plate theories. Reddy, e.g., fulfilled also the local Neumann boundary conditions on the upper and lower face of the plate in his third-order shear deformation theory but unlike us he used ad hoc assumptions. It should also be mentioned that we considered all loads of the plate problem in this contribution.

Last but not least, we will compare our results with the outcome of other authors. It will be shown that the Kirchhoff–Love plate theory [11] is a first-order complete plate theory and the Reissner plate theory [18] (without edge effects) is a second-order complete plate theory. Also, we compare our results with the publication of Kienzler and Schneider [10] and the publication of Kienzler and Kashtalyan [9].

2 Consistent-approximation approach

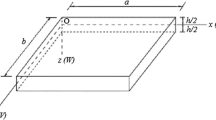
Let us assume a homogeneous, cuboid solid $\varOmega _x$ embedded in the three-dimensional Euclidean space. The boundary of this solid is separated into a Dirichlet part $\partial \varOmega _{x0}$ with prescribed displacements $u_{0i}$ (Latin indices have the range ${\{1,2,3\}}$; Greek indices have the range {1, 2}) and a Neumann part $\partial \varOmega _{xN}$ with applied surface loads $g_i$. We install a Cartesian coordinate system in the edge of the solid so that it is divided in half by the ($x_1$, $x_2$)-plane. This midplane is parallel to the upper and lower face of the solid and perpendicular to the $x_3$-direction. The thickness h of the solid is much smaller than the in-plane dimensions a and b (cf. Fig. 1). Therefore, we call it quasi two-dimensional continuum.

Fig. 1

Quasi-two-dimensional continuum

The surface loads $g_i^- =g_i(x_1,x_2,-\frac{h}{2})$ and $g_i^+ =g_i(x_1,x_2,\frac{h}{2})$ are applied at the upper and lower faces. We also allow for volume forces $f_i$ in all directions. Since we assume the material of the plate to be linear elastic and neglect all inertia effects (statics), we have to deal with the potential energy (or elastic potential)

$$\begin{aligned} E_{\mathrm {pot}}({\mathbf {u}})&=\int _{\varOmega _x} \sum _{i,j,r,s=1}^3 \dfrac{1}{2}E_{ijrs}u_{i|j}u_{r|s} \, \mathrm {d}V_x \nonumber \\&\quad - \int _{\varOmega _x}\sum _{i=1}^3 f_iu_i \, \mathrm {d}V_x - \int _{\partial \varOmega _{xN}}\sum _{i=1}^3g_iu_i \, \mathrm {d}A_x \end{aligned}$$

(1)

and its complement, the dual energy (or dual potential)

$$\begin{aligned} E_{\mathrm {dual}}(\varvec{\sigma })&= -\int _{\varOmega _x} \sum _{i,j,r,s=1}^3 \dfrac{1}{2}D_{ijrs}\sigma _{ij}\sigma _{rs} \, \mathrm {d}V_x \nonumber \\&\quad + \int _{\partial \varOmega _{x0}} \sum _{i,j=1}^3 \sigma _{ij}n_ju_{0i} \, \mathrm {d}A_x . \end{aligned}$$

(2)

Here, $E_{ijrs}$ denotes the fourth rank elasticity tensor with constant components and $D_{ijrs}$ is the fourth rank compliance tensor with constant components. Both potentials can be found, e.g., in [2]. But in contrast, here we are following [20] by multiplying the dual energy with − 1. Thus, the minimization problem of the dual energy turns into a maximization problem and the extreme values of the potential and dual energy coincide (cf. [14, (2.5)]). With ${\mathbf {u}} =u_i$, we denote the displacement distribution, $\varvec{\sigma } =\sigma _{ij}$ is the stress field and ${\mathbf {n}} =n_j$ represents the unit normal vector. For differentiation with respect to $x_i$ the abbreviation

$$\begin{aligned} \dfrac{\partial ()}{\partial x_i} =()_{|i} \end{aligned}$$

(3)

is introduced. It should be mentioned that the quantities $u_{0i}$, $g_i$ and $f_i$ are sufficiently smooth given data.

Due to the principles of minimal potential energy and maximal dual energy, we necessarily have to calculate the first variations of both and equate them to zero:

$$\begin{aligned} \delta E_{\mathrm {pot}}({\mathbf {u}};{\mathbf {v}})&\overset{!}{=} 0, \end{aligned}$$

(4)

$$\begin{aligned} \delta E_{\mathrm {dual}}(\varvec{\sigma };\varvec{\mu })&\overset{!}{=} 0 . \end{aligned}$$

(5)

With ${\mathbf {v}} =v_i$ (virtual displacements) and $\varvec{\mu } =\mu _{ij}$ (virtual stresses), the test functions are defined. If we integrate these terms by parts in all three coordinate directions and make use of the fundamental lemma of the calculus of variations, the local form of the equilibrium equations, the local Neumann boundary conditions and the local Dirichlet boundary conditions are found, cf. [20].

However, we want to derive two-dimensional theories from the 3D theory. The following way is analogous to the procedure of deriving one-dimensional theories in Schneider and Kienzler [20]:

We first introduce dimensionless² coordinates by the characteristic in-plane dimension a

$$\begin{aligned} \xi _i =\dfrac{x_i}{a} , \end{aligned}$$

(6)

and abbreviate the differentiation with respect to these dimensionless coordinates by the comma notation

$$\begin{aligned} \dfrac{\partial ()}{\partial \xi _i} =a \dfrac{\partial ()}{\partial x_i} =a ()_{|i} =(),_i . \end{aligned}$$

(7)

Furthermore, the displacements $u_i$ are non-dimensionalized by a, the surface loads $g_i$ are non-dimensionalized by a characteristic stiffness G, which might be chosen as the shear modulus for isotropy, and both potentials (1) and (2) are non-dimensionalized by $G\,a^3$. Then, in case of the dimensionless potential energy, we integrate its first variation by parts only in $\xi _1$- and $\xi _2$-direction, substitute the dimensionless test functions $\nicefrac {v_i}{a}$ by their infinite Taylor series

$$\begin{aligned} \dfrac{v_i(\xi _i)}{a}&= \sum _{n=0}^{\infty } \underbrace{\dfrac{1}{n!}\left[ \dfrac{1}{a}\dfrac{\partial ^n v_i}{\partial \tau _3^n}(\xi _1,\xi _2,\tau _3)\right] _{\tau _3=0}}_{=: \, {{}^{n}}{}{v}_i(\xi _1,\xi _2)}\xi _3^n, \end{aligned}$$

(8)

and make use of the fundamental lemma of the calculus of variations. In that way, we obtain from (4) the two-dimensional equilibrium equations

$$\begin{aligned}&\forall \, i \in \{1,2,3\} , n \in {\mathbb {N}}_0: \nonumber \\&\delta {{}^{n}}{}{v}_i: {{}^{n}}{}{\mathcal {M}}_{i1,1}(u_i) + {{}^{n}}{}{\mathcal {M}}_{i2,2}(u_i) - n\cdot {{}^{n-1}}{}{\mathcal {M}}_{i3}(u_i) =-{{}^{n}}{}{p}_i \end{aligned}$$

(9)

and the Neumann conditions at the midplane boundary

$$\begin{aligned}&0 =\sum _{i =1}^3 \sum _{n =0}^{\infty } \left\{ \mathbf {1 }_{P_{\xi N}}(\{0,1\})\left[ \int _0^{\frac{b}{a}} {{}^{n}}{}{v}_i\left( {{}^{n}}{}{\mathcal {M}}_{i1}(u_i)-{{}^{n}}{}{\mathcal {M}}_{Ni1}\right) n_1\mathrm {d}\xi _2\right] \right. \nonumber \\&\left. \qquad + \mathbf {2 }_{P_{\xi N}}\left( \left\{ 0,b\text {/}{a}\right\} \right) \left[ \int _0^{1} {{}^{n}}{}{v}_i\left( {{}^{n}}{}{\mathcal {M}}_{i2}(u_i)-{{}^{n}}{}{\mathcal {M}}_{Ni2}\right) n_2\mathrm {d}\xi _1\right] \right\} . \end{aligned}$$

(10)

In case of the dimensionless dual energy, we perform the same steps as for the potential energy but substitute the dimensionless test functions $\mu _{ij}\text {/G}$ by their infinite Taylor series

$$\begin{aligned} \dfrac{\mu _{ij}(\xi _i)}{G} =&\sum _{n=0}^{\infty } \underbrace{\dfrac{1}{n!}\left[ \dfrac{1}{G}\dfrac{\partial ^n \mu _{ij}}{\partial \tau _3^n}(\xi _1,\xi _2,\tau _3)\right] _{\tau _3=0}}_{=: \, {{}^{n}}{}{\mu }_{ij}(\xi _1,\xi _2)}\xi _3^n \end{aligned}$$

(11)

and insert also the Taylor series of $u_{i}\text {/}{a}$ and $u_{0 i}\text {}{a}$. Starting from (5), we end up with the Dirichlet conditions at the midplane boundary

$$\begin{aligned} 0 =&\sum _{i =1}^3 \sum _{n=0}^{\infty } \left\{ \mathbf {1 }_{P_{\xi 0}}(\{0,1\})\left[ \int _0^{\frac{b}{a}} \left( {{}^{n}}{}{u}_{0 i} - {{}^{n}}{}{u}_i\right) {{}^{n}}{}{\mathcal {M}}_{i1}(v_i)n_1\mathrm {d}\xi _2\right] \nonumber \right. \\&\left. \quad + \mathbf {2 }_{P_{\xi 0}}\left( \left\{ 0,{b}\text {/}{a}\right\} \right) \left[ \int _0^{1} \left( {{}^{n}}{}{u}_{0 i} - {{}^{n}}{}{u}_i\right) {{}^{n}}{}{\mathcal {M}}_{i2}(v_i)n_2\mathrm {d}\xi _1\right] \right\} .\end{aligned}$$

(12)

With

$$\begin{aligned} {{}^{n}}{}{\mathcal {M}}_{ij}&:= \int _{-\frac{h}{2a}}^{\frac{h}{2a}} \left( \dfrac{\sigma _{ij}}{G}\right) \xi _3^n \, \mathrm {d}\xi _3 , \end{aligned}$$

(13)

$$\begin{aligned} {{}^{n}}{}{\mathcal {M}}_{Ni\alpha }n_{\alpha }&:= \int _{-\frac{h}{2a}}^{\frac{h}{2a}} \left( \dfrac{g_i}{G}\right) \xi _3^n \, \mathrm {d}\xi _3 \end{aligned}$$

(14)

and

$$\begin{aligned} {{}^{n}}{}{p}_i :=&\int _{-\frac{h}{2a}}^{\frac{h}{2a}} \left( \dfrac{a\,f_i}{G}\right) \xi _3^n \, \mathrm {d}\xi _3 + \left( \dfrac{g_i}{G}\right) \left( \xi _1,\xi _2,\frac{h}{2a}\right) \left( \sqrt{3}\,c\right) ^n \nonumber \\&\quad + \left( \dfrac{g_i}{G}\right) \left( \xi _1,\xi _2,-\frac{h}{2a}\right) \left( -\sqrt{3}\,c\right) ^n, \end{aligned}$$

(15)

the stress resultants, the given stress resultants at the Neumann boundary $P_{\xi N}$ (subset of $\partial \varOmega _{xN}$ in the midplane) and the load resultants are defined, respectively. The quantities ${{}^{n}}{}{u}_{i}$ and ${{}^{n}}{}{u}_{0 i}$ describe the Taylor coefficients of the dimensionless displacement distribution and the Taylor coefficients of the given dimensionless displacement distribution at the Dirichlet boundary $P_{\xi 0}$ (subset of $\partial \varOmega _{x0}$ in the midplane). The indicator function $\mathbf{1 }_{S}(M)[F]$ is defined as the sum of F over the set of M which coincides with the subset $S \subset M$ in $\xi _1$-direction and the indicator function $\mathbf{2 }_{S}(M)[F]$ is defined analogously in $\xi _2$-direction. Finally, with $c =\nicefrac {h}{(\sqrt{12}\,a)}$ the plate parameter is introduced in (15). The problem in terms of (9), (10) and (12) is the so-called quasi-two-dimensional problem. It should be mentioned that it is equivalent to the 3D theory [21]. So, until now, we have neither made an approximation nor we have caused any error.

Equations (9), (10) and (12) are valid for the plate problem as well as for the disc problem. It can be shown that both problems are decoupled for at least monoclinic material (with the midplane as symmetry plane). In the following, we assume the material to be isotropic, so we can deal with the isolated plate problem. As a consequence, the Taylor series expansions of the dimensionless displacements are reduced to

$$\begin{aligned} \left( \dfrac{u_{\alpha }}{a}\right) =&{{}^{1}}{}{u}_{\alpha } \, \xi _3 + {{}^{3}}{}{u}_{\alpha }\,\xi _3^3 + {{}^{5}}{}{u}_{\alpha }\,\xi _3^5 + {{}^{7}}{}{u}_{\alpha }\,\xi _3^7 + \cdots \quad , \nonumber \\ \left( \dfrac{u_{3}}{a}\right) =&{{}^{0}}{}{u}_3\,\xi _3^0 + {{}^{2}}{}{u}_3\,\xi _3^2 + {{}^{4}}{}{u}_3\,\xi _3^4 + {{}^{6}}{}{u}_3\,\xi _3^6 + \cdots \quad . \end{aligned}$$

(16)

For the Taylor series expansions of the dimensionless volume forces, we get an analogous representation

$$\begin{aligned} \left( \dfrac{a\,f_{\alpha }}{G}\right) =&{{}^{1}}{}{f}_{\alpha } \, \xi _3 + {{}^{3}}{}{f}_{\alpha }\,\xi _3^3 + {{}^{5}}{}{f}_{\alpha }\,\xi _3^5 + {{}^{7}}{}{f}_{\alpha }\,\xi _3^7 + \cdots \quad ,\nonumber \\ \left( \dfrac{a\,f_{3}}{G}\right) =&{{}^{0}}{}{f}_3\,\xi _3^0 + {{}^{2}}{}{f}_3\,\xi _3^2 + {{}^{4}}{}{f}_3\,\xi _3^4 + {{}^{6}}{}{f}_3\,\xi _3^6 + \cdots \quad . \end{aligned}$$

(17)

Note, that the omitted summands of (16) and (17) belong to the disc problem. By splitting $g_i^-$ and $g_i^+$ into their symmetrical (S) and antisymmetrical (A) parts, we define the dimensionless surface loads (on the upper and lower face of the plate) for the plate problem:

$$\begin{aligned} \frac{g_{\alpha }^{A\pm }}{G}&=\pm \dfrac{g_{\alpha }^+-g_{\alpha }^-}{2G} =\pm \dfrac{{\hat{g}}_{\alpha }^+-{\hat{g}}_{\alpha }^-}{2}, \nonumber \\ \frac{g_{3}^{S\pm }}{G}&=\dfrac{g_3^+ + g_{3}^-}{2G} =\dfrac{{\hat{g}}_3^+ + {\hat{g}}_{3}^-}{2} . \end{aligned}$$

(18)

The surface loads $g_{\alpha }^{S\pm }$ and $g_{3}^{A\pm }$ belong to the disc problem and will not be treated. Note that, e.g., $g_3^+ =g_3^{S+} + g_3^{A+}$.

If we insert Hooke’s law,³ the kinematic relations and (16) in (13), the formulae (9), (10) and (12) represent a system of infinitely many PDEs for infinitely many displacement coefficients. Therefore, it cannot be solved without any approximation. Within the present paper, we will follow the consistent-approximation approach first introduced by Naghdi [15]. This approach is based on the fact that both the potential energy and the dual energy⁴ can be represented as series expansions in powers of $c^2$:

$$\begin{aligned} E_{\mathrm {pot}}({\mathbf {u}})&=Ga^3\left( (\bullet )+c^2(\bullet )+c^4(\bullet )+\cdots \right) , \end{aligned}$$

(19)

$$\begin{aligned} E_{\mathrm {dual}}(\varvec{\sigma })&=Ga^3\left( (\bullet )+c^2(\bullet )+c^4(\bullet )+\cdots \right) . \end{aligned}$$

(20)

This is achieved by the insertion of the Taylor series of the dimensionless displacements, volume loads and surface loads into the dimensionless potentials and subsequent integration in the thickness direction. Here, the plate parameter c appears quite naturally:

$$\begin{aligned} \int _{-\frac{h}{2a}}^{\frac{h}{2a}}\xi _3^k \, \mathrm {d}\xi _3 =\left\{ \begin{aligned}&\dfrac{1}{k+1}\dfrac{h}{a}\left( \sqrt{3}c\right) ^k&\quad \text {if } k \text { even}, \\&0&\quad \text {if } k \text { odd} . \end{aligned} \right. \end{aligned}$$

(21)

The main idea of the consistent-approximation approach is to keep all summands of the potentials up to a certain magnitude and neglect all summands of smaller magnitudes. Because they are very small for thin plates, powers of $c^2$ can estimate these magnitudes quite well. For example with $\nicefrac {h}{a} =\nicefrac {1}{10}$, it is $c^2 =8.33 \cdot 10^{-4}$ and $c^4 =6.94 \cdot 10^{-7}$. Thus, in an Nth-order theory, we consider all terms which are multiplied by $c^{2n}$, $n \le N$ and omit all terms which are multiplied by $c^{2m}$, $m > N$. We will further denote the omitted terms by $O(c^{2m})$, following the Big O notation. When we further talk about the magnitude, we refer to the powers of $c^2$. In contrast, with the order of a plate theory we designate the hierarchic equation systems. For the here introduced generic plate theories the order of the theory coincides with the highest power of $c^2$. Note that the presented approximation approach is completely different to the approach associated with the name Vekua,⁵ because with the latter the potentials are truncated with regard to the powers of the thickness variable and not the plate parameter!

So, for the two-dimensional equilibrium equations of the zeroth-order theory, we only have to take the terms with $c^0$ into account. If we do so, we get the generic PDE system of Table 1. Here, $()'$ denotes the derivative with respect to $\xi _1$, $()^{\bullet }$ denotes the derivative with respect to $\xi _2$, $\varDelta =()'' + ()^{\bullet \bullet }$ is the two-dimensional Laplace operator, the $(\bullet )$-symbol is the place holder for the displacement in the same column and RHS is the shorthand for right-hand side.

Note that the rows of the equation systems are ordered in dependence of the virtual displacements they are emerged from (cf. (9)). So, the equation for the first row is the one that is generated by the variation with respect to the virtual displacement with the smallest left-upper index, here ${{}^{0}}{}{v}_3$. Than the equations which result from the variation with respect to the virtual displacement with the next higher left-upper index follow, here with respect to ${{}^{1}}{}{v}_1$ and ${{}^{1}}{}{v}_2$. If, like in this case, the left-upper index is equal, the variation with respect to the virtual displacement with the smallest right lower index comes first. This ordering schema holds for every plate theory in this paper. Furthermore, all terms on the left-hand side of one row have to be summed up to build an PDE with the RHS.

Table 1 Zeroth-order generic PDE system

For the first-order theory, we have to consider, on the other hand, all terms with $c^0$ and $c^2$. The corresponding generic PDE system is shown in Table 2 with $\nu$ as Poisson’s ratio.

Table 2 First-order generic PDE-system

Finally, for the second-order theory, we have to consider all terms with $c^0$, $c^2$ and $c^4$. The corresponding generic PDE system is depicted in “Appendix” in Table 4.

3 Pseudo-reduction method

To reduce the PDE system emerging from an Nth-order generic plate theory, we make use of the pseudo-reduction method. In this method, we have to find a set of main variables, as few as possible, in order to reduce the PDE system to a few main PDEs, which are entirely written in the main variables, and several reduction PDEs, each written in the main variables and one non-main variable. Solving the main PDEs yields the main variables. The reduction PDEs can be solved afterward by insertion of the main variables. This gives us the non-main variables. So, the advantage of the pseudo-reduction method is that solving the reduction equations is much easier than solving the initial PDE system. All equations together, reduction PDEs and main PDEs, have to solve the initial PDE system identically (therefore it is no real reduction). In every step of the pseudo-reduction method, the consistent-approximation approach is applied so that we omit consequently all terms with the magnitude $c^{2(N+1)}$.

Because the PDEs are truncated power series in the characteristic plate parameter c, multiplications and divisions by powers of $c^2$ would change the accuracy of the given equations. For that reason, we have to treat each product of different powers of the plate parameter with the same displacement coefficient as independent variable. In consequence, we have more variables than equations and so the PDE system is underdetermined. To get additional equations, we apply multiplications by powers of the plate parameter $c^2$ to the PDE system. If we truncate the result again with the consistent-approximation approach, we indeed get valid equations. On the other hand, divisions by powers of the plate parameter $c^2$ are not allowed because they would lead to PDEs with displacements from higher-order plate theories (for details, cf. [19]).

As already mentioned in the Introduction, we will neglect edge-effects and therewith all “Reissner-like” variables in the present publication. These will be dealt with in a forth-coming paper. Therefore, we invariably can make use of the assumption that differentiations with respect to the dimensionless coordinates $\xi _1$ and $\xi _2$ does not change the magnitude of a function:

$$\begin{aligned} f({{}^{l}}{}{u}) =O\left( c^k\right) \quad \Leftrightarrow \quad \varDelta f({{}^{l}}{}{u}) =O\left( c^k\right) . \end{aligned}$$

(22)

So the magnitude of a PDE is not affected by differentiation (cf. [21]).

As the only main variable, we choose the deflection ${{}^{0}}{}{u}_3$ because it significantly describes the deformation of the plate (the influence of the slopes ${{}^{1}}{}{u}_1$ and ${{}^{1}}{}{u}_2$ is much smaller). Furthermore, in Sect. 7, it will turn out that this choice is appropriate because the results based on it fulfill the specific local conditions.

With ${{}^{0}}{}{u}_3$ as our main variable and by the use of assumption (22), pseudo-reduction of the 0th-order plate theory (cf. Table 1) yields:

$$\begin{aligned} {{}^{1}}{}{u}_1 =&-\left( {{}^{0}}{}{u}_3 \right) ' + O\left( c^2\right) , \end{aligned}$$

(23)

$$\begin{aligned} {{}^{1}}{}{u}_2 =&-\left( {{}^{0}}{}{u}_3 \right) ^{\bullet } + O\left( c^2\right) . \end{aligned}$$

(24)

If we insert (23) and (24) in equation (I) of Table 1, it is identically satisfied. So, there is no main PDE for the zeroth-order plate theory. In consequence, the corresponding stress resultants are identically zero, and therefore the zeroth-order generic plate theory allows only for rigid body motions:

$$\begin{aligned} {{}^{0}}{}{u}_3 =&\beta _{1} \xi _{1} + \beta _{2} \xi _{2} +\beta _{0} + O\left( c^2\right) \quad \quad \quad \text {with } \quad \beta _0, \beta _{\alpha } =\mathrm {const.} \quad , \end{aligned}$$

(25)

$$\begin{aligned} {{}^{1}}{}{u}_{\alpha } =&-\beta _{\alpha } + O\left( c^2\right) . \end{aligned}$$

(26)

Note: By the consistent-approximation approach, there normally have to be load resultants on the right-hand side of the equation system of Table 1. In this case equation, (I) would automatically yield

$$\begin{aligned} {{}^{0}}{}{p}_3 =0 + O\left( c^2\right) . \end{aligned}$$

(27)

Thus, all load resultants are of the magnitude $c^2$ and have to be considered for the first time in the first-order plate theory [8].

By applying the pseudo-reduction method to the first-order generic plate theory, we obtain from the equations (V) and (VI) (cf. Table 2):

$$\begin{aligned} c^{2} {}^{1}u_{1}&= -c^2\left( {}^{0}u_{3} \right) ' + O\left( c^4\right) , \end{aligned}$$

(28)

$$\begin{aligned} c^2 {}^{1}u_2&= -c^2\left( {}^{0}u_{3} \right) ^{\bullet }+ O\left( c^4\right) . \end{aligned}$$

(29)

With (28) and (29) we get from (IV):

$$\begin{aligned} c^2 {}^{2}u_{3} = \dfrac{\nu }{2(1-\nu )}c^2 \varDelta ^{0}u_{3} + O\left( c^4\right) . \end{aligned}$$

(30)

The remaining three equations from Table 2 contain the four independent non-main variables ${}^{1}u_1, {}^{1}u_2,$ $c^2 {}^{3} {u}_1, c^2 {}^{3} {u}_2$ and the two main variables ${{}^{0}}{}{u}_3$ and $c^2 {}^{0} {u}_3$. To establish in this underdetermined system a main PDE, we use the linear combination: $(\mathrm {I})-(\mathrm {II})'-(\mathrm {III})^{\bullet }$. So, contrary to the principle of the pseudo-reduction method, the emerging reduction PDEs have several non-main variables. Following that rule, we can eliminate five variables (which are expressed in two sets of linear combinations) and obtain

$$\begin{aligned} \dfrac{2}{1-\nu }c^2\varDelta \varDelta {{}^{0}}{}{u}_3 =&\dfrac{a}{h}\left( {{}^{0}}{}{p}_3+\left( {{}^{1}}{}{p}_1\right) '+\left( {{}^{1}}{}{p}_2\right) ^{\bullet }\right) + O\left( c^4\right) \nonumber \\ \Leftrightarrow \quad K\varDelta \varDelta {{}^{0}}{}{u}_3 =&a^3 \left( {{}^{0}}{}{P}_3+\left( {{}^{1}}{}{P}_1\right) '+\left( {{}^{1}}{}{P}_2\right) ^{\bullet }\right) + O\left( c^4\right) \quad , \end{aligned}$$

(31)

which is the classical Kirchhoff–Love plate-differential equation (with additional loads in $x_1$ and $x_2$ direction). Here, we made use of the dimensionalized load resultants

$$\begin{aligned} {{}^{n}}{}{P}_i =G\,{{}^{n}}{}{p}_i \end{aligned}$$

(32)

and the plate stiffness

$$\begin{aligned} K =2 \dfrac{G h c^2 a^2}{1-\nu } =\dfrac{E h^3}{12\left( 1-\nu ^2\right) } \end{aligned}$$

(33)

with E as Young’s modulus and G as shear modulus (characteristic stiffness). As it turns out, the first-order generic plate theory coincides with the classical plate theory of Kirchhoff. In [8], it has been shown that also the boundary conditions of the classical theory (involving Kirchhoff’s ersatz-shear forces) are recovered. Note that multiplications of the equations from Table 2 with $c^2$ lead only to the results (28) and (29) and thus are unnecessary.

Applying the pseudo-reduction method to the second-order plate theory proceeds analogously to the application for the first-order theory (cf. Table 4). So, for reasons of shortness, we omit the procedure for the second-order theory and refer to [8, Section 4.4] where it can be found in detail. There it turns out that the second-order generic plate theory coincides with the classical plate theory of Reissner.

So, the results of the generic plate theories are in accordance with the classical theories. But, as a great disadvantage, not all non-main variables in the first- and second-order generic plate theory can be reduced independently from each other (cf. linear combination above or [8, (47)]).

4 Modularity of the displacement coefficients

In their treatise [10], Kienzler and Schneider observed that the reduction equations contain only even powers of the plate parameter c (cf. (23), (24), (28) and (29)). So, they suggested to represent these coefficients in power series of $c^2$ themselves. We adopt this idea and split the displacement coefficients into the following infinite sum

$$\begin{aligned} {{}^{j}}{}{u}_i ={{}^{j}}{}{u}_i^0 + {{}^{j}}{}{u}_i^2 + {{}^{j}}{}{u}_i^4 + {{}^{j}}{}{u}_i^6 + \cdots \quad . \end{aligned}$$

(34)

Here, ${{}^{j}}{}{u}_i$ is any displacement coefficient and we call the corresponding summands displacement coefficient parts (dcp). The magnitude of the dcps is given by the right-upper index. For example, the dcp ${{}^{j}}{}{u}_i^{2}$ is of the magnitude $c^2$, whereas ${{}^{j}}{}{u}_i^{4}$ is of $c^4$.

With reference to (34), we can recognize that the reduction equations will change if we change the order of the plate theory. The reason for this is that we have to consider additional dcps if we increase the order of the plate theory. For example, in the zeroth-order theory, ${{}^{1}}{}{u}_1$ contains the dcp ${{}^{1}}{}{u}_1^{0}$, and in the first-order theory, it contains the sum of ${{}^{1}}{}{u}_1^{0}$ and ${{}^{1}}{}{u}_1^{2}$. Therefore, the reduction equations cannot remain unchanged among different orders.

Driven by this observation, we want to know if the reduction equations written in the dcps will change, too. So, we take at first a look at the first-order generic plate theory (cf. Table 2). Splitting the displacement coefficients with (34) and truncating the result with an error of $O(c^4)$ yields

$$\begin{aligned}&I: \quad \varDelta \left( {{}^{0}}{}{u}_3^{0} + {{}^{0}}{}{u}_3^{2}\right) + \left( {{}^{1}}{}{u}_1^{0} + {{}^{1}}{}{u}_1^{2}\right) ' + \left( {{}^{1}}{}{u}_2^{0} + {{}^{1}}{}{u}_2^{2}\right) ^{\bullet } + c^2 \varDelta {{}^{2}}{}{u}_3^{0} + 3c^2\left( {{}^{3}}{}{u}_1^{0}\right) ' \nonumber \\&\quad + 3c^2\left( {{}^{3}}{}{u}_2^{0}\right) ^{\bullet } \overset{O\left( c^4\right) }{=} -\dfrac{a}{h}{{}^{0}}{}{p}_3^{0} ,\nonumber \\&II: \quad \cdots \nonumber \\&\quad \vdots \quad \ddots \end{aligned}$$

(35)

It should be mentioned that we have also split the load resultants with respect to their magnitude into so-called load resultant parts (lrp)

$$\begin{aligned} {{}^{n}}{}{p}_i ={{}^{n}}{}{p}_i^{0} + {{}^{n}}{}{p}_i^{2} + {{}^{n}}{}{p}_i^{4} + {{}^{n}}{}{p}_i^{6} + \cdots \quad . \end{aligned}$$

(36)

One can easily comprehend this partition by observing equation (15) and (21). In contrast to the dcps, the right-upper index has to be added by two to show the magnitude of the lrps (cf. (27)). E.g., ${{}^{0}}{}{p}_3^{0}$ has the magnitude $c^{0+2}=c^2$ and ${{}^{4}}{}{p}_3^{4}$ has the magnitude $c^{4+2}=c^6$. Note that many lrps vanish because of their definition (15). For the lrps of the load resultant ${{}^{2}}{}{p}_3$, for example, the least possible magnitude is $c^4$ (because of the surface loads) and so ${{}^{2}}{}{p}_3^0$ is zero. To solve the PDE system (35), trivially both sides of the equations have to be equal. In detail, this implies that only terms of the same magnitude can be compared. Comparing terms of different magnitudes, however, yields to conflicts because, e.g., in

$$\begin{aligned} {{}^{0}}{}{u}_3^{0} =k \cdot {{}^{1}}{}{u}_1^{2} \quad \text {with} \quad k \in {\mathbb {R}} \end{aligned}$$

(37)

${{}^{0}}{}{u}_3^{0}$ has per definition the magnitude $c^0$ and therefore cannot contain ${{}^{1}}{}{u}_1^{2}$ of $c^2$ (and also vice versa). As a consequence, the PDE system (35) has to be separated into two PDE systems–one for $c^0$ and one for $c^2$–which have to be satisfied independently. If we truncate the system now with an error of $O(c^2)$, which means neglecting all terms of $c^2$, we get:

$$\begin{aligned}&I: \quad \varDelta \left( {{}^{0}}{}{u}_3^{0}\right) + \left( {{}^{1}}{}{u}_1^{0}\right) ' + \left( {{}^{1}}{}{u}_2^{0}\right) ^{\bullet } \overset{O\left( c^2\right) }{=} 0, \nonumber \\&II: \quad \cdots \nonumber \\&\quad \vdots \quad \ddots \end{aligned}$$

(38)

This system exactly corresponds to the system of Table 1 and because of that the dcps of both cases have to be equal. Next, we have to prove if the neglected terms which contain the zeroth-order dcps lead to conflicts. These terms are in the first-order theory $c^2\,{{}^{1}}{}{u}_1^0$ and $c^2\,{{}^{1}}{}{u}_2^0$ from (V) and (VI). According to Sect. 3, $c^2\,{{}^{1}}{}{u}_1$ and $c^2\,{{}^{1}}{}{u}_2$ are determined by (28) and (29), and therefore there is no conflict in the first-order equation system. So, we only have to prove that (28) and (29) coincide with the results of the zeroth-order dcps ${{}^{1}}{}{u}_1^0$ and ${{}^{1}}{}{u}_2^0$. This proof is made below (cf. (44) and (45)) and thus the unchangeability of the zeroth-order reduction equations, written in the dcps, among the zeroth- and first-order theory has been proved. Note, that this unchangeability implies further that also the dcps are unchangeable within a specific problem (because than the PDEs are solved). So, for shortness, we will call it in the following only the unchangeability of the dcps.

To show the systematic of our proof, we now take a look at the second-order generic plate theory (cf. Table 4). Inserting the splits (34) and (36) and truncating the result with an error of $O(c^6)$ yields to

$$\begin{aligned}&I: \quad \varDelta \left( {{}^{0}}{}{u}_3^{0} + {{}^{0}}{}{u}_3^{2} + {{}^{0}}{}{u}_3^{4}\right) + \left( {{}^{1}}{}{u}_1^{0} + {{}^{1}}{}{u}_1^{2} + {{}^{1}}{}{u}_1^{4}\right) ' + \left( {{}^{1}}{}{u}_2^{0} + {{}^{1}}{}{u}_2^{2} + {{}^{1}}{}{u}_2^{4}\right) ^{\bullet } \nonumber \\&\quad + c^2 \varDelta \left( {{}^{2}}{}{u}_3^{0} + {{}^{2}}{}{u}_3^{2}\right) + 3c^2\left( {{}^{3}}{}{u}_1^{0} + {{}^{3}}{}{u}_1^{2}\right) ' + 3c^2\left( {{}^{3}}{}{u}_2^{0} + {{}^{3}}{}{u}_2^{2}\right) ^{\bullet } \nonumber \\&\quad +\dfrac{9}{5}c^4\varDelta {{}^{4}}{}{u}_3^{0} + 9c^4\left( {{}^{5}}{}{u}_1^{0}\right) ' + 9c^4\left( {{}^{5}}{}{u}_2^{0}\right) ^{\bullet } \overset{O\left( c^6\right) }{=} -\dfrac{a}{h}{{}^{0}}{}{p}_3^{2}, \nonumber \\&II: \quad \cdots \nonumber \\&\quad \vdots \quad \ddots \end{aligned}$$

(39)

Here, for the reasons given above, the PDE system has to be separated into three PDE systems–for $c^0$, $c^2$ and $c^4$–which have to be satisfied independently. If we truncate (39) with an error of $O(c^2)$, the system (38) is recovered. So, the zeroth-order dcps from (39) have to be equal to the coefficients of the zeroth-order generic plate theory, too. If we instead truncate (39) with an error of $O(c^4)$, the system (35) is recovered. Thus, the first-order dcps from (39) have to be equal to the first-order dcps from (35) and, with the same line of reasoning like from above, the zeroth-order dcps fulfill the reduction equations $c^2\,{{}^{1}}{}{u}_1$ and $c^2\,{{}^{1}}{}{u}_2$ (cf. (44) and (45)). Until now, we again showed that the zeroth-order dcps are unchangeable among the zeroth- and first-order theory. To proof that both the zeroth- and first-order dcps are unchangeable among the zeroth-, first- and second-order theory, they must not lead to conflicts in the reduction equations of the second-order theory. Here, like at the end of Sect. 3, we refer to the results of [8, Section 4.4]. We checked all of those reduction equations with the zeroth- and first-order dcps (an example is treated in (46)) and as a consequence, we proved the unchangeability of the zeroth- and first-order dcps up to the second-order theory.

The exemplary and systematic proofs of the generic plate theories up to the second order lead us to assume strongly that all dcps are unchangeable over all orders of plate theories. Because this unchangeability of the dcps implies a modular structure of the displacement coefficients, we call this characteristic the modularity of the displacement coefficients (short: modularity). Furthermore, we assume that the modularity is also valid for all one- and two-dimensional theories (e.g., the beam theory) and even for general anisotropy, provided they are all based on the consistent-approximation approach and therefore have the same structure. This additional assumption is based on the fact that we also proved (not shown here) the unchangeability of the zeroth- and first-order dcps up to the second-order theory for the rod and beam theory.

With the modularity of the displacement coefficients, the results of Sect. 3 are accessible to a new interpretation. If we, e.g., apply the split (34) to the results (23) and (24), we get

$$\begin{aligned} {{}^{1}}{}{u}_1^0 \overset{O\left( c^2\right) }{=}&-\left( {{}^{0}}{}{u}_3^0\right) ', \end{aligned}$$

(40)

$$\begin{aligned} {{}^{1}}{}{u}_2^0 \overset{O\left( c^2\right) }{=}&-\left( {{}^{0}}{}{u}_3^0\right) ^{\bullet } . \end{aligned}$$

(41)

So, the dcps of $u_1$ and $u_2$ with the biggest magnitude have already been calculated and are fixed for all orders N. Applying the modularity to eqs. (28) and (29) yields

$$\begin{aligned} c^2 \left( {{}^{1}}{}{u}_1^0\right) \overset{O\left( c^4\right) }{=}&-c^2\left( {{}^{0}}{}{u}_3^0\right) ', \end{aligned}$$

(42)

$$\begin{aligned} c^2 \left( {{}^{1}}{}{u}_2^0\right) \overset{O\left( c^4\right) }{=}&-c^2\left( {{}^{0}}{}{u}_3^0\right) ^{\bullet } \end{aligned}$$

(43)

and this opens, despite all similarities to (28) and (29), a different perspective. Take, for example, eq. (28). Here, ${{}^{1}}{}{u}_1$ contains ${{}^{1}}{}{u}_1^0$ as well as ${{}^{1}}{}{u}_1^2$ and ${{}^{0}}{}{u}_3$ contains ${{}^{0}}{}{u}_3^0$ as well as ${{}^{0}}{}{u}_3^2$. So it would be wrong to conclude that ${{}^{1}}{}{u}_1 =-\left( {{}^{0}}{}{u}_3\right) '$ because eq. (28) can only give information about the dcps of $c^0$. In contrast, in eq. (42), there are on both sides only dcps of magnitude $c^0$ and they can be compared. Note that by using the modularity, multiplications or divisions by powers of $c^2$ are allowed. But if we do so, we have to increase or decrease the error $O(c^{2(N+1)})$. For eqs. (42) and (43), we consequently calculate

$$\begin{aligned}&c^2 \left( {{}^{1}}{}{u}_1^0+{{}^{1}}{}{u}_1^2+\cdots \right) =-c^2\left( {{}^{0}}{}{u}_3^0+{{}^{0}}{}{u}_3^2+\cdots \right) ' \nonumber \\&\quad \Rightarrow \quad c^2 \left( {{}^{1}}{}{u}_1^0\right) \overset{O\left( c^4\right) }{=} -c^2\left( {{}^{0}}{}{u}_3^0\right) ' \nonumber \\&\quad \Leftrightarrow \quad \quad {{}^{1}}{}{u}_1^0 \, \overset{O\left( c^2\right) }{=} -\left( {{}^{0}}{}{u}_3^0\right) ', \end{aligned}$$

(44)

$$\begin{aligned}&c^2 \left( {{}^{1}}{}{u}_2^0+{{}^{1}}{}{u}_2^2+\cdots \right) =-c^2\left( {{}^{0}}{}{u}_3^0+{{}^{0}}{}{u}_3^2+\cdots \right) ^{\bullet } \nonumber \\&\quad \Rightarrow \quad c^2 \left( {{}^{1}}{}{u}_2^0\right) \overset{O\left( c^4\right) }{=} -c^2\left( {{}^{0}}{}{u}_3^0\right) ^{\bullet } \nonumber \\&\quad \Leftrightarrow \quad {{}^{1}}{}{u}_2^0 \, \overset{O\left( c^2\right) }{=} -\left( {{}^{0}}{}{u}_3^0\right) ^{\bullet }. \end{aligned}$$

(45)

So, we finally end up with the same result as in (40) and (41), which is reasonable because of the modularity. Note that the multiplications and divisions by powers of $c^2$ are only equivalence transformations for dcps.

In addition to the results of Sect. 3, we exemplarily want to treat a second-order reduction equation with the modularity. Here, we choose equation (63) from [8, Section 4.4]. By identifying w and $\psi _{\alpha }$ with ${{}^{0}}{}{u}_3$ and ${{}^{1}}{}{u}_{\alpha }$ and adopting the modularity, we get

$$\begin{aligned} c^2\left( {{}^{0}}{}{u}_3\right) _{,\alpha } + c^2 {{}^{1}}{}{u}_{\alpha } + 3c^4{{}^{3}}{}{u}_{\alpha } \overset{O\left( c^6\right) }{=}&-\dfrac{1}{2}c^4\dfrac{4+\nu }{1-\nu }\varDelta \left( {{}^{0}}{}{u}_3\right) _{,\alpha } \nonumber \\ \Rightarrow \quad c^2\left( {{}^{0}}{}{u}_3^0 + {{}^{0}}{}{u}_3^2\right) _{,\alpha } + c^2 \left( {{}^{1}}{}{u}_{\alpha }^0 + {{}^{1}}{}{u}_{\alpha }^2\right) + 3c^4{{}^{3}}{}{u}_{\alpha }^0 \overset{O\left( c^6\right) }{=}&-\dfrac{1}{2}c^4\dfrac{4+\nu }{1-\nu }\varDelta \left( {{}^{0}}{}{u}_3^0\right) _{,\alpha } \quad . \end{aligned}$$

(46)

This result can be separated into two equations for different orders. In equation one, we treat all terms with the magnitude $c^2$:

$$\begin{aligned} c^2\left( {{}^{0}}{}{u}_3^0\right) _{,\alpha } + c^2 {{}^{1}}{}{u}_{\alpha }^0&=0 \nonumber \\ \Leftrightarrow \quad c^2 {{}^{1}}{}{u}_{\alpha }^0&=-c^2\left( {{}^{0}}{}{u}_3^0\right) _{,\alpha }\quad . \end{aligned}$$

(47)

With equation (47) the results (44) and (45) are recovered and therefore there is no conflict. In equation two, we treat all terms with the magnitude $c^4$. Under consideration of (49), (50), (52) and (53) and by neglecting all forces in $x_1$ and $x_2$ direction (simplification of [8]), we arrive at

$$\begin{aligned} c^2\left( {{}^{0}}{}{u}_3^2\right) _{,\alpha } + c^2 {{}^{1}}{}{u}_{\alpha }^2 + 3c^4{{}^{3}}{}{u}_{\alpha }^0&=-\dfrac{1}{2}c^4\dfrac{4+\nu }{1-\nu }\varDelta \left( {{}^{0}}{}{u}_3^0\right) _{,\alpha } \nonumber \\ \Leftrightarrow \quad 0&=0 \quad \surd \quad . \end{aligned}$$

(48)

Thus, it is proved that the reduction equation (46) is fulfilled by the zeroth- and first-order dcps.

5 Complete plate theories

With the modularity, we are now able to eliminate the disadvantage that not all non-main variables in the generic plate theories can be determined independently. For this purpose, we recall the generic PDE systems of the zeroth- and first-order plate theory and make use of the modularity. In the zeroth-order generic PDE system there are three dcps to determine: ${{}^{0}}{}{u}_3^0$, ${{}^{1}}{}{u}_1^0$ and ${{}^{1}}{}{u}_2^0$. The second and third equations in Table 1 yield the two reduction equations (40) and (41). So, the dcps ${{}^{1}}{}{u}_1^0$ and ${{}^{1}}{}{u}_2^0$ can each be determined with only dependence on the main variable ${{}^{0}}{}{u}_3^0$. Because of the linear dependence between the three zeroth-order equations (cf. Sect. 3), there is no main PDE in this order. Therefore, we add the main variable to the loads on the RHS of the zeroth-order equation system and treat it initially like given data. Thus, we end up with a simple-underdetermined PDE system.

In the first-order generic PDE system there are seven unknown dcps. At first, ${{}^{0}}{}{u}_3^0$ from the zeroth-order theory appears through the terms $c^2\,{{}^{1}}{}{u}_1^0$, $c^2\,{{}^{1}}{}{u}_2^0$ and $c^2\,{{}^{0}}{}{u}_3^0$ (cf. Table 2, II, III and IV). The other six dcps are: ${{}^{0}}{}{u}_3^2, {{}^{1}}{}{u}_1^2$, ${{}^{1}}{}{u}_2^2$, ${{}^{2}}{}{u}_3^0$, ${{}^{3}}{}{u}_1^0$ and ${{}^{3}}{}{u}_2^0$. Like in the zeroth-order theory, we add ${{}^{0}}{}{u}_3^2$ to the loads on the RHS of the PDE system. For the six unknown dcps on the left-hand side, we need six linear independent equations. But the generic PDE system of Table 2 provides only four linear independent equations, because the last two equations are equivalent to the second and third from the zeroth-order PDE system (cf. (44) and (45)). The missing equations can be obtained from the second-order generic plate theory. There, the fifth and sixth equation contain only dcps of the first order (cf. Table 4). So, we just have to increase the error of the last two equations of Table 2 to $O(c^6)$ to obtain six linear independent equations for the first-order theory. But, because of ${{}^{0}}{}{u}_3^2$ on the RHS, the resulting system is again a simple-underdetermined PDE system.

We call a plate theory complete, if we are able to determine all dcps in only dependence of the main variable (according to the principle of the pseudo-reduction method). By applying the pseudo-reduction method to the first-order simple underdetermined PDE system, we will show in Sect. 6 that there are only two reduction equations (for ${{}^{1}}{}{u}_1^2$ and ${{}^{1}}{}{u}_2^2$) depending on ${{}^{0}}{}{u}_3^2$. So, the main PDE is entirely written in the main variable ${{}^{0}}{}{u}_3^0$. As shown in Sect. 6, the main PDE of the second-order simple underdetermined PDE system (for construction cf. Fig. 2) is also entirely written in the main variable ${{}^{0}}{}{u}_3^2$. Thus, the supernumerary variable of the first-order simple underdetermined PDE system can be determined by treating the next-higher-order simple underdetermined PDE system. Therefore, we can finally call the simple first-order underdetermined PDE system a first-order complete plate theory.⁶ In the following, we assume that the supernumerary variable can always be calculated in the next higher-order simple underdetermined PDE system. So, all simple underdetermined PDE systems which are built like in Fig. 2 are complete plate theories. Calculations of complete plate theories to the order of ten have confirmed that assumption.

So, we have already received a zeroth- and first-order complete plate theories. To get an Nth-order complete plate theory, we have to use the scheme in Fig. 2. This scheme shows how to build a complete plate theory by using different magnitudes.

Fig. 2

Scheme for complete plate theories

At first, we ignore the colors and the dashed line: Every row in the scheme illustrates the instruction to build the complete plate theory of exactly one specific order. We start with the zeroth order and end with the fourth order. The vertical dots indicate that the next orders are built with the same systematic. On the axis below, we can see the total number of equations of one order. So, the zeroth-order theory has all in all three equations, the first-order theory has six equations and so on. Furthermore, we use the ordering scheme from the end of Sect. 2. Thus, we now know not only how many equations we need in one specific order but also which equations to choose.

For every row or rather every order the equations of the corresponding PDE system are divided in blocks of different magnitudes. These blocks are each depicted in a separate rectangular. In addition to the total number of equations, the axis below indicates also the total number of equations for every block and the sequence of the equations in the PDE system to be formed. So, for the first-order complete theory the first four equations (I–IV) have the magnitude $c^2$ and the next two equations (V–VI) are of $c^4$ (this structure agrees with the result from above). For the second-order complete plate theory the first four equations have the magnitude $c^4$, the next three are of $c^6$ and the last two are of $c^8$.

To explain the systematic structure of the further orders we now have to take the colors into account. Both colors, orange and green, indicate the seclusion of a block. If a block is orange, then it is not secluded and gets an extra equation in the next higher-order theory. Instead a green block has the maximum amount of equations. This amount will not change in any higher-order theory. For the next theories (third, fourth, ...), we always get three new equations, respectively. Two of them are found in the addition of one orange block (the last two equations) and one equation is added to the last block of the lower-order theory which therefore becomes secluded (green).

Furthermore, by increasing the order of a theory (e.g., first to second order) the magnitude of every block changes in a systematic way: The magnitude of every first block increases by two ($c^{2N}$) while increasing the order N of the theory. All other blocks of the same order N increase by two in sequence of their occurrence on the axis. So, the last block has always the magnitude $c^{4N}$. Note, if we omit the first equation, the green block always contains three equations and the orange block always contains two equations. For visualization we have marked this observation in Fig. 2 with a dashed line.

Table 3 First-order complete plate theory

With the found scheme of Fig. 2, we get for the first- and second-order complete plate theories the PDE systems of Tables 3 and 5 (in “Appendix”), respectively. In these systems, all equations have only the magnitude which is given in the scheme. So, in contrast to the generic PDE systems, we do not deal with lower-approximated equations. We omit, e.g., the equations V and VI of Table 2 in the first-order complete plate theory. Note that the omitted equations are fulfilled identically by lower-order dcps. To get to the systems of Tables 3 and 5, we inserted the already calculated lower-order dcps (e.g., ${{}^{1}}{}{u}_1^0$ in equation II of Table 2), made use of the lrps (cf. (36)) and put every summand which contains none of the $3(N+1)$ unknowns to the right-hand side of the PDE system.

So, with the results of this Section we can determine all non-main variables independently from each other and thus have eliminated the disadvantage of the generic plate theories. In addition, the pseudo-reduction method now can be applied like solving an ordinary linear equation system (e.g., with Cramer’s Rule) and this is much easier than the procedure described in [19].

6 Results and comparison with other authors

As basis for the comparison with other authors and for the next Section, we first reduce the PDE systems of the complete plate theories. The results of the zeroth-order complete plate theory are the equations (40) and (41). For the first-order PDE system in Table 3, we achieve the reduction equations

$$\begin{aligned} {{}^{1}}{}{u}_1^2&=\dfrac{a}{h}{{}^{1}}{}{p}_1^0 - \left( {{}^{0}}{}{u}_3^2\right) ' - \dfrac{3}{1-\nu }c^2\left( \varDelta {{}^{0}}{}{u}_3^{0}\right) ', \end{aligned}$$

(49)

$$\begin{aligned} {{}^{1}}{}{u}_2^2&=\dfrac{a}{h}{{}^{1}}{}{p}_2^0 - \left( {{}^{0}}{}{u}_3^2\right) ^{\bullet } - \dfrac{3}{1-\nu }c^2\left( \varDelta {{}^{0}}{}{u}_3^{0}\right) ^{\bullet }, \end{aligned}$$

(50)

$$\begin{aligned} {{}^{2}}{}{u}_3^0&=\dfrac{\nu }{2(1-\nu )}\varDelta {{}^{0}}{}{u}_3^{0}, \end{aligned}$$

(51)

$$\begin{aligned} {{}^{3}}{}{u}_1^0&=\dfrac{2-\nu }{6(1-\nu )}\left( \varDelta {{}^{0}}{}{u}_3^{0}\right) ', \end{aligned}$$

(52)

$$\begin{aligned} {{}^{3}}{}{u}_2^0&=\dfrac{2-\nu }{6(1-\nu )}\left( \varDelta {{}^{0}}{}{u}_3^{0}\right) ^{\bullet } \end{aligned}$$

(53)

and the main PDE

$$\begin{aligned} K \varDelta \varDelta {{}^{0}}{}{u}_3^{0} =a^3\left( {{}^{0}}{}{P}_3^{0} + \left( {{}^{1}}{}{P}_1^{0}\right) ' + \left( {{}^{1}}{}{P}_2^{0}\right) ^{\bullet }\right) . \end{aligned}$$

(54)

Omitting the loads in $x_1$- and $x_2$-direction, this equation is again the classical Kirchhoff–Love plate-differential equation (cf. (31)) and the quantities ${{}^{n}}{}{P}_i^{k}$ are the dimensionalized lrps. Finally, for the second-order PDE system of Table 5, we get

$$\begin{aligned} {{}^{1}}{}{u}_1^4 =&\dfrac{3}{2}\dfrac{a}{h}{{}^{1}}{}{p}_1^2 - \left( {{}^{0}}{}{u}_3^4\right) ' - \dfrac{3}{1-\nu }c^2\left( \varDelta {{}^{0}}{}{u}_3^{2}\right) ' - \dfrac{35}{192}\dfrac{\nu }{1-\nu }\dfrac{1}{c^2}\dfrac{a}{h}\left( {{}^{4}}{}{p}_3^4\right) ' \nonumber \\&\quad + \dfrac{45}{32}\dfrac{\nu }{1-\nu }\dfrac{a}{h}\left( {{}^{2}}{}{p}_3^2\right) ' - \dfrac{3}{64}\dfrac{(80+23\nu )}{1-\nu }c^2\dfrac{a}{h}\left( {{}^{0}}{}{p}_3^{0}\right) ' \nonumber \\&\quad - \dfrac{3}{4}\dfrac{1}{(1-\nu )}c^2\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) '' + \left( {{}^{1}}{}{p}_2^{0}\right) '^{\bullet }\right) , \end{aligned}$$

(55)

$$\begin{aligned} {{}^{1}}{}{u}_2^4 =&\dfrac{3}{2}\dfrac{a}{h}{{}^{1}}{}{p}_2^2 - \left( {{}^{0}}{}{u}_3^4\right) ^{\bullet } - \dfrac{3}{1-\nu }c^2\left( \varDelta {{}^{0}}{}{u}_3^{2}\right) ^{\bullet } - \dfrac{35}{192}\dfrac{\nu }{1-\nu }\dfrac{1}{c^2}\dfrac{a}{h}\left( {{}^{4}}{}{p}_3^4\right) ^{\bullet } \nonumber \\&\quad + \dfrac{45}{32}\dfrac{\nu }{1-\nu }\dfrac{a}{h}\left( {{}^{2}}{}{p}_3^2\right) ^{\bullet } - \dfrac{3}{64}\dfrac{(80+23\nu )}{1-\nu }c^2\dfrac{a}{h}\left( {{}^{0}}{}{p}_3^{0}\right) ^{\bullet } \nonumber \\&\quad - \dfrac{3}{4}\dfrac{1}{(1-\nu )}c^2\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) '^{\bullet } + \left( {{}^{1}}{}{p}_2^{0}\right) ^{\bullet \bullet }\right) , \end{aligned}$$

(56)

$$\begin{aligned} {{}^{2}}{}{u}_3^2 =&\dfrac{\nu }{2(1-\nu )}\varDelta {{}^{0}}{}{u}_3^{2} - \dfrac{3}{64}\dfrac{(7-30\nu )}{1-\nu }\dfrac{a}{h}{{}^{0}}{}{p}_3^{0} - \dfrac{35}{192}\dfrac{(1-2\nu )}{1-\nu }\dfrac{1}{c^4}\dfrac{a}{h}{{}^{4}}{}{p}_3^4 \nonumber \\&\quad + \dfrac{25}{32}\dfrac{(1-2\nu )}{1-\nu }\dfrac{1}{c^2}\dfrac{a}{h}{{}^{2}}{}{p}_3^2 + \dfrac{1}{8}\dfrac{1}{(1-\nu )}\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) ' + \left( {{}^{1}}{}{p}_2^{0}\right) ^{\bullet }\right) , \end{aligned}$$

(57)

$$\begin{aligned} {{}^{3}}{}{u}_1^2 =&\dfrac{(2-\nu )}{6(1-\nu )}\left( \varDelta {{}^{0}}{}{u}_3^2\right) ' + \dfrac{35}{576}\dfrac{1}{1-\nu }\dfrac{1}{c^4}\dfrac{a}{h}\left( {{}^{4}}{}{p}_3^4\right) ' - \dfrac{25}{96}\dfrac{1}{1-\nu }\dfrac{1}{c^2}\dfrac{a}{h}\left( {{}^{2}}{}{p}_3^2\right) ' \nonumber \\&\quad - \dfrac{1}{6}\dfrac{1}{c^2}\dfrac{a}{h}{{}^{1}}{}{p}_1^2 + \dfrac{1}{64}\dfrac{(39-16\nu )}{1-\nu }\dfrac{a}{h}\left( {{}^{0}}{}{p}_3^{0}\right) ' \nonumber \\&\quad + \dfrac{1}{24}\dfrac{\left( 3-2\nu \right) }{(1-\nu )}\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) '' + \left( {{}^{1}}{}{p}_2^{0}\right) '^{\bullet }\right) , \end{aligned}$$

(58)

$$\begin{aligned} {{}^{3}}{}{u}_2^2 =&\dfrac{(2-\nu )}{6(1-\nu )}\left( \varDelta {{}^{0}}{}{u}_3^2\right) ^{\bullet } + \dfrac{35}{576}\dfrac{1}{1-\nu }\dfrac{1}{c^4}\dfrac{a}{h}\left( {{}^{4}}{}{p}_3^4\right) ^{\bullet } - \dfrac{25}{96}\dfrac{1}{1-\nu }\dfrac{1}{c^2}\dfrac{a}{h}\left( {{}^{2}}{}{p}_3^2\right) ^{\bullet } \nonumber \\&\quad - \dfrac{1}{6}\dfrac{1}{c^2}\dfrac{a}{h}{{}^{1}}{}{p}_2^2 + \dfrac{1}{64}\dfrac{(39-16\nu )}{1-\nu }\dfrac{a}{h}\left( {{}^{0}}{}{p}_3^{0}\right) ^{\bullet } \nonumber \\&\quad + \dfrac{1}{24}\dfrac{\left( 3-2\nu \right) }{(1-\nu )}\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) '^{\bullet } + \left( {{}^{1}}{}{p}_2^{0}\right) ^{\bullet \bullet }\right) , \end{aligned}$$

(59)

$$\begin{aligned} {{}^{4}}{}{u}_3^0 =&\dfrac{175}{3456}\dfrac{(1-2\nu )}{1-\nu }\dfrac{1}{c^6}\dfrac{a}{h}{{}^{4}}{}{p}_3^4 - \dfrac{35}{192}\dfrac{(1-2\nu )}{1-\nu }\dfrac{1}{c^4}\dfrac{a}{h}{{}^{2}}{}{p}_3^2 + \dfrac{(27-70\nu +8\nu ^2)}{384(1-\nu )}\dfrac{1}{c^2}\dfrac{a}{h}{{}^{0}}{}{p}_3^{0} \nonumber \\&\quad - \dfrac{1}{48}(1+\nu )\dfrac{1}{c^2}\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) ' + \left( {{}^{1}}{}{p}_2^{0}\right) ^{\bullet }\right) ,\end{aligned}$$

(60)

$$\begin{aligned} {{}^{5}}{}{u}_1^0 =&-\dfrac{35}{3456}\dfrac{1}{1-\nu }\dfrac{1}{c^6}\dfrac{a}{h}\left( {{}^{4}}{}{p}_3^4\right) ' + \dfrac{7}{192}\dfrac{1}{1-\nu }\dfrac{1}{c^4}\dfrac{a}{h}\left( {{}^{2}}{}{p}_3^2\right) ' \nonumber \\&\quad - \dfrac{(59-32\nu +8\nu ^2)}{1920(1-\nu )}\dfrac{1}{c^2}\dfrac{a}{h}\left( {{}^{0}}{}{p}_3^{0}\right) ' - \dfrac{1}{240}(3-\nu )\dfrac{1}{c^2}\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) '' + \left( {{}^{1}}{}{p}_2^{0}\right) '^{\bullet }\right) , \end{aligned}$$

(61)

$$\begin{aligned} {{}^{5}}{}{u}_2^0 =&-\dfrac{35}{3456}\dfrac{1}{1-\nu }\dfrac{1}{c^6}\dfrac{a}{h}\left( {{}^{4}}{}{p}_3^4\right) ^{\bullet } + \dfrac{7}{192}\dfrac{1}{1-\nu }\dfrac{1}{c^4}\dfrac{a}{h}\left( {{}^{2}}{}{p}_3^2\right) ^{\bullet } \nonumber \\&\quad - \dfrac{(59-32\nu +8\nu ^2)}{1920(1-\nu )}\dfrac{1}{c^2}\dfrac{a}{h}\left( {{}^{0}}{}{p}_3^{0}\right) ^{\bullet } - \dfrac{1}{240}(3-\nu )\dfrac{1}{c^2}\dfrac{a}{h}\left( \left( {{}^{1}}{}{p}_1^{0}\right) '^{\bullet } + \left( {{}^{1}}{}{p}_2^{0}\right) ^{\bullet \bullet }\right) . \end{aligned}$$

(62)

And the second-order main PDE results in

$$\begin{aligned} K \varDelta \varDelta {{}^{0}}{}{u}_3^{2} =&a^3\left( {{}^{0}}{}{P}_3^{2} + \left( {{}^{1}}{}{P}_1^{2}\right) ' + \left( {{}^{1}}{}{P}_2^{2}\right) ^{\bullet } + \dfrac{\nu }{2(1-\nu )}\varDelta {{}^{2}}{}{P}_3^{2} \right. \nonumber \\&\left. - \dfrac{1}{10}\dfrac{(4+\nu )}{(1-\nu )}c^2\left( 6 \, \varDelta {{}^{0}}{}{P}_3^{0} + \left( \varDelta {{}^{1}}{}{P}_1^{0} \right) ' + \left( \varDelta {{}^{1}}{}{P}_2^{0} \right) ^{\bullet } \right) \right) . \end{aligned}$$

(63)

In Reissner’s theory only normal surface traction on the upper and lower face of the plate is considered. So, if we want to compare his theory with the second-order complete plate theory, we have to omit the surface loads in $x_1$- and $x_2$-direction and all volume loads. If we do so, we get from (63) to:

$$\begin{aligned} K \varDelta \varDelta {{}^{0}}{}{u}_3^{2} =&a^3\left( - \dfrac{6}{10}\dfrac{(4+\nu )}{(1-\nu )}c^2 \, \varDelta {{}^{0}}{}{P}_3^{0} + \dfrac{\nu }{2(1-\nu )}\varDelta {{}^{2}}{}{P}_3^{2} \right) \nonumber \\ \Leftrightarrow \quad K \varDelta \varDelta {{}^{0}}{}{u}_3^{2} =&a^3\dfrac{c^2}{10(1-\nu )}\left( 5\nu \dfrac{1}{c^2}\varDelta {{}^{2}}{}{P}_3^{2}-6(4+\nu )\varDelta {{}^{0}}{}{P}_3^{0}\right) . \end{aligned}$$

(64)

To further simplify (64) and compare it with Reissner’s theory, we have to look at the dependencies between the load resultants. Based on (15), we find with (17) and (18)

$$\begin{aligned} {{}^{0}}{}{p}_3^{0}= & {} \dfrac{h}{a}{{}^{0}}{}{f}_3 + \left( {\hat{g}}_3^+ + {\hat{g}}_3^- \right) , \quad {{}^{2}}{}{p}_3^{2} =c^2\dfrac{h}{a}{{}^{0}}{}{f}_3 + 3c^2\left( {\hat{g}}_3^+ + {\hat{g}}_3^- \right) , \nonumber \\ {{}^{4}}{}{p}_3^{4}= & {} \dfrac{9}{5}c^4\dfrac{h}{a}{{}^{0}}{}{f}_3 + 9c^4\left( {\hat{g}}_3^+ + {\hat{g}}_3^- \right) ,\nonumber \\ {{}^{0}}{}{p}_3^{2}= & {} c^2\dfrac{h}{a}{{}^{2}}{}{f}_3,\nonumber \\ {{}^{1}}{}{p}_1^{0}= & {} \sqrt{3}c\left( {\hat{g}}_1^+ - {\hat{g}}_1^- \right) , \quad {{}^{1}}{}{p}_1^{2} =c^2\dfrac{h}{a}{{}^{1}}{}{f}_1 ,\nonumber \\ {{}^{1}}{}{p}_2^{0}= & {} \sqrt{3}c\left( {\hat{g}}_2^+ - {\hat{g}}_2^- \right) , \quad {{}^{1}}{}{p}_2^{2} =c^2\dfrac{h}{a}{{}^{1}}{}{f}_2 , \end{aligned}$$

(65)

which in the case of negligible volume forces leads to the relations:

$$\begin{aligned} {{}^{2}}{}{p}_3^{2} =&3c^2{{}^{0}}{}{p}_3^{0}, \nonumber \\ {{}^{4}}{}{p}_3^{4} =&9c^4{{}^{0}}{}{p}_3^{0} . \end{aligned}$$

(66)

These definitions and relations are also valid for the dimensionalized lrps and thus, we can simplify equation (64) to

$$\begin{aligned} K \varDelta \varDelta {{}^{0}}{}{u}_3^{2} =&-a^3\left( \dfrac{3}{10}\dfrac{(8-3\nu )}{(1-\nu )}c^2 \, \varDelta {{}^{0}}{}{P}_3^{0} \right) . \end{aligned}$$

(67)

Until now, we cannot compare this result with Reissner’s theory because in his approach, the main PDE is expressed by an energetic mean of the transverse displacement ${{}^{0}}{}{u}_3$. In our complete plate theory, we can get that energetic mean from the Dirichlet conditions at the midplane boundary (12). But the derivation is very elaborate and thus will be the subject of a forthcoming paper. Here, we refer to Kienzler and Schneider [10] and obtain from their work

$$\begin{aligned} {{}^{K}}{}{w} ={{}^{0}}{}{u}_3 + \dfrac{3}{10}\dfrac{\nu }{1-\nu }c^2\varDelta {{}^{0}}{}{u}_3 \end{aligned}$$

(68)

for the energetic mean of the transverse displacement ${{}^{K}}{}{w}$. By applying the modularity to (68) the first and second-order parts of ${{}^{K}}{}{w}$

$$\begin{aligned} {{}^{K}}{}{w}^0 =&{{}^{0}}{}{u}_3^0, \end{aligned}$$

(69)

$$\begin{aligned} {{}^{K}}{}{w}^2 =&{{}^{0}}{}{u}_3^2 + \dfrac{3}{10}\dfrac{\nu }{1-\nu }c^2\varDelta {{}^{0}}{}{u}_3^0 \end{aligned}$$

(70)

are found. If we rearrange equation (70) and insert it into (67), we obtain

$$\begin{aligned} K \varDelta \varDelta \left( {{}^{K}}{}{w}^2 - \dfrac{3}{10}\dfrac{\nu }{1-\nu }c^2\varDelta {{}^{0}}{}{u}_3^0\right) =&-a^3\left( \dfrac{3}{10}\dfrac{(8-3\nu )}{(1-\nu )}c^2 \, \varDelta {{}^{0}}{}{P}_3^{0} \right) \nonumber \\ \Leftrightarrow \quad K \varDelta \varDelta {{}^{K}}{}{w}^2 =&-a^3\left( \dfrac{3}{10}\dfrac{(8-3\nu )}{(1-\nu )}c^2 \, \varDelta {{}^{0}}{}{P}_3^{0} \right) \nonumber \\&\quad + \dfrac{3}{10}\dfrac{\nu }{1-\nu }c^2 K \varDelta \varDelta \varDelta {{}^{0}}{}{u}_3^0. \end{aligned}$$

(71)

The second term on the right side can be further simplified by Kirchhoff’s equation (54). But, like Reissner, we first have to neglect all surface loads in $x_1$- and $x_2$-direction and all volume loads. Thus, we obtain from (54)

$$\begin{aligned} K \varDelta \varDelta {{}^{0}}{}{u}_3^{0} =a^3\,{{}^{0}}{}{P}_3^{0}. \end{aligned}$$

(72)

Finally, by applying the Laplace operator to this equation and inserting it into (71), we arrive at

$$\begin{aligned} K \varDelta \varDelta {{}^{K}}{}{w}^2 =&-a^3\left( \dfrac{6}{5}\dfrac{(2-\nu )}{(1-\nu )}c^2 \, \varDelta {{}^{0}}{}{P}_3^{0} \right) . \end{aligned}$$

(73)

Like the second-order generic plate theory, Reissner’s plate theory contains both the second- and first-order main PDE. The reason for that is because in a Nth-order generic plate theory we consider all terms which are multiplied by $c^{2n}$, $n \le N$, whereas in a Nth-order complete plate theory we only take terms of the magnitude $c^{2N}$ into account. Therefore, we have to add equation (72) to (73) in order to compare it with Reissner’s theory. So, by substitution of ${{}^{0}}{}{u}_3^0$ with ${{}^{K}}{}{w}^0$ (cf. (69)), we finally achieve

$$\begin{aligned} K \varDelta \varDelta \left( {{}^{K}}{}{w}^0 + {{}^{K}}{}{w}^2\right)&=a^3\left( {{}^{0}}{}{P}_3^{0} - \dfrac{6}{5}\dfrac{(2-\nu )}{(1-\nu )}c^2 \, \varDelta {{}^{0}}{}{P}_3^{0} \right) + O\left( c^6\right) \nonumber \\ \Rightarrow \quad K \varDelta \varDelta {{}^{K}}{}{w}&=a^3\left( {{}^{0}}{}{P}_3^{0} - \dfrac{6}{5}\dfrac{(2-\nu )}{(1-\nu )}c^2 \, \varDelta {{}^{0}}{}{P}_3^{0} \right) + O\left( c^6\right) . \end{aligned}$$

(74)

This result in fact corresponds to the classical Reissner plate theory and thus also to the second-order generic plate theory (cf. Sect. 3). But it does not coincide with Mindlin’s plate theory (cf. [10]). At this point, we would like to emphasize that Reissner’s and Mindlin’s theories are similar but not identical. Differences are elaborated in [16, 22].

The results of the complete plate theories of the zeroth up to the second order also coincide with the results of Kienzler and Schneider [10] after a change of variables from the transverse displacement of the middle surface ${{}^{0}}{}{u}_3$ to its energetically averaged main variable ${{}^{K}}{}{w}$. This coincidence is obviously reasonable because Kienzler and Schneider showed in their paper that their results also fulfill the specific local conditions (cf. Sect. 7). The only relevant difference, besides the omitting of loads in $x_1$- and $x_2$-direction and volume-loads, is the modularity of ${{}^{K}}{}{w}$. Like mentioned before, this variable emerges when evaluating the Dirichlet conditions at the midplane boundary (12). With it, we obtain the most compact representation of an Nth-order complete or generic plate theory. Moreover, by rewriting the complete plate theories as functions of ${{}^{K}}{}{w}$, we can investigate hidden patterns between theories of different orders. This will also be treated in an upcoming paper. Anyway, the averaged main variable is the only one that was not split in [10], while we here applied the modularity consequently to every variable. This leads us to different results of the dcps which, however, can be transformed into one another.

Due to the accordance between the complete plate theories and the results of Kienzler and Schneider, the comparison with other theories (e.g., Reddy’s theory) can be taken from their paper (cf. [10, Section 6]). So, we see that so far all results of the complete plate theories coincide with the classical theories of Kirchhoff and Reissner and there is no contradiction with the generic plate theories.

7 Fulfillment of the specific local conditions

Now, we prove whether the reduction equations of the complete plate theories fulfill also the specific local conditions. Because we only treat the plate problem within this paper, we have to apply the symmetric and antisymmetric parts of the surface loads according to (18) for the local Neumann boundary conditions on the upper and lower face of the plate. With ${\mathbf {n}}_u^{\mathrm {T}} =(0, 0, -1)$ and ${\mathbf {n}}_l^{\mathrm {T}} =(0, 0, 1)$ as the unit normal vectors of the upper and lower face of the plate (${\mathbf {a}}^{\mathrm {T}}$ is the transposition of ${\mathbf {a}}$ ), the following six local Neumann boundary conditions are found:

$$\begin{aligned} \begin{array}{ll} {\sigma _{33}}\mid _{\frac{h}{2a}} =g_3^{S+}, \qquad \qquad \qquad &{} {\sigma _{33}}\mid _{-\frac{h}{2a}} =-g_3^{S-}, \\ {\sigma _{31}}\mid _{\frac{h}{2a}} =g_1^{A+}, \qquad \qquad \qquad &{} {\sigma _{31}}\mid _{-\frac{h}{2a}} =-g_1^{A-}, \\ {\sigma _{32}}\mid _{\frac{h}{2a}} =g_2^{A+}, \qquad \qquad \qquad &{} {\sigma _{32}}\mid _{-\frac{h}{2a}} =-g_2^{A-} . \end{array} \end{aligned}$$

Due to Hooke’s law, the kinematic relations and the displacements (16), the stress $\sigma _{33}$ only contains the variable $\xi _3$ with odd powers. On the other hand, the stresses $\sigma _{31}$ and $\sigma _{32}$ are entirely written with even powers of $\xi _3$. Consequently, the relations

$$\begin{aligned} {\sigma _{33}}\mid _{\frac{h}{2a}} =&-{\sigma _{33}}\mid _{-\frac{h}{2a}}, \nonumber \\ {\sigma _{31}}\mid _{\frac{h}{2a}} =&{\sigma _{31}}\mid _{-\frac{h}{2a}}, \nonumber \\ {\sigma _{32}}\mid _{\frac{h}{2a}} =&{\sigma _{32}}\mid _{-\frac{h}{2a}} \end{aligned}$$

(75)

are observed. According to (18), the surface loads are axisymmetric in $x_3$-direction and point-symmetric in $x_1$- and $x_2$-direction. So, with these symmetries and the relations (75), the six local Neumann boundary conditions on the upper and lower face of the plate can be reduced to the following three:

$$\begin{aligned} 1) \quad {\sigma _{33}}\mid _{\frac{h}{2a}}&=g_3^{S+}, \\ 2) \quad {\sigma _{31}}\mid _{\frac{h}{2a}}&=g_1^{A+}, \\ 3) \quad {\sigma _{32}}\mid _{\frac{h}{2a}}&=g_2^{A+} . \end{aligned}$$

Together with the three equilibrium equations in the local form

$$\begin{aligned} 4) \quad \left( \sigma _{11}\right) _{,1} + \left( \sigma _{21}\right) _{,2} + \left( \sigma _{31}\right) _{,3}&=-f_1 a, \\ 5) \quad \left( \sigma _{12}\right) _{,1} + \left( \sigma _{22}\right) _{,2} + \left( \sigma _{32}\right) _{,3}&=-f_2 a, \\ 6) \quad \left( \sigma _{13}\right) _{,1} + \left( \sigma _{23}\right) _{,2} + \left( \sigma _{33}\right) _{,3}&=-f_3 a, \end{aligned}$$

there are overall six conditions to prove. It can be shown that the results of the complete plate theories up to the second order fulfill these six conditions a priori. To our best knowledge, this is the first time that the specific local conditions are fulfilled a priori by plate theories. Reddy [17], e.g., made ad-hoc assumptions (e.g., $\sigma _{33} =0$) and determined the resulting displacement coefficients partially by the local Neumann boundary conditions on the upper and lower face of the plate. And Kienzler and Schneider [10] determined free dcps by the specific local conditions. The displacement coefficients or dcps of both fulfill the specific local conditions if then only a posteriori.

Exemplary, we take the last equilibrium Eq. 6) and apply Hooke’s law, the kinematic relations, (16), (17) and the modularity to it. In this way, we get:

$$\begin{aligned}&\left( \sigma _{13}\right) _{,1} + \left( \sigma _{23}\right) _{,2} + \left( \sigma _{33}\right) _{,3} =-f_3 a \\&\quad \Rightarrow \; G\Big [\left( {{}^{0}}{}{u}_3^0 + {{}^{0}}{}{u}_3^2 + {{}^{0}}{}{u}_3^4\right) '' + \left( {{}^{2}}{}{u}_3^0 + {{}^{2}}{}{u}_3^2\right) ''\xi _3^2 + \left( {{}^{4}}{}{u}_3^0\right) ''\xi _3^4 + \left( {{}^{1}}{}{u}_1^0 + {{}^{1}}{}{u}_1^2 + {{}^{1}}{}{u}_1^4\right) ' \\&\qquad + 3\left( {{}^{3}}{}{u}_1^0 + {{}^{3}}{}{u}_1^2\right) '\xi _3^2 + 5\left( {{}^{5}}{}{u}_1^0\right) '\xi _3^4 + \left( {{}^{0}}{}{u}_3^0 + {{}^{0}}{}{u}_3^2 + {{}^{0}}{}{u}_3^4\right) ^{\bullet \bullet }\\&\qquad + \left( {{}^{2}}{}{u}_3^0 + {{}^{2}}{}{u}_3^2\right) ^{\bullet \bullet }\xi _3^2 + \left( {{}^{4}}{}{u}_3^0\right) ^{\bullet \bullet }\xi _3^4 + \left( {{}^{1}}{}{u}_2^0 + {{}^{1}}{}{u}_2^2 + {{}^{1}}{}{u}_2^4\right) ^{\bullet } \\&\qquad + 3\left( {{}^{3}}{}{u}_2^0 + {{}^{3}}{}{u}_2^2\right) ^{\bullet }\xi _3^2 + 5\left( {{}^{5}}{}{u}_2^0\right) ^{\bullet }\xi _3^4 + \dfrac{2(1-\nu )}{1-2\nu }\left( 2\left( {{}^{2}}{}{u}_3^0 + {{}^{2}}{}{u}_3^2\right) + 12{{}^{4}}{}{u}_3^0 \, \xi _3^2\right) \\&\qquad + \dfrac{2\nu }{1-2\nu }\bigg (\left( {{}^{1}}{}{u}_1^0 + {{}^{1}}{}{u}_1^2 + {{}^{1}}{}{u}_1^4\right) ' + 3\left( {{}^{3}}{}{u}_1^0 + {{}^{3}}{}{u}_1^2\right) '\xi _3^2 + 5\left( {{}^{5}}{}{u}_1^0\right) '\xi _3^4 \\&\qquad + \left( {{}^{1}}{}{u}_2^0 + {{}^{1}}{}{u}_2^2 + {{}^{1}}{}{u}_2^4\right) ^{\bullet } + 3\left( {{}^{3}}{}{u}_2^0 + {{}^{3}}{}{u}_2^2\right) ^{\bullet }\xi _3^2 + 5\left( {{}^{5}}{}{u}_2^0\right) ^{\bullet }\xi _3^4\bigg )\Big ] \\&\quad =-G\left( {{}^{0}}{}{f}_3 + {{}^{2}}{}{f}_3 \, \xi _3^2 + {{}^{4}}{}{f}_3 \, \xi _3^4\right) . \end{aligned}$$

The comparison of the terms with the variable $\xi _3^0$ and the magnitude $c^0$ leads under consideration of (40), (41) and (51) to:

$$\begin{aligned}&\left( {{}^{0}}{}{u}_3^0\right) '' + \left( {{}^{1}}{}{u}_1^0\right) ' + \left( {{}^{0}}{}{u}_3^0\right) ^{\bullet \bullet } + \left( {{}^{1}}{}{u}_2^0\right) ^{\bullet } + \dfrac{4(1-\nu )}{1-2\nu }{{}^{2}}{}{u}_3^0 \\&\quad + \dfrac{2\nu }{1-2\nu }\left( \left( {{}^{1}}{}{u}_1^0\right) ' + \left( {{}^{1}}{}{u}_2^0\right) ^{\bullet }\right) =0 \\&\quad \Leftrightarrow \quad 0 =0 \quad \surd \quad . \end{aligned}$$

The comparison of the terms with the variable $\xi _3^0$ and the magnitude $c^2$ leads under consideration of (32), (33), (49), (50), (54), (57) and (65) to:

$$\begin{aligned}&\left( {{}^{0}}{}{u}_3^2\right) '' + \left( {{}^{1}}{}{u}_1^2\right) ' + \left( {{}^{0}}{}{u}_3^2\right) ^{\bullet \bullet } + \left( {{}^{1}}{}{u}_2^2\right) ^{\bullet } + \dfrac{4(1-\nu )}{1-2\nu }{{}^{2}}{}{u}_3^2 \\&\quad + \dfrac{2\nu }{1-2\nu }\left( \left( {{}^{1}}{}{u}_1^2\right) ' + \left( {{}^{1}}{}{u}_2^2\right) ^{\bullet }\right) =-{{}^{0}}{}{f}_3 \\&\quad \Leftrightarrow 0 =0 \quad \surd \quad . \end{aligned}$$

Finally, the comparison of the terms with the variable $\xi _3^2$ and the magnitude $c^0$ leads under consideration of (32), (33), (51), (52), (53), (54), (60) and (65) to:

$$\begin{aligned}&\left( {{}^{2}}{}{u}_3^0\right) '' + 3\left( {{}^{3}}{}{u}_1^0\right) ' + \left( {{}^{2}}{}{u}_3^0\right) ^{\bullet \bullet } + 3\left( {{}^{3}}{}{u}_2^0\right) ^{\bullet } + \dfrac{24(1-\nu )}{1-2\nu } {{}^{4}}{}{u}_3^0 \\&\quad + \dfrac{2\nu }{1-2\nu }\left( 3\left( {{}^{3}}{}{u}_1^0\right) ' + 3\left( {{}^{3}}{}{u}_2^0\right) ^{\bullet }\right) =0\\&\quad \Leftrightarrow 0 =0 \quad \surd \quad . \end{aligned}$$

All other combinations of $c^n$ and $\xi _3^k$ cannot be checked within the framework of a second-order complete plate theory because they require higher-order dcps.

It has been proved in [20] that generic plate theories are Nth-order series expansions of the exact solution of the 3D theory. Kienzler and Kashtalyan [9] confirmed this result by a particular example for which a closed-form solution of the 3D theory is available. It is thus obvious that the reduction equations of the complete plate theories satisfy the specific local conditions up to their respective order of approximation. So, our result is reasonable.

After determination of additional dcps through the specific local conditions, the two coefficients ${{}^{0}}{}{u}_3^4$ and ${{}^{0}}{}{u}_3^6$ still remain undetermined in [10]. The above mentioned paper [9] of Kienzler and Kashtalyan solved that problem by employing an exact solution of the three dimensional theory of linear elasticity for a special case of plate support and loading. This exact solution is developed into a Taylor series and then compared with the displacement ansatz of Kienzler and Schneider (cf. [10, (57)]) under the same loading and supporting conditions term by term. The comparison gives the reduction PDEs of ${{}^{0}}{}{u}_3^4$ and ${{}^{0}}{}{u}_3^6$. As it turns out, the third and fourth-order complete plate theories lead to the same outcome for both reduction PDEs but in a more systematic way.

8 Conclusion

By partial integration only in $\xi _1$- and $\xi _2$-direction, substitution of the test functions by its Taylor series and applying the fundamental lemma of the calculus of variations, we obtain from the first variations of the dimensionless potential energy and its dimensionless complement the quasi two-dimensional problem. This problem contains the two-dimensional equilibrium equations, the Neumann conditions at the midplane boundary and the Dirichlet conditions at the midplane boundary. By assuming the material to be isotropic, we are able to treat the plate problem independently from the disc problem. In the quasi-two-dimensional problem, the geometric constant $c =\nicefrac {h}{\left( \sqrt{12}a\right) }$ emerges in even powers. Because of its fast decaying behavior, we use it to approximate the quasi-two-dimensional problem. With this so-called consistent-approximation approach, we achieve a Nth-order generic plate theory by containing all terms with the magnitude $c^{2m}, \,m \le N$ and omitting all terms with the magnitude $c^{2n}, \, n>N$. Thus, we obtain PDE systems with $3(N+1)$ equations and as many unknown displacement coefficients. To reduce these PDE systems we apply the pseudo-reduction method. As a result, the main PDE, which is the only one that needs to be solved, and a set of reduction PDEs, that express the non-main variables in terms of the main variable, are obtained.

The zeroth- and first-order generic plate theories are calculated and it is shown that the main PDE of the first order coincides with the classical Kirchhoff–Love plate theory. But, as a great disadvantage, not all non-main variables in the first- and second-order generic plate theory can be determined independently. By adopting a split of the displacement coefficients, introduced by Kienzler and Schneider [10], it is proved up to the second-order generic plate theory that the zeroth- and first-order main and reduction PDEs written in the dcps remain unchanged. Moreover, we assume that this unchangeability is a characteristic of any-order generic plate theories and call it modularity of the displacement coefficients. We presume this modularity also for all one- and two-dimensional generic theories (e.g., the beam theory) and even for general anisotropy. As justification for our assumption, we use the systematics of our proof and analogous proofs for the generic rod and beam theories.

Applied to the zeroth-, first- and second-order generic plate theories, the modularity shows that partially the same reduction PDEs appear in different orders. We identify this outcome as reason why not all non-main variables can be determined independently from each other. We solve this problem by putting equations from different orders of the generic plate theories together to so-called complete plate theories. For example, the first-order complete plate theory receives its first four equations from the first-order generic plate theory and the last two equations from the second-order generic plate theory. These theories are called complete because all dcps can be determined in only dependence of the main variable. By searching for complete plate theories of second and third order, a scheme to set up a complete plate theory of any order is found. A proof that the complete plate theories, gained by that scheme, always lead to systems, where every dcp can be determined in only dependence of the main variable, is subject of ongoing research.

The results of the zeroth-, first- and second-order complete plate theories are inserted in the local form of the equilibrium equations and the local Neumann boundary conditions on the upper and lower face of the plate. It is shown that they fulfill a priori the specific local conditions in the framework of the approximation under consideration.

By comparing the results of the complete plate theories with other authors, it is shown that they coincide with the classical theories of Kirchhoff and Reissner and the results of Kienzler and Schneider [10]. For the latter, the specific local conditions were also fulfilled, however, a posteriori.

Last but not least, by calculating the third- and fourth-order complete plate theories, we easily achieve the PDEs for ${{}^{0}}{}{u}_3^4$ and ${{}^{0}}{}{u}_3^6$. These two dcps, which could not be calculated in [10], were previously elaborately determined in Kienzler and Kashtalyan [9].

Appendix

See Tables 4 and 5.

Table 4 Second-order generic PDE-system

Table 5 Second-order complete plate theory