1 Introduction

Mechanics of metamaterials is gaining an increased interest owing to additive manufacturing technologies allowing us to craft sophisticated structures with different length scales. For weight reduction, material is saved by introducing a substructure. Substructure-related change in materials response is already known [1,2,3], studied under different assumptions [4,5,6,7,8,9], and verified experimentally [10,11,12,13]. Substructure-related change leads to metamaterials, and this phenomenon is explained by theoretical arguments by assuming conventional elasticity in the smaller length scale (microscale) leading to generalized elasticity in the larger length scale (macroscale) [14,15,16,17,18].

For constructing theories, different length scales are often incorporated in science. For example, consider the microscale being simply the molecular structure or the lattice structure in a crystalline material conferring anisotropy upon the response at the macroscale [19,20,21,22]. Another prominent structure-related anisotropy occurs in composite materials, where the microscale is composed of fibers and matrix. The alignment of fibers, and how different plies are stacked up, causes the anisotropy as well as values of effective parameters at the macroscale [23,24,25,26,27]. Porous materials are frequently modeled as a full material with voids as given inclusions at the microscale, we refer to [28,29,30,31,32,33]. Additive manufacturing is capable of building metamaterials as demonstrated in [34,35,36,37,38,39]. Also adding texture in 3-D printing introduces a substructure. Especially in metal 3-D printing technologies, the microscale itself is anisotropic [40,41,42]. We emphasize that at the macroscale, in all examples above, the microscale structure is not detectable such that the materials substructure is smeared out that is called homogenization.

As applied to generalized mechanics, the use of homogenization techniques is challenging [43, 44], since generalized mechanics is still evolving [45,46,47]. There exist different homogenization techniques [48,49,50,51,52,53,54]. In generalized mechanics [55, 56], often a representative volume element (RVE) is exploited as in [57, 58], although the use of an RVE in generalized mechanics is difficult to justify [59, 60]. Yet there exist direct approaches [61, 62] by computational homogenization methods [63,64,65,66,67,68] as well as techniques based on gamma-convergence [69, 70]. By means of asymptotic analysis [71,72,73,74] as already applied in [75,76,77,78], we decompose variables into global and local variations [79,80,81], and this separation makes possible to solve the elasticity problem analytically, leading to closed form relations between (known) parameters at the microscale and (sought after) parameters at the macroscale. This approach has been applied in one-dimensional problems for reinforced composites [82, 83] and in two-dimensional continuum [84,85,86,87] mostly numerically. From extensive studies [88,89,90,91,92,93], we know that this method is adequate for determining metamaterials parameters. We briefly explain the derivation based on [94] and extend the method to the three-dimensional case by providing a numerical procedure by means of the finite element method (FEM). Especially in honeycomb type, infill substructure is our interest [95]. The substructure introduces higher order effects as expected, and we determine the parameters by a computational homogenization based on the asymptotic analysis. The code uses open-source packages under GNU public license [96] from the FEniCS project [97], and we make the code publicly available in [98] in order to increase the scientific exchange.

2 Asymptotic homogenization

We begin with the assertion that the deformation energy at the microscale is equivalent to the deformation energy at the macroscale,

$$\begin{aligned} \begin{aligned} \int _{\Omega } { w^\text {m}} \,\mathrm {d}V = \int _{\Omega } { w^\text {M}} \,\mathrm {d}V,\\ \end{aligned}\end{aligned}$$
(1)

for the same domain, \(\Omega \), occupied by the continuum body. We use the standard continuum mechanics notation with \(\,\mathrm {d}V\) meaning the infinitesimal volume element, expressed in Cartesian coordinates as \(\,\mathrm {d}V=\,\mathrm {d}x \,\mathrm {d}y \,\mathrm {d}z\). There is only one coordinate system used for both scales. We use a material frame, so the location of material particles is denoted by \(\varvec{X}=(X_1,X_2,X_3)=(x,y,z)\). Furthermore, we use “m” and “M” denoting microscale and macroscale, respectively. The domains for both scales are equivalent, large enough for allowing homogenization and small enough such that the substructure has a significant effect at the macroscale. We emphasize that a large enough domain—analogously macroscale with a large enough length scale—converges to the classical elasticity approach.

Since we model an elastic body, the deformation energy depends solely on space derivatives of displacements. At each length scale, there exists one displacement field, \(u^\text {m}_i\), \(u^\text {M}_i\). We stress that displacements and their derivatives are different such that the energy density is different in each position. Nevertheless, for the whole body, the total energy is equivalent at both scales. This assertion is the key axiom in nearly all homogenization theories based on the intuition that the energy applied on the body is the same although we observe a different displacement recorded by a 10 MP camera via digital image correlation (DIC) compared to a displacement field captured under a microscope.

We simplify the analysis by assuming that the system at the microscale is composed of linear elastic material(s) such that the energy is quadratic in displacement gradients given by strains, \(\varvec{\varepsilon }^\text {m}\), with a known stiffness tensor, \(\varvec{C}^\text {m}\), as follows:

$$\begin{aligned} \begin{aligned} w^\text {m}= \frac{1}{2} C^\text {m}_{ijkl} \varepsilon ^\text {m}_{ij} \varepsilon ^\text {m}_{kl} , \ \ \varepsilon ^\text {m}_{ij} = \frac{1}{2} ( u^\text {m}_{i,j} + u^\text {m}_{j,i} + u^\text {m}_{k,i} u^\text {m}_{k,j} ), \end{aligned} \end{aligned}$$
(2)

where the comma denotes a space derivative in \(\varvec{X}\), and we understand Einstein’s summation convention over repeated indices. For the sake of simplicity, we henceforth use linearized strain measure,

$$\begin{aligned} \begin{aligned} \varepsilon ^\text {m}_{ij} = \frac{1}{2} ( u^\text {m}_{i,j} + u^\text {m}_{j,i} ), \end{aligned}\end{aligned}$$
(3)

and the usual (minor) symmetries of the stiffness, \(C^\text {m}_{ijkl}=C^\text {m}_{jikl}=C^\text {m}_{ijlk}\), we obtain

$$\begin{aligned} \begin{aligned} w^\text {m}= \frac{1}{2} C^\text {m}_{ijkl} u^\text {m}_{i,j} u^\text {m}_{k,l}. \end{aligned}\end{aligned}$$
(4)

The system at the microscale possesses different materials. For the substructure, for example in an additively manufactured porous structure, we model the structure itself with its stiffness tensor and the voids with a nearly zero stiffness. In other words, the material is heterogeneous at the microscale. At the macroscale, the system is assumed to be homogeneous and to obey materially and geometrically linear strain gradient elasticity modeled by the following deformation energy density:

$$\begin{aligned} \begin{aligned} w^\text {M}= \frac{1}{2} C^\text {M}_{ijkl} u^\text {M}_{i,j} u^\text {M}_{k,l} + \frac{1}{2} D^\text {M}_{ijklmn} u^\text {M}_{i,jk} u^\text {M}_{l,mn} + G^\text {M}_{ijklm} u^\text {M}_{i,j} u^\text {M}_{k,lm}, \end{aligned}\end{aligned}$$
(5)

with analogous symmetries \(C^\text {M}_{ijkl}=C^\text {M}_{jikl}=C^\text {M}_{ijlk}\) as well as \(D^\text {M}_{ijklmn}=D^\text {M}_{ijklmn}=D^\text {M}_{ikjlmn}=D^\text {M}_{lmnijk}\) and \(G^\text {M}_{ijklm}=G^\text {M}_{jiklm}=G^\text {M}_{ijkml}\). We stress that \(\varvec{G}^\text {M}=0\) if the macroscale is of centro-symmetric substructure and \(\varvec{D}^\text {M}=0\) leads to conventional elasticity with substructure-related anisotropy without higher-order (strain gradient) terms.

First, we introduce a so-called geometric center:

$$\begin{aligned} \begin{aligned} \overset{\text {c}}{\varvec{X}} = \frac{1}{V} \int _{\Omega } \varvec{X} \,\mathrm {d}V, \end{aligned}\end{aligned}$$
(6)

and, assuming enough continuity, approximate the macroscale displacement by the Taylor expansion around the value at the geometric center by truncating after quadratic terms. The choice of quadratic terms is justified by the nonlocality of the theory; in other words, we aim for the strain gradient theory incorporating second derivatives. All higher terms than the second derivative will be neglected. The expansion of displacement gradients reads

$$\begin{aligned} \begin{aligned} {u^\text {M}_i}(\varvec{X}) = {u^\text {M}_i}\Big |_{\overset{\text {c}}{\varvec{X}}} + u^\text {M}_{i,j} \Big |_{\overset{\text {c}}{\varvec{X}}} (X_j-\overset{\text {c}}{X}_j) + \frac{1}{2} u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{\varvec{X}}} (X_j-\overset{\text {c}}{X}_j) (X_k-\overset{\text {c}}{X}_k) . \end{aligned}\end{aligned}$$
(7)

Since \({u^\text {M}_i}\Big |_{\overset{\text {c}}{\varvec{X}}}\) is a vector evaluated at \(\overset{\text {c}}{\varvec{X}}\), its gradient vanishes leading to

$$\begin{aligned} \begin{aligned} u^\text {M}_{i,l}(\varvec{X})&= u^\text {M}_{i,j} \Big |_{\overset{\text {c}}{\varvec{X}}} \delta _{jl} + \frac{1}{2} u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{\varvec{X}}} ( \delta _{jl} (X_k-\overset{\text {c}}{X}_k) + (X_j-\overset{\text {c}}{X}_j) \delta _{kl} ), \\&= u^\text {M}_{i,l} \Big |_{\overset{\text {c}}{\varvec{X}}} + u^\text {M}_{i,lk} \Big |_{\overset{\text {c}}{\varvec{X}}} (X_k-\overset{\text {c}}{X}_k) , \\ u^\text {M}_{i,lm}(\varvec{X})&= u^\text {M}_{i,lk} \Big |_{\overset{\text {c}}{\varvec{X}}} \delta _{km} = u^\text {M}_{i,lm} \Big |_{\overset{\text {c}}{\varvec{X}}}. \end{aligned}\end{aligned}$$
(8)

Second, we introduce spatial averaging for displacement gradients by using the latter expansions and the fact that terms evaluated at \(\overset{\text {c}}{\varvec{X}}\) are constant within the domain

$$\begin{aligned} \begin{aligned} \langle {u}_{i,j}^\text {M}\rangle&=\frac{1}{V}\int _{\Omega } u^\text {M}_{i,j} \,\mathrm {d}V= u^\text {M}_{i,j}\Big |_{\overset{\text {c}}{\varvec{X}}} + u^\text {M}_{i,jk}\Big |_{\overset{\text {c}}{\varvec{X}}} \bar{I}_k, \\ \langle {u}_{i,jk}^\text {M}\rangle&=\frac{1}{V}\int _{\Omega } u^\text {M}_{i,jk}\,\mathrm {d}V= u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{\varvec{X}}}, \end{aligned}\end{aligned}$$
(9)

with

$$\begin{aligned} \begin{aligned} \bar{I}_k = \frac{1}{V} \int _{\Omega } (X_k-\overset{\text {c}}{X}_k) \,\mathrm {d}V = \frac{1}{V} \int _{\Omega } X_k \,\mathrm {d}V - \frac{1}{V} \int _\Omega \overset{\text {c}}{X}_k \,\mathrm {d}V = 0, \end{aligned}\end{aligned}$$
(10)

since integration is additive and we have inserted Eq. (6). Thus, we obtain

$$\begin{aligned} \begin{aligned} \langle {u}_{i,j}^\text {M}\rangle = u^\text {M}_{i,j}\Big |_{\overset{\text {c}}{\varvec{X}}} , \ \ \langle {u}_{i,jk}^\text {M}\rangle = u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{\varvec{X}}}. \end{aligned}\end{aligned}$$
(11)

Third, we use the spatial averaged values in the expansions (7) and (8)

$$\begin{aligned} \begin{aligned} u_i^\text {M}(\varvec{X})&= u^\text {M}_i\Big |_{\overset{\text {c}}{\varvec{X}}} + \langle {u}_{i,j}^\text {M}\rangle (X_j-\overset{\text {c}}{X}_j) + \frac{1}{2} \langle {u}_{i,jk}^\text {M}\rangle (X_j-\overset{\text {c}}{X}_j) (X_k-\overset{\text {c}}{X}_k) , \\ u^\text {M}_{i,j}(\varvec{X})&= \langle {u}_{i,j}^\text {M}\rangle + \langle {u}_{i,jk}^\text {M}\rangle (X_k-\overset{\text {c}}{X}_k), \\ u^\text {M}_{i,jk}(\varvec{X})&= \langle {u}_{i,jk}^\text {M}\rangle . \end{aligned}\end{aligned}$$
(12)

Obviously, we circumvent using any spatial averaging techniques [99,100,101]. Finally, we insert the latter into the energy definition and take out spatial averaged terms out of the integral

$$\begin{aligned} \int _\Omega w^\text {M}\,\mathrm {d}V= & {} \int _\Omega \bigg ( \frac{1}{2} C^\text {M}_{ijlm} u^\text {M}_{i,j} u^\text {M}_{l,m} + \frac{1}{2} D^\text {M}_{ijklmn} u^\text {M}_{i,jk} u^\text {M}_{l,mn} + G^\text {M}_{ijklmn} u^\text {M}_{i,j} u^\text {M}_{k,lm} \bigg ) \,\mathrm {d}V \nonumber \\= & {} \frac{1}{2} C^\text {M}_{ijlm} \int _{\Omega } u^\text {M}_{i,j} u^\text {M}_{l,m} \,\mathrm {d}V + \frac{1}{2} D^\text {M}_{ijklmn} \int _{\Omega } u^\text {M}_{i,jk} u^\text {M}_{l,mn} \,\mathrm {d}V + G^\text {M}_{ijklm} \int _{\Omega } u^\text {M}_{i,j} u^\text {M}_{k,lm} \,\mathrm {d}V \nonumber \\= & {} \frac{1}{2} C^\text {M}_{ijlm} \int _{\Omega } \Big ( \langle {u}_{i,j}^\text {M}\rangle +\langle {u}_{i,jk}^\text {M}\rangle (X_k-\overset{\text {c}}{X}_k) \Big ) \Big (\langle {u}_{l,m}^\text {M}\rangle + \langle {u}_{l,mn}^\text {M}\rangle (X_n-\overset{\text {c}}{X}_n) \Big ) \,\mathrm {d}V \nonumber \\&+ \frac{1}{2} D^\text {M}_{ijklmn} \int _{\Omega } \langle {u}_{i,jk}^\text {M}\rangle \langle {u}_{l,mn}^\text {M}\rangle \,\mathrm {d}V + G^\text {M}_{ijlmn} \int _{\Omega } \Big ( \langle {u}_{i,j}^\text {M}\rangle +\langle {u}_{i,jk}^\text {M}\rangle (X_k-\overset{\text {c}}{X}_k) \Big ) \langle {u}_{l,mn}^\text {M}\rangle \,\mathrm {d}V \nonumber \\= & {} \frac{V}{2} \bigg ( C^\text {M}_{ijlm} \langle {u}_{i,j}^\text {M}\rangle \langle {u}_{l,m}^\text {M}\rangle + \big ( C^\text {M}_{ijlm} \bar{I}_{kn} + D^\text {M}_{ijklmn} + 2 G^\text {M}_{ijlmn} (X_k-\overset{\text {c}}{X}_k) \big ) \langle {u}_{i,jk}^\text {M}\rangle \langle {u}_{l,mn}^\text {M}\rangle \nonumber \\&+ 2 G^\text {M}_{ijlmn} \langle {u}_{i,j}^\text {M}\rangle \langle u^\text {M}_{l,mn}\rangle \bigg ), \end{aligned}$$
(13)

by using

$$\begin{aligned} \bar{I}_{kn} = \frac{1}{V} \int _{\Omega } (X_k-\overset{\text {c}}{X}_k)(X_n-\overset{\text {c}}{X}_n) \,\mathrm {d}V. \end{aligned}$$
(14)

By following the asymptotic homogenization method, we use a so-called homothetic ratio, \(\epsilon \), for a separation of length scales and introduce the local coordinates,

$$\begin{aligned} y_j= \frac{1}{\epsilon }( X_j - \overset{\text {c}}{X}_j ). \end{aligned}$$
(15)

Therefore, the macroscale relations in Eq. (12) become

$$\begin{aligned} \begin{aligned} u_i^\text {M}(\varvec{X})&= u^\text {M}_i\Big |_{\overset{\text {c}}{\varvec{X}}} + \epsilon y_j \langle {u}_{i,j}^\text {M}\rangle + \frac{1}{2} \epsilon ^2 y_j y_k \langle {u}_{i,jk}^\text {M}\rangle , \\ u^\text {M}_{i,j}(\varvec{X})&= \langle {u}_{i,j}^\text {M}\rangle + \epsilon y_k \langle {u}_{i,jk}^\text {M}\rangle , \\ u^\text {M}_{i,jk}(\varvec{X})&= \langle {u}_{i,jk}^\text {M}\rangle . \end{aligned}\end{aligned}$$
(16)

With the assumption that the displacement field is a smooth function at the macroscale and \(\varvec{y}\)-periodic in local coordinates, the mean local fluctuations vanish within the chosen domain, \(\Omega \). In other words, the effective property at the macroscale is constant representing the “oscillatory” property at the microscale. The difference between the effective (macroscale) and oscillatory (microscale) property is the fluctuation to vanish. In this regard, we decompose the microscale displacement

$$\begin{aligned} \varvec{u ^\text {m}}(\varvec{X}) = \overset{0}{\varvec{u}}( \varvec{X}, \varvec{y}) + \epsilon \overset{1}{\varvec{u}}(\varvec{X},\varvec{y}) + \epsilon ^2 \overset{2}{\varvec{u}}(\varvec{X}, \varvec{y}) + \mathcal {O}(\epsilon ^3), \end{aligned}$$
(17)

where \(\overset{n}{\varvec{u}}( \varvec{X}, \varvec{y})\) (n = 0, 1, 2) are \(\varvec{y}\)-periodic. In other words, the chosen domain, \(\Omega \), acts as a representative volume element (RVE) within that we seek the effective property.

We use the well-known least action principle for solving the displacement by starting off with the Lagrange function, \(\rho f_i u^\text {m}_i - w^\text {m}\), where the gravitational specific (per mass) force, \(f_i\), and the mass density, \(\rho \), are given. For finding the variation of the action functional by the arbitrary test functions, \(\updelta \varvec{u}\), we perform an integration by part where the domain boundaries, \(\partial \Omega \), are identical to those from neighboring RVEs. Since the normal vectors, \(\varvec{n}\), of neighboring surfaces, \(\,\mathrm {d}A\), are opposite, all boundaries vanish

$$\begin{aligned} \begin{aligned} 0&= \updelta \int _\Omega \big ( \rho f_i u^\text {m}_i - w^\text {m}\big ) \,\mathrm {d}V , \\ 0&= \int _\Omega \big ( \rho f_i \updelta u^\text {m}_i - C^\text {m}_{ijkl} u^\text {m}_{k,l} \updelta u^\text {m}_{i,j} \big ) \,\mathrm {d}V , \\ 0&= \int _\Omega \Big ( \rho f_i + \big ( C^\text {m}_{ijkl} u^\text {m}_{k,l} \big )_{,j} \Big ) \updelta u^\text {m}_i \,\mathrm {d}V - \int _{\partial \Omega } C^\text {m}_{ijkl} u^\text {m}_{k,l} n_j \updelta u^\text {m}_i \,\mathrm {d}A , \\ 0&= \rho f_i + \big ( C^\text {m}_{ijkl} u^\text {m}_{k,l} \big )_{,j} . \end{aligned}\end{aligned}$$
(18)

Derivative of the microscale displacement from Eq. (17) after inserting Eq. (15) reads

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j}&= \Big ( \overset{0}{u}_i( \varvec{X}, \varvec{y}) + \epsilon \overset{1}{u}_i (\varvec{X},\varvec{y}) + \epsilon ^2 \overset{2}{u}_i(\varvec{X}, \varvec{y}) + \mathcal {O}(\epsilon ^3) \Big )_{,j} \\&= \overset{0}{u}_{i,j} + \epsilon \overset{1}{u}_{i,j} + \epsilon ^2 \overset{2}{u}_{i,j} + \frac{\delta _{kj}}{\epsilon } \frac{\partial }{\partial y_k} \Big ( \overset{0}{u}_i + \epsilon \overset{1}{u}_i + \epsilon ^2 \overset{2}{u}_i \Big ) + \mathcal {O}(\epsilon ^3) \\&= \overset{0}{u}_{i,j} + \frac{\partial \overset{0}{u}_i}{\partial y_j} \frac{1}{\epsilon }+ \epsilon \overset{1}{u}_{i,j} + \frac{\partial \overset{1}{u}_i}{\partial y_j} + \epsilon ^2 \overset{2}{u}_{i,j} + \epsilon \frac{\partial \overset{2}{u}_i}{\partial y_j} + \mathcal {O}(\epsilon ^3). \end{aligned}\end{aligned}$$
(19)

Inserting the latter in Eq. (18) and once more using the chain rule in combination with Eq. (15), we obtain

$$\begin{aligned} \begin{aligned}&\rho f_i + \Bigg ( C^\text {m}_{ijkl} \bigg ( \overset{0}{u}_{k,l} + \frac{\partial \overset{0}{u}_k}{\partial y_l} \frac{1}{\epsilon }+ \epsilon \overset{1}{u}_{k,l} + \frac{\partial \overset{1}{u}_k}{\partial y_l} + \epsilon ^2 \overset{2}{u}_{k,l} + \epsilon \frac{\partial \overset{2}{u}_k}{\partial y_l} \bigg ) \Bigg )_{,j} \\&\quad + \,\frac{1}{\epsilon }\frac{\partial }{\partial y_j} \Bigg ( C^\text {m}_{ijkl} \bigg ( \overset{0}{u}_{k,l} + \frac{\partial \overset{0}{u}_k}{\partial y_l} \frac{1}{\epsilon }+ \epsilon \overset{1}{u}_{k,l} + \frac{\partial \overset{1}{u}_k}{\partial y_l} + \epsilon ^2 \overset{2}{u}_{k,l} + \epsilon \frac{\partial \overset{2}{u}_k}{\partial y_l} \bigg ) \Bigg ) =0 \end{aligned}\end{aligned}$$
(20)

where separation of coefficients multiplied by the same order in \(\epsilon \) and setting every term zero—since \(\epsilon \) and \(\epsilon ^2\) terms are independent—results in

$$\begin{aligned}&\frac{1}{\epsilon ^2} \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m}\frac{\partial \overset{0}{u}_k}{\partial y_l} \Big ) = 0, \nonumber \\&\frac{1}{\epsilon }\Bigg ( \bigg ( C^\text {m}_{ijkl} \frac{\partial \overset{0}{u}_k}{\partial y_l} \bigg )_{,j} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m}\overset{0}{u}_{k,l} \big ) + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} \frac{\partial \overset{1}{u}_k}{\partial y_l} \Big ) \Bigg ) = 0,\nonumber \\&\rho f_i + \big ( C^\text {m}_{ijkl} \overset{0}{u}_{k,l} \big )_{,j} + \Big ( C^\text {m}_{ijkl} \frac{\partial \overset{1}{u}_k}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m}\overset{1}{u}_{k,l} \big ) + \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m}\frac{\partial \overset{2}{u}_k}{\partial y_l} \Big ) = 0, \nonumber \\&\epsilon \Bigg ( \big ( C^\text {m}_{ijkl} \overset{1}{u}_{k,l} \big )_{,j} + \Big ( C_{ijkl}^\text {m}\frac{\partial \overset{2}{u}_k}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m}\overset{2}{u}_{k,l} \big ) \Bigg ) =0, \nonumber \\&\epsilon ^2 \big ( C^\text {m}_{ijkl} \overset{2}{u}_{k,l} \big )_{,j} = 0. \end{aligned}$$
(21)

Since \(C^\text {m}_{ijkl}\) depends on \(\varvec{y}\), for example consider two distinct materials at the microscale, from the first relation, we immediately conclude that \(\overset{0}{u}_i=\overset{0}{u}_i(\varvec{X})\). By using this dependency, we introduce the multiplicative decomposition

$$\begin{aligned} \begin{aligned} \overset{1}{u}_i = \overset{0}{u}_{a,b}(\varvec{X}) \varphi _{abi}(\varvec{y}) , \ \ \overset{2}{u}_i = \overset{0}{u}_{a,bc}(\varvec{X}) \psi _{abci}(\varvec{y}), \end{aligned}\end{aligned}$$
(22)

with the unknown tensors \(\varphi _{abc}\) and \(\psi _{abcd}\). The latter decomposition is a general procedure in tensor calculus and the unknown tensors, \(\varvec{\varphi }\), \(\varvec{\psi }\), have no underlying assumptions. As a consequence, for \(\varvec{u}^\text {m}\), we have the following expression:

$$\begin{aligned} \begin{aligned} u^\text {m}_i = \overset{0}{u}_i(\varvec{X}) + \epsilon \overset{0}{u}_{a,b}(\varvec{X}) \varphi _{abi}(\varvec{y}) + \epsilon ^2 \overset{0}{u}_{a,bc}(\varvec{X}) \psi _{abci}(\varvec{y}) + \mathcal {O}(\epsilon ^3), \end{aligned}\end{aligned}$$
(23)

with the first term—the sole term depending only on \(\varvec{X}\), all the other terms depend on \(\varvec{y}\) as well—corresponding to the macroscale displacement,

$$\begin{aligned} \begin{aligned} \varvec{u}^\text {M}= \overset{0}{\varvec{u}}(\varvec{X}). \end{aligned}\end{aligned}$$
(24)

By using Eq. (24) in Eq. (23), we obtain the displacement gradient,

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j}&= \Big ( u^\text {M}_i + \epsilon u^\text {M}_{a,b} \varphi _{abi} + \epsilon ^2 u^\text {M}_{a,bc} \psi _{abci} \Big )_{,j} + \mathcal {O}(\epsilon ^3) \\&= u_{i,j}^\text {M}+ \frac{\partial \varphi _{abi}}{\partial y_j} u^\text {M}_{a,b} + \epsilon \varphi _{abi} u^\text {M}_{a,bj} + \epsilon \frac{\partial \psi _{abci}}{\partial y_j} u^\text {M}_{a,bc} + \epsilon ^2 \psi _{abci} u^\text {M}_{a,bcj} + \mathcal {O}(\epsilon ^3) \\&= \underbrace{\Big (\delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \Big )}_{L_{abij}} u^\text {M}_{a,b} + \epsilon u^\text {M}_{a,bc} \underbrace{\Big ( \varphi _{abi} \delta _{jc} + \frac{\partial \psi _{abci} }{\partial y_j} \Big )}_{N_{abcij}} + \epsilon ^2 \psi _{abci} u^\text {M}_{a,bcj} + \mathcal {O}(\epsilon ^3), \end{aligned}\end{aligned}$$
(25)

and, after inserting Eq. (16), we acquire

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j} = L_{abij} \langle u^\text {M}_{a,b} \rangle + \epsilon \langle u^\text {M}_{a,bc} \rangle y_c L_{abij} + \epsilon \langle u^\text {M}_{a,bc} \rangle N_{abcij}, \end{aligned}\end{aligned}$$
(26)

since we incorporate up to the second gradients in Eq. (7). By using \(M_{abcij} = y_c L_{abij} + N_{abcij}\), we calculate the energy at the microscale

$$\begin{aligned} \begin{aligned} \int _{\Omega } w^\text {m}\,\mathrm {d}V&= \frac{1}{2} \int _{\Omega ^P} \Big ( C_{ijkl}^\text {m}L_{abij} L_{cdkl} \langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,d}^\text {M}\rangle +2 \epsilon C_{ijkl}^\text {m}L_{abij} M_{cdekl} \langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,de}^\text {M}\rangle \\&\quad + \epsilon ^2 C_{ijkl}^\text {m}M_{abcij} M_{defkl} \langle {u}_{a,bc}^\text {M}\rangle \langle {u}_{d,ef}^\text {M}\rangle \Big ) \,\mathrm {d}V \\&= \frac{V}{2}\Big ( \bar{C}_{abcd} \langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,d}^\text {M}\rangle + 2\bar{G}_{abcde}\langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,de}^\text {M}\rangle + \bar{D}_{abcdef}\langle {u}_{a,bc}^\text {M}\rangle \langle {u}_{d,ef}^\text {M}\rangle \Big ). \end{aligned}\end{aligned}$$
(27)

with

$$\begin{aligned}&\bar{C}_{abcd} = \frac{1}{V} \int _{\Omega } C_{ijkl}^\text {m}L_{abij} L_{cdkl} \,\mathrm {d}V, \nonumber \\&\bar{G}_{abcde} = \frac{\epsilon }{V} \int _{\Omega } C_{ijkl}^\text {m}L_{abij} M_{cdekl} \,\mathrm {d}V, \nonumber \\&\bar{D}_{abcdef} = \frac{\epsilon ^2}{V} \int _{\Omega } C_{ijkl}^\text {m}M_{abcij} M_{defkl} \,\mathrm {d}V. \end{aligned}$$
(28)

Immediately we observe by comparing with Eq. (13),

$$\begin{aligned}&C^\text {M}_{ijlm} = \bar{C}_{ijlm}, \nonumber \\&G^\text {M}_{ijlmn} = \bar{G}_{abcde}, \nonumber \\&C^\text {M}_{ijlm} \bar{I}_{kn} + D^\text {M}_{ijklmn} + 2 \epsilon y_k G^\text {M}_{ijlmn}= \bar{D}_{ijklmn} , \end{aligned}$$
(29)

where

$$\begin{aligned} \begin{aligned} \bar{I}_{kn} = \int _{\Omega ^P} (X_k-\overset{\text {c}}{X}_k)(X_n-\overset{\text {c}}{X}_n) \,\mathrm {d}V =\epsilon ^2 \int _{\Omega ^P}y_k y_n \,\mathrm {d}V. \end{aligned}\end{aligned}$$
(30)

Therefore, \(\varvec{C}^\text {M}\), \(\varvec{D}^\text {M}\), \(\varvec{G}^\text {M}\) are determined once \(\varvec{\varphi }\) and \(\varvec{\psi }\) are calculated by using the substructure. For these variables, we will obtain corresponding field equations in the following.

By inserting Eq. (23) in Eq. (21)\(_{2}\) and using \(\overset{0}{\varvec{u}}=\overset{0}{\varvec{u}}(\varvec{X})\), we obtain

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial y_j} \big ( C^\text {m}_{ijkl} \overset{0}{u}_{k,l} \big ) + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} \frac{\partial \overset{0}{u}_{a,b}\varphi _{abk}}{\partial y_l} \Big )&= 0, \\ \frac{\partial C^\text {m}_{ijkl}}{\partial y_j} \delta _{ak}\delta _{bl} \overset{0}{u}_{a,b} + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} \frac{\partial \varphi _{abk}}{\partial y_l} \Big ) \overset{0}{u}_{a,b}&= 0, \\ \frac{\partial }{\partial y_j} \Bigg ( C^\text {m}_{ijkl} \underbrace{\Big ( \delta _{ak}\delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l} \Big ) }_{L_{abkl}} \Bigg )&= 0. \end{aligned}\end{aligned}$$
(31)

Analogously, by exploiting Eq. (21)\(_{3}\) and inserting the latter, we acquire

$$\begin{aligned} \begin{aligned} \rho f_i + \big ( C^\text {m}_{ijkl} \overset{0}{u}_{k,l} \big )_{,j} + \Big ( C^\text {m}_{ijkl} \frac{\partial \overset{0}{u}_{a,b} \varphi _{abk}}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \big ( C^\text {m}_{ijkl} \overset{0}{u}_{a,bl}\varphi _{abk} \big ) + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} \frac{\partial \overset{0}{u}_{a,bc}\psi _{abck}}{\partial y_l} \Big )&= 0 , \\ \rho f_i + C^\text {m}_{ijkl} \overset{0}{u}_{k,lj} + C^\text {m}_{ijkl} \overset{0}{u}_{a,bj} \frac{\partial \varphi _{abk}}{\partial y_l} + \frac{\partial }{\partial y_j} \big ( C^\text {m}_{ijkl} \varphi _{abk} \big ) \overset{0}{u}_{a,bl} + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} \frac{\partial \psi _{abck}}{\partial y_l} \Big ) \overset{0}{u}_{a,bc}&= 0 , \\ \rho f_i + C^\text {m}_{ickl} \overset{0}{u}_{a,bc} \underbrace{\Bigg ( \delta _{ak} \delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l} \Bigg )}_{L_{abkl}} + \overset{0}{u}_{a,bc} \frac{\partial }{\partial y_j} \Bigg ( C^\text {m}_{ijkl} \underbrace{ \Big ( \varphi _{abk} \delta _{cl} + \frac{\partial \psi _{abck}}{\partial y_l} \Big ) }_{N_{abckl}} \Bigg )&= 0 \end{aligned}\end{aligned}$$
(32)

Equations (21)\(_{4,5}\) are identically fulfilled

$$\begin{aligned} \begin{aligned} \big ( C^\text {m}_{ijkl} \overset{1}{u}_{k,l} \big )_{,j} + \Big ( C^\text {m}_{ijkl} \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} \overset{2}{u}_{k,l} \Big )&= 0 , \\ C^\text {m}_{ijkl} \overset{0}{u}_{a,blj} \varphi _{abk} + C^\text {m}_{ijkl} \frac{\partial \overset{0}{u}_{a,bcj} \psi _{abck}}{\partial y_l} + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} \overset{0}{u}_{a,bcl} \psi _{abck} \Big )&= 0 , \\ C^\text {m}_{ijkl} \overset{2}{u}_{k,lj}&= 0, \\ C^\text {m}_{ijkl} \overset{0}{u}_{a,bclj} \psi _{abck}&= 0, \end{aligned}\end{aligned}$$
(33)

since we incorporate only up to the second derivative in Eq. (7).

In the case of the macroscale, with the least action principle by means of the Lagrange function, \(\rho f_i u^\text {M}_i - w^\text {M}\), we obtain after using integration by parts twice and letting the domain boundaries vanish

$$\begin{aligned} \begin{aligned} 0&= \updelta \int _\Omega \big ( \rho f_i u^\text {M}_i - w^\text {M}\big ) \,\mathrm {d}V , \\ 0&= \int _\Omega \Big ( \rho f_i \updelta u^\text {M}_i - C^\text {M}_{ijkl} u^\text {M}_{k,l} \updelta u^\text {M}_{i,j} - D^\text {M}_{ijklmn} u^\text {M}_{l,mn} \updelta u^\text {M}_{i,jk} - G^\text {M}_{ijklm} \updelta u^\text {M}_{i,j} u^\text {M}_{k,lm} - G^\text {M}_{ijklm} u^\text {M}_{i,j} \updelta u^\text {M}_{k,lm} \Big ) \,\mathrm {d}V , \\ 0&= \rho f_i + C^\text {M}_{ijkl} u^\text {M}_{k,lj} - D^\text {M}_{ijklmn} u^\text {M}_{l,mnjk} + G^\text {M}_{ijklm} u^\text {M}_{k,lmj} - G^\text {M}_{kjilm} u^\text {M}_{k,jlm} , \\ 0&= \rho f_i + C^\text {M}_{ijkl} u^\text {M}_{k,lj} , \end{aligned}\end{aligned}$$
(34)

since the stiffness tensors are constant at the macroscale, as well as we incorporate only up to the second derivative in Eq. (7). By using this relation in Eq. (32), we get

$$\begin{aligned} \begin{aligned} -C^\text {M}_{icab} u^\text {M}_{a,bc} + C^\text {m}_{ickl} \overset{0}{u}_{a,bc} L_{abkl} + \overset{0}{u}_{a,bc} \frac{\partial }{\partial y_j} \Bigg ( C^\text {m}_{ijkl} N_{abckl} \Bigg )&= 0, \\ -C^\text {M}_{icab} + C^\text {m}_{ickl} L_{abkl} + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} N_{abckl} \Big )&= 0. \end{aligned}\end{aligned}$$
(35)

By solving Eqs. (31) and (35)\(_2\), we calculate \(\varvec{\varphi }\) and \(\varvec{\psi }\).

3 Method of solution

We sum up the methodology proposed herein. Consider a metamaterial with a given substructure at the microscale, \(\varvec{y}\). Modeling the substructure with the given \(\varvec{C}^\text {m}\) by means of the finite element method leads to a numerical solution of \(\varvec{\varphi }\) by satisfying Eq. (31):

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial y_j} \Bigg ( C^\text {m}_{ijkl} L_{abkl} \Bigg ) = 0 , \ \ L_{abkl} = \delta _{ak}\delta _{bl} + \frac{\partial \varphi _{abk}}{\partial y_l}. \end{aligned}\end{aligned}$$
(36)

By using the solution, from Eqs. (28), (29), we determine

$$\begin{aligned} \begin{aligned} C^\text {M}_{abcd} = \bar{C}_{abcd} = \frac{1}{V} \int _{\Omega } C_{ijkl}^\text {m}L_{abij} L_{cdkl} \,\mathrm {d}V. \end{aligned}\end{aligned}$$
(37)

The macroscale stiffness tensor, \(\varvec{C}^\text {M}\), is used in Eq. (35)\(_2\) in order to acquire \(\varvec{\psi }\) by fulfilling

$$\begin{aligned} \begin{aligned} -C^\text {M}_{icab} + C^\text {m}_{ickl} L_{abkl} + \frac{\partial }{\partial y_j} \Big ( C^\text {m}_{ijkl} N_{abckl} \Big ) = 0 , \ \ N_{abckl} = \varphi _{abk} \delta _{cl} + \frac{\partial \psi _{abck}}{\partial y_l}. \end{aligned}\end{aligned}$$
(38)

With this solution, we construct

$$\begin{aligned} \begin{aligned} M_{abcij} = y_c L_{abij} + N_{abcij} , \ \ \bar{I}_{kn} =\epsilon ^2 \int _{\Omega ^P}y_k y_n \,\mathrm {d}V. \end{aligned}\end{aligned}$$
(39)

and determine

$$\begin{aligned} \begin{aligned} G^\text {M}_{abcde}&= \bar{G}_{abcde} = \frac{\epsilon }{V} \int _{\Omega } C_{ijkl}^\text {m}L_{abij} M_{cdekl} \,\mathrm {d}V, \\ \bar{D}_{abcdef}&= \frac{\epsilon ^2}{V} \int _{\Omega } C_{ijkl}^\text {m}M_{abcij} M_{defkl} \,\mathrm {d}V, \\ D^\text {M}_{ijklmn}&= \bar{D}_{ijklmn} - C^\text {M}_{ijlm} \bar{I}_{kn} - 2 \epsilon y_k G^\text {M}_{ijlmn}. \end{aligned}\end{aligned}$$
(40)

The outcome is determining the components of \(\varvec{C}^\text {M}\) tensor of rank four, \(\varvec{G}^\text {M}\) tensor of rank five, and \(\varvec{D}^\text {M}\) tensor of rank six.

In particular, for the numerical solution of Eq. (36) as well as Eq. (38), we follow the standard procedure of the finite element method [102] and utilize a finite dimensional Hilbertian Sobolev space for trial functions. The same space is used for the test functions as well, called the Galerkin procedure. The triangulation of the structure in \(\varvec{y}\) is established by using tetrahedrons, and we solve the discrete problem by minimizing the weak form. In order to get the weak forms, Eqs. (36), (38) are multiplied by arbitrary test functions of their ranks for reducing to a scalar integrated over the volume of the structure, \(\Omega \). For fulfilling the \(\varvec{y}\) periodicity, all boundaries are modeled as periodic boundaries by tying the nodes on corresponding surfaces. In other words, for a cube from left to right along \(X_1\)-axis, each node, say, on the left surface has to have the same displacement as its counterpart with the same \(X_2\), \(X_3\) coordinates on the right surface. Hence, technically, all boundaries are of Dirichlet type and the test functions vanish on all boundaries, for an alternative approach of weak periodicity, we refer to [103]. We use herein a strong coupling with the same mesh on corresponding boundaries, since we use the RVE only at the level of parameter determination.

All the implementation is carried out in the FEniCS platform; we refer to [104] for an introduction with examples. The weak form is obtained after integrating by parts; we stress that the periodic boundary condition causes that boundary integrals vanish. Moreover, we omit distinguishing between the functions and their discrete representations, since they never occur in the same equation. In order to calculate \(\varvec{\varphi }\) and \(\varvec{\psi }\), by utilizing Eqs. (31) and (35)\(_2\), we obtain the following weak forms:

$$\begin{aligned}&\int _\Omega C^\text {m}_{ijkl} L_{abkl} \frac{\partial \updelta \varphi _{abi}}{\partial y_j} \,\mathrm {d}V = 0 , \ \ \nonumber \\&\int _\Omega \bigg ( -C^\text {M}_{icab} \updelta \psi _{abci} + C^\text {m}_{ickl} L_{abkl} \updelta \psi _{abci} - \Big ( C^\text {m}_{ijkl} N_{abckl} \Big ) \frac{\partial \updelta \psi _{abci} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0 , \ \ \end{aligned}$$
(41)

are solved separately by setting a, b, c indices. This fact is of importance so we write out explicitly, how it is meant to do. Because of the minor symmetry, \(C^\text {M}_{ijkl}=C^\text {M}_{ijlk}\), we know that \(L_{abkl}=L_{bakl}\) and \(\varphi _{abi}=\varphi _{bai}\) such that we solve six weak forms

$$\begin{aligned} \begin{aligned} \int _\Omega C^\text {m}_{ijkl} L_{11kl} \frac{\partial \updelta \varphi _{11i}}{\partial y_j} \,\mathrm {d}V = 0 , \ \ \int _\Omega C^\text {m}_{ijkl} L_{22kl} \frac{\partial \updelta \varphi _{22i}}{\partial y_j} \,\mathrm {d}V = 0 , \ \ \int _\Omega C^\text {m}_{ijkl} L_{33kl} \frac{\partial \updelta \varphi _{33i}}{\partial y_j} \,\mathrm {d}V = 0 , \ \ \\ \int _\Omega C^\text {m}_{ijkl} L_{23kl} \frac{\partial \updelta \varphi _{23i}}{\partial y_j} \,\mathrm {d}V = 0 , \ \ \int _\Omega C^\text {m}_{ijkl} L_{13kl} \frac{\partial \updelta \varphi _{13i}}{\partial y_j} \,\mathrm {d}V = 0 , \ \ \int _\Omega C^\text {m}_{ijkl} L_{12kl} \frac{\partial \updelta \varphi _{12i}}{\partial y_j} \,\mathrm {d}V = 0 , \ \ \end{aligned}\end{aligned}$$
(42)

in order to obtain \(\varphi _{11i}\), \(\varphi _{22i}\), \(\varphi _{33i}\), \(\varphi _{23i}\), \(\varphi _{13i}\), \(\varphi _{12i}\), respectively. We use these values in Eq. (37). This method is admissible under the assumption that for each ab in Voigt’s notation indices, \(\varvec{\varphi }\) components are per se independent. Also the use in Eq. (37) is justified since we obtain 21 components of the stiffness tensor as follows:

$$\begin{aligned} \begin{aligned} C^\text {M}_{1111}&= \frac{1}{V} \int _\Omega C^\text {m}_{ijkl} L_{11ij} L_{11kl} \,\mathrm {d}V , \ \ L_{11kl} = \delta _{1k}\delta _{1l} + \frac{\partial \varphi _{11k}}{\partial y_l}, \\ C^\text {M}_{1122}&= \frac{1}{V} \int _\Omega C^\text {m}_{ijkl} L_{11ij} L_{22kl} \,\mathrm {d}V , \ \ L_{22kl} = \delta _{2k}\delta _{2l} + \frac{\partial \varphi _{22k}}{\partial y_l}, \\&\quad \dots \\ C^\text {M}_{1212}&= \frac{1}{V} \int _\Omega C^\text {m}_{ijkl} L_{12ij} L_{12kl} \,\mathrm {d}V , \ \ L_{12kl} = \delta _{1k}\delta _{2l} + \frac{\partial \varphi _{12k}}{\partial y_l} \ . \end{aligned}\end{aligned}$$
(43)

Of course, depending on the substructure, it may be the case that some of \(\varvec{\varphi }\) components are equivalent; however, this symmetry is metamaterial specific. In the same manner, from Eq. (41), we use \(\psi _{abci}=\psi _{baci}\) and for \(i=1\) we solve

$$\begin{aligned} \begin{aligned} \int _\Omega \bigg ( -C^\text {M}_{1c11} \updelta \psi _{11c1} + C^\text {m}_{1ckl} L_{11kl} \updelta \psi _{11c1} - \Big ( C^\text {m}_{1jkl} N_{11ckl} \Big ) \frac{\partial \updelta \psi _{11c1} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \\ \int _\Omega \bigg ( -C^\text {M}_{1c22} \updelta \psi _{22c1} + C^\text {m}_{1ckl} L_{22kl} \updelta \psi _{22c1} - \Big ( C^\text {m}_{1jkl} N_{22ckl} \Big ) \frac{\partial \updelta \psi _{22c1} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \\ \int _\Omega \bigg ( -C^\text {M}_{1c33} \updelta \psi _{33c1} + C^\text {m}_{1ckl} L_{33kl} \updelta \psi _{33c1} - \Big ( C^\text {m}_{1jkl} N_{33ckl} \Big ) \frac{\partial \updelta \psi _{33c1} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \\ \int _\Omega \bigg ( -C^\text {M}_{1c23} \updelta \psi _{23c1} + C^\text {m}_{1ckl} L_{23kl} \updelta \psi _{23c1} - \Big ( C^\text {m}_{1jkl} N_{23ckl} \Big ) \frac{\partial \updelta \psi _{23c1} }{\partial y_j} \bigg ) \,\mathrm {d}V= 0, \\ \int _\Omega \bigg ( -C^\text {M}_{1c13} \updelta \psi _{13c1} + C^\text {m}_{1ckl} L_{13kl} \updelta \psi _{13c1} - \Big ( C^\text {m}_{1jkl} N_{13ckl} \Big ) \frac{\partial \updelta \psi _{13c1} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \\ \int _\Omega \bigg ( -C^\text {M}_{1c12} \updelta \psi _{12c1} + C^\text {m}_{1ckl} L_{12kl} \updelta \psi _{12c1} - \Big ( C^\text {m}_{1jkl} N_{12ckl} \Big ) \frac{\partial \updelta \psi _{12c1} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \end{aligned}\end{aligned}$$
(44)

for \(i=2\)

$$\begin{aligned} \begin{aligned}&\int _\Omega \bigg ( -C^\text {M}_{2c11} \updelta \psi _{11c2} + C^\text {m}_{2ckl} L_{11kl} \updelta \psi _{11c2} - \Big ( C^\text {m}_{2jkl} N_{11ckl} \Big ) \frac{\partial \updelta \psi _{11c2} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \\&\quad \dots \\&\int _\Omega \bigg ( -C^\text {M}_{2c12} \updelta \psi _{12c2} + C^\text {m}_{2ckl} L_{12kl} \updelta \psi _{12c2} - \Big ( C^\text {m}_{2jkl} N_{12ckl} \Big ) \frac{\partial \updelta \psi _{12c2} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \end{aligned}\end{aligned}$$
(45)

for \(i=3\)

$$\begin{aligned} \begin{aligned}&\int _\Omega \bigg ( -C^\text {M}_{3c11} \updelta \psi _{11c3} + C^\text {m}_{3ckl} L_{11kl} \updelta \psi _{11c3} - \Big ( C^\text {m}_{3jkl} N_{11ckl} \Big ) \frac{\partial \updelta \psi _{11c3} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0, \\&\quad \dots \\&\int _\Omega \bigg ( -C^\text {M}_{3c12} \updelta \psi _{12c3} + C^\text {m}_{3ckl} L_{12kl} \updelta \psi _{12c3} - \Big ( C^\text {m}_{3jkl} N_{12ckl} \Big ) \frac{\partial \updelta \psi _{12c3} }{\partial y_j} \bigg ) \,\mathrm {d}V = 0. \end{aligned}\end{aligned}$$
(46)

In this way, we solve for \(\psi _{11c1}\dots \psi _{12c3}\) separately and use them to obtain \(\varvec{G}^\text {M}\) and \(\varvec{D}^\text {M}\) by means of Eq. (40).

4 Results and discussion

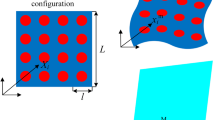
By virtue of 3-D printers, it is possible to manufacture complex structures with voids inside. Voids result in a porous structure at the microscale. We stress that the voids are introduced on purpose, and we assume that the microscale material is full. For example in fused deposition modeling (FDM), the filaments are made of non-porous material and the porosity is caused by design. This layer-by-layer manufacturing technique is coded by a software called slicer. Slicer converts the structure from the CAD design into a G-code providing the motion of the nozzle laying the melt material, i.e., print the material as a thick viscous fluid located at the given positions. For the purpose of weight reduction, all slicer software programs introduce an infill ratio, exchanging the full material with a pre-configured periodic lattice structure. Decreasing the infill ratio increases the porosity at the macroscale. One such typical honeycomb structure is a hexagonal lattice configuration as seen in Fig. 1, the CAD is utilized in Salome, the open-source integration platform for numerical simulation. The full material is replaced with this configuration, for which we compute the higher order terms for any homothetic ratio, \(\epsilon \), with the assumption that the linear isotropic material at the microscale might be linear anisotropic strain gradient at the macroscale. For the particular RVE as seen in Fig. 1, the homothetic ratio is unity, i.e., the infill ratio is around 50% meaning that the half of the space is filled with the (orange) material. The homothetic ratio is inversely related to the infill ratio, for decreasing \(\epsilon \) the infill ratio increases, where \(\epsilon =0\) reads 100% infill ratio meaning that the material is full and no substructure emerges. Obviously, for 100% infill ratio, the higher-order terms, \(\varvec{G}^\text {M}\), \(\varvec{D}^\text {M}\) vanish in Eq. (40).

Fig. 1
figure 1

Honeycomb structure in Salome and a possible representative volume element (RVE) are shown opaque within the transparent structure, orange denotes the 3-D printed material and gray is void (air) modeled with a significantly low modulus

Full size image
Fig. 2
figure 2

Used mesh of 68,371 tetrahedrons for the RVE, leading to 15,618 nodes, triangulation is obtained in Salome by using NetGen and Mephisto algorithms

Full size image
Fig. 3
figure 3

Demonstration of the periodic boundary conditions along X-axis, the same mesh is used such that the Y and Z coordinates are matching for nodes to be defined as the same degree of freedom

Full size image

By using the RVE, the mesh is generated in Salome by using NetGen and Mephisto algorithms as seen in Fig. 2. We emphasize that the periodic boundary conditions need corresponding meshes on the “neighboring” surfaces. An example is demonstrated in Fig. 3, where along the \(X_1=X\) axis, the boundary surfaces are visible. All nodes on both surfaces have the same \(X_2=Y\) and \(X_3=Z\) coordinates such that the degrees of freedom on each node are set equivalent to the corresponding node on the neighboring surface. As the periodic boundaries reflect the given solution, they are Dirichlet boundary conditions, which means that the macroscale and microscale solutions match along the boundaries as well. Although this condition is not a priori set into the formulation, the use of RVE enforces matching boundaries. From the computational point of view, using Dirichlet boundary conditions on all surfaces makes the problem well-defined. Hence, there are no emerging numerical problems, where we used multifrontal massively parallel sparse direct solver (mumps) for solving the weak forms and Gaussian quadrature for integration.

As usual, we write out the stiffness tensor in Voigt’s notation with A, B standing for combination of two indices in the order: 11, 22, 33, 23, 13, 12 such that the rank four tensor, \(C^\text {M}_{ijkl}\), is represented in a matrix notation,

$$\begin{aligned} \begin{aligned} C^\text {M}_{AB} = \begin{pmatrix} C^\text {M}_{1111} &{} C^\text {M}_{1122} &{} C^\text {M}_{1133} &{} C^\text {M}_{1123} &{} C^\text {M}_{1113} &{} C^\text {M}_{1112} \\ C^\text {M}_{2211} &{} C^\text {M}_{2222} &{} C^\text {M}_{2233} &{} C^\text {M}_{2223} &{} C^\text {M}_{2213} &{} C^\text {M}_{2212} \\ C^\text {M}_{3311} &{} C^\text {M}_{3322} &{} C^\text {M}_{3333} &{} C^\text {M}_{3323} &{} C^\text {M}_{3313} &{} C^\text {M}_{3312} \\ C^\text {M}_{2311} &{} C^\text {M}_{2322} &{} C^\text {M}_{2333} &{} C^\text {M}_{2323} &{} C^\text {M}_{2313} &{} C^\text {M}_{2312} \\ C^\text {M}_{1311} &{} C^\text {M}_{1322} &{} C^\text {M}_{1333} &{} C^\text {M}_{1323} &{} C^\text {M}_{1313} &{} C^\text {M}_{1312} \\ C^\text {M}_{1211} &{} C^\text {M}_{1222} &{} C^\text {M}_{1233} &{} C^\text {M}_{1223} &{} C^\text {M}_{1213} &{} C^\text {M}_{1212} \\ \end{pmatrix}, \end{aligned}\end{aligned}$$
(47)

where obviously the major symmetry holds true, \(C^\text {M}_{AB}=C^\text {M}_{BA}\), although this identity is not explicitly stated in the notation. Analogously we use \(\alpha \), \(\beta \) for three indices in the order: 111, 221, 331, 231, 131, 121, 112, 222, 332, 232, 132, 122, 113, 223, 333, 233, 133, 123 in order to be able to represent higher order terms in a matrix form as well. Specifically, for \(G^\text {M}_{ijklm}\) we have

(48)

and for \(D^\text {M}_{ijklmn}\) we obtain

(49)

where the symmetry holds true, \(D^\text {M}_{\alpha \beta }=D^\text {M}_{\alpha \beta }\). Therefore, we determine 21 components for \(C^\text {M}_{AB}\), 108 components for \(G^\text {M}_{A\alpha }\), and 171 components for \(D^\text {M}_{\alpha \beta }\) in this work for the honeycomb structure by means of the approach explained in Eqs. (36)–(40).

Computed for an RVE of 240 mm \(\times \,277.12\) mm \(\times \,20\) mm along X, Y, Z axes, respectively, made of an isotropic material with the Young’s modulus of 110 GPa and Poisson’s ratio of 0.35, we demonstrate the results in Voigt-like notation introduced above. For the stiffness tensor, we obtain

$$\begin{aligned} \begin{aligned} C^\text {M}_{AB} = \begin{pmatrix} 16 &{} 10 &{} 9 &{} 0 &{} 0 &{} 0 \\ 10 &{} 11 &{} 7 &{} 0 &{} 0 &{} 0 \\ 9 &{} 7 &{} 43 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 8 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 8 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 3 \\ \end{pmatrix} \text {\,GPa}, \end{aligned}\end{aligned}$$
(50)

where we round off 0.1 GPa in all components. For the higher-order terms, results depend on the arbitrary infill ratio set by the homothetic ratio \(\epsilon \), as follows:

(51)

with \(\pm 0.1\) kN/mm accuracy as well as

(52)

with 0.1 TN accuracy, where 1 TN\(\hat{=}10^{12}\) N. A general sensitivity analysis of higher-order terms is inadequate, in other words, comparison between the displacement altering because of \(\varvec{G}^\text {M}\) and \(\varvec{D}^\text {M}\) components is impossible. The structure dependence on the homothetic ratio \(\epsilon \) as well as loading and boundary conditions affect the sensitivity. Therefore, we have written out all terms with their own accuracy and circumvent ourselves from reducing the complexity of the outcome.

Since the topology is hexagonal, centro-symmetry is lacking such that \(\varvec{G}^\text {M}\) tensor of rank 5 fails to vanish. All components \(D^\text {M}_{\times 33\times \times \times }\) regarding the second gradient along Z-axis are zero due to the chosen geometry. Obviously, the periodic boundaries along Z-axis create hollow hexagonal tubes without “porosity.” Such a porous structure is indeed the case in XY-plane. Therefore, out of XY-plane the homogenization introduces a weakened structure, visible as \(C^\text {M}_{3333}\) being less than the half of the Young’s modulus of the material itself; however, no higher-order terms occur.

It is challenging to directly relate the homothetic ratio to the physical length scale, and further studies are necessary in order to justify this study’s parameters.

5 Conclusions

Generalized mechanics has been already studied in 1950s as a purely academic research. Additive manufacturing opens the door for crafting structures with substructures (microscale), called infills, leading to different length scales performing simultaneously at the macroscale, thus making the generalized elasticity necessary for accurate modeling. Involving strains, conventional elasticity necessitates 21 material parameters. Generalized elasticity with strain gradients introduces additional to the 21 (different) parameters in \(\varvec{C}^\text {M}\) rank 4 tensor, another 108 parameters in \(\varvec{G}^\text {M}\) rank 5, and 171 parameters in \(\varvec{D}^\text {M}\) rank 6 tensors. Asymptotic analysis results in micro-macro-scale relations that we briefly yet thoroughly demonstrated in this work. Finally, a new methodology is proposed for using the substructure and determining all the parameters in generalized elasticity by using computations based on the finite element method (FEM). In order to present the method on a particular case of hexagonal honeycomb substructure, open-source codes-based numerical implementation is established under GNU public license [96], the code is available in [98] in order to allow a transparent scientific exchange.