Discrete versus homogenized continuum modeling in finite deformation bias extension test of bi-pantographic fabrics

Abstract

A 2D-continuum model describing finite deformations in plane of discrete bi-pantographic fabrics has been recently obtained by applying an asymptotic procedure based on a set of local generalized coordinates. Rectangular bi-pantographic prototypes were additively manufactured by selective laser sintering using polyamide as raw material. Displacement-controlled bias extension tests were performed on such specimens for total elastic deformations up to ca. 25%. Experimental force measurements, complemented by discrete displacement measurements obtained by local digital image correlation, were used to fit the continuum model. In the present paper, a global and minimal set of generalized coordinates, alternative to the one used for the homogenization, is introduced for the discrete model. The mechanical constitutive parameters appearing in the discrete model are then found by means of collected experimental data. Finally, a comparison between experiments, the discrete and the continuum model is presented. It is concluded that (a) the discrete model and the experimental data are in excellent agreement, and that (b) the continuum retains the relevant phenomenology of the discrete system even for a rather low number of cells.

1 Introduction

Recently, [1, 2] presented the derivation by an asymptotic homogenization procedure [3,4,5,6] of a 1D-continuum model [7,8,9,10,11] being capable of describing finite deformations in plane of a discrete spring [12,13,14,15,16,17,18,19] pantographic structure [20,21,22,23,24,25,26,27] looking like an expanding barrier, referred to as pantographic beam.

Based on such results, Barchiesi et al. [28, 29] generalized to finite deformations the homogenization of bi-pantographic fabrics, first achieved by Seppecher et al. [6]. Bi-pantographic fabrics are conceived as assemblies of discrete pantographic beams (see Fig. 1) leading at macroscopic scale to second gradient materials in plane. (For a representative account of second gradient and generalized continua, the reader is referred to [30,31,32,33,34,35,36,37,38,39].) For such materials, the deformation energy density depends upon the second gradient of the deformation. In bi-pantographic structures, such a dependence is given through the rate of change in orientation and stretch of material lines directed along the constituting pantographic beams.

Fig. 1

Additively manufactured bi-pantographic rectangular specimen

In the spirit of meta-materials [40,41,42], rectangular bi-pantographic specimens shown in Fig. 1 were designed and additively manufactured [43,44,45] by selective laser sintering (SLS) aimed at obeying the theoretical discrete model. Displacement-controlled bias extension tests were performed on these specimens for total elastic deformations up to ca. 25%. Experimental deformation measurements obtained by local digital image correlation (DIC) and force–displacement measurements were used to fit the continuum model.

In Sect. 2, we briefly recall the main results regarding the homogenization of the discrete model, including micro–macro correspondences needed to compare numerical results obtained for descriptions at different scales, i.e., discrete at micro-scale and continuum at macro-scale. The bias extension test considered in the present study is further introduced. Motivated by computational and implementation convenience, we successively introduce in Sect. 3 a minimal set of generalized coordinates for the discrete model, which is alternative to the one used for the homogenization. In Sect. 4, we fit the constitutive parameters of the discrete model by using collected experimental data. We then compare experiments, micro- and macro-modeling. Finally, in Sect. 5, some conclusions are drawn.

2 Homogenized continuum

In the undeformed configuration (Fig. 2b), the discrete structure is formed by cells arranged upon straight lines within the reference domain $\Omega$, in direction of the unit basis vectors $\mathbf{e}_x,\mathbf{e}_y\in \mathbb {E}^2$, being $\mathbb {E}^2$ the two-dimensional Euclidean vector space. The set $\Omega \subseteq \mathbb {R}^2$ has boundary $\partial \Omega$ being the disjoint union of $N_\Omega \in \mathbb {N}$ smooth line sets $\partial \Omega _k$, $k\in [1;N_\Omega ]$, pairwise intersecting in distinct vertices (see Fig. 2a). The quantity $\mathbf{p}_{i,j} \in \mathbb {R}^2$ (see Fig. 2b, d) is the current position of the point at position $\mathbf{P}_{i,j}$ in the reference configuration. In Fig. 2c, elastic elements are colored in black (extensional Hooke elastic springs, stiffness $k_\mathrm{E}$), red (rotational Hooke elastic springs, stiffness $k_\mathrm{F}$), blue (rotational Hooke elastic springs, stiffness $k_\mathrm{F}$) and green (rotational Hooke elastic springs, stiffness $k_\mathrm{S}$). The homogenization target is a 2D-continuum whose kinematics is characterized by its placement function $\varvec{\chi }:\ \Omega \rightarrow \mathbb {R}^2$, or, equivalently, by its displacement function ${\mathbf{u}}:\ \Omega \rightarrow \mathbb {E}^2$ such that ${\mathbf{u}}({x,y})={\varvec{\chi }}({x,y})-x\ \mathbf{e}_x-y\ \mathbf{e}_y$, where x and y denote the coordinates of the undeformed configuration given in the basis $\{\mathbf{e}_x, \mathbf{e}_y\}$. For the sake of conciseness, we introduce the index $\alpha$ ranging within the set $\{x,y\}$. We also introduce the maps $\rho _\alpha :\Omega \rightarrow \mathbb {R}^+$ and $\vartheta _\alpha :\Omega \rightarrow [0,2\pi )$ aimed at rewriting the tangent vector field $\frac{\partial \varvec{\chi }}{\partial \alpha }$ to deformed material lines directed along $\mathbf{e}_\alpha$ in the reference configuration as

$$\begin{aligned} \begin{aligned}&\frac{\partial \varvec{\chi }}{\partial x}(x,y) = \rho _x(x,y)\left\{ \left[ \cos {\vartheta _x(x,y)}\right] \mathbf{e}_x+\left[ \sin {\vartheta _x(x,y)}\right] \mathbf{e}_y\right\} \; , \\&\frac{\partial \varvec{\chi }}{\partial y}(x,y) = \rho _y(x,y)\left\{ \left[ \cos {\vartheta _y(x,y)}\right] \mathbf{e}_y+\left[ \sin {\vartheta _y(x,y)}\right] \mathbf{e}_x\right\} \;. \end{aligned} \end{aligned}$$

(1)

Hence, the quantity $\rho _\alpha$, henceforth referred to as $\alpha$-stretch, is the length of the vector $\Vert {\partial \varvec{\chi }}/{\partial \alpha } \Vert$ tangent to the deformed material lines directed along $\mathbf{e}_\alpha$ in the reference configuration. Letting $\varepsilon \rightarrow 0$ in Fig. 2b while keeping fixed the overall dimension of the system, and suitably scaling the force elements’ stiffnesses, Barchiesi et al. [29] have shown that the deformation energy for the homogenized macro-model reads as

$$\begin{aligned} \begin{aligned} \mathfrak {E}&= \int _{\Omega }\sum _\alpha \biggl \{K_{S}\left[ \cos ^{-1}\left( 1-\frac{\rho _\alpha ^2}{\frac{1}{2\cos ^2\gamma }}\right) -\pi +2\gamma \right] ^2 \\&\quad +K_{E}K_{F}\biggl [ \frac{\rho _\alpha ^{2}\cos ^{2}\gamma -1}{\rho _\alpha ^{2}\cos ^{2}\gamma \left( K_{E}-8K_{F}\cos ^{2}\gamma \right) -K_{E}}\left( \frac{\partial \vartheta _\alpha }{\partial \alpha }\right) ^2\\&\quad +\frac{\rho _\alpha ^{2}\cos ^{2}\gamma }{\left( 1-\rho _\alpha ^{2}\cos ^{2}\gamma \right) \left[ 8K_{F}+\rho _\alpha ^{2}\left( K_{E}-8K_{F}\cos ^{2}\gamma \right) \right] }\left( \frac{\partial \rho _\alpha }{\partial \alpha }\right) ^2\biggl ] \biggl \} \ \mathrm {d}A \end{aligned} \end{aligned}$$

(2)

being $K_\mathrm{S}$, $K_\mathrm{E}$ and $K_\mathrm{F}$ the scaled macro-stiffnesses corresponding to the micro-stiffnesses $k_\mathrm{S}$, $k_\mathrm{E}$ and $k_\mathrm{F}$, respectively. It is worth recalling [46] that for the above continuum deformation energy we can prescribe conditions at the smooth boundaries on (a) the normal placement gradient, (b) the placement function, and conditions on the placement function at vertices, i.e., singular points of the boundary.

Fig. 2

Bi-pantographic fabrics. a Domain $\Omega$, b undeformed configuration of (i, j)th cell (including neighboring elements), c force elements of a single cell, d deformed configuration of (i, j)th cell (including neighboring elements)

To compare the numerical results of the micro- and macro-model, beyond the micro–macro identification of independent kinematic descriptors

$$\begin{aligned} \varvec{\chi }(x_i,y_j)=\mathbf{p}_{i,j} \; , \end{aligned}$$

(3)

the following micro–macro correspondences, obtained by neglecting non-leading $\varepsilon$-terms in Taylor expansions of corresponding continuum quantities evaluated at discrete points, are considered

$$\begin{aligned} \begin{aligned}&\rho _x\left( x_{i},y_i\right) \leftrightarrow \frac{\Vert \mathbf{p}_{i+1,j}-\mathbf{p}_{i,j}\Vert }{\varepsilon } \;,&\quad&\rho _y\left( x_i,y_j\right) \leftrightarrow \frac{\Vert \mathbf{p}_{i,j+1}-\mathbf{p}_{i,j}\Vert }{\varepsilon } \;. \end{aligned} \end{aligned}$$

(4)

For the shearing angle (see Fig. 3), we can identify the micro–macro correspondence

$$\begin{aligned} \left[ \pi /2-\arccos \left( \frac{\nabla \varvec{\chi }\ \mathbf{e}_x\cdot \nabla \varvec{\chi }\ \mathbf{e}_y}{\Vert \nabla \varvec{\chi }\ \mathbf{e}_x\Vert \Vert \nabla \varvec{\chi }\ \mathbf{e}_y\Vert }\right) \right] _{(x,y)=(x_i,y_j)} \leftrightarrow \pi /2-\arccos \left( \frac{(\mathbf{p}_{i+1,j}-\mathbf{p}_{i,j})\cdot (\mathbf{p}_{i,j+1}-\mathbf{p}_{i,j})}{\Vert \mathbf{p}_{i+1,j}-\mathbf{p}_{i,j}\Vert \Vert \mathbf{p}_{i,j+1}-\mathbf{p}_{i,j}\Vert }\right) \; . \end{aligned}$$

(5)

Fig. 3

Angle $\arccos \left( \frac{(\mathbf{p}_{i+1,j}-\mathbf{p}_{i,j})\cdot (\mathbf{p}_{i,j+1}-\mathbf{p}_{i,j})}{\Vert \mathbf{p}_{i+1,j}-\mathbf{p}_{i,j}\Vert \Vert \mathbf{p}_{i,j+1}-\mathbf{p}_{i,j}\Vert }\right)$ for the undeformed (left) and deformed (right) configurations

Introducing for the discrete system the nodal displacements $\mathbf{u}_{i,j} \in \mathbb {E}^2$ such that $\mathbf{u}_{i,j}=\mathbf{p}_{i,j}-\mathbf{P}_{i,j}$, by the micro–macro identification (3), we have $\mathbf{u}(x_i,y_j)=\mathbf{u}_{i,j}$. Therefore, we can define the following micro–macro correspondences at the boundaries (cf. Fig. 4)

$$\begin{aligned} \begin{aligned}&\frac{\partial \mathbf{u}}{\partial x}(x_i,y_j) \leftrightarrow \frac{\mathbf{u}_{i+1,j}-\mathbf{u}_{i,j}}{\varepsilon }\mathrm {\ and\ }\frac{\partial \mathbf{u}}{\partial y}(x_i,y_j) \leftrightarrow \frac{\mathbf{u}_{i,j+1}-\mathbf{u}_{i,j}}{\varepsilon }\mathrm {\ for\ all\ }(x_i,y_j)\in \partial \Omega _1\;,\\&\frac{\partial \mathbf{u}}{\partial x}(x_i,y_j) \leftrightarrow \frac{\mathbf{u}_{i,j}-\mathbf{u}_{i-1,j}}{\varepsilon }\mathrm {\ and\ }\frac{\partial \mathbf{u}}{\partial y}(x_i,y_j) \leftrightarrow \frac{\mathbf{u}_{i,j}-\mathbf{u}_{i,j-1}}{\varepsilon }\mathrm {\ for\ all\ }(x_i,y_j)\in \partial \Omega _3\;. \end{aligned} \end{aligned}$$

(6)

The bias extension test¹ is commonly used in textile mechanics as a standard experiment to measure the in-plane combined shearing and tensile response of materials made up of two families of fibers. Such a mono-axial extension test is performed on rectangle-shaped specimens having long sides aligned with the loading direction. Constituting fibers—pantographic ones in the present study—are initially oriented at ± 45-degrees to the loading direction. In the present study, the test is modeled by a domain having the shape of a rectangle (with sides 187 mm $\times$ 119 mm and $\gamma$ in Fig. 2b equal to $\pi /6$, see Fig. 4) and being subjected to the following essential boundary conditions:

$$\begin{aligned} \begin{aligned}&\mathbf{u}(x,y)=0\mathrm {\ at\ }(x,y)\in \partial \Omega _1\;,&\qquad&\mathbf{u}(x,y)=\bar{u}\mathbf{e}_{\zeta }\mathrm {\ at\ }(x,y)\in \partial \Omega _3,\ \bar{u}\in \mathbb {R} \; , \\&[\nabla \mathbf{u}(x,y)]\mathbf{e}_\zeta (x,y)=0\mathrm {\ at\ }(x,y)\in \partial \Omega _1\;,&\qquad&[\nabla \mathbf{u}(x,y)] \mathbf{e}_\zeta (x,y)=0\mathrm {\ at\ }(x,y)\in \partial \Omega _3\;.\\ \end{aligned} \end{aligned}$$

(7)

Fig. 4

Schematics of the reference domain $\Omega$ considered in the boundary value problem for the macro-model. Point A in the picture is at the center of the square having as side the (left) shortest side of the domain. Point B is at the center of the domain

Shearing angles at points B and A in Fig. 4 are connected to the transverse contraction of the specimen (hence shearing stiffness) and fiber bending (hence effective fiber bending stiffness), respectively. Indeed, shearing deformation is maximum in B and, since the gray dashed triangle adjacent to the (left) shortest side behaves quasi-rigidly, fiber bending is maximum in A. Fiber extension is maximum at specimen corners—close to corners in the present study—and, therefore, effective fiber extensional stiffness is strongly related to fiber extension at specimen corners. For the discrete system, we have $\varepsilon {=}12.02$ mm, see Fig. 6. The correspondence between boundary conditions (7) for the continuum model and those for the discrete model are schematized in Table 1.

Table 1 Boundary conditions for micro- and macro-model

3 Micro-model revisited

For solving the discrete micro-model directly and without making any of the hypotheses assumed for the derivation of the continuum model, it is much more convenient to introduce an alternative global, minimal set of generalized coordinates than the one used for the homogenization, i.e., the kinematics of the discrete system is entirely described by the coordinates of the nodal points. The bi-pantographic fabric is modeled as a discrete elastic spring system that is embedded in the two-dimensional Euclidean vector space $\mathbb {E}^2$. The static equilibrium conditions are obtained by the principle of virtual work, which in the case of our elastic system coincides with the principle of stationary total potential energy. Consequently, only the system’s potential energy and its corresponding variation have to be formulated. The system is composed of extensional and rotational springs only. First, we introduce the potential energies of a standard extensional and rotational spring element. Subsequently, we explain the kinematics of the bi-pantographic fabric, which includes some cumbersome but necessary bookkeeping of the relevant degrees of freedom for each spring contribution. Lastly, we state the principle of virtual work for the constrained discrete system subjected to kinematic boundary conditions.

The springs are formulated between nodal points, which are depicted as white filled circles, see Fig. 5. The position $\mathbf{r}= \zeta \mathbf{e}_{\zeta } + \varsigma \mathbf{e}_{\varsigma } \in \mathbb {E}^2$ of a typical nodal point is commonly addressed by its Cartesian coordinates $\mathbf{x}= (\zeta , \varsigma ) \in \mathbb {R}^2$ with respect to the orthonormal basis vectors $\mathbf{e}_{\zeta },\mathbf{e}_{\varsigma } \in \mathbb {E}^2$. If not stated otherwise, $\mathbb {R}^f$-tuples are considered in the sense of matrix multiplication as $\mathbb {R}^{f\times 1}$-matrices, i.e., as “column vectors”. Let $\mathbf{q}^\text {e}= (\zeta _1,\varsigma _1,\zeta _2,\varsigma _2) \in \mathbb {R}^4$ be the coordinates of two points interconnected by an extensional spring as depicted in Fig. 5a. Introducing the abbreviations $\Delta \zeta = \zeta _2 - \zeta _1$ and $\Delta \varsigma = \varsigma _2 - \varsigma _1$, the distance between the two points is

$$\begin{aligned} l(\mathbf{q}^\mathrm {e}) = \sqrt{\Delta \zeta ^2 + \Delta \varsigma ^2} = \sqrt{(\zeta _2 - \zeta _1)^2 + (\varsigma _2 - \varsigma _1)^2} \; . \end{aligned}$$

(8)

The derivative with respect to $\mathbf{q}^\mathrm {e}$ is the “row vector”

$$\begin{aligned} \frac{\partial l}{\partial \mathbf{q}^\mathrm {e}}(\mathbf{q}^\mathrm {e}) = \frac{1}{l(\mathbf{q}^\mathrm {e})}(-\Delta \zeta ,-\Delta \varsigma ,\Delta \zeta ,\Delta \varsigma ) \in \mathbb {R}^{1 \times 4}\;. \end{aligned}$$

(9)

The potential of an extensional spring with stiffness $k_\mathrm {e} > 0$ and undeformed length $l_0 > 0$ is the function

$$\begin{aligned} \mathcal {E}^\mathrm {e}(k_\mathrm {e},l_0,\mathbf{q}^\mathrm {e}) = \frac{1}{2} k_\mathrm {e} [l(\mathbf{q}^\mathrm {e}) - l_0]^2 \; . \end{aligned}$$

(10)

The derivative of the potential (10) with respect to $\mathbf{q}^\mathrm {e}$ is the function

$$\begin{aligned} {\mathbf{f}^\mathrm {e}}^{\mathsf {T}}(k_\mathrm {e},l_0,\mathbf{q}^\mathrm {e}) = \frac{\partial \mathcal {E}^\mathrm {e}}{\partial \mathbf{q}^\mathrm {e}}(k_\mathrm {e},l_0,\mathbf{q}^\mathrm {e}) = k_\mathrm {e} [l(\mathbf{q}^\mathrm {e}) - l_0 ] \frac{\partial l}{\partial \mathbf{q}^\mathrm {e}}(\mathbf{q}^\mathrm {e}) \in \mathbb {R}^{1\times 4} \; . \end{aligned}$$

(11)

Fig. 5

a Kinematics of an extensional spring. b Kinematics of a rotational spring

Rotational springs are interactions between three nodal points. Let $\mathbf{q}^\text {r}=(\zeta _1,\varsigma _1,\zeta _2,\varsigma _2,$ $\zeta _3,\varsigma _3) \in \mathbb {R}^6$ be the Cartesian coordinates of three nodal points as depicted in Fig. 5b. With the abbreviations $\Delta \zeta _1 = \zeta _2-\zeta _1$, $\Delta \zeta _2 = \zeta _3-\zeta _2$, $\Delta \varsigma _1 = \varsigma _2-\varsigma _1$ and $\Delta \varsigma _2 = \varsigma _3-\varsigma _2$, the distances between the respective points are

$$\begin{aligned} l_1(\mathbf{q}^\text {r}) = \sqrt{\Delta \zeta _1^2 + \Delta \varsigma _1^2} \; , \qquad l_2(\mathbf{q}^\text {r}) = \sqrt{\Delta \zeta _2^2 + \Delta \varsigma _2^2} \; , \end{aligned}$$

(12)

with the corresponding derivatives

$$\begin{aligned} \begin{aligned} \frac{\partial l_1}{\partial \mathbf{q}^\mathrm {r}}(\mathbf{q}^\mathrm {r})&= \frac{1}{l_1(\mathbf{q}^\mathrm {r})} (-\Delta x_1, -\Delta \varsigma _1, \Delta x_1, \Delta \varsigma _1, 0, 0) \in \mathbb {R}^{1 \times 6}\; , \\ \frac{\partial l_2}{\partial \mathbf{q}^\mathrm {r}}(\mathbf{q}^\mathrm {r})&= \frac{1}{l_2(\mathbf{q}^\mathrm {r})} (0,0,-\Delta x_2, -\Delta \varsigma _2, \Delta x_2, \Delta \varsigma _2) \in \mathbb {R}^{1 \times 6} \; . \end{aligned} \end{aligned}$$

(13)

The angles between the $\mathbf{e}_\zeta$-axis and the vectors $\Delta \zeta _1 \mathbf{e}_\zeta + \Delta \varsigma _1 \mathbf{e}_\varsigma$ and $\Delta \zeta _2 \mathbf{e}_\zeta + \Delta \varsigma _2 \mathbf{e}_\varsigma$, respectively, are introduced by the relations

$$\begin{aligned} \phi _1(\mathbf{q}^\text {r}) = \tan ^{-1}\left( \frac{\Delta \varsigma _1}{\Delta \zeta _1}\right) \; , \qquad \phi _2(\mathbf{q}^\text {r}) = \tan ^{-1}\left( \frac{\Delta \varsigma _2}{\Delta \zeta _2}\right) \end{aligned}$$

(14)

with the corresponding derivatives

$$\begin{aligned} \begin{aligned} \frac{\partial \phi _1}{\partial \mathbf{q}^\mathrm {r}}(\mathbf{q}^\mathrm {r})&= \frac{1}{l_1(\mathbf{q}^\mathrm {r})^2} (\Delta \varsigma _1, -\Delta \zeta _1, -\Delta \varsigma _1, \Delta \zeta _1, 0, 0) \in \mathbb {R}^{1 \times 6}\; , \\ \frac{\partial \phi _2}{\partial \mathbf{q}^\mathrm {r}}(q^\mathrm {r})&= \frac{1}{l_2(\mathbf{q}^\mathrm {r})^2} (0,0,\Delta \varsigma _2, -\Delta \zeta _2, -\Delta \varsigma _2, \Delta \zeta _2) \in \mathbb {R}^{1 \times 6}\; . \end{aligned} \end{aligned}$$

(15)

Note, numerically $\tan ^{-1}$ is implemented by an atan2-function with a range $(-\pi ,+\pi ] \subset \mathbb {R}$. The potential energy of a rotational spring with stiffness $k_\mathrm {r} > 0$ and undeformed angle $-\pi < \phi _0 \le \pi$ is

$$\begin{aligned} \mathcal {E}^\mathrm {r}(k_\mathrm {r},\phi _0,\mathbf{q}^\mathrm {r}) = \frac{1}{2} k_\mathrm {r} [\phi _2(\mathbf{q}^\mathrm {r}) - \phi _1(\mathbf{q}^\mathrm {r}) - \phi _0]^2 \; . \end{aligned}$$

(16)

Straightforwardly, the derivative with respect to $\mathbf{q}^\text {r}$ leads to the $\mathbb {R}^{1\times 6}$ matrix

$$\begin{aligned} {\mathbf{f}^\mathrm {r}}^{\mathsf {T}}(k_\mathrm {r},\phi _0,\mathbf{q}^\mathrm {r}) = \frac{\partial \mathcal {E}^\mathrm {r}}{\partial \mathbf{q}^\mathrm {r}}(k_\mathrm {r},\phi _0,\mathbf{q}^\mathrm {r}) = k_\mathrm {r}[\phi _2(\mathbf{q}^\mathrm {r}) - \phi _1(\mathbf{q}^\mathrm {r}) - \phi _0]\bigg (\frac{\partial \phi _2}{\partial \mathbf{q}^\mathrm {r}}(\mathbf{q}^\mathrm {r})- \frac{\partial \phi _1}{\partial \mathbf{q}^\mathrm {r}}(\mathbf{q}^\mathrm {r}) \bigg ) \; . \end{aligned}$$

(17)

Fig. 6

Reference configuration of the discrete model. The (i, j)th vertex and the (i, j)th cell are highlighted by a red dot and a red square, respectively. A close up shows the arrangement of the nodal points in the undeformed reference configuration

The bi-pantographic fabric is characterized by a periodic substructure, which is captured in the discrete model by identical cells composed of extensional and rotational springs. The cells themselves do interact with each other by sharing nodal points with adjacent cells and by additional rotational springs. In the undeformed reference configuration, the cells are quadratic with width $\sqrt{2}\varepsilon$, see Fig. 6. Each cell has 4 nodal points as vertices, which are globally addressed by the row-column indices (i, j) within the range $i = \{0,1,\dots ,N\}$ and $j = \{0,1,\dots ,M\}$. Consequently, the fabric consists of $N \cdot M$ cells with $(N+1)(M+1)$ cell vertices. Besides the 4 vertices, in each cell, there are 9 additional nodal points required to capture the complex behavior of the bi-pantographic fabric. In the reference configuration, these nodal points are arranged symmetrically as depicted in Fig. 6.

Fig. 7

Deformed configuration of the discrete model. The (i, j)th vertex and the (i, j)th cell are highlighted by a red dot and a red quadrilateral, respectively. A close up shows the arrangement of the nodal points in the deformed configuration and their interaction by extensional and rotational springs

In the deformed configuration, the Cartesian coordinates of the cell vertices are denoted $\mathbf{x}_{(i,j)} = (\zeta _{(i,j)}, \varsigma _{(i,j)}) \in \mathbb {R}^2$. As depicted in Fig. 7, the Cartesian coordinates of the kth nodal point within cell (i, j) are $\mathbf{x}^k_{(i,j)} = (\zeta ^k_{(i,j)}, \varsigma ^k_{(i,j)}) \in \mathbb {R}^2$. Note that the coordinates of the cell vertices have different denotations depending on their respective application on cell or fabric level. Thus, the $f = 2 [(N+1)(M+1) + 9 N\cdot M ]$ generalized coordinates of the discrete system are the Cartesian coordinates of all nodal points of the fabric

$$\begin{aligned} \mathbf{q}= (\mathbf{x}_{(0,0)}, \ldots , \mathbf{x}_{(M,N)}, \mathbf{x}^4_{(0,0)}, \ldots , \mathbf{x}^{12}_{(0,0)}, \ldots , \mathbf{x}^4_{(M-1,N-1)}, \ldots , \mathbf{x}^{12}_{(M-1,N-1)}) \in \mathbb {R}^f \; . \end{aligned}$$

(18)

Table 2 Assignments of coordinates of nodal points to spring coordinates within cell (i, j)

For a compact formulation of the total potential energy of the system, it is convenient to introduce spring coordinates, i.e., sets of coordinates that involve only the coordinates of the relevant nodal points for each spring. We begin with the interactions in each cell (i, j) by considering Fig. 7 together with Table 2, where the explicit assignments of the nodal coordinates to the spring coordinates are specified. The axial stiffnesses of the fibers in the fabric are modeled by 16 extensional springs each with stiffness $k_\mathrm {e}$ and undeformed length $l_0 = \tfrac{\sqrt{3}}{3} \varepsilon$. The coordinates required for the kth spring are given by $\mathbf{q}^\mathrm {e}_{(i,j)k} \in \mathbb {R}^4$. The resistance of the pins with respect to torsion is captured by 8 rotational springs, depicted in Fig. 7 by green arcs, with stiffness $k_\mathrm {r1}$. The energy of the lth rotational spring is formulated with $\mathbf{q}^\mathrm {r1}_{(i,j)l} \in \mathbb {R}^6$ and the undeformed angle $\phi _0 = (-1)^l \pi /3$. The bending stiffness of the fibers within each cell is included by 4 rotational springs with stiffness $k_\mathrm {r2}$ influencing the coordinates $\mathbf{q}^\mathrm {r2}_{(i,j)m} \in \mathbb {R}^6$. The cells interact with each other by sharing nodal points with adjacent cells. However, we also have to account for the bending stiffness of the fibers at each cell vertex for $i=1,\dots ,N-1$ and $j=1,\dots ,M-1$. These bending stiffnesses are realized by rotational springs with stiffness $k_\mathrm {r3} = k_\mathrm {r2}$ and corresponding spring coordinates $\mathbf{q}^\mathrm {r3}_{(i,j)m} \in \mathbb {R}^6$, which are specified in Fig. 8. To extract the spring coordinates from the generalized coordinates (18), the Boolean connectivity matrices $\mathbf{C}^\mathrm {e}_{(i,j)k} \in \mathbb {R}^{4\times f}$ and $\mathbf{C}^\mathrm {r1}_{(i,j)l},\mathbf{C}^\mathrm {r2}_{(i,j)m},\mathbf{C}^\mathrm {r3}_{(i,j)m} \in \mathbb {R}^{6\times f}$ are defined by the relations

$$\begin{aligned} \mathbf{q}^\mathrm {e}_{(i,j)k} = \mathbf{C}^\mathrm {e}_{(i,j)k} \mathbf{q}\; , \quad \mathbf{q}^\mathrm {r1}_{(i,j)l} = \mathbf{C}^\mathrm {r1}_{(i,j)l} \mathbf{q}\; , \quad \mathbf{q}^\mathrm {r2}_{(i,j)m} = \mathbf{C}^\mathrm {r2}_{(i,j)m} \mathbf{q}\; , \quad \mathbf{q}^\mathrm {r3}_{(i,j)m} = \mathbf{C}^\mathrm {r3}_{(i,j)m} \mathbf{q}\; . \end{aligned}$$

(19)

Fig. 8

Assignments of coordinates of nodal points to spring coordinates for interaction between cells

Using the spring coordinates of Table 2 and Fig. 8 together with the potential energies (10) and (16), the total potential energy of the discrete bi-pantographic fabric is

$$\begin{aligned} \begin{aligned} \mathcal {E}(\mathbf{q})&= \sum _{i = 0}^{N-1}\sum _{j=0}^{M-1} \left( \sum _{k = 0}^{15} \mathcal {E}^\mathrm {e}(k_\mathrm {e},l_0,\mathbf{C}^\mathrm {e}_{(i,j)k} \mathbf{q}) + \sum _{l = 0}^7 \mathcal {E}^\mathrm {r}(k_\mathrm {r1},(-1)^l \tfrac{\pi }{3}, \mathbf{C}^\mathrm {r1}_{(i,j)l} \mathbf{q}) \right. \\&\quad \left. + \sum _{m = 0}^3 \mathcal {E}^\mathrm {r}(k_\mathrm {r2},0, \mathbf{C}^\mathrm {r2}_{(i,j)m} \mathbf{q}) \right) +\sum _{i = 1}^{N-1}\sum _{j=1}^{M-1} \sum _{m = 0}^3 \mathcal {E}^\mathrm {r}(k_\mathrm {r3},0, \mathbf{C}^\mathrm {r3}_{(i,j)m} \mathbf{q}) \; . \end{aligned} \end{aligned}$$

(20)

Let $\hat{\mathbf{q}}(\varepsilon )$ be a function of $\varepsilon$ that includes the actual coordinates $\mathbf{q}$ for static equilibrium in the case of $\varepsilon = 0$, i.e., $\hat{\mathbf{q}}(0) = \mathbf{q}$. Then, the variation of the total potential energy $\mathcal {E}$ induced by $\hat{\mathbf{q}}$ is

$$\begin{aligned} \delta \mathcal {E}(\mathbf{q}) = \frac{\partial \mathcal {E}}{\partial \mathbf{q}}(\mathbf{q}) \frac{\mathrm {d}\hat{\mathbf{q}}}{\mathrm {d}\varepsilon }(0)= \mathbf{f}^{\mathsf {T}}(\mathbf{q}) \delta \mathbf{q}\; , \end{aligned}$$

(21)

where $\delta \mathbf{q}= \frac{\mathrm {d}\hat{\mathbf{q}}}{\mathrm {d}\varepsilon }(0)$ are the virtual displacements, $\mathbf{f}(\mathbf{q}) = (\partial \mathcal {E}/\partial \mathbf{q})^{\mathsf {T}}(\mathbf{q})$ are the internal generalized forces and the transposed of a matrix is indicated by $(\cdot )^{\mathsf {T}}$. Using (11) and (17) together with the total potential energy (20), the internal generalized forces of the bi-pantographic fabric are obtained by

$$\begin{aligned} \begin{aligned} \mathbf{f}^{\mathsf {T}}(\mathbf{q})&= \frac{\partial \mathcal {E}}{\partial \mathbf{q}}(\mathbf{q}) \\&= \sum _{i = 0}^{N-1}\sum _{j=0}^{M-1} \left( \sum _{k = 0}^{15} \mathbf{f}^\mathrm {e}(k_\mathrm {e},l_0,\mathbf{C}^\mathrm {e}_{(i,j)k} \mathbf{q})\mathbf{C}^\mathrm {e}_{(i,j),k} + \sum _{l = 0}^7 \mathbf{f}^\mathrm {r}(k_\mathrm {r1},(-1)^l \tfrac{\pi }{3}, \mathbf{C}^\mathrm {r1}_{(i,j)l} \mathbf{q})\mathbf{C}^\mathrm {r1}_{(i,j)l} \right. \\&\quad \left. + \sum _{m = 0}^3 \mathbf{f}^\mathrm {r}(k_\mathrm {r2},0, \mathbf{C}^\mathrm {r2}_{(i,j)m} \mathbf{q})\mathbf{C}^\mathrm {r2}_{(i,j)m} \right) +\sum _{i = 0}^{N-1}\sum _{j=0}^{M-1} \sum _{m = 0}^3 \mathbf{f}^\mathrm {r}(k_\mathrm {r3},0, \mathbf{C}^\mathrm {r3}_{(i,j)m} \mathbf{q})\mathbf{C}^\mathrm {r3}_{(i,j)m} \; . \end{aligned} \end{aligned}$$

(22)

Kinematic boundary conditions are imposed by perfect bilateral constraints $0 = \mathbf{g}(\mathbf{q}) \in \mathbb {R}^m$ with a virtual work contribution $\delta W^\mathrm {c} = \delta \mathbf{g}^\mathsf {T} \varvec{\lambda }= \delta \mathbf{q}^\mathsf {T} \mathbf{W}(\mathbf{q}) \varvec{\lambda }$, where $\mathbf{W}(\mathbf{q})^\mathsf {T}=\frac{\partial \mathbf{g}}{\partial \mathbf{q}}(\mathbf{q}) \in \mathbb {R}^{m \times f}$ is the matrix of generalized force directions and $\varvec{\lambda }\in \mathbb {R}^m$ the vector of constraint forces. The discrete system is now in static equilibrium if and only if the total virtual work of internal generalized forces and constraint forces vanishes for all virtual displacements, i.e.,

$$\begin{aligned} \delta \mathbf{q}^{\mathsf {T}}(\mathbf{f}(\mathbf{q}) + \mathbf{W}(\mathbf{q})\varvec{\lambda }) = 0 \quad \forall \delta \mathbf{q}\in \mathbb {R}^f \end{aligned}$$

(23)

and the constraint equations $\mathbf{g}(\mathbf{q}) = 0$ are satisfied. Thus, the equilibrium configuration is determined by the set of nonlinear equations

$$\begin{aligned} \begin{bmatrix} \mathbf{f}(\mathbf{q}) + \mathbf{W}(\mathbf{q})\varvec{\lambda }\\ \mathbf{g}(\mathbf{q}) \end{bmatrix} = 0 \end{aligned}$$

(24)

which can be solved, at least locally, by a Newton–Raphson iteration scheme.

4 Results

Specimens were 3D-printed using selective laser sintering (SLS). Polyamide powder PA2200 was used as raw material. A top view of the manufactured specimen, with a zoom on relevant details, is shown in Fig. 1. The micro-model’s kinematics prescriptions in the third and sixth rows of Table 1 are realized by connecting adjacent hinge axes in the vicinity of gripping areas, see Fig. 1. Stocky rhomboidal elements are used to this end, which can be assumed to be rigid for the studied load cases.

An increasing displacement was prescribed horizontally on the right side of the specimen with a loading rate of 15 mm/min meant to be quasi-static in relation to the weight of the specimen. Kinematic experimental acquisition was achieved by non-stereo digital image correlation (DIC). Pictures of the surface during deformation were acquired (0.5 fps, i.e., nominally for 1 mm displacement increments) by means of a Canon EOS 600D camera with a definition of 4272 $\times$ 2848 pixels and an 8-bit dynamic range. The sought kinematics is given by the in-plane displacements of the hinges at positions $\mathbf{p}_{i,j}$’s of the bi-pantographic structure. The displacements of these (discrete) points are retrieved via local DIC (i.e., using zones of interest or ZOIs [47] centered on each hinge). The simplest approach seeks the rigid body translation of each considered ZOI, as originally performed in particle image velocimetry [48, 49]. An in-depth illustration of the application of the above-mentioned DIC techniques to the present study is beyond the scopes of this article. Therefore, it is omitted. For more details on the design, manufacturing and experimental testing of bi-pantographic specimens, we refer to [29].

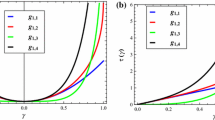
Parameters for the discrete ($k_\mathrm{F}$, $k_\mathrm{E}$ and $k_\mathrm{S}$) model and the continuum ($K_\mathrm{F}$, $K_\mathrm{E}$ and $K_\mathrm{S}$) one were independently found by fitting the three curves (see Fig. 9). The first one (Fig. 9 (left)) is the total reaction force versus $\bar{u}$. The second one (Fig. 9 (center)) is the shearing angle at point A (cf. Fig. 4) versus $\bar{u}$. Finally, the third one (Fig. 9 (right)) is the shearing angle at point B, which is strongly related to the transverse contraction of the specimen, against $\bar{u}$.

Fig. 9

Total reaction force with changed sign (N) versus prescribed displacement $\bar{u}$ (mm) along the direction $e_\zeta$ (left), shearing angle at point A ($^\circ$) versus prescribed displacement $\bar{u}$ (mm) along the direction $e_\zeta$ (center), and shearing angle ($^\circ$) at point B versus prescribed displacement $\bar{u}$ (mm) along the direction $e_\zeta$ (right)

Table 3 Parameters’ value for discrete and continuum models as found by way of fitting

Parameters’ value for discrete and continuum models as found by way of the fitting procedure described above is reported in Table 3. Deformed configurations as predicted by modeling, i.e., $\mathbf{p}_{i,j}$’s for the discrete model and $\varvec{\chi }(x_i,y_j)$ for the continuum model, are compared for different $\bar{u}$’s with experimental data, and are plotted in Fig. 10. Discrete and continuum modeling substantially overlap, and the agreement with experiments is remarkably good. It is worth noticing that experimental data are noticeably not-completely symmetric, which might be a point to address in future. A contour plot of the y-stretch $\rho _y$ is shown in Fig. 11 for discrete and continuum models. Again, micro–macro agreement is very good even for such a rather small number of cells.

Fig. 10

Deformed configurations as predicted by the discrete and continuum models, i.e., $\mathbf{p}_{i,j}$’s for the discrete model and $\varvec{\chi }(x_i,y_j)$ for the continuum one, for different $\bar{u}$’s are compared with experimentally measured ones. Abscissas and ordinates are expressed in mm

Fig. 11

y-stretch $\rho _y$ for discrete and continuum models. Abscissas and ordinates are expressed in mm

5 Conclusion

In the present article, we performed a preliminary comparison between discrete and homogenized continuum modeling in the finite deformation regime analysis of a recently designed specimen with bi-pantographic micro-structure. From obtained evidences, we conclude that the metamaterials synthesis problem has been successfully accomplished and that the agreement between homogenized continuum and discrete system is very good already for low numbers of cells. Possible outlooks include the investigation of lower-scale approaches based on granular micro-mechanics [50,51,52], the use of semi-discrete descriptions in which continuous beam elements replacing assemblies like those in Fig. 2d are solved by iso-geometric analyses [53,54,55,56,57,58,59] and the study of different boundary prescriptions [60].