Abstract
Potential deleterious health effects to astronauts induced by space radiation is one of the most important long-term risks for human space missions, especially future planetary missions to Mars which require a return-trip duration of about 3 years with current propulsion technology. In preparation for future human exploration, the Radiation Assessment Detector (RAD) was designed to detect and analyze the most biologically hazardous energetic particle radiation on the Martian surface as part of the Mars Science Laboratory (MSL) mission. RAD has measured the deep space radiation field within the spacecraft during the cruise to Mars and the cosmic ray induced energetic particle radiation on Mars since Curiosity’s landing in August 2012. These first-ever surface radiation data have been continuously providing a unique and direct assessment of the radiation environment on Mars. We analyze the temporal variation of the Galactic Cosmic Ray (GCR) radiation and the observed Solar Energetic Particle (SEP) events measured by RAD from the launch of MSL until December 2020, i.e., from the pre-maximum of solar cycle 24 throughout its solar minimum until the initial year of Cycle 25. Over the long term, the Mars’s surface GCR radiation increased by about 50% due to the declining solar activity and the weakening heliospheric magnetic field. At different time scales in a shorter term, RAD also detected dynamic variations in the radiation field on Mars. We present and quantify the temporal changes of the radiation field which are mainly caused by: (a) heliospheric influences which include both temporary impacts by solar transients and the long-term solar cycle evolution, (b) atmospheric changes which include the Martian daily thermal tide and seasonal CO\(_2\) cycle as well as the altitude change of the rover, (c) topographical changes along the rover path-way causing addition structural shielding and finally (d) solar particle events which occur sporadically and may significantly enhance the radiation within a short time period. Quantification of the variation allows the estimation of the accumulated radiation for a return trip to the surface of Mars under various conditions. The accumulated GCR dose equivalent, via a Hohmann transfer, is about \(0.65 \pm 0.24\) sievert and \(1.59 \pm 0.12\) sievert during solar maximum and minimum periods, respectively. The shielding of the GCR radiation by heliospheric magnetic fields during solar maximum periods is rather efficient in reducing the total GCR-induced radiation for a Mars mission, by more than 50%. However, further contributions by SEPs must also be taken into account. In the future, with advanced nuclear thrusters via a fast transfer, we estimate that the total GCR dose equivalent can be reduced to about 0.2 sievert and 0.5 sievert during solar maximum and minimum periods respectively. In addition, we also examined factors which may further reduce the radiation dose in space and on Mars and discuss the many uncertainties in the interpreting the biological effect based on the current measurement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multiple space agencies have been looking into the possible human deep space exploration programs to our neighbour planet Mars. However, space radiation presents risks not only for the lifetime of satellites and the performance of instruments onboard, but also the health of astronauts. There are three primary types of energetic particle radiation in space, the particles in the radiation belts of planetary magnetospheres, galactic cosmic rays (GCRs) and solar energetic particles (SEPs). Table 1, adapted from Feynman and Gabriel (2000), summarizes some major radiation effects induced by these particles with different types and energies. For deep space missions outside Earth’s magnetosphere and radiation belts, e.g., to the Moon and to Mars, high-energy GCR and SEP-induced radiation effects are the main concern as shown in the table. Note that all acronyms used in this article are given in Table 3 and 4 in the Abbreviatons.
1.1 Types of radiation relevant for a Mars mission
Radiation in deep space that can be hazardous for a potential Moon/Mars mission consists of omnipresent highly energetic GCRs, sporadic and possibly highly intense SEPs, and secondary radiation as primary particles (either GCRs or SEPs) pass through the spacecraft hull or the planetary atmosphere. SEPs and GCRs have different origins, properties, and distributions in space and time.
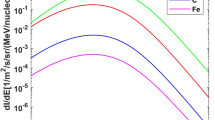
Left: GCR differential flux of protons (\(Z=1,\) azure), helium ions (\(Z=2,\) orange) and heavier nuclei (\(Z>2,\) green) as calculated by the Badhwar–O’Neill model (O’Neill 2010). Solidlines and dashed lines indicate the GCR flux at solar minimum and maximum periods respectively. Right: The proton spectra of 50 large SEP events, integrated over each event duration, of events detected from August 1997 to 2006 near Earth. More explanation can be found in the text
Cosmic rays have been extensively studied at the Earth (Grieder 2001). Remarkably, their energy spectrum has been measured with proton energies extending above \(10^{20}\) eV, several orders of magnitude above what the most powerful man-made particle accelerators can produce on Earth. At energies above \(\sim 10\) GeV/nuc, the energy spectrum follows a power law with a small spectral break near \(5 \times 10^{15}\) eV, commonly referred to as the knee, where the spectrum steepens. There exists another spectral break near \(3\times 10^{18}\) eV, usually called the ankle, where the spectrum turns up again. Below the ankle energy the particles are most commonly interpreted as originating from supernova explosions within the galaxy (Biermann and Sigl 2001) and are called galactic cosmic rays (GCRs). However, the detailed origin of these high-energy cosmic particles is still one of the most fundamental problems of modern astro-particle physics. In the current article, we focus on the radiation effect of GCRs rather than their origin. On their way to the solar system, GCRs are continuously deflected by galactic magnetic fields, resulting in a flux that is nearly isotropic in the solar system. In the heliosphere, the intensity and composition of GCRs are rather stable, but evolve as the particle flux is modulated by the varying heliospheric magnetic field following the solar cycle (e.g., Cane et al. 1999). GCRs in the inner heliosphere include about 2% electrons and 98% atomic nuclei of which the latter are composed of about 87% protons, 12% helium, and \(\sim 1\%\) heavier nuclei \((Z\ge 3)\) (Simpson 1983). (Abundances vary slightly depending on the phase of the solar cycle.) The decrease (increase) in GCR intensity near solar maximum (minimum) is reflected in the data from neutron monitors which measure the GCR-induced neutrons generated in Earth’s atmosphere (e.g., Feynman and Gabriel 2000). Figure 1 (left) shows the differential GCR flux as a function of energy for protons, helium ions and heavier ions as modeled by the Badhwar–O’Neill model (O’Neill 2010). The model numerically solves the Fokker–Planck equation that takes into account diffusion, convection, and adiabatic deceleration of GCR particles propagating inward through the heliosphere. The GCR flux is more modulated during solar maximum and is significantly lower than that during solar minimum for particles below about 1 GeV/nuc.
On the other hand, SEPs are energetic particles (mainly protons and electrons) emitted from the Sun and accelerated by solar eruptions. Therefore, SEP events are more likely to occur during solar maximum. SEPs generally have energies from suprathermal of a few keV up to several hundreds of MeV (occasionally even reaching 1 or 2 GeV or more) and can reach significantly higher fluxes at these energies compared to GCRs. Figure 1 (right) shows the proton spectra (integrated over each event duration) of 50 large SEP events reconstructed from measurements of the Geostationary Operational Environmental Satellite (GOES) and the Advanced Composition Explorer (ACE) satellite at the deep space environment near Earth from August 1997 to 2006 (Nymmik 2015; Khaksarighiri et al. 2021). A SEP event normally lasts between a few hours and a few days. Compared to the GCR flux (per day) shown in the left panel, the SEP event flux can be orders of magnitude higher especially at energies below a few hundreds of MeV.
Two different acceleration mechanisms are believed to be most responsible for accelerating SEPs: magnetic reconnection during solar flares and shock acceleration at Coronal Mass Ejection (CME)-driven shocks (e.g., Kallenrode 2003). The shock acceleration can also be differentiated into coronal CME shock or interplanetary shock-related acceleration.
Solar flares are related to magnetic reconnection processes in the low solar corona (Aschwanden 2002, and references therein). The majority of the particles accelerated in these structures remain confined, causing characteristic photon emissions in the X-ray and ultraviolet range lasting for several minutes to hours as electrons are decelerated when they run into regions of denser plasma (Bremsstrahlung emission). Some flares are associated with gamma rays indicating accelerated ions (Vilmer et al. 2011). In particular, the neutron-capture line at 2.223 MeV of gamma rays is formed when energetic protons and ions of 10–100 MeV/nuc collide with the nuclei in the dense chromosphere and produce neutrons which are further thermalized and captured by an ambient proton to form deuterium. A fraction of the flare-accelerated particles, however, can escape the acceleration region along open magnetic field lines, streaming into the interplanetary medium, often causing intense radio emissions. The composition of these particles is typically electron- and iron rich with an enhanced \(^3\)He/\(^4\)He ratio due to resonant wave–particle interaction in the acceleration region (Roth and Temerin 1997; Paesold et al. 2003). As the flare site generally has a limited extent, the flare-accelerated SEPs often have a narrow injection into the interplanetary space along the interplanetary magnetic field (IMF) lines whose large-scale form is that of an archimedean (Parker) spiral. Therefore, most commonly, an observer needs to be magnetically connected to the flare site to be affected by flare-accelerated SEPs. Such events are generally impulsive and of short duration.
In contrast, shock acceleration at CME-driven shocks is more likely responsible for long-lasting and wide-spread large SEP events (Reames 2013). Besides, as the shock wave propagates across the solar corona and through the interplanetary medium, it may continue accelerating particles from the ambient plasma or from contiguous and/or previous solar events (e.g., Desai and Giacalone 2016; Gopalswamy et al. 2002). These energetic particles stream out from the shock front guided by IMF lines as the shock propagates through the heliosphere. The acceleration at a wide shock structure and the possible continuous acceleration often result in a gradual and long-lasting time profile of the SEPs. However, the SEP spectrum and its time evolution also depend on the development of the shock, the superthermal seed population on its path, as well as the location of the observer and its connection to the evolving shock. As shown in many studies (e.g., Bain et al. 2016; Battarbee et al. 2018; Desai and Giacalone 2016; Gopalswamy et al. 2004; Guo et al. 2018a; Lario et al. 2013, 2017; Luhmann et al. 2017), the intensities of SEP events have different evolution profiles depending on various factors, such as: (1) the heliolongitude of the source region with respect to the observer location, (2) the strength of the shock and its efficiency at accelerating particles, (3) the evolution of the shock (its speed, size, shape and efficiency in particle acceleration), (4) the presence of a seed particle population to be (re-)accelerated, (5) the energy considered, (6) the solar wind conditions for the propagating particles, and (7) the heliospheric structures which may serve as discontinuity boundaries for propagating particles.
Finally, primary GCRs and SEPs passing through the spacecraft hull or Martian atmosphere may undergo inelastic interactions with the ambient atomic nuclei, losing some or all their energy and also creating secondary particles via spallation and fragmentation processes. These secondary particles may further interact with the ambient material during their propagation (and in the case of Mars, with the Martian regolith if they reach the surface), finally resulting in very complex spectra including both primary and secondary particle radiation inside the space vehicle or at the surface of Mars (e.g., Wilson et al. 1999; Kim et al. 2014).
1.2 Biological radiation effects for a human Mars mission
For a potential human mission to Mars which generally requires a long mission duration (\(\gtrsim 3\) years), risks induced by exposure to space radiation have been classified as one of the potential “show stoppers” (Walsh et al. 2019; Cucinotta et al. 2017). Therefore, the assessment of such radiation and the evaluation of its biological consequences have been given a high priority in the field of space exploration.
Chronic exposure to the GCR radiation environment does not immediately endanger the astronauts’ life, but it increases the probability of late-term consequences (e.g., Cucinotta and Durante 2006; Kennedy 2014), such as development of cancer and cataracts or damage to the central nervous system (CNS) and/or cardiovascular system and hereditary effects (Iancu et al. 2018). On the other hand, intense SEP events, apart from contributing to the above stochastic effect, can be also associated with deterministic effects. Deterministic effects occur above a threshold and increase with increasing exposure; whereas for stochastic effects, the probability of the radiation effect increases with increasing exposure (Straume 2015).
In NASA’s Human Research Roadmap (A Risk Reduction Strategy for Human Space Exploration https://humanresearchroadmap.nasa.gov), the integrated research plan divides the space radiation risks into the following categories: risk of acute and late CNS effects from radiation exposure, risk of acute radiation syndromes due to SEP events, risk of degenerative tissue or other health effects from radiation exposure, and risk of radiation carcinogenesis. The degenerative tissue risks include the effects of radiation on the heart, circulatory, endocrine, digestive, lens and other tissue systems (bone, muscle, etc.). Here, we provide an introductory summary of the biological effects of space radiation, while interested readers can find a detailed review on the topic by Kennedy (2014).
Most fundamentally, ionizing radiation may induce cancer via particle interaction with Deoxyribonucleic acid (DNA) molecules, either through direct ionization process or by generating secondary particles and activating free radicals in the cell which further interact with the DNA chains. These interactions can lead to cell death or, worse, DNA misrepair, which may have consequences for cell reproduction (Cucinotta and Durante 2006; Barcellos-Hoff et al. 2015). In particular, GCR ions with high (H) atomic number (Z) and energy (E) (HZE ions), despite of their low abundance, can be extremely damaging because the energy deposited in an individual cell is proportional to the square of the particle’s charge. Thus, HZE ions may contribute significantly to the cell damage disproportionately to their relatively small abundances.
Radiation can also interfere with the CNS. Biological experiments using animal models have revealed the capability of radiation to significantly decrease the structural complexity and synaptic integrity of neurons throughout different regions of the brain, inducing compromised cognitive performance of mice (Parihar et al. 2016). Sokolova et al. (2015) have studied the potential radiation damage on the hippocampus of mice, which is an important structure for the formation of long-term episodic memory and found that 1 Gy (energy deposited by radiation per unit mass 1 Gy = 1 J/kg) of proton radiation can produce long-term changes to neuronal electrophysiological states.
Although the human head and brain structure is different from that of a mouse, it is still expected that some neurological impact can be induced by radiation above a certain level. The NASA Space-Permissible Exposure Limit (SPEL) for short-term radiation exposure of CNS is 0.5 Gy in 30 days (Cucinotta et al. 2014). Khaksarighiri et al. (2021) have modeled the dose distribution inside a realistic human head structure induced by GCRs and SEP spectra of historical events, and found that the drastically enhanced dose induced by some SEP events inside the brain could actually exceed 0.5 Gy, with a potential mission-critical radiation effect.
Radiation can also induce degenerative tissue risks, including cataracts which occur with an increased rate as has been observed in astronauts (Cucinotta et al. 2001a; Rastegar et al. 2002). This is a long term effect which generally develops at a delayed stage. However, a mission to Mars would likely last for several years and astronauts need to spend a considerable amount of time in space where medical treatment is limited. In this case, radiation induced cataracts may also become a critical issue. In fact, epidemiological studies among Chernobyl workers, bomb survivors, astronauts, radiological technicians, and those undergoing diagnostic or radiotherapeutic procedures resulted in a re-evaluation in International Commission of Radiation Protection (ICRP) who proposed lowering of the radiation cataract threshold to 0.5 Gy/year (ICRP 2012). This threshold could be reached in a short time when exposed to large SEP events without sufficient protection.
Another important degenerative risk is circulatory diseases which are recently considered as an important risk for a mission to Mars (Cucinotta et al. 2013b). Space radiation may induce detrimental influences on certain parameters related to cardiovascular and circulatory diseases, with particularly strong effects leading to chronic vascular dysfunction (e.g., Soucy et al. 2011) and angiogenesis (e.g., Grabham and Sharma 2013). It has been reported that doses of 2–5 Gy \(^{56}\)Fe ion radiation targeted to specific arterial sites in some mice accelerated the development of atherosclerosis (Yu et al. 2011). It should be noted that these are very high doses of heavy ions compared to expected space exposures.
Last but not least, SEP events are capable of significantly increasing the absorbed dose to astronauts during an interplanetary mission, producing Acute Radiation Syndrome (ARS, https://www.cdc.gov/nceh/radiation/emergencies/arsphysicianfactsheet.htm), skin injury, and depletion of the blood forming organs (BFO), possibly even leading to death (Wu et al. 2009). ARS takes place when large amount of dose (i.e., greater than 0.7 Gy) is delivered to the entire body within a short period of time (usually a matter of minutes). Clinically, ARS can be classified as hematopoietic syndrome (with dose exposure between 0.7 and 10 Gy), gastrointestinal syndrome (usually when dose is above 10 Gy), and neurovascular syndrome (usually when dose is above 10 Gy). Symptoms of the hematopoietic syndrome are induced due to the high radiation dose (Gy level) damaging hematopoietic cells located in the bone marrow, with consequent blood count changes (Kennedy 2014). The survival rate of patients with this syndrome decreases with increasing dose. With the occurrence of a full gastrointestinal syndrome, body infection, dehydration, and electrolyte imbalance often appear and death usually occurs within 2 weeks. And the last stage of ARS with dose above 10 Gy normally induce death within 3 days.
Most SEPs have protons with energies below tens of MeV and an extra-vehicular activity (EVA) spacesuit has a sufficient thickness to stop protons below 30 MeV. It is generally believed that the likelihood of ARS risk during internal vehicle activity is extremely small. However, a large SEP event with abundant particles above hundreds of MeV may induce possible ARS of astronauts during intra-vehicular activity (IVA), or Lunar- or Mars-EVAs without sufficient shielding protection. For different SEP events, doses absorbed by different tissues are different due to self-shielding of the human body. Hu et al. (2009) have calculated the radiation doses that could have been received by astronauts during previous major SEP events. For the August 1972 SPE, they estimated that the event could have delivered doses of 2.69 and 0.46 Gy to skin and BFO, respectively for astronauts in a spacecraft (an aluminum sphere of 5 g/cm\(^{2}\) thickness). During EVA situations (an aluminum sphere of 0.3 g/cm\(^{2}\) thickness), the absorbed dose would be significantly higher, i.e., 32 and 1.38 Gy to skin and BFO, respectively. These problematic scenarios can be avoided or mitigated by operational measures, such as SEP event forecasting and monitoring, and by ready access to shielded locations. More discussions on radiation mitigation during SEP events can be found in Sect. 8.
1.3 Motivation to understand the Mars radiation environment
Unlike Earth, Mars has no global intrinsic magnetic field and only a thin atmosphere, with a column depth about 2% that of Earth’s. The thin atmosphere is not sufficient to stop a significant fraction of GCRs, although it stops a large share of SEPs in typical events. Primary GCRs and SEPs can interact with the Martian atmosphere, producing secondaries that make the surface radiation field different from that in space. This also happens in space as particles can interact with the spacecraft material. In particular, secondary neutrons are of considerable concern from the perspective of radiation protection. Unlike charged particles, neutrons do not undergo ionization energy loss and penetrate through matter easily, particularly those in the “fast” energy range on the order of MeV, where their biological weighting factors are large (e.g., ICRP 2012). Therefore, the assessment of the radiation environment associated with a Mars mission, including the cruise phase in deep space and the Martian surface stay, is necessary and fundamental to mitigate radiation risks for near-future robotic and crewed missions to Mars.
To evaluate such radiation risks for deep space and planetary missions, in particular in preparation for future human exploration of Mars, the Radiation Assessment Detector (RAD, Hassler et al. 2012) was designed to detect and analyze energetic particle radiation during the cruise to Mars and on the Martian surface as part of the Mars Science Laboratory (MSL, Grotzinger et al. 2012). The direct scientific goals of RAD important for future human Mars exploration are (Hassler et al. 2012): (1) to measure energetic particle spectra at the surface of Mars, (2) to measure dose and determine dose equivalent rates for human explorers on Mars, and (3) to use these measurements to enable validation of Mars atmospheric transmission models and radiation transport codes.
The MSL spacecraft, containing the Curiosity rover, was launched on November 26, 2011 (during the rising phase of solar cycle 24), and landed on Mars on August 6, 2012 after a 253 day cruise, setting down on the floor of Gale Crater, northwest of Aeolis Mons (Mount Sharp), and about 4.4 km below Martian zero elevation. During both the cruise phase and the surface mission period (for more than 8 years until the time of this writing), MSL/RAD has provided the first assessment of the radiation environment in such environments (Zeitlin et al. 2013; Hassler et al. 2014) which is fundamental for evaluating the radiation risks and the consequent biological effects likely to be encountered during a future Mars mission.
Top: The monthly value (gray) and smoothed monthly value (black) of sunspot numbers over different solar cycles in comparison with Cycle 24. Bottom: The normalized value of monthly sunspot number and the normalized value of the dose rate measured by RAD (transparent red for the original data while red line for the monthly data) on the surface of Mars. The normalization is done dividing the data by their median value of Cycle 24 to illustrate the magnitude of the evolution
Solar cycle 24 has been widely recognized as one of the weakest ones compared to historical records of sunspot numbers, as shown in Fig. 2 (top panel). The monthly sunspot data are downloaded from the World Data Center SILSO, Royal Observatory of Belgium, Brussels (http://www.sidc.be/silso/monthlyssnplot). As clearly shown in the bottom panel of Fig. 2, the GCR-induced radiation dose rate as measured by MSL/RAD on Mars rose by about 50% from the maximum of Solar cycle 24 until its deep minimum. The anti-correlation between the sunspot number and the GCR flux is nicely shown in the monthly data, even reflecting some short-term activities, e.g., the enhanced solar activity in 2017 September and the Forbush decrease (more details in Sect. 4.1) caused by the interplanetary counterparts of the solar eruption arriving at Mars (e.g., Lee et al. 2018; Guo et al. 2018a).
RAD data contain temporal variations at different time scales arising from different sources. In this paper, we present and study the temporal variation of the radiation measured by RAD from August 2012 until the end of 2020. Besides the occasional and prominent enhancement due to SEPs, the background GCR variations are mainly due to three causes: (a) heliospheric influences which include both long-term solar cycle evolution and temporal impacts by solar transients, (b) atmospheric depth variations which can be attributed to the Martian daily thermal tide and seasonal CO\(_2\) cycle, as well as the altitude change of the rover as it gradually climbs Mount Sharp, and (c) highly localized topographical effects which may partly shield/change the radiation field as the rover traverses variable Martian terrain. We present and quantify the temporal changes of the radiation field caused by different effects and discuss the possible radiation risks associated with future human exploration of the red planet under different conditions.
The paper is organized as following. We will first give an introduction of the RAD instrument and its measured quantities in Sect. 2. The following sections will address the above-mentioned three causes of the GCR variations with the atmospheric effect shown in Sect. 3, the heliospheric impacts in Sect. 4 and the topographic influences in Sect. 5. In Sect. 6, we estimate the accumulated GCR-induced radiation level for a round-trip mission (two cruise phases plus the surface stay) to Mars under different heliospheric conditions. In Sect. 7, we further address the characteristics and effects of SEPs, in particular the ones detected by RAD during its cruise to and on the surface of Mars. In Sect. 8, comparing MSL/RAD measurements with other available measurements, e.g., the Liulin-MO detectors on board the ExoMars Trace Gas Orbiter, and with the state-of-the-art modeling results, we discuss about potential reduction of the GCR and SEP radiation during the cruise phase and the surface stay, respectively. We also provide further interpretations of the associated risk of a Mars mission in Sect. 9. A brief summary and conclusion follow in Sect. 10.
2 The Radiation Assessment Detector (RAD)
The design of RAD allows it to detect energetic particles, both charged and neutral, and to determine radiation dose rates. A sketch of the RAD sensor head design is shown in Fig. 3. RAD acquires data for a specified period of time (typically 16 min), then packages its data and stores them in non-volatile memory. Each data acquisition period is referred to as an observation. The observation data, telemetered to Earth several times per day, are used to characterize the radiation environment. Important measurement quantities that are derived from the raw data include the absorbed dose rates in plastic (similar to tissue) and in silicon, histograms of deposited energy, the average quality factor, the dose equivalent rate, the spectra of charged particles typically from about 10 to 100 MeV/nuc for the most abundant H and He ions (heavier ions can be resolved up to hundreds of MeV/nuc with less spectral resolution) and even the high-energy neutral particle spectra via an inversion method. In this section, we briefly define and explain these terms, apart from the particle detection and calibration. The charged and neutral particle measurement is another important research topic of RAD and provide important data for benchmarking space radiation transport models. Interested readers can find more information on the charged particle measurement in several papers already in the literature: Ehresmann et al. (2014, 2017), the inverted neutral particle spectra on Mars in Köhler et al. (2014) and Guo et al. (2017b) as well as the data-model comparison in e.g., Matthiä et al. (2016, 2017) and Guo et al. (2019a).

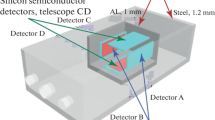
Image reproduced with permission from Guo et al. (2015a), copyright by ESO; adapted from Hassler et al. (2012)
Schematic view of the RAD sensor head, consisting of three silicon detectors (A, B and C, each having the thickness of 300 \(\upmu \text{m}\)), a caesium iodide scintillator (D with a height of 28 mm) and a plastic scintillator (E with a height of 18 mm). Absorbed dose values are simultaneously recorded in detector B and E. The D and E scintillators are surrounded by a plastic anticoincidence scintillator (F). For detecting charged particles, A, B, C, D and E are used as a telescope. Neutral particles (both neutrons and gammas) are detected in D and E using C and F as anticoincidence.
In this paper, we mainly focus on and discuss about the assessment of the radiation dose-related quantities and their time-variation which are fundamental for evaluating the radiation risks and the consequent biological effects likely to be encountered during a typical Mars mission. A few important dosimetric measurements are defined and explained in the following subsections.
2.1 Dose rate
Most importantly, the radiation dose rate, defined as the energy deposited by radiation per unit mass and time (e.g., in the unit of J/kg/day or Gray/day or Gy/d), is measured continuously. RAD dose measurements are taken using two concurrent methods in active dosimeters: the silicon detector “B” and the plastic scintillator “E”. The latter has a composition similar to that of human tissue, and it is also more sensitive to neutrons than silicon detectors. Figure 4 shows the time profile of RAD measured radiation dose rate since the MSL landing until December 2020. The original measurement shown is taken at a 16-min cadence and smoothed data have a smoothing window of 1 day. The absorbed dose in the silicon B detector, after subtracting the background contribution by the rover’s radioisotope thermoelectric generator (RTG), is smaller than that in the plastic E detector due to the different ionization potential of the two different detector materials.
RAD-recorded Martian surface dose rates in silicon detector B and plastic detector E since MSL landing until 2020 December. The silicon dose rate has been corrected for the background radiation contributed by the rover RTG. The dose rate measured in “B” is plotted in gray (B dose) and the daily smoothed values are plotted in orange (smt B dose); the dose rate measured in “E” is plotted in azure (E dose) and the daily smoothed values are plotted in black (smt E dose). Five SEP events detected on the surface of Mars are marked with numbers from 1 to 5
The Curiosity rover is dependent on the RTG power which contributes to the dose rate seen in the B detector, but not effectively to the E detector, as determined and measured by RAD before the MSL spacecraft was launched to Mars. Based on that measurement and the further calibration of RAD, we estimated the RTG contribution to the B dose rate was about 84 \(\upmu \)Gy/day during the cruise phase of the spacecraft flying from Earth to Mars, and is 66 \(\upmu \)Gy/day on the surface of Mars (Zeitlin et al. 2016). The latter value has been subtracted in the B dose rate shown in the figure. We note that the ratio of the B dose to the E dose seems to have decreased slightly over the course of 8 years, from about 0.75 to 0.72. Considering that the RTG radiation should decrease slowly with time, this indicates that the constant RTG background subtraction in B might be an over-correction in the later phase of the data present. If we assume that the E/B dose should be constant like the initial phase after landing, we estimate that the RTG contribution to the B dose rate averaged about 58 \(\upmu \)Gy/day for the last 2 years of data shown. This is roughly consistent with the 87.7 year half-life of the \(^{238}\)Pu that powers the RTG.
Figure 4 also shows that the E detector has much better statistics, which is mainly due to its large geometric factor. Since E also is a tissue-equivalent material, its absorbed dose is rather comparable to that in water, which is commonly used as a proxy for human tissue. (There is only a difference of \(\sim 3\%\) in ionization potential between plastic and water.) As noted above, it is also the case that the E detector dose rate appears to be unaffected by the background from Curiosity’s RTG. In this study, therefore, we generally use the dose recorded in the E detector, unless specifically noted otherwise. The E dose rate was around 200 \(\upmu \)Gy/day from late 2012 until early 2015 and slowly and steadily increased during the declining phase of the past solar cycle, until it flattened at around 320 \(\upmu \)Gy/day during the deep solar minimum of 2019–2020.
Since MSL’s landing on Mars, RAD has recorded only 5 prominent SEP events as also shown in Fig. 4, with the most significant one taking place on 2017-09-10 during the declining phase of solar cycle 24. This event was also observed as a ground level event on Earth, making it the first solar energetic particle event seen at the surface of two planets. Some particles were also transported across magnetic field lines throughout the heliosphere and were detected at the back side of the Sun where the eruption was centered (Guo et al. 2018a). RAD observed that the flux of protons with energies below about 100 MeV was increased by a factor of 30 (Ehresmann et al. 2018; Hassler et al. 2018), and the dose rate doubled over the course of several hours after the event onset. The dose rate leveled off at sustained peak rates for about 12 h before declining over the following 36 h. Though in many ways an impressive event, particularly considering the phase of the solar cycle, the integrated dose would not have posed any radiation risks to humans (Zeitlin et al. 2018). (More detailed discussion about this event can be found in Sect. 7.3.) Calculations of particle transport through the Martian atmosphere show that some historical SEP events with higher intensities could pose even higher radiation levels for astronauts on the Martian surface (Norman et al. 2014; Townsend et al. 2006; Guo et al. 2018c, 2019b). More direct measurements of the SEP-induced radiation field are needed for us to better verify its associated risks for future astronauts on Mars.
2.2 LET histogram
The B silicon detector is also used to produce a Linear Energy Transfer (LET, i.e., \(\text{d}E/\text{d}x\)) histogram for an incoming charged particle that satisfies a telescope acceptance cone path and penetrates through B. The cone is defined by a coincidence of hits in the A and B detectors, both of which are 300 \(\upmu \)m thick. Two view cones can be defined for the LET spectrum measurement, one using the inner ring of the A detector, and the other using the outer ring. The inner cone has an half angle of 18\(^\circ \) and the full cone has an half angle of 32\(^\circ \). With the measured deposited energy (\(\text{d}E\)) in the B detector, a \(\text{d}E/\text{d}x\) histogram can be constructed. Then an approximate silicon-to-water factor (\(\sim 1.79,\) Zeitlin et al. 2019) is applied to convert the LET measured in silicon to an estimated LET spectrum in water. (The conversion factor is accurate at the ±5% level.) Figure 5 (top) shows a comparison between the LET histograms recorded during the cruise phase and early surface phase. At about 0.2 keV/\(\upmu \)m of LET, the minimum ionizing proton peak formed by relativistic high-energy protons (and other highly relativistic, singly charged particles such as pions and muons) is clearly seen in both histograms. It is also apparent that on the surface of Mars, there is a reduction at high LET, where heavy charged particles \((Z > 2)\) contribute. This is mostly because the vertical column depth of the Martian atmosphere averaged about 21 g/cm\(^2\) during this period and heavy ions are likely to fragment when going through this much of atmosphere. During the cruise phase, the RAD field of view (FOV) was non-uniformly shielded with half of the FOV only lightly shielded (< 10 g/cm\(^2\), Zeitlin et al. 2013), thus allowing a larger ratio of heavier ions contributing to the high LET part of the spectrum.
Top: A comparison of charged-particle LET spectrum measured during the early phase on the Mars surface from 7 August 2012 to 1 June 2013 (black) with that measured during cruise (red) inside the MSL spacecraft with variable shielding. Image reproduced with permission from Hassler et al. (2014), copyright by AAAS. Bottom: The ICRP quality factor (ICRP 1992) as a function of LET in water
2.3 Quality factor and dose equivalent
The conventional method of radiation risk estimation uses a quality factor which is a function only of LET in water, \(Q(\text{LET})\) according to ICRP (1992). \(Q(\text{LET})\) is a dimensionless quantity used in radiation biology to relate dose—a physical quantity, as measured by RAD and other instruments—to dose equivalent, a quantity that is intended to represent the risk of cancer induction, albeit with large uncertainty. As shown in Fig. 5 (bottom), Q is equal to 1 for LET less than 10 keV/\(\upmu \)m; it then increases linearly and peaks at LET of 100 keV/\(\upmu \)m; finally at even higher LET values, it decreases inversely to its square root. The average quality factor \(\langle Q \rangle \), is then defined as the convolution of \(Q(\text{LET})\) with the LET histogram normalized by the integrated LET histogram. Therefore the LET distribution determines the value of \(\langle Q \rangle \), which is particularly sensitive to the high LET part of the histogram populated by heavy ions, as this is the region where \(Q(\text{LET})\) acts as a large weighting factor. The \(\langle Q \rangle \) value calculated based on the data shown in Fig. 5 is \(3.05 \pm 0.3\) for the Martian surface case compared to \(3.82 \pm 0.3\) for the cruise phase. Given the similar solar modulation conditions of the two periods, the difference between their \(\langle Q \rangle \) values is mainly due to the more effective Mars atmospheric shielding against heavy ions in the LET view cone of RAD, i.e., the same reason for the difference in the LET histograms explained in the previous paragraph. Over the course of the mission, \(\langle Q \rangle \) values have declined compared to this early measurement, and in more recent data average about 2.3; see Zeitlin et al. (2019) and Sect. 3.2 for details.
Multiplying the measured dose with the above estimated \(\langle Q \rangle \), we can obtain the dose equivalent (in sievert or Sv) which can be related to the radiation risk of lifetime cancer induction via population studies (Cucinotta and Durante 2006). There are other definitions used in the field of radiation biology (equivalent dose, effective dose, etc.) which use the same SI unit (Sv); this may be a source of confusion when these disparate quantities are compared to one another (ICRP 2013, and also more details in Sect. 9). Although no standard upper limit has been established for a deep space mission to Mars, some space agencies have adopted 1 sievert as the astronaut career exposure limit for low-Earth orbit (LEO) missions. In terms of the RAD measurement, we estimate the LET-based dose equivalent as it is not possible to precisely detect the type and the original energy of each incident particle in space or on the Martian surface, as would be needed to, for example, calculate organ doses.
3 Atmospheric effects on the surface radiation environment
3.1 The Martian atmosphere at Gale Crater
Mars has a much thinner atmosphere than Earth. The Martian surface atmospheric pressure is less than 1% of that of Earth. The dominant composition of the Martian atmosphere is about 95% CO\(_2\) (Owen et al. 1977), of which 25% may condense or sublimate seasonally onto the winter poles driving a global evolution of the seasonal CO\(_2\) mass exchange in the air and consequently surface pressure changes (Tillman 1988; Zurek 1988). One Martian year lasts 668 sols, equal to 687 Earth days. Each Mars year (MY) starts with the Martian solar longitude \((L_{\text{s}})\) being \(0^\circ \), i.e., spring equinox, followed by the summer solstice \((L_{\text{s}} = 90^\circ ),\) the autumnal equinox \((L_{\text{s}} = 180^\circ )\) and finally the winter solstice \((L_{\text{s}} = 270^\circ ).\) April 11, 1955 \((L_{\text{s}}\) is \(0^\circ )\) is defined as the beginning of MY 1. There are two pressure peaks in each MY, as shown in Fig. 7 in red, with the higher one corresponding to the southern hemisphere early summer and the lower peak to the northern hemisphere early summer. This is due to the high eccentricity of Mars’s orbit with the planet being closer to the Sun during the southern hemisphere summer.
In addition to seasonal effects, the Martian atmosphere exhibits a strong thermal tide excited by direct solar heating of the atmosphere on the day side and strong infrared cooling on the night side. Heating causes an inflation of the atmosphere with a simultaneous drop in the atmospheric column depth and surface pressure. In Gale Crater, the thermal tide produces a diurnal variation of column mass of about \(\pm 5\%\) relative to the median, as measured by the Rover Environmental Monitoring Station (REMS, Gómez-Elvira et al. 2012). Two periods of the REMS measured surface pressure and its changes over each Martian day are shown in Fig. 6a, c. The magnitude of the diurnal pressure cycle at Gale Crater is substantially greater than previous surface measurements. This is likely due to the topography of the crater environment, which yields hydrostatic adjustment flows that amplify the daily tides (Haberle et al. 2014). Here and below, we use “daily” to refer to each Martian day which lasts for 24 h, 39 min and 35 s.
3.2 The influence of the atmosphere on the surface radiation
It is shown in Fig. 6a, c that daily changes of the RAD recorded dose rate are anti-correlated with the REMS measured atmospheric pressure, which is a direct measure of the atmospheric vertical column depth. That is, when the atmospheric pressure (and thus, column mass) increases, the surface dose rate decreases and vice versa. This reveals a shielding effect of the atmosphere on the surface radiation environment (Rafkin et al. 2014). Data and models (Guo et al. 2017a; Zeitlin et al. 2019; Singleterry Jr et al. 2011) suggest that the underlying cause of the observed diurnal effect is the fragmentation of heavy ions in the predominantly CO\(_2\) atmosphere; as atmospheric depth increases, a decreasing share of heavy ions (which make a disproportionately large contribution to dose) survive transport to the surface intact.
a/c RAD detected dose rate in E detector and REMS measured surface pressure [Pa] in two different periods (each lasting for 26 sols) under different solar modulation conditions indicated by the average modulation potential \({\overline{\varPhi }}\). b/d Superposed hourly perturbation of dose rate versus that in pressure during the period of data shown in a/c. The yellow highlighted data in a indicate a SEP event and a Forbush decrease and are excluded from the superposed fitting on the right (the data during these two periods are still shown as blue dots in b). The linear fit to the data are shown in yellow in b and d and the fitted slope \(\kappa \) is shown with a unit of \(\upmu \)Gy/day/Pa
The RAD dose rate is continuously changing due to other effects such as the heliospheric influences which complicate the quantification of the diurnal effect. As marked in Fig. 6a in yellow, the diurnal oscillation of the dose rate is disturbed during the SEP event and the subsequent Forbush decrease which is caused by the impact of an interplanetary coronal mass ejection (e.g., Cane et al. 2000, more details in Sect. 4.1). To isolate and quantify the diurnal atmospheric effect, a superposed epoch method can be applied: first the hourly variations of the dose rate from the daily mean value can be extracted as \(\delta ~{D}_{\mathrm{hourly}} = {D}_{\mathrm{hourly}} - \bar{{D}}_{\mathrm{daily}}\); second, the hourly variation of the pressure from the daily mean value can be similarly extracted as \(\delta ~{P}_{\mathrm{hourly}}\); finally, \(\delta ~{D}_{\mathrm{hourly}}\) can be correlated with \(\delta ~{P}_{\mathrm{hourly}}\) over multiple days (Rafkin et al. 2014; Guo et al. 2015b, 2017a). The anti-correlation is well fit by a linear regression with the parameter \(\kappa \) (\(\upmu \)Gy/day/Pa) representing the anti-correlation dependence, as shown Fig. 6b, d for the data shown in (a) and (c), respectively. In this procedure, we have also excluded the data periods strongly influenced by heliospheric disturbances such as the highlighted SEP and Forbush decrease in (a).
The fitted \(\kappa \) in two periods shown in Fig. 6 are significantly different. This is mainly due to the different phases of the solar cycle in these two periods (Guo et al. 2017a). In the period shown in Fig. 6a, which has a duration of 26 sols (approximately one Solar rotation as seen from Mars), the average modulation potential \(\varPhi \) is about 610 MV. For the 26-sol period shown in (b), the average \(\varPhi \) is about 490 MV, corresponding to weaker solar modulation of the primary GCRs. \(\varPhi \) represents the heliospheric modulation of GCR flux, based on Earth-based neutron monitor measurements. There is a network of neutron monitors distributed around the Earth, which have provided a decades-long record of solar modulation of GCRs. Monthly averages values of \(\varPhi \) based on neutron monitor measurements (Usoskin et al. 2017) can be found here: http://cosmicrays.oulu.fi/phi/phi.html. A more detailed discussion of solar modulation can be found in Sect. 4.3.2. Modulation of the GCRs is energy dependent: lower energy particles are more influenced, and their flux is more depressed during stronger solar modulations. The atmospheric shielding effect is also energy dependent, as less energetic particles are more easily slowed down or stopped by the atmosphere. The effects of atmospheric shielding and solar modulation are asynchronous, and operate on very different time scales (11 years vs. \(\sim \) 2–3 years). At times, the effects go in the same direction (e.g., high modulation potential and high pressure, tending to maximize the suppression of low-energy ions), or can work in opposite directions (e.g., high modulation with low pressure, or vice-versa). When solar modulation is weak, the share of lower energy GCRs incident at the top of the atmosphere is comparatively large, and we would expect the atmospheric shielding effect to become more evident. The data bear this out: \(|{\kappa }| = 0.21\) for \(\varPhi = 490\) MV and \(|{\kappa }| = 0.14\) for \(\varPhi = 610\) MV, as shown in Fig. 6.
Guo et al. (2017a) have simulated this atmospheric effect and its dependence on solar modulation conditions, combining modeled GCR spectra and particle transport calculations of the primary GCRs through the Martian atmosphere. The modeled results agree qualitatively well with the measurement, showing that the atmospheric shielding effect is more obvious under weaker solar modulation conditions, and also predict that the diurnal effect would be depressed or even vanish as solar modulation becomes stronger. The RAD data reported here begin before the maximum of solar cycle 24 and continue through the maximum (2014–2015) and into the declining phase and the associated deep solar minimum (more details in Sect. 4). Modulation during the solar maximum of Cycle 24 was much weaker compared to the previous cycles, and the diurnal response of the surface dose rate has been observed to be always anti-correlated with the atmospheric pressure throughout this period. Data collected during a much stronger solar maximum are needed to validate the model prediction.
In Fig. 7, the black dots represent the proportionality factor \(\kappa \) (multiplied by 1000) between the dose rate and pressure variations calculated in intervals of 26 sols using the above-mentioned superposed epoch method. Its evolution over more than four Martian years of the MSL surface mission, from August 2012 until October 2020, is displayed in the figure. The dose rate, surface pressure and \(\varPhi \) values over the same time range are also shown with each value being the 26-sol binned result and the error bar being the standard deviation. The choice of binning data into each 26 sols is to average out the solar modulation difference at Earth where \(\varPhi \) is estimated and at Mars within one solar rotation period which is about 26 sols at Mars.
Dose rate, pressure, and modulation potential \(\varPhi \) collected in the time range from Sol 1 to 2894 (lower x ticks; Sol 1 corresponds to the day of MSL landing) or 2012-08-06 to 2020-09-26 (upper x ticks). Left y axis: The 26 sol binned RAD plastic dose rate (\(\upmu \)Gy/d, gray) and derived pressure dose rate correlation \(|\kappa |\) (\(\upmu \)Gy/day/Pa and scaled up 1000 times, black); right y axis: The 26 sol binned surface pressure (Pascal, red) measured by REMS and \(\varPhi \) (MV, magenta) derived from Earth neutron monitor data. Vertical shaded period (sol 2070 to 2150) corresponds to a global Martian storm in 2018. Odd/even Martian Years (MY) are marked using gray/white background
Figure 7 clearly shows that the Martian surface dose rate is anti-correlated with the solar modulation potential \(\varPhi \) in the long term and this will be studied in more detail in Sect. 4. It also shows that the atmospheric shielding effect as fitted by \(|\kappa |\) is also evolving in the long term and becomes larger towards the solar minimum for the reasons explained earlier.
Some exceptions to these trends are visible in the most recent Martian year. For instance, as highlighted in azure from sol 2080 to 2150 (June–August of 2018), there was a global Martian dust storm (Guzewich et al. 2019), during which the \(|\kappa |\) values drastically dropped to below 0.1 \(\upmu \)Gy/day/Pa. A closer look at the daily surface pressure shows that, during the storm, it evolved in a more complex pattern than the usual daily thermal tide and had a larger diurnal dynamic range. But the daily variation range of the dose rate was slightly decreased, resulting in a smaller value of \(|\kappa |\). This deviation from the larger trend is not fully understood at present. If the dusty atmosphere contained a significant fraction of heavier elements, as the soil does, we would expect a modified relation between column depth and surface dose rate; however, the mass of dust in the atmosphere during the storm is far too small to explain the observed change in \(\kappa \).
Another example is shown for the period from around Sol 1440 to 1640 when \(|\kappa |\) had a persistent drop. This is most likely due to the high inclination angle (up to about 30\(^\circ \)) of the rover during its climb. As shown in Fig. 17, the rover altitude increased by about 150 m within this period. The overall atmospheric pressure of the two most recent Martian years, as observed by Curiosity’s REMS instrument in Gale Crater, is lower than the previous years at the same season, mainly because the rover was climbing higher in altitude towards Mount Sharp. Since the beginning of the mission until late 2020, the rover climbed more than 400 m (more details in Sect. 5.2). During some periods, the inclination of the rover deck relative to the zenith causes the detector to view different portions of the sky. Since the radiation on the Martian surface is dependent on the zenith angle, this could lead to changes in \(\kappa \) during those periods.
Although \(|\kappa |\) has notable variations, its value has been in the range from 0.1 and 0.2 \(\upmu \)Gy/day/Pa for most of the mission. A maximum value of \(\sim 0.21~\upmu \)Gy/day/Pa was seen during the deep solar minimum; this can be considered an upper limit of the atmospheric influence on the dose rate in Gale crater. Figure 7 also shows the seasonal evolution of the Martian atmospheric changes over 4 Martian years. The pressure varies between 690 and 960 Pa throughout a Martian year for the first 3 years and between 660 and 920 in the last year. Since the diurnal atmospheric changes affect the dose rate, it is sensible to deduce that the seasonal atmospheric variation, which changes over a larger amplitude compared to the diurnal oscillations, would also result in dose rate changes at a seasonal time scale. However, Fig. 7 clearly shows that the heliospheric modulation has a stronger influence, and the seasonal atmospheric influence is only embedded therein. Using the upper limit of \(|\kappa | \sim 0.21~\upmu \)Gy/day/Pa during solar minimum and the dynamic range of seasonal pressure of about 270 Pa, we can derive that the seasonal atmosphere-induced dose rate variation is \(\lesssim 57~\upmu \)Gy/day between minimal and maximal seasonal pressure values. This is about 19% of the average dose rate of \(\sim 300~\upmu \)Gy/day during solar minimum of Cycle 24. Thus, it may be important to take into account the seasonal atmospheric effect on the surface radiation for future Martian mission planning, especially during solar minimum conditions.
Another important effect of the atmospheric influence on the surface radiation is the variation of the quality factor which is used to derive the dose equivalent from dose, as explained in Sect. 2. Zeitlin et al. (2019) have reported that when the atmospheric column depth varies in the long term (due to both seasonal changes and elevation of the rover) which changes between about 20 and 24 g/cm\(^2\), the \(\langle Q \rangle \) value also changes between 2.1 and 2.7, with the smaller value obtained for larger atmospheric depth. This is expected: As the atmosphere thickens, the shielding against heavy ions—which contributes more to a larger \(\langle Q \rangle \)—becomes more efficient due to nuclear fragmentation. For instance, using measured cross sections (Zeitlin et al. 1997), the nuclear mean free path of an iron ion is only about 12 g/cm\(^2\), roughly half of the typical vertical column depth at Gale Crater. As a consequence, the \(\langle Q \rangle \) value is anti-correlated with the atmospheric column depth (or the surface pressure).
4 Modulation of GCR radiation by solar activity
GCRs in the solar system are constantly affected by variations of the heliospheric magnetic fields, both on short and long time scales. In the long term, the GCR flux was first observed to vary inversely with sunspot number (Forbush 1954, 1958) since the transport of GCRs towards the inner heliosphere is modulated by the intensity of the heliospheric magnetic field (Parker 1965), which evolves with the 22-year Hale cycle. Figure 2 already showed the anti-correlation between GCR radiation measured on Mars and sunspot number in Cycle 24.
In the short term, the GCR flux can also be altered temporarily in the form of Forbush decreases (Forbush 1937; Lockwood 1971) by transient heliospheric structures with enhanced magnetic fields such as interplanetary coronal mass ejections (ICMEs, Cane 2000) and stream interaction regions (SIRs, Richardson 2004). Forbush decreases (FDs) can often be identified as a temporary and rapid depression in the GCR intensity followed by a comparatively slower recovery phase, and typically last for a few days. CMEs are eruptions of magnetic structures from the Sun caused by magnetic reconfiguration or reconnection, often launched with a speed as fast as thousands of kilometers per second. CMEs often drive a shock ahead of them while propagating outwards in the heliosphere. SIRs are formed due to high speed streams (HSS) arising from coronal holes running into the slow solar wind in interplanetary space and SIRs often occur recurrently as corotating interaction regions (CIRs) since coronal holes may exist stably for several Carrington rotations and the consequent GCR modulation occurs periodically.
In this section, we will give an overview and discuss about the ICME-induced FDs, recurrent FDs related to CIRs, and the long-term solar-cycle modulations of GCRs as measured by RAD on Mars.
4.1 ICME-induced Forbush decreases on Mars
The observation of a FD event is usually studied at one point in the interplanetary space, mostly on and near Earth, while the same FD may look different at other locations in the heliosphere. This is mainly related to the fact that (1) an ICME and its shock’s intensity, speed, orientation and interaction with the ambient solar wind are different at different parts of the structure (e.g., nose or flank) and may change drastically as it propagates outward from the Sun through the heliosphere, and (2) the GCRs are transported from the outer heliosphere to the inner part and particles of different types and energies respond differently to the outward propagating and evolving shocks and magnetic ejecta (Dumbović et al. 2020).
The textbook example of a two-step FD often relates the first step to the encounter of the shock front and the following sheath region (if existent), which is the part between the leading shock and the trailing magnetic ejecta. The sheath is characterized by enhanced solar wind speed and turbulence which affect the diffusion coefficients of GCRs (Wibberenz et al. 1998). During the propagation of an ICME, the sheath keeps evolving as it is affected by different processes (Manchester et al. 2005; Janvier et al. 2019; Freiherr von Forstner et al. 2020) such as the pileup of solar wind in front, reconnection with the following ejecta, expansion or contraction due to the variation of the speed of the driving ejecta and the ambient solar wind, or lateral transport of plasma away from the ICME apex. The second step occurs as the closed magnetic structure of the ejecta significantly hinders perpendicular diffusion transport of GCRs across the magnetic field (Krittinatham and Ruffolo 2009). Due to the evolution of the magnetic flux rope, there is a concurrent process of flux rope expansion and increased diffusion of GCRs into the rope as the ICME propagates (Dumbović et al. 2018). Both the evolution of the sheath and the following magnetic structure drive the evolution of the FD profiles.
Therefore, observations of FDs at multiple heliospheric locations are important for us to understand the propagation of the solar eruptions and the reaction of the GCRs. The observation of FD events has been carried out extensively at Earth since decades. Since its landing, MSL/RAD has been providing another chance to observe FDs and the associated ICMEs at a unique view point in the heliosphere. Such studies are also helpful for us to understand the space weather context at Mars, especially when in situ plasma measurements are lacking (e.g., Witasse et al. 2017; Winslow et al. 2018; Guo et al. 2018a, b; Wang et al. 2018; Dumbović et al. 2019; Freiherr von Forstner et al. 2018, 2019, 2020; Papaioannou et al. 2019). Here we focus on RAD-detected FDs on Mars.

Images adapted from Freiherr von Forstner et al. (2018), copyright by AGU
Upper left: Cartoon illustration of the opposition phase constellation ideal for observations of the same ICME passing both Earth and Mars. Upper right: An example of an ICME event detected first at Earth and later at Mars as FDs. Lower-left: Histogram of ICME speed changes of 15 events between 1 au and Mars. \({\bar{v}}\) is the calculated mean speed between 1 au and Mars based on the time delay of the FD onset at two locations and \(v_{1 {\mathrm{AU}}}\) is the measured speed at 1 au. Lower-right: Comparison of the ratio \({\bar{v}}/v_{1 {\mathrm{AU}}}\) to \(v_{\mathrm{sw}} - v_{1 {\mathrm{AU}}}\), where \(v_{\mathrm{sw}}\) is the ambient solar wind speed measured at ACE. The colors denote the ICME speed at 1 au. The Pearson correlation coefficient r and the probability p that such a data set was produced by an uncorrelated system are displayed.
Tracking the propagation and evolution of ICMEs FDs can be used to identify the arrival of ICMEs at an observer’s location, and thus it is possible to track the propagation of a single ICME when multiple observers detect FDs at different heliospheric distances along the path of the ICME. Since the interaction of GCRs and the ICME shock/sheath region, as well as the magnetic structure, occurs continuously as the ICME propagates, FDs are expected to reflect the evolutionary properties of the outward propagating ICME, including its speed, size, shock strength, magnetic field strength in the ejecta, etc. Witasse et al. (2017) have studied the journey of an ICME, ejected at the Sun on 14 October 2014, throughout the solar system. The ICME did not pass Earth, but was unambiguously identified using the associated FDs at Mars (with 1.5 astronomical unit (au) distance from the Sun, 3 days after the CME launch), comet 67P/Churyumov–Gerasimenko (3.1 au, 8 days after launch), and Saturn (9.9 au, 29 days after launch) in the outer heliosphere. At observation points closer to the Sun, the associated FD was seen to be steeper , deeper and shorter than at points farther from the Sun. Similarly, Winslow et al. (2018) studied the FD caused by an ICME as it passed Mercury, Moon and Mars throughout the inner heliosphere and also found that the associated FD is steeper and deeper closer to the Sun, and the magnitude of the FD becomes smaller with heliocentric distance. Furthermore, Freiherr von Forstner et al. (2018) have studied 15 ICME events which first passed by an observer at 1 au, i.e., at either Earth or the STEREO spacecraft at 1 au, and later also reached Mars. Using the delay time of the FD onset at two locations, they estimated the ICMEs’ transit times between 1 and 1.5 au and found that the deceleration of ICMEs due to their interaction with the ambient solar wind may continue beyond 1 au, as illustrated in Fig. 8. Another comparison of a larger set of FDs at Earth and Mars shows a linear correlation between the total amplitude and the maximum hourly decrease of FDs, but the relations of these two quantities have different slopes at Earth and Mars (Freiherr von Forstner et al. 2020). With the help of a theoretical model, this statistical difference of the FD property suggests that the ICME sheath region may have broadened by a factor between about 1.5 and 1.9 en route from Earth to Mars, indicating a continuation of a slight decrease of the expansion factor in comparison with results obtained from Mercury to Venus and to Earth by Janvier et al. (2019).
a, b WSA-Enlil simulation snapshots showing the propagation of the three CMEs associated with the 10 September 2017 eruption, in Heliocentric Earth Ecliptic (HEE) coordinates, at different times: a the fast third CME approaches the previously merged two CMEs (CME1 + 2) from behind; b merged 3 CMEs nearly arrived at Mars. The colors shown are the modeled radial solar wind speeds in the ecliptic plane. c The modeled propagation and interaction of 3 CMEs and the shock propagation in the direction of Mars based on the Drag-based model (DBM). d The in situ RAD observation (normalized to background level before the SEP onset) of the 10 September 2017 SEP event and the FD on 13 September as well as DBM-modeled ICME arrival time at Mars.
Association with complex/interacting events The biggest FD as observed by MSL/RAD so far is related to the second largest flare (class X8.2) in solar cycle 24, which took place on 10 September 2017 from the Active Region 12673 at S08W88. Within one day, the same region launched two CMEs, followed by a third extremely fast CME accompanied by an intense shock, which triggered an EUV wave spreading rapidly across the entire solar surface (Veronig et al. 2018; Lee et al. 2018). The flare and shock accelerated SEPs up to about 2 GeV, which were transported through a wide range of the heliosphere and detected on the surface of both Earth and Mars (Guo et al. 2018a). The CME-related shock was very wide (at least 220\(^{\circ }\) in its longitudinal extent) and it impacted Earth about 2 days after the launch. In the direction of Mars (about 160\(^\circ \) away from Earth in heliospheric longitude), it propagated faster and arrived at Mars only about 9 h later than at Earth. Using both an analytical drag-based model (DBM, Vršnak et al. 2013) and the MHD ENLIL model to describe the interplanetary journey of the ICMEs, Guo et al. (2018a) studied the propagation of the 3 CMEs and associated shocks towards the two planets and found that the shock propagation was rather different in the two directions (Fig. 9). Towards Earth, the shock was not driven by a magnetic structure and experienced more deceleration on its way. Towards Mars, the very fast CME and the shock driven by it caught up with the previous 2 CMEs, which likely swept the way for the successive one to experience less drag; all three CMEs had similar directions and speeds one faster than another and they likely merged as an entity and propagated further together as shown in Fig. 9. The arrival of the shock and the merged CME caused the largest FD in the RAD measurements so far (\(\sim \) 23% and larger than the 18–19% as observed during the 2014 October event reported by Witasse et al. 2017).
Another FD as large as 15% on July 27, 2017 has been analyzed by Dumbović et al. (2019) in comparison with the in situ ICME signatures at STEREO-A (46\(^\circ \) from Mars). Combined with DBM and ENLIL modeled results, they found out that there were two CMEs interacting with each other and also with the ambient solar wind. This adds to the complexity of the event, resulting in a long, multi-step interplanetary disturbance at Mars, where different substructures correspond to different steps of the FD, adding up to a large-amplitude FD. This provides an alternative interpretation of two-step FDs rather than the classic sheath–ejecta scenario.
Statistics and energy dependence of FDs on Mars Guo et al. (2018b) have performed a statistical study of 121 FDs recorded in the RAD dose rate observations from 2014 until 2016 and found the mean amplitude of FDs observed by RAD at Gale crater is about 4–5% and the probability distribution of FD magnitudes can be well fitted by a power law with the index being \(-2.08\pm 0.32\). Similar results were obtained for terrestrial FDs from 1957 to 2016 with a power-law index of \(-2.31\pm 0.11\) (Belov et al. 2015). Papaioannou et al. (2019) have further compiled a catalog of 424 FDs seen by RAD from 2012 to 2016 and showed that the average amplitude of FDs at Mars is higher by a factor of 1.5–2 compared to the size of the FDs detected during the same period at Earth. This difference is mainly due to the different energy ranges of the GCRs measured in the two data sets. At Earth, neutron monitor measurements are used to derive the GCR flux at a fixed rigidity of 10 GV (Belov 2008). Rigidity is particle momentum per unit charge and 10 GV protons have an energy about 9 GeV. The atmospheric cutoff energy for particles reaching RAD is lower, about 160 MeV (Guo et al. 2018c). Measurements of FDs at different neutron monitor stations with different geomagnetic cutoff rigidities, have shown that there is an energy dependence of the FD amplitude (Cane 2000; Lingri et al. 2016) and recovery time (Usoskin et al. 2008) due to the energy-dependent modulation of the GCR: The strength of the modulation, the amplitude of the FDs, and the recovery time are anti-correlated with the kinetic energy of the GCR particles. Therefore, FDs caused by the same ICME detected with a lower cutoff energy generally have a larger amplitude than those with a higher cutoff energy that can be caused by a thicker atmosphere, a stronger magnetosphere or a higher response-energy range of the detector. Of course, the ICME evolution from Earth to Mars would also result in a different FD profile (likely shallower and more gradual) as described earlier. However, the statistical comparison here suggests that the energy range of the primary GCRs leading to the detected FD may have a larger impact on the FD amplitude, especially when the corresponding energy ranges of the original GCRs are very different at each observer. This highlights the importance of understanding and quantifying the energy-dependent modulation of the GCR particles by solar transients (e.g., Guo et al. 2020), enabling the use of FDs to infer the properties of ICMEs.
4.2 Recurrent Forbush decreases on Mars
High-speed solar wind streams from coronal holes may interact with the preceding slow solar wind, forming a region of compressed plasma at the leading edge of a stream interaction region (SIR). SIRs are characterized by high solar wind density and corresponding dynamic pressure as well as high magnetic field strength (Smith and Wolfe 1976). Since coronal holes may persist over several months, the streams often recur for more than one solar rotation and lead to so-called corotating interaction regions (CIRs). Observations have shown that the high-speed streams that drive the CIRs typically follow the magnetic sector boundaries and the solar wind rarefaction region forms in the declining speed region of the high-speed stream (Gosling and Pizzo 1999). They are particularly prominent features of the solar wind during the declining and minimum phases of the 11-year solar cycle.
The RAD detector has identified many FDs on the surface of Mars, which have been studied statistically by Guo et al. (2018b) and Papaioannou et al. (2019). However, using only the FDs identified in the GCR flux, it can be difficult to tell if the cause is an ICME or SIR. Arriving two years after the landing of MSL, the Mars Atmosphere and Volatile EvolutioN (MAVEN) orbiter has also been monitoring space weather conditions at Mars since September 2014 (Lee et al. 2017). The solar wind ion analyzer and the magnetometer on board can be used to study the solar wind plasma parameters and the IMF vector at Mars, which are particularly helpful to identify solar transients such as SIRs and ICMEs at Mars.
Compared to depressions caused by ICMEs, SIR-related depressions are in general more symmetrical and of smaller amplitudes as observed at Earth (e.g., Melkumyan et al. 2019). As discussed in Sect. 4.1, ICME-related depressions typically consist of two parts: the first part is associated with an open, compressed and turbulent shock–sheath region and the second with a closed magnetic structure which can be successfully modeled via perpendicular diffusion of GCRs into an expanding flux rope (Dumbović et al. 2020). In contrast, SIRs do not have closed magnetic field regions and thus, their interaction with particles may include contributions from all mechanisms of GCR transport, i.e, diffusion, drift, adiabatic cooling and convection (Parker 1965).
SIR properties at Mars Recently, Huang et al. (2019) have used the MAVEN measurements during the period from October 2014 to November 2018 and identified 149 SIRs and their associated shocks at Mars. Geyer et al. (2021) further analyzed these events comparing in-situ solar wind data at Earth and Mars using as well the remote sensing image of the Solar coronal holes. Comparing the properties of SIRs at Mars to those at Earth, these studies found that (1) most SIRs are well formed at 1 au; (2) the average duration of SIRs at Mars is about 37.0 h, comparable to that at Earth (36.7 h) indicating that there is no significant expansion as they move radially outward up to 1.5 au; (3) the crest of the HSS profile broadens by about 17%, and the magnetic field and total pressure by about 45% around the stream interface; (4) the maximum magnetic field strength and pressure of SIRs decrease significantly from 1 to 1.5 au; (5) occurrence rate of fast forward shocks is about three times as high at Mars than at Earth.
Top: The locations of planets in the inner heliosphere in HEE coordinates on 2016-07-07 and 2016-09-27, downloaded from http://stereo-ssc.nascom.nasa.gov/cgi-bin/make_where_gif. The nominal Parker spiral under a solar wind speed of 400 km/s is over-plotted to show that Mars and Earth are magnetically connected in a. Bottom: The interplanetary magnetic field, solar wind speed, proton density and temperature as well as the ground-based GCR measurement at Earth (green) and Mars (orange) from June 10 until September 26, 2016 for 4 solar rotations. The Pearson correlation coefficient between the data at Earth and Mars for each solar rotation is marked for each dataset. The topographical shielding of dose due to the MSL rover parking at Murray Buttes (Sect. 5) is marked as a red shaded area. More information can be found in the text
As an example, during the second half of the year 2016, some CIRs and recurrent FDs were observed at both Earth and Mars. Coincidentally, the opposition phase of Mars took place on May 30, 2016 when Earth and Mars were aligned on the same side of the Sun. Geyer et al. (2021) have studied the evolution of the HSS properties in this period from the Sun to Earth and to Mars. They found that multiple coronal holes and several CIRs reappeared for at least 5 solar rotations between the end of May and the end of September. In order to better understand the SIR-associated FD properties at Mars in comparison to those at 1 AU, a synergistic study of the MAVEN plasma and IMF observations together with the GCR measurements is needed. Figure 10 shows the ground-based GCR measurements together with the plasma and magnetic field observations at both planets during the above-mentioned period. The Earth solar wind measurements are plotted based on the hourly the Advanced Composition Explorer (ACE) data included in the OMNI dataset (https://omniweb.gsfc.nasa.gov) and the ground-based Oulu neutron monitor count rate data have been downloaded from the Neutron Monitor database (http://www01.nmdb.eu). The MAVEN data are archived here (https://lasp.colorado.edu/maven/sdc/public/) and only the measurements taken outside the Mars magnetosphere when the spacecraft was in the solar wind are plotted.
Similar temporal evolution of a given solar wind parameter between Earth and Mars can be seen in the figure. The Pearson correlation coefficient (cc) between Earth and Mars observations has been calculated for each solar rotation. The correlation between the ground-based GCR measurements is, based on the cc values, slightly better than that for other parameters, in particular for the first two solar rotations in June and July. The relative position of the planets in HEE coordinates is shown in Fig. 10a for early July and in (b) for late September. The nominal Parker spiral under a solar wind speed of 400 km/s is over-plotted, showing that Mars and Earth were connected to the Sun via the same IMF line around July 7, 2016. As the stream interaction regions also form roughly along the IMF lines (Richardson 2004), Mars and Earth observe the CIR structure at the same time around these days. We should note that 400 km/s is the typical ambient slow solar wind while the actual speed may vary up to about 600 km/s which would result in a Parker spiral with less curvature.
The magnitude of the magnetic field and plasma density at Mars are slightly smaller than those recorded at Earth due to Mars’ greater distance from the Sun. The outward propagating solar wind has similar speeds at 1 and 1.5 au. The temporal variations of GCRs at both locations are very similar except for a short period at Mars highlighted in red, which is due to extra shielding of the GCR by a surface butte close to the rover as analyzed in more detail in Sect. 5.4. The modulated GCR temporal evolution at both planets is similar, yielding a cc value \(> 0.7\) during the first two solar rotations shown. The magnitudes of the modulation in Oulu and MSL/RAD data are also very comparable, despite the very different cutoff energies of the two ground-based measurements. The cutoff energy for MSL/RAD is about 160 MeV, based on the atmosphere above it, and about 500 MeV for Oulu based on its geomagnetic latitude. The energy dependence of the CIR-induced GCR modulation is not fully understood; a better understanding is needed to explain the magnitude of the GCR evolution. Furthermore, the radial evolution of the CIR needs to be taken into account. For instance, the occurrence of shocks has been evaluated to be more frequent at 1.5 au while the shock strength becomes weaker at Mars (Huang et al. 2019; Geyer et al. 2021), and the SIR structure tends to expand at larger heliospheric distances (e.g., Gosling and Pizzo 1999). The radial evolution of the SIR and how this affects the corresponding GCR depression is still an open question.
4.3 Evolution due to long-term solar modulation
4.3.1 Comparison of GCR variations at Earth ground, in space and on Mars
The long-term evolution of the Martian surface radiation collected during the second half of Solar cycle 24 through the deep minimum until the beginning of Cycle 25 can be compared with long-term GCR measurements carried out by instruments at other locations. In Fig. 11, we compare RAD observations with the GCR flux measured by the ground-based Oulu neutron monitor count rate at Earth and the Earth L1 measurement by Solar and Heliospheric Observatory (SOHO) from August 2012 until December 2020. Neutron monitors collect the count of secondary particles generated by the primary cosmic ray flux at the top of the Earth atmosphere and its time evolution reflects that of the primary GCRs. The Electron Proton Helium Instrument (EPHIN) is part of the Comprehensive Suprathermal and Energetic Particle Analyzer (COSTEP, Müller-Mellin et al. 1995) on the SOHO satellite. As a proxy for the measurement of GCRs, we utilize the channel for particles penetrating through all detectors with minimum ion energies of 53 MeV/nuc (Kühl and Heber 2019).
From top to bottom: Normalized Oulu neutron monitor count rate, normalized EPHIN integral channel (for ions \(> 50\) MeV/nuc), and normalized MSL/RAD dose rate. The original data and the daily-smoothed data are shown in different shades of azure. The normalization is done by scaling the data with the median value (averaged in the time range of MSL/RAD)
To facilitate the comparison of the relative change of the GCR flux from different measurements, we normalized each data set by dividing the values by the median of the daily smoothed data (the time range for calculating the median is set to be after MSL’s landing on Mars so that all three normalized data sets have the same time reference). As shown, for the given time range, the Oulu neutron monitor count rate changed by \(\pm \sim 8\%,\) the EPHIN GCR flux changed by \(\pm \sim 40\%\) and the RAD GCR dose rate changed by \(\pm \sim 25\%.\) The largest variation of the long-term GCR rate over the full solar cycle is detected in the EPHIN measurement carried out in deep space. There are also more SEP events seen in this data set, as it has the lowest energy cutoff. This allows for the detection of lower energy SEP particles which do not reach the surface of Mars or the top of Earth’s atmosphere due to geomagnetic shielding. As shown, SEP events are more present during stronger solar activities when the background GCR flux is lower.
GCRs incident on matter undergo both electromagnetic and nuclear interactions. At Mars, these interactions occur in the atmosphere, altering the observed spectra as described in Sect. 3. Incident GCRs and SEPs can generate secondaries via fragmentation and spallation interactions in the atmosphere, but in terms of modulation effects, ionization energy loss is the more important process. This is because low-energy particles with insufficient range to penetrate the atmosphere simply stop before reaching the surface. This means that, for example, protons with incident energies less than 165 MeV (± 25 MeV, depending on the seasonal surface pressure, Guo et al. 2018c) do not reach the surface of Mars. Higher-energy primaries that survive traversal of the atmosphere are detected as lower energy particles on the surface of Mars. (In some cases, the energy loss is negligible—e.g., a 1 GeV proton loses \(< 5\%\) of its energy in traversing the atmosphere above RAD.) Ionization energy loss in the atmosphere produces a species-dependent cutoff energy (165 MeV/nuc for \(^1\)H and \(^4\)He, but \(\sim \) 800 MeV/nuc for \(^{56}\)Fe) and a general shift from the low-energy to higher energy parts of the GCR spectra. Since the high energy component of the GCRs is less modulated by solar activity, the surface flux is less sensitive to solar modulation conditions than the primary GCR flux is. Guo et al. (2020) have modeled this effect using a GEANT4 based model implemented with the Martian atmospheric and regolith properties (as previously used in Guo et al. 2018c) and showed that under a given heliospheric modulation potential, the change of GCR rate on the surface of Mars is smaller than that in deep space.
On the surface of Earth, where the atmosphere is much thicker (about 50 times greater than in Gale Crater), the atmosphere prevents virtually all primary GCRs from reaching Earth’s surface. Ground-based neutron monitors measure secondary neutrons generated in the atmosphere, predominantly by high-energy GCRs. To enter the atmosphere and potentially interact, incident GCRs must have energies above the local geomagnetic cutoff; in the case of the Oulu monitor, this corresponds to proton energies \(\gtrsim \) 500 MeV (Usoskin et al. 2002). The cutoff energy is higher for neutron monitors at lower latitudes, where geomagnetic shielding is stronger. Since the neutron flux at the surface of Earth is dominated by neutrons produced by high-energy ions, neutron monitor measurements in essence give large weight to the less-modulated part of the GCR energy spectrum. The relative amplitude of the heliospheric modulation is, accordingly, much smaller on the surface of Earth compared to that seen on Mars or in deep space as shown in Fig. 11.
4.3.2 The modulation potential \(\varPhi \)
One commonly used parameter to describe the modulation of GCRs by the heliospheric activity is the modulation potential \(\varPhi \), which corresponds to the mean electric potential that approximates the energy loss a cosmic ray particle experiences traversing the solar system into the inner heliosphere (Gleeson and Axford 1968; Usoskin et al. 2005). Although the physical definition of \(\varPhi \) appears imprecise, it has useful practical application—e.g., it is the only parameter in the so-called force field modulation model (Gleeson and Axford 1968). Usoskin et al. (2005) calculated the monthly values of the modulation potential \(\varPhi \) (http://cosmicrays.oulu.fi/phi/phi.html), reconstructed using the data from the worldwide neutron monitor network and calibrated with direct balloon and space-borne measurements of the cosmic ray energy spectrum, including that obtained by the PAMELA (Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics) data (Usoskin et al. 2017).
Top: Time profile of the monthly Oulu neutron monitor count rate (left y-axis, azure) and the monthly Solar modulation potential \(\varPhi \) (right y-axis, black) over 50+ years. Bottom: the correlation between the two parameters and a fit of this correlation. The function of the fit is given in the legend. The monthly \(\varPhi \) derived based on the function is marked as red circles in the top panel
We plot the monthly \(\varPhi \) value together with the monthly Oulu neutron monitor count rate in the top panel of Fig. 12, and we also correlate these two parameters in the bottom panel. The correlation coefficient between the two data sets is as good as 0.99 and a non-linear fit to the data is applied. The fitted function is then used to derive the monthly \(\varPhi \) values based on the monthly Oulu count rate and the resulting \(\varPhi \) is over-plotted in the top panel, which agrees well with the original \(\varPhi \) values. Based on this correlation, we can derive the \(\varPhi \) values measured at Earth directly from the Oulu data, which can be daily or binned into each solar-rotation period as shown in Fig. 7.
We expect the \(\varPhi \) value at Mars to be different from that at Earth at a given time due to the different heliospheric locations of the two planets: First, there exists a radial gradient of the modulation as the GCRs are propagating inward through the heliosphere. Using multiple spacecraft observations, Honig et al. (2019) found the GCR fluxes increase by about 2.96% per au between 1 and 4.5 au. Roussos et al. (2020) found the radial gradient to be about 2–3.5% depending on the phase of the solar cycle using data at 1 and 9.5 au. In any case, the GCR gradient between Earth and Mars is very small and in the order of 1–2%. Second, there is a longitudinal difference of the modulation due to not only the drift effect of the global GCR propagation but also possibly the varying distance of the observer form the heliospheric current sheet. More importantly, short-term solar transients (CMEs and SIRs) may significantly affect the local modulation condition within a constrained longitudinal cone. Generally short-term longitudinal effects can be minimized by averaging data over a solar rotation period. In this study, to derive the Martian surface radiation based on a parameter that is readily known, we always refer to \(\varPhi \) values derived at Earth and we use the monthly derived value or the per-Carrington-rotation binned value to account for the longitudinal effect.
4.3.3 The correlation between \(\varPhi \) and Martian surface radiation
In the top panel of Fig. 13, we plot the monthly \(\varPhi \) value as discussed in the last section together with the dose rate measured by MSL/RAD plastic detector on the surface of Mars from August 2012 until June 2020. The monthly binned RAD data are also plotted over the daily data and the 2-\(\sigma \) atmospheric-related variations are marked in the shaded area. The atmospheric influence is constrained by the maximum dependence of the dose rate on pressure \(|\kappa | = 0.21~\upmu \)Gy/day/Pa, and the standard deviation of the seasonal pressure variation is \(\sim \) 60 Pa, so that the uncertainty of the atmosphere-induced dose variation can be estimated to be about \(\sigma = 12.6~\,\upmu \)Gy/day.
Top: Time profile of the monthly solar modulation potential \(\varPhi \) (left y-axis, black) and the radiation dose rate on Mars seen by RAD (right y-axis, red for daily values, black for monthly binned data, azure-shaded area for 2-\(\sigma \) atmosphere-related variations) from 2012 August until 2020 June. Bottom: The correlation between the two parameters and a fit of this correlation together with the 95% prediction interval (azure-shaded) and the confidence interval (orange-shaded)
The two parameters are seen to be strongly anti-correlated and the correlation coefficient between the two data sets is as good as \(-0.97\). In a previous study (Guo et al. 2015b), we subtracted the seasonal atmospheric influence to obtain the dose rate assuming a fixed pressure. Here we take the pressure-induced variation as an uncertainty in the long-term data which can then be propagated as an error through the fitting of the two data sets.
Guo et al. (2015b) studied the \(\varPhi \)-dose correlation with a smaller range of data collected from 2012 to 2014 and used both linear and non-linear functions for fitting the data. The correlation model then had the combined uncertainty of both fitting results. Using data recorded for about 8 years, with larger variations, we are now able to discern that the non-linear correlation would better represent the dose dependence on the solar modulation potential \(\varPhi \). The fitted non-linear function is shown in the bottom panel of Fig. 13 and written as:
where \(D_{\mathrm{mars}}\) is the Martian surface dose rate, A and B are fitted parameters which are \(19.8 \pm 4.9~\upmu \)Gy/day and \(118.6 \pm 2.5\) mGy MV/day.
This empirical function can be used to estimate the Martian surface radiation dose rate based on the solar modulation potential \(\varPhi \) measured at Earth. Note that the estimation would be more sensible for the monthly averaged data rather than daily values. This is because Earth and Mars, as they orbit around the Sun, are located at different locations in the heliosphere which may have different short-term modulations as explained in Sect. 4.3.2.
It is also important to note that the empirical function is based on data collected from the pre-maximum of Cycle 24 through its declining phase over the deep solar minimum. As shown, the \(\varPhi \) ranges between about 370 and 710 MV and the value at the solar maximum is much smaller than that measured in some previous solar cycles. For instance, the \(\varPhi \) value was slightly higher than 1200 MV during the peak of Cycle 22 (Fig. 12 top panel). Therefore, the fitted function has much larger uncertainties at large \(\varPhi \) values as shown by the 95% confidence interval in Fig. 13. More RAD data collected over a stronger solar maximum would be needed to better define the function parameters. It should also be kept in mind that the RAD data were acquired under considerably more atmospheric shielding than would be present for a mission operating at the median elevation on Mars (\(\sim \) 22 g/cm\(^{2}\) vs. 16 g/cm\(^{2}\), with higher doses under a smaller atmospheric depth as a consequence (See Sect. 3.2).
4.3.4 Empirical modeling of the Martian surface radiation
This empirical function obtained above (in Sect. 4.3.3) can be used to estimate the Martian surface radiation environment, at Gale Crater or similar altitudes on Mars, under different solar modulation conditions. This is shown in terms of the dose rate and the consequent dose equivalent rate in Fig. 14. Based on monthly mean solar modulation \(\varPhi \) values collected from solar cycle 20 to 24, as shown in the top panel of the figure, we apply the empirical function to model the dose rate evolution throughout these 5 solar cycles. It is shown that the Martian surface dose rate ranges between \(\sim \) 100 and 390 \(\upmu \)Gy/day between solar maximum and minimum.
Top: Monthly solar modulation potential \(\varPhi \) estimated at Earth for the last 5 solar cycles since 1964 until 2020 (left y-axis, black) as well as the RAD-measured dose rate on Mars from 2012 August to 2020 June (right y-axis, red). Bottom: Measured (in red) and modeled monthly dose rate (azure, left y-axis) as well as dose equivalent rate (blue, right y-axis) based on the monthly \(\varPhi \) in the top panel. The shaded areas of the modeled dose rate and dose equivalent rate indicate their respective uncertainties propagated through the model
As described in Sect. 2, the dose equivalent can be estimated as the product of the absorbed dose and the LET-derived average quality factor \(\langle Q \rangle \). Taking into account the variation of \(\langle Q \rangle =2.4 \pm 0.3\), as mainly driven by the atmospheric variations (Zeitlin et al. 2019, also explained in Sect. 3.2), we also estimate the time-evolving dose equivalent rate and its corresponding uncertainty as plotted in the bottom panel of Fig. 14. The dose equivalent rates under different solar activities are within the range of about 0.25 and 0.95 mSv/day. The previous estimation of the dose equivalent rate, as modeled in Guo et al. (2015b) based on a smaller range of RAD measurement from 2012 to 2014, was between 0.35 and 1.15 mSv/day. The new result based on more statistics is mostly consistent with, but slightly lower than the previous one. This is also because the previous estimation had taken into account an extra linear fit which is shown to be unlikely based on the larger dataset.
4.3.5 The radiation environment during the cruise phase to Mars
Prior to making measurements on the Martian surface, MSL/RAD collected data during its transit to Mars. It was switched on December 6, 2011 and, with few interruptions, measured through July 14, 2012 when it was temporarily switched off in preparation for the landing. Figure 15 (Zeitlin et al. 2013) shows the RAD dose rate data collected during more than seven months of cruise phase. This was the first measurement of the GCR radiation environment inside the shielding of the spacecraft traveling from Earth to Mars. In principle, MSL spacecraft has an environment similar to future missions to the planet, and thus the RAD measurement provides insight into the potential radiation hazard for astronauts going to Mars. Discussions of comparison with other cruise phase radiation measurement can be found in Sect. 8.1.1.

Image reproduced with permission from Zeitlin et al. (2013), copyright by AAAS
Dose rates recorded in a silicon detector and in a plastic scintillator (tissue equivalent) during the MSL’s cruise to Mars. There are five observed SEP events marked with numerals.
During solar quiet times, the dose rate in free space is mostly due to primary GCR ions and their secondaries generated through interaction with the spacecraft materials. The GCR dose rate measured by the plastic scintillator “E” was about \(461 \pm 92~\upmu \)Gy/day and the dose equivalent rate is about \(1.58 \pm 0.22\) mSv/day (Zeitlin et al. 2019). (This revised value, about 15% smaller than our original estimate in Zeitlin et al. (2013), was based on a reanalysis of the cruise data using an improved method to remove RTG background from the measured LET spectrum, as well as a revised silicon to water conversion factor.) For a given incident flux, the dose rate in silicon is generally less than the dose rate in plastic because of the comparatively large ionization potential of silicon.
A close look at the GCR radiation reveals that there are many variations related to solar modulation as shown in Figure 2 of Guo et al. (2015a). The variation of the GCR-induced dose rate at MSL occurs nearly simultaneously with the variation of the neutron monitor count rate at Earth, indicating that both reflect similar heliospheric conditions. This is reasonable as the longitudinal separation between MSL and Earth was rather small during the cruise phase. Also, during most of the cruise phase, the spacecraft was more or less located on the same Parker spiral as Earth, i.e., MSL was magnetically well connected to Earth, known as the Hohmann–Parker effect (Hohmann 1994; Posner et al. 2013, Sect. 7.2.1).
Using a similar methodology as that for quantifying the radiation on the surface of Mars as discussed above in Sects. 4.3.3 and 4.3.4, one can also obtain the correlation between \(\varPhi \) and the cruise phase radiation measurement (Guo et al. 2015a). The correlation can be also extrapolated to a wider range including more extreme solar modulation conditions for estimating the dose rate and dose equivalent rate for different levels of solar activity. The modeled dose equivalent rate during solar maximum of Cycle 22 (\(\varPhi \approx 1200\) MV) has been found to be as low as \(1 \pm 0.5\) mSv/day (the large error bar results from the extrapolation of the model uncertainty), which is considerably lower than the RAD cruise measurement of \(1.58 \pm 0.22\) mSv/day during the maximum of Cycle 24. The modeled dose equivalent rate during solar minimum periods (\(\varPhi \approx 350\) MV) is about \(2.9 \pm 0.8\) mSv/day.
5 Topographical factors influencing the surface radiation
5.1 Overview of the rover route
The Curiosity rover landed in Gale Crater on Mars at a smooth region called “Yellowknife Bay” (4.35\(^\circ \) S 137.27\(^\circ \) E) as marked in yellow text at the top right corner of bottom map in Fig. 16. The base image of the map is from the High Resolution Imaging Science Experiment (HiRISE) camera on NASA’s Mars Reconnaissance Orbiter. Mount Sharp forms the central peak within Gale Crater and is dry and sandy today, but it may have had surface liquid water such as rivers and lakes more than 3.5 billion years ago (e.g., Williams et al. 2013; Horvath and Andrews-Hanna 2017). While climbing up Mount Sharp, the Curiosity rover has been following the path where ground water may have existed, such as the Clay Unit area (May 2019).

Image credit: NASA/JPL-Caltech/Univ. of Arizona. The high-resolution image can be found here http://mars.nasa.gov/resources/25077/curiositys-traverse-map-through-sol-2800/
Top: The zenith tilt angle (azure stars) and the elevation (black line) of the Curiosity rover in MOLA coordinates through the first 2800 sols (until June 22, 2020). Bottom: The route map through the first 2800 Martian sols, which adds to 22.65 km in total. The sol number of each drive is marked along the line. The scale bar is 1 km.
The rover path over the first 2800 sols (from August 6, 2012 until June 22, 2020) is shown in a yellow curve in Fig. 16 (bottom): It headed from the northeast towards the southwest and slowly turned towards southeast. Important geological features along the drive are shown in white text. The rover climbed about 400 m in the course of 2800 sols as shown in the top panel of Fig. 16. During the first 1400 sols, the altitude only rose less than 100 m while in the following 600 sols the rover climbed about 250 m. This can also be seen in the topographic map at the bottom where the sol number of each drive is marked along the line.
Figure 16 also shows the zenith tilt angle of the rover body after each drive (the inclination can vary slightly during each drive). RAD is mounted so that its central axis is perpendicular to the rover deck, that is, RAD’s field of views are centered on the vertical when the rover is on flat ground. Along the traverse of Curiosity, the rover body was generally not exactly horizontal, as it would be on level ground; rather, it was tilted at angles up to about 30\(^\circ \) from the zenith, with an average value of 7.3\(^\circ \). When the rover is tilted, RAD’s viewing cone is not centered on the zenith. Based on the center of mass, the vehicle can withstand a tilt of at least 50\(^\circ \) in any direction without overturning, but automatic sensors limit the rover from exceeding 30\(^\circ \) tilts (Makovsky et al. 2009).
5.2 The effect of the increased altitude on the radiation variation
The Curiosity rover gained altitude as it traversed the lower slopes of Mt. Sharp, the atmospheric column mass above RAD has (for a given time in the seasonal cycle) decreased over time. In the course of 2800 sols, the rover climbed about 400 m, resulting in a noticeable decrease of the average surface pressure (proportional to the atmospheric column depth) above RAD.
Figure 17 plots the MSL/REMS measured pressure since the rover landing on August 6, 2012 until October 2020, over Mars year (MY) 31 until MY 35. Curiosity landed in the late summer of the northern hemisphere (or late winter of the southern hemisphere) when most of the CO\(_2\) had condensed at the south pole. This effect makes northern summer the season with lowest annual pressure. Pressure data from Mars Years 32, 33, 34, and parts of 31 and 35 are shown in the figure. For the Mars years for which the data are complete, the annual average pressures are 835 Pa for MY32, 832 Pa for MY33, and 808 Pa for MY34. The annual pressure of MY34 is about 3% lower than the previous year by about 30 Pascal, clearly in correspondence with the difference in average elevation between the 2 years.
Atmospheric pressure measured by MSL/REMS (red curve) and the elevation (azure curve) of the Curiosity rover in MOLA coordinates. A Martian year lasts for 687 Earth days. Each odd/even Mars year (MY) is marked using gray/white background. Vertical dashed lines divide each Martian year into 4 seasons following the sequence of Spring equinox (Ls = 0\(^\circ \)), Summer solstice (Ls = 90\(^\circ \)), Autumnal equinox (Ls = 180\(^\circ \)) and Winter solstice (Ls = 270\(^\circ \))
Employing the pressure–dose anti-correlation obtained in Guo et al. (2017a) or the updated analysis in Sect. 3.2, we assume \(|\kappa | \sim 0.21~\upmu \)Gy/day/Pa when the solar modulation is weak, as is the case in the time period considered here. We can infer that the elevation change resulted in an increase of up to 6 \(\upmu \)Gy/day of the measured dose rate. However, this small effect coincided with increased GCR flux as solar modulation declined during this time period, which is a much larger effect—the reduced solar modulation caused an increase of the dose rate by about 100 \(\upmu \)Gy/day (see e.g., Fig. 13).
For a given GCR spectrum, \(\langle Q \rangle \) should increase as the rover elevation increases and the atmospheric shielding decreases. However, the GCR spectrum was not constant in this time period due to the weakening modulation, which preferentially allows more protons into the inner heliosphere. This effect appears to have compensated for any increase in \(\langle Q \rangle \) that might have arisen from the thinner atmosphere above RAD. The result is that \(\langle Q \rangle \) remained in a narrow range, between 2.1 and 2.5, since the middle of MY33 (Zeitlin et al. 2019).
5.3 The zenith angle dependence of the dose
The GCR flux in the heliosphere can be considered as an isotropic field. In the absence of a global magnetosphere, these particles mainly interact with the Martian atmosphere as they propagate through it and may cause a change of the particle directionality on the surface of Mars. On Earth’s surface, there is a larger directional flux of particles from the zenith than from the horizon. Wimmer-Schweingruber et al. (2015) have studied the zenith angle dependence of the particle fluxes on the surface of Mars and found that within the narrow range of tilt angles \((\le 15^\circ ),\) there is a dependence of the flux \(\propto \cos ^\gamma (\theta )\) with \(\gamma =1.18\pm 0.07\). This value is close to the value of 1.0 that describes an isotropic field, and quite different from that at sea level on Earth where \(\gamma \approx 2\). The study used data collected throughout the first 806 sols, during which the rover tilt angle was within a maximum value of 15\(^{\circ }\). An updated study to understand the flux directionality over a wider range of zenith angles is possible with more recent data.
Intuitively, the total dose should not depend on the tilt angle of the detector, considering that a perfect detector equally accepts and records particles coming in from all directions to contribute to the dose measurement. If the detection efficiency is independent of the incident angle, then the total dose integrated over all directions is constant independent of rotation or inclination in an isotropic field. However, two effects cause deviations from this ideal scenario. First, the radiation field on the surface of Mars is not perfectly isotropic due to the \(1/\cos {\theta }\) dependence of the column depth particles traverse to reach the surface. Second, there is inhomogeneous shielding internal to RAD in the vicinity of the two detectors used for dose rate measurements. The B detector field of view is, to a good approximation, shielded only by the atmosphere in its upper hemisphere, but is heavily shielded in the lower hemisphere. As a result, fewer albedo particles reach it than reach E. On the other hand, for a downward-traveling particle to reach E, it must first traverse the A, B, C, and D detectors. Particles traversing D may encounter as much as 13 g/cm\(^2\) of mass, which in some cases exceeds their range, or—in the case of energetic heavy ions—may cause them to undergo nuclear fragmentation. Alternatively, particles arriving at E from the side or bottom must first pass through the anti-coincidence detector F, which presents about 1.2 g/cm\(^2\) of shielding. The combination of an anisotropic field and angle-dependent detection efficiency suggests there could be an influence of the tilt angle of the rover on the measured dose rate. However, this dependence, if it exists, is embedded as a minor effect among stronger influences—the heliospheric variation, daily and seasonal atmospheric modulation, and decrease of pressure due the increase of the rover’s elevation. A direct comparison of the dose rate versus the rover tilt angle does not show any evidence of a correlation. For general considerations, then, we assume that the dose collected from all directions is, to a good approximation, independent of the inclination angle of the rover.
Despite the preceding conclusion, we note that it may be possible to further probe differences in the dose contributed by particles arriving from different zenith angles. The B and E dosimetry triggers record particles coming in from all directions and do not differentiate the directionality of particles when recording their contributions to dose. A subset of particles arrives within the AB view cone and are recorded in the LET histograms (Sect. 2), separated into a narrow inner view cone and a larger outer one. The inner cone spans about 36\(^\circ \) while the outer one has a full acceptance angle up to 64\(^\circ \) (Zeitlin et al. 2016). At least in principle, we can use these differing fields of view to obtain the dose in each: within the inner LET cone, within the outer LET cone, and outside the LET cone (when considering the difference between total dose and the LET dose). Combined with the tilt angle of the rover, which ranges between 0 and 30\(^\circ \), future work can be done to investigate the dependence of dose on the zenith angle, taking into consideration that the surface pressure variation should also have a concurrent effect in the data.
5.4 Regolith shielding at Murray Buttes
Figure 18 shows one of the photos of the Murray Buttes taken by the rovers Mast Camera on Aug. 18, 2016 (Sol 1434). The two prominent mesas in this view are about 80 m apart. The one on the left reaches about 8 meters above the surrounding plane and is about 100 m from Curiosity’s position. The mesa on the right is about 10 m high. Its top is about 82 m from the rover. Upper Mount Sharp is the large mound dominating the horizon behind the two mesas. A few weeks later, on sol 1455, as Curiosity continued heading south, it drove close to a butte (not shown in this figure) where it was subsequently parked for nearly 13 sols. The dose rate measured by the RAD E detector in this period is shown in Fig. 19.

Image credit: NASA/JPL-Caltech/MSSS. High-resolution original image can be downloaded here: https://mars.nasa.gov/resources/8059/martian-mesas-in-murray-buttes-area-sol-1434/?site=msl
The component images of this mosaic were taken by the right-eye camera of the rover’s Mast Camera on Aug. 18, 2016 (Sol 1434) in the area called Murray Buttes. The left edge of this view is northeast from the rover; the right edge is southeast. More details are in the text.

Adapted from Guo et al. (2021)
a The RAD E dose rate measurement from May 2016 until January 2017. Original data are in gray and smoothed daily values are in black. Each solar rotation period of about 26 sols is separated by vertical azure lines. b Superposition of the normalized daily dose rates for the five rotations which are marked from I to V in a. The time of each solar rotational period ranges from sol 1 to 26. The period, when Curiosity was parked, is shaded in red in a and marked between dashed vertical lines in b. Data for each period are normalized by the data outside the dashed-line-delimited window. The average normalized value for the parked period is 0.953 with a standard deviation of 0.006 as indicated by the horizontal red solid line. The average normalized values during this window of the superposed time are shown in different horizontal lines for previous 4 solar rotational cycles and their average value is about 1.0.
As previously shown and discussed in Sect. 4.2 and Fig. 10, the RAD dose rate variation during this period is modulated by the CIRs which appear periodically following the solar rotation. As shown again in Fig. 19a, the RAD measured dose rate repeats very similar evolution patterns throughout the first 4 solar rotation periods followed by a period which includes the 13 sols during which the rover was parked near a butte, as marked in a red shaded area. The regularity of GCR variation in the following solar rotation cycles started deteriorating as the CIR structures became unstable due to the evolution of the coronal holes at the solar surface—these often experience growing and decaying phases (Heinemann et al. 2018).
The parked period clearly shows a sudden drop and a quick recovery of the dose rate at its beginning and end, respectively. The obvious explanation is that a significant part of the sky was blocked by the butte where cosmic ray ions were stopped before reaching RAD. As the dose rate is varying in time, one can not quantify the reduction by simply calculating the dose rate difference before and during the parking. The modulation of the GCR radiation during this period (in which there were no major solar eruptions) is mainly driven by recurrent CIRs that follow the periodic rotation of the Sun (Geyer et al. 2021), we expect that the measured dose rate would have been equal to the dose rate during the same phase of the previous cycles, if no extra butte shielding had been present. To illustrate this idea, we superpose the RAD measurements during each of the first five solar rotation cycles, which are marked from I to V in Fig. 19a. The normalized dose rate during each solar rotation are plotted with a time window of 26 sols in the bottom panel of the figure. The normalization is done as dividing the daily dose rate by the mean value of the daily dose rate outside the dashed-line-delimited window. The \(\sim 13\) sols of the parked period is marked between dashed vertical red lines, and the dose rate during the parking is clearly lower than the dose rate recorded at the same point in the previous 4 cycles. The average dose rate for the parked period is \(238\pm 2~\upmu \)Gy/day, or \(0.953 \pm 0.006\) in the normalized data frame. The average dose rate for previous 4 solar rotational cycles during this 13 sol range of the superposed time is 253 ± 1 \(\upmu \)Gy/day, or \(0.999 \pm 0.009\) in the normalized data frame. We conclude that the dose rate dropped by 15 ± 2 \(\upmu \)Gy/day of dose rate, or \({5\% \pm 1\%},\) during the parked period.
It is also important to note that the reduction of the dose seen by RAD at the butte is the difference between the shielded radiation from the sky direction and the secondary albedo radiation coming from the butte itself (Guo et al. 2021). The resulting \(\sim 5\%\) of reduction in dose rate is not significant enough to efficiently protect the future astronauts from cosmic radiation on Mars, but it is suggestive of an operational approach that would exploit features of the local terrain to shield habitats and other frequently occupied structures. This is the first direct illustration that an existing geological structure such as a simple butte may serve as a potential radiation shelter for future habitats on Mars (Ehresmann et al. 2021; Guo et al. 2021).
As the Martian surface contains various natural geological shelters, such as cave skylights (Cushing et al. 2007) and lava tubes (Léveillé and Datta 2010), it is of great interest to assess the feasibility and practicality to use such natural structures for radiation sheltering. Since no radiation measurement has been taken within such shelters, modeling work is essential to help evaluate the effectiveness and required depth of potential natural shields. More discussion of the potential benefits of using Martian surface materials to reduce the radiation during astronauts’ stay on Mars can be found in Sect. 8.2.
6 GCR-induced radiation for a return trip to Mars
Considering the variations of the GCR radiation as analyzed and discussed earlier, we now estimate the accumulated GCR-induced radiation level for a round-trip mission (two cruise phases plus the surface stay) to Mars under different conditions.
6.1 Transfer orbits to Mars
For a potential human mission to Mars, we consider two different types of Mars transfer orbit: the Hohmann transfer (Hohmann 1994) and a fast transfer through advanced propulsion (Durante 2014) and on-orbit staging (Folta et al. 2012). The Hohmann transfer orbit generally uses the lowest possible amount of energy in traveling between two planets orbiting the Sun in circular orbits of different radii in the same plane, and so is used to deliver the maximum mission payload mass with the fixed amount of energy that can be imparted by a particular rocket. For a space mission between Earth and Mars, a Hohmann transfer window occurs every 26 months and requires a travel time (one way) of about 7–8 months. The most recent route of a Hohmann transfer for the Mars 2020 mission is shown in Fig. 20. A typical round-trip mission scenario to Mars using a Hohmann transfer trajectory both ways thus includes about 400–500 days of transit time and 500 days of surface stay.
The route of a typical Mars mission (Mars 2020 in this case) takes to the Red Planet via the Hohmann transfer, including planned trajectory correction maneuvers (TCMs) to adjust the flight path. TCMs can be differently planned depending on the time of the mission. The travel time is about 210 days in this case.
In the future, a much faster transfer to Mars may be realized (Durante 2014) through the implementation of on-orbit staging combined with a network of pre-positioned fuel supplies (at low Earth orbit in advance of mission hardware or crew). For the required energy power nuclear thrusters are under consideration such as nuclear thermal rockets (NTR), nuclear electric propulsion (NEP) or nuclear thermal-electric rockets (NTER) which is a hybrid NTP/NEP system (Bruno et al. 2013; Dujarric et al. 2013). During an Earth-Mars conjunction phase (when both planets are in line on the same side of the Sun, i.e., with the nearest distance), a return trip to Mars can be reduced to about 120 days from Earth to Mars, a 14 day stay and a 75 day return.
6.2 Accumulated GCR exposure for a return mission to Mars’s surface
Based on the above two different transfer scenarios, we can assess the accumulated GCR-induced exposure level for a round-trip mission to Mars using the empirical modeling of the cruise and surface radiation environments under various conditions, especially during different phases of solar activity. The time-varying atmospheric influence on the dose rate as derived from the observations has been included as an uncertainty in the empirical modeling of the Martian surface environment (Sect. 4.3.4, Figs. 13 and 14). The topographical effect as reported in Sect. 5 has a small effect \(\sim 5\%\) on the dose as observed by RAD so far and is not considered as a factor in the current estimation here.
The dose equivalent derived based on the empirical model as discussed in Sects. 4.3.4 and 4.3.5 can be estimated for a round-trip mission to Mars. The results are given for two different transfer orbits under various solar minimum and maximum periods as shown in Table 2. The table suggests that the shielding of GCRs by heliospheric magnetic fields during solar maximum periods is efficient in reducing the GCR-induced exposure for a Mars mission, reducing the mission dose equivalent by more than 50%.
In the case of a Hohmann transfer with up to 500 days of transit time and about 500 days of surface stay, the mission dose equivalent (H) is about \(1.59 \pm 0.12\) Sv during solar minimum \((\varPhi = 350 \) MV), and about \(0.65 \pm 0.24\) Sv during solar maximum \((\varPhi = 1000\) MV). For solar activity in between these two conditions, we chose \(\varPhi = 650\) MV, and find the accumulated dose equivalent is about \(1.02 \pm 0.13\) Sv. This is quite consistent with the value obtained by Hassler et al. (2014), who estimated a value about 1.01 Sv based on RAD’s cruise measurement and the first 300 sols of surface measurement under similar solar modulation conditions. The shorter missions enabled by advanced propulsion would obviously provide major benefits in reducing crew exposure, particularly in deep space where the only available shielding comes from the vehicle. Discussion of the feasibility of such technological advances is beyond the scope of this paper.
We should note that these values are estimated based on a fixed \(\varPhi \) value for the total mission duration to highlight the different scenario of missions performed during different solar cycles. Considering a Hohmann return trip lasting for about 3 years, the solar modulation would of course evolve during this period. Therefore, the actual total dose equivalent during solar maximum is likely to be larger than the given value, and the actual dose equivalent during solar minimum is likely to be smaller than the predicted value. In other words, the values given in the table for solar max and min can be considered as lower and upper bounds, respectively.
Of course, additional contribution to the radiation by SEPs could also play an important role, especially during solar maximum when accumulated GCR contribution is minimum. However, exposure from SEPs is more uncertain than exposure to GCRs. Currently, there is no reliable way of predicting their occurrence rate and cumulative fluence or dose for the duration of a round-trip mission to Mars. The RAD-observed few SEP events and their radiation dose, during MSL’s cruise and surface phases will be discussed in the Sect. 7.
7 Solar particle events
In contrast to the continuous flux of GCRs which are modulated by the heliospheric magnetic fields following the solar cycle, SEP events are sporadic, often impulsive (meaning they have a fast rise time), and could be extremely hazardous without adequate shielding. There have been numerous studies of SEP events arriving at Earth detected by different instruments and at the STEREO spacecraft orbiting around the Sun at 1 au. These observations are important to improve our understanding of the physics and properties of SEP events as will be briefly reviewed in Sect. 7.1.
Concerning the radiation environment encountered during a potential Mars trip, we will review the SEP events detected by MSL/RAD during its cruise phase to Mars and on Mars’s surface since its launch in 2012 in Sects. 7.2 and 7.3.
7.1 SEP acceleration, transport and interaction with shielding
Above, we briefly described the characteristics of SEPs in terms of the acceleration and transport mechanisms in Sect. 1.1. To date, the accurate prediction of the occurrence, property and effects of solar particle events is not yet possible due to the complex acceleration and transport processes involved.
First, the acceleration of SEPs by magnetic reconnection, wave–particle interaction and shocks associated with solar flares and CMEs is a complicated phenomenon. The relative importance of different acceleration mechanisms depends on many parameters of the magnetic and plasma conditions of the solar eruptions, which are neither precisely observed nor fully understood (Cliver 2016). In addition, theories of particle acceleration by shocks require the presence of a “seed population”, i.e., suprathermal particles, at the Sun and/or in the interplanetary medium, that are difficult to quantify. The study of solar eruptions and acceleration of SEPs is a very challenging and active research topic involving many solar physicists and heliospheric scientists. A detailed discussion of this topic is beyond the scope of this paper and can be found in several review articles (e.g., Kallenrode 2003; Reames 2013).
Second, accelerated particles need to be transported through the interplanetary space to reach observers at Earth, Mars, or in interplanetary space. Normally, SEPs, being charged, are most efficiently transported when the observer is magnetically connected to the open field close to the acceleration region. Therefore the earliest onset and highest particle fluxes as seen at Earth tend to be related to flares and CMEs on the western flank of the Sun where the observer’s magnetic footpoint locates. However, as shown by numerous observations—especially using multi-spacecraft observations from different viewpoints (e.g., Richardson et al. 2014; Battarbee et al. 2018; Lario et al. 2013, 2017; Dresing et al. 2014; Guo et al. 2018a; Palmerio et al. 2021, etc.)—SEPs can be distributed more widely in the heliosphere than the acceleration source. This is because additional cross-field transport processes take place near the Sun and/or in the solar wind. These processes include particle drift motion (e.g., Marsh et al. 2013), pitch-angle scattering (e.g., Effenberger and Litvinenko 2014), cross-field diffusion (e.g., Dröge et al. 2010), meandering effects due to turbulent field (e.g., Laitinen et al. 2016), and influence of the propagation due to non-nominal IMF caused by pre-existing CMEs (e.g., Rouillard et al. 2016) or co-rotating interaction regions (e.g., Guo et al. 2018a). The relative role of the above processes that transport and spread particles in the interplanetary space depends on the solar wind turbulence, the particle type and energy etc., and thus differs from event to event (e.g., Li 2017).
Finally, after propagating through the interplanetary space, SEPs may further interact with the local shielding such as planetary atmospheres or the spacecraft structures, which may significantly modify the radiation field. Particles may lose all or part of their energy while interacting with the material, and can also generate secondaries via nuclear interactions (such as neutrons, electrons, gammas, muons, etc.) which contribute to the radiation hazard. The interaction of the primary cosmic particles with the Martian atmosphere has been described in detail in Sect. 3. Compared to GCRs, SEPs normally have a lower energy range and are more easily stopped by the material that they transverse through. For instance, Mars’s atmosphere can stop protons below energy of about 160 MeV from reaching the surface at Gale Crater (Guo et al. 2018c). A spacesuit can generally stop protons below about 30 MeV (Wu et al. 2009). Depending on the in situ shielding conditions, a large SEP event with abundant protons with energy larger than tens or hundreds of MeV may result in a whole-body dose above the threshold \((\sim 0.7\) Gy) required to trigger acute radiation syndrome, ARS (Sect. 1.2).
In summary, a better understanding of the underlying physics in the processes of the acceleration, injection and interplanetary transport of SEPs is the key to advancing our space weather applications and to forecasting potential transient radiation hazards for space missions. The dynamic, sporadic and complex nature of eruptive solar events make this one of the most challenging research topics in heliospheric physics. Studies of SEPs must take into account the characteristics of flares, CMEs, shocks, seed particle populations, and the conditions for particle acceleration and propagation combining high-resolution multi-point observations. New data from Parker Solar Probe (Fox et al. 2016) and Solar Orbiter (Müller et al. 2013) may fill some of the existing knowledge gaps, and eventually enable accurate, physics-based forecasting of SEP events and their properties.
7.2 SEP events detected during MSL’s cruise to Mars
The MSL/RAD measurement during the 8 months of cruise phase was the first radiation measurement within a spacecraft in transit to Mars. The measured dose rate is shown in Fig. 15. Five SEP events were observed during the cruise phase, providing an opportunity to better understand potential SEP-induced radiation hazards for deep space missions. We will address their properties in two aspects: their time evolution and their effects on the radiation environment inside the spacecraft, which depend on the SEP intensity and energy spectrum.

Image adapted from Zeitlin et al. (2013)
Spacecraft position and dose rates for three of the five SEP events seen by RAD during the cruise phase. Top: The heliospheric location of MSL in respect to other spacecraft (in HEE coordinates) and their nominal magnetic connections to the Sun under 400 km/s of solar wind speed (black for MSL and blue for Earth). Bottom: RAD dose rates (black lines) and GOES-11 165–500 MeV proton count rate (blue lines, arbitrary units).
7.2.1 SEP time evolution and the Hohmann–Parker effect
Figure 21 shows a comparison between RAD SEP event data (black) to data from the Geostationary Operational Environmental Satellite (GOES-11) 165–500 MeV proton count rate (blue) during MSL’s cruise phase (Zeitlin et al. 2013). The location of MSL is marked in HEE coordinates in the upper panels, which show that during most of the cruise phase, MSL was magnetically connected with Earth via the nominal magnetic field (the Parker spiral) under a solar wind speed of 400 km/s. This is also known as the Hohmann–Parker effect (Hohmann 1994; Posner et al. 2013): spacecraft on outbound and inbound minimum-energy transfer orbits stay magnetically connected within a small angular distance with its origin planet (during the early cruise phase) or its destination planet (at a later stage).
In general, the dose rate onsets and peaks in the RAD data occur at later times than those in the GOES data. The SEP events in January and May 2012 show similar impulsive-onset time profiles at both MSL and Earth. This is expected when there is a good connection to the injection site, which allows energetic particles—at least in the early onset phase of the event—to arrive along the field lines. This suggests that near-Earth real-time SEP measurements can be used to forecast SEP events for the cruise from Earth to Mars, at least when the perturbation of the Parker spiral is small (Posner and Strauss 2020, and more discussions in Sect. 8.1.3).
In contrast to the January and May SEP events, the 7–10 March event shows strikingly different features in the GOES and MSL profiles. In addition to the fact that GOES and RAD (partly because it was under shielding) measured different energy ranges of the initial SEP spectrum, this event was also very complex, with eruptions of 2 X-class flares and 2 fast halo CMEs launched within 2 h on 7 March 2012 (Ding et al. 2016). Solar activity on 7 March 2012 started with an X5.4 flare (onset: 00:02UT, peak: 00:24UT, end: 00:40UT) at E27\(^\circ \) on the solar disk (seen from Earth) accompanied by a CME first observed above the occluding disk in the Large Angle and Spectrometric Coronagraph (LASCO) on board SOHO at 00:24UT, with a speed of 2684 km/s. The second flare of class X1.3 (onset: 01:05UT, peak: 01:14UT, end: 01:23UT) was at E17\(^\circ \), accompanied by a halo CME appearing at 01:36UT with a speed of 1825 km/s. The SEPs were also widespread and were observed at multiple vantage points including Earth, MSL, STEREO-A, STEREO-B, and Mercury. Analysis of the March event combining Earth, STEREO-A and STEREO-B data concludes that particles released during this event were more likely associated with the first eruption (Richardson et al. 2014; Ding et al. 2016). The release time of the protons and electrons detected by STEREO-B which was best-connected to the eruption at the Sun agreed well with the start time of the type II radio bursts associated with the first CME shock. However, the second CME as a magnetic obstacle propagating towards the direction of Earth and MSL may have changed the nominal Parker spiral of the observers, causing different time profiles observed at two locations. The Hohmann–Parker effect was not valid in this case. Therefore, complex events as such involving flares, CMEs and shocks pose challenges in predicting their onset using the observation near Earth. SEPs associated with these types of events often reach high energy and intensity, so that such events are potentially hazardous, and real-time data acquired near Earth may not be particularly useful in predicting the conditions in interplanetary space.
7.2.2 SEP-induced radiation
The MSL/RAD cruise data were obtained under the pre-maximum phase of an unusually weak solar cycle. The SEP fluxes observed by RAD are dominantly protons, for which the quality factor is approximately 1 (Sect. 2). Dose and dose equivalent rates are therefore approximately equal. The two events from 23 to 29 January had a dose equivalent of 4.0 mSv as measured inside the MSL spacecraft; two from 7 to 15 March had a combined dose equivalent of 19.5 mSv, and one on 17 May of 2012 had a dose equivalent of 1.2 mSv (Zeitlin et al. 2013). The summed dose equivalent of the five observed SEPs is 24.7 mSv, roughly 5% of the contribution to the total cruise dose equivalent (\(\approx 466\) mSv), or approximately equal to 15 days of GCR dose equivalent during low solar activity. During the peak of a more-active solar maximum one would generally expect a bigger contribution of SEP-related radiation risk.
The radiation environment inside a spacecraft is highly dependent on the spacecraft shielding distribution and on the spectrum of incoming SEPs (Wilson et al. 1999). Low-energy particles are easily shielded, while higher energy ones may only be slowed down by shielding, and are more likely to generate secondary particles. Production of fast neutrons by high-energy SEPs is potentially a concern, but in typical events, the proton spectrum is “soft” (i.e., strongly peaked at low energy) and the induced fast neutron flux is small.
Shielding conditions may vary significantly depending on the spacecraft’s design, the materials used to construct the craft, and the location within the spacecraft. In the case of MSL, the shielding around RAD was highly non-uniform (Zeitlin et al. 2013). A ray-tracing analysis showed that nearly 30% of the solid angle above RAD was only lightly shielded (\(< 5\) g/cm\(^{2}\)), while the 50% of the solid angle in the lower hemisphere was shielded by 8–10 g/cm\(^{2}\). The remaining 20% of the solid angle was heavily shielded (\(\ge \) 20 g/cm\(^{2}\)). The shielding depth averaged over all incident directions was roughly 16 g/cm\(^{2}\). The less-shielded paths to RAD were easily penetrated by SEPs; it is likely that a crewed vehicle would have a more uniform shielding distribution and a smaller share of lightly shielded rays.
7.3 SEP radiation detected by MSL on Mars
During the 8 years of measurement on Mars, RAD has detected only a few solar particle events (distinguished as five peaks in the dose rate) as shown previously in Fig. 4, all of which are small apart from the 2017 September 10th event (Zeitlin et al. 2018; Ehresmann et al. 2018; Guo et al. 2018a; Hassler et al. 2018).
7.3.1 The 2017 September SEP event
For the 10 September 2017 event, Guo et al. (2018a) have analyzed this event concerning the eruption and propagation of CMEs and SEPs from the Sun into the heliosphere. The arrival of CMEs and the resulted Forbush decrease at Mars have been discussed in Sect. 4.1 (Fig. 9). The SEP onset as seen in the dose rate data is about 19:50UT on 10 September. The event peaked on 11 September, from about 4:00 to 14:00 UT and fell gradually until the Forbush decrease due to the arrival of the shock front of the interplanetary coronal mass ejection at Mars. GCR rates dropped by 23% instantaneously or by about 20% below the rates prior to the event.

Image reproduced with permission from Zeitlin et al. (2018), copyright by AGU
Dose rates as measured on Mars using the B silicon detector (after conversion from silicon to water with a factor of 1.3) and E plastic scintillator. a Dose rates include contributions from GCRs. b Dose rates with GCR contributions subtracted.
Figure 22a shows the dose rates as recorded in the silicon B and plastic E detectors for this event. Prior to the onset, the background GCR dose rate in the B detector averaged to be \(\sim 244~\,\upmu \)Gy/day after converting from silicon dose to water dose, and the E dose rate averaged 268 \(\upmu \)Gy/day in plastic (Zeitlin et al. 2018). The 10% difference in GCR response is probably a combination of three factors: (1) the E detector is more sensitive to neutrons than the B detector; (2) the E detector is far thicker than B (18 mm of plastic vs 0.3 mm of silicon) so that nuclear interactions in the detector itself are much more probable in E—these can cause large energy depositions; (3) low-energy albedo particles traveling upward from the Martian surface are likely to deposit energy in E but to stop in the RAD stack before reaching B.
Figure 22b shows the same dose rate data with the average pre-event GCR background subtracted. During the SEP event, the B dose rate exceeded the E dose rate because E is embedded further down in the stack and is, therefore, more shielded from low-energy solar particles that reach B but stop before reaching E. (Many such particles stop in the D detector, directly above E.) Integrating the B or E dose rates for the period from the start of the SEP event until the arrival of the shock front at Mars, we find that the SEP contributed 445 \(\upmu \)Gy of dose as measured by the shallow B detector (converted to water dose), and 298 \(\upmu \)Gy of dose as measured by the deeper E detector. Both values are about 20% less than those reported in Zeitlin et al. (2018), which were affected by an error in the averaging methodology.
As described in Sect. 2, based on particles entering the A \(\cdot \) B coincidence cone, RAD measures the LET histogram which can be used to estimate the average quality factor, \(\langle Q \rangle \), for converting the measured dose to dose equivalent. For the most intense portion of the SEP event, \(\langle Q \rangle \) was 1.17, much lower than the value of 2.3 found for GCR-only periods before and after the event (Zeitlin et al. 2018). Therefore, despite the significant dose rate increase (2–3 times) during the event, the peak dose equivalent rate in the B detector, which can be considered to be approximating a skin exposure, was only about 50% greater than the GCR dose equivalent rates. In terms of deterministic acute radiation effects (critical when absorbed dose above the level of cGy) as introduced in Sect. 1.2, this event was far below the threshold at which acute health issues appear.
To better assess the radiation contribution by this event, Zeitlin et al. (2018) calculated the integrated dose and dose equivalent comparing (I) a 30 day GCR background period prior to the start of the event, and for (II) the SEP and FD period which is the 30 day window starting with the onset of the event as seen on Mars. For the B detector, integrated dose (converted to water) during period (I) is about 7.3 and 7.7 mGy during period (II); for the E detector, the integrated dose is about 8.1 and 8.2 mGy during two periods respectively; the total dose equivalent during two periods are 16.5 and 16.6 mSv, respectively. Due to the effect of the Forbush decrease, the total dose and dose equivalent during two periods are almost identical.
Note that Mars was not magnetically connected to the acceleration site at the beginning of the event (Lee et al. 2018; Guo et al. 2018a) and the ICME was propagating towards Mars. If there had been a better magnetic connection for SEP arrivals and a less significant impact of the ICME, the dose rate and integrated dose increases would likely have been much larger during the event.
7.3.2 The other four SEP events
Figure 23 shows the dose rate data of the first four SEP events RAD detected on Mars before the 2017 September event. The average pre-event GCR background is calculated as the average dose rate in the course of 2 days since 3 days before the event onset. The background level is marked for B and E in azure and orange dotted lines, respectively. The duration of each SEP event is highlighted in the red area. The integrated B dose (after conversion from silicon dose to water dose that is more comparable to tissue dose as measured in E) and E dose for each SEP event are calculated with the background contribution subtracted. They are 42 \(\upmu \)Gy in B and 26 \(\upmu \)Gy in E for event 1 starting on 2013-04-11, 77 \(\upmu \)Gy in B and 61 \(\upmu \)Gy in E for event 2 starting on 2013-10-11, 25 \(\upmu \)Gy in B and 17 \(\upmu \)Gy in E for event 3 starting on 2014-01-07, and finally 214 \(\upmu \)Gy in B and 168 \(\upmu \)Gy in E for event 4 on 2014-09-01.
Dose rates as measured on Mars during the first four SEP events detected by MSL/RAD in the B silicon detector (after conversion from silicon to water with a factor of 1.3, gray lines) and E plastic scintillator (black lines). The pre-event background value is marked for each event with the azure dotted line for B and the orange dotted line for E. The duration of each SEP event is highlighted in the red area. The SEP event integrated E or B dose subtracting the background GCR contribution is summarized in the title for each event
During the SEP event, the B dose rate exceeded the E dose rate for every event because E is embedded further down and more shielded from low-energy solar particles. Protons arriving RAD within the telescope view cone need about 100 MeV to penetrate D and reach E. The ratio of total event dose in E to that in B is 0.62, 0.79, 0.68 and 0.79 for each of the four events respectively. Similarly, this ratio is 0.67 for the 2017-09-10 event. Considering the instrument self-shielding of B and E respectively, this suggests that radiation induced by SEP events on the Martian surface for internal human organs should be smaller than the skin exposure and also highlights in the importance of shielding protection especially during SEP events, such as via extra shielding provided by the habitat and the spacecraft.
In summary, the RAD measurement so far suggests that the SEP-induced radiation is smaller than expected due to (a) the efficient shielding of the Martian atmosphere against typical low-energy SEPs, particularly on or near the floor of a deep crater such as Gale, and (b) the extremely weak nature of Solar Cycle 24 which makes it difficult to generalize the current assessment to other solar cycles. More measurements collected during a much stronger solar maximum are essential for assessing the SEP contribution to the radiation for a mission to Mars.
8 Reduction of radiation exposure for a round-trip mission to Mars’s surface
Hitherto, there has not been any officially defined upper limit of the radiation an astronaut may accumulate during missions beyond the LEO (NCRP 2000). However, space agencies and private sector companies who are planning for crewed missions to Mars are obliged to minimize, where and when possible, the radiation exposures received by astronauts. In this section, based on our analysis of the RAD cruise and surface measurements conducted so far, we try to compare the results to other available measurements as well as the state-of-the-art modeling results of the deep space and Martian radiation environments. We then discuss the possible approaches to mitigate exposures during both solar quiet and eruption periods.
In addition to MSL/RAD, three other radiation detectors have operated during a cruise to Mars: (1) the Martian Radiation Environment Experiment (MARIE, Badhwar 2004) on board the 2001 Mars Odyssey spacecraft which was launched in April 2001 and injected into orbit around Mars in October 2001, i.e., during the maximum of Solar cycle 23. (2) the Liulin-MO detectors (Semkova et al. 2018) on board the Exomars Trace Gas Orbiter (TGO) launched on March 14, 2016 and injected into orbit around Mars on October 19 and thus measuring the cruise radiation during the declining phase of Solar cycle 24. (3) the Mars Energetic Particle Analyzer (MEPA, Tang et al. 2020) on board the first Chinese Mars exploration mission (Tianwen-1) which, at the time of writing, is cruising towards Mars since its launch on 2020 July 23 and will start orbiting Mars in February 2021 (deep solar minimum at the beginning of Cycle 25). A synergistic analysis of these measurements throughout different solar cycle and shielding conditions would be extremely valuable. However, MARIE was only turned on three times during its cruise phase and there were SEPs occurring during the first two times, and it temporarily stopped communicating during the third and final turn-on during cruise. As a result, no usable GCR dosimetry data was obtained by MARIE during Mars Odyssey’s cruise. Data from MEPA during its cruise to Mars are still unavailable at the time of writing, leaving only the TGO Liulin-MO measurement available for comparison with the RAD measurements (Sect. 8.1.1).
On the surface of Mars, RAD has made the only radiation environment measurements to date. MARIE, Liulin-MO and MEPA are all mounted on Mars orbiters and measure (or measured) a radiation environment more akin to free space (albeit with \(\sim \) 2\(\pi \) shielding due to the body of the planet). Cross-comparison of RAD with other measurements must take into account the shielding effect of the atmosphere and the effects of albedo particles that escape the Martian surface. This could be a research topic for future studies.
In the last decades, much effort has been devoted to calculating the Martian surface radiation using GCR models and particle transport codes (e.g., Simonsen et al. 1990; Saganti et al. 2004; Keating et al. 2005; De Angelis et al. 2006; Dartnell et al. 2007; Ehresmann et al. 2011; McKenna-Lawlor et al. 2012; Kim et al. 2014; Gronoff et al. 2015; Guo et al. 2018c). There are various particle transport codes such as HZETRN (Slaba et al. 2016; Wilson et al. 2016), PHITS (Sato et al. 2013), MCNP6 (Werner et al. 2017), GEANT4/PLANETOCOSMICS (Desorgher 2005) and the most recent GEANT4/AtRIS (Banjac et al. 2018; Guo et al. 2019a) which can be employed for studying particle interactions with the Martian atmosphere. With the successful operation of RAD on the surface, benchmarking models against real data has become possible. In particular, two workshops concerning model-vs-data comparisons have been organized (https://www.boulder.swri.edu/rad_modeling_workshop2/). The focus of the workshops was comparing predictions from different models of the Martian surface quiet time environment to the in situ RAD measurements. After optimizing the models for input parameters and physics lists, HZETRN, PHITs and GEANT4 all seem to match reasonably well with the measurements of the RAD dose rate and surface spectra of charged particles as summarized by Matthiä et al. (2017). Detailed discussions of different models, their features, limitations, etc., are beyond the scope of the current article. Interested readers can find relevant results collected in a special issue of Life Sciences in Space Research (Hassler et al. 2017).
The particle transport models, once validated against data, can provide valuable insight into the subsurface radiation environment which is an important factor to understand the possible mitigation of the radiation exposure for future habitats on Mars. This will be discussed in Sect. 8.2.1.
8.1 Reduction of the radiation exposure in transit
We estimated the accumulated GCR radiation in Sect. 6 under three representative solar modulation conditions and two orbit trajectories as shown in Table 2. For each scenario, most of the contribution to the radiation for a return trip to Mars results from the cruise phases. The estimation of the cruise phase radiation environment is based on the shielding configuration of the MSL spacecraft carried out during a very weak solar maximum. The shielding effect could differ depending on (a) the spacecraft material and design and (b) the type and energy of the incoming particles, which vary following the solar activity evolution. In the case of the MSL spacecraft, the shielding conditions around RAD were highly non-uniform as described in Sect. 7.2.2 (and also in Zeitlin et al. 2013).
8.1.1 Cruise phase radiation assessment by TGO Liulin-MO
As a comparison, another estimation of dose equivalent rate in interplanetary space during the cruise to Mars has been obtained based on the Liulin-MO detectors on board the TGO of the ExoMars program (Semkova et al. 2018). The averaged spacecraft shielding around the Liulin-MO detectors is about 10 g/cm\(^{2}\) which is smaller than the mean depth within RAD’s FOV, but close to the median depth. The measured dose equivalent rate from GCRs is about \(2.0 \pm 0.3\) mSv/day for the cruise period from April 22 until September 15, 2016, somewhat higher than the rate of \(1.58 \pm 0.22\) mSv/day measured by MSL/RAD in 2012. The difference is mainly driven by the difference in solar modulation in the two time periods. Modulation during MSL’s cruise to Mars in 2012 was characterized by an average \(\varPhi \) of \(\sim \) 565 MV, while for TGO’s cruise in 2016, the average \(\varPhi \) was \(\sim \) 444 MV. Empirical modeling (Guo et al. 2015a) shows that the TGO-measured dose equivalent rate is in excellent agreement with that found by MSL/RAD when this difference is taken into account. This seems to suggest that the different shielding conditions of TGO and MSL did not significantly influence the GCR radiation environment therein. More measurements carried out under different shielding and solar modulation conditions during cruises to Mars would be highly valuable.
8.1.2 Challenges in shielding of GCRs in deep space
It has long been known that shielding against GCRs is problematic, since a large share of them are highly energetic and therefore have ranges in matter that exceed any practical bulk shielding depth. Calculations show that it is non-trivial to incorporate vehicular design and shielding parameters in assessing the possible reduction of GCR radiation within spacecraft in the interplanetary space. Cucinotta et al. (2006) argued that, because of their higher energies, the cancer risk from GCRs cannot be eliminated using operational approaches and practical amounts of shielding. An important consideration in any shielding design is the production of secondary neutrons, which have a high biological relevance. Interactions of high-energy ions with the spacecraft hull may also produce high-multiplicity showers of secondaries.

Image reproduced with permission from Slaba et al. (2015)
Comparison of selected GCR particle energy spectra in free space (left pane) and behind 5 g/cm\(^2\) of aluminum and 30 g/cm\(^2\) of water (right pane) during solar minimum.
It is well known that moderate depths of bulk shielding provide effective shielding against the SEPs produced in typical events. But when high-energy particles are more abundant as in GCRs, increased shielding may produce a more intense environment inside the vehicle. As shown in Fig. 24, for protons, neutrons and helium ions, the GCR spectral intensities behind 5 g/cm\(^2\) of aluminum and 30 g/cm\(^2\) of water shielding are higher than those in free space, especially below a few hundreds of MeV/nuc, as modeled by Slaba et al. (2015). A uniform shielding of the entire space habitat to reach at least \(\sim \) 20–30 g/cm\(^2\) is estimated to reduce the GCR effective dose by only about 25% (Cucinotta et al. 2005). Attaining even this modest improvement is impractical for deep space exploration missions due to the limited takeoff mass and volume restrictions of existing space launch systems. As a reference, the Apollo module, which is the only vehicle to date that has transported humans outside of LEO, had an average shielding of 6.15 g/cm\(^2\), which can only effectively shield protons with energies up to 75 MeV (Clowdsley et al. 2005).
Superconducting shield The idea of using a large superconducting magnet to generate an active shield against deep space charged particles around the spacecraft dates back to the 1960s (von Braun 1969), and was subsequently evaluated in several configurations (e.g., Wilson et al. 1997; Townsend et al. 1990; Hoffman et al. 2005). Recently, under the European Space Radiation Superconducting Shield project, Vuolo et al. (2016) carried out detailed Monte Carlo simulations in which spacecraft and magnets were modeled together with a simplified mechanical structure supporting the superconducting magnet coils. Radiation transport through magnetic fields and materials and the generation of secondaries were simulated for a deep-space mission scenario. They found that when modeling the production of secondaries considering structures supporting the active shielding systems and the habitat, the radiation protection efficiency of the magnetic field is severely limited compared to previous studies, when only the magnetic field was modeled around the crew and primary charged particles were simply deflected. It is clear that active shielding using toroidal magnetic configurations is far from sufficiently mature enough to be seriously considered for spaceflight.
To summarize, state-of-the-art measurements and modeling results suggest that to most efficiently reduce the accumulated radiation during the cruise to Mars, which is mostly contributed by GCRs, the preferred time window of the mission is during solar maximum periods when GCRs are significantly depressed. As shown in Table 2, during solar maximum, the cruise GCR dose equivalent can be less than half of that during solar maximum periods. Like all operational choices, this one comes with a tradeoff: while a mission at solar maximum is beneficial in terms of GCR exposure, it is also more likely to experience one or more intense SEP events, a contingency that must be carefully planned for.
8.1.3 Warning and shielding of SEPs
However, as SEP events occur more frequently during solar maximum, timely warnings/alarms against SEP radiation and optimized shielding design are necessary for mitigating SEP-associated risks. Wilson et al. (1999) estimated that the risk of early health effects following a SEP event can be effectively reduced to an acceptable level by the proper use of operational warning and dosimetry systems along with an adequate storm shelter for crew protection.
SEP alerts Since Apollo missions, radiation dosimeters have been available to astronauts for self-alert of SEP events (NCRP 1988). This would provide a reliable operational nowcast for the crew. Reliable physics-based models of short- or long-term prediction of SEP events have not yet been developed, as discussed in Sect. 7.1. Nevertheless, some real time data-based warning systems have been developed in the past years. In a statistical analysis of SEP events observed between 1998 and 2002 by the COSTEP instrument on the SOHO satellite, Posner (2007) found that SEP events often start in situ with the arrival of relativistic electrons, followed by exponential increases of proton intensities. Therefore, using real-time electron measurements, it is possible to enable up to about 1 h of warning for energetic protons, which have larger biological radiation effects. This is the so-called Relativistic Electron Alert System for Exploration (REleASE) warning system. Furthermore, following the Hohmann transfer orbit (Hohmann 1994), the spacecraft remains close to the interplanetary magnetic field lines that connect Earth and/or Mars with the Sun (Hohmann–Parker effect, see Sect. 7.2.1), provided the field lines remain more or less unperturbed. This would enable a SEP warning system for the spacecraft during the cruise phase using data based on a two-tier warning system at Earth and Mars (Posner and Strauss 2020). For astronauts on the way from Earth to Mars, the REleASE system would provide advance warning time with a minimum of about 22 min at 1 au and a maximum near 42 min at Mars’ distance from the Sun. The protons used for the time-delay analysis in respect to relativistic electrons have energies below 50 MeV, which stop in about 3 g/cm\(^2\) of aluminum-equivalent shielding. More energetic relativistic protons arrive faster, leaving little forewarning time. The vehicle material will also modify the radiation behind the shielding. Therefore, an effective SEP warning or alert system, tailored for various local shielding conditions, is essential for alarming astronauts with quantitative estimations of the risk level. For instance, the Earth–Moon–Mars Radiation Environment Module (EMMREM, Schwadron et al. 2010) has been developed to provide the SEP dose rates under various aluminum-equivalent shielding thicknesses in deep space. Measurements of energetic particles near 1 au can be ingested into the module and projected to various locations throughout the inner heliosphere. Future potential particle detection near Mars, such as being part of an in situ space weather monitor at Mars–Sun L1 point (Sánchez-Cano et al. 2019), would also be of great benefit for such modeling and forecasting systems.
PREDICCS Based on the aforementioned modules and various near real-time data, PREDICCS (Predictions of radiation from REleASE, EMMREM, and Data Incorporating the CRaTER, COSTEP, and other SEP measurements) is an online tool (https://prediccs.sr.unh.edu/) to model the interplanetary radiation environment (Schwadron et al. 2012). It first uses near real-time particle measurements from various instruments near Earth (depending on the years of operation). Then the time series of SEP proton measurements are used as input for further simulating the particle transport across interplanetary space, giving proton spectra outputs. Finally, the dose rate induced by these the SEP protons absorbed in a water slab target behind an aluminum shielding is given. To test the model, Quinn et al. (2017) calculated the accumulated event dose predicted by PREDICCS for the 5 SEP events encounter by RAD during its cruise to Mars (Sect. 7.2.1) when the spacecraft was magnetically connected with Earth. The comparison of the event dose with actual RAD data reveals some discrepancies, but the tool shows potential to be used as a real-time warning system.
Storm shelters and shielding garment It has been well studied that hydrogenous materials and light elements are expected to be more effective radiation shields than aluminum, which is used in current spacecraft hulls. Particle transport calculations suggested that the use of polymers as shielding material in place of an equal mass of aluminum would reduce crew exposures without increasing the vehicle mass (Wilson et al. 1995; Guetersloh et al. 2006), although structural issues present a major challenge for this approach. If the vehicle shielding is insufficient, upon the onset of SEP events as alerted by active dosimeters or forecasting systems, additional shielding can be applied such as within a “storm shelter” polyethylene shielding (Wilson et al. 1999) and/or the adoption of wearable shielding spacesuits (Wilson et al. 2006; Vuolo et al. 2017). The shelter could serve for astronauts to be protected during the most intense phase of the event, typically lasting for hours. On the other hand, the garment would work better for smaller SEP events or for a later phase of an event when the SEP is less intense with a softer energy spectrum. This would also allow astronauts to move around more freely to perform necessary operations for the mission. Vuolo et al. (2017) have carried out simulations of an anthropomorphic phantom in an average SEP environment and estimated the shielding performance based on different materials. Water-filled spacesuits have been selected to be the first choice material after a trade-off analysis between shielding effectiveness and availability of resources in the space habitat. In case of extraordinary events, the combination of shelter and garments might be a necessary mitigation strategy.
In summary, the cruise phase GCR radiation can be most efficiently reduced by choosing a mission window around solar maximum when the interplanetary GCR flux is lower. Material shielding against GCRs is challenging and impractical for deep space cruises. However, during solar maximum years, more SEP events may impose acute radiation hazards and this requires extra operational planning to alert for and additionally shield these events. Physics-based forecasting approaches a few days before the onset of a SEP event have not yet achieved success, with a large number of false alarms and many events not being predicted at all. Some real-time measurement-based nowcasting tools (using data acquired near Earth where particle fluxes are well measured) have been recently developed, which show a promising potential to predict the cruise radiation at locations magnetically connected to Earth.
8.2 Reduction of exposures during a stay on Mars
The data-based estimation of the radiation variation on the surface of Mars is relying on the RAD measurement at Gale Crater where the average atmospheric depth is about 21.5 g/cm\(^2\) with a seasonal pressure variation up to about 25%. Mars has many valleys, craters and also the highest mountain in the solar system, hence atmospheric column depth varies drastically from place to place. Exposures must therefore be re-evaluated when the atmospheric thickness differs significantly. Calculation of the Martian radiation environment with different atmospheric depth shows that the dose and dose equivalent rate may change between 10 and 20% (depending on the solar modulation), when the atmospheric column mass is between 15 and 25 g/cm\(^2\) (Guo et al. 2017a). The continuation of the current RAD operation as the Curiosity rover climbs up Mt. Sharp is critical for us to better assess the atmospheric influence of the surface radiation environment over a larger range.
Landing in a region with a relatively thick atmosphere provides several advantages to the landing system (longer descent time, less rapid deceleration, more drag). It seems likely that such a location will be chosen for a future human mission. Therefore, the radiation environment at Gale Crater is not expected to be substantially different from the radiation fields at other craters where future missions may land.
8.2.1 Regolith shielding
To reduce the radiation dose during a human stay on Mars, astronauts may make use of natural geological structures as radiation shelters. This would be part of a larger strategy of in situ resource utilization (Starr and Muscatello 2020). Observations from the orbit of Mars revealed that possible cave skylights (Cushing et al. 2007) or lava tubes (Léveillé and Datta 2010) are not uncommon on the Martian surface. The regolith shielding can be particularly helpful during highly intense SEP events, and also serve to achieve a steady reduction of long-term exposure to continuous GCR-induced radiation (Simonsen et al. 1990; Kim et al. 1998; Dartnell et al. 2007; Röstel et al. 2020).

Image reproduced with permission from Röstel et al. (2020), copyright by the authors
Required subsurface shielding for peak (\(\varPhi ={1000}~\text{MV}\)), average (\(\varPhi ={580}~\text{MV}\)) and weak solar modulation (\(\varPhi ={400}~\text{MV}\)) scenarios. Gray and Red bars show the required shielding depths for achieving an equivalent dose reduction to 200 and 100 mSv/year, respectively. From left to right, different regolith rock types are presented including basaltic andesite rock (AR), iron-rich sandstone (SS), Sulfur concrete (SC), an inhomogeneous scenario for Arabia Terra (AT), where a soil mixture of 10% water by weight underlies 30 g/cm\(^2\) of dry rock, a homogeneous mixture of 10% water and 90% basaltic andesite rock by weight (W10), and finally a homogeneous mixture of 50% water and 50% basaltic andesite rock by weight (W50) as an extreme case. The left three cases represent a dry scenario while the right three are “wet” surface with high content of hydrogen.
Recently, Röstel et al. (2020) have modeled the GCR radiation environment on the surface and at the subsurface of Mars and suggested that sufficient shielding depth may limit the annual equivalent dose to be under 100 mSv. Equivalent dose was used in these calculations; this is derived from legal concerns related to radiation protection standards. It is not directly comparable to the dose equivalent obtained from RAD data, which is a “point estimate” based on the measured energy deposition spectrum weighted by the ICRP60 quality factor (ICRP 1992). (See further discussion in Sect. 9). As shown in Fig. 25, this required shielding depth is between 80 cm and 2.5 m depending on the solar modulation and soil composition, with hydrated soil requiring less shielding. Materials with significant hydrogen content can efficiently reduce the equivalent dose due to hydrogen’s superior performance as a shield against energetic charged particles, and due to its moderation of biologically effective fast neutrons.
When planning for field excursions away from such habitats, sheltering at the vicinity of a butte can also be useful, as suggested by the RAD observations during the time Curiosity was parked in the Murray buttes region (Ehresmann et al. 2021; Guo et al. 2021, and see Sect. 5). This could be mission saving during emergency situations when intense SEPs arrive at Mars.
8.2.2 SEP radiation modeling
As measurements of SEP-induced radiation enhancements are scarce on the surface of Mars (Sect. 7.3), modeling the potential surface SEP radiation becomes essential to understand the potential risk induced by large SEP events. Townsend et al. (2011) considered the transport of possible historical Carrington-type SEP events through the Martian atmosphere and also through various hemispherical configurations of aluminum shielding to estimate the resulting organ doses and effective doses of such extreme events. In nearly all scenarios, only thinly shielded crews on the summit of Olympus Mons (21 km above mean elevation) appear to exceed exposure limits induced by the largest SEP considered.
As the chance of encountering a Carrington-type event is extremely small, Guo et al. (2018c) have calculated the induced Martian surface dose and dose equivalent rates of more than 30 significant solar events (measured in situ by SOHO from between 1995 December and 2015 December), to provide insights into the possible variety of Martian surface radiation enhancement throughout a normal solar cycle. In the worst case, integrated dose equivalent resulting from a 2 h exposure to the SEPs reaches approximately 8 mSv (comparable to a chest CT scan). Furthermore, by analyzing and correlating the parameterized properties of the SEP spectra and the resulting surface dose rate, Guo et al. (2019b) found that the SEP intensity at the pivot energy of about 300 MeV alone can determine the surface dose rate. This is because of the effective atmospheric shielding of particles below about 150 MeV from reaching the surface and the nature of the SEP spectra where the high-energy component has significantly less flux. The results suggest that to mitigate radiation risks for future Mars missions, detecting or predicting the particle flux at 300 MeV during large SEP events may provide an instantaneous alert for a potential hazardous radiation environment on Mars. In conjunction with the aforementioned SEP event forecasting tools (Sect. 8.1.3) and active dosimeter alarms (NASA 2014), astronauts performing EVA on the surface can plan on returning to base or seeking for shelters or rock formations as a temporary shield.
Another potential possibility to reduce the surface radiation is to use Martian magnetic anomalies provided by crustal magnetic fields (Acuna et al. 1999). However, GCRs with energies above a few GeVs are unlikely to be shielded due to their large Larmor radii. (A proton of 10 GV rigidity or 9 GeV energy crossing a magnetic field of about 1500 nT (see Figure 2 of Acuna et al. 1999) has a gyroradius \(\sim \) 21,000 km which is larger than the scale of Mars.) For lower-energy particles during SEP events, Emoto et al. (2018) simulated particle trajectories entering a two-dimensional magnetic fields (while ignoring their interaction with the atmosphere) and found that the radiation shielding depends on the incident particle angle, energy and the geometry of the magnetic field. With the configuration of an idealized magnetic anomaly, protons below about 1 GeV can be efficiently shielded when they enter from one side, but unaffected when they arrive from the opposite side. Therefore, in practice, the potential application of radiation shielding using crustal magnetic fields needs careful consideration of the realistic configuration of the magnetic fields, the incident particle directionality and its dependence on the altitude (taking into account the particle interaction with the atmosphere), as well as the mass, charge and energy of incident particles.
9 A comment on further interpretation of the health risk
In general, the study of radiation impact on humans is challenging and often has large uncertainties in the quantification of the biological effect. There are very limited data for human beings in space under exposure to SEP/GCR HZE ions. The biological effects and health risk estimation primarily depends on biophysical calculations and animal experiments, as briefly described in Sect. 1.2.
So far, we have thoroughly assessed the MSL/RAD measured quantities such as dose, LET and dose equivalent and their time variations expected for a potential Mars mission. These measurements have directly answered a few of the critical questions gathered from previous NASA Radiation Health Program’s Annual Investigator Meetings and Workshops (Cucinotta et al. 2001b), such as: “What is the Martian radiation environment?” and “What is the solar cycle dependence of space radiation?”. However, since the biological effects associated with these quantities remain incompletely understood (e.g., Cucinotta et al. 2013a), it is difficult to directly relate our assessments to potential health risks of astronauts. Some of the limitations in predicting the space radiation health risk based on physical measurements and the current state of radiobiology knowledge are discussed below.
The dose rate in the RAD E detector includes a small contribution from neutral particles (mostly neutrons), typically on the order of 10 \(\upmu \)Gy/day, or about 5% of the total E dose rate. This contribution is measured using the C and F detectors as anticoincidence to obtain neutral particle energy deposition spectra in the D and E detectors (Fig. 3). Both D and E are sensitive to neutrons and gamma-rays, each with a different response function to the two kinds of neutral-particle radiation. An inversion method was developed to transform the measured spectra into gamma-ray and neutron energy spectra (Köhler et al. 2011). Dose and dose equivalent rates can be determined by convolution of the neutron energy spectrum with standard energy-dependent conversion coefficients such as those given by the US Nuclear Regulatory Commission (NRC 2018), ICRP (ICRP 1996), etc. Neutron spectra for two different periods in the Mars surface mission have been obtained (Köhler et al. 2014; Guo et al. 2017b); we consider the latter to be more accurate than the earlier one, in which counting rates were overestimated due to an error in one of the correction factors that was applied to the raw data.
Compared to charged particle dosimetry, the uncertainties inherent in neutron dosimetry are considerably larger. The primary reason for this is that the detector response functions, on which the inversion method is based, rely on Monte Carlo calculations, which in turn depend on nuclear cross section databases with significant associated uncertainties. The uncertainties are particularly significant for neutron energies above 20 MeV, which is an important part of the neutron energy spectrum RAD measures. It is also the case that the detection thresholds for neutral particles are, of necessity, set much higher in RAD than the inherent noise levels of the D and E detectors. This is because of the constant, high-rate bombardment of these detectors by relatively low-energy neutrons and gamma-rays that originate from the RTG. As a consequence of the high thresholds, the measurement of neutrons is limited to the energy range above about 8 MeV. Model calculations (e.g., Röstel et al. 2020) suggest that a considerable share of the neutron dose equivalent on the Martian surface (\(\sim \) 40%) comes from neutrons with energies less than this, which RAD cannot measure. At the other end of the energy range, RAD becomes inefficient for neutron detection above a few hundred MeV, because as neutron energy increases, so does the probability that a recoil proton created in the E detector plastic will have sufficient range to escape and trigger the F veto detector. Calculations show that another \(\sim \) 10% of the dose equivalent may be lost from this effect. The dose equivalent obtained from inversion and convolution with conversion coefficients can therefore be interpreted as a lower bound on the true neutron dose equivalent, which is likely to be on the order of double the measured value.
As noted earlier, the RAD dose equivalent is not the so-called equivalent dose or effective dose. The equivalent dose is established for legal concerns in terrestrial applications when the incident particle types are known as well as their energy ranges. Space radiation cannot be so easily characterized (Sect. 1.1), and may change drastically in time and location as discussed. The equivalent dose is the weighted dose generally used in radiation protection and gives a safe bound of the biological effectiveness, as, for instance, the radiation weighting factor of all particles heavier than protons is set to be 20 independent of their energy ICRP (2010). The effective dose is yet another quantity used in radiation protection; it is calculated as the sum of the tissue weighted equivalent dose as \(\sum _{T} w_T H_T\), where T stands for a certain tissue with \(w_T\) being the tissue weighting factor and \(H_T\) being the equivalent dose induced by particles transported to the surface of an organ/tissue. The tissue weighting factor \(w_T\) is specific for each organ or tissue of the body (ICRP 2007). The factors vary considerably; bone marrow as 0.12, compared to about 0.01 for the brain. These weighting factors are estimates and have large uncertainties, as they do not account for gender, age or other health conditions of the individual. Previous models have predicted effective doses of approximately 1–2 mSv/day in interplanetary space and approximately 0.5–1 mSv/day on the Martian surface (e.g., Cucinotta and Durante 2006). Although dose equivalent and effective dose are derived differently, these values are similar to the RAD measured dose equivalent rate as well as to our extrapolations to different solar modulation conditions, which are 1–2 mSv/day in deep space and 0.3–0.9 mSv/day on the surface of Mars (Table 2).
Furthermore, there are large uncertainties in extrapolating from radiation effects on terrestrial populations or medical studies to effects on astronauts (Cucinotta et al. 2001b). Epidemiological data, mainly from survivors of the atomic bombs in Japan (Pierce et al. 1996; Preston et al. 2003), have been used to make cancer risk estimations of sparsely ionising particles such as \(\gamma \)-rays and X-rays. The bomb survivor cohort includes a small share of high-LET exposures from neutrons, but the exposures were dominantly to low-LET radiation that was essentially instantaneous. Radiation exposure in space is a drastically different scenario, and extrapolation of bomb survivor data to the astronaut cohort is highly problematic. The US National Council on Radiation Protection is currently engaged in the “Million Worker Study” (Boice Jr et al. 2018) which is focused on occupational exposures and which may ultimately prove more relevant to the study of chronic radiation exposures in healthy populations.
Besides, the low dose and dose rate radiation exposure derived for long-term exploration missions can not be easily realized in ground-based experiments which are often performed using rodent models exposed to mono-energetic single-ion beams (e.g., Sokolova et al. 2015; Parihar et al. 2015). Due to constraints in the accelerator environment, doses are generally delivered over very short periods of time, typically over a few minutes (e.g., Loucas and Cornforth 2013). Because many radiobiology studies are designed to elucidate mechanisms of cancer induction, and because it is necessary to observe a statistically significant signal above the non-negligible natural background, doses historically were much higher than human crews would be exposed to during interplanetary space travel (e.g., Durante et al. 2002, 2005). Recognizing these issues, steps have recently been taken at the NASA Space Radiation Laboratory to better align the exposures given to model systems with crew exposures, including the provision of mixed radiation fields, lower dose rates, and protracted exposures (Simonsen et al. 2020).
Using animal models poses difficult questions regarding the extrapolation of measured effects to humans. Differences in anatomy, metabolism, and lifespan complicate interpretation (Williams et al. 2010). As an example, LD50 defines the required dose necessary to cause fatality in 50% of those exposed. The LD50 for mice is at least two times higher than that for humans, as shown in Morris and Jones (1988).
Additionally, studies of the synergistic effects of radiation combined with the unusual set of stressors experienced in spaceflight—microgravity, isolation and emotional stress—indicate an increased susceptibility to infection and delayed wound healing (Sanzari et al. 2011). Yatagai et al. (2019) proposed that the combined effects between microgravity and space radiation might occur through the window of cellular responses, including damaging and signaling by reactive oxygen species, damage responses on DNA (repair, replication, transcription, etc.), and expression of genes and proteins (regulation by chromatin, epigenetic control, etc.). This is an unsettled field of research at present, and no firm conclusions about synergistic effects can yet be drawn (Moreno-Villanueva et al. 2017).
In conclusion, health risk projections for space radiation exposures are based on many factors that are, at best, incompletely understood, for the reasons discussed above. Risk predictions such as REIC and REID (radiation exposure-induced cancer and death, respectively) are therefore highly uncertain. Different agencies such as NCRP, NASA, and the US nuclear industry have adopted different career dose limits or different approaches to evaluate the risk (Cucinotta et al. 2013a). NASA’s radiation standard limits astronaut exposures to a 3% risk of exposure induced death at the upper 95% confidence interval of the risk estimate. Central estimates of exposure limits for 30- to 60-year-old never-smokers range from 600 to 1000 mSv and 800 to 1200 mSv for females and males, respectively. Exposure limits at the 95% confidence levels are about one third of the central values (Cucinotta and Chappell 2011). These limits are applicable for LEO missions; deep-space limits are not yet defined. As described above, the accumulated GCR dose for a round-trip mission via a Hohmann transfer under solar minimum and medium conditions (1–1.5 Sv in Table 2) so that would be problematic in the NASA framework for LEO. Reduction of the mission dose from GCRs during solar maximum is promising, but the additional contribution by SEPs could be highly hazardous during solar maximum. In recent years, much effort has been devoted to developing biological countermeasures as reviewed by Kennedy (2014). But their mechanisms and effects are not fully understood and their application in space flight is not yet mature. As suggested by Durante (2014), the best solution to the space radiation problem, and also to other health risks related to microgravity and isolation, could be reduction of the transit time. This can only be achieved using nuclear propulsion, possibly a mixed system combining thermal and electric nuclear power, but this field also needs major developments for practical applications.
10 Summary and conclusion
One of the most significant risks for human health in space is the exposure to energetic particles, which are mostly GCRs during solar quiet time and occasionally SEPs during solar storms. This becomes especially challenging for future planetary missions such as to Mars, which, with current propulsion methods, require a return-trip duration of about 3 years following the most energy-efficient Hohmann transfer. To evaluate the relevant radiation environments for future human exploration, the RAD was designed to detect and analyze the most biologically hazardous energetic particle radiation on the Martian surface as part of the MSL mission. Since the landing of MSL on Mars on August 6, 2012, RAD has been operating continuously and providing the first-ever and unique measurements of the energetic particle radiation environment on the Martian surface.
In this review article, we have analyzed and discussed the radiation dose measured by RAD during its cruise phase and on Mars’s surface, and the factors that give rise to temporal variations. The RAD data obtained to date span the time from the pre-max of Solar Cycle 24 throughout its solar minimum, into the initial year of Cycle 25. Over the long time scale, the Martian surface GCR radiation was observed to increase by about 50% due to the weakened solar activity and heliospheric magnetic fields. On shorter time scales, RAD has also detected dynamic variations in the radiation field on Mars, reflecting the pass-by of solar magnetic eruptions, the atmospheric diurnal and seasonal evolution, as well as small effects from local topography as the rover traverses the lower slopes of Mount Sharp. RAD detected 5 prominent SEP events during the cruise to Mars and has observed another 5 events while operating on the Martian surface. The largest and most recent event at the time of this writing took place on September 10, 2017 and was also observed as a ground level event on Earth.
We have presented and quantified the variations of the surface GCR radiation field which are caused by three factors as summarized below.
-
The atmospheric column mass varies for three reasons (Sect. 3): the Martian daily thermal tide, the seasonal CO\(_2\) condensation cycle, and the altitude change of the rover. The latter is also a topographical factor as presented in Sect. 5.2. The diurnal pressure variations measured by MSL/REMS reach \(\pm 5\%\) relative to the median, or up to around 80 Pa between daily minimum and maximum pressures. The seasonal CO\(_2\) cycle induced pressure ranges up to about 270 Pa between minimum and maximum values. The pressure has been observed to decrease by roughly 30 Pa as the rover has climbed up Mt. Sharp, as seen by comparing the annual mean values of MY 34 to the previous two Martian years. Analyzing the diurnal pressure–dose correlation using a superposed method, we have isolated and quantified the diurnal pressure oscillation induced dose rate changes (Rafkin et al. 2014; Guo et al. 2015b, and Sect. 3.2). The anti-correlation between the pressure and dose changes reveals that the Martian atmosphere is providing modest shielding against GCRs at Gale Crater. However, this effect is not constant and it mostly depends on the primary particle spectra on top of the atmosphere. During solar minimum, when the low-energy component of the primary GCR flux is relatively high, this effect is more prominent as lower energy particles are more easily stopped by the atmosphere. During solar maximum, the atmospheric modulation is weaker or may even vanish (in terms of its effect on dose rate) as suggested by model results (Guo et al. 2017a). Throughout the weak solar cycle 24, the atmospheric shielding effect has been well observed and the quantified correlation has been used to derive the seasonal pressure change-induced dose variation which is up to 57 \(\upmu \)Gy/day, about 19% of the average dose rate \(\sim \) 300 during the past solar minimum. Despite its modest effect on dose rates, atmospheric shielding plays a significant role in reducing the radiation quality factor \(\langle Q \rangle \) via the process of nuclear fragmentation of GCR heavy ions. In free space, \(\langle Q \rangle \) is expected to be in the range from 6 to 7, whereas RAD has measured values in the range from 2 to 2.5 in Gale Crater. Consequently, the dose equivalent, which is the multiplication of \(\langle Q \rangle \) and the dose, always decreases as the atmosphere thickness increases. Moreover, the atmosphere also stops a large share of SEPs in typical events.
-
The heliospheric impact includes both short-term influences by solar transients and the long-term solar cycle evolution (Sect. 4). On short time scales, the GCR flux can be altered temporarily in the form of Forbush decreases (FDs) by transient heliospheric magnetic structures such as interplanetary coronal mass ejections and stream interaction regions. FDs have been observed since decades at Earth by ground neutron monitors; now RAD has also provided a new dataset of the FDs observed at Mars since 2012 August (Guo et al. 2018b; Papaioannou et al. 2019). These FDs have been analyzed in various works for identifying the shock, CME and SIR arrival at Mars and for studying the propagation and evolution of such solar transients and their space weather effect at Mars in synergy with in situ plasma and magnetic field measurements or even when such measurements are missing (Witasse et al. 2017; Winslow et al. 2018; Guo et al. 2018a; Wang et al. 2018; Dumbović et al. 2019; Freiherr von Forstner et al. 2018, 2019, 2020). Over the time period from August 2012 until June 2020, the RAD GCR dose rate increased by \(\sim \) 50%. In comparison, the Earth Oulu neutron monitor (with a much larger atmospheric cutoff at Earth) count rate rose by \(\sim \) 15%, and the EPHIN GCR (with a low energy cutoff of about 50 MeV) flux changed by \(\gtrapprox \) 200%. The different GCR variation at detectors with different energy responses reveals the energy-dependent modulation of the GCR particles by the heliospheric magnetic fields. Using the modulation potential \(\varPhi \), which is a practical parameter to successfully describe the heliospheric modulation, we have formulated a quantitative description of the radiation on Mars based on existing correlation of the monthly \(\varPhi \) and RAD data (Eq. 1), through which the atmospheric influence is included as an uncertainty of the quantification. The resulting non-linear function can be used to extrapolate the Martian surface radiation under other extreme solar modulation conditions.
-
Last but not least, as the rover explores along its pathway, topographical features also influence the radiation detected by RAD (Sect. 5). A particularly interesting feature is that when the rover was parked close to a butte, which partly obscured the sky view, the dose rate dropped by about 15 ± 2 \(\upmu \)Gy/day or nearly 5%. This provides the first in situ illustration that the existing surface structures may serve as a potential radiation shelter for future habitats on Mars.
The quantification of the variation of the radiation field not only helps us to understand the potential radiation risks for future human exploration of the red planet under different conditions, but also highlights the advantage of using RAD as a space weather monitor on Mars. Together with other measurements in Mars orbit by, e.g., MAVEN and Mars Express, RAD has been used to analyze the arrival of solar storms at Mars (e.g., Lee et al. 2018; Guo et al. 2018a) and to help understand the dynamic space weather condition at Mars.
We also compared the RAD cruise-phase measurement to that of Liulin-MO on TGO results (Semkova et al. 2018) of the cruise journey in 2016, which are in agreement considering the different levels of solar modulation in 2012 and 2016. At the time of writing, another instrument MEPA (Tang et al. 2020) on board the Chinese Mars Tianwen-1 mission is cruising towards Mars. Both Liulin-MO and MEPA monitor the orbiter radiation environment of Mars and can be used synergistically with RAD to assess the global radiation at Mars at different spatial and temporal scales. In particular, the concurrent measurement of the radiation on top of the atmosphere versus that at Gale Crater can be used to better quantify the atmospheric effect, validate particle transport models and more precisely constrain the incoming GCR/SEP spectra at Mars.
Based on the above assessment of the radiation during the cruise to Mars and on the surface, we estimated the accumulated GCR radiation level for a round-trip mission to Mars using the empirical modeling of the radiation environment under various conditions, especially under different solar modulation conditions (Sect. 6). The cruise-phase dose or dose equivalent contributes more than the surface phase for a round-trip mission. Overall, the shielding of the GCR radiation by heliospheric magnetic fields during solar maximum periods reduces the total GCR-induced radiation for a Mars mission by more than 50% (Table 2). As shown in Table 2, the accumulated GCR dose equivalent, via a Hohmann transfer, is about \(0.65 \pm 0.24\) and \(1.59 \pm 0.12\) during solar maximum and minimum periods respectively. With future nuclear thrusters via a fast transfer, the total GCR dose equivalent would be about 0.2 and 0.5 during maximum and minimum periods respectively. Contributions by SEPs must be taken into account; these cannot be easily assessed due to their high variability from cycle to cycle and from event to event. We discussed SEP properties and reviewed the RAD-observed SEP events during the extreme weak solar cycle 24 in Sect. 7.
We then examined parameters related to mitigation considerations for further reducing radiation exposures in space and on Mars in Sect. 8, such as spacecraft material, the possibility (not yet feasible) of shielding using superconducting magnets, SEP alert and storm shelters, as well as Martian subsurface habitats.
Finally, we also commented on the many uncertainties in the quantification of health risks in Sect. 9. The GCR exposure for a return mission via a Hohmann transfer under solar minimum and medium conditions is, in terms of dose equivalent, about 1–1.5 Sv, which would be problematic for the cancer risk considerations of NASA in the current framework, which is presently only applicable to LEO missions. (Limits for deep-space missions are not yet defined.) The reduction of GCR exposure that can be achieved by planning a mission for a solar maximum timeframe is promising, but adds the potentially high risk of large, unpredictable contributions by SEP events. Substantial technological development allowing for a fast Mars transfer might be the best solution to the space radiation risk, and also to other health issues such as microgravity and isolation for such a revolutionary endeavor of humanity.
References
Acuna M, Connerney J, Lin R, Mitchell D, Carlson C, McFadden J, Anderson K, Rème H, Mazelle C, Vignes D et al (1999) Global distribution of crustal magnetization discovered by the Mars Global Surveyor MAG/ER experiment. Science 284(5415):790–793. https://doi.org/10.1126/science.284.5415.790
Aschwanden MJ (2002) Particle acceleration and kinematics in solar flares: a synthesis of recent observations and theoretical concepts. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-2541-5
Badhwar GD (2004) Martian radiation environment experiment (MARIE). Space Sci Rev 110(1–2):131. https://doi.org/10.1007/978-0-306-48600-5_4
Bain H, Mays M, Luhmann J, Li Y, Jian L, Odstrcil D (2016) Shock connectivity in the 2010 August and 2012 July solar energetic particle events inferred from observations and ENLIL modeling. Astrophys J 825(1):1. https://doi.org/10.3847/0004-637x/825/1/1
Banjac S, Herbst K, Heber B (2018) The Atmospheric Radiation Interaction Simulator (AtRIS)—description and validation. J Geophys Res. https://doi.org/10.1029/2018JA026042
Barcellos-Hoff MH, Blakely EA, Burma S, Fornace AJ Jr, Gerson S, Hlatky L, Kirsch DG, Luderer U, Shay J, Wang Y et al (2015) Concepts and challenges in cancer risk prediction for the space radiation environment. Life Sci Space Res 6:92–103. https://doi.org/10.1016/j.lssr.2015.07.006
Battarbee M, Guo J, Dalla S, Wimmer-Schweingruber R, Swalwell B, Lawrence D (2018) Multi-spacecraft observations and transport simulations of solar energetic particles for the May 17th 2012 event. Astron Astrophys 612:A116. https://doi.org/10.1051/0004-6361/201731451
Belov AV (2008) Forbush effects and their connection with solar, interplanetary and geomagnetic phenomena. Proc IAU 4(S257):439–450. https://doi.org/10.1017/S1743921309029676
Belov A, Abunin A, Abunina M, Eroshenko E, Oleneva V, Yanke V, Papaioannou A, Mavromichalaki H (2015) Galactic cosmic ray density variations in magnetic clouds. Sol Phys 290(5):1429–1444. https://doi.org/10.1007/s11207-015-0678-z
Biermann PL, Sigl G (2001) Introduction to cosmic rays. In: Lemoine M, Sigl G (eds) Physics and astrophysics of ultra-high-energy cosmic rays. Lecture notes in physics, vol 576. Springer, Berlin, pp 1–26. https://doi.org/10.1007/3-540-45615-5_1
Boice JD Jr, Ellis ED, Golden AP, Girardi DJ, Cohen SS, Chen H, Mumma MT, Shore RE, Leggett RW (2018) The past informs the future: an overview of the Million Worker Study and the Mallinckrodt Chemical Works Cohort. Health Phys 114(4):381–385. https://doi.org/10.1097/HP.0000000000000825
Bruno C, Durante M, Dujarric C (2013) Propulsion requirements for a safe human exploration of Mars. In: 64th International astronautical congress, Beijing, China. IAF, pp IAC–13–C4.7.8
Cane HV (2000) Coronal mass ejections and Forbush decreases. Space Sci Rev 93(1–2):55–77. https://doi.org/10.1007/978-94-017-1187-6_4
Cane H, Wibberenz G, Richardson I, Von Rosenvinge T (1999) Cosmic ray modulation and the solar magnetic field. Geophys Res Lett 26(5):565–568. https://doi.org/10.1029/1999GL900032
Cane HV, Richardson IG, St Cyr OC (2000) Coronal mass ejections, interplanetary ejecta and geomagnetic storms. Geophys Res Lett 27(21):3591–3594. https://doi.org/10.1029/2000GL000111
Cliver E (2016) Flare versus shock acceleration of high-energy protons in solar energetic particle events. Astrophys J 832(2):128. https://doi.org/10.3847/0004-637x/832/2/128
Clowdsley M, Nealy J, Wilson J, Anderson B, Anderson M, Krizan S (2005) Radiation protection for lunar mission scenarios. In: Space 2005. AIAA, Reston, VA, pp AIAA 2005-6652. https://doi.org/10.2514/6.2005-6652
Cucinotta FA, Chappell LJ (2011) Updates to astronaut radiation limits: radiation risks for never-smokers. Radiat Res 176(1):102–114. https://doi.org/10.1667/RR2540.1
Cucinotta FA, Durante M (2006) Cancer risk from exposure to galactic cosmic rays: implications for space exploration by human beings. Lancet Oncol 7(5):431–435. https://doi.org/10.1016/S1470-2045(06)70695-7
Cucinotta F, Manuel F, Jones J, Iszard G, Murrey J, Djojonegro B, Wear M (2001a) Space radiation and cataracts in astronauts. Radiat Res 156(5):460–466. https://doi.org/10.1667/0033-7587(2001)156[0460:sracia]2.0.co;2
Cucinotta FA, Schimmerling W, Wilson JW, Peterson LE, Badhwar GD, Saganti PB, Dicello JF (2001b) Space radiation cancer risk projections for exploration missions: uncertainty reduction and mitigation. Technical Report. NASA JSC-29295, NASA
Cucinotta FA, Kim MHY, Ren L (2005) Managing lunar and Mars mission radiation risks part I: cancer risks, uncertainties, and shielding effectiveness. Technical Report TP-2005-213164, NASA. https://ntrs.nasa.gov/citations/20050196720
Cucinotta FA, Kim MHY, Ren L (2006) Evaluating shielding effectiveness for reducing space radiation cancer risks. Radiat Meas 41(9–10):1173–1185. https://doi.org/10.1016/j.radmeas.2006.03.011
Cucinotta FA, Kim M, Chappell LJ (2013a) Space radiation cancer risk projections and uncertainties—2012. Technical Report. TP-2013-217375, NASA
Cucinotta FA, Kim MHY, Chappell LJ, Huff JL (2013b) How safe is safe enough? Radiation risk for a human mission to Mars. PLoS One 8(10):e74988. https://doi.org/10.1371/journal.pone.0074988
Cucinotta FA, Alp M, Sulzman FM, Wang M (2014) Space radiation risks to the central nervous system. Life Sci Space Res 2:54–69. https://doi.org/10.1016/j.lssr.2014.06.003
Cucinotta FA, To K, Cacao E (2017) Predictions of space radiation fatality risk for exploration missions. Life Sci Space Res 13:1–11. https://doi.org/10.1016/j.lssr.2017.01.005
Cushing GE, Titus TN, Wynne JJ, Christensen PR (2007) THEMIS observes possible cave skylights on Mars. Geophys Res Lett 34:17201. https://doi.org/10.1029/2007GL030709
Dartnell L, Desorgher L, Ward J, Coates A (2007) Modelling the surface and subsurface Martian radiation environment: implications for astrobiology. Geophys Res Lett 34:L02207. https://doi.org/10.1029/2006GL027494
De Angelis G, Wilson J, Clowdsley M, Qualls G, Singleterry R (2006) Modeling of the Martian environment for radiation analysis. Radiat Meas 41(9):1097–1102. https://doi.org/10.1016/j.nuclphysbps.2006.12.035
Desai M, Giacalone J (2016) Large gradual solar energetic particle events. Living Rev Sol Phys 13:3. https://doi.org/10.1007/s41116-016-0002-5
Desorgher L (2005) PLANETOCOSMICS software user manual. http://cosray.unibe.ch/~laurent/planetocosmics/. Accessed 22 Feb 2021
Ding LG, Cao XX, Wang ZW, Le GM (2016) Large solar energetic particle event that occurred on 2012 March 7 and its VDA analysis. Res Astron Astrophys 16:122. https://doi.org/10.1088/1674-4527/16/8/122. arXiv:1604.05303 [astro-ph.SR]
Dresing N, Gómez-Herrero R, Heber B, Klassen A, Malandraki O, Dröge W, Kartavykh Y (2014) Statistical survey of widely spread out solar electron events observed with STEREO and ACE with special attention to anisotropies. Astron Astrophys 567:A27. https://doi.org/10.1051/0004-6361/201423789
Dröge W, Kartavykh YY, Klecker B, Kovaltsov GA (2010) Anisotropic three-dimensional focused transport of solar energetic particles in the inner heliosphere. Astrophys J 709:912–919. https://doi.org/10.1088/0004-637X/709/2/912
Dujarric C, Santovincenzo A, Summerer L (2013) The Nuclear Thermal Electric Rocket: a proposed innovative propulsion concept for manned interplanetary missions. Prog Propuls Phys 4:293–312. https://doi.org/10.1051/eucass/201304293
Dumbović M, Heber B, Vršnak B, Temmer M, Kirin A (2018) An analytical diffusion-expansion model for Forbush decreases caused by flux ropes. Astrophys J 860(1):71. https://doi.org/10.3847/1538-4357/aac2de
Dumbović M, Guo J, Temmer M, Mays ML, Veronig A, Heinemann SG, Dissauer K, Hofmeister S, Halekas J, Möstl C et al (2019) Unusual plasma and particle signatures at Mars and STEREO-A related to CME–CME interaction. Astrophys J 880(1):18. https://doi.org/10.3847/1538-4357/ab27ca
Dumbović M, Vršnak B, Guo J, Heber B, Dissauer K, Carcaboso F, Temmer M, Veronig A, Podladchikova T, Möstl C et al (2020) Evolution of coronal mass ejections and the corresponding Forbush decreases: modelling vs multi-spacecraft observations. Sol Phys 295:104. https://doi.org/10.1007/s11207-020-01671-7
Durante M (2014) Space radiation protection: destination Mars. Life Sci Space Res 1:2–9. https://doi.org/10.1016/j.lssr.2014.01.002
Durante M, George K, Wu H, Cucinotta F (2002) Karyotypes of human lymphocytes exposed to high-energy iron ions. Radiat Res 158(5):581–590. https://doi.org/10.1667/0033-7587(2002)158[0581:KOHLET]2.0.CO;2
Durante M, George K, Gialanella G, Grossi G, La Tessa C, Manti L, Miller J, Pugliese M, Scampoli P, Cucinotta F (2005) Cytogenetic effects of high-energy iron ions: dependence on shielding thickness and material. Radiat Res 164(4):571–576. https://doi.org/10.1667/RR3362.1
Effenberger F, Litvinenko YE (2014) The diffusion approximation versus the telegraph equation for modeling solar energetic particle transport with adiabatic focusing. I. Isotropic pitch-angle scattering. Astrophys J 783(1):15. https://doi.org/10.1088/0004-637x/783/1/15
Ehresmann B, Burmeister S, Wimmer-Schweingruber RF, Reitz G (2011) Influence of higher atmospheric pressure on the Martian radiation environment: implications for possible habitability in the Noachian epoch. J Geophys Res 116(A15):10106. https://doi.org/10.1029/2011JA016616
Ehresmann B, Zeitlin C, Hassler DM, Wimmer-Schweingruber RF, Böhm E, Böttcher S, Brinza DE, Burmeister S, Guo J, Köhler J et al (2014) Charged particle spectra obtained with the Mars Science Laboratory Radiation Assessment Detector (MSL/RAD) on the surface of Mars. J Geophys Res 119(3):468–479. https://doi.org/10.1002/2013JE004547
Ehresmann B, Zeitlin CJ, Hassler DM, Matthiä D, Guo J, Wimmer-Schweingruber RF, Appel JK, Brinza DE, Rafkin SC, Böttcher SI, Burmeister S, Lohf H, Martin C, Böhm E, Reitz G (2017) The charged particle radiation environment on Mars measured by MSL/RAD from November 15, 2015 to January 15, 2016. Life Sci Space Res 14:3–11. https://doi.org/10.1016/j.lssr.2017.07.004
Ehresmann B, Hassler D, Zeitlin C, Guo J, Wimmer-Schweingruber RF, Matthiä D, Lohf H, Burmeister S, Rafkin S, Berger T et al (2018) Energetic particle radiation environment observed by RAD on the surface of Mars during the September 2017 event. Geophys Res Lett 45(11):5305–5311. https://doi.org/10.1029/2018GL077801
Ehresmann B, Hassler D, Zeitlin C, Guo J, Wimmer-Schweingruber RF, Khaksari S, Löffler S (2021) Natural radiation shielding on Mars measured with the MSL/RAD instrument. J Geophys Res 126:e2021JE006851. https://doi.org/10.1029/2021JE006851
Emoto K, Takao Y, Kuninaka H (2018) A preliminary study on radiation shielding using Martian magnetic anomalies. Biol Sci Space 32:1–5. https://doi.org/10.2187/bss.32.1
Feynman J, Gabriel SB (2000) On space weather consequences and predictions. J Geophys Res 105(A5):10543–10564. https://doi.org/10.1029/1999JA000141
Folta D, Vaughn F, Rawitscher G, Westmeyer P (2012) Fast Mars transfers through on-orbit staging. In: Concepts and approaches for Mars exploration. LPI, p 4181. https://www.lpi.usra.edu/meetings/marsconcepts2012/pdf/4181.pdf
Forbush SE (1937) On the effects in cosmic-ray intensity observed during the recent magnetic storm. Phys Rev 51:1108–1109. https://doi.org/10.1103/PhysRev.51.1108.3
Forbush SE (1954) World-wide cosmic ray variations, 1937–1952. J Geophys Res 59(4):525–542. https://doi.org/10.1029/JZ059i004p00525
Forbush SE (1958) Cosmic-ray intensity variations during two solar cycles. J Geophys Res 63(4):651–669. https://doi.org/10.1029/JZ063i004p00651
Fox NJ, Velli MC, Bale SD, Decker R, Driesman A, Howard RA, Kasper JC, Kinnison J, Kusterer M, Lario D, Lockwood MK, McComas DJ, Raouafi NE, Szabo A (2016) The solar probe plus mission: humanity’s first visit to our star. Space Sci Rev 204:7–48. https://doi.org/10.1007/s11214-015-0211-6
Freiherr von Forstner JL, Guo J, Wimmer-Schweingruber RF, Hassler DM, Temmer M, Dumbović M, Jian LK, Appel JK, Čalogović J, Ehresmann B, Heber B, Lohf H, Posner A, Steigies CT, Vršnak B, Zeitlin CJ (2018) Using Forbush decreases to derive the transit time of ICMEs propagating from 1 AU to Mars. J Geophys Res 123(1):39–56. https://doi.org/10.1002/2017JA024700
Freiherr von Forstner JL, Guo J, Wimmer-Schweingruber RF, Temmer M, Dumbović M, Veronig A, Möstl C, Hassler DM, Zeitlin CJ, Ehresmann B (2019) Tracking and validating ICMEs propagating toward Mars using STEREO heliospheric imagers combined with Forbush decreases detected by MSL/RAD. Space Weather 17(4):586–598. https://doi.org/10.1029/2018SW002138
Freiherr von Forstner JL, Guo J, Wimmer-Schweingruber RF, Dumbović M, Janvier M, Démoulin P, Veronig A, Temmer M, Papaioannou A, Dasso S et al (2020) Comparing the properties of ICME-induced Forbush decreases at Earth and Mars. J Geophys Res 125(3):e2019JA027662. https://doi.org/10.1029/2019JA027662
Geyer P, Temmer M, Guo J, Heinemann SG (2021) Properties of stream interaction regions at Earth and Mars during the declining phase of SC 24. Astron Astrophys 649:A80. https://doi.org/10.1051/0004-6361/202040162
Gleeson L, Axford W (1968) Solar modulation of galactic cosmic rays. Astrophys J 154:1011. https://doi.org/10.1086/149822
Gómez-Elvira J, Armiens C, Castañer L, Domínguez M, Genzer M, Gómez F, Haberle R, Harri AM, Jiménez V, Kahanpää H et al (2012) REMS: the environmental sensor suite for the Mars Science Laboratory rover. Space Sci Rev 170(1–4):583–640. https://doi.org/10.1007/s11214-012-9921-1
Gopalswamy N, Yashiro S, Michałek G, Kaiser ML, Howard RA, Reames DV, Leske R, von Rosenvinge T (2002) Interacting coronal mass ejections and solar energetic particles. Astrophys J Lett 572:L103–L107. https://doi.org/10.1086/341601
Gopalswamy N, Yashiro S, Krucker S, Stenborg G, Howard RA (2004) Intensity variation of large solar energetic particle events associated with coronal mass ejections. J Geophys Res. https://doi.org/10.1029/2004JA010602
Gosling JT, Pizzo VJ (1999) Formation and evolution of corotating interaction regions and their three dimensional structure. Space Sci Rev 89:21–52. https://doi.org/10.1023/A:1005291711900
Grabham P, Sharma P (2013) The effects of radiation on angiogenesis. Vasc Cell 5(1):19. https://doi.org/10.1186/2045-824X-5-19
Grieder PK (2001) Cosmic rays at Earth: researcher’s reference manual and data book. Elsevier, Amsterdam. https://doi.org/10.1016/B978-0-444-50710-5.X5000-3
Gronoff G, Norman RB, Mertens CJ (2015) Computation of cosmic ray ionization and dose at Mars. I: a comparison of HZETRN and Planetocosmics for proton and alpha particles. Adv Space Res 55(7):1799–1805. https://doi.org/10.1016/j.asr.2015.01.028
Grotzinger JP, Crisp J, Vasavada AR, Anderson RC, Baker CJ, Barry R, Blake DF, Conrad P, Edgett KS, Ferdowski B, Gellert R, Gilbert JB, Golombek M, Gómez-Elvira J, Hassler DM, Jandura L, Litvak M, Mahaffy P, Maki J, Meyer M, Malin MC, Mitrofanov I, Simmonds JJ, Vaniman D, Welch RV, Wiens RC (2012) Mars Science Laboratory Mission and Science Investigation. Space Sci Rev 170(1):5–56. https://doi.org/10.1007/s11214-012-9892-2
Guetersloh S, Zeitlin C, Heilbronn L, Miller J, Komiyama T, Fukumura A, Iwata Y, Murakami T, Bhattacharya M (2006) Polyethylene as a radiation shielding standard in simulated cosmic-ray environments. Nucl Instrum Methods Phys Res Sect B 252(2):319–332. https://doi.org/10.1016/j.nimb.2006.08.019
Guo J, Zeitlin C, Wimmer-Schweingruber RF, Hassler DM, Posner A, Heber B, Köhler J, Rafkin S, Ehresmann B, Appel JK et al (2015a) Variations of dose rate observed by MSL/RAD in transit to Mars. Astron Astrophys 577:A58. https://doi.org/10.1051/0004-6361/201525680
Guo J, Zeitlin C, Wimmer-Schweingruber RF, Rafkin S, Hassler DM, Posner A, Heber B, Koehler J, Ehresmann B, Appel JK et al (2015b) Modeling the variations of dose rate measured by RAD during the first MSL Martian year: 2012–2014. Astrophys J 810(1):24. https://doi.org/10.1088/0004-637X/810/1/24
Guo J, Tony Slaba C, Zeitlin Cand, Wimmer-Schweingruber RF, Badavi FF, Böhm E, Böttcher S, Brinza DE, Ehresmann B, Hassler DM, Matthiä D, Rafkin S (2017a) Dependence of the Martian radiation environment on atmospheric depth: modelling and measurement. J Geophys Res 122(2):329–341. https://doi.org/10.1002/2016JE005206
Guo J, Zeitlin C, Wimmer-Schweingruber R, Hassler DM, Köhler J, Ehresmann B, Böttcher S, Böhm E, Brinza DE (2017b) Measurements of the neutral particle spectra on Mars by MSL/RAD from 2015-11-15 to 2016-01-15. Life Sci Space Res 14:12–17. https://doi.org/10.1016/j.lssr.2017.06.001
Guo J, Dumbović M, Wimmer-Schweingruber RF, Temmer M, Lohf H, Wang Y, Veronig A, Hassler DM, Mays LM, Zeitlin C et al (2018a) Modeling the evolution and propagation of 10 September 2017 CMEs and SEPs arriving at Mars constrained by remote sensing and in situ measurement. Space Weather 16:1156–1169. https://doi.org/10.1029/2018SW001973
Guo J, Lillis R, Wimmer-Schweingruber RF, Zeitlin C, Simonson P, Rahmati A, Posner A, Papaioannou A, Lundt N, Lee CO et al (2018b) Measurements of Forbush decreases at Mars: both by MSL on ground and by MAVEN in orbit. Astron Astrophys 611:A79. https://doi.org/10.1051/0004-6361/201732087
Guo J, Zeitlin C, Wimmer-Schweingruber RF, McDole T, Kühl P, Appel JC, Matthiä D, Krauss J, Köhler J (2018c) A generalized approach to model the spectra and radiation dose rate of solar particle events on the surface of Mars. Astron J 155(1):49. https://doi.org/10.3847/1538-3881/aaa085
Guo J, Banjac S, Röstel L, Terasa JC, Herbst K, Heber B, Wimmer-Schweingruber RF (2019a) Implementation and validation of the GEANT4/AtRIS code to model the radiation environment at Mars. J Space Weather Space Clim. https://doi.org/10.1051/swsc/2019004
Guo J, Wimmer-Schweingruber RF, Wang Y, Grande M, Matthiä D, Zeitlin C, Ehresmann B, Hassler DM (2019b) The pivot energy of solar energetic particles affecting the Martian surface radiation environment. Astrophys J Lett 883(1):L12. https://doi.org/10.3847/2041-8213/ab3ec2
Guo J, Wimmer-Schweingruber RF, Dumbović M, Heber B, Wang Y (2020) A new model describing Forbush decreases at Mars: combining the heliospheric modulation and the atmospheric influence. Earth Planet Phys 4(1):62–72. https://doi.org/10.26464/epp2020007
Guo J, Khaksarighiri S, Wimmer-Schweingruber R, Ehresmann B, Hassler D, Zeitlin C et al (2021) Directionality of the Martian surface radiation and derivation of the upward albedo radiation. Geophys Res Lett 48(15):e2021GL093912. https://doi.org/10.1029/2021GL093912
Guzewich SD, Lemmon M, Smith CL, Martínez G, de Vicente-Retortillo Á, Newman CE, Baker M, Campbell C, Cooper B, Gómez-Elvira J, Harri AM, Hassler D, Martin-Torres FJ, McConnochie T, Moores JE, Kahanpää H, Khayat A, Richardson MI, Smith MD, Sullivan R, de la Torre Juarez M, Vasavada AR, Viúdez-Moreiras D, Zeitlin C, Zorzano Mier MP (2019) Mars Science Laboratory Observations of the 2018/Mars year 34 global dust storm. Geophys Res Lett 46(1):71–79. https://doi.org/10.1029/2018GL080839
Haberle R, Gómez-Elvira J, Torre Juárez M, Harri AM, Hollingsworth J, Kahanpää H, Kahre M, Lemmon M, Martín-Torres F, Mischna M et al (2014) Preliminary interpretation of the REMS pressure data from the first 100 sols of the MSL mission. J Geophys Res 119(3):440–453. https://doi.org/10.1002/2013JE004488
Hassler DM, Zeitlin C, Wimmer-Schweingruber RF, Böttcher SI, Martin C, Andrews J, Böhm E, Brinza D, Bullock M, Burmeister S et al (2012) The Radiation Assessment Detector (RAD) investigation. Space Sci Rev 170(1):503–558. https://doi.org/10.1007/s11214-012-9913-1
Hassler DM, Zeitlin C, Wimmer-Schweingruber RF, Ehresmann B, Rafkin S, Eigenbrode JL, Brinza DE, Weigle G, Böttcher SI, Böhm E et al (2014) Mars’s surface radiation environment measured with the Mars Science Laboratory’s Curiosity Rover. Science 343(6169):1244797. https://doi.org/10.1126/science.1244797
Hassler DM, Norbury JW, Reitz G (2017) Mars Science Laboratory Radiation Assessment Detector (MSL/RAD) modeling workshop proceedings. Life Sci Space Res 14:1–2. https://doi.org/10.1016/j.lssr.2017.06.004
Hassler D, Zeitlin C, Ehresmann B, Wimmer-Schweingruber RF, Guo J, Matthiä D, Rafkin S, Berger T, Reitz G (2018) Space weather on the surface of Mars: impact of the September 2017 events. Space Weather 16(11):1702–1708. https://doi.org/10.1029/2018SW001959
Heinemann SG, Temmer M, Hofmeister SJ, Veronig AM, Vennerstrøm S (2018) Three-phase evolution of a coronal hole. I. 360\(^{\circ }\) Remote sensing and in situ observations. Astrophys J 861:151. https://doi.org/10.3847/1538-4357/aac897. arXiv:1806.09495 [astro-ph.SR]
Hoffman J, Fisher P, Batishchev O (2005) Use of superconducting magnet technology for astronaut radiation protection. Technical report, NIAC. Final Report for NIAC Phase I Contract CP 04-01
Hohmann W (1994) Die Erreichbarkeit der Himmelskörper. Untersuchungen über das Raumfahrtproblem. Oldenbourg, München. https://doi.org/10.1515/9783486751406
Honig T, Witasse OG, Evans H, Nieminen P, Kuulkers E, Taylor MG, Heber B, Guo J, Sánchez-Cano B (2019) Multi-point galactic cosmic ray measurements between 1 and 4.5 AU over a full solar cycle. Ann Geophys. https://doi.org/10.5194/angeo-37-903-2019
Horvath DG, Andrews-Hanna JC (2017) Reconstructing the past climate at Gale Crater, Mars, from hydrological modeling of late-stage lakes. Geophys Res Lett 44(16):8196–8204. https://doi.org/10.1002/2017GL074654
Hu S, Kim MHY, McClellan GE, Cucinotta FA (2009) Modeling the acute health effects of astronauts from exposure to large solar particle events. Health Phys 96(4):465–476. https://doi.org/10.1097/01.HP.0000339020.92837.61
Huang H, Guo J, Wang Z, Lin H, Zheng J, Cui J, Xu X, Wang Y, Feng X, Wei Y, Wan W (2019) Properties of stream interactions and their associated shocks near 1.52 au: MAVEN Observations. Astrophys J 879(2):118. https://doi.org/10.3847/1538-4357/ab25e9
Iancu OD, Boutros SW, Olsen RH, Davis MJ, Stewart B, Eiwaz M, Marzulla T, Belknap J, Fallgren CM, Edmondson EF et al (2018) Space radiation alters genotype-phenotype correlations in fear learning and memory tests. Front Genet 9:404. https://doi.org/10.3389/fgene.2018.00404
ICRP (1992) Recommendations of the International Commission on Radiological Protection (ICRP) 1990. Eur J Nucl Med 19(2):77–79. https://doi.org/10.1007/BF00184120
ICRP (1996) ICRP Publication 74, conversion coefficients for use in radiological protection against external radiation. Ann ICRP 26(3/4):1–205
ICRP (2007) The ICRP 2007 recommendations. Radiat Protect Dosim 127(1–4):2–7. https://doi.org/10.1093/rpd/ncm246
ICRP (2010) Conversion coefficients for radiological protection quantities for external radiation exposures. Ann ICRP 40(2–5):1–257. https://doi.org/10.1016/j.icrp.2011.10.001
ICRP (2012) ICRP publication 118: ICRP statement on tissue reactions and early and late effects of radiation in normal tissues and organs—threshold doses for tissue reactions in a radiation protection context. Ann ICRP 41(1–2):1–322. https://doi.org/10.1016/j.icrp.2012.02.001
ICRP (2013) ICRP publication 123: assessment of radiation exposure of astronauts in space. Ann ICRP 42(4):1–339. https://doi.org/10.1016/j.icrp.2013.05.004
Janvier M, Winslow RM, Good S, Bonhomme E, Démoulin P, Dasso S, Möstl C, Lugaz N, Amerstorfer T, Soubrié E, Boakes PD (2019) Generic magnetic field intensity profiles of interplanetary coronal mass ejections at Mercury, Venus, and Earth from superposed epoch analyses. J Geophys Res 124(2):812–836. https://doi.org/10.1029/2018JA025949. arXiv:1901.09921 [physics.space-ph]
Kallenrode M (2003) Current views on impulsive and gradual solar energetic particle events. J Phys G 29(5):965. https://doi.org/10.1088/0954-3899/29/5/316
Keating A, Mohammadzadeh A, Nieminen P, Maia D, Coutinho S, Evans H, Pimenta M, Huot JP, Daly E (2005) A model for Mars radiation environment characterization. IEEE Trans Nucl Sci 52(6):2287–2293. https://doi.org/10.1109/TNS.2005.860748
Kennedy AR (2014) Biological effects of space radiation and development of effective countermeasures. Life Sci Space Res 1:10–43. https://doi.org/10.1016/j.lssr.2014.02.004
Khaksarighiri S, Guo J, Wimmer-Schweingruber R, Narici L (2021) An easy-to-use function to assess deep space radiation in human brains. Sci Rep 11(1):1–12. https://doi.org/10.1038/s41598-021-90695-5
Kim MHY, Thibeault SA, Simonsen LC, Wilson JW (1998) Comparison of Martian meteorites and Martian regolith as shield materials for galactic cosmic rays. Technical Report. TP-1998-208724, NASA. https://ntrs.nasa.gov/citations/19980237030
Kim MHY, Cucinotta FA, Nounu HN, Zeitlin C, Hassler DM, Rafkin SCR, Wimmer-Schweingruber RF, Ehresmann B, Brinza DE, Böttcher S, Böhm E, Burmeister S, Guo J, Köhler J, Martin C, Reitz G, Posner A, Gómez-Elvira J, Harri AM, The MSL Science Team (2014) Comparison of Martian surface ionizing radiation measurements from MSL-RAD with Badhwar–O’Neill 2011/HZETRN model calculations. J Geophys Res 119(6):1311–1321. https://doi.org/10.1002/2013JE004549
Köhler J, Ehresmann B, Martin C, Böhm E, Kharytonov A, Kortmann O, Zeitlin C, Hassler D, Wimmer-Schweingruber RF (2011) Inversion of neutron/gamma spectra from scintillator measurements. Nucl Instrum Methods Phys Res Sect B 269(22):2641–2648. https://doi.org/10.1016/j.nimb.2011.07.021
Köhler J, Zeitlin C, Ehresmann B, Wimmer-Schweingruber RF, Hassler D, Reitz G, Brinza D, Weigle G, Appel J, Böttcher S et al (2014) Measurements of the neutron spectrum on the Martian surface with MSL/RAD. J Geophys Res 119(3):594–603. https://doi.org/10.1002/2013JE004539
Krittinatham W, Ruffolo D (2009) Drift orbits of energetic particles in an interplanetary magnetic flux rope. Astrophys J 704(1):831–841. https://doi.org/10.1088/0004-637X/704/1/831
Kühl P, Heber B (2019) Revising more than 20 years of EPHIN ion flux data—a new data product for space weather applications. Space Weather 17(1):84–98. https://doi.org/10.1029/2018SW002114
Laitinen T, Kopp A, Effenberger F, Dalla S, Marsh M (2016) Solar energetic particle access to distant longitudes through turbulent field-line meandering. Astron Astrophys 591:A18. https://doi.org/10.1051/0004-6361/201527801
Lario D, Aran A, Gómez-Herrero R, Dresing N, Heber B, Ho G, Decker R, Roelof E (2013) Longitudinal and radial dependence of solar energetic particle peak intensities: STEREO, ACE, SOHO, GOES, and MESSENGER observations. Astrophys J 767(1):41. https://doi.org/10.1088/0004-637X/767/1/41
Lario D, Kwon RY, Richardson IG, Raouafi NE, Thompson B, Von Rosenvinge TT, Mays ML, Mäkelä PA, Xie H, Bain H et al (2017) The solar energetic particle event of 2010 August 14: connectivity with the solar source inferred from multiple spacecraft observations and modeling. Astrophys J 838(1):51. https://doi.org/10.3847/1538-4357/aa63e4
Lee C, Hara T, Halekas J, Thiemann E, Chamberlin P, Eparvier F, Lillis R, Larson D, Dunn P, Espley J et al (2017) MAVEN observations of the solar cycle 24 space weather conditions at Mars. J Geophys Res 122(3):2768–2794. https://doi.org/10.1002/2016JA023495
Lee CO, Jakosky BM, Luhmann JG, Brain DA, Mays ML, Hassler DM, Holmström M, Larson DE, Mitchell DL, Mazelle C, Halekas JS (2018) Observations and impacts of the 10 September 2017 solar events at Mars: an overview and synthesis of the initial results. Geophys Res Lett 45(17):8871–8885. https://doi.org/10.1029/2018GL079162
Léveillé RJ, Datta S (2010) Lava tubes and basaltic caves as astrobiological targets on Earth and Mars: a review. Planet Space Sci 58(4):592–598. https://doi.org/10.1016/j.pss.2009.06.004
Li G (2017) Particle acceleration and transport in the inner heliosphere. Sci China Earth Sci 60(8):1440–1465. https://doi.org/10.1007/s11430-017-9083-y
Lingri D, Mavromichalaki H, Belov A, Eroshenko E, Yanke V, Abunin A, Abunina M (2016) Solar activity parameters and associated Forbush decreases during the minimum between cycles 23 and 24 and the ascending phase of cycle 24. Sol Phys 291(3):1025–1041. https://doi.org/10.1007/s11207-016-0863-8
Lockwood JA (1971) Forbush decreases in the cosmic radiation. Space Sci Rev 12(5):658–715. https://doi.org/10.1007/BF00173346
Loucas BD, Cornforth MN (2013) The LET dependence of unrepaired chromosome damage in human cells: a break too far? Radiat Res 179(4):393–405. https://doi.org/10.1667/RR3159.2
Luhmann J, Mays M, Odstrcil D, Li Y, Bain H, Lee C, Galvin A, Mewaldt R, Cohen C, Leske R et al (2017) Modeling solar energetic particle events using ENLIL heliosphere simulations. Space Weather 15(7):934–954. https://doi.org/10.1002/2017SW001617
Makovsky A, Ilott P, Taylor J (2009) Mars Science Laboratory telecommunications system design. Design and performance summary series, vol 14. DESCANSO/JPL, Pasadena. https://descanso.jpl.nasa.gov/DPSummary/summary.html
Manchester IWB, Gombosi TI, De Zeeuw DL, Sokolov IV, Roussev II, Powell KG, Kóta J, Tóth G, Zurbuchen TH (2005) Coronal mass ejection shock and sheath structures relevant to particle acceleration. Astrophys J 622(2):1225–1239. https://doi.org/10.1086/427768
Marsh M, Dalla S, Kelly J, Laitinen T (2013) Drift-induced perpendicular transport of solar energetic particles. Astrophys J 774(1):4. https://doi.org/10.1088/0004-637X/774/1/4
Matthiä D, Ehresmann B, Lohf H, Köhler J, Zeitlin C, Appel J, Sato T, Slaba T, Martin C, Berger T et al (2016) The Martian surface radiation environment—a comparison of models and MSL/RAD measurements. J Space Weather Space Clim 6(27):1–17. https://doi.org/10.1051/swsc/2016008
Matthiä D, Hassler DM, de Wet W, Ehresmann B, Firan A, Flores-McLaughlin J, Guo J, Heilbronn LH, Lee K, Ratliff H, Rios RR, Slaba TC, Smith M, Stoffle NN, Townsend LW, Berger T, Reitz G, Wimmer-Schweingruber RF, Zeitlin C (2017) The radiation environment on the surface of Mars—summary of model calculations and comparison to RAD data. Life Sci Space Res 14:18–28. https://doi.org/10.1016/j.lssr.2017.06.003
McKenna-Lawlor S, Gonçalves P, Keating A, Morgado B, Heynderickx D, Nieminen P, Santin G, Truscott P, Lei F, Foing B et al (2012) Characterization of the particle radiation environment at three potential landing sites on Mars using ESA’s MEREM models. Icarus 218(1):723–734. https://doi.org/10.1016/j.icarus.2011.04.004
Melkumyan AA, Belov AV, Abunina MA, Abunin AA, Eroshenko EA, Yanke VG, Oleneva VA (2019) Comparison between statistical properties of Forbush decreases caused by solar wind disturbances from coronal mass ejections and coronal holes. Adv Space Res 63(2):1100–1109. https://doi.org/10.1016/j.asr.2018.10.009
Moreno-Villanueva M, Wong M, Lu T, Zhang Y, Wu H (2017) Interplay of space radiation and microgravity in DNA damage and DNA damage response. npj Microgravity 3(1):1–8. https://doi.org/10.1038/s41526-017-0019-7
Morris M, Jones T (1988) A comparison of dose–response models for death from hematological depression in different species. Int J Radiat Biol 53(3):439–456
Müller D, Marsden RG, St Cyr OC, Gilbert HR, The Solar Orbiter Team (2013) Solar Orbiter. Sol Phys 285(1):25–70. https://doi.org/10.1007/s11207-012-0085-7
Müller-Mellin R, Kunow H, Fleißner V, Pehlke E, Rode E, Röschmann N, Scharmberg C, Sierks H, Rusznyak P, McKenna-Lawlor S et al (1995) COSTEP-comprehensive suprathermal and energetic particle analyser. Sol Phys 162:483–504. https://doi.org/10.1007/978-94-009-0191-9_13
NASA (2014) Space flight human-system standard, volume 1, revision A: crew health. Technical Report. NASA-STD-3001 VOL 1, NASA. https://standards.nasa.gov/standard/nasa/nasa-std-3001-vol-1
NCRP (1988) Guidance on radiation received in space activities. Technical Report, No. 98, National Council on Radiation Protection and Measurements
NCRP (2000) Recommendations of dose limits for low Earth orbit. Technical Report. NCRP Report 132, National Council on Radiation Protection and Measurements
Norman RB, Gronoff G, Mertens CJ (2014) Influence of dust loading on atmospheric ionizing radiation on Mars. J Geophys Res 119(1):452–461. https://doi.org/10.1002/2013JA019351
NRC (2018) §20.1004 Units of radiation dose. In: Code of Federal Regulations: NRC Regulations Title 10. GPO, Washington, DC. https://www.nrc.gov/reading-rm/doc-collections/cfr/part020/part020-1004.html
Nymmik R (2015) Database of Solar Energetic Particles (SEP) fluences, measured from August 1997 till 2006. http://smdc.sinp.msu.ru/index.py?nav=model-sep
O’Neill PM (2010) Badhwar–O’Neill 2010 galactic cosmic ray flux model-revised. IEEE Trans Nucl Sci 6(57):3148–3153. https://doi.org/10.1109/TNS.2010.2083688
Owen T, Biemann K, Rushneck D, Biller J, Howarth D, Lafleur A (1977) The composition of the atmosphere at the surface of Mars. J Geophys Res 82(28):4635–4639. https://doi.org/10.1029/JS082i028p04635
Paesold G, Kallenbach R, Benz A (2003) Acceleration and enrichment of \(^{3}\)He in impulsive solar flares by electron firehose waves. Astrophys J 582(1):495. https://doi.org/10.1086/344593
Palmerio E, Kilpua EK, Witasse O, Barnes D, Sánchez-Cano B, Weiss AJ, Nieves-Chinchilla T, Möstl C, Jian LK, Mierla M et al (2021) CME magnetic structure and IMF preconditioning affecting SEP transport. Space Weather 19(4):e2020SW002654. https://doi.org/10.1029/2020SW002654
Papaioannou A, Belov A, Abunina M, Guo J, Anastasiadis A, Wimmer-Schweingruber RF, Eroshenko E, Melkumyan A, Abunin A, Heber B et al (2019) A catalogue of Forbush decreases recorded on the surface of Mars from 2012 until 2016: comparison with terrestrial FDs. Sol Phys 294(6):66. https://doi.org/10.1007/s11207-019-1454-2
Parihar VK, Allen B, Tran KK, Macaraeg TG, Chu EM, Kwok SF, Chmielewski NN, Craver BM, Baulch JE, Acharya MM et al (2015) What happens to your brain on the way to Mars. Sci Adv 1(4):e1400256. https://doi.org/10.1126/sciadv.1400256
Parihar VK, Allen BD, Caressi C, Kwok S, Chu E, Tran KK, Chmielewski NN, Giedzinski E, Acharya MM, Britten RA, Baulch JE, Limoli CL (2016) Cosmic radiation exposure and persistent cognitive dysfunction. Sci Rep 6:34774. https://doi.org/10.1038/srep34774
Parker EN (1965) The passage of energetic charged particles through interplanetary space. Planet Space Sci 13:9–49. https://doi.org/10.1016/0032-0633(65)90131-5
Pierce DA, Shimizu Y, Preston DL, Vaeth M, Mabuchi K (1996) Studies of the mortality of atomic bomb survivors report. 12, Part I. Cancer: 1950–1990. Radiat Res 146(1):1–27. https://doi.org/10.2307/3579391
Posner A (2007) Up to 1-hour forecasting of radiation hazards from solar energetic ion events with relativistic electrons. Space Weather. https://doi.org/10.1029/2006SW000268
Posner A, Strauss R (2020) Warning time analysis from SEP simulations of a two-tier REleASE system applied to Mars exploration. Space Weather 18(4):e2019SW002354. https://doi.org/10.1029/2019SW002354
Posner A, Odstrĉil D, MacNeice P, Rastaetter L, Zeitlin C, Heber B, Elliott H, Frahm R, Hayes J, von Rosenvinge T et al (2013) The Hohmann–Parker effect measured by the Mars Science Laboratory on the transfer from Earth to Mars: consequences and opportunities. Planet Space Sci 89:127–139. https://doi.org/10.1016/j.pss.2013.09.013
Preston DL, Shimizu Y, Pierce DA, Suyama A, Mabuchi K (2003) Studies of mortality of atomic bomb survivors Report 13: solid cancer and noncancer disease mortality: 1950–1997. Radiat Res 160(4):381–407. https://doi.org/10.1667/RR3049
Quinn PR, Schwadron NA, Townsend LW, Wimmer-Schweingruber RF, Case AW, Spence HE, Wilson JK, Joyce CJ (2017) Modeling the effectiveness of shielding in the Earth–Moon–Mars radiation environment using PREDICCS: five solar events in 2012. J Space Weather Space Clim 7:A16. https://doi.org/10.1051/swsc/2017014
Rafkin SC, Zeitlin C, Ehresmann B, Hassler D, Guo J, Köhler J, Wimmer-Schweingruber R, Gomez-Elvira J, Harri AM, Kahanpää H et al (2014) Diurnal variations of energetic particle radiation at the surface of Mars as observed by the Mars Science Laboratory Radiation Assessment Detector. J Geophys Res 119:1345–1358. https://doi.org/10.1002/2013JE004525
Rastegar Z, Eckart P, Mertz M (2002) Radiation-induced cataract in astronauts and cosmonauts. Graefes Arch Clin Exp Ophthalmol 240(7):543–547. https://doi.org/10.1007/s00417-002-0489-4
Reames DV (2013) The two sources of solar energetic particles. Space Sci Rev 175(1):53–92. https://doi.org/10.1007/s11214-013-9958-9
Richardson IG (2004) Energetic particles and corotating interaction regions in the solar wind. Space Sci Rev 111:267–376. https://doi.org/10.1023/B:SPAC.0000032689.52830.3e
Richardson I, von Rosenvinge T, Cane H, Christian E, Cohen C, Labrador A, Leske R, Mewaldt R, Wiedenbeck M, Stone E (2014) > 25 MeV proton events observed by the high energy telescopes on the STEREO A and B spacecraft and/or at Earth during the first seven years of the STEREO mission. Sol Phys 289(8):3059–3107. https://doi.org/10.1007/978-1-4939-2038-9_27
Röstel L, Guo J, Banjac S, Wimmer-Schweingruber RF, Heber B (2020) Subsurface radiation environment of Mars and its implication for shielding protection of future habitats. J Geophys Res Planets 125(3):e2019JE006246. https://doi.org/10.1029/2019JE006246
Roth I, Temerin M (1997) Enrichment of \(^{3}\)He and heavy ions in impulsive solar flares. Astrophys J 477(2):940. https://doi.org/10.1086/303731
Rouillard AP, Plotnikov I, Pinto RF, Tirole M, Lavarra M, Zucca P, Vainio R, Tylka AJ, Vourlidas A, De Rosa ML, Linker J, Warmuth A, Mann G, Cohen CMS, Mewaldt RA (2016) Deriving the properties of coronal pressure fronts in 3D: application to the 2012 May 17 ground level enhancement. Astrophys J Lett 833:45. https://doi.org/10.3847/1538-4357/833/1/45. arXiv:1605.05208 [astro-ph.SR]
Roussos E, Dialynas K, Krupp N, Kollmann P, Paranicas C, Roelof EC, Yuan C, Mitchell DG, Krimigis SM (2020) Long- and short-term variability of galactic cosmic-ray radial intensity gradients between 1 and 9.5 au: observations by Cassini, BESS, BESS-Polar, PAMELA, and AMS-02. Astrophys J 904(2):165. https://doi.org/10.3847/1538-4357/abc346
Saganti PB, Cucinotta FA, Wilson JW, Simonsen LC, Zeitlin C (2004) Radiation climate map for analyzing risks to astronauts on the Mars surface from galactic cosmic rays. Space Sci Rev 110(1–2):143–156. https://doi.org/10.1007/978-0-306-48600-5_5
Sánchez-Cano B, Lester M, Andrews DJ, Opgenoorth H, Lillis R, Leblanc F, Fowler CM, Fang X, Vaisberg O, Mayyasi M, Holmberg M, Guo J, Hamrin M, Mazelle C, Peter K, Pätzold M, Stergiopoulou K, Goetz C, Ermakov VN, Shuvalov S, Wild J, Blelly PL, Mendillo M, Bertucci C, Cartacci M, Orosei R, Chu F, Kopf AJ, Girazian ZR, Roman MT (2019) Mars’ plasma system. Scientific potential of coordinated multi-point missions: “The next generation” (A White Paper submitted to ESA’s Voyage 2050 Call). arXiv e-prints arXiv:1908.05497 [physics.space-ph]
Sanzari JK, Wilson JM, Wagner EB, Kennedy AR (2011) The combined effects of reduced weightbearing and ionizing radiation on splenic lymphocyte population and function. Int J Radiat Biol 87(10):1033–1038. https://doi.org/10.3109/09553002.2011.595875
Sato T, Niita K, Matsuda N, Hashimoto S, Iwamoto Y, Noda S, Ogawa T, Iwase H, Nakashima H, Fukahori T et al (2013) Particle and heavy ion transport code system, PHITS, version 2.52. J Nucl Sci Technol 50(9):913–923. https://doi.org/10.1080/00223131.2013.814553
Schwadron N, Townsend L, Kozarev K, Dayeh M, Cucinotta F, Desai M, Golightly M, Hassler D, Hatcher R, Kim MY et al (2010) Earth–Moon–Mars radiation environment module framework. Space Weather. https://doi.org/10.1029/2009SW000523
Schwadron NA, Baker T, Blake B, Case AW, Cooper JF, Golightly M, Jordan A, Joyce C, Kasper J, Kozarev K, Mislinski J, Mazur J, Posner A, Rother O, Smith S, Spence HE, Townsend LW, Wilson J, Zeitlin C (2012) Lunar radiation environment and space weathering from the Cosmic Ray Telescope for the Effects of Radiation (CRaTER). J Geophys Res 117(E12):E00H13. https://doi.org/10.1029/2011JE003978
Semkova J, Koleva R, Benghin V, Dachev T, Matviichuk Y, Tomov B, Krastev K, Maltchev S, Dimitrov P, Mitrofanov I, Malahov A, Golovin D, Mokrousov M, Sanin A, Litvak M, Kozyrev A, Tretyakov V, Nikiforov S, Vostrukhin A, Fedosov F, Grebennikova N, Zelenyi L, Shurshakov V, Drobishev S (2018) Charged particles radiation measurements with Liulin-MO dosimeter of FREND instrument aboard ExoMars Trace Gas Orbiter during the transit and in high elliptic Mars orbit. Icarus 303:53–66. https://doi.org/10.1016/j.icarus.2017.12.034
Simonsen L, Nealy J, Townsend L, Wilson J (1990) Radiation exposure for manned Mars surface missions. Technical Report. 2979, NASA. https://ntrs.nasa.gov/citations/19900009041
Simonsen LC, Slaba TC, Guida P, Rusek A (2020) NASA’s first ground-based Galactic Cosmic Ray Simulator: enabling a new era in space radiobiology research. PLoS Biol 18(5):e3000669e3000669. https://doi.org/10.1371/journal.pbio.3000669
Simpson J (1983) Elemental and isotopic composition of the galactic cosmic rays. Annu Rev Nucl Part Sci 33(1):323–382. https://doi.org/10.1146/annurev.ns.33.120183.001543
Singleterry RC Jr, Blattnig SR, Clowdsley MS, Qualls GD, Sandridge CA, Simonsen LC, Slaba TC, Walker SA, Badavi FF, Spangler JL et al (2011) OLTARIS: on-line tool for the assessment of radiation in space. Acta Astronaut 68(7):1086–1097. https://doi.org/10.1016/j.actaastro.2010.09.022
Slaba TC, Blattnig SR, Norbury JW, Rusek A, La Tessa C, Walker SA (2015) GCR simulator reference field and a spectral approach for laboratory simulation. Technical Report. TP-2015-218698, NASA. https://ntrs.nasa.gov/citations/20150003791
Slaba TC, Wilson JW, Badavi FF, Reddell BD, Bahadori AA (2016) Solar proton exposure of an ICRU sphere within a complex structure part II: ray-trace geometry. Life Sci Space Res 9:77–83. https://doi.org/10.1016/j.lssr.2016.05.001
Smith EJ, Wolfe JH (1976) Observations of interaction regions and corotating shocks between one and five AU: pioneers 10 and 11. Geophys Res Lett 3(3):137–140. https://doi.org/10.1029/GL003i003p00137
Sokolova IV, Schneider CJ, Bezaire M, Soltesz I, Vlkolinsky R, Nelson GA (2015) Proton radiation alters intrinsic and synaptic properties of CA1 pyramidal neurons of the mouse hippocampus. Radiat Res 183(2):208–218. https://doi.org/10.1667/RR13785.1
Soucy KG, Lim HK, Kim JH, Oh Y, Attarzadeh DO, Sevinc B, Kuo MM, Shoukas AA, Vazquez ME, Berkowitz DE (2011) HZE \(^{56}\)Fe-ion irradiation induces endothelial dysfunction in rat aorta: role of xanthine oxidase. Radiat Res 176(4):474–485. https://doi.org/10.1667/RR2598.1
Starr SO, Muscatello AC (2020) Mars in situ resource utilization: a review. Planet Space Sci 182:104824. https://doi.org/10.1016/j.pss.2019.104824
Straume T (2015) Medical concerns with space radiation and radiobiological effects. In: Pelton JN, Allahdadi F (eds) Handbook of cosmic hazards and planetary defense. Springer, Cham, pp 259–293. https://doi.org/10.1007/978-3-319-03952-7_4
Tang S, Wang Y, Zhao H, Fang F, Qian Y, Zhang Y, Yang H, Li C, Fu Q, Kong J et al (2020) Calibration of Mars energetic particle analyzer (MEPA). Earth Planet Phys 4(4):355–363. https://doi.org/10.26464/epp2020055
Tillman JE (1988) Mars global atmospheric oscillations: annually synchronized, transient normal-mode oscillations and the triggering of global dust storms. J Geophys Res 93(D8):9433–9451. https://doi.org/10.1029/JD093iD08p09433
Townsend LW, Wilson JW, Shinn JL, Nealy JE, Simonsen LC (1990) Radiation protection effectiveness of a proposed magnetic shielding concept for manned Mars missions. SAE Transact 99:965–971. https://doi.org/10.4271/901343
Townsend LW, Stephens DL, Hoff J, Zapp E, Moussa H, Miller T, Campbell C, Nichols T (2006) The Carrington event: possible doses to crews in space from a comparable event. Adv Space Res 38(2):226–231. https://doi.org/10.1016/j.asr.2005.01.111
Townsend L, PourArsalan M, Hall M, Anderson J, Bhatt S, DeLauder N, Adamczyk A (2011) Estimates of Carrington-class solar particle event radiation exposures on Mars. Acta Astronaut 69(7):397–405. https://doi.org/10.1016/j.actaastro.2011.05.020
Usoskin I, Alanko K, Mursula K, Kovaltsov G (2002) Heliospheric modulation strength during the neutron monitor era. Sol Phys 207(2):389–399. https://doi.org/10.1023/A:1016266801300
Usoskin I, Alanko-Huotari K, Kovaltsov G, Mursula K (2005) Heliospheric modulation of cosmic rays: monthly reconstruction for 1951–2004. J Geophys Res 110:A12108. https://doi.org/10.1029/2005JA011250
Usoskin I, Braun I, Gladysheva O, Hörandel J, Jämsén T, Kovaltsov G, Starodubtsev S (2008) Forbush decreases of cosmic rays: energy dependence of the recovery phase. J Geophys Res 113(A7):A07102. https://doi.org/10.1029/2007JA012955
Usoskin IG, Gil A, Kovaltsov GA, Mishev AL, Mikhailov VV (2017) Heliospheric modulation of cosmic rays during the neutron monitor era: calibration using PAMELA data for 2006–2010. J Geophys Res 122(4):3875–3887. https://doi.org/10.1002/2016JA023819
Veronig AM, Podladchikova T, Dissauer K, Temmer M, Seaton DB, Long D, Guo J, Vršnak B, Harra L, Kliem B (2018) Genesis and impulsive evolution of the 2017 September 10 coronal mass ejection. Astrophys J 868(2):107. https://doi.org/10.3847/1538-4357/aaeac5
Vilmer N, MacKinnon AL, Hurford GJ (2011) Properties of energetic ions in the solar atmosphere from \(\gamma \)-ray and neutron observations. Space Sci Rev 159(1–4):167. https://doi.org/10.1007/s11214-010-9728-x
von Braun W (1969) Will mighty magnets protect voyagers to planets? Popul Sci 198:98100
Vršnak B, Žic T, Vrbanec D, Temmer M, Rollett T, Möstl C, Veronig A, Čalogović J, Dumbović M, Lulić S, Moon YJ, Shanmugaraju A (2013) Propagation of interplanetary coronal mass ejections: the drag-based model. Sol Phys 285(1):295–315. https://doi.org/10.1007/s11207-012-0035-4
Vuolo M, Giraudo M, Musenich R, Calvelli V, Ambroglini F, Burger W, Battiston R (2016) Monte Carlo simulations for the space radiation superconducting shield project (SR2S). Life Sci Space Res 8:22–29. https://doi.org/10.1016/j.lssr.2015.12.003
Vuolo M, Baiocco G, Barbieri S, Bocchini L, Giraudo M, Gheysens T, Lobascio C, Ottolenghi A (2017) Exploring innovative radiation shielding approaches in space: a material and design study for a wearable radiation protection spacesuit. Life Sci Space Res 15:69–78. https://doi.org/10.1016/j.lssr.2017.08.003
Walsh L, Schneider U, Fogtman A, Kausch C, McKenna-Lawlor S, Narici L, Ngo-Anh J, Reitz G, Sabatier L, Santin G, Sihver L, Straube U, Weber U, Durante M (2019) Research plans in Europe for radiation health hazard assessment in exploratory space missions. Life Sci Space Res 21:73–82. https://doi.org/10.1016/J.LSSR.2019.04.002
Wang Y, Shen C, Liu R, Liu J, Guo J, Li X, Xu M, Hu Q, Zhang T (2018) Understanding the twist distribution inside magnetic flux ropes by anatomizing an interplanetary magnetic cloud. J Geophys Res 123(5):3238–3261. https://doi.org/10.1002/2017JA024971. arXiv:1803.01353 [astro-ph.SR]
Werner CJ et al (2017) MCNP users manual-code version 6.2. Technical Report. LA-UR-17-29981, Los Alamos National Laboratory. https://mcnp.lanl.gov/mcnp_manual.shtml
Wibberenz G, le Roux J, Potgieter M, Bieber J (1998) Transient effects and disturbed conditions. Space Sci Rev 83(1):309–348. https://doi.org/10.1023/A:1005083109827
Williams JP, Brown SL, Georges GE, Hauer-Jensen M, Hill RP, Huser AK, Kirsch DG, MacVittie TJ, Mason KA, Medhora MM et al (2010) Animal models for medical countermeasures to radiation exposure. Radiat Res 173(4):557–578. https://doi.org/10.1667/RR1880.1
Williams RM, Grotzinger JP, Dietrich W, Gupta S, Sumner D, Wiens R, Mangold N, Malin M, Edgett K, Maurice S et al (2013) Martian fluvial conglomerates at Gale Crater. Science 340(6136):1068–1072. https://doi.org/10.1126/science.1237317
Wilson JW, Badavi FF, Cucinotta FA, Shinn JL, Badhwar GD, Silberberg R, Tsao C, Townsend LW, Tripathi RK et al (1995) HZETRN: description of a free-space ion and nucleon transport and shielding computer program. Technical Report. TP-3495, NASA. https://ntrs.nasa.gov/citations/19950022109
Wilson JW, Miller J, Konradi A, Cucinotta FA (eds) (1997) Shielding strategies for human space exploration. NASA Conference Publication, vol 3360. NASA, Hampton, VA. https://ntrs.nasa.gov/citations/19980137598
Wilson JW, Cucinotta F, Shinn J, Simonsen L, Dubey R, Jordan W, Jones T, Chang C, Kim M (1999) Shielding from solar particle event exposures in deep space. Radiat Meas 30(3):361–382. https://doi.org/10.1016/S1350-4487(99)00063-3
Wilson JW, Anderson BM, Cucinotta FA, Ware J, Zeitlin CJ (2006) Spacesuit radiation shield design methods. SAE Transact 115:277–293. https://doi.org/10.4271/2006-01-2110
Wilson JW, Slaba TC, Badavi FF, Reddell BD, Bahadori AA (2016) Solar proton exposure of an ICRU sphere within a complex structure: combinatorial geometry. Life Sci Space Res 9:69–76. https://doi.org/10.1016/j.lssr.2016.05.002
Wimmer-Schweingruber RF, Köhler J, Hassler DM, Guo J, Appel JK, Zeitlin C, Böhm E, Ehresmann B, Lohf H, Böttcher SI et al (2015) On determining the zenith angle dependence of the Martian radiation environment at Gale Crater altitudes. Geophys Res Lett 42(24):10557–10564. https://doi.org/10.1002/2015GL066664
Winslow RM, Schwadron NA, Lugaz N, Guo J, Joyce CJ, Jordan AP, Wilson JK, Spence HE, Lawrence DJ, Wimmer-Schweingruber RF et al (2018) Opening a window on ICME-driven GCR modulation in the inner solar system. Astrophys J 856(2):139. https://doi.org/10.3847/1538-4357/aab098
Witasse O, Sánchez-Cano B, Mays ML, Kajdič P, Opgenoorth H, Elliott HA, Richardson IG, Zouganelis I, Zender J, Wimmer-Schweingruber RF, Turc L, Taylor MGGT, Roussos E, Rouillard A, Richter I, Richardson JD, Ramstad R, Provan G, Posner A, Plaut JJ, Odstrcil D, Nilsson H, Niemenen P, Milan SE, Mandt K, Lohf H, Lester M, Lebreton JP, Kuulkers E, Krupp N, Koenders C, James MK, Intzekara D, Holmstrom M, Hassler DM, Hall BES, Guo J, Goldstein R, Goetz C, Glassmeier KH, Génot V, Evans H, Espley J, Edberg NJT, Dougherty M, Cowley SWH, Burch J, Behar E, Barabash S, Andrews DJ, Altobelli N (2017) Interplanetary coronal mass ejection observed at STEREO-A, Mars, comet 67P/Churyumov–Gerasimenko, Saturn, and New Horizons en route to Pluto: comparison of its Forbush decreases at 1.4, 3.1, and 9.9 AU. J Geophys Res 122(8):7865–7890. https://doi.org/10.1002/2017JA023884
Wu H, Huff JL, Casey R, Kim MH, Cucinotta FA (2009) Risk of acute radiation syndromes due to solar particle events. In: McPhee JC, Charles JB (eds) Human health and performance risks of space exploration missions. Evidence reviewed by the NASA Human Research Program. NASA Technical Report, vol SP-2009-3405. NASA, pp 171–191. https://humanresearchroadmap.nasa.gov/evidence/
Yatagai F, Honma M, Dohmae N, Ishioka N (2019) Biological effects of space environmental factors: a possible interaction between space radiation and microgravity. Life Sci Space Res 20:113–123. https://doi.org/10.1016/j.lssr.2018.10.004
Yu T, Parks BW, Yu S, Srivastava R, Gupta K, Wu X, Khaled S, Chang PY, Kabarowski JH, Kucik DF (2011) Iron-ion radiation accelerates atherosclerosis in apolipoprotein E-deficient mice. Radiat Res 175(6):766–773. https://doi.org/10.1667/RR2482.1
Zeitlin C, Heilbronn L, Miller J, Rademacher S, Borak T, Carter T, Frankel K, Schimmerling W, Stronach C (1997) Heavy fragment production cross sections from 1.05 GeV/nucleon \(^{56}\)Fe in C, Al, Cu, Pb, and CH\(_2\) targets. Phys Rev C 56(1):388. https://doi.org/10.1103/PhysRevC.56.388
Zeitlin C, Hassler DM, Cucinotta FA, Ehresmann B, Wimmer-Schweingruber RF, Brinza DE, Kang S, Weigle G, Böttcher S, Böhm E, Burmeister S, Guo J, Köhler J, Martin C, Posner A, Rafkin S, Reitz G (2013) Measurements of energetic particle radiation in transit to Mars on the Mars Science Laboratory. Science 340(6136):1080–1084. https://doi.org/10.1126/science.1235989
Zeitlin C, Hassler D, Wimmer-Schweingruber RF, Ehresmann B, Appel J, Berger T, Böhm E, Böttcher S, Brinza D, Burmeister S et al (2016) Calibration and characterization of the Radiation Assessment Detector (RAD) on curiosity. Space Sci Rev 201(1–4):201–233. https://doi.org/10.1007/s11214-016-0303-y
Zeitlin C, Hassler D, Guo J, Ehresmann B, Wimmer-Schweingruber RF, Rafkin S, Freiherr von Forstner J, Lohf H, Berger T, Matthiä D et al (2018) Analysis of the radiation hazard observed by RAD on the surface of Mars during the September 2017 solar particle event. Geophys Res Lett 45(12):5845–5851. https://doi.org/10.1029/2018GL077760
Zeitlin C, Hassler D, Ehresmann B, Rafkin S, Guo J, Wimmer-Schweingruber RF, Berger T, Matthiä D (2019) Measurements of radiation quality factor on Mars with the Mars Science Laboratory Radiation Assessment Detector. Life Sci Space Res 22:89–97. https://doi.org/10.1016/j.lssr.2019.07.010
Zurek RW (1988) Free and forced modes in the Martian atmosphere. J Geophys Res 93(D8):9452–9462. https://doi.org/10.1029/JD093iD08p09452
Acknowledgements
RAD is an instrument supported by NASA (HEOMD) under JPL subcontract 1273039 to SWRI, and in Germany by DLR (under German Space Agency grants 50QM0501, 50QM1201, and 50QM1701) to the Christian-Albrechts-University of Kiel. MSL/RAD and MSL/REMS data are archived in the NASA planetary data systems’ planetary plasma interactions node (http://ppi.pds.nasa.gov/). We acknowledge the sunspot data provided by the World Data Center SILSO, Royal Observatory of Belgium, Brussels (http://www.sidc.be/silso/monthlyssnplot), the NM data provided here http://www.nmdb.eu, the solar modulation potential given by http://cosmicrays.oulu.fi/phi/phi.html, the OMNI dataset accessible here https://omniweb.gsfc.nasa.gov, the EPHIN data maintained here http://ulysses.physik.uni-kiel.de/costep/level3/l3i/, and the MAVEN data downloadable here https://lasp.colorado.edu/maven/sdc/public/. J. G. and Y. W. are supported by the Strategic Priority Program of the Chinese Academy of Sciences (Grant no. XDB41000000), the National Natural Science Foundation of China (Grant no. 42074222) and the CNSA pre-research Project on Civil Aerospace Technologies (Grant no. D020104). We thank Arik Posner, Stephan Böttcher, Eddie Weigle, Lars Seimeiz, Eckart Böhm, Cesar Martin, Henning Lohf, Jan Köhler, Günther Reitz, Daniel Matthiä, Thomas Berger, David Brinza, Joe Peterson, etc. who have contributed to RAD at different times of its development.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guo, J., Zeitlin, C., Wimmer-Schweingruber, R.F. et al. Radiation environment for future human exploration on the surface of Mars: the current understanding based on MSL/RAD dose measurements. Astron Astrophys Rev 29, 8 (2021). https://doi.org/10.1007/s00159-021-00136-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00159-021-00136-5