Common envelope evolution: where we stand and how we can move forward

Abstract

This work aims to present our current best physical understanding of common-envelope evolution (CEE). We highlight areas of consensus and disagreement, and stress ideas which should point the way forward for progress in this important but long-standing and largely unconquered problem. Unusually for CEE-related work, we mostly try to avoid relying on results from population synthesis or observations, in order to avoid potentially being misled by previous misunderstandings. As far as possible we debate all the relevant issues starting from physics alone, all the way from the evolution of the binary system immediately before CEE begins to the processes which might occur just after the ejection of the envelope. In particular, we include extensive discussion about the energy sources and sinks operating in CEE, and hence examine the foundations of the standard energy formalism. Special attention is also given to comparing the results of hydrodynamic simulations from different groups and to discussing the potential effect of initial conditions on the differences in the outcomes. We compare current numerical techniques for the problem of CEE and also whether more appropriate tools could and should be produced (including new formulations of computational hydrodynamics, and attempts to include 3D processes within 1D codes). Finally we explore new ways to link CEE with observations. We compare previous simulations of CEE to the recent outburst from V1309 Sco, and discuss to what extent post-common-envelope binaries and nebulae can provide information, e.g. from binary eccentricities, which is not currently being fully exploited.

Introduction: the importance of common-envelope evolution

Common-envelope evolution (CEE) is the name given to a short-lived phase in the life of a binary star during which two stars orbit inside a single, shared envelope. CEE is believed to be a vital process in the evolution of a large number and wide diversity of binary stars. This almost certainly includes the progenitors of Type Ia supernovae, X-ray binaries and double neutron stars. Hence understanding the outcome of CEE is required in order to understand the production of the most important cosmological standard candles, the nearest known black holes and the most promising stellar-mass gravitational-wave sources.

The reason for the importance of CEE is relatively simple to explain, especially for compact binaries. The stars which produced the compact component of many interesting systems must once have been orders-of-magnitude larger than would fit within the present-day system. CEE is currently accepted as allowing the formation of these systems. The standard reference for CEE is Paczynski (1976). This cites private communication with Ostriker, along with Ron Webbink’s Ph.D. thesis, for the origin of this idea (see also van den Heuvel 1976). After the ejection of the common envelope (CE), the remains of the binary stars can then be left in the tight orbits we observe.

However, once a CE phase begins, envelope ejection is not inevitable. When CEE leads to envelope ejection (and a tighter binary) and when it leads to a merger is one of the questions which we can still not answer from our own theoretical understanding: all we have been able to do with comparative certainty is appeal to the existence of apparently post-CE binaries. Work which discussed the physical situation involved in CEE was published before 1976 (Bisnovatyi-Kogan and Sunyaev 1971; Sparks et al. 1974; Refsdal et al. 1974), and interest in such cases helped to inspire the realization that CEE might be a formation mechanism for close binaries. Nonetheless, today’s theoretical picture of the endpoint of CEE—and the consequent utility of CEE for producing observed systems—is more based on evolutionary necessity than physical calculation. In the absence of a complete physical solution, simplified treatments containing free parameters, have been adopted (see Sect. 1.3 for an introduction to the history of this process, and for details of the recipes see Sects. 3 and 5). The free parameters in these simplified treatments are sometimes tuned to match observations, and sometimes values are assumed in order to make predictions. That is problematic since there is little reason to believe that these parameters should take a global value; the time scales and energy sources and sinks could (and probably do) vary considerably between situations.

In general it is also not sufficient to state that CE must act in a certain way in order to produce the observed systems, since perhaps alternative formation channels are available. For example, population synthesis codes are able to reproduce the observed population of black-hole low-mass X-ray binaries if they set CE ejection efficiencies to high enough values, but the best physical constraints we have seem to preclude the formation of one subset of them (Podsiadlowski et al. 2003, and references therein). Taking this formation restriction seriously, rather than assuming CEE is somehow efficient enough, led to the proposal of new formation mechanisms which might also help explain, e.g., the strange abundances of the donors in these systems (Justham et al. 2006; Chen and Li 2006; Ivanova 2006; Podsiadlowski et al. 2010).

Since CEE remains central to our understanding of the formation of many types of system, it is uncomfortable that in many cases we are still fitting parameters with few physical constraints. CEE is one of the most important unsolved problems in stellar evolution, and is arguably the most significant and least-well-constrained major process in binary evolution (for alternative reviews see Taam and Sandquist 2000; Webbink 2008; Taam and Ricker 2010).

A crucial astrophysical process

Because CEE is important in the formation of a wide variety of systems, a discussion of the astrophysical importance of CEE in the context of compact binaries could easily be lengthy; we will give a very incomplete survey.

As with most astrophysical processes, we cannot wait long enough to watch the formation of many systems by CEE. Nor can we normally infer the precise prior history of individual systems. So in order to make quantitative tests of our formation theories we model entire populations of objects and then compare the properties of those synthesized populations to reality. The tools which allow us to do this are called population synthesis codes. To distinguish this type of population synthesis from those used in other areas of astrophysics, the more specific term binary population synthesis (BPS) is often used. Such calculations turn statistical descriptions of stellar initial conditions—such as the initial mass function (IMF) and binary separation distribution—into predictions for, e.g., the formation rates for different type of stellar exotica, or the expected present-day distribution for the masses and orbital-periods of the type of compact binary under investigation. To do this, BPS simulates the evolution of many different binary systems. Obtaining meaningful results for rare classes of system or event (such as X-ray binaries or type Ia supernovae) may require calculating the evolution of hundreds of millions of individual binary systems; hence BPS codes necessarily include simplified and parametrized descriptions of evolutionary processes such as CEE. Sometimes BPS is used to try to determine which values of CEE parameters best reproduce reality, although the many uncertainties and nonlinearities involved in binary evolution mean that this must be done cautiously. Nonetheless, BPS certainly enables us to see how our poor understanding of CEE converts to uncertainties in predictions, as we now illustrate.

One currently important example is how uncertainties in the outcome of CEE carry through into large uncertainties in theoretical predictions for compact-object merger rates, as have been used to help justify observational facilities such as LIGO. Gravitational-wave observatories clearly have an interest in the expected merger rates of compact objects in the local universe, in order to try to predict the rate of events they should detect. Such mergers, when resulting from primordial binaries, are typically expected to involve at least one CE phase in their production. Some of the merger event rate could also be produced following dynamical interactions in dense stellar systems (e.g. globular clusters).

Taking results from population synthesis calculations, Abadie et al. (2010), quote ‘realistic’ rates for mergers of a NS with a stellar-mass BH which span more than two orders of magnitude (the full range quoted in their Table 7 covers four orders of magnitude). Whilst there are certainly other significant unknowns, almost the full range of uncertainty within the set of rates quoted as realistic can emerge just from altering how one class of systems entering CEE during a particular evolutionary phase is treated (Belczynski et al. 2007), and the potential occurrence of a special case of CEE can produce one of the higher realistic rates (Dewi et al. 2006). The BPS rates for the merger of two stellar-mass BHs quoted in Abadie et al. (2010) are even more uncertain (a range of more than three orders of magnitude for the field-binary models considered realistic), and again changes in just how CEE is treated could encompass most of that range of rates (e.g. for Belczynski et al. 2007, with otherwise identical assumptions, the presence or absence of a single CE channel can affect the BH-BH merger rate by a factor of 500).

Another type of compact-object mergers—of carbon–oxygen white dwarfs (CO WDs)—is potentially also responsible for type Ia supernovae (SN Ia). Indeed, the paper regularly cited for introducing the energy parameterization of CEE (see Sect. 3, Webbink 1984) was aiming to study WD–WD mergers, including them as potential progenitors of SN Ia (see also Iben and Tutukov 1984). If these double-degenerate mergers need to be of roughly Chandrasekhar mass or more in order to lead to an explosion then the individual CO WDs need to be relatively massive. In turn, this suggests that the core evolution of the stars which produced the CO WDs was not truncated very early; hence the initial binary separation needs to have been wide enough to allow at least the primary to evolve into a relatively massive CO WD. At the point when both WDs have been formed, the orbital separation needs to be small enough for gravitational radiation to be able to lead to a merger within the age of the universe. This is another classic case where CEE is required to turn a long-period binary into a short-period one. Figure 1 schematically illustrates potential evolutionary scenarios leading to such a WD–WD merger. There are two distinct possibilities for the character and outcome of the first mass transfer episode. Probably currently physically preferable is that the first mass-transfer episode is stable; in this scenario then such double-degenerate SN Ia progenitors only require one CE phase in their production. However, the dominant formation channel which emerges from many BPS predictions typically involves an unstable first episode of mass transfer followed by CEE. If this second option does dominate then CEE would be involved twice in forming potential double-degenerate SN Ia. In this case then the energy transfer during CEE must be extremely efficient (≳50 %) in order to keep the binary fairly wide after the first CE phase. Hence population synthesis predictions for the rates of such mergers tend to adopt very high CE efficiencies, and tend to be very sensitive to reductions in that efficiency. For example, in the calculations by Ruiter et al. (2011), perfect CE efficiency (specifically $\alpha_{\rm CE} \lambda$=1, for which see Sect. 3) predicts a Chandrasekhar-mass CO WD merger rate just consistent with the empirical SN Ia rate. However, a reduction in overall CE energetic efficiency by a factor of 8 reduces the predicted rate of SN Ia from the CO WD merger channel by more than three orders of magnitude at 100 Myr after the starburst and makes the merger rate almost completely negligible from ≈3 Gyr after the starburst; the overall predicted SN Ia rate here falls far below the observed rate. Unfortunately we cannot firmly state whether the first mass-transfer phase leads to CEE or not, since we lack a sufficiently detailed knowledge of mass transfer stability. However, this specific example has been the subject of considerable debate (see Sect. 5). Understanding the general stability of mass transfer is a problem strongly related to CEE itself and will also be discussed later (Sect. 6).

Fig. 1

Examples of evolutionary channels where CEE plays a crucial role in the formation of the final system. The leftmost column presents a variety of ways to form potential SN Ia progenitors, including double-degenerate mergers and accretion onto a CO WD from a non-degenerate companion. The middle and rightmost columns illustrate the formation of systems containing neutron stars: one route by which a binary millisecond pulsar may form, and one way to produce a double pulsar (formation of which could also involve an additional CE phase before the first SN). Other variations of these channels exist. Abbreviations: ZAMS—zero age main sequence, RLO—Roche-lobe overflow, CE—common envelope, CO WD—carbon-oxygen white dwarf, He—He star, HMXB—high-mass X-ray binary, LMXB—low-mass X-ray binary, MSP—millisecond pulsar, NS—neutron star, SN—supernova

Instead of, or in addition to, WD–WD mergers then SN Ia might be produced by accretion onto a CO WD in single-degenerate systems (see, e.g., Whelan and Iben 1973). These systems also involve CEE in their formation, so an improved understanding of CEE should help us to understand their production. However, the predicted formation rates of SN Ia through single-degenerate progenitors tend to be less strongly dependent on CE efficiency than predictions for the double-degenerate systems. Indeed, in the models of Ruiter et al. (2011) then the calculations which assume a lower CE efficiency lead to an increase in the single-degenerate SN Ia rate at some epochs (see also, e.g., Han and Podsiadlowski 2004, where the highest assumed CE efficiency produces the lowest overall SN Ia rate for each otherwise equivalent set of models). If population calculations are to help determine which channels actually produce SN Ia then tighter physical constraints on CE ejection, along with a better understanding of when mass transfer leads to CEE, would be very helpful. We note in passing that birthrates of particular classes of system are not necessarily monotonically dependent on CE ejection efficiency (see, e.g., Table 2 of Willems et al. 2005).

The formation of both classes of gamma-ray bursts (GRBs) probably also involves CEE. Some GRBs are believed to result from compact object mergers (as above); these are associated with the observed set of short-duration, harder-spectrum bursts. The typically longer-duration observational subclass of GRBs, whose parent populations are strongly linked with recent star formation, are also likely to have CEE in their formation channels (Fryer et al. 1999). These are thought to arise from a special-case of core-collapse in massive stars; it is believed that the cores should be rotating rapidly enough to cause a massive accretion disc to form as the core collapses. In addition, the progenitor star is expected to have lost its envelope, both on theoretical grounds (to enable the jet of the GRB to escape) and on observational grounds (when these GRBs have been linked with a supernova, this supernova has been of a stripped-envelope star, typically a broad-lined type Ic supernova). Stripping the envelope and spinning-up the core can be achieved by several channels involving CEE (for a review of this and of alternative possibilities, see Fryer et al. 2007; also Podsiadlowski et al. 2010). One notable recently observed GRB has been explained using a specific CEE-based model (see Thöne et al. 2011; for the underlying model see, e.g., Fryer and Woosley 1998).

The physics of CEE also has the potential to revolutionize our understanding of the evolution of ‘single’ stars. A star might have its evolution altered by CE-type in-spiral of a planet or brown dwarf. In particular, it has been proposed that planets might eject the envelopes of some red giants (Soker 1998; see also Nelemans and Tauris 1998; Soker and Harpaz 2000; Soker and Hadar 2001; De Marco and Soker 2011). Planet-driven envelope ejection might potentially explain the formation of single low-mass white dwarfs (as proposed by Nelemans and Tauris 1998; see also the discussion and comparison of alternatives in Justham et al. 2010). This possibility is now being driven by observation as well as theory. Maxted et al. (2006) have observed a low-mass white dwarf (≈0.39M _⊙) with a close brown-dwarf (0.053M _⊙) companion (see also, e.g., Setiawan et al. 2010). We should perhaps consider the long-term evolution of every ‘single’ star with planets as effectively that of a binary (or multiple) system with an extreme mass ratio.

An extraordinary physical problem

Despite the importance of CEE, it is essentially unsolved. The situation is extremely challenging for both computation and analytic treatment; from beginning to end the problem involves a complex mix of physical processes operating over a huge range of scales. A relatively common problem would be one in which a neutron star (NS) spirals into the envelope of a giant. Simulations of such a CE event might need to cover a range in time scale of ∼10¹⁰ (i.e. from perhaps 1 s, which is already three orders of magnitude longer than the dynamical time scale of the NS, to ∼1000 yr, the thermal time of the envelope and plausible duration of the CE phase; note that this ignores the duration of the onset of CEE. An interesting range in scale could be ∼10⁸ (i.e. from ≈10 km, the size of the NS, to ≈1000R _⊙), and even more if the details of the accretion onto the NS are important (as it might be; see Sect. 9), or if shocks within the envelope need to be resolved more accurately than this allows. There is no prospect of simulations with anything like a resolution of (10⁸)³ in the relevant future, nor ones which continue for 10¹⁰ time steps. Even for less extreme examples, in which the in-spiralling secondary is not a compact object, comprehensive models are still beyond the reach of our ability. Calculations trying to capture the most important aspects of CEE have been attempted for many years (Taam et al. 1978; Meyer and Meyer-Hofmeister 1979), but even today’s sophisticated simulations necessarily ignore some almost certainly significant physics (see Sects. 7 and 8).

A little history: how we arrived at the current situation

Whilst the physical complexity and numerical demands of CEE still leave us with a very incomplete understanding of how it proceeds, it was recognized early on that very general considerations of energy and angular momentum conservation might provide useful constraints on the outcomes. We note that those early thoughts were not vastly less physically sophisticated than the pictures used today. These fundamental constraints would then enable population synthesis studies. The aim was to model the evolution of an ensemble of hypothetical binaries in order to unravel the evolutionary channels that lead to the wide variety of highly evolved binaries actually observed, and also perhaps to predict families of evolved binaries yet to be discovered or recognized.

The earliest treatment of CEE to be widely employed was one assuming that the energy needed to eject the common envelope was derived entirely from orbital energy dissipation (van den Heuvel 1976). The current rationale for neglecting other possible sources and sinks of energy is discussed below in Sect. 3, although even at the very beginning it was recognized that there were several possible complications. Paczynski (1976) identified frictional drag as driving transfer of both orbital energy (as heat) and angular momentum from the binary orbit to the common envelope, and realized that a combination of angular momentum and energy conservation would drive the envelope expansion. Moreover, Paczynski (1976) also discusses the fact that the expanding envelope could be expected to radiate energy away at an increasing rate, and that the consequences of such effects for the overall scenario are hard to quantify.

In the energy formalism that was adopted, the energy budget for the binary is fixed at the onset of mass transfer and the post-common-envelope system is constrained to have an orbital energy which is negative enough to provide the energy necessary for envelope ejection. In reality, common-envelope ejection cannot be completely efficient (since, for example, the ejecta carry away some terminal kinetic energy), and so an efficiency parameter, $\alpha_{\rm CE}$, was introduced to characterize the fraction of dissipated orbital energy actually used to eject the common envelope (Livio and Soker 1988).

When it comes to quantifying the different terms appearing in the energy budget, elementary orbital mechanics tells us unambiguously that the total orbital energy (potential plus kinetic) of a binary with separation a is $E_{\rm orb} = -Gm_{1} m_{2}/2a$. Evaluation of the envelope binding energy, $E_{\rm bind}$, is a more problematic affair (see Sect. 3). Webbink (1984) introduced a simple parameterization, $E_{\rm bind} = Gm_{1} m_{\rm1,env}/R_{1}$ based on evaluation of the gravitational potential energy plus internal energy of envelopes of a handful of models of giant branch stars he had on hand; ionization/dissociation energy was neglected. Unfortunately, his paper failed to stipulate which energy terms were included or excluded in the approximation for $E_{\rm bind}$, but the simple expression introduced there was clearly intended only to provide an order-of-magnitude estimate of $E_{\rm bind}$.

More realistic evaluation of $E_{\rm bind}$ depends on the detailed structure of the donor envelope. To that end, an additional factor, λ, was introduced (de Kool 1990) to allow for differences in envelope structure:

$$ E_{\rm bind} = G \frac{m_{1} m_{\rm1,env}}{\lambda R_{1}} $$

(1)

As conceived, λ depends on the structure of the donor star, although in practice it is sometimes treated as a free parameter.

The introduction of the λ parameter should have improved matters quantitatively. It would have been desirable to define this factor in the inverse, i.e. $E_{\rm bind} = \lambda Gm_{1} m_{1,\rm env}/R_{1}$, thereby avoiding nasty singularities when $E_{\rm bind}$ changes sign (because of the recombination term), but the convention is now irredeemably established. Unfortunately, when (de Kool 1990) introduced λ, he included only the gravitational term, and this seems to have led to the notion that the internal energy was somehow separable from it. Of course the Virial Theorem tells us that these terms are strongly related, though not necessarily in a simple way. So when (Dewi and Tauris 2001) turned to this issue, they introduced, in addition to $\lambda_{\rm g}$ parameterizing the gravitational potential energy, a second $\lambda_{\rm b}$ to parameterize the sum of gravitational and internal energy, and the issue immediately arose over which, if either, parameterization should be used. Further, as is noted now, the formal values of λ depend strongly on where one places the mass cut for the ejected envelope.

While λ was invented to improve and simplify calculations, particularly for population synthesis, it is now clear that not only is having a fixed value for all possible systems wrong, but it is also still not certain how to calculate λ for any given star, however well-known that star’s structure is. We will return to this in more detail in Sect. 3.

The next formalism to be invented was based on conservation of angular momentum. The historical necessity for this alternative, known as the γ-formalism (Nelemans et al. 2000), was to find at least some explanation for formation of the known double-white dwarf (DWD) binaries. There it seemed that the standard energy formalism failed, as it could only explain the observed systems if energy is generated during CEE, i.e. $\alpha_{\rm CE}>1$. (More precisely stated, an unknown source of energy appeared to be needed to replace the expected role of the orbital energy source, since the orbital energy actually acts as a further energy sink for these systems.) Apparent violation of energy conservation law is rather stressful for a physicist, so a less obviously troublesome conservation law was called upon to help. Again, as no self-consistent numerical simulations could have been performed at the time, the angular momentum budget had to be parametrized and then its free parameter has been fine-tuned using the observations of several known-to-the-date DWD systems. This did not resolve the apparent energy generation problem, only hid it. Nonetheless, it opened a discussion about the possibility to eject an envelope by some other mechanism other than a standard common envelope event. We will consider this formalism in more detail in Sect. 5. Note that the current explanation for the increase of the binary separation during this first mass-transfer phase is that it is quasi-conservative, such that the mass transfer is driven by nuclear energy input and thermal expansion. So there is no longer any apparent need to resort to unexplained energy generation.

In nature, during a real CEE, both fundamental conservation laws must—of course—be obeyed. However, neither of these two simplified formalisms were designed to simultaneously obey both conservation laws. It has to be understood that these approximate methods were invented mainly because of our inability—which continues to the present day—to self-consistently model a complete CEE event. However, after many years of use in population synthesis, the severe limitations of these educated guesses seem to have sometimes been forgotten. These expressions can—all too easily—be used to make apparently predictive statements which may have limited justification.

To summarize, an energy formalism first emerged based on the argument that common-envelope ejection must be a dynamical process. If its duration were as long as a thermal time scale, the input from available energy sources could be lost to radiation, but also other additional energy sources might well play a role. A complete combination of all possible sinks and sources acting on different time scales would lead to a very complex and difficult picture. In this work we will examine the physics underlying CEE, and see to what extent we can hope to move beyond these uncertain simplifications.

This work

This work aims to take a physical approach to the problem of CEE. It considers CEE from first principles, trying not to let preconceptions and potentially misinterpreted observations or population synthesis calculations mislead us. Hence it does not aim to be a comprehensive review of all possible implications of the common envelope problem, but it does hope to build the state-of-the-art in understanding CEE.

Section 2 gives an overview of a notional CE event, dividing it into phases within which different processes are dominant, and also pointing to relevant sections within the remainder of the text. Section 3 then considers at length the overall energy balance within CEE, whilst Sect. 4 considers the situation at the end of the CE phase. Section 5 briefly discusses the application of angular momentum conservation to CEE. In Sect. 6 we look at the conditions which produce and precede CEE. Section 7 then compares the results from different modern hydrodynamic simulations, and Sect. 8 discusses the best present-day simulation tools along with potential future improvements in those methods. Section 9 discusses the possibility of hypercritical accretion. Section 10 considers what we can learn from observations of post-CE systems; there we also compare observations of a recent transient event, which may well have been produced by CEE, to the expectations produced by CEE simulations. The conclusions, Sect. 11, include a list of some promising directions for possible progress.

Main phases

It is convenient to break down the progression of an idealized CE event into several distinct phases, where each phase operates on its own time scale (Podsiadlowski 2001, see also Fig. 2):

Fig. 2

The main potential phases of a CE event prior to the envelope ejection or the merger. This example is for a 1.6M _⊙ red giant and a 0.3M _⊙ WD, using data from one-dimensional hydrodynamical simulations in Ivanova (2002). Not all phases are expected to happen during all CE events. The dashed lines represent locations at fixed mass coordinates, and the dotted line shows the location of the in-spiralling secondary

I: Loss of corotation

During this stage a stable and probably non-eccentric binary, where the rotation of the donor is also likely to be synchronized with the orbit, is transformed into its complete antithesis—a spiralling-in binary.

The start of the spiral-in could be caused by, e.g.:

• 1. A dynamically unstable (runaway) mass transfer. This happens if the donor, either due to its evolution or due to its immediate reaction upon mass loss, expands relative to its Roche lobe (for more details see Sect. 6).

• 2. An instability such as the Darwin instability (Darwin 1879), or a secular tidal instability (Hut 1980; Lai et al. 1993; Eggleton and Kiseleva-Eggleton 2001). The Darwin instability occurs when the spin angular momentum of the system is more than a third of its orbital angular momentum (see also Sect. 6.2).

• 3. The reaction of the accretor leads to matter filling the binary orbit. For example, if mass transfer proceeds at too great a rate to be accreted by the compact companion, but the system is also unable to quickly expel the mass, then a common-envelope is naturally formed. Potential cases include an envelope temporarily trapped around a neutron-star being fed at super-Eddington rates (Begelman 1979; Houck and Chevalier 1991; King and Begelman 1999), or reincarnation of an accreting white dwarf which tries to form a red giant (Nomoto et al. 1979; Nomoto et al. 2007); or perhaps even in nova systems when the expansion of the nova shell engulfs the companion.

The loss of corotation itself occurs on a dynamical time scale. Prior to that moment, however, the stellar structure is strongly affected by the mass-transfer history before the dynamical instability sets in. This preparatory stage could last hundreds of years, from dozens of dynamical time scales to a thermal time scale (see Sect. 6 and Podsiadlowski et al. 2002a).

II: Plunge-in and its termination

A rapid spiral-in, during which the orbital energy is deposited in the envelope, drives its expansion and may lead to its dynamical ejection right away, or to a rapid merger of both stars. This stage is purely dynamical and is the best studied stage to-date. Typical hydrodynamical simulations for CEE ending with a merger or with a binary formation are shown on Figs. 3 and 4, and for more technical details see discussion in Sect. 7.

Fig. 3

Common envelope event with a 1.2M _⊙ early giant and 0.6M _⊙ MS star, resulting in a merger of two stars. Simulation performed for this review by J. Lombardi and R. Scruggs, simulated with 2.2×10⁵ SPH particles. For more technical details on the code, see Gaburov et al. (2010) and Lombardi et al. (2011). Video for the simulation is available as Electronic Supplementary Material 2. Visualization (images and on-line video) are generated using SPLASH (Price 2007)

Fig. 4

Common envelope event with 0.88M _⊙ giant and 0.6M _⊙ MS star, likely leading to the formation of a close binary. Shown are density slices in the orbital plane (left) and in the perpendicular plane (right) at different times, each panel is 430R _⊙ on a side. Simulations were carried out with the gird-based code ENZO (O’Shea et al. 2005), and a resolution of 256³ cells. The image was created for this review by J.-C.Passy. Video for the simulation is available as Electronic Supplementary Material 3. For more details on simulations see Passy et al. (2012a) and Sect. 7

III: Self-regulating spiral-in

The envelope may expand enough that the spiral-in slows down. In this way a self-regulating state can be formed, in which frictional luminosity released by the spiral-in is transported to the surface where it is radiated away (Meyer and Meyer-Hofmeister 1979). This is expected to happen, for example, in some cases if the rate of spiral-in is determined by the local density in the region of the secondary: too little instantaneous heating means that the local density rises, increasing the rate of spiral-in and therefore heating (and vice versa). This phase is non-dynamical and operates on the thermal time scale of the envelope. How this difference in time scale affects the energetics of CEE is discussed in Sect. 3. Recent hydrodynamic simulations of phase II have found non-local energy dissipation (Ricker and Taam 2008; Passy et al. 2012a); if those long-range effects continue to dominate beyond the initial dynamical spiral-in then it is less clear whether a self-regulating state is likely to form.

IV: Termination of the self-regulating phase

The self-regulated spiral-in ends with the ejection of the envelope (e.g., via delayed dynamical ejection, Ivanova 2002; Han et al. 2002), or when either of the secondary or core of the primary overfills its Roche lobe. The second case can result in a (slow) merger (Ivanova 2002; Ivanova and Podsiadlowski 2003b), but also provides a further route for envelope ejection (Ivanova et al. 2002; Podsiadlowski et al. 2010). This phase takes several dynamical time scales.

In principle, a self-regulated spiral-in (‘phase III’) could also be followed by another dynamical plunge (‘phase II’) if the mechanism maintaining self-regulation somehow ends. That plunge could in turn be followed by another self-regulated phase. It is not clear how unlikely such a repeat is to happen in reality, but there seems to be no first-principles physical reason why the sequence of phases could not be I–II–III–II–III–[…]–IV in some cases.

V: Post-CE evolution

The final properties of the post-CE system are not necessarily set until some time after envelope ejection. For example, the eccentricity of a surviving binary can be changed by any remaining circumstellar matter, which might well include a circumbinary disk. Thermal evolution of the remnant cores might drive further mass transfer, and winds from the remnant cores could widen the system. (For more details see Sect. 10.)

The energy budget during CEE

The standard way to predict the fate of a common-envelope phase is known as the energy formalism (van den Heuvel 1976; Webbink 1984; Livio and Soker 1988; Iben and Livio 1993), in which the energy difference between the orbital energies before and after the event is compared with the energy required to disperse the envelope to infinity, $E_{\rm bind}$:

$$ E_{\rm bind} = \Delta E_{\rm orb} = E_{\rm orb,i} - E_{\rm orb,f} = -\frac{ G m_1 m_2}{2 a_{\rm i}} + \frac{ G m_{1\rm,c} m_2}{2 a_{\rm f}} $$

(2)

Here $a_{\rm i}$ and $a_{\rm f}$ are the initial and final binary separations, m ₁ and m ₂ are the initial star masses and $m_{1\rm,c}$ is the final mass of the star that lost its envelope $m_{1,\rm env}$. As not all the available orbital energy can be used to drive the envelope ejection, the concept of common-envelope efficiency is introduced, which is parametrized as $\alpha_{\rm CE}$. This is the fraction of the available orbital energy which is usefully used in ejecting the envelope.

We could alternatively state the energy budget for CEE by writing that the combined total energy of the immediate products of CEE cannot be greater than the total energy of the system at the onset of CEE. This statement plus a few approximations leads to Eq. (2). We also need to decide which physical contributions should be counted in this energy budget, but if they are physically complete then $\alpha_{\rm CE}$ should never need to exceed unity.

There are subtly different ways of writing the energy formalism. However, all implicitly assume that the ejected material departs with precisely the local escape velocity, i.e. $\alpha_{\rm CE} = 1$ does not only imply perfect energy transfer, but also perfect fine-tuning. Since kinetic energy scales as the square of velocity, matter would need to escape within a factor of ≈1.4 of the escape velocity for $\alpha_{\rm CE} > 0.5$ to be allowed.

A significant technical improvement in the application of this formalism was the inclusion of a second parameter, λ, to account for the particular structure of each star in calculating $E_{\rm bind}$ for that star (de Kool 1990; Dewi and Tauris 2000; Dewi and Tauris 2001). Following this addition, the most commonly used form for the energy formalism in population studies is now

$$ \frac{m_1 m_{\rm1, env}}{\lambda R_1} = \alpha_{\rm CE} \biggl( -\frac { G m_1 m_2}{2 a_{\rm i}} + \frac{ G m_{1\rm,c} m_2}{2 a_{\rm f}} \biggr) $$

(3)

This expression allows the two free parameters to be simply joined into a single unknown, $\alpha_{\rm CE}\lambda$, and this convenient combination can be commonly seen in population synthesis papers. Of course, using a global value for the product $\alpha_{\rm CE}\lambda$ does lose the advantage gained when using λ to describe the individual binding energy of specific stars.

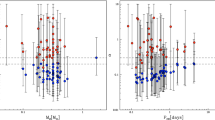
We note that different definitions of λ exist in the literature, depending on whether the authors include only the contribution from gravitational binding energy or also the internal energy of the star (see Fig. 5). The value of λ can change greatly between stars, so using a global value in calculations is unsatisfactory. An important physical question associated with this is how to determine the boundary between the remnant core and the ejected envelope, since λ can be extremely sensitive to that location (Tauris and Dewi 2001); this is discussed in Sect. 4.

Fig. 5

λ as a function of mass shown on example of 20M _⊙ star when it has R=750R _⊙ (Z=0.02, overshooting 0.2 of the pressure scale and no wind loss). For comparison shown $\lambda_{\rm g}$ when only gravitational binding energy is taken into account (thin solid line) and when internal energy is taken into account as well (thick solid line). Dotted lines correspond to several possible core definitions, as discussed in Sect. 4.1

Note that the envelope does not just need to become unbound from the giant, as it must also be lost from the binary. Equation (2), even when using detailed binding-energy calculations for the giant star, neglects this. (One way of thinking about this is that the zero of potential energy for the envelope is redefined between the initial and final states.) The appropriate correction would usually be small, but it is often forgotten.

When calculating $E_{\rm bind}$, it is vital to know whether to include only the gravitational terms. Webbink (1984) performed a full integration over both the gravitational binding energy and the thermal energy of the gas, since they are inextricably linked (but did not include recombination energy, for which see Sect. 3.3.2), but early parametrizations only included the gravitational terms. Physically it might be preferable for, e.g., the thermal energy of the gas to be thought of as a potential source of energy rather than as something which reduces the magnitude of the binding energy; in either case we need to think about how internal energy might be converted to mechanical work if it is to help eject the envelope. This depends partly on the time scales over which the CE event happens, as we will discuss below. Likewise, those time scales help to control whether other energy sources can contribute to the ejection besides the orbital energy reservoir.

Applicability of the energy formalism: time scales and energy conservation

It is crucial to realize that the standard energy formalism (as in Eq. (2)) was introduced to explain a common envelope event as an event taking place on a dynamical time scale. The formalism also presumes that only the energy stored in the binary orbit, or in the initial internal energy of the common envelope, could play a role in the envelope ejection. If the energy formalism is mis-applied (for example, to quasi-conservative—thermal or nuclear time scale—mass transfer) then artifacts like an apparent efficiency greater than unity ($\alpha_{\rm CE}\gg1$, i.e. non-conservation of energy) could easily take place. This would clearly be misleading and unphysical, but the situation could arise since this approximation neglects some potentially important energy sources and sinks. Among the likely sinks are radiative losses from the common envelope and energy stored in microscopic or macroscopic degrees of freedom (i.e. internal energy of the matter and terminal kinetic energy of the ejecta). Prospective sources are nuclear energy input—either from burning at the base of the common envelope or from burning ignited at the surface of the accretor—and accretion energy from matter retained by the companion star. Note that, although mass transfer involves the liberation of gravitational potential energy to heat the accreted envelope, this exchange of gravitational potential energy for thermal energy neither introduces new energy sources nor new energy sinks.

The longer the CE phase lasts, the more opportunity there is for deviation from the energetically closed system described above. For example if the event takes place on a thermal time scale or longer, then energy lost in radiation from the envelope’s photosphere might have to be taken into account. For static equilibrium models we might feel justified in assuming that this loss is balanced by heating from the stellar core, but this is unlikely to remain true as the star’s structure alters during the CE event. Either the radiation from the surface or heating from the core might be larger in different CE events. Predicting future radiative losses in general would be challenging if not impossible.

Similarly, predicting the details of changes in the nuclear energy sources during CEE is not straightforward, since their output might increase (see Sect. 3.3.4) or fade away due to adiabatic expansion of the core in response to mass loss. Qualitatively, however, it seems reasonable to expect that if the donor star is in thermal equilibrium at the onset of mass transfer, then radiative losses initially balance nuclear energy input. Then radiative losses seem likely to grow relative to input from nuclear sources. This is because we anticipate that the emitting area will probably increase whilst the nuclear sources, if anything, seem most likely to decline in output, since the internal decompression attending mass loss will tend to quench nuclear burning.

Qualitatively it is also possible to argue that accretion during CEE is not commonly significant for non-degenerate companion. The common envelope itself typically possesses much higher specific entropy than the surface of the accretor, with the consequence that matter accreted by the companion star reaches pressure equilibrium at the surface of that star with much higher temperature, and vastly lower density, than the accretor’s initial surface layer. A temperature inversion or roughly isothermal layer is expected to bridge this entropy jump with the result that, over the duration of the CEE (which is much shorter than the thermal time scale of the accretor), the accretor is thermally isolated from the common envelope, while the common envelope itself becomes increasingly tenuous. If this picture is correct then one would expect very little net accretion onto a non-degenerate companion star (Webbink 1988; Hjellming and Taam 1991). For degenerate companions, in this same context, the ignition of nuclear burning at the surface of the accretor might be inhibited by the very high entropy of accreted material—which would be extremely buoyant, and difficult to compress to ignition conditions—although detailed simulations of the process should be performed (see also Sects. 3.3.5 and 9).

It should be clear that it is very difficult to make any general statements once the common envelope ejection is non-dynamical. Once the spiral-in or the envelope preliminary expansion takes place on a time scale longer than dynamical, energy conservation in the simple original form above is not expected to work.

Relating loss of orbital energy to heat input and outflow of the envelope

The energy from orbital decay is often assumed to thermalize locally, typically by viscous dissipation in the region of the in-spiralling secondary. However, hydrodynamic simulations (Ricker and Taam 2012) form large-scale spiral waves, with tidal arms trailing the orbit of the binary. Spiral shocks transfer angular momentum to the matter in the envelope. Furthermore, some of the energy in those spiral shocks will be dissipated as heat a long way from the secondary.

It also seems possible that some matter is flung out as a result of these spiral waves, i.e. orbital kinetic energy is directly transferred to the kinetic energy of the envelope. If the spiral-in ends during the dynamical plunge-in, without entering a self-regulating phase, then a significant fraction of the orbital energy transferred to the ejected envelope might not have been thermalized.

Avoiding a thermal intermediate stage would have the clear advantage that the energy input is less likely to be radiated away, but might reduce the chance that any other heat source could help with that part of the ejection. If we could decide to what extent the envelope is ejected directly (by kinetic energy imparted from spiral shocks) or indirectly (by heating and a pressure gradient)—an apparently simple distinction—then it might help us conclude how much the suggestions in the following subsection are likely to be helpful.

The results of Ricker and Taam (2012) are discussed in more detail in Sect. 7. Here we note that ≈25 % of the envelope is ejected during their dynamical plunge-in calculations. The distribution of entropy production within the envelope may well be different during any subsequent self-regulated spiral-in. The dominant driving mechanism for further envelope loss might therefore also change.

Is orbital energy the only relevant source of energy?

Section 3.1 hopefully made it clear that there could easily be scope for additional sources of energy to participate in CE ejection. In the following we discuss several possibilities. The first is widely accepted, though physically unproven to help, but the others are less normally included.

Internal energies

It has become standard practice to include the internal energy of the envelope in CE binding energy calculations. It is arguably physically clearer to think of the internal energy reservoir as another energy source, and we shall do so here, but it is also natural to modify the definition of $E_{\rm bind}$ such that it becomes the sum of the potential energy and internal energy of the envelope. This has typically been calculated using detailed stellar models via

$$ E_{\rm bind} = - \int_{\rm core}^{\rm surface} \bigl( \varPsi(m) + \epsilon(m) \bigr) \,dm $$

(4)

Here Ψ(m)=−Gm/r is the gravitational potential and ϵ is the specific internal energy. If integrated over the whole star, Eq. (4) gives the total energy of the star. However, when applied only to a part of the star, it is no longer formally valid, in part due to how gravity is taken into account.

This contribution of internal energies was first explicitly applied by Han et al. (1994), and can make a very large difference from the energetic ease of envelope ejection during some phases of stellar evolution. Some authors only allow a fraction of the available internal energy reservoir to contribute to the ejection, in which case a second efficiency parameter, $\alpha_{\rm th}$ is used to denote the fraction of the internal energy which is available to help eject the envelope.

Equation (4) neglects the response of the core, which we discuss further in Sect. 4. Here we note that, if the core expands during mass loss, this could do mechanical work on the envelope. So the binding energy should formally be calculated as the difference between the initial (E _i) and final (E _f) total energies of the star:

(5)

where the integrals are now through the whole star, not just the envelope (Ge et al. 2010; Deloye and Taam 2010). For stars with degenerate cores it seems unlikely that this correction is large, but it has not yet been definitively shown to be unimportant.

It is not guaranteed that the internal energy should make a significant contribution. The simplest physical version of this change seems to presume that a significant part of the envelope expansion is subsonic, i.e. that pressure equilibrium can be maintained. Otherwise the envelope’s gas would seem unable to transfer its internal energy into envelope expulsion via thermal pressure.

Furthermore, some stars appear marginally unbound when their internal energy is included in the binding energy calculation, yet they retain their envelopes. Evidently, a net excess of internal energy over gravitational binding energy is not a sufficient condition to unbind the envelope, even when this situation is maintained over many dynamical time scales. Of course it is easy to speculate that the CE event might somehow trigger the release of this energy.¹ Arguments have been made that positive internal energy is the condition which determines spontaneous envelope ejection for single stars, and that this helps to match the intial-final mass relation (Han et al. 1994; Meng et al. 2008). If this is the case, then at metallicities ⪆0.02, stars with initial mass ⪅1.0M _⊙ do not ignite helium (Meng et al. 2008).

Internal energy, thermal energy and recombination energy

It seems worth exploring the details of the ‘internal energy’ term included in Eq. (4). In particular, we wish to highlight that the contributions used separate into two distinct groups.

The natural components of internal energy are the thermal terms familiar from kinetic theory, which we collectively label $U_{\rm th}$. These measure the energy of the matter relative to the state where stationary (cold) electrons and ions are separated to infinity, i.e. the natural zero-energy state. This combines the internal kinetic energy of the particles and the energy stored in radiation. Per unit volume, we write

$$ \frac{U_{\rm th}}{V} = a T^{4} + \sum_{\mathrm{particles}} \sum_{\mathrm{d.o.f.}} \frac{k_{\rm B}T}{2} $$

(6)

where the summations are over the particles (including molecules) present, and their available degrees of freedom. (We have not written down the corrections to the electron energies due to Coulomb interactions and degeneracy, which are not likely to be significant in stellar envelopes.)

The second set of contributions arise because we expect that more energy than $U_{\rm th}$ is available to be released from the matter in the envelope during envelope ejection. The plasma can recombine and some atoms will form molecules; those processes will release binding energy. This extra store of available energy is typically referred to as recombination energy, $\Delta E_{\rm recomb}$. It can be calculated by adding the appropriate ionization and dissociation potentials for each ion and atom present, though it is usual to neglect dissociation of any other molecule than $\rm H_{2}$. We note that recombination energy was suggested much earlier to be a potential driving mechanism for the ejection of ordinary planetary nebulae (Lucy 1967; Roxburgh 1967; Paczyński and Ziółkowski 1968).

These two, very different, components have been mixed into ‘internal energy’ when discussing envelope ejection and stellar binding energies (see, e.g., Han et al. 1994, 2002). One of the reasons why this might be physically confusing is that recombination energy does not contribute to the standard internal energy which enters the virial theorem. This is also one of the reasons why recombination energy is potentially helpful in CE ejection. For a stellar envelope which is dominated by gas pressure such that the gravitational binding energy is $U_{\rm th}/2$ then, if $\Delta E_{\rm recomb} = U_{\rm th}$, the star’s envelope would be formally unbound even before CEE.

Their relative magnitude can be crudely estimated by comparing the value of $k_{\rm B}$ (i.e. 8.6×10⁻⁵ eV K⁻¹) with the ionization potentials of hydrogen and helium (79.1 eV/ion for He, 13.6 eV/ion for H). Assuming a 10:1 ratio of hydrogen to helium (by number) gives an average of ≈ 20 eV available per ion, in which case energy stored in thermal terms dominates energy stored in the ionization state of the plasma for temperatures above ∼2×10⁵ K.

So there seems very likely to be a strong contrast in where the energy release from these two components will happen. The thermal terms, with specific energy ${\sim}3/2 k_{\rm B}T$ per particle in most giant envelopes, will store and release energy at high temperatures, i.e. deep within the star. The release of binding energy during recombination and molecule formation will take place at relatively low temperatures.

The fact that the gravitational potential well is deepest far from the possible recombination zones seems worth pursuing. This might help explain how internal energy can help CE ejection, even though stars which are marginally unbound after calculating the integral in Eq. (4) (when including recombination terms) are stable to perturbations. When the CE spiral-in has made the envelope expand and cool enough then recombination would be triggered, perhaps giving the final push to make a loose envelope unbound.

On the other hand, it is also possible that recombination energy is liberated so close to the surface that it is more easily convected to the surface and radiated away. The helium recombination zones in red giants are typically well below the photosphere (at optical depths ≫100), so if the giant structure is roughly preserved during CEE then we do expect the energy from recombination to be thermalized. Even if the envelope above the recombination zone became optically thin in the continuum, line-driven expansion might still be favored by remaining optically thick in the recombination lines. However, there is very little mass above those recombination zones, and the recombination zones themselves tend to help drive convection.

The distinction between the recombination and kT components is not normally made. It may be that using a single $\alpha_{\rm th}$ parameter for all internal energy contributions is currently sufficient for use in population synthesis, and we should certainly be careful about introducing yet another fitting parameter. Nonetheless, if we aim to understand the physics underlying CEE then in future work it seems sensible to aim to deal separately with the thermal and recombination terms.

Tidal heating

Tidal heating is sometimes discussed as an additional effect which might help the envelope ejection, and sometimes presumed to work more efficiently than orbital energy taken into account in the energy formalism. This deserves a special note of clarification. Tidal heating is clearly not an energy source but rather a transfer mechanism, taking energy out of the binary orbit and stellar spin.

The orbital energy reservoir is no larger than if tidal heating is ignored, and that contribution has already been taken into account in the energy budget even in the original energy formalism. In this respect then tidal heating obeys exactly the same law of energy conservation as would dynamical spiral-in.

In principle there might be a small correction, due to the energy stored in the stellar spin, whilst corotation is enforced. Energy stored in spins is usually ignored in the energy balance equation. Yet it only seems likely to be at all helpful if the giant is rotating faster than corotation, and is spun down as tides take effect. This is the opposite of the strongly expected situation. Indeed, taking into account spin energy in the overall energy budget seems most likely to make the situation worse: some of the available orbital energy will go into enforcing corotation.

Moreover, the tidal heating time scale seems likely to be longer than that of the dynamical spiral-in. In which case, the star can lose more of this orbital energy via radiation from the surface layers than if tidal heating was ignored. So potentially tidal heating can decrease the efficiency if energy conservation is applied using Eq. (2).

So, for several reasons, invoking tidal heating should not increase the amount of energy available to eject the envelope. It should not result in $\alpha_{\rm ce} > 1$.

Nuclear energy

Another energy source that could play a role in the envelope ejection is nuclear fusion (Ivanova 2002; Ivanova and Podsiadlowski 2003b). If one considers a binary that is doomed to merge, but does not yet merge during the dynamical plunge-in phase, then during the self-regulating spiral-in phase a non-compact companion (e.g., a main sequence star) will, at some point, start to overfill its Roche lobe. This can be considered to be the end of the normal spiral-in. Due to continued frictional drag from the envelope on the mass-losing companion, the orbit continues to shrink, forcing the mass transfer to continue and even to increase. A stream of hydrogen-rich material can then penetrate deep into the giant’s core, reaching even the He burning shell and leading to its complete explosion (Ivanova et al. 2002), since the released nuclear energy during explosive hydrogen burning could exceed the binding energy of the He shell (in massive stars this can be a few times 10⁵¹ erg). The rest of the CE is much less tightly bound and is also ejected during the same explosion. This leaves behind a compact binary consisting of the core of the giant and whatever remains of the low-mass companion after the mass transfer. The companion is not expected to remain Roche lobe filling immediately after the explosion.

Such explosive CE ejection could both help a less massive companion to survive the CE (this makes the formation of low-mass black-hole X-ray binaries more plausible). It also seems to naturally produce a fast-rotating core which has been stripped of both hydrogen and helium (Podsiadlowski et al. 2010). The remnant star could then produce both a long-duration γ-ray burst and a type Ic SN, helping to explain their observational connection.

Accretion energy

Another potential source of energy is the luminosity of accretion onto the secondary during the common envelope phase (see, e.g., Ivanova 2002; Voss and Tauris 2003). The Eddington luminosity would release ∼5×10⁴⁵ ergs per year per 1M _⊙ of the accretor. In which case, if a slow spiral-in lasts from 100 to 1000 years, the energy released through accretion could become comparable to the energy release from the binary orbit via tidal interaction and viscous friction (for the comparison of contributions in the case of different masses for a donor and a giant, see Ivanova 2002). In most cases, standard methods predict that the available accretion rate for an in-spiralling companion exceeds its Eddington-limited accretion rate. However, hydrodynamical simulations found that whilst the spiral-in is still dynamical, the commonly used Bondi–Hoyle–Lyttleton prescription for estimating the accretion rate onto the companion significantly overestimates the true rate (Ricker and Taam 2012), in which case the contribution of accretion to the energy budget could easily be negligible (see also Sect. 9).

The balance between orbital energy release and accretion luminosity should change at different stages of the CE process. When a compact object is orbiting inside the outer regions of the envelope of the giant (where the binding energy per unit mass is low and the spiraling-in time scale is long) then it seems easiest for accretion energy release to dominate orbital energy deposition. A special case of accretion energy release would occur if an in-spiralling compact object orbits deeply enough to cause the core to overfill its Roche lobe (Soker 2004). This might cause a brief, powerful release of accretion energy to help envelope ejection. If that process occurs, it might disfavor the formation of Thorne–Żytkow objects (Thorne and Zytkow 1975, 1977).

Accretion energy release might be able to help envelope ejection in ways other than via heating. Kinetic outflows—jets—might be driven by accretion onto an in-spiralling compact companion. Soker (2004) argued that this should be the expected outcome for an in-spiralling WD or NS. Many parameters are poorly determined for this entire process, but Soker argues that the jets can blow hot bubbles within the envelope, causing some mass loss and potentially slowing the spiral-in.

How important are magnetic fields?

The role of magnetic fields in CEE is far from understood. The rapidly rotating envelope expected during a CEE phase provides an environment in which a magnetic dynamo may well operate effectively, but such dynamos could only redistribute energy already present in the system. Dynamos are not energy sources, and any increase in magnetic energy must be matched by decreases in other parts of the energy budget. Hence overall CE energetics are broadly not altered by the presence or absence of dynamo action.

Nonetheless, strong B-fields created by the dynamo would be expected to suppress differential rotation of the CE (e.g., Regos and Tout 1995; Potter et al. 2012). That angular momentum transport could greatly alter the spiral-in process, and would also be relevant to our understanding of whether energy dissipation is broadly local or non-local with respect to the in-spiralling star (as discussed in Sect. 3.2).

Despite the above, it is less clear whether magnetic fields are likely to be significant for the main phase of CE ejection. Qualitatively, we might expect that magnetic fields are more likely to be dynamically important in the outer layers than the inner ones, and it is these inner layers which contribute most to the envelope’s binding energy and are most important for determining the fate of the final spiral-in. In normal, non-degenerate, stars with very large surface magnetic fields, their magnetic fields only make a small contribution in the inner layers to the hydrostatic stresses (since B ²/8πP≪1). Hence we consider it unlikely that forces arising from magnetic fields will be directly dominant during the final common-envelope ejection.

However, magnetic fields could drive additional wind-type mass-loss during a common envelope (e.g., see Regos and Tout 1995); this could reduce the amount of material which has to be ejected by canonical CEE, hence potentially altering the overall outcome. A large-scale α−Ω dynamo during CEE has been argued to produce compact remnants with large magnetic moments (Tout et al. 2008; Potter and Tout 2010). It may also alter the outflow geometry, possibly shaping the post-CE nebulae in collimated bipolar outflows (Nordhaus et al. 2007).

Does enthalpy help to unbind the envelope?

Above we have given some possible extensions to the canonical energy formalism. In particular, we have explored a set of potential additional energy sources which might help unbind the envelope. However, it has recently been proposed by Ivanova and Chaichenets (2011) that the standard framework is seriously physically incomplete if the CE ejection happens during the self-regulating phase.

In particular, Ivanova and Chaichenets (2011) argued that the condition to start outflows is similar to the energy requirement in Eq. (4), but with an additional P/ρ term, familiar from the Bernouilli equation:

$$ E_{\rm flow}= - \int_{\rm core}^{\rm surface} \biggl( \varPsi(m) + \epsilon (m) + \frac{P(m)}{\rho(m)} \biggr) \,dm $$

(7)

Since P/ρ is non-negative, the condition to start outflows during slow spiral-in occurs before the envelope’s total energy become positive. As a result, this “enthalpy” formalism helps to explain how low-mass companions can unbind stellar envelopes without requiring an apparent $\alpha_{\rm CE} > 1$. Although this consideration may change the requirements for the energy budget, we emphasize that this was derived without reference to the total energy budget for envelope ejection, and it arises from a condition that separates stable envelopes from envelopes that are unstable with respect to the generation of stationary outflows.

This would be a radical change in the standard picture of CE energetics; understanding this question is clearly important. An energetic debate over whether the arguments in Ivanova and Chaichenets (2011) are correct is still continuing, and we outline two opposing points of view below; there are others.

Against: energy redistribution during dynamical envelope ejection

The P/ρ contribution in the Bernouilli equation expresses the fact that the pressure gradient helps to accelerate the envelope outwards.

Hence the gas expelled from the outer regions carries more kinetic energy than what would be calculated without the work of the pressure included. But this energy comes at the expense of the energy of the inner regions of the envelope. So the P/ρ term is important, but this only redistributes energy rather than being a new, previously forgotten, energy source.

This can be demonstrated by a simple case. Consider a gas of adiabatic index γ with a uniform initial pressure P ₀ and initial density ρ ₀, occupying a cylindrical pipe in the region x _l <x<x _r (where x _l is left and x _r right, corresponding to the inner and outer edges of the envelope). At t=0 the valve at x _r is opened.

This classic problem is solved in Sect. 99 of Landau and Lifshitz (1959). The velocity of the gas at the right (outer) edge reaches a value of v _r =2C _s /(γ−1), where C _s =γP ₀/ρ ₀ is the initial sound speed. Its specific kinetic energy $2 C^{2}_{s}/ (\gamma -1)^{2}$ (e.g., $(9/2) C^{2}_{s}$ for γ=5/3), is much larger than the initial specific internal energy $C^{2}_{s} /\gamma(\gamma-1)$ (e.g., $(9/10) C^{2}_{s}$ for γ=5/3). This ‘extra’ energy comes at the expense of the energy of gas elements further to the left (i.e. further inside). A rarefaction wave propagates to the left and reduces the internal energy of the gas there. The further to the left a mass segment is, the lower its velocity is.

The same qualitative flow structure holds for the ejected CE. The pressure gradient accelerate the outer parts of the envelope at the expense of the inner parts. The energy is unevenly distributed: the outer parts escape with a speed much above the escape velocity, but the very inner parts might not reach the escape velocity. They will fall back, unless extra energy is deposited to the still-bound envelope segments.

This uneven energy distribution is clearly shown for a case where the energy is deposited over a short time in the inner part of the envelope (Kashi and Soker 2011). The inner parts of the envelope expand at velocities below the escape velocity. They fall back to the binary system. If they contain sufficient angular momentum, a circumbinary disk might be formed. Note, however, that this may no longer be valid if the orbiting companion continues to add energy at the base of the envelope, or if heat can flow outwards from the core on a short enough time scale.

To maintain a negative pressure gradient (which accelerates outward) in the inner regions during the ejection process, the bottom of the envelope must gain sufficient heat from the core (which requires a sufficiently long time scale for ejection), or by continued energy input from the binary (the conditions on which are unclear). However, in the simple case where the envelope is energetically isolated after the start of envelope ejection then the P/ρ term only redistributes energy within the envelope.

For: outflows during self-regulating spiral-in

The arguments above assume that the ejection time scale is short, but the derivation of Eq. (7) implicitly required that ejection happens on a thermal time scale. The arguments which lead to the use of Eq. (7) rather than Eq. (4) were based on considering stellar stability criteria. The original assumption for the energy formalism is that the energy required to eject the envelope equals $E_{\rm bind}$. This is based on either of two assumptions: that an envelope is dispersed once its total energy $W_{\rm env}>0$, or that an envelope with $W_{\rm env}>0$ is unstable. The connection between W and $E_{\rm bind}$ presumes that $E_{\rm bind}$ is in fact $W_{\rm env}$. But Ivanova and Chaichenets (2011) argued that those assumptions are not foolproof, as both a star with W>0 can be kinetically stable (Bisnovatyi-Kogan and Zel’Dovich 1967), and a star’s stability condition against adiabatic perturbations is not the same as having W>0.

Ivanova and Chaichenets (2011) instead considered quasi-steady surface outflows, which would develop on the same time scale as it takes for the envelope to redistribute heat released during the spiral-in, i.e. the thermal time scale of the envelope. These outflows could only take place if slow spiral-in occurred, not during a dynamical plunge-in phase. It is important to realize that such steady flows do not behave the same way as the non-stationary flows described in Sect. 3.4.1. Since the base of the envelope could have time to take energy from the core, the final total energy requirement for envelope ejection might be more than that given by Eq. (7). However, the energy which might be released by the reaction of the core cannot easily be evaluated at the start of the CE phase; full mass-loss calculations would be needed.

Summary

Whether enthalpy helps with CE ejection may therefore be determined by the time scale over which the ejection occurs.

Both arguments above might be correct in different binary systems. If the envelope can be ejected during the dynamical plunge-in, then the envelope may act as a closed energetic system (depending on the time scale of ejection compared to the time scale of energy input from the binary orbit). But if that rapid ejection does not happen, and the spiral-in reaches the self-regulating phase, then it may becomes possible for quasi-steady outflows to develop on the thermal time scale of the envelope, and also for further heat input to come from the core or from the binary orbit. In cases where the P/ρ term only acts to redistribute energy within the ejected envelope then it might make the overall ejection more difficult, in other cases it might be helpful. A priori it is not clear which situation is more likely to be common.

Although it is still unclear to what extent enthalpy helps with CE ejection, both sides of the debate above suggest that the P/ρ term might be vital in determining the point which defines the depth from which the envelope is ejected, i.e. the bifurcation point which separates the material which remains bound from the material which escapes. How to physically determine this location will be addressed in the next section.

The end of the CE phase & the fate of the remnant

The previous section discussed the widely used energy formalism and variations upon it. The main question which the energy formalism is trying to answer is where does the spiral-in stop? That is: can we take the initial conditions of a CE phase and predict the outcome? If a merger is avoided, what does the remaining binary look like?

It is not sufficient to conclude that there is, in principle, sufficient useful energy available to eject the envelope. Perhaps spiral-in does stop as soon as sufficient gravitational potential energy has been released to unbind the envelope, but this standard assumption is at best crude. Physically, it might be that (almost all) the envelope is ejected, but the spiral-in of the companion still continues until it merges with the core. (A post-CE binary might alternatively merge during thermal relaxation following envelope ejection.)

Even more fundamentally, it is not trivial to define the boundary between the ‘core’ and the ‘envelope’. Nor is it clear how close that boundary is to the bifurcation point which separates the material which is ejected from that which stays bound. So far we have treated these points as if they were well-known, but they are not. These locations are needed in order to calculate $E_{\rm bind}$ correctly, and different definitions can lead to large differences in CE outcome (Tauris and Dewi 2001).

Locating the bifurcation point

A number of possible criteria can be found in the literature which aim to define the boundary between the remaining core and the ejected envelope. Some are related to plausible definitions of the core mass, some attempt to predict a natural bifurcation point on other grounds.

Obvious possibilities are the minimum possible core mass (the hydrogen-exhausted core) and the maximum possible core mass (the transition between the radiative zone of the H-burning shell and the bottom of the outer convective envelope). Equivalent descriptions of the latter point include: (i) where the entropy profile has a transition between the increasing and flat parts (Tauris and Dewi 2001); (ii) where the effective polytropic index is discontinuous (Hjellming and Webbink 1987). The proposed conditions can be grouped into three main categories as follows:

• 1. Connected to the nuclear energy generation:

  • at the maximum nuclear energy generation within the H shell (Tauris and Dewi 2001),

  • at the maximum nuclear energy generation plus a condition on the mass of the remaining envelope, which itself is a function of the evolutionary status of the donor (for low mass red giants and asymptotic giant branch stars, De Marco et al. 2011),

  • where the nuclear energy generation falls below some threshold (De Marco et al. 2011).

• 2. Based on the chemical composition:

  • the central mass which contains less than 10 % hydrogen (Dewi and Tauris 2000),

  • core is everything below the location where X=15 % (Xu and Li 2010).

• 3. Connected with thermodynamic quantities:

  • where ∂ ²logρ/∂ ² m=0 within the H-burning shell (Bisscheroux 1998),

  • where the function of the binding energy $y=\sinh^{-1}(E_{\rm bind})$ has the transition between a sharp increase and a fairly slow increase in the outer envelope (Han et al. 1994),

  • where the value of P/ρ is at its maximum within the H-burning shell; this could be described as the point of maximum compression, or maximum sonic velocity (Ivanova 2011),

  • by using the entropy profile to predict the surface luminosity of any possible remnant. Comparison of this predicted luminosity with the current nuclear luminosity might suggest whether that potential remnant would expand or contract (on a thermal time scale) after being exposed.

Not all the definitions are applicable to every star: some only work for low-mass giants or asymptotic giant branch stars, and some conditions cannot be found or determined uniquely in all the stars (e.g., the condition ∂ ²logρ/∂ ² m=0 does not always give a unique answer for massive stars). In Fig. 5 we demonstrate how different definitions of the bifurcation point can work.

As the binding energy within the hydrogen shell greatly exceeds the binding energy of the outer convective envelope, different core definitions for the same star could lead to final binary separations different by factors of up to 100 (Tauris and Dewi 2001; Ivanova 2011, 2012); for the star illustrated in Fig. 5 the different core definitions predict envelope binding energies which vary by a factor of 34. It is therefore of paramount importance to find the bifurcation (core boundary) point as accurately as possible. For that, understanding the physical reasons behind the existence of such a point is very important.

Most of the core definitions are simply ad hoc and do not carry much meaning except that they could be used as fixed comparison points between different population studies. However, some (e.g., the thickness of the remaining envelope) are based on a known feature of low-mass giants (those which have degenerate cores): the ability to re-expand their envelope back to a giant structure if the remaining envelope mass exceeds some (small) value (Deinzer and von Sengbusch 1970). In general, the envelope mass that still re-expands needs to be found for every core mass, but when adopting a criterion it is usually approximated as some small fixed mass.

The definition in which the core is determined by the compression point, $m_{\rm cp}$, is in some sense a generalization of the case of low-mass giants described above. Here the bifurcation is also based on opposite reactions of different parts of the H shell to the very rapid mass loss; both immediately after the envelope ejection and subsequently on a thermal time scale. However, this type of divergence point for giant stars exists in all giants, including massive ones. In the general case, it can be said that if mass is removed to below the divergence point then the remnant contracts on its thermal time scale. On the other hand, if mass remains above the divergence point then the star expands during its thermal readjustment. During that thermal reexpansion the remnant could either develop an outer convective envelope or experience strong thermal pulses. This divergence point does not reliably coincide with any of the other proposed bifurcation points described above.

Additional characteristics of that bifurcation point $m_{\rm cp}$ have been found (for more details see Ivanova 2011, 2012), where the most important is that the energy expense required to shed the envelope down to $m_{\rm cp}$ is minimal, if both the expansion during CEE and thermal readjustment after CE ejection are considered. This is related to the question of whether the enthalpy formalism for the energy balance should be applied (see Sect. 3.4 above), but it seems that $m_{\rm cp}$ should be the natural bifurcation point whether the ejection is on a thermal time scale or dynamical. Hence it seems plausible that $m_{\rm cp}$ could be the long-searched-for and physically motivated point which defines where the spiral-in stops.

Interaction with a post-CE disk

If not all of the envelope is ejected then, due to angular momentum conservation and further interaction of the fall-back gas with the binary system, a circumbinary disk may well be formed (Kashi and Soker 2011; De Marco et al. 2011). Various numerical simulations have also suggested that a substantial fraction of the envelope might stay bound (e.g., Sandquist et al. 1998; Lombardi et al. 2006; Passy et al. 2012a). That circumbinary disk is expected to have a thick structure (e.g., Soker 1992, 2004; Sandquist et al. 1998) and its interaction with the binary system may further reduce the orbital separation (Kashi and Soker 2011). In the context of the energy formalism it would effectively mean that $\alpha_{\rm CE} \ll1$ and so in many cases this could lead to a merging immediately after the dynamical phase of the CE. Kashi and Soker (2011) find that this effective value of $\alpha_{\rm CE} < 1$ (see also Ivanova 2011) can explain the recent findings of De Marco et al. (2011): they also found that the value of $\alpha_{\rm CE}$ they deduce from observations is much smaller than what their numerical simulations of the CE phase give (De Marco et al. 2008, 2009, 2011).

The angular momentum budget

We have previously considered energy conservation as a constraint on CEE. The total angular momentum of the system should also be conserved, but as of yet this law has been less widely applied when studying CEE.

From first principles it seems surprising that angular momentum would be the dominant factor in determining the final state of any CEE in which the binary separation (a) is significantly reduced. This is because most of the transfer of angular momentum is expected to happen at wide separations ($J \propto\sqrt{a}$). In contrast, most of the gravitational energy release (∝1/a) should occur later in CEE, i.e. when the post-CE separation is being finalized. Nonetheless, the physical necessity of angular momentum conservation may be particularly useful in understanding the early stages of CEE, and CE phases where a does not significantly decrease.

The plunge

The need for a dynamical plunge-in at the very beginning of CEE can be qualitatively understood by considering when the orbital energy and angular momentum have to be shed from a spiraling-in binary. If we write the orbital energy E of a binary in terms of its eccentricity e, angular momentum J, total mass M, and reduced mass μ,

$$ E = - \frac{G^2 M^2 \mu^3 (1-e^2)}{2J^2} $$

(8)

we see that in the limit that dE≈0 (with M and μ assumed constant),

$$ \frac{de^2}{1-e^2} \approx-2 \frac{dJ}{J} $$

(9)

This suggests that, in the regime when the orbital energy E is almost constant (i.e., at the start of the spiral-in), the binary’s eccentricity grows roughly as fast as angular momentum J is transferred to the envelope.

The orbit is not expected to circularize until $a/R \lesssim r_{\rm g}^{4/3}$, where R is the radius of the common envelope, and r _g its dimensionless radius of gyration (then $I=r_{\rm g}^{2} M R^{2}$ is the moment of inertia) and for giants $r_{\rm g}^{2}\approx0.1$.

The γ-formalism

Considering conservation of angular momentum might avoid some of the problems with trying to apply energy conservation that we outlined in Sect. 3. This gives physical motivation for trying an alternative parametrization. In this subsection we begin by considering such a parametrization: the γ-formalism, in which angular momentum is considered to be the deterministic quantity (Nelemans et al. 2000; Nelemans and Tout 2005). The governing equation is:

$$ \frac{\Delta J_{\rm lost}}{J_{\rm i}}= \frac{J_{\rm i} - J_{\rm f}}{J_{\rm i}} = \gamma\frac{m_{1,\rm e}}{m_1+m_2} $$

(10)

where $J_{\rm i}$ and $J_{\rm f}$ are the orbital angular momenta of the initial and the final binaries, and $m_{1, \rm e} =m_{1} - m_{1, \rm c}$ is the mass of the ejected envelope.

This has come to be widely used in BPS studies as an alternative to the standard energy-based methods for predicting the outcome of general CE events. However, the γ-formalism was first proposed in an attempt to explain a narrower set of systems for which the standard energy prescription for CEE appeared to be particularly problematic. For clarity we first address the more restricted original set of cases, and in the next subsection (Sect. 5.3) we consider the potential broader application of angular-momentum based parametrizations like the γ-formalism to predicting the outcomes of canonical CEE.

The origins of the γ-formalism

The γ-formalism was developed in order to explain some particular DWD systems (Nelemans et al. 2000; Nelemans and Tout 2005). These were thought to have formed following two CE episodes, during the first of which the orbital period might have increased. This requirement arose because the older WD in those DWD systems has a smaller mass, and since radius and core mass are coupled in low-mass giants, the orbital separation at the onset of the second mass-transfer episode had to be wider than at the onset of the first one. The energy formalism would not naturally describe a CE phase which widened the binary orbit as appeared to have happened for these systems. Moreover, since that relationship between giant radius and core mass allows the properties of the pre-CE systems to be reconstructed, the γ-value for each unstable mass-transfer episode can also be inferred (Nelemans et al. 2000). Intriguingly, that reconstruction method found that all those observed DWD systems could be explained by very similar values of γ. This led to interest in whether the narrow range of inferred γ-values was related to a deeper meaning. In addition, it was also suggested that Eq. (10) provides a better tool than the energy formalism for predicting the post-CE properties of a wide range of binaries—using a single value of γ for all occurrences—including those where the method originally used to reconstruct the pre-CE properties of the DWD systems would not work (Nelemans and Tout 2005).

The sensitivity of the outcome to γ

The narrow range of γ produced by reconstruction techniques did suggest that the method could be very valuable. The ability to predict the outcomes of CEE for several disparate classes of system using one value of γ would make it a powerful tool, and understanding the origin of a universal γ-value might help to illuminate the physics taking place during CEE. However, Webbink (2008) explained that this may be understood as an intrinsic property of the formalism itself rather than giving deeper insight into CEE. In this way both the success in the initial fitting and later problems in the application of the γ-formalism for other types of binary may arise from the mathematical consideration of how the γ-formalism (as described by Eq. (10)) performs a transformation of an initial binary into a post-CE binary. Specifically, a small range of γ is capable of leading to a very wide range of outcomes: the mapping from the initial to final separation is very sensitive to γ (see Webbink 2008 and Woods et al. 2010, and for a more formal mathematical explanation see Woods et al. 2011). This naturally leads to reconstruction methods inferring a small range of γ, as if the process itself is divergent, the inverse process is convergent. In this case a wide range of outcomes (observed binary separations) was connected to a narrow range of inputs (γ values). This sensitivity to small changes in γ suggests that Eq. (10) should be at least reformulated.

The physical basis of the γ-formalism

Equation (10) is a fitting mechanism for the outcome of a mysterious period of canonically unstable RLOF. Beyond this, there is no clear physical picture of the underlying processes which the γ-formalism represents. One could interpret Eq. (10) as describing the angular momentum which is carried away by each particle of mass ejected from the system. However, the prescription only gives the overall angular-momentum loss at the end of the mass-ejection phase; it contains no assumptions about the specific angular momentum loss at each instant. Nonetheless, as this review aims to understand the physics of CEE, we direct the interested reader to Sects. 7.2 and 8.3, which discuss angular momentum transport and loss in simulations of CEE. Hopefully our understanding of the physics of CEE will soon improve enough to allow predictions to simultaneously take advantage of both energy and angular-momentum conservation.

Since the systems to which the γ-formalism was first applied are precisely the ones with which the energy formalism struggled, it is clear that the γ-formalism does not automatically describe a CEE phase where a limit from simple energy conservation is expected. Replacing the energy formalism with a different parametrization does not solve the apparent physical problem if energy generation during CEE is required to form a particular post-CE system. Some systems predicted by the γ-formalism can be described as having apparently violated energy conservation during their formation if only orbital and thermal energies are available. This suggests that the time scale of the ejection in the γ-formalism is longer than the thermal time scale of the stellar envelope, which makes it more plausible that an additional energy source—such as the star’s own fusion energy—could be used (see Sect. 3.1). We stress that introducing Eq. (10) does not solve the underlying issue in the formation of the DWD binaries (i.e. exactly what happened during the first MT episode) to which it was first applied, even if it was an effective parametrization of the outcome.

Resolving the problem of DWD formation with mass-transfer stability?

The proposal of the γ-formalism highlighted a set of mass transfer episodes which apparently led to orbital expansion via CEE. However, an expanding orbit—as required to explain the DWD systems which the γ-formalism was first used to parametrize—can be a consequence of stable mass transfer. The first Roche-lobe overflow episode in the formation of those DWD systems was not necessarily unstable, and hence did not necessarily lead to CEE (as recently argued by Woods et al. 2012). In this case the progenitor systems that form DWDs are different from those that form DWDs via CEE and the γ-formalism.² This means that use of the γ-formalism does not substitute for following the MT episode in detail. Further study is required to finally determine which systems form DWDs, but the existing work related to the formation of these systems should certainly remind us that understanding mass-transfer stability is as important as understanding CEE itself.

Angular-momentum based parametrizations of classical, in-spiralling CEE

As noted previously, angular momentum is probably the most natural conserved quantity to consider when the binary separation does not significantly decrease. That condition does apply to the systems for which the γ-formalism was developed. However, the majority of canonical CEE cases involve a major spiral-in; indeed, that reduction in separation was the serious problem which CEE was invented to solve. Nonetheless, since angular-momentum conservation is physically true it seems worth considering whether a formalism similar to the γ-formalism could be used for all CEE events.

Moreover, numerous population synthesis studies have already adopted the γ-formalism as an alternative way of predicting the outcome of general CE phases (normally only to compare with the standard α–λ prescription). Hence it is important to consider whether such use is likely to lead to undesirable outcomes. A simple test finds that blanket use of the standard γ-prescription with a single value of γ and a typical initial binary population leads to apparent energy input in a large fraction—roughly half—of the CE events that avoid merger.³ If the γ-formalism—or a similar angular-momentum-based prescription—becomes the standard way to predict outcomes of CEE in population synthesis then this high fraction of events which require unexplained energy input should receive greater attention. We emphasize that any purely angular-momentum-based prescription is a fundamentally different way of treating CEE from one where the outcome is guaranteed to be limited by the available orbital energy. The γ-formalism is not only an alternative choice of parametrization; it is also a qualitatively different picture.

Angular-momentum-based fitting for CE with significant spiral-in

Motivated by the above, we now analytically examine the behaviour of an angular-momentum based prescription for situations with significant spiral-in. We do this by taking the γ-formalism and adding the additional condition that the orbital energy decreases during CEE.

If we assume circular, Keplerian post-CE orbits then for each such CE event we can define two limiting values of γ:

• $\gamma_{\rm E}$: The value of γ for which Eq. (10) predicts that the post-CE orbital energy will be higher than the pre-CE orbital energy.

• $\gamma_{\rm M}$: The value of γ for which Eq. (10) predicts that the system will merge. We define this cautiously, such that for $\gamma_{\rm M}$ all of the orbital angular momentum of the system is carried away by the envelope ejection; mergers could happen for less extreme values than $\gamma_{\rm M}$.

From the above definitions can be derived a relation between $\gamma_{\rm E}$ and $\gamma_{\rm M}$, specifically:

$$ \frac{\gamma_{\rm E}}{\gamma_{\rm M}} = 1 - \sqrt{ \biggl( \frac{M_{\rm c}}{M_{1}} \biggr)^{3} \biggl(\frac{M_{1}+M_{2}}{M_{\rm c} +M_{2}} \biggr)} $$

(11)

where M ₁ and M ₂ are the pre-CE masses of the components and $M_{\rm c}$ is the core mass of the primary star (i.e. $M_{\rm c}=M_{1}-M_{\rm ej}$, where $M_{\rm ej}$ is the mass ejected during CEE). The above can be rewritten as

$$ \frac{\gamma_{\rm E}}{\gamma_{\rm M}} = 1 - \biggl( (1-x )^{3/2} \biggl(1-\frac{x}{k} \biggr)^{-1/2} \biggr) $$

(12)

where $x=M_{\rm ej}/M_{1}$, i.e. the fractional mass of the pre-CE primary star which is ejected during the CE event, k=1+(1/q) and q=M ₁/M ₂ is the mass ratio of the system prior to CEE. Note that k is a weak function of q for the range of likely cases at the onset of CEE (i.e. from q≫1 to q≈1, which correspond to k≈1 and k≈2). For those two limits:

• When k≈1 (i.e. q≫1) then Eq. (12) simply reduces to $(\gamma_{\rm E}/\gamma_{\rm M}) \approx x$.

• When q=1 then the binomial expansion, truncated after the first two powers of x, gives $(\gamma_{\rm E}/\gamma_{\rm M}) \approx(5/4)x-(3/32)x^{2}$.

The above indicates that the range of γ between $\gamma_{\rm E}$ and $\gamma_{\rm M}$ is dominated by the fractional mass ejection from the primary. Cases where the surviving core mass is a small fraction of the donor mass—in which case x is a large fraction of unity—are expected to be common. It should be clear that in such systems the range of γ between $\gamma_{\rm E}$ and $\gamma_{\rm M}$ is a small fraction of $\gamma_{\rm M}$. This is related to the more general sensitivity of the formalism discussed in Sect. 5.2.2.

Appendix A uses model stellar structures to numerically demonstrate the limited range between γ _E and γ _M for some unexceptional cases. Importantly, the range of values between γ _E and γ _M is expected to differ from system to system (see also Webbink 2008; Woods et al. 2010, 2011). Hence a single global value of γ seems unlikely to be effective in describing all CE phases for which there is significant spiral-in and significant mass ejection.

Wider application of the γ-formalism

As noted previously, the specific successes of the γ-formalism have led to some population synthesis studies adopting it as a general alternative to the energy formalism. Some comparisons of the observed populations of post-CE binaries with population synthesis models have found inconsistencies with the γ-formalism when applying it to general CE events (see, e.g., Davis et al. 2010; Zorotovic et al. 2010). However, we have argued elsewhere against drawing over-strong conclusions about the process of CEE from population synthesis alone, and the same principle should apply here.

Nonetheless, use of the γ-formalism to make predictions for systems other than those for which it was calibrated should be done cautiously. This is especially true for systems which undergo serious spiral-in, or for which the final orbital energy is lower than the initial; then the outcomes predicted will be highly sensitive to the chosen value of γ, as explained above. In particular, it seems very unlikely that a single value of γ could apply to all CE phases which occur in the Universe. Avoiding unexplained energy input in a significant fraction of post-CE binaries requires fine-tuning of γ for particular cases. We have made clear that the parameters in the energy formalism are also likely to be different for different systems, hence such variation in γ is not a fundamental argument against the use of a parametrization based on angular momentum, but it is a strong practical warning to those who make and interpret BPS models (especially combined with the high sensitivity of the current γ-formalism to changes in γ).

Overall, the classes of CEE to which the γ-formalism might currently be well-suited are almost certainly limited. Population synthesis modellers who intend to employ the γ-formalism should consider this point. The recent work by Toonen et al. (2012) adopts a set of restrictions which may be useful guidelines: they do not apply the γ-prescription for a second episode of dynamically unstable mass transfer, nor when the companion star is a compact remnant, nor when the dynamical instability is due to a tidal instability.

The onset of the common-envelope phase

The onset of the common-envelope phase is not immediate. This process involves both the time during which unstable RLOF is turning into the common-envelope phase and also the recent pre-RLOF evolution of the donor.

Enhanced mass loss before RLOF

The donor might lose a significant amount of its mass during the approach to RLOF, i.e. before the actual RLOF starts. Mass lost through a tidally enhanced wind was proposed by Tout and Eggleton (1988) to explain the observed mass-ratio inversion in some RS CVn binaries. In addition, very massive stars that approach the Humphreys–Davidson limit could be subject to enhanced winds, and even spontaneous envelope loss (e.g., Vanbeveren 1991; Eggleton 2002). AGB superwinds might also be enhanced or triggered by the presence of a close companion (e.g., Chen et al. 2011). One of the driving mechanisms for AGB superwinds is likely connected to pulsations, and such pulsations can be either amplified (e.g., due to tidal interactions) when the star is close to its Roche Lobe (RL), or strong pulsations can start earlier than it would be in a case of a single star. A similar effect might happen for stars which are close to other pulsation instabilities, such as the Cepheid instability (Eggleton 2002). Another potential driving mechanism for enhanced winds can be connected to the rotational velocity of the star. The rate-of-rotation of the donor is likely to increase prior to RLOF due to synchronization of the stellar spin with the orbit via tidal interactions (Bear and Soker 2010). So it seems possible that during this pre-RLOF stage a star might lose mass at the same rate as AGB superwinds, $10^{-4}M_{\odot}\,{\rm yr}^{-1}$ (or at an even greater rate for massive stars). This mass loss occurs without loss of orbital energy (i.e. without reducing the semi-major axis of the orbit before the onset of the main CE phase). Note, however, that wind loss will tend to widen the binary, which may lead to avoidance of CEE; it should certainly increase the stability of RLOF against CEE.

The obvious consequences of any enhanced mass loss prior the onset of CE, compared to evolution as a single star of the same mass, is that both the mass of the envelope and its binding energy can be decreased due to matter redistribution. This may lead to an apparent increase of $\alpha_{\rm CE}$ for the overall sequence of events. The binding energy decrease at the tip of the AGB is even argued to lead to a state when the envelope becomes almost unbound or blown away by a superwind, and a binary may even completely avoid the formation of a common envelope (Chen et al. 2011). Even after the secondary enters the giant envelope, the rotational velocity could be high enough to keep inducing an enhanced mass-loss rate. Significantly more systems might survive the CE phase if these preceding spin-up and mass-loss phases were taken into account.

Duration of tidal interactions before dynamical instability

Generally we can estimate that tidal interaction becomes significant when the orbital separation is two–three times larger than the giant radius: see, e.g., Portegies Zwart and Meinen (1993) for immediate tidal interactions. Due to continuous tidal interaction during the time a donor evolves near the tip of the RGB or AGB, $\tau_{\rm ev}$, a giant donor is argued to be tidally spun-up even at larger separations (Soker 1996):

$$ a_{\rm max} \simeq5 R_\mathrm{g} \biggl( \frac{\tau_{\rm ev}}{10^6~{\rm yr} } \biggr)^{1/8} \biggl( \frac{M_2}{0.1M_\odot} \biggr)^{1/8} F(L_{\rm g},R_{\rm g},M_{\rm env}) $$

(13)

where $F(L_{\rm g},R_{\rm g},M_{\rm env})$ is a slowly varying function of the primary’s luminosity, radius, and envelope mass, respectively. Note that there are a number of uncertainties and simplifications within that expression. It is based on Zahn’s impressive theory of tidal spin interactions (Zahn 1977, 1989), but the numerical factor should be treated with caution, as it is often found that this must be tuned to match observed binary systems. However, the important point here is qualitative: $a_{\rm max}$ increases with the mass of the companion.

In order to avoid the onset of CEE after synchronization has been achieved, the system needs to remain stable against the Darwin instability (Darwin 1879). Qualitatively, this instability is a consequence of the fact that removing angular momentum from the binary orbit causes the orbital period to decrease, i.e. spin faster. Hence, in a tidally locked binary, if the giant extracts angular momentum from the orbit (e.g. by expanding and thereby changing its moment of inertia) then tidal locking forces it to extract additional angular momentum from the orbit in order to stay synchronized (since the orbital period will itself have been decreased by the star’s initial demands). It should be clear that if the moment of inertia of the binary orbit is far larger than the moment of inertia of the individual stars then this exchange of angular momentum will not destabilize the system. However, in some cases there are no stable solutions, i.e. if the attempts by the orbit to supply the spin angular momentum demanded by the star are unable to lead to equilibrium. When such a runaway occurs then the stars merge (i.e., in this case, enter CEE). Quantitatively, the condition to avoid that instability—assuming that the system is tidally locked—is that the orbital moment of inertia $I_{\rm orb}$ be more than 3 times $I_{\rm g}$ the giant’s moment of inertia $I_{\rm orb} > 3 I_{\rm g} = 3 r_{\rm gyr}^{2} M_{\rm env} R_{\mathrm{g}}^{2}$ (Hut 1980). Here $r_{\rm gyr}$ is the gyration radius of the giant and is usually about 0.1. We have also made the usual simplifying assumption that the moment of inertia of the giant is much larger than that of the other star. A more massive companion makes the system more stable with respect to Darwin instability. As the giant’s radius grows, the binary system becomes less stable; for a discussion of the competition between orbital separation increase due to mass loss and orbit decrease due to tidal interaction, and the possible onset of the Darwin instability, see Bear and Soker (2010).

It follows that more massive secondaries could be more efficient in bringing the giant envelope to synchronization before entering the CE phase. They are also more efficient in maintaining this stage for a long time. During that time the giant loses more of its envelope in the wind. When the CE finally occurs, as the wind carries angular momentum and/or the giant expands, there is less mass in the envelope. More massive secondaries would therefore tend to have less mass to expel during the CE phase, and so would end the CE phase with a wider orbital separation. In the energy formalism a larger final orbital separation indicates a larger value of $\alpha_{\rm CE}$. Because of this, massive secondaries could be expected to appear to cause larger values of $\alpha_{\rm CE}$. However, more massive companions would be expected to have larger post-CE separations even with the same $\alpha_{\rm CE}$, simply since they carry more pre-CE orbital energy. So the post-CE observational signature of these tidal interactions is not unique.

Nonetheless, this prediction based on pre-RLOF tidal interactions is in fact contrary to that deduced from observations by De Marco et al. (2011), who find that there is a possible negative correlation between the mass ratio of the two stars and the value of $\alpha_{\rm CE}$. Namely, for larger M ₂/M _g the average value of $\alpha_{\rm CE}$ is smaller, as also found by Davis et al. (2011) (although Zorotovic et al. 2010 do not find indications for a dependence of α on the mass of the companion; also, there are enormous observational selection effects favoring short orbital periods). It can be noted that the final separations from observations are all low, irrespective of the mass ratio. De Marco argues that, without needing to make complex reconstructions, this already tells you that the low mass systems have a larger α in the energy formalism.

Soker argues that a possible reconciliation of the apparent contradiction between the finding of De Marco et al. (2011) and his estimate may come from the distribution of initial binary parameters (e.g., more massive secondaries could reside closer to their parent star and so they enter the CE phase at earlier epoch). However, so far there is no observational evidence for such distributions. Alternatively, the difference in effective $\alpha_{\rm CE}$ could arise because the difference in mass affects the physics of the CE ejection. For example perhaps CEE involving more massive companions occurs on a shorter time scale; that could affect the energy redistribution within the envelope to make complete envelope ejection more difficult (see the discussion in Sect. 3.4). And, finally, it may simply mean that tidally induced synchronization before RLOF does not play a significant role in the outcome of CEE.

RLOF and the development of dynamical instability

Once a model donor star overfills its Roche lobe, a theoretical criterion is usually applied to try to determine whether the mass transfer is dynamically unstable. If the RLOF is dynamically unstable, it is usually expected to lead to CEE. However, some special-case systems do exist which we would expect to have experienced dynamically unstable mass transfer seem to have avoided CEE (see the discussion in Podsiadlowski et al. 1992).

The standard analysis of the stability of mass transfer compares the differential reaction of the Roche lobe to mass transfer to the reaction of the donor to mass loss on different time scales (see Hjellming and Webbink 1987). For the purpose of this analysis, the donor has often been treated as a composite polytrope (Hjellming and Webbink 1987; Soberman et al. 1997a). The donor’s reaction is mainly a function of whether the envelope is convective or radiative. However, it is wrong to forget that the existence of a core can make a substantial difference from mass transfer stability (Hjellming and Webbink 1987; Soberman et al. 1997a; unfortunately this is not an unusual misconception—see, e.g., the discussion in Podsiadlowski 2001 and references therein). As an example, a commonly used critical mass ratio ($q_{\rm crit}$) for the stability of RLOF from convective donors with isentropic envelopes is $q_{\rm crit} \simeq2/3$; this value is only relevant for fully convective stars, as stars with cores are more stable (Hjellming and Webbink 1987; Soberman et al. 1997a).

A polytropic equation of state has also been used to derive an analytic solution for the mass transfer rate during the lead up to runaway (Webbink and Iben 1987; Webbink 2010). This phase is difficult to treat self-consistently with a full stellar evolution code so, although the assumptions used are highly idealized, this solution may be of use in setting up the initial conditions of hydrodynamic simulations of CEE.

Recent progress has been made in studying the problem of mass transfer stability using the adiabatic approximation but using realistic stellar structures rather than polytropic stellar models (Ge et al. 2010). These studies have preliminary shown significant differences to the old criteria for when the instability occurs, as well as considerable changes for the same star at different points along the giant branch. The more detailed models show greater stability, with $q_{\rm crit}$ as large as 10 for some of the stars (Ge et al. as reported at KIAA workshop on common envelopes in 2011).

Nonetheless, such work carries the main disadvantage of old studies: the adiabatic approach literally means that the reaction of the star is studied by keeping the entropy profile (at each mass coordinate) fixed. The thermal adjustment time of the outer layers of the star is so short that, even when the mass transfer is taking place on time scales shorter than the global thermal time scale of the star, the entropy profile within the star can deviate considerably during mass transfer from the fixed profile used in adiabatic codes (Podsiadlowski et al. 2002b; Woods and Ivanova 2011; Passy et al. 2012b). In particular, the superadiabatic spike near the surface of the star is not lost in the way that the adiabatic approximation predicts; some of the strong expansion predicted in adiabatic codes is suppressed by retaining this spike.

A further stabilising effect present in reality but absent in adiabatic codes is the finite time taken for the development of the dynamical instability after the start of mass transfer (see the discussion in Han et al. 2002). The critical mass ratio also depends on how conservative the mass transfer is, where less conservative mass transfer leads to more stability and higher $q_{\rm crit}$ (see, e.g., Podsiadlowski et al. 1992; Kalogera and Webbink 1996; Soberman et al. 1997b; Han et al. 2001; Woods et al. 2012). The dynamical stability of RLOF could also be increased by tidal spin-orbit couplings (Tauris and Savonije 2001).

Adiabatic codes are elegant, and provide a clean & well-defined answer about when instability occurs. Adiabatic codes could also be modified by adding artificial thermal relaxation, essentially placing a superadiabatic blanket on top of an adiabatic envelope. Indeed Ge et al. (2010) found that in this case the reaction of the star is typically calculated to lie between the predictions from detailed stellar codes and those produced by adiabatic calculations. However, any modern detailed stellar/binary evolutionary code can also provide $q_{\rm crit}$, without needing to resort to the adiabatic approximation. For example, Han et al. (2002) explicitly calculate values of $q_{\rm crit}$ for use in their own population synthesis calculations; Chen and Han (2008) also use a full stellar evolution code to investigate $q_{\rm crit}$ in detail. Of course both approaches are approximations, and therefore potentially misleading, since neither type of code is really treating the full three-dimensional problem. It may even be that the structure in the vicinity of the inner Lagrangian point is closer to the predictions from adiabatic codes, since there the superadiabatic layer may not be able to rebuild itself (for studies of the flow in this region, see Paczyński and Sienkiewicz 1972 and Fig. 3.6 of Eggleton 2006).

3D and hydrodynamic effects

Fully understanding the onset of CE might well require the inclusion of physics beyond standard stellar calculations. There are two important factors affecting how dynamically unstable the initial phase will be, according to current studies by means of 3D hydrodynamical simulations:

• how strongly the donor is in or out of corotation with the binary,

• what is the value of the total angular momentum.

These two issues are worthy of further consideration. If the initial conditions for hydrodynamic CE simulations are such that the donor is not in corotation with the binary, or if the companion is simply placed at the surface of the donor, then the dynamical plunge-in phase is being forced to start artificially quickly. In both of those cases then the system as a whole is missing some of the angular momentum which it should possess (for companions massive enough that we expect them to spin-up the giant’s envelope). Neither of the approximations reflects the real situation, and the consequences are not yet well understood.

Unfortunately such initial conditions have been commonly used in published simulations, but the degree of non-corotation varies from one research group to another. If we compare two cases: one with 95 % of the appropriate orbital velocity required for corotation in Ricker and Taam (2012) against 0 % as in Passy et al. (2012a), it seems that the more rapid initial rotation may help to eject more material to infinity from the system. Conversely, less rotation could lead to more material being trapped, perhaps in a bound circumbinary disk (this comparison is considered in more detail in Sect. 7). Determining what the angular momentum distribution is in a binary system when the donor overfills its Roche lobe is an important question in properly treating the initial stages of CEE, and is important input in order to make the most of computer time.

Onset of CE from dynamically stable RLOF

It is possible that mass-transferring binaries which do not experience CEE following a standard dynamical instability are still dragged into CEE. This might happen because the accretor cannot accept matter at the rate at which it is being transferred, and also the system as a whole cannot eject the matter rapidly enough. In this case a de facto common envelope could be built up around the stars. Until relatively recently it was thought that thermal-time-scale mass transfer in X-ray binaries could lead to CEE in this way. However, it is now acknowledged that Cygnus X-2 passed through such a thermal-time-scale phase and avoided CEE (King and Ritter 1999; Podsiadlowski and Rappaport 2000; Tauris et al. 2000; Kolb et al. 2000). Another relevant system in this context is SS433, which seems to be transferring matter at ${{\gtrsim} }10^{-4}M_{\odot}\,{\rm yr^{-1}}$ but—so far—appears to have avoided CEE (Blundell et al. 2001; Podsiadlowski 2001).

Double-core evolution is a special case of this (Brown 1995, see also Dewi et al. 2006). In this case the CE phase ejects the envelopes of both stars. Unusually, it requires the mass ratio to be close to 1 (typically within a few percent). If the primary then overfills its Roche lobe as a giant, then accretion onto the secondary might cause it to expand and also overfill its Roche lobe. This leads to a joint CE, in this case formed by matter from both stars, and in-spiral of both cores.

Comparison of state-of-the-art 3D simulations

3D hydrodynamic simulations of common-envelope evolution have been carried out by Ricker and Taam (2012) (hereafter RT) using the grid-based, adaptive mesh refinement (AMR) code FLASH (Fryxell et al. 2000) and by Passy et al. (2012a) (hereafter PDM) using the grid-based code Enzo (O’Shea et al. 2005) in single grid mode and the Lagrangian code SNSPH (Fryer et al. 2006).

The star simulated by PDM was a 0.88M _⊙, 85R _⊙ giant with companions in the mass range 0.1 to 0.9M _⊙, and RT considered a 1.05M _⊙, 31.6R _⊙ giant with a 0.6M _⊙ companion. As the initial masses are similar, the main difference between the initial conditions chosen for these simulations were the initial conditions for the rotation, where RT considered a donor which is almost in corotation with the orbital motion (spun up to 95 % of the orbital angular velocity), whilst PDM took the case when the giant is not rotating at all (see also Sect. 6.4).

In PDM, the grid-based models with 256³ resolution and the Lagrangian 500000 particle models reach essentially the same conclusions, which gives some confidence that there are no major numerical issues in the simulations. The effective resolution of the RT simulations was 2048³.

Final separations and envelope ejection

The dynamical in-fall phase lasts of the order of 50 days in RT and 10 to 100 days in PDM, and the final separations are between a few and ∼30R _⊙. The final orbital separation in RT are few times smaller than the PDM simulations with the same companion mass. However, for both groups these final separations are systematically larger than the observed separations of post-common envelope binaries (De Marco et al. 2011; Zorotovic et al. 2010). One explanation is that the phase immediately following the dynamical in-spiral phase further alters the post-common envelope binary separation. Kashi and Soker (2011) suggested that even a small amount of fall-back mass can create a circumbinary disk which can then tighten the immediately post-CE binary orbit through tidal interactions.

In the RT simulations about 25 % of the envelope is ejected. The PDM simulations stop at the end of the dynamical spiral-in, at which point most of the envelope is still loosely bound—only a small fraction of the stellar envelope is unbound. If this result is physical then the next phase of evolution seems likely to be an in-falling envelope that will then form a disk. The fall-back disk envisaged by Kashi and Soker (2011) is far less massive than the mass of the fall-back material in the PDM simulation (at only 1–10 % of the total envelope mass). The difference in the amount of ejected matter may simply be consistent with RT producing a shorter final binary period. The reason why RT and PDM systematically disagree about the final orbital period is not clear, though different initial conditions seem a likely reason.

Angular momentum

The main difference in initial conditions between RT and PDM is the amount of angular momentum in the giant donor envelope before the spiral-in phase. Since this should affect the speed of the initial plunge, such a difference could easily lead to differing outcomes, perhaps playing an important role in determining the ejection efficiency. Yet the simulations of Sandquist et al. (1998) found that primary spin did not substantially alter the results for their heavier primaries, though for smaller mass ratios than considered by RT. Tidal spin-up of the primary should be efficient for larger companion masses, while for the lower masses (e.g., M ₂≤0.05M _⊙) it might make little or no difference and the primary could be spinning slowly. So, even if pre-CE spin is a factor in ejecting the common envelope, it could apply only to some interactions.

Nonetheless this pre-in-spiral stage should be considered carefully, as it seems likely to be important in affecting the simulations. In PDM the companion is always placed on the primary’s surface with a Keplerian velocity, where the in-spiral starts immediately. Clearly this is unrealistic, since the companion would interact with the giant tidally and through wind accretion for a reasonably long time before falling in. What is not clear is how this initial phase influences the outcome of the interaction. A comparison test ran with the companion placed 5 % farther out or with an orbital velocity slightly larger than the Keplerian value in Passy et al. (2012a) did not alter the final results, though it resulted in marginally larger eccentricity.

We note that RT find that the outflowing matter carries significant angular momentum. That is, the highest velocity components are in the tangential direction rather than in the radial direction. PDM, on the other hand, find the opposite; this difference should be pursued further.

Variations with initial mass ratio

Sandquist et al. (1998) found that the fraction of ejected mass increases with mass ratio (companion mass to red giant) of the system. The result found in RT (for systems with mass ratios closer to unity) are consistent with this trend.

In PDM, lower mass companions take longer to in-spiral, in particular initially, and come to rest at smaller orbital separations, as one might expect (although note that these are not the final separation as the envelope is still bound). However, not only do the observed post-common envelope systems cluster at smaller orbital separations, these separations do not appear to be a function of mass ratio nor secondary mass.⁴ The observations therefore suggest that more massive secondaries (i.e. systems with larger mass ratios, q) are less efficient at unbinding the envelope and so they sink deeper into the envelope despite having plenty of orbital energy to deliver. This is in line with what was determined by De Marco et al. (2011) and independently by Davis et al. (2011). Alternatively, more massive companions might suffer further in-spiral after the envelope is ejected due to one or more alternative physical mechanism(s).

Energetics and $\alpha_{\rm CE}$

RT find that, for their hydrodynamic transfer of orbital energy to the envelope, $\alpha_{\rm CE}$ is ∼25 % based on the amount of matter ejected. PDM deemed it inappropriate to calculate the values of $\alpha_{\rm CE}$ when the envelope has not been ejected. Clearly further energy sources might help envelope ejection if they were included (see Sect. 3). One obvious candidate for inclusion in simulations is the reservoir of recombination energy; it has not yet been shown whether that energy release can be efficiently converted into kinetic energy of the envelope.

Eccentricity

In PDM, the initial eccentricity of the orbit is zero for most of their simulation. By the end of the dynamical in-fall phase a small eccentricity is driven into the system (e∼0.1). Their two simulations where the companion was placed further out or had a larger-than-Keplerian orbital velocity, resulting in a mild initial eccentricity, finished with slightly larger eccentricities than the simulations that were started in circular orbits. Eccentricity measurements on real post-common-envelope systems have not yet reached the level of precision to test this.

Entering self-regulation?

A vital question is whether the endpoints of the simulations in both RT and PDM are simply the start of a longer, self-regulated phase. In the terminology of Sect. 2 is this the end of phase II and the start of phase III? Alternatively, has phase II ended with envelope ejection and no further spiral-in (or a rapid merger)? It would be unrealistic for calculations like this to follow phase III. Furthermore, since the in-spiral time scales involved become so long, it would be natural for calculations like this to look like they are converging on a steady-state in either case.

It might be that, if 25 % of the envelope is ejected in this phase (as found by RT), the rest is ejected in a separate later phase of the CE event, following a period of self-regulated spiral-in. Asymptotically slowing calculations are very sensibly stopped so as not to waste computer time, but we encourage thought as to how to distinguish whether such simulations are entering a phase of self-regulation.

As the time scale of these simulations starts to approach the thermal time scale, processes other than pure hydrodynamics begin to become important. This is the regime in which 1D stellar-evolution type codes seem most useful, as they can typically include more physics than is present in 3D hydro codes. However, we should still be careful to check that assumed symmetries are not too problematic.

Numerical methods

At present it is not possible to treat the whole common-envelope problem with only a single code and a realistic amount of computer time. The dynamical plunge-in phase could be treated with some hydrodynamic codes. The pre- and post-plunge-in stages (the onset of mass transfer and the slow spiral-in) are each likely to occur on a thermal time scale or longer, and could only be treated with a code that includes a full equation of state, and both radiative and convective energy transfer. An appropriate code for these longer phases would be a stellar-evolution code that is adapted to treat at least some specific features of the common envelope evolution, although such codes would currently only treat the problem in 1D and so could miss other key aspects of the situation.

Existing 3D hydrodynamic methods and their limits

A wide variety of numerical tools are available to model the stages of common envelope evolution which are dominated by hydrodynamics. In principle, Lagrangian codes are the most straightforward and accurate: comparing pressures at the centers of adjacent zones gives the acceleration on each zone edge. However, Lagrangian grids suffer in multi-dimensional problems, as the zone edges can become tangled. Eulerian codes avoid mesh tangling, but the relative motion between the matter and mesh leads to numerical advection. A number of advances to the Eulerian grid-based technique have increased the power of Eulerian techniques in modeling common envelope: nested grids, rotating grids, adaptive mesh refinement (AMR). Modern computers also allow sufficiently high resolution smooth particle hydrodynamics (SPH) calculations to study CEE. In addition, adaptive Lagrangian–Eulerian (ALE), particle-in-cell and spectral methods are becoming more common in astrophysics. All of these computational methods provide a wide range of choices for modelers of common envelope evolution. Here we discuss these techniques, focusing on their application to common envelope model simulations.

An important aspect of numerical modeling is understanding the strengths and weaknesses of a given technique and how these strengths and weaknesses will affect the results in a given application. We present an introductory summary of these below.

ALE, as the name implies, tries provide the best features of both Lagrangian and Eulerian codes. Usually they behave like Lagrangian code, with Eulerian-like re-zoning available to avoid mesh tangling. Unfortunately the increased complexity can produce new difficulties. ALE codes are strong in problems such as core-collapse where the stellar core collapses, nearly spherically, several orders of magnitude in space before turbulence sets in. In such problems, a strict Lagrangian code, followed by an Eulerian turbulence calculation takes advantage of the strengths of the adaptive Lagrangian–Eulerian technique. It is not clear that the common-envelope problem has features where a pure Lagrangian capability will be important and ALE’s strengths may not be well-suited for the common envelope problem.

Particle-in-cell codes are generally adopted where detailed microphysics must be modeled, and we are not at this stage for common envelope calculations. Finally, the sensitivity of spectral methods to boundary conditions make complex problems such as modeling the common envelope process daunting. At this point, it is not clear that these 3 “new” techniques are ideally suited for the problems associated with CEE. Instead, we will focus on basic grid-based and SPH techniques.

Strengths of Eulerian, grid-based codes

• History and Code Base: The long history of grid-based schemes in computational physics has led to a number of schemes developed to better model shocks and include additional physics such as radiation transport.

• Tracing space, not mass: Grid-based codes are ideal for low-mass flows: e.g., winds, mass streams in accreting binaries, and the low-density cavities that might be formed during CEE.

Weaknesses of Eulerian, grid-based codes

• Advection term: The advection term in the hydrodynamic equations of a grid-based code generally does not allow strict momentum or angular momentum conservation and it leads to numerical diffusion of heat and materials. Local non-conservation leads to global non-conservation. For calculations of the common-envelope problem, the lack of angular momentum conservation can alter the final result.

• Tracing mass: Grid-based codes are not ideal for tracing mass, and that makes following the ejecta in a common envelope calculation difficult.

• Shock modeling schemes: Although the shock modeling schemes used in grid-based codes are ideal for shocks along the grid, they are not so accurate off-axis and conserve total energy often at the expense of getting erroneous internal energy estimates.

• The re-zoning in AMR cannot simultaneously conserve energy, density and pressure gradients and some care must be given to re-zoning algorithms.

Strengths of smooth particle hydrodynamics

• Linear and Angular momentum are conserved. However, strict conservation is not maintained with gravity implementations.

• Ideally suited for problems tracing mass, e.g., the ejecta in a common envelope phase.

Weaknesses of smooth particle hydrodynamics

• Low-mass streams are difficult to model. SPH is not an ideal tool to model the initial onset of the common envelope phase (though see, e.g., Church et al. 2009).

• Low-density bubbles or cavities formed inside the (departing) envelope might also suffer from poor resolution.

• Most implementations use artificial viscosity to model shocks. This typically broadens the shock front, preventing crisp shock models. In addition, the artificial viscosity may over-estimate the amount of friction in the flow.

• Setup is generally more difficult. For example, careful thought and wisdom is needed to make the best choice of particle mass for a particular problem.

• Few off-the-shelf packages are available with which to include additional physics.

For further discussion of the practical strengths and weaknesses of SPH see, e.g., Price (2012); for more formal reviews see, e.g., Rosswog (2009) and Springel (2010).

In any CE calculation adopting either grid- or particle-based schemes, we must worry about how the scheme implements gravity. Typically, SPH schemes use tree-based gravity schemes, as do many AMR codes (Barnes and Hut 1986; Warren and Salmon 1993, 1995). Multipole schemes are also prevalent in grid-based codes. Each gravity routine carries with it numerical artifacts and these must be understood. Tree-based schemes are accompanied by a multipole acceptability criterion (MAC) and this can be easily tuned to determine the errors in the gravity routine (Salmon and Warren 1994).

Boundary conditions can also pose problems for both grid- and particle-based schemes.

Code comparison can be an extremely powerful tool to distinguish between the numerical artifacts of different schemes, as performed for CEE by Passy et al. (2012a).

Finally, we stress that any numerical scheme must be used with care. Understanding the weaknesses of a technique is critical to interpreting the results.

A novel generalization of mesh-less methods

As with other approaches, new numerical methods can be developed. In Electronic Supplementary Material 1 we demonstrate this by showing that Lagrangian particle-based methods are a subset of more general mesh-less finite-volume schemes. The spatially discrete equations have the same form and properties as the ones for mesh-based finite volume numerical schemes, whilst the geometrical quantities (corresponding to volumes and areas in mesh-based schemes) are expressed as spatial integrals in mesh-less schemes. As a concrete example we also show that several approximations are needed to obtain the SPH equations in closed form suitable for numerical integration, and these approximations introduce certain inaccuracies. The approximation can be improved with high-order numerical quadratures, but the computational cost and complexity of these may well be comparable to that of unstructured mesh construction in mesh-based schemes. This mesh-less generalization breaks down the artificial differences between mesh- and particle-based methods, and hopefully opens the way for codes which have the advantages of both types.

1D simulations: what can be learned?

Early attempts at simulating the CE phase in one dimension produced some successes. The simulations of Meyer and Meyer-Hofmeister (1979) set the time scale for CE evolution at around 1000 years. However, these simulations were unable to model higher-dimensional effects such as the preferential ejection of material in the orbital plane (Bodenheimer and Taam 1984) or the spiral shocks and circulation currents generated by the in-falling cores (Taam and Sandquist 2000). If these effects are not included, simulations of CE evolution lead to very different results and often suggest no mass ejection at all.

Clearly we would like to be able to run full three-dimensional high-resolution hydrodynamic simulations of the CE phase for multiple systems, but unfortunately the computing power required to do so on a reasonable time scale is still many years away. It would be extremely useful if we could use detailed three-dimensional models to gain sufficient understanding of the non-spherical processes so that we could derive a one-dimensional parameterization of the missing effects. One-dimensional models have the strong advantage that they can be run sufficiently quickly that the CE phase of a large number of systems can be modeled at the expense of relatively little computing time. This would allow us to come up with quantitative prediction for the outcome of a CE phase for a wide range of systems.

The early one-dimensional simulations of Meyer and Meyer-Hofmeister (1979) assumed that the angular momentum in the CE was deposited into the envelope by the spiraling cores and then redistributed diffusively by convection leading to a steady state distribution satisfying

$$ \frac{\partial}{\partial r} \biggl({\mu r^4\frac{\partial\varOmega }{\partial r}} \biggr)=0 $$

(14)

where μ is the convective diffusion coefficient which was taken to be uniform. This is a very simple approximation which could easily be improved upon given our current knowledge. In particular, we stress that it is essential to restore the time-dependence of the angular momentum distribution because the evolution of the envelope can occur on a dynamical time scale.

An example of a similar model including some of the missing physical effects is:

(15)

where we have used a model similar to Meyer and Meyer-Hofmeister (1979)—based on angular momentum conservation—but we have included a number of important terms:

• U is a term for advection of angular momentum by circulation, similar to the Eddington–Sweet circulation expected in rotating stars (Zahn 1992).

• μ, the standard diffusion coefficient, has been retained, but we can now reasonably model its spatial variation. It has been noted that some numerical simulations predict a single convective cell in the CE (Taam and Ricker 2010). This may require revising the diffusion coefficient from the one predicted by standard mixing-length theory. Note that this diffusion coefficient assumes angular momentum is transported by shear-induced turbulence or some similar process so that the system tends towards solid body rotation.

• ν is an additional diffusion coefficient. This represents the alternative possibility that fluid parcels are able to retain their angular momentum. In this case the system tends towards a state of uniform specific angular momentum (e.g., Arnett and Meakin 2010).

• $\dot{J}$, the source term on the right-hand side, describes how angular momentum is deposited in the envelope. In the standard approximation this is a delta function. However, models show that spiral shocks produced by the cores are responsible for depositing much of the angular momentum (Taam and Sandquist 2000) so it seems more sensible to choose a smoother function.

The forms of U, μ, ν and $\dot{J}$ are currently unknown. More work is needed to derive reasonable prescriptions for them based on three-dimensional results.

We can also use three-dimensional results to refine our models for accretion of material by the cores, the rate at which they deposit energy into the envelope and the rate of mass loss from the system. With sensible treatments for these effects, a one-dimensional approximation of CE evolution could be used to predict how the ejection time scales and post-CE properties of binary systems might vary for a wide variety of initial conditions.

Compact objects and hypercritical accretion

Stars spiralling into the envelope of their companion are usually expected to be limited in the rate at which they can accrete to the rate at which the force of the radiation released in the accretion is equal to the inward gravitational force in a spherical model, i.e. the Eddington rate. For a neutron star accreting hydrogen-rich matter, this limiting rate is ∼1.6×10⁻⁸ M _⊙ yr⁻¹. Although a derivation based on spherical accretion is not strictly valid when accreting material with angular momentum, in most astrophysical phenomena, the maximum accretion rate onto a neutron star lies within a factor of a few of this value.

But the accretion rates in common envelope evolution can be so high that the emitted radiation is trapped within the flow. At these accretion rates, the temperatures at the base of an accreting neutron star are sufficiently high to drive neutrino emission. These neutrinos can remove the potential energy released from accretion without generating any significant radiation force to prevent further accretion. In such conditions, the neutron star could accrete well above the Eddington rate, a process known as hypercritical accretion.

If hypercritical accretion happens, it might prevent the formation of some neutron-star X-ray binaries and close double-neutron-star systems through the canonical CE formation channel. This led to the proposal of double-core CE evolution as an alternative mechanism for the formation of such systems (Brown 1995, see also Dewi et al. 2006). Hypercritical accretion could also prevent the formation of Thorne–Żytkow objects (Thorne and Zytkow 1975, 1977).

For hypercritical accretion to occur, the photon radiation must be trapped in the flow. One way to estimate this trapping is to compare the in-fall velocity of the accreting material to the diffusion velocity of the radiation(Chevalier 1993). The accretion velocity ($v_{\rm acc}$) is given by the accretion rate assuming a spherical inflow:

$$ v_{\rm acc} = \dot{M}_{\rm acc}/\bigl(4 \pi r^2 \rho \bigr) $$

(16)

where $\dot{M}_{\rm acc}$ is the accretion rate onto the neutron star and ρ is the density at radius r. The corresponding diffusion velocity ($v_{\rm diff}$) is

$$ v_{\rm diff} = r/t_{\rm diff} = r \frac{\lambda_{\rm mfp} c}{r^2} = c/(\rho\kappa r) $$

(17)

where $t_{\rm diff} = (r/\lambda_{\rm mfp})^{2} \lambda_{\rm mfp}/c$ is the diffusion time, $\lambda_{\rm mfp} = 1/(\rho\kappa)$ is the mean free path of the photon, κ is the photon opacity (for ionized hydrogen, this is 0.2 cm² per g), and c is the speed of light. For the radiation to be trapped in the flow, $v_{\rm diff}$ must be less than $v_{\rm acc}$. Solving for the accretion rate, we find

(18)

If we assume Bondi–Hoyle accretion, the accretion rate exceeds this value for many massive giants (Fryer et al. 1996). Actual accretion rates can be 1–2 orders of magnitude less than the Bondi–Hoyle accretion rate because the accretion radius (r) is smaller than the effective Bondi–Hoyle radius. Even so, if the neutron star spirals deeply into the giant envelope, the photons will be trapped, allowing the possibility of hypercritical accretion, i.e. the Eddington limit might be beaten.

For hypercritical accretion to work, neutrinos must effectively cool the accreting material. We can use equilibrium atmospheres to calculate the neutrino cooling time scale (Fryer et al. 1996). This calculation assumes that, as the material piles onto the neutron star, it convects and forms a constant entropy atmosphere on top of the neutron star. The neutrino cooling time scale must be shorter than the photon diffusion time scale for it to dominate the cooling. By comparing these time scales, Fryer et al. (1996) found that this criterion corresponds to material entropies below 600k _B per nucleon. Typical stellar material has entropy below 50k _B per nucleon, i.e. well below that threshold. However, shock heating will raise the entropy (S) of the accretion flow above values typical for stellar material (Fryer et al. 1996):

$$ S=374 \biggl( \frac{M_{\rm NS}}{1.4M_\odot} \biggr)^{7/8} \biggl( \frac{\dot{M}_{\rm acc}}{10^{-4}M_\odot\,{\rm yr^{-1}}} \biggr)^{1/4} \biggl( \frac{r}{10^{10}~{\rm cm}} \biggr)^{-3/8} $$

(19)

where $M_{\rm NS}$ is the mass of the neutron star. Nonetheless, this constraint is less restrictive than Eq. (18) so we can assume that if the photons are trapped in the flow neutrino cooling will allow hypercritical accretion.

However, we repeat that this derivation assumed that the unstable accretion atmosphere will efficiently convect such that the entropy remains in instantaneous equilibrium throughout that atmosphere. In nature, this convection is explosive and will likely drive outflows that can ultimately reduce the rate of mass accretion. These uncertainties make it difficult to determine the exact criterion for hypercritical accretion. To an order of magnitude, hypercritical accretion is likely to occur if the estimated Bondi–Hoyle accretion rate is greater than 10⁻² M _⊙ yr⁻¹. Below this value detailed calculations are required. However, the Bondi–Hoyle–Lyttleton prescription significantly overestimates the rate observed in simulations (see Sect. 3.3.5 and the detailed discussion in Ivanova 2011); if current simulations are producing the correct answer for the accretion rate then it is unlikely that hypercritical accretion will take place during CEE (100 times less than estimated Bondi–Hoyle accretion rate, or 10⁻³ M _⊙ yr⁻¹ Ricker and Taam 2012).

Linking with observations

Since a CE event is short-lived, it might be argued that we are highly unlikely to catch it while it occurs (although see Sect. 10.2), in which case we could only observe the resulting post-CE systems (including post-CE nebulae). Our lack of full-scale simulations of all the phases does not improve the situation, as we have few definitive physical predictions to offer.

As explained in Sect. 8, 3D simulations currently only help with understanding the appearance of dynamical-time-scale events, i.e. very short-lived phases which are unlikely to be observed. Even their predictions for post-CE appearance are only directly applicable for CEE events which end after the dynamical plunge-in phase. On the other hand, the appearance of a CE object during a long-lasting self-regulating phase is currently provided only by 1D calculations and, since it is certain that systems undergoing CEE (or merging) will not be spherically symmetric, we must be cautious about applying 1D calculations when we do see systems undergoing CEE or during mergers. At least if a CE ends in a merger, the evolution of this merger product can be understood by means of a regular stellar code, once the structure of the merger product is determined.

So far, the community has mostly only been able to link models to observations for populations of post-CE systems. Even in this case, we stress that comparisons are usually performed within the framework of the α-formalism. These studies principally aim to calibrate our existing parameterization, fine-tuning $\alpha_{\rm CE}$-values using post-CE masses and periods (recent examples, Zorotovic et al. 2010; Davis et al. 2010, 2011; De Marco et al. 2011). Other parameters (e.g. α _th) can be added, and the parameters can be allowed to vary systematically between systems, but even this might well miss real physical complexity. As discussed in Sect. 3, there is no reason why the effective value of $\alpha_{\rm CE}$ cannot vary drastically even between systems with similar initial conditions. Moreover, the calibration results produced by different groups sometimes show opposite trends; see the discussions in Sects. 6.2, 7. Here we will pay attention to other characteristics of post-CE systems as possible keys to understanding common-envelope evolution.

A priori expectations of appearance during CEE

Whilst the plunge-in is proceeding, the envelope of the primary star expands. A giant donor rapidly evolves up its giant branch, though appearing colder than a regular giant of the same luminosity (Ivanova 2002; Podsiadlowski and Ivanova 2003), being closer to the Hayashi line. The degree of the expansion of the bound envelope at the end of the plunge-in phases—and therefore also during the self-regulating spiral-in—depends on the mass ratio, on the primary initial mass and on its radius (or luminosity), although it is not currently possible to specify the sensitivity with respect to these parameters.

As an example of the lack of our current understanding, we first describe some results taken from 1D simulations (described in full detail in Ivanova 2002 and in parts in Han et al. 2002; Ivanova and Podsiadlowski 2002, 2003b). A 1.6M _⊙ giant with a pre-spiral-in radius of about 140R _⊙ was found to expand 3-fold during a common envelope event with a 0.3M _⊙ companion, on a time-scale of 20 years. During the plunge-in phase, a 20M _⊙ giant with a pre-CE radius of 1100R _⊙ expanded by a factor of about 2.5 over 100 years when the companion had a mass of 5M _⊙, but when the companion had a mass of 1M _⊙ then the expansion was greater (a factor of 4) and the plunge-in is more rapid (taking place in only ∼50 years). In that second case, the spiral-in of the 1M _⊙ companion never changes to become self-regulating. The more aggressive spiral-in might partly explain why the lower-mass secondary produced greater envelope expansion, though the difference in spiral-in duration is less than a factor of two.

Using a giant of 0.9M _⊙ (with a radius an order of magnitude different from the 20M _⊙ star in the previous example), the 3D simulations of Passy et al. (2012a) found that the orbital decay of less massive companions takes slightly longer than for more massive companions. It is perhaps not surprising that a very different situation, modeled using very different methods, results in the opposite trend. But our lack of understanding of that difference is significant. We note that the degree of expansion of the bound envelope in the two cases is similar (a factor of several).

It might be that this particular time-scale comparison between codes is invalid, i.e. that we are not comparing physically quantities with similar meaning. We define the ‘fast plunge-in’ to start when the envelope begins to expand. In 1D, this fast plunge-in starts gradually, whilst in 3D it is forced to coincide with the start of the simulations due to the choice of initial conditions. Also the 3D results do not provide a single value for the radius of the envelope, so it is not clear when exactly fast envelope expansion started.

The stellar expansion is directly related to the increase in luminosity, by 4–16 times (by up to 3 magnitudes) for the cases described above. At the very end of the self-regulating spiral-in phase, if the binary is not fated to merge, the envelope experiences another fast expansion.

Before the envelope is ejected, 1D simulations find that this CE may also experience pulsations of increasing strength (see, e.g., the case with 1.6+0.3M _⊙ from Ivanova 2002), before becoming unbound. The period of pulsations is about several years; at least an order of magnitude longer than star’s dynamical time scale. There are no 3D simulations for this stage. Furthermore, the important time scale to develop these pulsations is significantly longer than the dynamical one, and existing 3D hydrodynamical codes do not contain all the physics necessary to reproduce them.

Likewise, none of the numerical methods (1D or 3D) used thus far is capable of obtaining the beginning of envelope ejection via outflows as discussed in Ivanova and Chaichenets (2011).

Observed transients as potential CE events or stellar mergers

Despite being a relatively short-lived event, CEE is expected to be accompanied by a rise in luminosity which could be detected as a transient event. V838 Mon-type eruptions and the great eruption of η Car have both been argued to be potentially caused by violent binary interactions.⁵ In particular, V1309 Sco (a V838 Mon-class event) seems to be the most promising case so far for an active CE event (or merger) being caught in action.

The discovery of V1309 Sco was reported by Nakano et al. (2008) and it was identified as a “red nova” or “V838 Mon-type eruption” using VLT/UVES followup observations by Mason et al. (2010). The eruption was detected early in September 2008 and took place in the field of view monitored by the OGLE project (Udalski 2003). Tylenda et al. (2011) reported the detection of the progenitor up to six years prior to the outburst. The pre-outburst primary was classified photometrically as an F-type giant (Rudy et al. 2008).

Prior to the outburst the object was an eclipsing contact binary with an orbital period of ∼1.4 days, however, the orbital period was not constant and decreased by 1.2 % between 2002 and the outburst in 2008. This orbital period is arguably too long to classify the progenitor as a W UMa-type binary, which would be expected to merge as the primary leaves the main sequence (Webbink 1976; Rasio 1995). However, the orbital period is also too short to say that the binary contained a very evolved giant. For such a primary, especially considering the apparently comparatively low mass of its companion, the theoretical prediction would be that a common envelope event would be likely to result in a merger rather than in envelope ejection.

Between 2002–2006 the light curve showed two maxima and two minima during each orbital period, but transitioned to a single maximum and minimum in 2007. During the same time, the brightness of the progenitor increased to I≃15.5 in April 2007 and then decreased by ∼1 magnitude until March 2008, when the brightness began to rise exponentially. At its peak in September 2008, the object was ∼6 magnitudes brighter than before the outburst (Tylenda et al. 2011).

During the first five months of the rise, the characteristic time scale for the increase in luminosity was 27 days. During the outburst and the subsequent decline the spectral type changed from F9 in September 2008 to M7 in April 2009 and M3 in October 2010 (Tylenda et al. 2011). This is similar to the observed evolution of V838 Mon itself (see, e.g., Tylenda 2005).

It is tempting to interpret these results as a binary that evolved from a contact system (before the second peak in the light curve disappears) to a stable common-envelope systems (after the second peak has disappeared but before the outburst) followed by a merger (when the exponential increase in the luminosity begins); see also Stȩpień (2011). It is noticeable that the behavior is qualitatively as predicted by simulations. Quantitative comparisons are less helpful, since no simulations for such a system have been published. Nonetheless the increases in luminosity and radius are much larger, and the post-outburst decline in luminosity also more rapid, than might have been expected based on the published simulations involving larger, more evolved giants (as described in Sect. 10.1).

So V1309 Sco seems like an excellent candidate for an individual system which has been observed during the CEE phase. The fact that we have evidence for a pre-outburst binary nature is especially compelling in that case. The resemblance to V838 Mon is strong enough for us to consider a link to CEE very likely in that case too. Indeed, stellar merger models were proposed as potential explanations very soon after the discovery of the V838 Mon outburst (see, e.g., Bond et al. 2003; Soker and Tylenda 2003; Retter and Marom 2003; Tylenda 2005; Tylenda et al. 2005).

A wider class of transients with similarities to V838 Mon also invite a possible CEE explanation: “red novae”. Those objects are not novae by their physical nature, despite their observational similarities; for that reason alternative names for this class have been suggested, including “intermediate-luminosity red transients” and “intermediate luminosity optical transients”. These events have luminosities between novae and supernovae, with peak absolute visual magnitudes of −13M _V to −15M _V . During the outburst the source is cold—hence red—unlike a normal classical nova. The energy involved in producing these events is order-of-magnitude comparable to the likely orbital energy release from CEE or the binding energy of the envelope (about 10⁴⁷ erg, Bond et al. 2009; Kulkarni et al. 2007). Specific examples of this class include M85 OT 2006-1 (Kulkarni et al. 2007; Ofek et al. 2008), NGC300 OT 2008 (Bond et al. 2009; though see Kashi et al. 2010 for an alternative scenario which involves rapid mass transfer from an extreme AGB star on its MS companion), PTF 10fqs (Kasliwal et al. 2011) and M31 RV (Bond 2011, and references within). The rate of similar events has been estimated to be as much as 20 % of the core collapse SN rate (Thompson et al. 2009). The observed ejecta velocities also broadly match what might be expected from CEE (or a stellar merger). Kasliwal et al. (2011) detected expansion velocities in PTF 10fqs of ${\sim}1000~{\rm km\,s}^{-1}$. For NGC300 OT 2008 a wide range of velocities have been published, from ${\sim} 75~{\rm km\,s}^{-1}$ (Bond et al. 2009), to ${\sim}1000~{\rm km\,s}^{-1}$ (Berger et al. 2009). The low-velocity end of that range is easily compatible with CEE, or a stellar merger model involving a large giant star. Velocities of ${\sim}1000~{\rm km\,s}^{-1}$ suggest that the primary star would have had to be less extended, but this still could be compatible with an early giant, as was observed in the example of V1309 Sco. For more discussion on a possible connection between intermediate luminosity red transients and CEEs see Ivanova et al. (2013).

Post-CE appearance

If the CE event results in a merger, then the initial post-event reaction of the star is the rapid evolution of a star out of its thermal equilibrium. In this case the star is overluminous, and contracts towards equilibrium as it radiates away excess energy. This contracting sequence, just like during the plunge-in phase, goes along the giant branch, though now towards smaller luminosities—during a spiral-in and subsequent merger, the primary star performs a loop on the HR diagram around the giant branch. After this fast contraction had finished, its further evolution depends on the details of mixing of the inner layers, and may be similar to a normal giant evolution (although perhaps with abnormal surface composition). Abnormal chemical compositions may include enhanced abundance of He (up to 0.4, Podsiadlowski and Ivanova 2003) or s-elements (Ivanova and Podsiadlowski 2003b), as well as unusual CNO ratios (Ivanova and Podsiadlowski 2003a). B[e] supergiants might well be post-merger systems (Podsiadlowski et al. 2006).

In some cases then post-merger massive stars are able to reach core-collapse as a blue supergiant. This explanation for the progenitor of SN 1987 A is now well-established, largely as a result of the distinctive triple-ring nebula which was formed following the merger (Podsiadlowski 1991, 1992; Podsiadlowski et al. 1991; Morris and Podsiadlowski 2006, 2007). Other information about the violent past of merger products could be provided by the shape of the nebula around it (e.g., Morris and Podsiadlowski 2009).

Post-merger giant stars could well be rapidly rotating, and giants with unusually high surface velocities have been identified (Garcia 2011). Stars where only the surface layers are rapidly rotating could be especially notable: potentially a low-mass companion is still orbiting in the outer, low-density, layers of the giant.

Let us now consider in more detail cases when CE leads to survival of the binary.

Post-CE eccentricities as a constraint on time of the ejecta

One potential constraint on CEE that has received little previous attention is the post-CE orbital eccentricity. If we detected post-CE eccentricity then it would be a useful indication in trying to understand the end of the preceding CE phase. However, eccentricity is fragile. For fixed angular momentum, circular orbits have the lowest energy, so energy dissipation can act to circularize orbits following the CE phase. So the effects of tidal circularization (Zahn 1977) largely rule out many binaries from giving us useful information on eccentricities (e.g. the large class of main-sequence + white dwarf binaries). However, binaries in the nuclei of planetary nebulae should still be helpful, since in their case there has been insufficient time since the ejection of the envelope for tides to have had a significant circularizing effect. Another promising exception is a single long-period main-sequence + white dwarf system we mention below.

Potentially useful classes of systems are white dwarf–white dwarf and white dwarf–neutron star binaries, along with systems containing an sdB star and a compact remnant. In these binaries post-CE circularization is expected to be ineffective. SdB stars are radiative, and relatively short-lived; tidal circularization is believed to be much less effective in radiative stars than ones with convective envelopes (Zahn 1977).

What might we learn? We expect that the two stars entering a CE to be in a near-circular orbit due to pre-CE tidal interactions. However, 3D simulations show that the eccentricity grows rapidly during the early spiral-in phase. Ejection immediately following the dynamical plunge might therefore leave residual eccentricity, which could potentially be used as a diagnostic of this phase. Current 3D hydrodynamic simulations produce small eccentricities at the end of this phase ≲0.1. However, if the system continues into a slower self-regulated spiral-in, the eccentricity built up during the previous plunge is likely to be damped away. Observed eccentricities (or lack of) may then largely tell us how effective and long-lasting this self-regulated phase is.

Another possibility is that the post-CE eccentricity could be increased by the presence of a dynamically significant, close circumbinary disk—if one exists. Tidal interactions with such a disk should be strongest at apastron, which tends to amplify any existing eccentricity (Artymowicz et al. 1991). Any observed eccentricities may indicate that such disks are present.

For the most part observed post-CE systems do not have significant eccentricities. Limits are typically of the order ϵ<0.05 from radial velocity work, although with more work upper limits on any eccentricity present of around 0.01 should not be hard to achieve (generally the determination of periods rather than eccentricities has been the target of radial velocity work). In eclipsing cases, one can reduce the errors by a further factor of 10 or so, and in pulsar binaries, one can reach uncertainties in eccentricity of order ϵ∼10⁻⁶. However, apparent eccentricity detections should be treated with caution as the measurement of eccentricity is always biased to be positive by whatever errors are present (since the probability distribution is necessarily one-sided). Applying a strict >5σ criterion, there are two cases of significant eccentricity amongst the sdB binaries which are PG1232-136 (ϵ=0.060±0.005) and [CW83] 1419-09 (ϵ=0.039±0.005) (Edelmann et al. 2005). One other interesting case is G 203-47, an M3.5V star in a 15-day orbit with a white dwarf and having an eccentricity of ϵ=0.068±0.004 (Delfosse et al. 1999). With only a few examples, against many non-detections, one should be wary of Kozai-cycle driven eccentricity (Kozai 1962), yet perhaps there is some potential for learning about the CE phase from eccentricities.

Planetary nebulae as a constraint on ejecta velocities and time scales

Approximately one in five planetary nebulae (PNe) are ejected common envelopes (Han et al. 1995; Bond 2000; Miszalski et al. 2009b). The potential role of CE ejection in shaping PNe morphology was considered very soon after CEE was proposed (Webbink 1979). Hence studying the diverse shapes and velocity distributions of nebulae like these should give us insights into the CE ejection mechanism. One may expect these PNe to all have the same shape in virtue of the common phenomenon that generated them. In particular one may expect a traditional bipolar shape, promoted by the loss of the AGB envelope in the equatorial plane (Sandquist et al. 1998; De Marco et al. 2003), followed by a spherical fast wind from the hot primary, which swept past the ejected common envelope. While this picture is expected, its realization can take various shapes—see Fig. 6 and Figs. 4 to 6 in De Marco (2009).

Fig. 6

Post-CE planetary nebulae with known compact binaries as central objects. Top left—Necklace Nebula (image credit: NASA, ESA, and the Hubble Heritage Team (STScI/AURA), for details see Corradi et al. 2011); top right—NGC 6337 (credit to Corradi, for more details see Corradi et al. 2000); bottom left—ETHOS 1 (credit to B. Miszalski, for more details see Miszalski et al. 2011; Boffin and Miszalski 2011); bottom right—NGC 6778 (credit: Guerrero and Miranda 2012)

Initially, shapes around the few known post-CE PNe appeared not to be systematically bipolar (Bond and Livio 1990; Zijlstra 2007). It was noted, however, that post-CE PNe lack the multiple structures that may form over several phases of varying mass-loss, in line with their AGB evolution having been interrupted. Morris (1981) and Soker (1997) suggested that bipolarity in PNe is promoted by those binary interactions that avoid a common envelope phase. However, later studies based on a larger number of post-CE PNe, showed that there is at least a tendency for post-CE PNe to have bipolar shapes (De Marco 2009; Miszalski et al. 2009a), or a shape that results from a faded bipolar structure. In addition, common-envelope PNe also seem to share a propensity to exhibit low ionization features, knots and filaments embedded in larger, toroidal structures (Miszalski et al. 2009a). Shaping of PNe by magnetic fields has also been considered, although (Jordan et al. 2012) find no observational evidence for significant magnetic fields in their sample of central stars of aspherical PNe. It has been argued that at least one highly collimated pre-PN can be shaped by magnetic fields (Vlemmings et al. 2006). Although pre-PN central stars are not likely descendants from common envelopes, it is highly likely that wider binary interactions caused the magnetic fields in the first place (for theoretical arguments against shaping of PNe by single star, global magnetic fields see Soker (2006); see also Sect. 3.3.6).

A detailed kinematic analysis of post-CE PNe should be able to give significant insight on the common envelope ejection phases and time scales. As an example, Mitchell et al. (2007) carried out a detailed kinematical analysis of the eclipsing post-common envelope binary central star of PN Abell 63. In this edge-on object, a tube-like disk is expanding at 17±1 km s⁻¹ along the orbital plane and two tenuous, collimated lobes with bright caps are expanding perpendicularly to the plane of the disk and the plane of the orbit at $126\pm23~{\rm km\,s}^{-1}$. The lobes appear to have preceded the disk formation by a few thousands years. Very similar kinematics are seen in other post-common envelope PNe, such as ETHOS 1 (Miszalski et al. 2011, bottom left image on Fig. 6) and the “Necklace” (Corradi et al. 2011, top left image on Fig. 6). One interpretation of these objects is that a collimated outflow (perhaps even a jet) was active during or shortly before the envelope was ejected. On the other hand the kinematic analysis of NGC6778 shows that the two jet pairs are kinematically younger than the main nebula. These two jet pairs also have different velocities and seem to be curved (Guerrero and Miranda 2012). Further detailed studies of PN around post-CE central stars should provide us with a great deal of insight onto the CE phase.

Double-core common-envelope evolution

In standard CEE, it is typically assumed that only one of the pre-CE stars has a well-developed core and extended envelope, whilst the in-spiralling companion star is assumed to be relatively dense. The special case where both stars have expanded to giant-type structures by the onset of CEE is referred to as double-core CEE.⁶ Successful envelope ejection from double-core CEE would expose both cores, i.e. it would result in a binary composed of the cores of both the pre-CEE stars. This possibility was briefly mentioned earlier in the context of the onset of CEE, since double-core CEE does not normally begin following tidal instability or dynamically unstable mass transfer (see Sect. 6.5). So, if double-core CEE ever occurs, this fact would at least increase our understanding of which systems undergoing mass transfer are unstable to entering CEE. Observational confirmation that double-core CEE occurs—or does not occur—is not yet available, but it seems worth continuing to investigate known systems to try to constrain the incidence of this process. For example, the existence of double He-rich hot subdwarf binaries might provide evidence that double-core CEE does happen in some cases (Justham et al. 2011). The formation of double neutron-star binaries was the original motivation for suggesting double-core CEE, and some of them may indeed be produced through this channel (Brown 1995; Dewi et al. 2006). However, the different spins of the observed double neutron star systems suggest that these known systems did not evolve through double-core CE. It also seems plausible that the apparent mild recycling of the older neutron stars in the observed systems is due to mass transferred during the thermal core readjustment following a normal, single, envelope ejection (Ivanova 2011).

Conclusions and directions for future work

We have attempted to reassess everything that we know to-date from the theoretical point of view about the physics of CEE and related events. This has included comparing and trying to understand the main features of the most recent hydrodynamic simulations of CEE, along with the relevant numerical methods. We have also briefly discussed some of the more direct—and hence hopefully less misinterpretable—observational constraints.

Most importantly, we have tried to understand CEE from a physical point of view with the eventual aim of replacing the existing top-down parametrizations (such as the energy formalism) with a bottom-up description. However, it is clear that this problem is exceptionally complex. Any individual CEE event consists of several sub-phases occurring on a wide range of time scales and under the influence of diverse physical mechanisms. No existing numerical method is capable of grasping it all. Moreover, pen-and-paper arguments still do not agree on which are the dominant physical processes, and which physics (if any) can be neglected.

In order to make progress, therefore, we need to determine how to study the phases within CEE in a self-consistent way, whereby the outcome of one phase becomes a realistic initial condition for the next phase. In addition to dividing CEE into separate phases in time, each phase can be attacked from different directions: we can try to define useful self-contained problems which are both manageable and interesting.

It should be clear from this work that there are still many points of disagreement within the community. For example, a strong constituency believes that CEE is an intrinsically 3D problem: if that is correct, then great care would have to be taken over which 1D simulations, if any, would be worthwhile to perform. Nonetheless, there are some theoretical and modeling goals which we think are both useful and realistically tractable. These include:

• 1. Understanding pre-CE evolution would help to better initialize CE simulations. We should aim to constrain:

  • The conditions needed to start a CE phase. Even the range of systems undergoing RLOF which lead to CEE via dynamically unstable mass transfer is not yet fully known.

  • The angular momentum distribution of the matter at the start of hydrodynamical simulations.

  • The pre-dynamically unstable phase. This includes the time between the start of RLOF and CEE as well as, e.g., enhanced winds before RLOF properly begins.

• 2. During CEE, we should concentrate on a better physical understanding of:

  • How one phase transforms into another phase, e.g. when a dynamical plunge-in becomes a self-regulated spiral-in, or when a self-regulated phase ends.

  • Whether and how recombination works in order to provide the envelope with momentum. At the very least we need to equip hydro codes such that ionization is included in their equations of state.

  • To what extent the energy from the binary orbit is transferred to the envelope through viscosity and local frictional heating, or through large-scale gravitational interactions (i.e. spiral waves).

  • How fine-tuned envelope ejection is, i.e. how close is the ejection velocity of each element to the local escape velocity.

  • The location of the bifurcation point that separates the ejected envelope from the bound remnant.

  • How outflowing envelopes are shaped, partly in order to allow comparison with the morphologies of PNe.

• 3. Developing and understanding codes and methods for CEE, by:

  • Comparing existing 3D hydrodynamic codes and results. This includes understanding the influence of the initial conditions as chosen by different groups, whether using the same or different types of code.

  • Attempting to treat the problem using coupled 1D and 3D codes, to try to take advantage of their differing strengths. For example, 3D hydro could be used to produce energy input source terms for a 1D code. Even grafting model atmospheres onto 3D simulations could help us understand the observational signatures of systems entering CEE.

  • Thoughtfully dividing the set of possible simulations into those which can be treated with 1D codes, and which need 3D.

Whilst it is too early to speak about a detailed comparison with observations, more observational constraints from post common-envelope binaries, and especially from observations of planetary nebulae, should be very helpful in further understanding (as well as for code verification). Specifically, observations on nebulae shapes and velocities may help to understand how the ejection proceeded.

The eccentricity, if any, of post-CE binaries may also help to identify and understand any CE events which resulted in envelope ejection immediately following the dynamical plunge-in. It is expected that eccentricity would be lost during the slow spiral-in, and might even be damped away during the process of envelope ejection. The presence of eccentricity might therefore be a clue that the envelope was ejected immediately after the fast spiral-in stage, not following a self-regulated spiral-in phase. Note, however, that observational biases tend to produce spurious apparent eccentricities, so it is easier to give upper limits on eccentricity than to be confident about detections.

One potential observation would give definitive information with the detection of a single object. If we find a single Thorne–Żytkow Object, we would have strong constraints on hypercritical accretion.

We note that the clarity and certainty of our understanding of CE physics is certainly not yet good enough to predict formation rates of many classes of system. For some post-CE systems the formation rate inferred from observations cannot currently be explained within the mainstream energy formalism when using physically realistic parameters (e.g., short-period black hole X-ray binaries). This definitely strongly reduces the reliability of predictions for formation rates, e.g. for systems with black holes, including close black hole-black hole binaries which are of interest for gravitational-wave astronomy.

Those who study the formation rates of binary systems by means of population synthesis must anticipate and acknowledge that current uncertainties in theoretically predicted rates could be about two orders of magnitude arising from uncertain CE energetics for systems where CEE is involved. (In addition to this, formation channels involving CEE also introduce other uncertainties, e.g. from $q_{\rm crit}$.) In some binary systems the major uncertainty comes from our poor understanding of the energetics involved (and it is hence related to $\alpha_{\rm CE}$), whilst in others it is due to an arbitrary choice of the remaining core’s mass (hence it is related to λ). This review discusses several ways in which these uncertainties might be reduced by more careful consideration of the physics involved. Attempts to observationally calibrate these parameters are only advisable if performed for well-defined classes of post-CE binaries, since there is very strong reason to expect they should not be global parameters. We stress that trying to determine the single effective value of $\alpha_{\rm CE}$ is very misguided: there will be different values in different cases, as the time-scales and energy sources and sinks should vary from one CE event to another.

We are convinced that much work remains to be done, however, we feel optimistic that the solution of the problem could be achieved within the next decade.

Appendix A: Analysis of energy- and angular-momentum based parametrizations of CEE using the E–J plane

Here we illustrate the energy and angular-momentum balance at the end of CEE resulting from two parametrizations common in the literature (the energy formalism and the γ-formalism). Clearly both energy conservation and angular momentum conservation should physically take place during CEE; here we examine the relationship between these parametrizations.

To compare the two prescriptions and their outcomes, it is necessary to adopt a relationship between orbital energy (E) and angular momentum (J). We choose to assume that the post-CE binaries have circular, Keplerian orbits. This seems reasonable (we do not expect high post-CE eccentricities) and relatively robust (since, at fixed E, a non-zero eccentricity [e] would lead to a correction in J by only a factor of $\sqrt{1-e^{2}}$). So for the γ-formalism, we take the post-CE orbital energy as it would be for a Keplerian binary (and for the energy formalism we fix J in the same way).

We will use the following to indicate the possible post-CE states from the different formalisms (see Figs. 7, 8 and 9):

• Black curves represent sets of possible outcomes produced by the γ-formalism, for given fixed values of γ.

• Blue lines are the sets of outcomes produced by the energy formalism, assuming $\alpha_{\rm CE}=1$.

Fig. 7

Orbital angular momentum J and energy E for a CE in a 2M _⊙+0.5M _⊙ binary (r _d=23R _⊙ and the hydrogen-exhausted core m _d,X =0.317M _⊙). The black star indicates the state of the binary at the onset of the CE. The solid line (red) shows the Keplerian E _orb−J _orb relation for the final binary assuming that the mass of the post-CE remnant consists of all the RG mass that was originally contained within the final Roche lobe (m _RL), in other words, the maximum possible remnant mass for this orbit. The shaded region contains Keplerian orbits for core masses bounded by $m_{\mathrm{c,min}} < m_{\mathrm{d, c}} < m_{\mathrm{c, max}}$ (see the text). A final state of the post-CE binary must lie within this area. The dashed lines (blue) represent the set of all possible final states as per the energy formalism (being a function of all possible core masses), for λ calculated using the stellar model and for λ=1. The dashed-dotted green line separates regions where the post-CE binary has more or less energy than at the start of the CE. The dotted green line separates regions where the post-CE is wider (a>a _i) than at the start of the CE and where it shrunk (a<a _i). The stellar model was calculated using the evolutionary code described in Ivanova (2002), Ivanova and Taam (2004)

Fig. 8

Orbital angular momentum and energy for a 2M _⊙+0.5M _⊙ binary (r _d=86R _⊙ and m _d,X =0.38M _⊙). Thick and thin solid red lines show the only possible final binary configurations for various adopted core masses. For comparison we also show the minimum energy expenditures to release the envelope (blue dashed line, see also the caption of Fig. 7). Black solid and dotted lines indicate possible final binary configurations, assuming angular momentum is lost in accordance with the γ-formalism, where the thick black solid lines show $\gamma_{\rm E}$ and $\gamma_{\rm M}$, i.e. the minimum and maximum γ that make a binary which avoids the need for energy input or merger. Dotted black lines show values of γ that lead to formation of binaries which satisfy those constraints for the full range of core mass definitions. Other line-styles are as in Fig. 7

Fig. 9

Left: Orbital angular momentum and energy for a 2M _⊙+1.5M _⊙ binary (r _d=86R _⊙ and m _d,X =0.38M _⊙). Right: Orbital angular momentum and energy for a 2M _⊙+0.35M _⊙ binary (r _d=86R _⊙ and m _d,X =0.38M _⊙). Line styles are as in Fig. 8

We emphasize that the above curves are not intended to represent the evolution during CEE, but only possible final states. They could only represent the evolution during CEE if the instantaneous value of γ or $\alpha_{\rm CE}$ is constant throughout the CE phase, which would be extremely unexpected. Each curve represents a collection of possible final states for fixed CE parameter (γ or $\alpha_{\rm CE}$), where different points on these curves represent different final remnant masses.

Note that final states higher in |E| tend to represent tighter binaries; orbital energy increases as the period decreases.

We also use the following conventions:

• The thick red line separates the merger region from the non-merger region. This represents the condition for the remnant core to not to overfill its Roche lobe, assuming that the remnant core does not expand upon mass loss. Since we know that a remnant core will almost always expand (see the discussion in Deloye and Taam 2010; Ivanova 2011), this definition usually represents the closest possible post-CE orbits. Realistically, the final position of the binary should be below this line—the actual state depends on how close the post-CE system is to being Roche-lobe filling.

• The dashed-dotted green line separates regions where the post-CE binary has more or less orbital energy than at the start of the CE.

• The dotted green line separates the region where the post-CE system is wider (a>a _i) than at the start of the CE from the region where the separation has decreased (a<a _i).

• Thin red lines show all Keplerian solutions for the minimum and maximum possible core masses (see below). For any given remnant mass these are straight lines on the E–J plane.

We mark the initial state of a binary with a star. We take into account the orbital energy $E_{\mathrm{orb, i}}$ and the rotational energy of the giant’s envelope (assumed to be synchronized with the initial orbit), as well as the orbital angular momentum $J_{\mathrm{orb, i}}$ and angular momentum of the giant’s envelope.

For this analysis, our choice of the lower bound on the possible core mass $m_{\mathrm{c, min}}$ is the hydrogen-exhausted core m _d,X (the region where X<10⁻¹⁰) and is rather standard. For the upper bound on the possible core mass $m_{\mathrm{c, max}}$ we choose the minimum between the central mass which contains less than 10 % hydrogen and the bottom of the outer convective envelope (m _BCE). The solutions/outcomes for the post-CE core masses above the maximum possible core mass (to the right of the right thin red line) are provided only to show the behavior throughout the E–J plane, but should not be considered as physically likely final states. (Note also that it is for those masses where the effect of remnant expansion should be the greatest.)

Based on our assumptions, only the solutions bounded from above by the thick solid merger line and lying within the region between minimum and maximum core masses are expected to be permitted for a self-consistent post-CE binary unless another—currently unidentified—energy source is available. This condition is independent of whether the energy formalism or the γ-formalism is used.

A.1 Examining outcomes of the α-formalism in the E–J plane

As an example, we consider a binary with a giant of 2M _⊙ and a WD of 0.5M _⊙, where the CE is initiated when the giant is evolved to a hydrogen-exhausted core mass m _d,X ∼0.317M _⊙ and has a radius of 23R _⊙ (see Fig. 7). In this figure, we shade the region containing the expected range of potential core masses. As we said above, only the strip bounded from above by the thick solid line and lying within the shaded region is permitted for a self-consistent final post-CE binary. As was discussed in Sect. 4, even for a properly computed λ, the final orbital separations can vary by over a factor of 10 in the region of likely core masses.

In the energy formalism, as expected, the post-CE binary cannot have more energy than the initial binary and still satisfy conservation of energy (see the dashed-dotted green line on Fig. 7), since some energy must be used to expel the common envelope to infinity. We can also find the position that a final binary would have if it kept the same orbital separation, for any valid post-CE mass of the donor $m_{\mathrm{c, min}}< m_{\mathrm{d,c}}<m_{\mathrm{d}}$. In the absence of another energy source, a widened orbit would violate energy conservation and so should not be produced by this energy formalism.

The whole range of possible states for a post-CE binary described by the energy formalism is bounded by the blue dashed line at the bottom, the solid red line at the top and the shaded red area. When the CE is initialized at a different giant radius (i.e. at a different orbital period), and accordingly a different m _d,X , the picture is qualitatively similar, although the uncertainty that is introduced by the core-mass definition could vary.

A.2 Examining outcomes of the γ-formalism in the E–J plane

Here we choose a 2M _⊙ giant, evolved to a hydrogen-exhausted core mass m _d,X ∼0.38M _⊙ and has a radius of 86R _⊙. This represents a common case in the study of Nelemans and Tout (2005), where many double WD binaries have an older companion of 0.5M _⊙ and a younger WD of 0.4M _⊙ (see Fig. 8). From Fig. 8, we see that the set of solutions for γ=1.5 roughly coincides with a possible final binary configuration for these particular companion masses.⁷ The set of γ≈1.5 solutions crosses the final binary configuration at approximately the location mandated by energy consideration. This may therefore help to explain why γ=1.5 is successful in fitting the observed systems which are thought to be similar to this one.

We can also study the restricted set of outcomes available when CEE is limited by the available orbital energy reservoir. We repeat this is not an assumption in the γ-formalism, but it is important for understanding how the γ-formalism related to canonical CEE, with a significant spiral-in, as described by the long-standing energy prescription. Here we make use of the limiting cases defined in Sect. 5.3.1, which represent the γ-values which lead to merger ($\gamma_{\rm M}$) or require an additional energy source ($\gamma_{\rm E}$).

For $\gamma> \gamma_{\rm M}=1.505$ this binary would merge as Eq. (10) predicts negative post-CE angular momentum. For $\gamma<\gamma_{\rm E}=1.38$, Eq. (10) produces an orbital separation such that a Keplerian post-CE binary could only be explained if some form of extra energy input was provided to the system during a CEE. Even within this narrow range of $\gamma_{\rm E}<\gamma<\gamma_{\rm M}$ some outcomes would require either energy generation or would be mergers: the details depend on the size of the core and on the exact definition of the ejected envelope. For smaller ejected masses, the range also becomes smaller. For example, in the case when CEE removes only the convective envelope (rather than removing the entire hydrogen burning shell to leave only the naked core), then γ>1.43 is required to produce a binary without apparent energy generation and γ<1.47 is required for the binary not to merge.

This behaviour is related to the sensitivity to the value of γ of the post-CE separations predicted using Eq. 10, as discussed in Sect. 5.2.2. For this particular binary, the change in the input γ values by as little as δγ=0.125, from 1.38 to 1.505, provides the difference in post-CE binary separations for spiral-ins by a factor of 20 for the same adopted core mass; any larger change would modify the outcome qualitatively into either a merger or an outcome with apparent energy generation.

Now consider the same 2M _⊙ giant, with the same $m_{\mathrm{c, min}}\sim0.4M_{\odot}$, but with a 1.5M _⊙ companion (Fig. 9, left). This is similar to some initial binaries considered to be progenitors for DWDs in van der Sluys et al. (2006). Assuming a spiral-in limited by the available orbital energy, this binary could survive without merging only between $\gamma_{\rm M}=2.108$ and $\gamma_{\rm E}=1.94$ (we note that this is close to values of γ used in some similar systems in van der Sluys et al. 2006, see their Table 6); orbital expansion happens for γ<1.5. Taking into account that not all of the hydrogen shell might be expelled and that the core has finite size, this range is reduced to γ≈1.99−2.06. With γ=1.5, the binary is even wider than it was at the beginning—the same effect as having negative α or a stellar wind. As a consequence, the binary becomes wider during mass loss (of course this is both legal and natural for the γ-formalism, since it was created to model exactly such widening for the first episode of MT in DWDs formation and includes no restrictions on the overall energy balance).

Another example involves a binary with a less massive companion (0.35M _⊙, Fig. 9, right). Keplerian solutions can easily be found for γ≈1.36−1.39, where the extreme cases are $\gamma_{\rm M} = 1.415$ and $\gamma_{\rm E} = 1.305$. With γ=1.5, the post-CE binary should merge if realistic core sizes are taken into account.

We stress that the analysis in this subsection assumes constraints which are not contained within the original γ-formalism, although those limits are natural ones in the absence of an additional, currently unidentified, energy source. It also takes the standard position that the post-CE systems have circular, Keplerian orbits. Nonetheless, we suggest that the overall results above indicate the γ-formalism, as currently expressed, is not ideal for making predictions about CE phases which are limited by the available orbital energy, or (similarly) those which involve a significant spiral-in and mass loss.