Multiscale topology optimization of an electromechanical dynamic energy harvester made of non-piezoelectric material

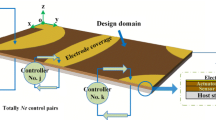
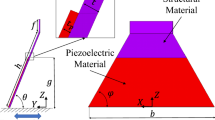
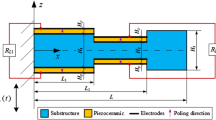
Abstract

In this work, a novel multiscale topology optimization method has been proposed for the design of electromechanical energy-harvesting systems converting mechanical vibrations into electric currents made of non-piezoelectric materials. At the microscopic scale, the material is assumed to be periodic, porous, and flexoelectric, although not piezoelectric. A first step of topology optimization is performed, in order to maximize the effective (homogenized) flexoelectric properties of the material, where a flexoelectric homogenization model is first formulated. As a result, the effective material, although made of a non-piezoelectric material, has apparent piezoelectric properties. In a second step, these properties are used to model the behavior of a dynamic electromechanical energy-harvesting system structure. A second topology optimization step, this time performed at the structural scale, aims to maximize the system electromechanical coupling factor (ECF) for a given forced vibration frequency, including the micro-inertial effect. At both scales, an isogeometric analysis method is employed to solve the strain-gradient problems numerically. We show that the optimized structure obtained offers significant gains in terms of ECF (by a factor of between 2 and 20) compared with non-optimized structures of the same volume, over a wide range of excitation frequencies. The procedure could open up new possibilities in the design of energy recovery systems without the use of piezoelectric materials.

Appendices

Appendix A

1.1 Matrices of material and IGA discretization

$B_\phi$, $B_u$ and $H_u$ are the matrices containing the gradient and Hessian of the corresponding basis functions $N_\phi$ and $N_u$ which are given by

$$\begin{aligned}&{\varvec{B}}_\phi =\begin{bmatrix} \frac{\partial N_1}{\partial x}&{}\cdots &{}\frac{\partial N_n}{\partial x}\\ \frac{\partial N_1}{\partial y}&{}\cdots &{}\frac{\partial N_n}{\partial y} \end{bmatrix},\ {\varvec{B}}_u=\begin{bmatrix} \frac{\partial N_1}{\partial x}&{}\cdots &{}\frac{\partial N_n}{\partial x}&{}0&{}\cdots ,&{}0\\ 0&{}\cdots &{}0&{}\frac{\partial N_1}{\partial y}&{}\cdots &{}\frac{\partial N_n}{\partial y} \\ \frac{\partial N_1}{\partial y}&{}\cdots &{}\frac{\partial N_n}{\partial y}&{}\frac{\partial N_1}{\partial x}&{}\cdots &{}\frac{\partial N_n}{\partial x} \end{bmatrix} \end{aligned}$$

(A1)

$$\begin{aligned}&\tilde{{\varvec{B}}}_u=\begin{bmatrix} \frac{\partial N_1}{\partial x}&{}\cdots &{}\frac{\partial N_n}{\partial x}&{}0&{}\cdots ,&{}0\\ 0&{}\cdots &{}0&{}\frac{\partial N_1}{\partial y}&{}\cdots &{}\frac{\partial N_n}{\partial y} \\ \frac{\partial N_1}{\partial y}&{}\cdots &{}\frac{\partial N_n}{\partial y}&{}0&{}\cdots &{}0\\ 0&{}\cdots &{}0&{}\frac{\partial N_1}{\partial x}&{}\cdots &{}\frac{\partial N_n}{\partial x} \end{bmatrix},\nonumber \\&{\varvec{H}}_u=\begin{bmatrix} \frac{\partial ^2 N_1}{\partial x^2}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial x^2}&{}0&{}\cdots &{}0 \\ 0&{}\cdots &{}0&{}\frac{\partial ^2 N_1}{\partial y^2}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial y^2} \\ \frac{\partial ^2 N_1}{\partial x \partial y}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial x \partial y}&{}0&{}\cdots &{}0 \\ 0&{}\cdots &{}0&{}\frac{\partial ^2 N_1}{\partial x \partial y}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial x \partial y} \\ \frac{\partial ^2 N_1}{\partial x \partial y}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial x \partial y}&{}\frac{\partial ^2 N_1}{\partial x^2}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial x^2}\\ \frac{\partial ^2 N_1}{\partial y^2}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial y^2}&{}\frac{\partial ^2 N_1}{\partial x \partial y}&{}\cdots &{}\frac{\partial ^2 N_n}{\partial x \partial y} \end{bmatrix} \end{aligned}$$

(A2)

The material parameters $\textbf{C}$, ${\varvec{\alpha }}$, ${\varvec{e}}$, ${\varvec{\mu }}$ and $\textbf{G}$ are defined in the 2D matrix form as

$$\begin{aligned}&\textbf{C}=\begin{bmatrix} c_{11}&{}c_{12}&{}0\\ c_{12}&{}c_{22}&{}0\\ 0&{}0&{}c_{44} \end{bmatrix},\ {\varvec{\alpha }}=\begin{bmatrix} \alpha _{11}&{}0\\ 0&{}\alpha _{33} \end{bmatrix},\ {\varvec{e}}=\begin{bmatrix} 0&{}0&{}e_{15}\\ e_{13}&{}e_{33}&{}0 \end{bmatrix} \end{aligned}$$

(A3)

$$\begin{aligned}&{\varvec{\mu }}=\begin{bmatrix} \mu _{11}&{}0&{}0&{}\mu _{12}&{}0&{}\mu _{44}\\ 0&{}\mu _{11}&{}\mu _{12}&{}0&{}\mu _{44}&{}0 \end{bmatrix} \end{aligned}$$

(A4)

$$\begin{aligned}&\textbf{G}=\ell ^2\begin{bmatrix} c_{11}&{}0&{}0&{}c_{12}&{}0&{}0\\ 0&{}c_{11}&{}c_{12}&{}0&{}0&{}0\\ 0&{}c_{12}&{}c_{11}&{}0&{}0&{}0\\ c_{12}&{}0&{}0&{}c_{11}&{}0&{}0\\ 0&{}0&{}0&{}0&{}c_{44}&{}0\\ 0&{}0&{}0&{}0&{}0&{}c_{44} \end{bmatrix} \end{aligned}$$

(A5)

Appendix B

1.1 Calculation of effective flexoelectric tensor

The strain and electric fields solutions, strain gradient fields solutions of the problem Eq. (3) can be expressed as the functions of the effective strain, electric and strain gradient fields as

$$\begin{aligned}&\varepsilon _{ij}=A^0_{ijpq}\overline{\varepsilon }_{pq}-B^0_{ijp}\overline{E}_{p}-A^1_{ijpqr}\overline{\nabla \varepsilon }_{pqr} \end{aligned}$$

(B1)

$$\begin{aligned}&E_i=D^0_{ipq}\overline{\varepsilon }_{pq}-h^0_{ip}\overline{E}_{p}-D^1_{ipqr}\overline{\nabla \varepsilon }_{pqr} \end{aligned}$$

(B2)

$$\begin{aligned}&\nabla \varepsilon _{ijk}=J^0_{ijkpq}\overline{\varepsilon }_{pq}-Q^0_{ijkp}\overline{E}_{p}-J^1_{ijkpqr}\overline{\nabla \varepsilon }_{pqr} \end{aligned}$$

(B3)

We define the displacement and electric fields matrices:

$$\begin{aligned}&\textbf{U}=\{\textbf{U}_\phi ;\textbf{U}_u\}, \ \textbf{V}=\{\textbf{V}_\phi ;\textbf{V}_u\}, \ \textbf{W}=\{\textbf{W}_\phi ;\textbf{W}_u\} \end{aligned}$$

(B4)

$$\begin{aligned}&\textbf{U}_u=[\textbf{u}^1,\textbf{u}^2,\textbf{u}^3], \ \textbf{V}_u=[\textbf{u}^4,\textbf{u}^5], \ \textbf{W}_u=[\textbf{u}^6,\textbf{u}^7,\textbf{u}^8,\textbf{u}^9,\textbf{u}^{10},\textbf{u}^{11}] \end{aligned}$$

(B5)

$$\begin{aligned}&\textbf{U}_\phi =[{\varvec{\phi }}^1,{\varvec{\phi }}^2,{\varvec{\phi }}^3], \ \textbf{V}_\phi =[{\varvec{\phi }}^4,{\varvec{\phi }}^5], \ \textbf{W}_\phi =[{\varvec{\phi }}^6,{\varvec{\phi }}^7,{\varvec{\phi }}^8,{\varvec{\phi }}^9,{\varvec{\phi }}^{10},{\varvec{\phi }}^{11}] \end{aligned}$$

(B6)

The displacement fields $\textbf{u}^i$ and the electric fields ${\varvec{\phi }}^i$ are the vector columns containing, respectively, the nodal displacement and electric potentials solution of the localization problems Eqs. (3) with the boundary conditions described in Table 5.

Table 5 Elementary solution corresponding to the prescribed macroscopic strain, electric potential, and strain gradient components

The matrices associated with the tensors $A^0$, $B^0$, $A^1$, $D^0$, $A^0$, $h^0$, $D^1$, $J^0$, $Q^0$ and $J^1$ in Eqs. (B1)–(B3) can be computed according to

$$\begin{aligned}&\textbf{A}^0({x})=\textbf{B}_u({x})\textbf{U}_u,\hspace{15pt}\textbf{B}^0(\textbf{x})=\textbf{B}_u({x})\textbf{V}_u,\hspace{15pt}\textbf{A}^1(\textbf{x})=\textbf{B}_u(\textbf{x})\textbf{W}_u; \end{aligned}$$

(B7)

$$\begin{aligned}&\textbf{D}^0({x})=-\textbf{B}_\phi ({x})\textbf{U}_\phi ,\hspace{15pt}\textbf{h}^0({x})=-\textbf{B}_\phi ({x})\textbf{V}_\phi , \hspace{15pt}\textbf{D}^1({x})=-\textbf{B}_\phi ({x})\textbf{W}_\phi \end{aligned}$$

(B8)

$$\begin{aligned}&\textbf{J}^0({x})=\textbf{H}_u({x})\textbf{U}_u,\hspace{15pt}\textbf{Q}^0({x})=\textbf{H}_u({x})\textbf{V}_u, \hspace{15pt}\textbf{J}^1({x})=\textbf{H}_u({x})\textbf{W}_u \end{aligned}$$

(B9)

Substituting Eqs. (B7)–(B9) into Eq. (14), we have the effective flexoelectric tensor in matrix form as

$$\begin{aligned}&\overline{{\varvec{\mu }}}=-\left\langle \textbf{V}_u^T \textbf{B}_u^T \textbf{C} \textbf{B}_u\textbf{W}_u-\textbf{V}_\phi ^T\textbf{B}_\phi ^T{\varvec{\alpha }}\textbf{B}_\phi \textbf{W}_\phi +\textbf{V}_u^T\textbf{H}_u^T{\varvec{\mu }}\textbf{B}_\phi \textbf{W}_\phi +\textbf{V}_\phi ^T\textbf{B}_\phi ^T{\varvec{\mu }}\textbf{H}_u\textbf{W}_u \right\rangle \end{aligned}$$

(B10)

Appendix C

1.1 Sensitivity analysis

To solve the effective flexoelectric coefficients enhancement problem in Eq. (54) for microstructure and the electromechanical coupling efficiency optimization problem Eq. (56) for energy harvester based on the gradient-based mathematical programming method, the adjoint method is employed to derive both the numerical sensitivities.

1.1.1 Microstructure analysis

The effective flexoelectric tensor can be written by compact form as

$$\begin{aligned}&\overline{{\varvec{\mu }}}=-\frac{1}{\Omega _m} \begin{bmatrix} \textbf{V}_\phi \\ \textbf{V}_u \end{bmatrix}^T \begin{bmatrix} \textbf{K}_{\phi \phi }&{}&{}\textbf{K}_{\phi u}\\ \textbf{K}_{\phi u}^T &{}&{}\textbf{K}_{uu} \end{bmatrix} \begin{bmatrix} \textbf{W}_\phi \\ \textbf{W}_u \end{bmatrix} \end{aligned}$$

(C1)

We define

$$\begin{aligned}&\textbf{K}_G= \begin{bmatrix} \textbf{K}_{\phi \phi }&{}&{}\textbf{K}_{\phi u}\\ \textbf{K}_{\phi u}^T &{}&{}\textbf{K}_{uu} \end{bmatrix} \end{aligned}$$

(C2)

By using the adjoint method, the corresponding Lagrangian $L^m$ for the effective flexoelectric tensor components optimization problem Eq. (54) is formed by introducing adjoint vectors $\lambda ^{m}_1$ and $\lambda ^m_2$ as:

$$\begin{aligned}&L^m=\overline{{\varvec{\mu }}}-(\textbf{V}^T\textbf{K}_G-{\textbf{F}_V}^T){\varvec{\lambda }}^m_1-({\varvec{\lambda }}^m_2)^T(\textbf{K}_G\textbf{W}-{\textbf{F}_W}^T) \end{aligned}$$

(C3)

Where $\textbf{V}^T\textbf{K}_G-{\textbf{F}_V}^T=0$ and $\textbf{K}_G\textbf{W}-{\textbf{F}_W}^T=0$ are the IGA discrete forms of Eq. (11) with boundary condition shown in Table 5, and they hold for arbitrary vectors $\lambda ^{m}_1$ and $\lambda ^m_2$. Differentiating the Lagrangian $L^m$ with respect to the design variable $\rho ^m$ gives:

$$\begin{aligned}&\frac{\partial L^m}{\partial \rho ^m}=\frac{\partial \overline{{\varvec{\mu }}}}{\partial \rho ^m}-\frac{\partial (\textbf{V}^T\textbf{K}_G-{\textbf{F}_V}^T)}{\partial \rho ^m}{\varvec{\lambda }}^m_1-({\varvec{\lambda }}^m_2)^T\frac{\partial (\textbf{K}_G\textbf{W}-{\textbf{F}_W}^T)}{\partial \rho ^m} \end{aligned}$$

(C4)

We finally obtain the adjoint sensitivity of effective flexoelectric components with respect to the density as

$$\begin{aligned}&\frac{\partial \overline{{\varvec{\mu }}}}{\partial \rho ^m}=\frac{1}{\Omega _m} \begin{bmatrix} \textbf{V}_\phi \\ \textbf{V}_u \end{bmatrix}^T \cdot \frac{\partial }{\partial \rho ^m}\left( \begin{bmatrix} \textbf{K}_{\phi \phi }&{}&{}\textbf{K}_{\phi u}\\ \textbf{K}_{\phi u}^T &{}&{}\textbf{K}_{uu} \end{bmatrix} \right) \cdot \begin{bmatrix} \textbf{W}_\phi \\ \textbf{W}_u \end{bmatrix} \end{aligned}$$

(C5)

1.1.2 Energy harvester analysis

For the energy harvester in dynamics, the first derivative of the objective function J with respect to the nodal design variable $\rho _{i,j}$ is calculated as

$$\begin{aligned}&\frac{\partial J}{\partial \rho _{i,j}}=\frac{\frac{\partial \Pi _m}{\partial \rho _{i,j}}\Pi _e-\Pi _m\frac{\partial \Pi _e}{\partial \rho _{i,j}}}{\Pi _e^2} \end{aligned}$$

(C6)

The terms $\frac{\partial \Pi _m}{\partial \rho _{i,j}}$ and $\frac{\partial \Pi _e}{\partial \rho _{i,j}}$ are derived by chain rules, respectively,

$$\begin{aligned}&\frac{\partial \Pi _m}{\partial \rho _{i,j}}=\frac{\partial \Pi _m}{\partial \bar{\bar{\rho }}_{i,j}} \cdot \frac{\partial \bar{\bar{\rho }}_{i,j}}{\partial \bar{\rho }_{i,j}} \cdot \frac{\partial \bar{\rho }_{i,j}}{\partial \rho _{i,j}} \end{aligned}$$

(C7)

$$\begin{aligned}&\frac{\partial \Pi _e}{\partial \rho _{i,j}}=\frac{\partial \Pi _e}{\partial \bar{\bar{\rho }}_{i,j}} \cdot \frac{\partial \bar{\bar{\rho }}_{i,j}}{\partial \bar{\rho }_{i,j}} \cdot \frac{\partial \bar{\rho }_{i,j}}{\partial \rho _{i,j}} \end{aligned}$$

(C8)

Furthermore, $\frac{\partial \Pi _m}{\partial \bar{\bar{\rho }}_{i,j}}$ and $\frac{\partial \Pi _e}{\partial \bar{\bar{\rho }}_{i,j}}$ is explicit calculated by introducing an adjoint vector ${\varvec{\lambda }}^c$ and ${\varvec{\lambda }}^e$, respectively. The corresponding Lagrangian equations are constructed as:

$$\begin{aligned}&L_{\Pi _m}= \Pi _m-{\varvec{\lambda }}^c_1(\textbf{K}_{tot}\textbf{U}_{tot}-\textbf{F}_{tot})-{\varvec{\lambda }}^c_2(\overline{\textbf{K}_{tot}\textbf{U}_{tot}}-\overline{\textbf{F}_{tot}}) \end{aligned}$$

(C9)

$$\begin{aligned}&L_{\Pi _e}=\Pi _e-{\varvec{\lambda }}^e_1(\textbf{K}_{tot}\textbf{U}_{tot}-\textbf{F}_{tot})-{\varvec{\lambda }}^e_2(\overline{\textbf{K}_{tot}\textbf{U}_{tot}}-\overline{\textbf{F}_{tot}}) \end{aligned}$$

(C10)

where the discrete system of coupling equilibrium equation $\textbf{K}_{tot}\textbf{U}_{tot}=\textbf{F}_{tot}$ is defined in Eq. (52), while $\overline{\textbf{K}_{tot}\textbf{U}_{tot}}=\overline{\textbf{F}_{tot}}$ is the corresponding conjugate counterpart. Both equilibrium equations hold for arbitrary ${\varvec{\lambda }}^c$ and ${\varvec{\lambda }}^e$. The sensitivities of the Lagrangian equations with respect to $\bar{\bar{\rho }}_{i,j}$ are written as

$$\begin{aligned} \frac{\partial L_{\Pi _m}}{\partial \bar{\bar{\rho }}_{i,j}}&=\frac{\partial \Pi _m}{\partial \bar{\bar{\rho }}_{i,j}}+\frac{\partial \Pi _m}{\partial \textbf{U}_{tot}}\cdot \frac{\partial \textbf{U}_{tot}}{\partial \bar{\bar{\rho }}_{i,j}}\nonumber \\&\quad +\frac{\partial \Pi _m}{\partial \overline{\textbf{U}}_{tot}}\cdot \frac{\partial \overline{\textbf{U}_{tot}}}{\partial \bar{\bar{\rho }}_{i,j}}\nonumber \\&\quad -{\varvec{\lambda }}^c_1\frac{\partial (\textbf{K}_{tot}\textbf{U}_{tot}-\textbf{F}_{tot})}{\partial \bar{\bar{\rho }}_{i,j}}-{\varvec{\lambda }}^c_2\frac{\partial (\overline{\textbf{K}_{tot}\textbf{U}_{tot}}-\overline{\textbf{F}_{tot}})}{\partial \bar{\bar{\rho }}_{i,j}} \end{aligned}$$

(C11)

$$\begin{aligned} \frac{\partial L_{\Pi _e}}{\partial \bar{\bar{\rho }}_{i,j}}&=\frac{\partial \Pi _e}{\partial \bar{\bar{\rho }}_{i,j}}+\frac{\partial \Pi _e}{\partial \textbf{U}_{tot}}\cdot \frac{\partial \textbf{U}_{tot}}{\partial \bar{\bar{\rho }}_{i,j}}\nonumber \\&\quad +\frac{\partial \Pi _e}{\partial \overline{\textbf{U}_{tot}}}\cdot \frac{\partial \overline{\textbf{U}_{tot}}}{\partial \bar{\bar{\rho }}_{i,j}}\nonumber \\&\quad -{\varvec{\lambda }}^e_1\frac{\partial (\textbf{K}_{tot}\textbf{U}_{tot}-\textbf{F}_{tot})}{\partial \bar{\bar{\rho }}_{i,j}}-{\varvec{\lambda }}^e_2\frac{\partial (\overline{\textbf{K}_{tot}\textbf{U}_{tot}}-\overline{\textbf{F}_{tot}})}{\partial \bar{\bar{\rho }}_{i,j}} \end{aligned}$$

(C12)

We finally obtain the sensitivities of mechanical and electrical energy w.r.t $\bar{\bar{\rho }}_{i,j}$,

$$\begin{aligned} \frac{d \Pi _m}{d \bar{\bar{\rho }}_{i,j}}&=\frac{1}{2}\overline{\textbf{U}}^T\frac{\partial \textbf{K}_{uu}}{\partial \bar{\bar{\rho }}}\textbf{U}\nonumber \\&\quad -Re\left\{ ({{\varvec{\lambda }}^c_1})^T\frac{\partial \overline{\textbf{K}_{tot}}}{\partial \bar{\bar{\rho }}}\overline{\textbf{U}_{tot}}+({\varvec{\lambda }}^c_2)^T\frac{\partial \textbf{K}_{tot}}{\partial \bar{\bar{\rho }}}\textbf{U}_{tot}\right\} \end{aligned}$$

(C13)

$$\begin{aligned} \frac{d \Pi _e}{d \bar{\bar{\rho }}_{i,j}}&=\frac{1}{2}\overline{{\varvec{\Phi }}}^T\frac{\partial \textbf{K}_{\phi \phi }}{\partial \bar{\bar{\rho }}}{\varvec{\Phi }}\nonumber \\&\quad -Re\left\{ ({{\varvec{\lambda }}^e_1})^T\frac{\partial \overline{\textbf{K}_{tot}}}{\partial \bar{\bar{\rho }}}\overline{\textbf{U}_{tot}}+({{\varvec{\lambda }}^e_2})^T\frac{\partial \textbf{K}_{tot}}{\partial \bar{\bar{\rho }}}\textbf{U}_{tot}\right\} \end{aligned}$$

(C14)

where $Re\left\{ \cdot \right\}$ mean the real part of the complex. The adjoint vectors are calculated by the following adjoint equations

$$\begin{aligned}&\overline{\textbf{K}_{tot}}{\varvec{\lambda }}^c_1=\frac{\partial \Pi _m}{\partial \overline{\textbf{U}_{tot}}} \end{aligned}$$

(C15)

$$\begin{aligned}&\textbf{K}_{tot}{\varvec{\lambda }}^c_2=\frac{\partial \Pi _m}{\partial \textbf{U}_{tot}} \end{aligned}$$

(C16)

$$\begin{aligned}&\overline{\textbf{K}_{tot}}{\varvec{\lambda }}^e_1=\frac{\partial \Pi _e}{\partial \overline{\textbf{U}_{tot}}} \end{aligned}$$

(C17)

$$\begin{aligned}&\textbf{K}_{tot}{\varvec{\lambda }}^e_2=\frac{\partial \Pi _e}{\partial \textbf{U}_{tot}} \end{aligned}$$

(C18)

To solve the adjoint equations, we can use the same mechanical and electric boundary condition as the problem Eq. (58). The derivatives of material density distribution field $\bar{\bar{\rho }}$ with respect to nodal density field $\rho$ presented in Eq. (C7), (C8) can be obtained as

$$\begin{aligned}&\frac{\partial \bar{\bar{\rho }}_{i,j}}{\partial \bar{\rho }_{i,j}}=R_{i,j}^{p,q}(\bar{\xi },\bar{\eta }) \end{aligned}$$

(C19)

$$\begin{aligned}&\frac{\partial \bar{\rho }_{i,j}}{\partial \rho _{i,j}}=\frac{w(r_{\bar{i},\bar{j}})}{\sum _{\hat{i}=1}^{n_s}\sum _{\hat{j}=1}^{m_s}w(r_{\hat{i},\hat{j}})} \end{aligned}$$

(C20)

Substituting Eqs. (C13), (C14)–(C19), (C20) into Eqs. (C7) and (C8), finally into Eq. (C6), the explicit sensitivity of objection function with respect to nodal density variable $\rho$ can therefore be obtained.