Microvascular materials leverage fluid within embedded vasculature to achieve dynamic functionality (Devi et al. 2021; Tan et al. 2018; Pety et al. 2017). Different properties are realized in a single host material through a distinct choice of fluid (Esser-Kahn et al. 2011). For example, circulating liquid coolant through the microchannels in a heated solid provides an effective mechanism for thermal regulation, i.e., active cooling (Wang et al. 2005; Kozola et al. 2010; Coppola et al. 2015; Zhao et al. 2021; Hadad et al. 2019; Coppola et al. 2016; Sun et al. 2023; Driesman et al. 2019). This makes microvascular materials an apt choice for applications such as battery and electronics packaging, where heat removal must be considered (Pejman et al. 2022; Chen et al. 2022; Deng et al. 2020; Pety et al. 2017).

Many real-world thermal applications do not operate under steady-state conditions. For example, electronic components such as CPUs undergoing fluctuations in computational load, or the battery system of electric vehicles during charging and discharging, are naturally prone to temperature changes. Since the performance and longevity of such components depend on their thermal stability, it is vital to have efficient thermal management systems with responsive cooling capabilities (Bandhauer et al. 2011; Kim et al. 2019). For instance, it is not only essential that these devices are capable of reducing temperature when experiencing high thermal loading, but also that this reduction occurs rapidly. This in turn underscores the need for a robust transient thermal design methodology for microvascular materials.

Previous developments in the design optimization space for microvascular systems include various frameworks to enhance steady-state thermal performance. Several design approaches have used multi-objective formulations for microvascular network optimization. Genetic algorithms (GAs) have been implemented to minimize the maximum temperature, void volume fraction of the channels, and the required pumping power of vascularized materials (Aragón et al. 2013, 2011, 2008; Li et al. 2017; Soghrati et al. 2014). While able to find a local minimum, genetic algorithms suffer from high computational cost as well as complicated vascular designs.

Soghrati et al. studied active cooling with a periodic (i.e., sinusoidal) vasculature where the amplitude and frequency were varied and the steady-state thermal response evaluated using the Interface Enriched Generalized Finite Element Method (IGFEM) (Soghrati et al. 2012, 2013, 2012). The suite of simulation results populated a parametric space to produce an optimized vascular configuration that minimized the maximum temperature at steady state, while considering the flow efficiency (i.e., pressure drop) and void fraction.

In subsequent work, a reduced order model (ROM) was introduced to more efficiently obtain the steady-state thermal response of active-cooling systems using a NURBS-based Interface Enriched Generalized Finite Element Method (N/IGFEM) (Tan et al. 2015). Simplifying assumptions to the governing equations reduce computational cost of thermal and hydraulic analysis components. Additionally, the N/IGFEM method provides the ability to handle thermal discontinuities across elements, i.e., microchannels approximated as line sources can intersect elements within a structured, non-conforming mesh.

Following, a shape optimization scheme was developed based on minimizing the P-norm temperature at steady state for a vascular carbon-fiber epoxy-matrix composite (Tan et al. 2016; Najafi et al. 2015, 2017). The P-norm temperature is a differentiable alternative to the maximum temperature objective, introduced because of the need to find the gradients in the optimization process. Under this framework, the thermal response of a two-dimensional (2D) system is approximated by the ROM with N/IGFEM. The design parameters in this shape optimization scheme are control points that define the microchannel geometry and network connections. Owing to the N/IGFEM advantage in handling thermal discontinuities across elements, remeshing is not needed as the channels evolve during optimization, thereby enhancing computational efficiency. The shape optimization approach was later extended to 3D using standard IGFEM, but again with the P-norm temperature serving as the objective function (Tan and Geubelle 2017). The ability to enact control points in an additional dimension produced vascular configurations with even lower steady-state temperatures.

In an extension of this work, multi-objective shape optimization employing the same ROM and N/IGFEM, produced microvascular cooling networks using the Normalized Normal Constraint (NNC) and \(\epsilon\)-constraint methods (Tan et al. 2018). The three objective functions minimized in this study were the P-norm temperature, variance in the temperature field, and fluid pressure drop. This work also incorporated the cross-sectional dimensions of the rectangular microchannels as design variables, which led to additional thermal performance gains and lower pressure drop compared to a fixed cross-section.

Pejman et al. evolved beyond this work and developed a Hybrid Topology and Shape Optimization (HyTopS) framework (Pejman et al. 2019). By introducing additional design parameters, this new scheme allowed for optimization of channel diameter simultaneously with the optimization of the network configuration. Vascular segments were removed from the network if the coolant flow rate fell below a minimum threshold. Experimental and computational comparisons showed that HyTopS can obtain optimized designs with better steady-state active-cooling efficiency than the scheme based on shape optimization alone. The HyTopS framework was also deployed to design a microvascular cooling network using Polynomial Chaos Expansion (PCE) (Pejman et al. 2021). The PCE implement allowed uncertainty to be incorporated into the optimization process for which the respective probabilistic designs outperformed those from a deterministic approach. Furthermore, the HyTopS method was implemented in the design of blockage tolerant vascular networks (Pejman et al. 2020).

A more recent method for gradient-based topology optimization (TO), formulated around the same ROM, was introduced for actively cooled microvascular materials (Pejman et al. 2021). Utilizing a conforming finite element mesh, a large network of microchannels was predefined as collapsed line sources on select element boundaries. During the optimization process, the diameters of the microchannels evolve to minimize the P-norm temperature. As with the HyTopS method, channels are automatically removed from the network design via a flow rate threshold. However, there are several advantages to this TO framework over the HyTopS framework. Because there is no shape optimization occurring, the analytical sensitivity derivation is easier to implement since there is no need to determine the velocity field. Due to the fixed channel locations on the element boundaries there are no thermal discontinuities across elements, and thus, standard FEM interpolation is used (as opposed to generalized FEM or interface-enriched IGFEM). In addition to the aforementioned advantages, a comparison between the shape, hybrid shape/topology, and topology optimization methods indicates that lower as well as more uniform temperatures are obtained with this latest approach.

However, despite the numerous developments in microvascular-based active-cooling design optimization, there have been no works considering transient thermal behavior. This leaves an immense knowledge gap in related research and real-world translation. Transient thermal topology optimization requires an analysis tool to capture the time-varying temperature response and a transient sensitivity analysis to obtain the gradients of the design variables. In this study, the finite element and adjoint methods are employed to calculate the solution field and sensitivities, respectively.

The remainder of this paper is organized as follows: In Sect. 2, the transient heat transfer formulation and finite element model are introduced. In Sect. 3, a model verification via Ansys Fluent is performed along with an experimental validation. In Sect. 4, the optimization framework accompanying the derivation of the adjoint sensitivity analysis is presented. Finally, in Sect. 5, application problems are provided to demonstrate the newfound capabilities of the transient optimization framework.

1 Transient finite element model

In order to capture the transient thermal response of microvascular materials, a Geometric Reduced Order Finite Element Model (GRO-FEM) is implemented (Tan et al. 2015). The GRO-FEM is used because, as an iterative process, topology optimization is computationally costly. By making valid approximations, the GRO-FEM can ease this computational expense.

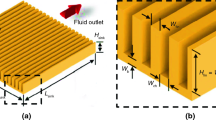
As depicted in Fig. 1, the domain of the model considered is a square plate with an embedded vascular network. The plate is composed of solid isotropic material and the vascular network contains flowing liquid coolant. The assumptions are as follows: since the thickness of the plate is small (< 1/20) compared to its length and width, a 2D analysis can be made. Also, since the diameters of the channels are small compared to their length, they are collapsed into line sources that lie on element boundaries. Because of this assumption, the wall temperature of the channel is assumed to be equal to the mixed mean fluid temperature of the coolant. The radiation heat transfer coefficient is obtained from the factorized Stefan–Boltzmann equation and added to the convection coefficient for a combined heat transfer coefficient (Tan et al. 2016). Additionally, the fluid flow is assumed to be fully developed, laminar, and steady state at the onset of active cooling. Conduction in the axial direction of flow is neglected due to the large Péclet number (compared to unity), indicating that advection dominates over axial conduction. Hagen-Poiseuille flow is assumed, i.e., the mass flow rate in each channel is linearly dependent on the pressure drop (Bahrami et al. 2005). Further details on obtaining the mass flow rate can be found in Appendix B.

In this model, the microvascular solid material is heated from the bottom surface by a uniform heat flux and cools via advective fluid flow and radiation plus convection from the top surface. The lateral surfaces/boundaries are considered adiabatic.

Fig. 1
figure 1

Illustration of the boundary value problem considered in the Geometric Reduced Order Finite Element (GRO-FEM) model for microvascular active cooling

Full size image

The works (Pejman et al. 2019, 2021; Zienkiewicz et al. 2005; Lewis et al. 2004; Zienkiewicz and Parekh 1970) were referenced in deriving this transient finite element model. The governing transient heat diffusion equation can be written in the weak form as:

$$\begin{aligned}&\int _{\Omega } \left( \nu \rho c \frac{\partial {T}}{\partial {t}} +\nabla \nu \cdot {\mathscr {K}} \nabla T + {\tilde{h}}\nu (T-T_{\text{amb}}) - \nu f\right) d\Omega \nonumber \\&\quad + \sum _{j=1}^{n_{ch}} \int _{\Gamma _f^{(j)}} \nu {\dot{m}}^{(j)}c_f{\textbf{t}}^{(j)} \cdot \nabla T d\Gamma = 0. \end{aligned}$$
(1)

In Eq. (1), \(\nu\) are the weight functions, \(\rho\) and \(c\) are the density and specific heat capacity of the solid host material, respectively, \({\mathscr {K}} = {\mathcal {K}}_p{\textbf{I}}\) is the host thermal conductivity tensor, \({\mathcal {K}}_p\) is the isotropic thermal conductivity of the solid material, \(T\) is the temperature field, \(T_{\text{amb}}\) is the ambient temperature, \(f\) is the distributed heat source applied to the bottom surface, \(n_{ch}\) is the number of microchannels, \({\dot{m}}^{(j)}\) is the mass flow rate of the \(j^{\textrm{th}}\) microchannel, \({\textbf{t}}^{(j)}\) is the unit tangent vector of the \(j^{\textrm{th}}\) microchannel in the flow direction, and \(c_{f}\) is the fluid coolant-specific heat capacity. \({\tilde{h}}=h_ {conv} +h_ {rad}\) is the equivalent (i.e., combined) heat transfer coefficient of the top surface and is found from the sum of the convection and the radiation components. The radiation component is found via the relation \(h_{\text{rad}} = 4\epsilon \sigma _{\text{B}} T^3_{\text{amb}}\), where \(\epsilon\) is the emissivity and \(\sigma _{\text{B}}\) is the Stefan–Boltzmann constant.

Using the finite element method (FEM), the physical domain of the problem can be discretized spatially. This gives approximations for the temperature field where,

$$\begin{aligned} T_{\text{e}}({\textbf{X}}) = \sum _{i=1}^{n^e}N_i({\textbf{X}})T_i={\textbf{N}}^e({\textbf{X}}){\textbf{T}}^e. \end{aligned}$$
(2)

In Eq. (2), \({\textbf{X}}\) are the spatial coordinates, \(n^e\) is the number of nodes in each element (e), \(N_i({\textbf{X}})\) are the shape functions, \(T_i\) is the temperature at each node, \({\textbf{N}}^e\) is the vector of shape functions for element e, and \(\mathbf {T^e}\) is the vector of nodal temperatures in element e. By taking the spatial derivative of (2) with respect to \({\textbf{X}}\), the thermal gradients are as follows:

$$\begin{aligned} \frac{{\partial } T_{\text{e}}({\textbf{X}})}{{\partial }{\textbf{X}}} = \frac{{\partial }{\textbf{N}}^e}{{\partial }{\textbf{X}}}{\textbf{T}}^e = {\textbf{B}}^e({\textbf{X}}){\textbf{T}}^e, \end{aligned}$$
(3)

where \({\textbf{B}}^e({\textbf{X}})\) is the partial derivative of \({\textbf{N}}^e({\textbf{X}})\) with respect to \({\textbf{X}}\). The derivative of temperature with respect to time can be written as:

$$\begin{aligned} \frac{{\partial } T_{\text{e}}({\textbf{X}})}{{\partial }t} = \sum _{i=1}^{n^e}N_i({\textbf{X}}){\dot{T}}_i={\textbf{N}}^e({\textbf{X}}){\dot{\textbf{T}}}^e, \end{aligned}$$
(4)

where \({\dot{T}}_i\) is the nodal time derivative of temperature, and \({\dot{\textbf{T}}}^e\) is the vector of nodal time derivatives of temperature for element e.

Using global finite element matrices, Eq. (1) can be represented as:

$$\begin{aligned} {\mathbb {C}}\mathbb {{\dot{T}}}+{\mathbb {K}}{\mathbb {T}}-{\mathbb {F}}=0, \end{aligned}$$
(5)

which is a set of spatially discretized ordinary differential equations. In Eqs. (5), \({\mathbb {K}}\) is the global stiffness matrix, \({\mathbb {C}}\) is the global capacitance matrix, \({\mathbb {F}}\) is the global force vector, \({\mathbb {T}}\) is the global nodal temperature vector, and \(\mathbb {{\dot{T}}}\) is the global nodal time derivative of temperature vector.

These global matrices are assembled from the numerically integrated element stiffness matrix \({\textbf{K}}^e\), element capacitance matrix \({\textbf{C}}^e\), and element force vector \({\textbf{F}}^e\) where:

$$\begin{aligned} {\textbf{K}}^e =&\int _{\Omega _{\text{e}}} \bigg ({\textbf{B}}^{e'}({\textbf{X}}){\mathscr {K}}{\textbf{B}}^e({\textbf{X}})+{\textbf{N}}^{e'}({\textbf{X}})\tilde{h}{\textbf{W}}^e({\textbf{X}})\bigg )\,d\Omega \nonumber \\&+\frac{1}{2}\sum _{j=1}^{n_{ch}}\int _{\Gamma _f^{(j)}\cap \partial \Omega _{\text{e}}} {\textbf{B}}^{e'}({\textbf{X}}){\textbf{t}}^{(j)}{\dot{m}}^{(j)}c_f{\textbf{W}}^e({\textbf{X}})\,d\Gamma , \end{aligned}$$
(6)
$$\begin{aligned} {\textbf{C}}^e =&\int _\Omega {\textbf{N}}^{e'}({\textbf{X}})\rho c {\textbf{N}}({\textbf{X}})\,d\Omega , \end{aligned}$$
(7)
$$\begin{aligned} {\textbf{F}}^e =&\int _\Omega {\textbf{W}}^{e'}({\textbf{X}})\big (f({\textbf{X}})+\tilde{h}T_{\text{amb}}\big )\,d\Omega . \end{aligned}$$
(8)

Here, the prime symbol \((\cdot )'\) indicates the transpose of \((\cdot )\). The term \({\textbf{W}}^e({\textbf{X}})\) in Eqs. (6) and (8) is the Streamline Upwind Petrov Galerkin (SUPG) function - a stabilizing term used to prevent oscillations in the solution due to the convection in the microchannels. Additional details regarding the SUPG term may be found in Pejman et al. (2019). In this model, it is assumed that there is no variation in temperature in the thickness direction of the plate. Thus, this dimension is handled by scaling the thermal conductivity in the stiffness matrix and specific heat capacity in the capacitance matrix by the plate thickness.

To discretize Eq. (5) temporally, a weighted residual finite element approach is taken. It is assumed that \({\mathbb {T}}\) varies linearly between each time step, and therefore can be approximated as:

$$\begin{aligned} {\mathbb {T}}(\tau ) = \sum _{ k=1 }^{l} N _{k}(\tau ){\mathbb {T}}_{k} = \left( 1-\frac{\tau }{\Delta t}\right) {\mathbb {T}}_{n-1}+\left( \frac{\tau }{\Delta t}\right) {\mathbb {T}}_{n}, \end{aligned}$$
(9)

where \(t\) is time, \(\Delta t\) is the time step size, \(\tau =t-t_{n-1}\), \(n\) is the number time step, \({\textbf{N}}\) is the vector of 1D Lagrangian shape functions, \(\mathbb {T}_{n-1}\) is the known global temperature vector of the current time step, \(\mathbb {T}_{n}\) is the unknown global temperature vector of the next time step, and \(l\) is the number of nodes in the temporally discretized element. In this study, the temperature is approximated to vary linearly between time steps (i.e., \(l=2\)), thus the weighted residual equation becomes:

$$\begin{aligned} \int _0^{\Delta t}W(\tau )[\mathbb {C}_n\mathbb {{\dot{T}}}+\mathbb {K}_{n}{\mathbb {T}}-\mathbb {F}_{n}]\,d\tau =0, \end{aligned}$$
(10)

where \(W(\tau )\) is an arbitrary weighting function. After introducing a weighting parameter:

$$\begin{aligned} \beta = \frac{1}{\Delta t}\frac{\int _0^{\Delta t}W(\tau )\tau \,d\tau }{\int _0^{\Delta t}W(\tau )\,d\tau }, \end{aligned}$$
(11)

Equation (10) can be re-written as:

$$\begin{aligned} \frac{1}{\Delta t}\mathbb {C}_{n}(\mathbb {T}_{n}-\mathbb {T}_{n-1})+\mathbb {K}_n[\mathbb {T}_{n-1}+\beta (\mathbb {T}_{n}-\mathbb {T}_{n-1})] - \mathbb {{\bar{F}}}_{n} = 0, \end{aligned}$$
(12)

where,

$$\begin{aligned} \mathbb {{\bar{F}}}_{n} = \mathbb {F}_{n} + \beta (\mathbb {F}_{n} - \mathbb {F}_{n-1}). \end{aligned}$$
(13)

By rearranging variables, Eq. (12) can be written as,

$$\begin{aligned} \mathbb {K}^*_{n}\mathbb {T}_{n} = \mathbb {F}^*_{n}, \end{aligned}$$
(14)

where \(\mathbb {K}^*_{n}\) and \(\mathbb {F}^*_{n}\) are defined as:

$$\begin{aligned}&\mathbb {K}^*_{n} = (\mathbb {C}_{n}+\beta \Delta t\mathbb {K}_{n}), \end{aligned}$$
(15a)
$$\begin{aligned}&\mathbb {F}^*_{n} = [(\mathbb {C}_{n}-(1-\beta )\Delta t\mathbb {K}_{n})\mathbb {T}_{n-1}+\Delta t \mathbb {{\bar{F}}}_{n}]. \end{aligned}$$
(15b)

Given an initial or current temperature profile, \(\mathbb {T}_{n}\) in Eq. (14) can be obtained using a linear solver such as Gaussian Elimination. In this study, the Unsymmetric-Pattern MultiFrontal Package (UMFPACK) is used for solving via Matlab’s backslash operator.

The constant \(\beta\) in Eq. (15) is used to determine the time stepping scheme when solving for the temperature distribution. For instance, if \(\beta =0\), an explicit scheme is used. If \(\beta =1\), an implicit scheme is used and setting \(\beta =\frac{1}{2}\) gives the semi-implicit Crank-Nicholson scheme. In this study, a value of \(\beta = 1\) (i.e., backward Euler) was used for all analyses.

2 Transient GRO-FEM model verification and validation

Previous works have verified/validated the GRO-FEM model under steady-state conditions (Tan et al. 2016; Pejman et al. 2019). To verify the new transient formulation and proper implementation of the 2D GRO-FEM, active-cooling simulation results are compared to a 3D Ansys Fluent simulation (2021). Experimental validation is also performed using an additively manufactured microvascular metal (Inconel 718, nickel-chromium superalloy).

Fig. 2
figure 2

Verification/validation problem description. Here, \({\dot{m}}_{in}\), \(T_{in}\), and \(P_{out}\) are the prescribed coolant inlet mass flow rate, prescribed coolant inlet temperature, and prescribed coolant outlet pressure, respectively. \(q^{\prime \prime }\) is the uniform heat flux applied to the bottom surface and \(\tilde{h}\) is the combined convection and radiation heat transfer coefficient of the top surface. The perimeter is insulated by polymer foam in the experiments and assumed adiabatic in the simulations

Full size image

Figure 2 provides the problem description. In the verification simulations, a microvascular plate (\(\approx\) 4 mm thick) with thermal properties of Inconel 718 (see Table 1) containing a 2-branch microchannel network is subject to the following boundary conditions: (i) applied heat flux from the bottom surface, (ii) adiabatic lateral surfaces, and (iii) convective and radiative heat loss from the top surface. In the simulations, the plate is discretized spatially with a structured mesh of 3200 triangular elements for the GRO-FEM model and a conforming mesh of 94374 elements for the Ansys Fluent model. Both simulations discretize temporally using a 1 s time step. Initially, the plate is at thermal equilibrium with no active cooling (i.e., fluid flow) occurring through the microchannels; we refer to this as the hot steady state (HSS). The plate is prescribed an initial HSS isothermal temperature of \({\textbf{T}}_0 = 75.87\) \(^{\circ }\)C in the simulations. At time t = 0, a constant coolant flow rate through the inlet is prescribed, reducing the temperature of the plate via advection. The coolant considered in these simulations is deionized water and the thermophysical properties for the simulations are indicated in Table 1. The transient thermal response of the plate is evaluated using the GRO-FEM and Ansys Fluent until reaching the cold steady state (CSS), i.e., when the plate is at thermal equilibrium with coolant flowing through the channels. In the GRO-FEM simulation, the CSS is defined such that the maximum nodal temperature variation between time steps is no more than 1x10\(^{-6}\) \(^{\circ }\)C/s. The Ansys Fluent verification simulation was evaluated at the same time that the GRO-FEM reached the CSS. The temperature profiles along the vertical centerline (\(x=0\)) for both transient simulations are plotted at 120, 300, 600, and 900 s in Fig. 3. The simulations agree with one another qualitatively, capturing the same undulating trend at each time stamp. Quantitatively, temperatures from the GRO-FEM model are lower than the Ansys Fluent simulation along the entire centerline, the differences being the highest at the channel locations with decreasing discrepancy between simulation platforms at later times.

There are a few possible sources for the differences between the GRO-FEM and Ansys Fluent. The Ansys model is 3D while the GRO-FEM model is simplified to 2D for computational efficiency. Moreover, there are differences in the equations that are solved for fluid flow and the radiation boundary condition. Ansys Fluent uses the set of nonlinear 3D Navier–Stokes equations to solve for the fluid velocity and the nonlinear Stefan–Boltzmann equation to solve for the radiation boundary condition. The GRO-FEM uses the linear Hagen-Poiseuille equation to obtain the fluid velocity and a factorized form of the Stefan–Boltzmann equation to resolve the radiation boundary condition, both potential contributors to differences between the simulation results.

Table 1 Thermophysical properties in validation comparison
Full size table
Fig. 3
figure 3

Centerline temperatures obtained from the transient GRO-FEM and Ansys Fluent at 120, 300, 600, and 900 s

Full size image
Fig. 4
figure 4

Experimental validation. a A micro-CT reconstruction of the 3D-printed Inconel 718 plate revealing the branched coplanar vascular network (scale bar = 10 mm); zoomed inset: optical micrograph showing the microchannel’s diamond-shaped cross-section (scale bar = 500 \(\mu\)m). b The average top surface temperature from infrared (IR) imaging and also the ambient temperature evolution recorded during the experiment

Full size image

For the validation experiment, the branched vascular network from the simulations is created in Inconel 718 (In718) using 3D-printing via selective laser melting (Fig. 4a). Due to the layer-by-layer metal powder melting process, a self-supporting diamond-shaped cross-section is constructed that has the same hydraulic diameter as the circular channels in the simulations. The In718 plate is placed atop a thin film resistive heater (Omega, KH608/2). The lateral sides of the plate are insulated with foam and the top surface is free to convect and radiate to the ambient atmosphere. The top surface is sandblasted and spray painted matte black to avoid reflections from the otherwise shiny metallic surface; the emissivity of the sanded/painted surface (\(\epsilon\) = 0.93) is measured according to ASTM standard E1933-14 (2018). During the experiment, an overhead infrared (IR) camera (FLIR, A655sc) measures the ambient and top surface temperatures. The plate is heated from the bottom surface via the resistive heater (q\(''\)=1000 \(W/m^2\)) until the HSS is reached. The system is considered at the HSS when the average top surface temperature does not vary by more than 0.2\(^{\circ }\)C within a 10 min interval (i.e., the resolution of the IR camera). Upon reaching the HSS, active cooling begins by pumping deionized water at room temperature (RT = 23\(^{\circ }\)C) through the vascular network via a peristaltic pump (Cole-Parmer, EW-07522-30) at a constant flow rate of 20.2 mL/min (i.e., within the laminar regime) until the CSS is achieved. The CSS is ascertained using the same temperature variation criterion as the HSS. The average top surface temperature evolution of the experiment for the transient heating and cooling processes is shown in Fig. 4b. The cold steady-state (CSS) temperature distributions for the validation experiment and both simulations are shown in Fig. 5 a-c. The GRO-FEM simulation captures the heat extraction along the vasculature with temperature gradients resembling the 3D simulation and experimental contours from IR imaging. The average and maximum surface temperatures versus time during the entire active-cooling segment are plotted in Fig. 5 d,e. The 3D simulation and the experimental validation agree closely with each other. The GRO-FEM simulation also captures the transient thermal evolution where this 2D model temperature prediction is generally lower than the other two results due to the simplifying assumptions of the GRO-FEM model. Table 2 summarizes the average and maximum surface temperatures of the experiment and both sets of simulations at the CSS. The average temperature between the experiment and 3D Ansys Fluent simulation at the CSS agree within \(\approx\) 0.5\(^{\circ }\)C, while the GRO-FEM agrees to within \(\approx\) 2\(^{\circ }\)C of the experiment. This is consistent with previous verification/validation studies of the steady-state GRO-FEM that found it produces lower average and maximum temperatures (for a similar boundary value problem) when compared to 3D simulations and experimental measurements (Tan et al. 2016; Pejman et al. 2019). However, the gain in computational efficiency of the GRO-FEM (via linearization) over Ansys Fluent is an attractive advantage, particularly in a transient and iterative optimization framework. To quantify the increased efficiency, the Ansys Fluent verification simulation required 188 min to solve, while the GRO-FEM verification took only 1.5 min to resolve the solution. Thus, based on the small differences in steady-state results and the close agreement of the temperature versus time plots, the transient GRO-FEM is deemed accurate enough given the benefit to reduce the computational cost in the iterative topology optimization framework described next.

Fig. 5
figure 5

Verification and validation of the transient GRO-FEM model. CSS top surface temperature distributions obtained from a the 2D GRO-FEM model, b 3D Ansys Fluent model, c validation experiment, and the respective evolution of d average and e maximum top surface temperatures versus time

Full size image
Table 2 Simulation and experimental top surface temperature comparison at CSS
Full size table

3 Transient topology optimization framework

In this section, the topology optimization framework is developed where the problem can be written mathematically as:

$$\begin{aligned} \min _{\mathbf {\alpha }} \quad&\theta (\mathbf {\alpha }) = G\left( {T_{n-1}^{Avg}}\left( \mathbf {\alpha }\right) ,{T_{n}^{Avg}}\left( \mathbf {\alpha }\right) ,\mathbf {\alpha }\right) \quad {n} \in [1,\ldots ,M] \end{aligned}$$
(16a)
$$\begin{aligned} s.t. \quad&H(\mathbf {\alpha }) = V(\mathbf {\alpha }) - V_{max} \le 0 \end{aligned}$$
(16b)
$$\begin{aligned}&I(\mathbf {\alpha }) = P(\mathbf {\alpha }) - P_{max} \le 0 \end{aligned}$$
(16c)
$$\begin{aligned}&\mathbb {C}_{n}{\dot{{\mathbb {T}}}}_{n}\left( \mathbf {\alpha }\right) +\mathbb {K}_{n}\left( \mathbf {\alpha }\right) {\mathbb {T}}_{n}\left( \mathbf {\alpha }\right) - \mathbb {F}_{n}=0 \quad {n} \in [1,\ldots ,M] \end{aligned}$$
(16d)
$$\begin{aligned}&\alpha _i = [0,1] \quad i \in [1,\ldots ,N], \end{aligned}$$
(16e)

where \(\theta\) is the objective function to be minimized, \(\mathbf {\alpha }\) is the vector of design variables (i.e., the microchannel diameters), \(G\) is a response functional, \(T^{Avg}\) is the average temperature of the domain, \(H\) is the volume constraint, \(V\) is the volume fraction of the microchannels in the design domain, \(V_{max}\) is the maximum allowable volume fraction of design variables, \(I\) is the pressure constraint, \(P\) is the inlet pressure, \(P_{max}\) is the maximum allowable inlet pressure, \(N\) is the number of design variables, \({n}\) is the time step, and \(M\) is the total number of time steps.

3.1 Design parameters

The design parameters used in this study contain a penalization factor introduced in Pejman et al. (2019) to reduce the number of intermediate diameters for manufacturability considerations. As such, the effective diameter is obtained from:

$$\begin{aligned} D^{(i)}_{eff} = D_{min}+\alpha ^\eta _i(D_{max,i}-D_{min}), \end{aligned}$$
(17)

where \(D^{(i)}_{eff}\) is the effective diameter of the \(i{\textrm{th}}\) microchannel, \(D_{min}\) is the minimum possible diameter of the microchannel to prevent numerical singularity, \(D_{max,i}\) is the largest possible microchannel diameter, \(\alpha\) is the set of design variables, and \(\eta\) is the penalization factor. In all of the optimization problems considered in this study, \(D_{max,i} = 450 \: \mu \text{m}\).

3.2 Objective function

The objective function to be minimized in this study is the area beneath the average temperature versus time curve as the plate actively cools from the hot steady state (HSS) to the cold steady state (CSS). By minimizing this area, it is intended that the CSS average temperature (T\(^\text {{Avg,CSS}}\)) and the time to reach this equilibrium (t\(_\text {{CSS}}\)) are reduced. This objective function is graphically depicted in Fig. 6. Here, the orange region represents the objective function for the initial design and the smaller blue region represents the objective function for the optimized design. In order to calculate the area, trapezoidal quadrature is implemented. Therefore, the objective function can be mathematically stated as:

$$\begin{aligned} G=\sum _ {n=1}^{M} \frac{\Delta t}{2}({T_ {n-1}^{Avg}}\left( \mathbf {\alpha }\right) +{T_{n}^{Avg}}\left( \mathbf {\alpha }\right) ) \end{aligned}$$
(18)

and

$$\begin{aligned} {T^{Avg}}\left( \mathbf {\alpha }\right) = \sum _{m=1}^{n_{node}}\left( \frac{T_m}{n_{node}}\right) , \end{aligned}$$
(19)

where n is the current time step, \(M\) is the total number of time steps, \(T^{Avg}\) is the average temperature in the domain, \(n_{node}\) is the number of nodes in the domain, \(T_m\) is the nodal temperature corresponding to node \(m\), and \(\Delta t\) is the time step of the transient analysis. In this framework, the total number of time steps \(M\) corresponds to the time required to reach the CSS. In all optimization problems conducted in this study, the CSS is such that the maximum nodal temperature deviation is not greater than 1x10\(^{-3}\) \(^{\circ }\)C/s between each time step.

Fig. 6
figure 6

Illustration of the objective function: the area below the average temperature versus time curve, for both the initial and optimized designs

Full size image

3.3 Adjoint sensitivity analysis

In order to calculate the sensitivities of the objective function, the adjoint method is used due to its accuracy and computational efficiency. In deriving this analysis, the following works were referenced (Tortorelli et al. 1994; Tortorelli and Haber 1989; Pejman et al. 2021, 2019; Michaleris et al. 1994; Vitola 2020). The adjoint sensitivity derivation is begun by taking the derivative of the objective function with respect to the design variables:

$$\begin{aligned} \frac{{\textrm{d}} \theta }{{\textrm{d}} \mathbf {\alpha } }&= \frac{{\textrm{d}} G\left( {\mathbb {T}}_{0}\left( \mathbf {\alpha }\right) ,{\mathbb {T}}_{1}\left( \mathbf {\alpha }\right) ,{\mathbb {T}}_{2}\left( \mathbf {\alpha }\right) ,\ldots ,{\mathbb {T}}_{M}\left( \mathbf {\alpha }\right) ,\mathbf {\alpha }\right) }{{\textrm{d}} \mathbf {\alpha } }\nonumber \\&= \sum _{n=1}^{M} \bigg ( \frac{{\partial }G}{{\partial }\mathbb {T}_{n-1}}\frac{{\partial }\mathbb {T}_{n-1}}{{\partial }\mathbf {\alpha } }+\frac{{\partial }G}{{\partial }\mathbb {T}_{n}}\frac{{\partial }\mathbb {T}_{n}}{{\partial }\mathbf {\alpha } }\bigg )+\frac{{\partial }G}{{\partial }\mathbf {\alpha }}. \end{aligned}$$
(20)

Because the response functional \(G\) is not explicitly a function of the design variable \(\mathbf {\alpha }\), the term \(\frac{{\partial }G}{{\partial }\mathbf {\alpha }}\) is zero. The terms \(\frac{{\partial }\mathbb {T}_{n}}{{\partial }\mathbf {\alpha } }\) and \(\frac{{\partial }\mathbb {T}_{n-1}}{{\partial }\mathbf {\alpha } }\) in Eq. (20) are implicit and therefore cannot be evaluated analytically. The strategy to handle these implicit terms is to use a Lagrange multiplier to eliminate them from the equation. To apply this strategy, a pseudo problem is introduced by taking the derivative of the transient scheme in matrix form (14) with respect to the design variable. After rearranging, the pseudo problem can be written as:

$$\begin{aligned} \mathbb {K}^*_{n}\frac{{\partial }\mathbb {T}_{n}}{{\partial }\mathbf {\alpha } } =&-\frac{{\partial }\mathbb {K}^*_{n}}{\partial \mathbf {\alpha } }\mathbb {T}_{n}+ \frac{{\partial }\mathbb {F}^*_{n}}{{\partial }\mathbf {\alpha } } \quad {n} \in [1,\ldots ,M] \end{aligned}$$
(21a)
$$\begin{aligned} \mathbb {K}_{0}\frac{{\partial }\mathbb {T}_{0}}{{\partial }\mathbf {\alpha } }=&-\frac{{\partial }\mathbb {K}_{0}}{{\partial }\mathbf {\alpha } }\mathbb {T}_{0}+ \frac{{\partial }\mathbb {F}_{0}}{{\partial }\mathbf {\alpha } } \end{aligned}$$
(21b)
$$\begin{aligned} \frac{{\textrm{d}} \theta }{{\textrm{d}} \mathbf {\alpha } } =&\sum _{n=1}^{M}\Big ( \frac{{\partial }G}{{\partial }\mathbb {T}_ {n-1}}\frac{{\partial }\mathbb {T}_ {n-1}}{{\partial }\mathbf {\alpha } }+ \frac{{\partial }G}{{\partial }\mathbb {T}_{n}}\frac{{\partial }\mathbb {T}_{n}}{{\partial }\mathbf {\alpha } }\Big )\nonumber \\&+\sum _{n=1}^{M} \Bigg (\mathbf {\lambda}_n\left( -\mathbb {K}^*_{n}\frac{{\partial }\mathbb {T}_{n}}{{\partial }\mathbf {\alpha } }- \frac{{\partial }\mathbb {K}^*_{n}}{{\partial }\mathbf {\alpha } }\mathbb {T}_{n}+ \frac{{\partial }\mathbb {F}^*_{n}}{{\partial }\mathbf {\alpha } }\right) \Bigg ) \nonumber \\&+\mathbf{\lambda} _0\Big (-\mathbb {K}_{0}\frac{{\partial }\mathbb {T}_{0}}{{\partial }\mathbf {\alpha } }-\frac{{\partial }\mathbb {K}_{0}}{{\partial }\mathbf {\alpha } }\mathbb {T}_{0}+ \frac{{\partial }\mathbb {F}_{0}}{{\partial }\mathbf {\alpha } } \Big ), \end{aligned}$$
(22)

where \(\mathbf {\lambda}_n\) is the Lagrange multiplier at time step \(n\). Because the terms \(-\mathbb {K}^*_{n}\frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } }-\frac{\partial \mathbb {K}^*_{n}}{\partial \mathbf {\alpha } }\mathbb {T}_{n}+ \frac{\partial \mathbb {F}^*_{n}}{\partial \mathbf {\alpha } }\) and \(-\mathbb {K}_{0}\frac{\partial \mathbb {T}_{0}}{\partial \mathbf {\alpha } }-\frac{\partial \mathbb {K}_{0}}{\partial \mathbf {\alpha } }\mathbb {T}_{0}+ \frac{\partial \mathbb {F}_{0}}{\partial \mathbf {\alpha } }\) are identically equal to zero, the Lagrange multiplier can be chosen arbitrarily, as its choice will have no impact on the value of the gradient of the objective function. This property is critical as the choice of the Lagrange multiplier will be used to eliminate the implicit terms in the gradient of the objective function. Here, the Lagrange multiplier will be selected as the adjoint variable obtained through solving an adjoint problem.

To progress toward solving for \(\mathbf {\lambda}_n\), Eq. (22) can be further evaluated by first considering the derivatives of the terms in the transient scheme with respect to the design variables \(\mathbf {\alpha }\). Here,

$$\begin{aligned} \frac{\partial \mathbb {K}^*_{n}}{\partial \mathbf {\alpha }} =&\beta \Delta t \frac{\partial \mathbb {K}_{n}}{\partial \mathbf {\alpha } }, \end{aligned}$$
(23a)
$$\begin{aligned} \frac{\partial \mathbb {F}^*_{n}}{\partial \mathbf {\alpha }} =&-(1-\beta )\Delta t \frac{\partial \mathbb {K}_{n}}{\partial \mathbf {\alpha } }\mathbb {T}_ {n-1}\nonumber \\&+[\mathbb {C}_{n}-(1-\beta )\Delta t \mathbb {K}_{n}]\frac{\partial \mathbb {T}_{n-1}}{\partial \mathbf {\alpha } }, \end{aligned}$$
(23b)

noting that \(\frac{\partial {\mathbb {C}}}{\partial \mathbf {\alpha } }\) and \(\frac{\partial {\mathbb {F}}}{\partial \mathbf {\alpha } }\) are zero since they are not explicitly dependent on the design variables \(\mathbf {\alpha }\). Next, the derivatives of the response function can be evaluated as:

$$\begin{aligned} \frac{\partial G}{\partial \mathbb {T}_ {n-1}}&= \frac{\Delta t}{2}\frac{\partial {T_{n-1}^{Avg}}}{\partial \mathbb {T}_ {n-1}}, \end{aligned}$$
(24a)
$$\begin{aligned} \frac{\partial G}{\partial \mathbb {T}_{n}}&= \frac{\Delta t}{2}\frac{\partial {T_{n}^{Avg}}}{\partial \mathbb {T}_{n}}, \end{aligned}$$
(24b)

where the derivative \(\frac{\partial {T^{Avg}}}{\partial {\mathbb {T}}}\) is equal to a vector of size \([1 \times n_{nodes}]\) with values of \(\frac{1}{n_{nodes}}\) for each entry. Subsequently, the derivatives in Eqs. (23) and (24), along with the finite element matrices constituting the transient scheme, are substituted into Eq. (22) to obtain the following relation:

$$\begin{aligned} \frac{{\textrm{d}} \theta }{{\textrm{d}} \mathbf {\alpha } } =&\sum _{n=1}^{M}\frac{\Delta t}{2}\Big ( \frac{\partial T_{n-1}^{Avg}}{\partial \mathbb {T}_{n-1}}\frac{\partial \mathbb {T}_{n-1}}{\partial \mathbf {\alpha } }+\frac{\partial T_{n}^{Avg}}{\partial \mathbb {T}_{n}}\frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } } \Big )\nonumber \\&+\sum _{n=1}^{M}\mathbf{\lambda} _n \Big (-[\mathbb {C}_{n}+\beta \Delta t \mathbb {K}_{n}] \frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } }-\beta \Delta t\frac{\partial \mathbb {K}_{n}}{\partial \mathbf {\alpha } }\mathbb {T}_{n}\nonumber \\&-(1-\beta )\Delta t \frac{\partial \mathbb {K}_{n}}{\partial \mathbf {\alpha } }\mathbb {T}_{n-1}+ [\mathbb {C}_{n}-(1-\beta )\Delta t\mathbb {K}_{n}] \frac{\partial \mathbb {T}_{n-1}}{\partial \mathbf {\alpha } } \Big )\nonumber \\&+\mathbf{\lambda} _0\Big (-\mathbb {K}_{0}\frac{\partial \mathbb {T}_{0}}{\partial \mathbf {\alpha } }-\frac{\partial \mathbb {K}_{0}}{\partial \mathbf {\alpha } }\mathbb {T}_{0}+ \frac{\partial \mathbb {F}_{0}}{\partial \mathbf {\alpha } } \Big ). \end{aligned}$$
(25)

Now, any terms in Eq. (25) that are associated with an implicit derivative are separated into an “implicit equation," \(\frac{{\textrm{d}} \theta _i}{{\textrm{d}} \mathbf {\alpha } }\). The implicit derivatives in this case are \(\frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } }\) and \(\frac{\partial \mathbb {T}_{n-1}}{\partial \mathbf {\alpha } }\). The remaining terms are placed in an “explicit equation,"\(\frac{{\textrm{d}} \theta _{\text{e}}}{{\textrm{d}} \mathbf {\alpha } }\). The implicit and explicit equations are defined by Eqs. (26a) and (26b), respectively:

$$\begin{aligned} \frac{{\textrm{d}} \theta _i}{{\textrm{d}} \mathbf {\alpha } } =&\sum _{n=1}^{M}\bigg (\frac{\Delta t}{2}\frac{\partial {T_{n-1}^{Avg}}}{\partial \mathbb {T}_{n-1}}\frac{\partial \mathbb {T}_{n-1}}{\partial \mathbf {\alpha } } + \frac{\Delta t}{2}\frac{\partial {T_{n}^{Avg}}}{\partial \mathbb {T}_{n}}\frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } }\nonumber \\&+\mathbf{\lambda} _{n}\bigg (-[\mathbb {C}_{n}+\beta \Delta t \mathbb {K}_{n}]\frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } }\nonumber \\&+[\mathbb {C}_{n}-(1-\beta )\Delta t \mathbb {K}_{n}\frac{\partial \mathbb {T}_{n-1}}{\partial \mathbf {\alpha } }]\bigg )\bigg ) \nonumber \\&-\mathbf{\lambda} _0\mathbb {K}_{0}\frac{\partial \mathbb {T}_{0}}{\partial \mathbf {\alpha } }, \end{aligned}$$
(26a)
$$\begin{aligned} \frac{{\textrm{d}} \theta _{\text{e}}}{{\textrm{d}} \mathbf {\alpha } } =&\sum _{n=1}^{M}\mathbf{\lambda} _n\bigg (-\beta \Delta t \frac{\partial \mathbb {K}_{n}}{\partial \mathbf {\alpha } }\mathbb {T}_{n}-(1-\beta )\Delta t \frac{\partial \mathbb {K}_{n}}{\partial \mathbf {\alpha } }\mathbb {T}_{n-1}\bigg )\nonumber \\&-\mathbf{\lambda} _0\frac{\partial \mathbb {K}_{0}}{\partial \mathbf {\alpha } }\mathbb {T}_{0}. \end{aligned}$$
(26b)

The summation in the implicit equation can then be expanded, and all terms of the same time step can be collected to solve for that time step’s respective Lagrange multiplier. There are two unknowns in each equation required to solve for the Lagrange multiplier, \(\mathbf{\lambda} _n\) and \(\mathbf{\lambda} _{n+1}\), except for the final time step which is only dependent on \(\mathbf{\lambda} _M\). Therefore, the solution strategy is to obtain and record the thermal response for each time step, and then working backwards beginning with \(n=M\), all of the adjoint variables (Lagrange multipliers) can be obtained through the solution of the following adjoint problems.

For \(n=M\) (final time step):

$$\begin{aligned} \bigg (\frac{\Delta t}{2}\frac{\partial {T_{M}^{Avg}}}{\partial \mathbb {T}_{M}} - \mathbf{\lambda} _M[\mathbb {C}_{M}+\beta \Delta t \mathbb {K}_{M}]\bigg )\frac{\partial \mathbb {T}_{M}}{\partial \mathbf {\alpha } } =0. \end{aligned}$$
(27)

The coefficient of \(\frac{\partial \mathbb {T}_{M}}{\partial \mathbf {\alpha } }\) is set equal to zero by solving for \(\mathbf{\lambda} _M\) such that:

$$\begin{aligned} \mathbf{\lambda} _M'=\frac{\Delta t}{2}([\mathbb {C}_{M}+\beta \Delta t \mathbb {K}_{M}]')^{-1}\frac{\partial {T_{M}^{Avg}}}{\partial \mathbb {T}_{M}}'. \end{aligned}$$
(28)

For \(n=1,\dots ,M-1\) (intermediate time step):

$$\begin{aligned}{} & {} \bigg (\Delta t\frac{\partial {T_{n}^{Avg}}}{\partial \mathbb {T}_{n}}-\mathbf{\lambda} _n[\mathbb {C}_{n}+\beta \Delta t\mathbb {K}_{n}]+\mathbf{\lambda} _{n+1}[\mathbb {C}_{n+1}\nonumber \\{} & {} \quad -(1-\beta )\Delta t\mathbb {K}_{n+1}]\bigg )\frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } } = 0. \end{aligned}$$
(29)

The coefficient of \(\frac{\partial \mathbb {T}_{n}}{\partial \mathbf {\alpha } }\) can be set equal to zero by solving for \(\mathbf{\lambda} _n\) such that:

$$\begin{aligned} \mathbf{\lambda} '_n= & {} \bigg ([\mathbb {C}_{n}+\beta \Delta t\mathbb {K}_{n}]'\bigg )^{-1}\bigg (\Delta t\frac{\partial {T_{n}^{Avg}}}{\partial \mathbb {T}_{n}}'+ [\mathbb {C}_{n+1}\nonumber \\{} & {} -(1-\beta )\Delta t\mathbb {K}_{n+1}]'\mathbf{\lambda} _{n+1}'\bigg ). \end{aligned}$$
(30)

For \(n=0\) (initial time):

$$\begin{aligned} \bigg (\frac{\Delta t}{2} \frac{\partial {T_{0}^{Avg}}}{\partial \mathbb {T}_{0}}+\mathbf{\lambda} _{1}[\mathbb {C}_{1}-(1-\beta )\Delta t\mathbb {K}_{1}]-\mathbf{\lambda} _0\mathbb {K}_{0}\bigg )\frac{\partial \mathbb {T}_{0}}{\partial \mathbf {\alpha } } = 0. \end{aligned}$$
(31)

The coefficient of \(\frac{\partial \mathbb {T}_0}{\partial \mathbf {\alpha } }\) is set equal to zero by solving for \(\mathbf{\lambda} _0\) such that:

$$\begin{aligned} \mathbf{\lambda} '_0=(\mathbb {K}_{0}')^{-1}\Bigg (\frac{\Delta t}{2} \frac{\partial {T_{0}^{Avg}}}{\partial \mathbb {T}_{0}}'-\mathbf{\lambda} _{1}[\mathbb {C}_{1}-(1-\beta )\Delta t\mathbb {K}_{1}]'\Bigg ). \end{aligned}$$
(32)

Now that \(\mathbf{\lambda} _n\) is known for each time step, Eq. (26b) can be solved, giving the sensitivity of the objective function.

As an additional note, for the optimization problems solved in this study, the initial temperatures of the microvascular material are prescribed. Therefore, the implicit derivative \(\frac{\partial \mathbb {T}_{0}}{\partial \mathbf {\alpha } }\) is automatically zero and does not need to be eliminated. Furthermore, because the initial condition assumes no flow at time \(t=0\), the term \(\frac{\partial \mathbb {K}_{0}}{\partial \mathbf {\alpha } }\) is zero. This eliminates \(\mathbf{\lambda} _0\) in the explicit Eq. (26b). Thus, solving for \(\mathbf{\lambda} _0\) with the initial conditions considered herein is not necessary.

Furthermore, the term \(\frac{\partial \mathbb {K}_{n}}{\partial \mathbf {\alpha } }\) in Eq. (26b) can be evaluated analytically by solving the element equation:

$$\begin{aligned} \frac{\partial \mathbf {K}_n^e}{\partial \mathbf {\alpha }} = \frac{1}{2}\sum ^{n_{ch}}_{j=1}\int _{\Gamma ^j_f\cap \partial \Omega }\mathbf {B}^{e'}t'^{(j)}\frac{\partial \dot{m}^{(j)}}{\partial \mathbf {\alpha }}c_f\mathbf {W}^ed\Gamma _f, \end{aligned}$$
(33)

and subsequently assembling into a global matrix. Further details on this derivative can be found in Pejman et al. (2021).

3.4 Optimization framework

In this optimization framework, all possible microchannels are predefined in a network grid and where the channels lie on the boundaries of the elements. An example of an 8x8 predefined vascular network along with an initial (reference) and final (optimized) network is shown in Fig. 7. Through the optimizer’s algorithm, channels may be created and along with existing channels, the diameters are increased or decreased to minimize the objective function. A continuation method is incorporated in this framework where the optimization processes repeat for successive penalization values of \(\eta =\) 1, 1.5, 2, 2.5, and 3 (Pejman et al. 2021). After the optimizer has converged at each penalization step, any channel whose flow rate falls below a defined threshold is removed. The critical flow rate threshold considered in this study is 0.3 mg/s (0.017 mL/min). In the framework developed here, the algorithm used is FMINCON SQP, available in MATLAB (MATLAB 2015).

Fig. 7
figure 7

An example of all predefined channel possibilities in the design space/grid, an example initial (reference) vasculature, as well as an example optimized design. For these example networks, the inlet is at the top left and the outlet is at the bottom right

Full size image

4 Application problems

4.1 Example problem 1: Uniform heat flux

In this first example, the transient optimizer is employed to design an actively cooled microvascular metal. The problem is defined as follows:

A 100 x 100 x 3 mm plate constructed of Inconel 718 is subject to the same boundary conditions as in the verification problem of Sect. 2 (Fig. 2). The design domain is discretized spatially using a conforming mesh of 5000 triangular elements and temporally using a 1 s time step. This discretization scheme is used for all optimization problems considered in this study. Initially, the material is at the isothermal hot steady state (HSS) temperature (\({{T}}_0 = 77.11\)). At time t = 0, constant coolant flow through the microchannel is initiated, reducing the temperature of the material until it reaches the cold steady state (CSS). The thermophysical properties of the solid plate and liquid coolant are shown in Table 3. The coolant used in all optimization problems is 50:50 ethylene glycol and water. The viscosity of the coolant is considered to be temperature-dependent, where \(\nu = 0.0069(T^{ch}_{avg}/273.15)^{-8.3}/\rho\) (Jarrett and Kim 2011). Here, \(\rho\) is the coolant density, \(T^{ch}_{avg} = \frac{1}{|\Omega _f|}\int _{\Omega _f}Td\Omega _f\) is the average microchannel temperature in Kelvin, \(\Omega _f\) is the domain of the un-collapsed microchannels, and \(|\Omega _f|\) is the volume of all microchannels in the plate. Figure 7a shows all of the possible channels in the optimization domain, with the reference configuration shown in Fig. 7b, and in all cases for this example, the coolant enters the vascular network at the top left and exits the outlet at the bottom right. Through the optimization process outlined in Sect. 3, the initial (reference) vascular network is evolved to minimize the objective function (area beneath the average temperature vs. time curve) as the solid host material is actively cooled by the flowing liquid.

In addition, two competing constraints are placed on the design: (i) maximum pressure drop and (ii) maximum volume fraction. The volume fraction constraint will prevent the optimizer from producing a design with all possible channels and the pressure drop constraint eliminates small diameter channels, which are often difficult to manufacture. The maximum pressure drop constraint in this problem is 55 kPa and the maximum volume fraction constraint is 0.5 %.

Fig. 8
figure 8

Example Problem 1: a vascular configurations, b flow rate distributions, and c CSS temperature distributions of the reference and optimized designs

Full size image
Fig. 9
figure 9

a Average temperature versus time during cooling for the reference and optimized designs in Example 1. b The objective value (area beneath average temperature vs. time) and c constraint evolution for each optimization iteration

Full size image
Table 3 Thermophysical properties for the example problem(s)
Full size table

Figure 8 shows the distribution of channel diameters, mass flow rates, and CSS temperatures for the reference and optimized design. The mass flow rate and channel distributions provide a depiction of the design changes made after the optimization process - where the optimization framework introduced channels to reduce the objective function. The temperature profile at CSS shows a lower and more uniform temperature field that is achieved with the optimized design.

Figure 9a is a plot of the average temperature vs. time for the reference and optimized designs, where the reduction in the objective function (i.e., the area beneath each respective curve) is apparent. As shown in Fig. 9b, the optimization algorithm converged in 145 iterations. Additionally, both prescribed pressure (55 kPa) and volume fraction (0.5 %) constraints were met, making this a viable solution. The spikes observed in the constraint values versus iteration plot (Fig. 9c) are due to the change of the penalization factor (\(\eta\)) during the continuation process. Table 4 compares the area beneath the average temperature vs. time curve, the average temperature at CSS, and the time required to reach CSS for the reference and optimized designs. The optimization process was able to reduce these three variables by 53.1%, 8.7%, and 53.1%, respectively.

Table 4 Table of the reference and optimized results from Example problem 1
Full size table

The difference in the reference design objective value in Table 4 and initial objective value in Fig. 9b at iteration zero is due to the microchannel thresholding/penalization. The reference design objective value in Table 4 considers that the channels are fully penalized and those below the mass flow rate threshold are already removed. The objective value of the initial design in Fig. 9b still considers all channels present and at lower penalization (i.e., \(\eta =1\) in Eq. (17)) at the beginning of the continuation process.

A further comparison of the optimized design from Example 1 is made with a more intuitive, engineered reference configuration as seen in Fig. 10a. In this reference design, a larger number of channels (equal to the volume constraint) are placed within the design domain. Figure 10b shows the average temperature vs. time for the intuitive reference and optimized designs during the cooling process. Here, it is seen that the optimized design’s performance is superior - with a 19.4% lower objective value (i.e, area beneath each respective curve) than the intuitive reference. The increased performance of the optimized design demonstrates this framework's capability of finding a better performing network configuration compared to a more conventional microchannel design.

Fig. 10
figure 10

a An intuitive reference design containing a volume of microchannels equal to the constraint. b The average temperature versus time during cooling for the intuitive reference and optimized designs in Example problem 1. The increased performance i.e., (faster cooling to a lower CSS temperature) of the optimized design demonstrates the framework's capability of finding a superior network compared to a more conventional microchannel design

Full size image

In an additional study, the effects of the initial design on the optimized configuration are evaluated. Figure 11 demonstrates the objective function evolution of a set of 25 initial designs. Also shown are 6 initial and optimized configurations (a-f) from this set. Here, it is seen that optimized designs with different channel configurations can still provide similar cooling performance by reaching the best local minimum. Some designs are trapped in other local minima during the optimization process (i.e., Fig 11d) where the resulting optimized channel configuration deviates further from the other optimized designs.

Fig. 11
figure 11

The objective function evolution of 25 different initial configurations. A set of 6 of the initial and optimized channel configurations are shown in a through f

Full size image

4.2 Example problem 2: Concentrated heat flux

In this second example, the effect of concentrated heat fluxes on the metal (Inconel 718) plate is studied. The material properties, reference design, and boundary conditions are the same as in Example 1, except that the inlet and outlet are now moved to the far left and far right center of the plate, respectively. The initial reference design is shown in Fig. 12b and 12(h). Design constraints are placed on the vascular network such that the maximum allowable pressure is 40 kPa and the maximum allowable volume fraction of channels is 0.5 %.

Simultaneously with the onset of coolant flow, concentrated heat fluxes of 30,000 \(W/m^2\) are applied in addition to a 1000 \(W/m^2\) uniformly distributed heat flux across the entire domain. Two concentrated heat flux cases are considered. For Case 1, the concentrated fluxes are located in the lower and upper left quadrants, and for Case 2, the heat fluxes are in the lower left and upper right quadrants. Figure 12 shows the concentrated heat flux locations, the reference and optimized vascular designs, temperature contours at the CSS, as well as transient active-cooling behavior. In response to the concentrated heat fluxes, the optimizer inserts channels and increases diameters to direct and increase coolant flow through high flux regions.

Fig. 12
figure 12

Example Problem 2: a Heat flux Case 1; b, c Reference/optimized vascular designs; d, e CSS temperature distributions; and f Transient average temperature vs. time behavior. g Heat flux Case 2; h, i Reference/optimized vascular designs; j, k CSS temperature distributions; and (l) Transient average temperature vs. time behavior

Full size image

As an additional evaluation, the optimized designs obtained in Example 2 (Fig. 12c and 12i) are compared with a more intuitive reference design as seen in Fig. 13a. Figure 13b and 13c show the average temperature versus time during cooling for the Concentrated Heat Flux 1 and 2 cases, respectively. Here, in both instances, the design optimized for a specific concentrated heat flux configuration outperforms the intuitive reference - with an 11.8% lower objective for the Concentrated Heat Flux 1 design and a 6.7% lower objective for the Concentrated Heat Flux 2 design. This again shows that this framework can identify a better performing microchannel design compared to a more conventional microchannel configuration.

Fig. 13
figure 13

a An intuitive reference design containing a volume of microchannels equal to the constraint. b The average temperature versus time during cooling for the intuitive reference and optimized designs in Example problem 2: Concentrated Heat Flux 1. c The average temperature versus time during cooling for the intuitive reference and optimized designs in Example problem 2: Concentrated Heat Flux 2. The increased performance (faster cooling to a lower CSS temperature) of the optimized design in both b and c confirms the framework's capability of finding a better performing network compared to a more conventional microchannel design

Full size image

4.3 Example problem 3: Varying flow rates

In this third example, minimization of the new transient objective function (area beneath the average temperature vs. time curve) is compared to a prior steady-state optimizer (Pejman et al. 2021). The steady-state optimization process minimizes the P-norm temperature at the CSS. The P-norm temperature objective function is used in place of the maximum temperature, since the latter is not a differentiable function - a requirement for this gradient-based optimization process.

The predefined vascular grid is the same as in the two prior examples. However, for this problem, a symmetry boundary condition is applied along the center channel (from the left inlet to the right outlet), which enhances the computational efficiency. The remaining boundary conditions and thermophysical properties are the same as in Example problem 1. The maximum allowable volume fraction of the channels in the design is 0.25 %. However, no pressure constraint is applied in this problem for fair comparison of results across varying flow rates (2.5, 5, 10 mL/min).

The aim here is to determine if the active-cooling performance and vascular designs produced by the transient optimizer will differ from the results produced by the steady-state optimizer, and if so, under which flow rates. Figure 14 shows the vascular network configurations, CSS temperature contours and average temperature versus time cooling curves for the designs produced by the transient and steady-state optimizers for the three flow rates considered.

The steady-state and transient optimizers produce different designs at all flow rates. The transient framework produces a distribution of smaller channels throughout the entire domain while the steady-state framework produces a more flow-directed design with fewer and larger channels. This is likely due to the initial transient isothermal conditions throughout the plate, where at the beginning of active cooling, flow is required everywhere in the domain. In contrast, the steady-state optimizer is only concerned with the temperature distribution at the CSS where flow is directed to the regions that are the warmest, i.e., closer to the outlet. The flow rate required to cool such proximal regions is lower than that needed for the entire domain, leading to less branching of the vasculature for the steady-state optimizer. As the flow rate is reduced, less branching is observed near the inlet for the steady-state designs, which prevents heating of the coolant prior to reaching the hottest regions of the plate.

Comparing the transient thermal performance of the designs obtained from the steady-state and transient optimizers (Fig. 14 (m-o)), the difference in area beneath the average temperature vs. time curves is small.

Fig. 14
figure 14

Example Problem 3: a, b Vascular designs obtained from the transient and steady-state optimizers for a coolant flow rate of 2.5 mL/min, and c, d respective CSS temperature distributions; e, f Vascular designs obtained from the transient and steady-state optimizers for a coolant flow rate of 5 mL/min, and g, h respective CSS temperature distributions; i, j Vascular designs obtained from the transient and steady-state optimizers for a coolant flow rate of 10 mL/min, and k, l respective CSS temperature distributions; m, n, o Transient active-cooling profiles for the reference, steady-state optimized, and transient optimized vascular networks at 2.5, 5, and 10 mL/min flow rates

Full size image
Table 5 Comparison of active-cooling performance at CSS for designs obtained from steady-state and transient optimization methods
Full size table

Thus, as summarized in Table 5, not much advantage is gained for transient optimization in comparison with minimizing the steady-state P-norm temperature. When also considering the additional cost of the transient GRO-FEM and sensitivity analysis, minimizing the P-norm temperature at steady state seems to provide an adequate design for nearly optimized transient performance of the microvascular system considered in this study. However, this may not necessarily be the case for other problems, e.g., those with time-varying boundary conditions.

As an additional investigation of the vascular networks produced by the transient optimization framework, each design was evaluated at the two other flow rates for which it was not optimized. For example, the design optimized at 2.5 mL/min was additionally evaluated at 5 and 10 mL/min. Figure 15 provides the CSS temperature contours, average CSS temperature, time to reach CSS, and the transient objective function. All of the steady-state temperature contours appear similar, but the transient objective function values are smaller for the optimized design, confirming that the transient framework performs as intended. In other words, the vascular designs optimized for a specific flow rate provided a transient cooling response with the least area beneath the average temperature versus time curve (objective function) when compared to designs optimized for a different flow rate.

Fig. 15
figure 15

Cross evaluation of the transient designs optimized for 2.5, 5, and 10 mL/min. Shown here are the vascular networks for each design and the CSS temperature profile at each flow rate. The dashed boxes indicate the best performance at the analyzed flow rates, which corresponds in all cases to the transient optimized networks. The best performance is characterized by having the lowest objective value at the analyzed flow rate

Full size image

5 Conclusion

In this work, transient topology optimization for active-cooling of microvascular plates has been achieved considering a Geometric Reduced Order Finite Element Model (GRO-FEM). The computationally efficient framework, verified and validated herein, has expanded the vascular design space beyond previous methods that are limited to steady-state heat transfer. The transient objective function, i.e., minimization of the area beneath the average temperature versus time curve, provides a robust criterion for gradient-based optimization with respective sensitivities derived from adjoint analysis.

The newfound capabilities of this transient optimization framework have been demonstrated via several active-cooling examples. The microvascular designs evolved from a reference configuration exhibit both faster cooling and lower cold steady-state temperatures under a uniform, as well as concentrated heat fluxes. In another example, while the vascular designs and resulting temperature contours are different for the new transient versus a prior steady-state optimizer (Pejman et al. 2021), the average temperature vs. time profiles are strikingly similar, revealing that a steady-state optimization is sufficient for the problems considered in this study (i.e., 2D design domains with relatively small diameter microchannels). However, this may not be the case under alternative microvascular system parameters, for example: temperature-dependent properties (e.g., thermal conductivity), time-varying boundary conditions (heat sources and losses), or design domains where the microchannels could traverse in 3-dimensions. Moreover, further transient objective functions (and sensitivities) could be developed. Such classes of problems represent ripe areas for future research that can build upon these latest findings and new optimization framework.