Abstract
Metamaterials open up a spectrum of artificially engineered properties otherwise unreachable in conventional bulk materials. For electromechanical energy conversion systems, lightweight materials with high hydrostatic piezoelectric coupling coefficients and negative Poisson’s ratio can be obtained. Thus, in this contribution, we explore the possibilities of piezoelectric metamaterials design by employing structural optimization. More specifically, we apply a sequential framework of topology and shape optimization to design piezoelectric metamaterials with negative Poisson’s ratio for electromechanical energy conversion under uniform pressure. Topology optimization is employed to generate the initial layout, whereas shape optimization fine tunes the design and improves durability and manufacturability of the structures with the help of a curvature constraint. An embedding domain discretization (EDD) method with adaptive domain and shape refinement is utilized for an efficient and accurate computation of the state problem in the shape optimization stage. Multiple case studies are conducted to determine the importance of desired stiffness characteristics, symmetry conditions and objective formulations on the design of piezoelectric metamaterials. Results show that the obtained designs are highly dependent on the desired stiffness characteristics. Moreover, the addition of the EDD-based shape optimization step introduces significant changes to the designs, confirming the usability of the sequential framework.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Metamaterials have seen growing interest in recent years due to the their exceptional properties that are otherwise unreachable in natural or conventional materials. Such properties can be achieved via an engineered geometry on the microstructural level, which, when periodically repeated, can reproduce the effective properties on the macroscopic level. The broad spectrum of reachable physical properties includes, e.g. acoustic and piezoelectric acoustic metamaterials for wave manipulation and enhanced sound absorption and insulation (Ji and Huber 2022), photonic metamaterials for ultrahigh-resolution imaging or cloaking devices (Soukoulis and Wegener 2011), piezoelectric metamaterials for vibration suppression and energy harvesting at wide bandgaps (Hu et al. 2017), electromagnetic or chiral metamaterials with applications in remote aerospace devices, military equipment or medical diagnostic devices (Valipour et al. 2022).
Piezoelectrics are particularly interesting from the perspective of metamaterial design due to their capability of electromechanical energy conversion. Therefore, they find application in actuation, sensing (Shaikh and Zeadally 2016), hydrophones, energy harvesting (Wei and Jing 2017) and many other engineering and medical devices (Vijaya 2012). Some of the inherent limitations of ceramic piezoelectrics, like brittleness and high stiffness, can be overcome, for instance, by introducing porosity in the microstructure (Della and Shu 2008; Kar-Gupta and Venkatesh 2006; Zhang et al. 2017). Moreover, progress in additive manufacturing has a crucial contribution in the development of piezoelectric materials with arbitrary geometries on the microscale level, including lead-free piezoelectrics like PVDF nanocomposites (Bodkhe et al. 2017) or BCZT cellular materials (Köllner et al. 2022). Porous piezoelectrics exhibit lower stiffness, brittleness and higher sensitivity, which is highly beneficial for ultrasonic transduction (Smith 1989) or ceramics for biomechanical structures (Mancuso et al. 2021).
By altering the geometry of the microstructure, some mechanical properties like stiffness or density can be tailored for specific applications but most importantly, materials with unconventional characteristics like negative effective Poisson’s ratio, so-called auxetic materials, can be obtained (Alderson and Alderson 2007; Carneiro et al. 2013). The exceptional ability of auxetic materials to contract in transverse directions under compressive load opens up a range of possibilities for energy harvesting (Zhao et al. 2022). Auxetic cellular honeycomb (HC) structures are the most popular auxetic metamaterials, widely studied in the literature due to their relatively simple geometry (Iyer and Venkatesh 2011; Iyer et al. 2015; Khan et al. 2019). Stress build-up within auxetic HC was verified numerically and experimentally (Whitty et al. 2003) and various configurations of auxetic HC were compared for their superior electromechanical properties towards energy harvesting applications (Köllner et al. 2023).
In the last two decades, the role of structural optimization methods, density-based and level-set topology optimization in particular (Bendsoe and Sigmund 2003; Wang et al. 2003), has immensely increased in engineering design. Geometries generated using structural optimization reach beyond designers intuition and broaden our horizons in understanding the relationship between shape, connectivity and the resultant properties of the structure. Advances in additive manufacturing only strengthen these developments, since they allow manufacturing of topology optimized shapes without engineer’s interference with the obtained structures. These developments have been successfully extended towards the generation of new geometries for metamaterials. Besides the classical, re-entrant design of HC for auxetic metamaterials, alternative designs of periodic microstructures have been generated mathematically using topology optimization for linear elastic materials (Neves et al. 2000; Zhang et al. 2007) with the objective to generate structures with desired stiffness properties, in Andreassen et al. (2014) with consideration of manufacturability and 3D geometries.
In Paulino et al. (2009), the optimal design of functionally graded composites was shown, which benefits from the presence of grey transition regions within density-based topology optimization. Topology optimization of thermomechanical microstructures was addressed in Moshki et al. (2022) using an alternating active-phase algorithm to handle the presence of multiple materials. Optimal design of biodegradable metamaterials for medical applications was addressed in Zhang et al. (2021). Alternative optimization methods like the ground structure approach (Li et al. 2021) or machine learning frameworks (Challapalli et al. 2021; Fernández et al. 2022) have been applied to generate optimal lattice structures or density-based structures (Kollmann et al. 2020).
Optimal microstructure designs for piezoelectric materials were shown in Silva et al. (1997), Sigmund et al. (1998) and Silva and Kikuchi (1999) with the objective function to maximize the hydrostatic coupling coefficient \(d_h\) or the figure of merit \(d_h \times g_h\). These studies on the design of piezoelectric microstructures using topology optimization give a detailed overview of how the results are affected by the choice of different objective functions focusing on energy conversion performance. The designs obtained in these works resulted in auxetic behaviour, proving that \(d_h\) is a good choice of objective function for hydrostatic applications. In Vatanabe et al. (2014), the design of piezoelectric microstructures was successfully explored using topology optimization for maximum phononic bandgaps. In Xu et al. (2017), the dynamic characteristics of piezoelectric microstructure were optimized using a bidirectional evolutionary structure optimization (BESO) method. The goal of this work was to maximize the damping dissipation velocity, which improves the active control performance. In Ding and Xu (2022), the design of piezoelectric microstructures for vibration suppression using the BESO method was introduced by considering the initial disturbance.
In addition to microstructural design for piezoelectric structures, recent advances in te optimal design of piezoelectric structures include reliability-based topology optimization with voltage uncertainty (Yang et al. 2022), which uses the PEMAP-P model that additionally considers the polarization direction as a design variable. In Donoso et al. (2023), a novel piezoelectric transducer design methodology is presented that focuses on optimizing electrode configurations for manufacturable and functional devices. In Wang et al. (2023), a velocity field level-set method is presented to determine the optimal material distribution of a piezoelectric layer on a plate with active vibration control. Compared to density-based topology optimization, the level-set method improved the accuracy of vibration control by avoiding intermediate densities.
Among various structural optimization methods the density-based approach to topology optimization (Bendsøe 1989), also referred to as the SIMP (Solid Isotropic Material with Penalization) method, is most widely studied due to its simple formulation and implementation (Andreassen et al. 2011; Aage et al. 2015), large design space (no initial guess of the design is necessary) and robustness. However, by using the material interpolation law and the lack of mechanical boundaries, it also poses certain challenges, in particular in imposing boundary-related constraints, e.g. curvature constraints. On the contrary, node-based shape optimization methods rely upon the direct update of the boundary of the structure (Ding 1986). The presence of the mechanical boundary guarantees an accurate solution of the state problem and enables simple incorporation of boundary-related constraints, like stress or curvature constraints. The main hurdle, however, is the limitation to small design updates and the necessity of a valid initial guess of the design. The standard approach to node-based shape optimization deals with an explicitly meshed structure and the design update concerns not only the boundary nodes (the factual design variables) but also the inner nodes (the dependent nodes), thereby greatly increasing the complexity of the regularization schemes. Some of these drawbacks are addressed in implicit boundary approaches, like, for instance, the level-set methods (Allaire et al. 2002), where larger design updates are not an issue due to the separation of the computational domain, which consists of a structured mesh, and the representation of the shape by a level-set function. Alternatively, node-based shape optimization using an embedding domain discretization (EDD) method was outlined in Riehl and Steinmann (2017), in which the variable shape is explicitly modelled by lower-dimensional segments, e.g. line segments in 2D; hence, the inner nodes of the variable shape are avoided. Moreover, a structured, adaptively refined background mesh is utilized as the computational domain. This approach alleviates the update of the inner elements of the variable shape and mitigates the complexity of regularization schemes, effectively enabling much larger design updates and at the same time facilitating more efficient computations with flexible refinement strategies for the background mesh.
To profit from the advantages of different structural optimization approaches, various combined methods were proposed (Sokolowski and Zochowski 1999; Norato et al. 2007; Eschenauer et al. 1994; Christiansen et al. 2014; Lian et al. 2017; Riehl and Steinmann 2015; Nguyen et al. 2020; Andreasen et al. 2020; Stankiewicz et al. 2021). In our work, we adapt the sequential approach as in Dev et al. (2022); Stankiewicz et al. (2022), in which a standard, density-based topology optimization is used to generate an initial structure and node-based shape optimization using EDD follows up to fine tune the design. This combination proved to be a good fit due to a number of reasons. First, the choice of EDD-based shape optimization requires generation of only the boundary of the shape (1D segments) after the topology optimization step, which greatly simplifies the transition step from topology to shape optimization. Secondly, a coarsely discretized domain for topology optimization is chosen, as we do not require highly accurate state problem computations, since it only provides the initial configuration of the shape optimization step. Next, we incorporate a shape curvature constraint as in Stankiewicz et al. (2022) to improve manufacturability and durability of the final design, which is otherwise a challenging task in topology optimization due to the lack of an explicit boundary. Finally, we exploit the advantages of both topology and shape optimization, as listed before, to provide a versatile and powerful structural optimization routine capable of designing complex geometries from a large design space, at the same time guaranteeing high accuracy of the state problem solutions and a variety of possible constraints.
The contribution of this work is twofold. Firstly, we develop a shape optimization methodology for the design of metamaterials by exploiting computational homogenization within the EDD framework. We investigate how shape optimization further improves the metamaterial after generating an initial design with topology optimization to verify the significance of such sequential approach. Secondly, we perform an advanced study on how the microstructural design of piezoelectric structures depends on the desired stiffness characteristics by running case studies with various constraint sets on both the “normal” stiffness coefficients as well as the “shear” stiffness coefficients. Moreover, a comparison of different objective functions for the generation of auxetic structures and of various symmetry conditions is performed.
The article is organized as follows. In Sect. 2 we introduce the theoretical background for the computation of effective materials properties of piezoelectric structures. We employ asymptotic expansion in order to provide analytical expressions for the effective materials tensors and for the computation of sensitivities. In Sect. 3 we outline the sequential optimization routine. Section 4 contains the results of the case studies and the discussion. The conclusions and future outlook are addressed in Sect. 5.
2 Theoretical background
2.1 Piezoelectricity
The direct piezoelectric effect is observed when electric charges accumulate on the surface of a non-conducting dielectric material due to mechanical strain. The converse piezoelectric effect occurs when mechanical stress is induced in response to an applied electric field.
The following theoretical formulations are outlined based on Ieee standard on piezoelectricity (1988). We adopt a standard tensor notation. For the formulation of the state problem, we consider a piezoelectric domain \(\Omega \). At any point in the domain \(\Omega \) , the mechanical balance of linear momentum has to be fulfiled, which, assuming there are no body forces acting on \(\Omega \), reads
and where \(\varvec{\sigma }\) is the Cauchy stress. Additionally, the electrostatic equation is formulated for an insulating material as follows;
where \(\varvec{D}\) is the electric displacement. Note that for the electric behaviour, we are only concerned with the quasistatic electric approximation; hence, no dynamic coupling with mechanical strains is considered. Mechanical strain is obtained as the symmetric gradient of the displacement field \(\varvec{u}\)
and the electric field is derived from a scalar electric potential \(\phi \)
By considering the mechanical and electrical properties of the structure as well as the piezoelectric coupling between them, the enthalpy density for a piezoelectric structure takes the form
where \(\varvec{C}\) is the elasticity tensor, \(\varvec{e}\) is the piezoelectric coupling tensor and \(\varvec{\epsilon }^S\) is the permittivity tensor. The linear constitutive relations are then obtained by taking derivatives of H w.r.t the field gradients
Equations (6) and (7) are represented in a stress-charge form, in which the elasticity tensor corresponds to the material stiffness, the piezoelectric coupling tensor and the permittivity tensor define the relation at constant strain between the electric field and the Cauchy stress and the electric displacement, accordingly. Alternatively, the constitutive relations can be represented in a strain-charge form, namely
where \(\varvec{S}= \left[ \varvec{C}\right] ^{-1}\) is the compliance matrix, \(\varvec{d}= \varvec{e}: \varvec{S}\) the piezoelectric tensor and \(\varvec{\epsilon }^T\) the permittivity tensor in the strain-charge format
The boundary conditions for a piezoelectric problem are given as follows
where \(\bar{\varvec{t}}\) and \(\bar{q}\) are prescribed tractions and free surface charges, respectively.
2.2 Homogenization for piezoelectrics
In the following, we briefly introduce the methodology to compute effective material properties of piezoelectric composites. In this work, the effective material properties are predicted numerically using the finite element method. For structural optimization purposes, the effective material properties require an analytical representation (Silva et al. 1997). Therefore, a first-order asymptotic expansion of the field variables (Chung et al. 2001) is employed according to the theory of homogenization in order to separate the micro- and macroscale:
where \(\varvec{y} = \varvec{x} / \epsilon \) (\(\epsilon \) is a small parameter) represents an upscaling of the microstructure that captures the heterogeneous nature of the material. \(\varvec{u}_0\) and \(\phi _0\) are independent of \(\varvec{y}\), since they describe the macroscopic (homogenized) part of the solution, while \(\varvec{u}_1\) and \(\phi _1\) represent the fluctuation part of the solution due to the material variation on the microscale. Hence, a portion of the microstructure is selected, the so-called unit cell or the representative volume element (RVE) \(\text {Y}= [0,y_1] \times [0,y_2] \times [0,y_3]\) that best approximates the complex behaviour of the structure when periodically repeated in all directions. The fluctuations of the solution can be further formulated as follows (Gałka et al. 1992)
where \(\varvec{\chi }\) is a third-order tensor consisting of characteristic displacements \(\varvec{\chi }^\mathrm{(ij)}\) (Torquato and Haslach Jr 2002), \(\varvec{\zeta }\) and \(\varvec{\psi }\) are second-order tensors, where \(\varvec{\zeta }^\mathrm{(k)}\) and \(\psi ^\mathrm{(ij)}\) are characteristic coupling functions and \(\varvec{\eta }\) is a first-order tensor, where \(\eta ^\mathrm{(k)}\) are characteristic potentials. Indexes \(\mathrm{(ij)}\) and \(\mathrm{(k)}\) indicate a relation to the corresponding unit tests, i.e. the \(\mathrm{(ij)}\)-th unit strain tests and \(\mathrm{(k)}\)-th unit electric field tests.
To obtain the respective microscopic strain and electric field tensors, we utilize the chain rule
By assuming that \(\epsilon \) is sufficiently small, we obtain the following kinematic relation for the partial derivative of the displacement field
and by employing Eqs. (14) and (15), we arrive at
At this point, we can express the total strains and total electric fields for each of the (ij)-th and (k)-th unit tests as
where \(\varvec{\varepsilon }_0^\mathrm{(ij)}\) and \(\varvec{E}_0^\mathrm{(k)}\) are the macroscopic (unit) strain and electric field due to \(\mathrm{(ij)}\)-th and \(\mathrm{(k)}\)-th unit tests. For a detailed derivation of the microscopic and macroscopic equations, we refer to (Gałka et al. 1992; Nelli Silva et al. 1999). In the following, we directly proceed to the homogenized tensors in the energy bilinear form. By utilizing the previously introduced quantities, they are given as follows.
d21 (d31), d22 (d33) and the combined \(d^h\) conversion on the example of the BTO crystal structure. The titanium atom (in red) is slightly off-centre in the vertical direction, indicating the polarization direction. When external loading is applied, the deformation of the structure causes the titanium atom to further displace, affecting the dipole moment and the resultant electric displacement \(\varvec{D}\). The light red atom indicates its original position before the application of the external load. (Color figure online)
whereas by using Eqs. (20)–(23) we obtain the expressions for individual material coefficients as follows
2.3 Chosen performance measures
Two performance measures are considered in this study for the objective function: the effective Poisson’s ratio \(\upsilon _{\textrm{H}}\) and the hydrostatic coupling (charge) coefficient \(d^h_{\textrm{H}}\). The purpose of this work is to design structures with improved energy conversion efficiency under uniform pressure field. The works of Silva et al. (1997), Sigmund et al. (1998), Silva and Kikuchi (1999) have shown that using the hydrostatic coupling (charge) coefficient \(d^h_{\textrm{H}}\) as an objective function leads to feasible, auxetic designs with good energy conversion efficiency under uniform pressure field. However, for better comparison, \(\upsilon _{\textrm{H}}\) is alternatively employed in the topology optimization step with the goal of initiating the shape optimization step with an auxetic structure. The choice of \(\upsilon _{\textrm{H}}\) or \(d^h_{\textrm{H}}\) is then examined to determine the differences in the topologies obtained using these objective functions. However, only \(d^h_{\textrm{H}}\) is used for the shape optimization step since the initial structure is already auxetic at this point.
Before proceeding with the definition of those measures, let us reformulate the effective material tensors using Voigt notation. The effective elastic tensor takes the form of a 3x3 matrix in two dimensions (for the two-dimensional case in this work we consider the direction 2 (Y) as the polarized direction) and for an orthotropic material is given by
Whereas the effective piezoelectric tensor \(\varvec{e}_{\textrm{H}}\) in the stress-charge form in the Voigt notation is defined as
Analogously, the effective piezoelectric tensor in the strain-charge form is given by
Now, the effective Poisson’s ratio is formulated by assuming a transversely isotropic behaviour on the macroscale
The second quantity of interest is the effective hydrostatic (charge) coupling coefficient \(d_{\textrm{H}}^h\) which relates the electric displacement in the polarization direction \(D^2_{\textrm{H}}\) with a hydrostatic pressure P under zero electric field \(\varvec{E}_0 = \varvec{0}\). For clarity, we recall Eq. (9) under the assumption of zero electric field
Then, by considering a hydrostatic pressure (in Voigt notation) \(\varvec{\sigma }= \left[ P, P, 0\right] \) , we obtain the following relation
effectively reducing to
since the (perpendicular to the polarization direction) electric displacement \(D^1_{\textrm{H}}\) is only related to \(\varvec{\sigma }_{\textrm{H}}\) by \(d^{31}_{\textrm{H}}\), effectively coupling only the shear stress \(\sigma ^{12}_{\textrm{H}}\) with \(D^1_{\textrm{H}}\), which is set to zero in the case of hydrostatic pressure. Thus, the sum \(d^h_{\textrm{H}} = d^{21}_{\textrm{H}} + d^{22}_{\textrm{H}}\) is the effective hydrostatic coupling (charge) coefficient of interest, which can be formulated as follows:
where \(\bar{\varvec{v}} = \left[ 1 \ 1\right] \) and \(\varvec{\bar{C}}_{\textrm{H}}\), \(\varvec{\bar{e}}_{\textrm{H}}\) are the simplified effective tensors, given as follows
Here, the second formulation involves only the material tensors in the stress-charge form, as required for the sensitivity analysis. For a clearer understanding of the meaning behind the hydrostatic piezoelectric coupling \(d^h\), in Fig. 1, the two possible ways of invoking the direct piezoelectric effect on the example of a BTO non-centro-symmetric crystal structure are shown, the sum of which make up for the \(d^h\) conversion. The slight displacement of the oxygen octahedron and the titanium atom along the direction 2 (Y) creates a dipole moment, which is further affected by the external loading and the resultant deformation. The left-hand image depicts the \(d^{21}\) (\(d^{31}\) in 3D) direct conversion, since the load is applied in the direction 1 (X), perpendicular to the polarization direction. In the second image, the material is loaded along the polarization direction, hence the \(d^{22}\) (\(d^{33}\) in 3D) conversion. However, under the hydrostatic loading conditions (as in the right-hand image), the effects of \(d^{21}\) and \(d^{22}\) conversion annihilate each other, effectively resulting in a very low conversion rate. This is a clear consequence of the fact that any bulk material exhibits a positive Poisson’s ratio. Hence, application of the metamaterial concept to design structures with negative Poisson’s ratio appears to be reasonable in order to account for higher conversion rates under hydrostatic loading.
3 Optimization strategy
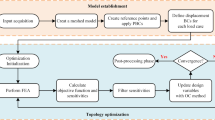
3.1 Sequential approach
In Dev et al. (2022), a sequential approach to topology and shape optimization was outlined, specifically to tackle the challenge of designing compliant mechanisms with a focus on durable flexure hinges, which require highly refined geometry and accurate numerical models. Topology optimization is the state of the art tool for structural design and has the capability to generate complex structures without initial guess of the geometry. Moreover, it is relatively simple to implement and robust. Nevertheless, shape optimization explicitly treats the boundary of the structure, providing an opportunity to consider boundary-related measures, like, for instance, the boundary stress or the curvature. In Fig. 2, the sequential approach to topology and shape optimization is sketched together with a brief overview of the advantages of each method. For detailed discussions on the applicability of this approach, refer to Dev et al. (2022), Stankiewicz et al. (2022).
3.2 Topology optimization
Density-based topology optimization employs pseudo-densities \(\rho _e \in \left[ 0, 1 \right] \) as design variables, which are assigned to every finite element, hence the subindex e. For pure elastic problems, SIMP (Solid Isotropic Material with Penalization) is the standard approach to determine the material properties of a structure with intermediate densities. For piezoelectric problems, the interpolation of each material tensor is analogous \(\{ \bullet \} \left( {\hat{\rho }}_e \right) = \left[ {\hat{\rho }}^{p}_e \left[ 1 - \rho _{\textrm{min}}\right] + \rho _{\textrm{min}}\right] \ \{ \bullet \}\), where \(\rho _{\textrm{min}} = 10^{-9}\) and for each material tensor we employ the following penalization factors: \(p = 3\) for \(\varvec{C}_e\) and \(p = 2\) for \(\varvec{e}_e\) and \(\varvec{\epsilon }^S_e\). We determined that this combination of penalization factors provides, for the case studies in this work, the best convergence towards black and white designs. The hat in \({\hat{\rho }}_e\) indicates the regularized pseudo-density. The three-step regularization consists of the density filtering for member size control and checkboard pattern avoidance (Bruns and Tortorelli 2001), smoothed Heaviside projection filter for the reduction of the grey transition region (Wang et al. 2011) and projection-based filter for symmetry constraints (Vatanabe et al. 2016).
The topology optimization step is defined according to the following setup
Both of the objective functions given in 2.3 are considered in this step: the effective Poisson’s ratio \(\upsilon _{\textrm{H}}\) and the effective hydrostatic piezoelectric coupling coefficient \(d_{\textrm{H}}^h\). However, \({\mathcal {F}}\left( {{\hat{\rho }}, \varvec{u}} \right) \) is not a multi-objective function, but rather, it is either \(\upsilon _{\textrm{H}}\) or \(d_{\textrm{H}}^h\) as shown in the results section. The minimization of the first objective is employed purely to generate an auxetic behaviour, whereas maximization of the second objective directly optimizes the electromechanical conversion efficiency under hydrostatic loading conditions. Such a choice of objectives allows to assess whether those responses can be used interchangeably, since both of the formulations should ultimately generate an auxetic structure. The effective orthotropy of the structure is ensured by the symmetry constraint imposed on the design variables. The sensitivities of above mentioned responses are obtained by means of the adjoint method, similar to Silva et al. (1997). The optimal solution is sought after by means of the Method of Moving Asymptotes (MMA) (Svanberg 1987).
3.3 Shape optimization
Following the initial generation of the structure layout using topology optimization, we utilize the shape generation tool as described in the beginning of the chapter and perform the fine tuning of the design by means of the shape optimization in the EDD setting. The EDD approach to shape optimization is outlined in detail in Riehl and Steinmann (2017) for linear elastic problems and further explored for simultaneous topology and shape optimization in Stankiewicz et al. (2021) and sequential topology and shape optimization of compliant mechanisms in Dev et al. (2022) in linear elasticity with boundary stress constraints and in Stankiewicz et al. (2022) in nonlinear elasticity with the addition of local adaptive refinement strategies and curvature constraint.
In Fig. 3, the adaptive refinement procedure for the EDD state problem in the last iteration of a sequentially optimized piezoelectric metamaterial is shown. The finite elements of the embedding domain are subdivided into the inner elements (coloured in red), boundary elements (cut by the shape, coloured in green) and the outer elements (coloured in white). A close-up of the locally refined region based on the curvature criterion is additionally shown in Fig. 4. For a detailed description on the adaptive refinement strategy for EDD, we refer to Stankiewicz et al. (2022).
Uniform and local adaptive refinement steps for EDD state problem. a–c depict a uniform refinement of all boundary elements of the embedding domain (coloured in green). d shows local refinement of the boundary elements based on the curvature criterion for locally improved accuracy. (Color figure online)
Usage of the adaptive refinement procedure for the domain and the shape guarantees accuracy of the solution and improves computational efficiency and the resolution of the shape curvature. In Fig. 5, three different discretizations are depicted that represent the design between the topology and shape optimization steps. In Table 1, the corresponding effective properties of the structure computed using each of the discretizations are given. The differences between the material coefficients reach even 45% for the case of \(C^{22}_{\textrm{H}}\). A number of factors contribute to such a large divergence in the predicted material values. On the one hand, we deal with the inherent limitations of density-based topology optimization, which are the presence of grey cells that require interpolation of the material tensor, and the staircase-like boundary. On the other hand, the shape extraction procedure is purely heuristic and does not guarantee a feasible design right away. The authors are aware that the precision of the topology optimization state problem can be improved by refining the mesh (at the cost of computational efficiency). However, specifically for the sequential approach, the current methodology is sufficient, as the shape optimization step guarantees an accurate solution to the state problem (as compared with the standard FEM) and efficient computation due to the adaptive refinement strategies.
Solution comparison of the state problem within the sequential optimization framework. a The density distribution at the final, converged iteration of the topology optimization step. b An EDD problem and c a standard FEM model, both based on the directly extracted shape from the topology optimization result in a
The problem definition for the shape optimization step is analogous to that of the topology optimization step, with the exception of using just \(d^h_{\textrm{H}}\) as the objective function and the addition of the curvature constraint
where the objective function is a function of the nodal positions of the boundary and \(\kappa \) stands for the curvature magnitude of the shape. The curvature magnitude is defined as the second derivative of the arclength parameterized plane curve \(\varvec{x} (s)\) as follows:
The discretized version of \(\kappa \) is obtained by employing Taylor series expansion to approximate \(\partial _s^2 \varvec{x}\), which for a node i, after some modifications, is given by
where \(\varvec{N}^i\) is the nodal normal vector calculated as a weighted average of the adjacent segment normals. For more details on the derivation of the curvature constraint, see Stankiewicz et al. (2022). Note that the implementation of the curvature constraint is integrated within the regularization procedure of the shape sensitivities. The regularization of the sensitivities, the bounding box as well as the curvature constraint are all realized via the traction method, which was first introduced in Azegami and Takeuchi (2006) and adapted to the EDD setting with the inclusion of the aforementioned geometrical constraints in Stankiewicz et al. (2022).
4 Numerical studies
In the following section, we conduct numerical experiments that evaluate the influence of various optimization setups and discuss the obtained results. First of all, we consider a well-known re-entrant honeycomb (see Fig. 6) and perform pure shape optimization to investigate its influence on an already established design and its dependency on various sets of constraints for the effective elastic tensor. Next, we conduct three studies of a complete design approach, i.e. sequential topology and shape optimization. In the first study, we compare the two different objectives for the topology optimization step, as given in the previous section. In the second study, we vary the values of the elastic coefficients and in the third study, we compare the possible symmetry conditions. Moreover, in each of the studies, we consider the influence of the constraint on the effective shear elastic coefficient.
4.1 Bulk properties
The bulk material used for the case studies in this work is barium titanate (BTO, chemical formula: \(\mathrm BaTiO_3\)). BTO is a lead-free alternative to the commonly used lead zirconate titanate (PZT), which finds application in piezoelectric energy harvesters. As typical for a ceramic material, BTO is highly brittle and stiff, which limits its application in terms of operational frequencies and deformation under vibrational energy harvesting or sensing. Hence, the application of the metamaterial concept to BTO offers great possibilities for improved deformability, larger operational frequency range and lightweight design. Since BTO cannot undergo large strains and for computational efficiency, only a geometrically linear model for the state problem is considered. In Appendix 1 all necessary material coefficients are given.
4.2 Shape optimization of engineered structures
The re-entrant honeycomb is the standard layout when it comes to auxetic structures. An exemplary design is shown in Fig. 6, and the effective material properties of which are the following
The \(d^\textrm{h}_{\textrm{H}}\) value is significantly superior as compared to the bulk material (\(d^\textrm{h} = 112 \mathrm{pC/N}\)). The normal stiffness in vertical direction (\(C^{22}_{\textrm{H}}\), direction Y) is more than twice higher than in the horizontal direction (\(C^{11}_{\textrm{H}}\), direction X). Moreover, the shear stiffness \(C^{33}_{\textrm{H}}\) is relatively small which signifies a potential instability under imperfect loading. In the following, we investigated two different target stiffness configurations by means of pure shape optimization. The problem setup, i.e. the objective and the constraints, is outlined in Table 2.Footnote 1 The optimization problems are each limited to 200 iterations of the Multiplier Method (Hestenes 1969; Rockafellar 1973). Therefore, we accept slight violations of the constraints as the optimization problems often do not reach the assumed tolerances.
We directly maximize the effective hydrostatic piezoelectric coupling coefficient \(d^h_{\textrm{H}}\) under the volume restriction of 40% of the unit cell. For the stiffness constraints, in case 1, we aim to obtain a structure with similar stiffness in both X and Y directions. In case 2, however, we try to preserve similar stiffness values as in the initial design. In both cases, we introduce the curvature constraint \(\kappa \le 5 \left[ \mathrm{1/mm}\right] \) which is equivalent to a minimum radius constraint of \(r > 0.2 \left[ {\text {mm}}\right] \) to avoid stress concentration.
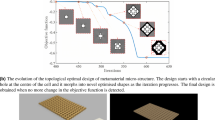
In Fig. 7, the resultant structures from the shape optimization of the re-entrant honeycomb are shown with the effective properties listed in Table 3.
To begin with, an interesting observation is that the objectives \(d^\textrm{h}_{\textrm{H}}\) and \(\upsilon _{\textrm{H}}\) lead to strongly similar designs, see, for instance, the cases 1, 3 and 2, 4, pairwise. Moreover, the improvement of \(d^\textrm{h}_{\textrm{H}}\) is negligible and the value of \(\upsilon _{\textrm{H}}\) is indeed better for the cases with lower \(C^{22}_{\textrm{H}}\) stiffness. For the cases 1 and 3, the value of \(C^{22}_{\textrm{H}} = 4\) has not been reached. We observe a tendency; however, the decrease of \(C^{22}_{\textrm{H}}\) is realized via a change in the angle of the diagonal member in the structure. Nevertheless, the design changes during shape optimization alone are in general very small, which heavily restricts possible setups of the optimization problems. Still, we draw the main conclusion of the first study that the design of the re-entrant honeycomb is mainly a question of the desired stiffness proportion between \(C^{11}_{\textrm{H}}\) and \(C^{22}_{\textrm{H}}\) rather than finding the maximal \(d^\textrm{h}_{\textrm{H}}\) value.
Close-up of the resulting structures of the shape optimization problems from Table 2. The black design is the initial configuration
4.3 Complete design approach
In the following, we explore the design possibilities of piezoelectric metamaterials by employing the sequential topology and shape optimization routine. We analyse three case studies, each time choosing different constraints to assess their influence on the design. We start with the objective function, for which the effective Poisson’s ratio \(\upsilon _{\textrm{H}}\) and effective hydrostatic piezoelectric coupling coefficient \(d_{\textrm{H}}^\textrm{h}\) are compared in the initial design generation phase by topology optimization. In conjunction with this, the presence of a constraint on the shear stiffness coefficient \(C^{33}_{\textrm{H}}\) is studied. In Table 4, the optimization setup is shown. The responses of interest are additionally highlighted.
Note that the objective for the shape optimization for all cases is \(d^\textrm{h}_{\textrm{H}}\), since this is the ultimate design goal. Regarding the stiffness characteristics, we require the same normal stiffness in both X and Y directions. The obtained structures together with the chosen effective properties are depicted in Table 5.
It is immediately apparent that significantly varying geometries were obtained for each setup, although the objective values remain practically the same. In particular, the case 5 generated the well-known re-entrant honeycomb structure. Nevertheless, all of the designs exhibit auxetic behaviour with Poisson’s ratios of \(\upsilon _{\textrm{H}} \approx -\,0.8\) or lower, which confirms the unanimity of both objective functions. The structures from the upper row in Table 5 exhibit very low shear stiffness coefficient \(C_{\textrm{H}}^{33}\) in relation to \(C_{\textrm{H}}^{11}\) and \(C_{\textrm{H}}^{22}\). By introducing the constraint \(C_{\textrm{H}}^{33} > 0.50\) , visibly different designs were obtained without affecting the objective values. A notable tendency observed is a shortened diagonal member, which is most visible in case 7. The effective elastic and piezoelectric tensors for the example of case 7 are given as follows:
which proves the feasibility of the structure with the imposed constraints on the elastic coefficients. However, we notice that the stiffness coefficients did not reach the lower limits although the structure formed very narrow hinges. This observation once again points our attention at the difference in accuracy between the state problems in the topology and shape optimization steps. Thus, taking into consideration manufacturability of the structures, an adjusted set of stiffness constraints for the shape optimization step appears to be a reasonable choice.
The second study is devoted to the influence of stiffness requirements in general, i.e. the constraints on all diagonal elastic coefficients \(C_{\textrm{H}}^\textrm{ii}\) were varied, with the requirement that the normal stiffness coefficients still remain similar \(C_{\textrm{H}}^{11} \approx C_{\textrm{H}}^{22}\). A summary of the problems setup for this study is given in Table 6.
For each case, the objective is to maximize the hydrostatic piezoelectric coupling coefficient \(d^\textrm{h}_{\textrm{H}}\), as the previous study has shown that this formulation is capable of generating auxetic structures in the topology optimization step. The cases 6 and 8 are taken from the previous study, hence the unordered numbering. Two new cases (9 and 10) consider higher stiffness requirements, whereas for the case 10, the constraint on \(C^{33}_{\textrm{H}}\) is increased twice as compared to the case 8. In Table 7, the resultant designs and their selected effective properties are given.
Besides the obvious geometrical differences, we observe a major decrease (in the absolute sense) of the effective Poisson’s ratio \(\upsilon _{\textrm{H}}\) for the stiffer structures (case 9 and 10). This highlights a trade-off between increased stiffness and the ability of a structure to exhibit auxetic deformation, although this did not affect the value of \(d^\textrm{h}_{\textrm{H}}\) significantly. The addition of the \(C_{\textrm{H}}^{33}\) (case 10) further drops the Poisson’s ratio to \(\upsilon _{\textrm{H}} = -\,0.53\). The effective elastic and piezoelectric material tensors for the example of case 10 read
where the value of \(C_{\textrm{H}}^{11}\) is slightly greater than the lower limit of 6 GPa. Nevertheless, the constraints were not violated which confirms the feasibility of the obtained design.
The third study concerns the possible symmetry conditions, which, for two-dimensional problems, besides the double XY-symmetry used for all previous studies, it includes single X- and Y-symmetries. The problem setups are listed in Table 8, where for all the symmetry cases, a study with and without the presence of the \(C_{\textrm{H}}^{33}\) constraint was conducted, similarly to the previous comparisons. The XY-symmetry cases are the same as in Table 7, hence the unordered numbering of the cases.
The presence of the symmetry condition in general is necessary to guarantee orthotropy of the material, without the need for an explicit orthotropy constraint. The resulting structures and their effective properties are given in Table 9.
The structures with the single symmetry condition are notably different, since a larger design space is available for the optimizer. The case 12 (Y-symmetry) generated an infeasible design with a close to zero value of \(C^{33}_{\textrm{H}}\). In this particular case, the addition of the constraint on \(C^{33}_{\textrm{H}}\) (see case 14) alleviated the issue and a feasible design was generated. Both of the designs with X-symmetry (case 11 and 13) reached relatively high values of \(C^{33}_{\textrm{H}}\); hence, there is practically no difference between them, except the opposite orientation. Similarly to the previous comparisons, the effective elastic and piezoelectric tensors are given for case 14
where the values of \(C^{11}_{\textrm{H}}\) and \(C^{33}_{\textrm{H}}\) are slightly above their lower limits, not affecting, however, the feasibility of the design.
As previously observed, the transition between the topology and the shape optimization leads to a jump in the effective material coefficients due to the reduced accuracy of the state problem in the topology optimization step, as well as due to the heuristics behind the shape generation step. Therefore, if one roughly knows the discrepancy between the effective coefficients when transitioning from topology to shape optimization, a reasonable approach is to select a different set of constraint values for each of the steps. For instance, a set of constraint values can be reduced by a certain amount for the topology optimization step and set back to the desired values only for the shape optimization step. Thus, in Table 10, we introduced adjustments to the constraint values on the stiffness coefficients for the shape optimization step on the examples of cases 5 and 7.
The case 5 is particularly peculiar for two reasons. First, the largest jump in the value occurred for \(C^{22}_{\textrm{H}}\), leading to the initial design for shape optimization yielding \(C^{22}_{\textrm{H}}\) almost two times greater than \(C^{11}_{\textrm{H}}\). Second, only an increase in the volume constraint from \(V \le 40\%\) to \(V \le 50\%\) facilitated the fulfilment of the constraint on \(C^{11}_{\textrm{H}}\). In Table 11, the \(C^{11}_{\textrm{H}}\) and \(C^{22}_{\textrm{H}}\) stiffness coefficients for the cases 5a and 5b are shown at different stages of the sequential optimization routine.
In the shape optimization phase, an attempt to retrieve the similarity of \(C^{11}_{\textrm{H}}\) and \(C^{22}_{\textrm{H}}\) stiffness coefficients was made by choosing the constraint value of \(C^\textrm{ii}_{\textrm{H}} \ge 5\) for both the coefficients, which turned out not be reachable for the case 5a. Therefore, the increase in the volume constraint enabled design changes effective enough to retrieve similar values of \(C^{11}_{\textrm{H}}\) and \(C^{22}_{\textrm{H}}\), both of them fulfiling the optimization constraints.
The resulting structures for the adjusted sets of constraints for the cases 5 and 7 are shown in Table 12. For the case 5, one can immediately see that an increase of the \(C^\textrm{ii}_{\textrm{H}}\) constraints by \(25\%\) leads to a reduction of the length of the diagonal members (case 5b), mostly because of the difficulty to fulfil the constraint on \(C^{11}_{\textrm{H}}\). Significantly greater stiffness coefficients could be imposed for the case 7, which shows very thin hinges in the original setup. Here, an increase of up to \(75\%\) of the stiffness coefficients’ constraints lead to a generation of hinge-free structures with greatly improved manufacturability.
In Fig. 8, a visualization of three metamaterials based on the cases 7, 10 and 14 is shown (for which the effective elastic and piezoelectric tensors were given as well). This rendering helps to notice the similarities between the designs obtained in this work. In particular, the topological equivalence between all the cases is evident in the stiffness study, the results of which are depicted in Table 7.
4.4 Role of fine tuning with shape optimization
Finally, the evolution of a sequential optimization problem is shown in two examples to illustrate the importance of the shape optimization step. In Fig. 9, the intermediate results of the sequential optimization of cases 7(b) and 10 are shown. These two examples were chosen to show two different aspects that are common when sequential optimization is applied to the design of piezoelectric microstructures.
Sequential optimization of the cases 7 and 10. From the left side: topology optimization results, generated shapes, shape optimization results. The case 7 depicts two final shapes: with unchanged constraint values (case 7, green arrow) and with modified constraint values (case 7b, orange arrow). (Color figure online)
Case 7 is presented to illustrate the accuracy issue due to material interpolation within topology optimization. For this reason, the difference between the member thickness after the shape generation and after the shape optimization is particularly noticeable. This is due to the large jump in stiffness values between the topology optimization result and the generated shape. The topology optimization result contains a relatively high number of cells with intermediate density (\(23\%\) cells with pseudo-density in the range \(\rho \in \left[ 0.01, 0.99\right] \)) after 500 iterations using the method of moving asymptotes (MMA). Therefore, the predicted material coefficients are not accurate and the resulting structure is not optimal with respect to the problem setup. As a result, an excessively stiff shape was obtained immediately after its generation. Consequently, the final structure of case 7 contains very thin features that are not suitable for manufacturing. Adjusting the stiffness constraints, as seen in case 7b, helped to obtain a manufacturable design.
Case 10 shows a large design evolution within the shape optimization alone, again caused by the jump in computed material properties after the shape generation. The shape optimization step finally approaches the stiffness constraints after a significant shortening of the diagonal members.
In Figs. 10 and 11, the evolution of the hydrostatic coupling coefficient \(d^\textrm{h}_{\textrm{H}}\) and the stiffness coefficients \(C^\textrm{ii}_{\textrm{H}}\), respectively, is plotted for cases 10 and 14. The iteration count encompasses the complete sequential procedure, i.e. the shape optimization iterations are counted starting from the last topology optimization iteration. In the \(d^\textrm{h}_{\textrm{H}}\) plot, one can immediately notice that the value is strongly overestimated in the early iterations due to the presence of the grey cells. Hence, the evolution of \(d^\textrm{h}_{\textrm{H}}\) is difficult to analyse until the design is completely black and white. However, one can clearly distinguish the transition from topology to shape optimization by the sudden drop of \(d^\textrm{h}_{\textrm{H}}\) in the late stage of optimization. In case 10, it occurred at about iteration 500 and in case 14 at iteration 300. The sudden drop of \(d^\textrm{h}_{\textrm{H}}\) indicates the error that even a converged topology optimization introduces in the computation of effective material parameters. This error is even more pronounced in the \(C^\textrm{ii}_{\textrm{H}}\) plot, where two spikes are shown at iteration 300 and 500, respectively. The normal stiffness coefficient \(C^\textrm{11}_{\textrm{H}}\) was constrained from both the bottom (6 GPa) and the top (7 MPa) to avoid excessive stiffness that occurred in other design attempts. The jump in value of up to \(70\%\) is visible for \(C^\textrm{11}_{\textrm{H}}\) in case 14 after shape generation, emphasizing the importance of design adaptation with shape optimization.
4.5 Discussion
Negligible difference between the values of the effective hydrostatic piezoelectric coupling coefficient \(d^\textrm{h}_{\textrm{H}}\), which for the cases considered in this work varies merely within the range of \(d^\textrm{h}_{\textrm{H}} \in \left[ 175, 181\right] \) (the value of \(d^\textrm{h}_{\textrm{H}} = 185\) for the case 12 is ignored due to the infeasibility of the design) suggests that decision about a suitable design of the piezoelectric metamaterial for hydrostatic pressure applications is not a question of maximized performance, but rather the desired stiffness characteristics. Depending on the applied loading conditions, optimal performance can be achieved by designing a structure, which deformation does not exceed the stress limits and also is compliant enough to provide a sufficient energy conversion., e.g. for energy harvesting applications.
The final design also largely depends on the requirements for the \(C_{\textrm{H}}^{33}\) values, since the well-known re-entrant honeycomb structures exhibit disproportionately low value of \(C_{\textrm{H}}^{33}\) as compared to \(C_{\textrm{H}}^{11}\) and \(C_{\textrm{H}}^{22}\), thus imposition of a \(C_{\textrm{H}}^{33}\) constraint significantly alters the design, providing structures more resistant to a potentially unwanted deformation when a metamaterial with large number of repeated cells is considered. Moreover, increased \(C_{\textrm{H}}^{33}\) contributes to a decrease of the absolute value of the Poisson’s ratio, without affecting, however, the value of \(d^\textrm{h}_{\textrm{H}}\).
Introduction of the symmetry conditions is an efficient way to guarantee orthotropy of the resultant metamaterial, simultaneously limiting the design space and hence improving the convergence to a feasible design. By imposing a double symmetry for X and Y planes, one can obtain a design equivalent to the re-entrant honeycomb (case 5).
The discrepancy between the computed material coefficients in the topology and shape optimization steps is tackled by selecting lower stiffness constraints for the topology optimization step and then by increasing them in the shape optimization step. This way, formation of narrow hinges is avoided in the final structure.
5 Conclusions
In this contribution, we applied the sequential topology and shape optimization framework (Dev et al. 2022) to design auxetic piezoelectric metamaterials made of (lead-free) barium titanate ceramic. By combining topology and shape optimization, we benefited from the advantages of each method. In the sequential framework, first topology optimization was utilized to generate the design layouts, in which the complexity of the designs was controlled by the regularization scheme: density filtering, projection and symmetry constraint. Next, by using a simple shape generation algorithm, we performed shape optimization to fine tune the designs. By exploiting the shape optimization, we profited from: (1) accurate and efficient computations of the state problem by the EDD method with adaptive base and shape refinement; and (2) presence of crisp boundary, which enabled consideration of the curvature constraint to control manufacturability and durability of the designed structures.
The case studies have shown that the design of a piezoelectric metamaterial for hydrostatic pressure applications mainly depends on the desired stiffness characteristics. By varying the constraint values for the elastic coefficients and symmetry conditions significantly varying structures were obtained. Minimization of the effective Poisson’s ratio and maximization of the hydrostatic piezoelectric coupling coefficient both lead to generation of auxetic structures. By employing the sequential optimization framework, we obtained exact designs with accurately computed effective material properties.
5.1 Outlook
Usage of brittle ceramic material motivated us to employ a geometrically linear model to compute the effective properties. However, for less brittle materials, like, for instance, PVDF, a geometrically nonlinear model would be beneficial to design structures with optimal material properties under larger deformations (despite the increased computational cost).
The sequential topology and shape optimization framework can be extended towards the design of metamaterials based on other applications or physical models, e.g. photonic metamaterials.
Furthermore, experimental investigation is planned in the future work to verify the applicability of the proposed optimization procedure and the obtained material properties. Although experimental studies are not within the scope of this contribution, in Fig. 12, we show test manufacturing of selected samples from the cases 5,7 and 10.
The selected samples were fabricated experimentally by ceramic injection moulding of barium titanate (BTO). The basic process for fabricating complex geometric structures has been described in detail in previous work (Biggemann et al. 2018; Köllner et al. 2023; Hoffmann et al. 2023). However, an adaptation of the process flow for complex structures was required. In order to optimize the injection moulding process, the positive moulds of structures were designed using OpenSCAD (Kintel and Wolf 2014) from the structures exported as STL. These CAD files were stereolithographically printed with an Anycubic Photon Mono 4K (Anycubic, Shenzhen, China) using Anycubic Translucent UV Resin (Anycubic, Shenzhen, China) with a z-resolution of 50 \(\upmu \)m. The printed templates were then moulded with a two-part RTV-2 silicone rubber (ELASTOSIL®M 4514 Wacker Chemie AG, Munich, Germany) to obtain a negative mould. Transfer moulding was performed with a ceramic feedstock containing \(55\, \mathrm vol\%\) BTO powder (Sigma Aldrich, Darmstadt, Germany), \(40\, \mathrm vol\%\) paraffin wax (Granopent®P, Carl Roth GmbH, Karlsruhe, Germany) and \(5\, \mathrm vol\%\) carnauba wax (Naturfarben, Carl Roth GmbH, Karlsruhe, Germany). Transfer moulding was carried out at 120 °C under vacuum (< 10 Pa). One of the difficulties in comparison with previous structures was that the areas of the struts in the centre of the structure and in the head and base areas were very thin. Typically, a minimum width of 6–8 mm is required to ensure non-destructive moulding from the silicone moulds. The debinding process, performed at 650 °C for 1 h in an Al2O3 crucible (CERAMTRADE, Bad Vilbel, Germany) with an \(\mathrm ZrO_2\) (Tosoh USA, Inc., Grove City, USA) powder bed, and the subsequent sintering process, performed at 1400 °C for 6 h, were performed on \(\mathrm ZrO_2\) substrates placed on porous mullite substrates (Annamullit®88, Compagnie de Saint-Gobain S.A., Courbevoie, France). Optimized heating and cooling rates of 0.1 to 5 K/min were used in these procedures.
Successful injection moulding and sintering of the selected structures prove that the geometries are manufacturable directly from the results of the sequential optimization procedure despite their geometric complexity.
Notes
From this point, we drop the notation of the units, since they remain the same for the whole article.
References
Aage N, Andreassen E, Lazarov BS (2015) Topology optimization using PETSC: an easy-to-use, fully parallel, open source topology optimization framework. Struct Multidisc Optim 51:565–572
Alderson A, Alderson K (2007) Auxetic materials. Proc Inst Mech Eng Part G 221(4):565–575
Allaire G, Jouve F, Toader A-M (2002) A level-set method for shape optimization. CR Math 334(12):1125–1130
Andreasen CS, Elingaard MO, Aage N (2020) Level set topology and shape optimization by density methods using cut elements with length scale control. Struct Multidisc Optim 62:685–707
Andreassen E, Clausen A, Schevenels M, Lazarov BS, Sigmund O (2011) Efficient topology optimization in matlab using 88 lines of code. Struct Multidisc Optim 43:1–16
Andreassen E, Lazarov BS, Sigmund O (2014) Design of manufacturable 3d extremal elastic microstructure. Mech Mater 69(1):1–10
Arndt D, Bangerth W, Blais B, Fehling M, Gassmöller R, Heister T, Heltai L, Köcher U, Kronbichler M, Maier M (2021) The deal II. Library, version 9.3. J Numer Math 29(3):171–186
Azegami H, Takeuchi K (2006) A smoothing method for shape optimization: traction method using the robin condition. Int J Comput Methods 3(01):21–33
Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1:193–202
Bendsoe MP, Sigmund O (2003) Topology optimization: theory, methods, and applications. Springer, New York
Biggemann J, Pezoldt M, Stumpf M, Greil P, Fey T (2018) Modular ceramic scaffolds for individual implants. Acta Biomater 80:390–400
Bodkhe S, Turcot G, Gosselin FP, Therriault D (2017) One-step solvent evaporation-assisted 3d printing of piezoelectric PVDF nanocomposite structures. ACS Appl Mater Interfaces 9(24):20833–20842
Bruns TE, Tortorelli DA (2001) Topology optimization of non-linear elastic structures and compliant mechanisms. Comput Methods Appl Mech Eng 190(26–27):3443–3459
Carneiro VH, Meireles J, Puga H (2013) Auxetic materials—a review. Mater Sci 31:561–571
Challapalli A, Patel D, Li G (2021) Inverse machine learning framework for optimizing lightweight metamaterials. Mater Des 208:109937
Christiansen AN, Nobel-Jørgensen M, Aage N, Sigmund O, Bærentzen JA (2014) Topology optimization using an explicit interface representation. Struct Multidisc Optim 49:387–399
Chung PW, Tamma KK, Namburu RR (2001) Asymptotic expansion homogenization for heterogeneous media: computational issues and applications. Compos A Appl Sci Manuf 32(9):1291–1301
Della CN, Shu D (2008) The performance of 1–3 piezoelectric composites with a porous non-piezoelectric matrix. Acta Mater 56(4):754–761
Dev C, Stankiewicz G, Steinmann P (2022) Sequential topology and shape optimization framework to design compliant mechanisms with boundary stress constraints. Struct Multidisc Optim 65(6):180
Ding Y (1986) Shape optimization of structures: a literature survey. Comput Struct 24(6):985–1004
Ding H, Xu B (2022) Material microstructure topology optimization of piezoelectric composite beam under initial disturbance for vibration suppression. J Vib Control 28(11–12):1364–1378
Donoso A, Aranda E, Ruiz D (2023) A new method for designing piezo transducers with connected two-phase electrode. Comput Struct 275:106936
Eschenauer HA, Kobelev VV, Schumacher A (1994) Bubble method for topology and shape optimization of structures. Struct Optim 8:42–51
Fernández M, Fritzen F, Weeger O (2022) Material modeling for parametric, anisotropic finite strain hyperelasticity based on machine learning with application in optimization of metamaterials. Int J Numer Methods Eng 123(2):577–609
Gałka A, Telega J, Wojnar R (1992) Homogenization and thermopiezoelectricity. Mech Res Commun 19(4):315–324
Hestenes MR (1969) Multiplier and gradient methods. J Optim Theory Appl 4(5):303–320
Hoffmann P, Köllner D, Simon S, Kakimoto K-I, Fey T (2023) Modular lead-free piezoceramic/polymer composites with locally adjustable piezoelectric properties. Open Ceram 13:100320
Hu G, Tang L, Banerjee A, Das R (2017) Metastructure with piezoelectric element for simultaneous vibration suppression and energy harvesting. J Vib Acoust 139(1):011012
IEEE standard on piezoelectricity (1988) ANSI/IEEE Std 176-1987. https://doi.org/10.1109/IEEESTD.1988.79638
Iyer S, Venkatesh T (2011) Electromechanical response of (3–0) porous piezoelectric materials: effects of porosity shape. J Appl Phys 110(3):034109
Iyer S, Alkhader M, Venkatesh T (2015) Electromechanical behavior of auxetic piezoelectric cellular solids. Scripta Mater 99:65–68
Ji G, Huber J (2022) Recent progress in acoustic metamaterials and active piezoelectric acoustic metamaterials—a review. Appl Mater Today 26:101260
Kar-Gupta R, Venkatesh T (2006) Electromechanical response of porous piezoelectric materials. Acta Mater 54(15):4063–4078
Khan K, Al-Mansoor S, Khan S, Khan MA (2019) Piezoelectric metamaterial with negative and zero Poisson’s ratios. J Eng Mech 145(12):04019101
Kintel M, Wolf C (2014) Openscad. GNU General Public License, p GNU General Public License 2(10)
Kollmann HT, Abueidda DW, Koric S, Guleryuz E, Sobh NA (2020) Deep learning for topology optimization of 2d metamaterials. Mater Des 196:109098
Köllner D, Tolve-Granier B, Simon S, Kakimoto K-I, Fey T (2022) Advanced estimation of compressive strength and fracture behavior in ceramic honeycombs by polarimetry measurements of similar epoxy resin honeycombs. Materials 15(7):2361
Köllner D, Simon S, Niedermeyer S, Spath I, Wolf E, Kakimoto K-I, Fey T (2023) Relation between structure, mechanical and piezoelectric properties in cellular ceramic auxetic and honeycomb structures. Adv Eng Mater 25(3):2201387
Li Z, Luo Z, Zhang L-C, Wang C-H (2021) Topological design of pentamode lattice metamaterials using a ground structure method. Mater Des 202:109523
Lian H, Christiansen AN, Tortorelli DA, Sigmund O, Aage N (2017) Combined shape and topology optimization for minimization of maximal von mises stress. Struct Multidisc Optim 55:1541–1557
Mancuso E, Shah L, Jindal S, Serenelli C, Tsikriteas ZM, Khanbareh H, Tirella A (2021) Additively manufactured batio3 composite scaffolds: a novel strategy for load bearing bone tissue engineering applications. Mater Sci Eng C 126:112192
Moshki A, Hajighasemi MR, Atai AA, Jebellat E, Ghazavizadeh A (2022) Optimal design of 3d architected porous/nonporous microstructures of multifunctional multiphase composites for maximized thermomechanical properties. Comput Mech 69(4):979–996
Nelli Silva E, Ono Fonseca J, Espinosa FM, Crumm A, Brady G, Halloran J, Kikuchi N (1999) Design of piezocomposite materials and piezoelectric transducers using topology optimization—Part I. Arch Comput Methods Eng 6:117–182
Neves MM, Rodrigues H, Guedes JM (2000) Optimal design of periodic linear elastic microstructures. Comput Struct 76(1–3):421–429
Nguyen TT, Bærentzen JA, Sigmund O, Aage N (2020) Efficient hybrid topology and shape optimization combining implicit and explicit design representations. Struct Multidisc Optim 62:1061–1069
Norato JA, Bendsøe MP, Haber RB, Tortorelli DA (2007) A topological derivative method for topology optimization. Struct Multidisc Optim 33:375–386
Paulino GH, Silva ECN, Le CH (2009) Optimal design of periodic functionally graded composites with prescribed properties. Struct Multidisc Optim 38:469–489
Riehl S, Steinmann P (2015) A staggered approach to shape and topology optimization using the traction method and an evolutionary-type advancing front algorithm. Comput Methods Appl Mech Eng 287:1–30
Riehl S, Steinmann P (2017) On structural shape optimization using an embedding domain discretization technique. Int J Numer Methods Eng 109(9):1315–1343
Rockafellar RT (1973) The multiplier method of hestenes and powell applied to convex programming. J Optim Theory Appl 12(6):555–562
Shaikh FK, Zeadally S (2016) Energy harvesting in wireless sensor networks: a comprehensive review. Renew Sustain Energy Rev 55:1041–1054
Sigmund O, Torquato S, Aksay IA (1998) On the design of 1–3 piezocomposites using topology optimization. J Mater Res 13(4):1038–1048
Silva EN, Kikuchi N (1999) Design of piezocomposite materials and piezoelectric transducers using topology optimization—Part III. Arch Comput Methods Eng 6(4):305
Silva EN, Fonseca JO, Kikuchi N (1997) Optimal design of piezoelectric microstructures. Comput Mech 19(5):397–410
Smith WA (1989) The role of piezocomposites in ultrasonic transducers. In: Proceedings., IEEE Ultrasonics Symposium, pp 755–766. IEEE
Sokolowski J, Zochowski A (1999) On the topological derivative in shape optimization. SIAM J Control Optim 37(4):1251–1272
Soukoulis CM, Wegener M (2011) Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat Photonics 5(9):523–530
Stankiewicz G, Dev C, Steinmann P (2021) Coupled topology and shape optimization using an embedding domain discretization method. Struct Multidisc Optim 64(4):2687–2707
Stankiewicz G, Dev C, Steinmann P (2022) Geometrically nonlinear design of compliant mechanisms: topology and shape optimization with stress and curvature constraints. Comput Methods Appl Mech Eng 397:115161
Svanberg K (1987) The method of moving asymptotes-a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373
Torquato S, Haslach H Jr (2002) Random heterogeneous materials: microstructure and macroscopic properties. Appl Mech Rev 55(4):62–63
Valipour A, Kargozarfard MH, Rakhshi M, Yaghootian A, Sedighi HM (2022) Metamaterials and their applications: an overview. Proc Inst Mech Eng Part L 236(11):2171–2210
Vatanabe SL, Paulino GH, Silva EC (2014) Maximizing phononic band gaps in piezocomposite materials by means of topology optimization. J Acoust Soc Am 136(2):494–501
Vatanabe SL, Lippi TN, Lima CR, Paulino GH, Silva EC (2016) Topology optimization with manufacturing constraints: a unified projection-based approach. Adv Eng Softw 100:97–112
Vijaya M (2012) Piezoelectric materials and devices: applications in engineering and medical sciences. CRC Press, Boca Raton
Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192(1–2):227–246
Wang F, Lazarov BS, Sigmund O (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidisc Optim 43:767–784
Wang Y, Kang Z, Zhang X (2023) A velocity field level set method for topology optimization of piezoelectric layer on the plate with active vibration control. Mech Adv Mater Struct 30(7):1326–1339
Wei C, Jing X (2017) A comprehensive review on vibration energy harvesting: modelling and realization. Renew Sustain Energy Rev 74:1–18
Whitty J, Alderson A, Myler P, Kandola B (2003) Towards the design of sandwich panel composites with enhanced mechanical and thermal properties by variation of the in-plane poisson’s ratios. Compos A Appl Sci Manuf 34(6):525–534
Xu B, Ding H, Xie YM (2017) Optimal design of material microstructure for maximizing damping dissipation velocity of piezoelectric composite beam. Int J Mech Sci 128:527–540
Yang B, Cheng C, Wang X, Meng Z, Homayouni-Amlashi A (2022) Reliability-based topology optimization of piezoelectric smart structures with voltage uncertainty. J Intell Mater Syst Struct 33(15):1975–1989
Zhang W, Wang F, Dai G, Sun S (2007) Topology optimal design of material microstructures using strain energy-based method. Chin J Aeronaut 20(4):320–326
Zhang Y, Xie M, Roscow J, Bao Y, Zhou K, Zhang D, Bowen CR (2017) Enhanced pyroelectric and piezoelectric properties of pzt with aligned porosity for energy harvesting applications. J Mater Chem A 5(14):6569–6580
Zhang H, Takezawa A, Ding X, Xu S, Duan P, Li H, Guo H (2021) Bi-material microstructural design of biodegradable composites using topology optimization. Mater Des 209:109973
Zhao J, Hu N, Wu J, Li W, Zhu Z, Wang M, Zheng Y, Dai H (2022) A review of piezoelectric metamaterials for underwater equipment. Front Phys 10:1180
Acknowledgements
The authors gratefully acknowledge financial support for this work by the Deutsche Forschungsgemeinschaft: Project number 399073171 (GRK2495/B) and 407523036.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
GS drafted the main idea, wrote the manuscript text, implemented the code and ran the case studies. CD contributed in the code implementation and gave substantial feedback. MW and TF manufactured the samples and wrote the corresponding description. PS supervised the work, gave substantial feedback and revised the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Replication of results
All the presented methodology is implemented in C++ utilizing the finite element library deal.II (Arndt et al. 2021). The version of the code, the executable, the parameter settings and the result files are available from the corresponding author upon request.
Additional information
Responsible Editor: Yoon Young Kim
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Bulk material properties: \(\textrm{BaTiO}_3\)
Appendix 1: Bulk material properties: \(\textrm{BaTiO}_3\)
For all the examples studied in this work, we utilize BTO material properties, given as follows: Material density:
Compliance tensor:
Piezoelectric tensor (strain-charge format):
Relative permittivity tensor (strain-charge format):
Elasticity tensor (inverse of the compliance tensor):
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stankiewicz, G., Dev, C., Weichelt, M. et al. Towards advanced piezoelectric metamaterial design via combined topology and shape optimization. Struct Multidisc Optim 67, 26 (2024). https://doi.org/10.1007/s00158-024-03742-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-024-03742-w