1 Introduction

Several engineering applications require or greatly benefit from the optimization of natural frequencies. This is usually done for performance reasons, safety improvement, disturbance rejection, human comfort, or noise reduction. A few examples of such applications in the field of structural dynamics are, e.g., resonators, bridges, energy harvesters, or car chassis (Nobari et al. 2015; Dunning et al. 2016; Townsend et al. 2019; Townsend and Kim 2019; Giannini et al. 2022).

Several techniques exist to optimize such structures, depending on the problem at hand and on the desired goal. In cases where the design is constrained to adopt a prescribed geometry, a parametric—or size—optimization (Choi and Kim 2005; Giannini et al. 2020) is usually recommended.

On the other hand, topology optimization techniques (Bendsoe and Sigmund 2004; Dunning and Kim 2015) can attain any suitable shape within the design space, thus increasing the overall freedom of the design process. There exist several approaches to topology optimization, such as Solid Isotropic Material with Penalization (SIMP) method (Bendsøe and Sigmund 1999), level-set method (Wang et al. 2003; Allaire et al. 2004), Evolutionary Structural Optimization (ESO) method (Xie and Steven 1993), and the more recent Moving Morphable Components (MMC) method (Guo et al. 2014). Among these, level-set optimization has been successfully adopted to solve a number of engineering problems, mainly due to its ability to define sharp interfaces without filtering stages, and to its computational efficiency derived from the fact that only the boundary is propagated, instead of the whole physical domain.

Some examples of level-set optimization related to dynamical systems include vibration problems (Allaire and Jouve 2005), repeated eigenfrequencies (Seyranian et al. 1994), buckling loads maximization (Dunning et al. 2016; Townsend and Kim 2019), energy harvesters (Townsend et al. 2019), or heat exchange systems (Hyun and Kim 2021a).

Despite the successful application of topology optimization in all these fields, the great majority of existing works focus on the deterministic performance of the structures at hand. While this leads to optimal structures under nominal conditions, their performance can be greatly affected by a change in loading conditions, working conditions, or environmental factors, among others.

Robust formulations have been adopted for structures subject to varying loads or uncertainties on the loading point. For instance, Dunning et al. (2011) proposed an approach to minimize the expected compliance, whereas Dunning and Kim (2013); Xu et al. (2019) presented algorithms that consider both the expected value and the variance of the compliance. On the other hand, Guest and Igusa (2008) applied a multi-load approach to truss structures subject to Gaussian uncertainties in the external loads and extended the method to consider uncertain nodal locations, whereas Chen et al. (2010) perform the optimization under random field uncertainties.

Similarly, there are works presenting formulations able to keep into account the variance of a manufacturing process, which may lead to over- or under-etching of a nominal structure geometry. For instance, Wang et al. (2011) introduced filtering stages to ensure mesh convergence at both global and local scales. These projection stages are used to optimize compliant mechanisms and heat conductors under a minimum length scale. In a similar way, Jang et al. (2012); Andreasen et al. (2020) exploit these filtering stages to implement a worst-case approach for compliance minimization, whereas Li et al. (2019) dealt with frequency maximization in the presence of possible over-etch. All these methods follow a worst-case approach, which sometimes leads to solutions that are too conservative. On the other hand, probabilistic methods, such as the Monte Carlo method (Rubinstein and Kroese 2016) or polynomial chaos expansion (Wiener 1938), are able to better describe the manufacturing uncertainty field, thus allowing the computation of the response statistics and their sensitivities. Among these are the works of Schevenels et al. (2011), Tootkaboni et al. (2012), Lazarov et al. (2012), Chen and Chen (2011) and Zhang and Kang (2017).

Concerning structural optimization in thermal environments, Chung et al. (2020) presented a level-set topology optimization technique for nonlinear thermoelasticity, whereas Kambampati et al. (2020) deals with stress-based topology optimization in presence of a spatially varying temperature field. Topology optimization approaches for thermal buckling criteria were presented by Wu et al. (2019), Gan and Wang (2022). Regarding dynamic problems, Yang and Li (2013, 2014) focused on dynamic compliance minimization.

The problem of eigenfrequencies stability in temperature is extremely relevant in several applications, with literature providing numerous theoretical and experimental studies of the phenomenon (Talebian et al. 2010; Wang et al. 2012). Perfect examples of this are microelectromechanical systems (MEMS). For instance, MEMS for time-keeping applications (Wu et al. 2020) are crucial in the electronics industry and represent a multi-billion dollar market (van Beek and Puers 2011). While resonators have historically been produced using quartz crystals, the recent advances in MEMS technology allowed us to obtain reliable, miniaturized, and cheap MEMS resonators and oscillators.

However, frequency drifts are among the biggest challenges that MEMS designers have to face, whether they are dealing with gyroscopes, oscillators, or micro-mirrors (Jiang et al. 2021; Ferguson et al. 2005; Wolter et al. 2005).

Even though specific MEMS architectures and/or feedback loops exist to keep the oscillating frequency at the desired value (Prache et al. 2016; Salvia et al. 2010), it would be beneficial to have layouts intrinsically robust to temperature variations. This, in fact, would keep the oscillating frequency as close as possible to the system’s resonance, thus reducing the amount of forcing needed to keep the device in motion. However, to the authors’ knowledge, there are no works in literature that present techniques able to reduce or minimize the variance of a system’s natural frequencies in presence of a varying temperature.

The rest of the paper is organized as follows. Section 2 briefly presents the most common existing approaches for reducing the temperature effects on MEMS resonators. After that, Sect. 3 shows how the thermal behavior of the material properties and the thermal expansion phenomenon affect the natural frequencies and the mode shapes of a structure. Then, the temperature-robust eigenfrequency optimization method is described, along with the statistical analysis and the sensitivity derivation. Different numerical examples of the proposed approach are presented in Sect. 5, including the application to a 1 MHz MEMS resonator. Finally, Sect. 6 presents the conclusions.

2 Existing approaches for reducing temperature effects

In the field of MEMS resonators for timing applications, the natural frequency sensitivity with respect to temperature variations is expressed through the Temperature Coefficient of Frequency (TCF, Wu et al. 2020):

$$\begin{aligned} \textrm{TCF} = \frac{1}{f_0} \frac{\partial f_0}{\partial T}, \end{aligned}$$
(1)

where \(f_0\) is the nominal value of the natural frequency. This term is usually measured in ppm/°C. Typically, silicon resonators exhibit a negative TCF around −30 ppm/°C, which is too high for industrial applications. Therefore, compensation techniques are required to achieve a low TCF and a highly stable timing reference.

The most common temperature compensation techniques are based either on passive or active approaches (Wu et al. 2020). An example of active compensation is electrostatic tuning, which exploits the electrostatic stiffness effect obtained through a bias voltage in capacitive MEMS. The bias voltage is carefully tuned to compensate for temperature-induced frequency variations. A TCF of 39 ppm over a temperature range between \(25~^{\circ }\textrm{C}\) and \(125~^{\circ }\textrm{C}\) has been achieved by Sundaresan et al. (2007). However, this approach is not always feasible since it requires large bias voltages which may not be suitable for standard CMOS. Another approach is electronic compensation, which is typically implemented through a Phase-Locked Loop (PLL) circuit coupled with a temperature sensor. Even though the PLL circuit inevitably increases the phase noise and the jitter of the output clock, this approach has been used to design a MEMS-based programmable oscillator with a TCF less than 0.1 ppm over a temperature range between −45 and 105 °C (Roshan et al. 2016). A different approach is a micro-oven control, where a MEMS resonator is placed inside a thermally isolated micro-oven whose temperature is controlled with a feedback circuit. For instance, the Oven-Controlled MEMS Oscillator (OCMO, Wojciechowski et al. 2015; Wojciechowski and Olsson 2015) is characterized by a TCF of around 0.3 ppm in the range of \(-45\) and \(85~^{\circ }\textrm{C}\).

Compared to active techniques, passive compensation approaches do not require additional power consumption or dedicated circuits. For instance, composite structures exploit the positive TCF of some materials, such as SiO2, to compensate for the negative TCF of silicon. Similarly, doping (Csavinszky and Einspruch 1963) allows for a decrease in the TCF of Silicon through heavy doping. Besides these techniques, which rely on material engineering, another passive approach is geometry engineering. The idea is to design a layout where the temperature dependence of the material properties is compensated by the thermal stresses, yielding a device with a low TCF. For instance, Hsu and Nguyen (1998) applies this approach to a low-frequency folded-beam MEMS device, whereas Hsu et al. (2000) designed a 10 MHz MEMS resonator with a TCF around −2.5 °C.

Typically, in industrial applications, a combination of active and passive compensation approaches is used. In particular, composite structures or doping is used to greatly reduce the initial TCF. Then, electronic compensation or micro-oven control is implemented to further improve the frequency robustness of such devices.

3 Temperature effects on the natural frequencies

In this Section, we show how considering only elasticity is not sufficient when optimizing a structure for frequency robustness in temperature, and it is necessary to take into account thermal stresses as well.

3.1 Influence of the material properties

The characteristic equation of a linear second-order vibrating system is

$$\begin{aligned} \left( -\omega ^2 \textbf{M} + \textbf{K} \right) \varvec{q} = \varvec{0}, \end{aligned}$$
(2)

where \(\textbf{M}\) and \(\textbf{K}\) are respectively the mass and stiffness matrices, \(\varvec{q}\) is the mode shape vector, and \(\omega\) is the natural frequency. Under the assumption of linear elastic material, the matrices \(\textbf{M}\) and \(\textbf{K}\) linearly depend on the material properties. Given that, for the applications considered (i.e., MEMS resonators), the frequency drift resulting from temperature changes is primarily due to the thermal behavior of Young’s modulus (Jiang et al. 2021) and that thermal stresses affect the \(\textbf{K}\) but not \(\textbf{M}\) (Wu et al. 2020), this study focuses on the changes related to the stiffness matrix.

For most isotropic materials, there is a wide range of temperature over which the change of Young’s modulus can be approximated to be linear (Ledbetter 1982),

$$\begin{aligned} E = E_0 \left( 1 + \beta _T \Delta T\right) = E_0 \phi , \end{aligned}$$
(3)

where \(E_0\) is the initial value for E, \(\Delta T\) is the temperature variation, and \(\beta _T\) is the linear thermal coefficient (Ledbetter 1982).

Since the matrix \(\textbf{K}\) linearly depends on Young’s modulus, Eq. (2) is rewritten as:

$$\begin{aligned} \left( -\omega ^2 \textbf{M} + \phi \textbf{K} \right) \varvec{q} = \varvec{0}, \end{aligned}$$
(4)

where the coefficient \(\phi\) accounts for the thermal behavior of Young’s modulus. Therefore, a reference angular frequency \(\omega _0\) is affected by a change in temperature according to

$$\begin{aligned} \omega = \omega _0 \sqrt{1 + \beta _T \Delta T}, \end{aligned}$$
(5)

In particular, in the case of silicon, Young’s modulus E tends to decrease (soften) with increasing temperatures (Shirai 2013), leading to a subsequent frequency decrease.

That is, if only Eq. (4) was considered, structures made of the same material but characterized by different natural frequencies at the same temperature will experience the same relative variation \(\omega /\omega _0\). Moreover, the mode shape associated with the natural frequency remains unaffected by the temperature change. Therefore, in order to introduce a dependency on the shape of the structure, thermal stresses need to be considered.

3.2 Influence of the thermal stress

A common approach to include the thermal stresses is to add to Eq. (2) the geometric stiffness matrix \(\mathbf {K_G}\) (Crisfield 1996; Liu et al. 2013):

$$\begin{aligned} \left( -\omega ^2 \textbf{M} + \textbf{K} + \mathbf {K_G}\right) \varvec{q} = \varvec{0}, \end{aligned}$$
(6)

The matrix \(\mathbf {K_G}\) depends on the nodal displacement vector \(\varvec{u_T}\), obtained from the solution of the static thermal expansion problem,

$$\begin{aligned} \textbf{K} \varvec{u_T} = \varvec{f_T}, \end{aligned}$$
(7)

where \(\varvec{f_T}\) is the equivalent force vector, proportional to the thermal expansion coefficient \(\alpha _k\), that accounts for the thermal stresses.

It is possible to show that \(\varvec{f_T}\) linearly depends on the temperature variation \(\Delta T\) (Crisfield 1996; Liu et al. 2013):

$$\begin{aligned} \varvec{f_T} = \Delta T\varvec{{\tilde{f}}_T}. \end{aligned}$$
(8)

Consequently, it is possible to write the normalized thermal expansion problem:

$$\begin{aligned} \textbf{K} \varvec{{\tilde{u}}_T} = \varvec{{\tilde{f}}_T}, \end{aligned}$$
(9)

where \(\varvec{u_T} = \Delta T\varvec{{\tilde{u}}_T}\).

It can be demonstrated (Crisfield 1996; Liu et al. 2013) that \(\mathbf {K_G}\) linearly depends on \(\Delta T\) as well:

$$\begin{aligned} \mathbf {K_G} = \Delta T\mathbf {{\tilde{K}}_G}. \end{aligned}$$
(10)

Moreover, \(\mathbf {K_G}\) linearly depends also on Young’s modulus. Therefore, considering both the thermal behavior of Young’s modulus (Eq. 3) and the thermal stresses (Eq. 9), the characteristic equation (Eq. 2) can be rewritten as

$$\begin{aligned} \left( - \omega ^2 \textbf{M} + \phi \textbf{K} + \phi \Delta T\mathbf {{\tilde{K}}_G} \right) \varvec{q} = \varvec{0}. \end{aligned}$$
(11)

In this work, the mass normalization conditions of the mode shapes are used:

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{q}^T \textbf{M} \varvec{q} = 1 \\ \varvec{q}^T \left( \phi \textbf{K} + \phi \Delta T\mathbf {{\tilde{K}}_G} \right) \varvec{q} = \omega ^2 \end{array} \right. \end{aligned}$$
(12)

The formulation in Eq. (11) is suitable for a topology optimization approach and will be used in the rest of this work.

4 Level-set topology optimization

In this Section, we show the statistical analysis used to compute the eigenfrequency expected value and variance. After that, we illustrate the temperature-robust level-set topology optimization algorithm.

4.1 Statistical analysis

The temperature difference \(\Delta T\) is assumed to follow a Gaussian distribution characterized by a mean value \(\mu\) and variance \(\sigma ^2\). The value of \(\Delta T\) affects the eigenfrequency according to Eq. (11). By applying the Law of the Unconscious Statistician (LOTUS) (Allen 2006, Section 18.3.4), the expected value of the natural frequency \(\mathbb {E}[\omega ]\) can be computed as follows:

$$\begin{aligned} \mathbb {E}[\omega ] = \int \omega (\Delta T) P(\Delta T) \mathrm{{d}}\Delta T, \end{aligned}$$
(13)

where \(P(\Delta T)\) is the Normal Probability Density Function associated with \(\Delta T\). Then, the variance is computed as

$$\begin{aligned} \mathbb {S}^2[\omega ] = \mathbb {E}[\omega ^2] - \mathbb {E}^2[\omega ]. \end{aligned}$$
(14)

To solve Eqs. (13) and (14), the natural frequency is linearized around \(\Delta T= \mu\):

$$\begin{aligned} \begin{aligned} \omega (\Delta T)&= \omega (\mu ) + \left. \frac{\partial \omega }{\partial \Delta T}\right| _\mu (\Delta T- \mu ) \\&= \omega (\mu ) + \omega _T(\mu ) (\Delta T- \mu ). \end{aligned} \end{aligned}$$
(15)

A simple way to approximate \(\omega _T\) is through finite differences. However, this approach would be associated with a high computational cost since it requires solving additional eigenvalue problems. For instance, the first-order forward and backward schemes require an additional solution. On the other hand, if the central difference scheme is used, two additional eigenvalue problems are required (at \(\Delta T= \mu \pm \sigma\)). Therefore, in this work, an analytical approach is used.

The expression of \(\omega _T\) is computed by differentiating Eq. (11):

$$\begin{aligned} \begin{aligned}&\varvec{q}^T \left( -2\omega \frac{\partial \omega }{\partial \Delta T} \textbf{M} + \phi \mathbf {{\tilde{K}}_G} \right. \\&\quad+ \left. \frac{\partial \phi }{\partial \Delta T} \left( \textbf{K} + \Delta T\mathbf {{\tilde{K}}_G} \right) \right) \varvec{q} = \varvec{0}. \end{aligned} \end{aligned}$$
(16)

Using the mass normalization conditions Eqs. (12) and (16) can be rewritten as:

$$\begin{aligned} -2\omega \frac{\partial \omega }{\partial \Delta T} + \omega ^2 m_T + \phi \varvec{q}^T \mathbf {{\tilde{K}}_G} \varvec{q} = \varvec{0}, \end{aligned}$$
(17)

where the coefficient \(m_T\) is defined as

$$\begin{aligned} m_T = \frac{1}{\phi } \frac{\partial \phi }{\partial \Delta T}. \end{aligned}$$
(18)

Finally, Eq. (17) allows to compute

$$\begin{aligned} \omega _T = \frac{\partial \omega }{\partial \Delta T} = \frac{\omega ^2 m_T + \phi \varvec{q}^T \mathbf {{\tilde{K}}_G} \varvec{q}}{2\omega }. \end{aligned}$$
(19)

Using the previous results, Eqs. (13) and (14) lead:

$$\begin{aligned} \mathbb {E}[\omega ]= & {} \omega (\mu ) \end{aligned}$$
(20)
$$\begin{aligned} \mathbb {S}^2[\omega ]= & {} \omega _T^2(\mu ) \sigma ^2. \end{aligned}$$
(21)

4.2 Temperature-robust eigenfrequency optimization

Equations (20) and (21) allow to define the temperature-robust eigenfrequency problem as follows:

$$\begin{aligned} \begin{array}{r c l} \max &{} &{} w_e \mathbb {E}[\omega ] - w_s \mathbb {S}^2[\omega ] \\ \mathrm {s.t.}&{} &{} \left( -\omega ^2 \textbf{M} + \phi \textbf{K} + \phi \Delta T\mathbf {{\tilde{K}}_G}\right) \varvec{q} = \varvec{0} \\ &{} &{} \textbf{K} \varvec{{\tilde{u}}_T} = \varvec{{\tilde{f}}_T} \\ &{} &{} A \le A_{\textrm{max}}, \end{array} \end{aligned}$$
(22)

where the objective function is a linear combination of \(\mathbb {E}[\omega ]\) and \(\mathbb {S}^2[\omega ]\), A indicates the area fraction (i.e., the fraction of the available design domain that is occupied by the material), and \(A_{\textrm{max}}\) refers to the maximum acceptable area fraction. This formulation aims at maximizing the expected natural frequency while minimizing its variance. The coefficients \(w_e\) and \(w_s\) are computed according to Asadpoure et al. (2011):

$$\begin{aligned} w_e= & {} \frac{w}{\mathbb {E}[\omega ^0]} \end{aligned}$$
(23)
$$\begin{aligned} w_s= & {} \frac{1 - w}{\mathbb {S}^2[\omega ^0]}, \end{aligned}$$
(24)

where \(0 \le w \le 1\), and \(\omega ^0\) is the eigenfrequency of the initial design. If \(w = 1\), only the expected value is maximized and the robust problem falls back into the deterministic case. On the other hand, if \(w = 0\), only the variance is minimized. To track the desired mode shape during the optimization process, the Modal Assurance Criterion (MAC) is implemented (Kim and Kim 2000; Pastor et al. 2012).

Problem (22) is solved iteratively using a level-set optimization method (Algorithm 1). Just like in the classical Level-Set Topology Optimization (LSTO, Allaire et al. 2002; Wang et al. 2003; Allaire et al. 2004), the Level-Set Method (LSM, Osher and Sethian 1988; Sethian 1999; Osher and Fedkiw 2006) is exploited to track and evolve the boundary of the structure throughout the robust optimization process (Fig. 1). The level-set function \(\Phi\) is propagated according to the Hamilton-Jacobi equation,

$$\begin{aligned} \frac{\partial \Phi (x)}{\partial t} + V_n(x) \vert \nabla \Phi (x) \vert = 0, \end{aligned}$$
(25)

where \(V_n(x)\) indicates the velocity field, obtained by extending the optimal boundary points velocities to the entire design domain (Osher and Fedkiw 2006).

Fig. 1
figure 1

The structure is represented by the black regions (b), where the level-set function \(\Phi\) is greater than zero. The boundary of this structure is the result of the intersection between \(\Phi\) and the black plane at the zero level in (a)

Full size image

At each iteration, the structure identified by the zero level-set of \(\Phi\) is discretized using the Marching Squares algorithm (Lorensen and Cline 1987; Maple 2003). This allows to compute the boundary points \(z_j\), which are the design variables of the optimization problem, as well as the area fractions \(\alpha _k\) of all the grid elements (Hyun and Kim 2021b). Figure 2 provides a graphical representation of the Marching Squares discretization. The area fractions are then used to define the structural matrices according to the Ersatz material approximation with a linear interpolation scheme for the material properties (Allaire et al. 2004).

Fig. 2
figure 2

Illustration of the Marching Squares algorithm. The zero level-set of \(\Phi\) is intersected with the domain mesh (blue points), which allows the approximation of the boundary (orange). Each grid element is then assigned an area fraction \(\alpha _k\) between 0 (white) and 1 (black). (Color figure online)

Full size image

The boundary point sensitivities are computed using the approach presented by Kambampati et al. (2021): the derivatives of \(\mathbb {E}[\omega ]\) and \(\mathbb {S}^2[\omega ]\) with respect to the area fractions \(\alpha _k\) of individual elements (Sect. 4.3) are combined with a local perturbation of the boundary points to obtain the shape sensitivities at the boundary points (Chen and Chen 2011; Wu et al. 2021). The sensitivities at the boundary points are used in the sub-optimization problem (Allaire et al. 2004) that is solved with IPOPT (Interior Point OPTimizer, Wächter and Biegler 2006), an open-source library for large-scale nonlinear constrained optimization.

The optimal velocities of the boundary points, which come from the solution to the sub-optimization problem, are then used to update the level-set function. This operation is performed by solving the level-set equation in its discrete form,

$$\begin{aligned} \Phi _i^{k+1} = \Phi _i^k - \Delta t V_{n,i}^k \vert \nabla \Phi _i^k \vert , \end{aligned}$$
(26)

where \(\Phi\) is the level-set function, k refers to the iteration number, i indicates a grid node, \(\Delta t\) is the time step of the propagation, and \(V_{n,i}\) indicates the velocity of node i (normal to the geometry boundary).

In this work, a fixed grid made of unitary square elements is used, along with the Hamilton-Jacobi Weighted Essentially Non-Oscillatory method (HJ-WENO, Osher and Fedkiw 2006) for spatial discretization, and a Forward Euler approach for time discretization. In addition, \(\Delta t = 1\) is used, leading to the following Courant-Friedrichs-Lewy (CFL) condition for numerical stability (Osher and Fedkiw 2006):

$$\begin{aligned} \max \left\{ V_n \right\} \le \alpha _{\textrm{CFL}} < 1. \end{aligned}$$
(27)

Throughout this work, \(\alpha _{\textrm{CFL}} = 0.2\) has proven to be a good trade-off between convergence and numerical stability.

Convergence is reached when all constraints are satisfied and the objective (or cost) variation between two successive iterations is sufficiently small in terms of relative difference.

figure a

4.3 Sensitivity analysis

In this Section, we present the analytical procedure used to to obtain the derivatives of the expected natural frequency \(\mathbb {E}[\omega ]\) and its variance \(\mathbb {S}^2[\omega ]\) with respect to the area fractions \(\alpha _k\) of the grid elements. These derivatives are then combined with local perturbation of the boundary points (Kambampati et al. 2021) to compute the boundary sensitivities of Problem (22).

While the derivative of the expected natural frequency \(\frac{\partial \mathbb {E}[\omega ]}{\partial \alpha _k}\) is derived by following an approach similar to that presented in Yang and Li (2013, 2014), the derivative of the frequency variance \(\frac{\partial \mathbb {S}^2[\omega ]}{\partial \alpha _k}\) requires a novel formulation that is presented later in this Section.

The derivative of \(\mathbb {E}[\omega ]\) with respect to \(\alpha _k\) is written as

$$\begin{aligned} \begin{aligned} \frac{\partial \mathbb {E}[\omega ]}{\partial \alpha _k}&= \frac{\varvec{q}^T \left( -\omega ^2 \frac{\partial \textbf{M}}{\partial \alpha _k} + \phi \frac{\partial \textbf{K}}{\partial \alpha _k} \right) \varvec{q}}{2 \omega } \\&\quad + \frac{\Delta T\phi \varvec{q}^T \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial \alpha _k} \varvec{q}}{2 \omega } \\&\quad + \frac{\Delta T\phi \left[ \varvec{q}^T \left( \sum _i \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial {\tilde{u}}_{T, i}} \frac{\partial {\tilde{u}}_{T, i}}{\partial \alpha _k} \right) \varvec{q} \right] }{2 \omega }, \end{aligned} \end{aligned}$$
(28)

where \({\tilde{u}}_{T,i}\) is the i-th element of \(\varvec{{\tilde{u}}_T}\) that is obtained by solving Eq. (9).

The term within square brackets in Eq.(28), can be rewritten in a compact form as

$$\begin{aligned} \varvec{\Lambda }^T(\varvec{q}, \varvec{q}) \frac{\partial \varvec{{\tilde{u}}_T}}{\partial \alpha _k}, \end{aligned}$$
(29)

where the operator \(\varvec{\Lambda }\) is defined as

$$\begin{aligned} \varvec{\Lambda }(\varvec{a}, \varvec{b}) = \left[ \begin{array}{c} \vdots \\ \varvec{a}^T \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial {\tilde{u}}_{T, i}} \varvec{b} \\ \vdots \end{array} \right] _{n \times 1}, \end{aligned}$$
(30)

with n being the number of degrees of freedom.

To avoid computing the term \(\frac{\partial {\tilde{u}}_{T, i}}{\partial \alpha _k}\), the adjoint method is used, yielding

$$\begin{aligned} \begin{aligned} \frac{\partial \mathbb {E}[\omega ]}{\partial \alpha _k}&= \frac{\varvec{q}^T \left( -\omega ^2 \frac{\partial \textbf{M}}{\partial \alpha _k} + \phi \frac{\partial \textbf{K}}{\partial \alpha _k} \right) \varvec{q}}{2 \omega } \\&\quad + \frac{\Delta T\phi \varvec{q}^T \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial \alpha _k} \varvec{q}}{2 \omega } \\&\quad + \frac{\Delta T\phi \varvec{\mu }^T \left( \frac{\partial \textbf{K}}{\partial \alpha _k} \varvec{{\tilde{u}}_T} - \frac{\partial \varvec{{\tilde{f}}_T}}{\partial \alpha _k} \right) }{2 \omega }, \end{aligned} \end{aligned}$$
(31)

where the adjoint vector \(\varvec{\mu }\) is computed by solving

$$\begin{aligned} \textbf{K} \varvec{\mu } = -\varvec{\Lambda }(\varvec{q}, \varvec{q}). \end{aligned}$$
(32)

Since the matrix \(\mathbf {{\tilde{K}}_G}\) depends linearly on \(\varvec{{\tilde{u}}_T}\) (Zienkiewicz and Taylor 2005), the derivative \(\frac{\partial \mathbf {{\tilde{K}}_G}}{\partial {\tilde{u}}_{T, i}}\) can be computed as

$$\begin{aligned} \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial {\tilde{u}}_{T, i}} = \frac{\mathbf {{\tilde{K}}_G} \left( {\tilde{u}}_{T, i} + \Delta {\tilde{u}}_{T, i} \right) - \mathbf {{\tilde{K}}_G} \left( {\tilde{u}}_{T, i} \right) }{\Delta {\tilde{u}}_{T, i}}, \end{aligned}$$
(33)

where \(\Delta {\tilde{u}}_{T, i}\) represents the displacement change of the i-th element of vector \(\varvec{{\tilde{u}}_T}\).

The sensitivity of the variance is computed as

$$\begin{aligned} \frac{\partial \mathbb {S}^2[\omega ]}{\partial \alpha _k} = 2 \mathbb {S}[\omega ] \frac{\partial \omega _T}{\partial \alpha _k} \sigma . \end{aligned}$$
(34)

To obtain the derivative of \(\omega _T\) with respect to \(\alpha _k\), we start by differentiating Eq. (17):

$$\begin{aligned} \begin{aligned} 2\omega \frac{\partial \omega _T}{\partial \alpha _k}&= 2\omega \frac{\partial \omega }{\partial \alpha _k}m_T - 2\frac{\partial \omega }{\partial \alpha _k}\omega _T \\&\quad + \phi \varvec{q}^T\frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k}\varvec{q} + 2 \phi \varvec{q}^T \mathbf {{\tilde{K}}_G} \frac{\partial \varvec{q}}{\partial \alpha _k}, \end{aligned} \end{aligned}$$
(35)

where the term \(\frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k}\) is the total derivative with respect to \(\alpha _k\).

Computing \(\frac{\partial \varvec{q}}{\partial \alpha _k}\) for all the grid elements would be computationally expensive. In order to avoid this operation, the adjoint method is used by exploiting the Static Modal Derivatives (SMD, Idelsohn and Cardona 1985a, b; Slaats et al. 1995; Varona et al. 2019) of Eq. (11) with respect to \(\alpha _k\):

$$\begin{aligned} \begin{aligned}&\phi \left( \textbf{K} + \Delta T\mathbf {{\tilde{K}}_G} \right) \frac{\partial \varvec{q}}{\partial \alpha _k} \\&+ \phi \left( \frac{\partial \textbf{K}}{\partial \alpha _k} + \Delta T\frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k} \right) \varvec{q} = \varvec{0}. \end{aligned} \end{aligned}$$
(36)

Combining Eqs. (35) and (36):

$$\begin{aligned} \begin{aligned} 2\omega \frac{\partial \omega _T}{\partial \alpha _k}&= 2\omega \frac{\partial \omega }{\partial \alpha _k} \left( m_T - \frac{\omega _T}{\omega } \right) \\&\quad +\phi \varvec{q}^T\frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k}\varvec{q} \\&\quad + 2 \phi \varvec{q}^T \mathbf {{\tilde{K}}_G} \frac{\partial \varvec{q}}{\partial \alpha _k} \\&\quad + \phi \varvec{\gamma }^T \left( \textbf{K} + \Delta T\mathbf {{\tilde{K}}_G} \right) \frac{\partial \varvec{q}}{\partial \alpha _k} \\&\quad + \phi \varvec{\gamma }^T \left( \frac{\partial \textbf{K}}{\partial \alpha _k} + \Delta T\frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k} \right) \varvec{q}, \end{aligned} \end{aligned}$$
(37)

To avoid the computation of \(\frac{\partial \varvec{q}}{\partial \alpha _k}\), we solve the adjoint equation

$$\begin{aligned} \left( \textbf{K} + \Delta T\mathbf {{\tilde{K}}_G} \right) \varvec{\gamma } = - 2 \mathbf {{\tilde{K}}_G} \varvec{q}, \end{aligned}$$
(38)

which allows to simplify Eq. (37) as follows:

$$\begin{aligned} \begin{aligned} 2\omega \frac{\partial \omega _T}{\partial \alpha _k}&= 2\omega \frac{\partial \omega }{\partial \alpha _k} \left( m_T - \frac{\omega _T}{\omega } \right) \\&\quad+ \phi \varvec{\gamma }^T \frac{\partial \textbf{K}}{\partial \alpha _k} \varvec{q} + \phi \varvec{y}^T \frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k} \varvec{q}, \end{aligned} \end{aligned}$$
(39)

where \(\varvec{y} = \varvec{q} + \Delta T\varvec{\gamma }\).

Using the \(\varvec{\Lambda }\) operator introduced in Eq. (30), it is possible to show that:

$$\begin{aligned} \varvec{y}^T \frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k} \varvec{q} = \varvec{y}^T \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial \alpha _k} \varvec{q} + \varvec{\Lambda }(\varvec{y}, \varvec{q})^T \frac{\partial \varvec{{\tilde{u}}_T}}{\partial \alpha _k}. \end{aligned}$$
(40)

As before, the adjoint method is used to avoid the computation of the term \(\frac{\partial \varvec{{\tilde{u}}_T}}{\partial \alpha _k}\). Equation (9) is differentiated as follows:

$$\begin{aligned} \textbf{K} \frac{\partial \varvec{{\tilde{u}}_T}}{\partial \alpha _k} + \frac{\partial \textbf{K}}{\partial \alpha _k} \varvec{{\tilde{u}}_T} + \frac{\partial \varvec{{\tilde{f}}_T}}{\partial \alpha _k} = \varvec{0}, \end{aligned}$$
(41)

Then, Eq. (40) and (41) are combined, yielding

$$\begin{aligned} \begin{aligned} \varvec{y}^T \frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k} \varvec{q}&= \varvec{y}^T \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial \alpha _k} \varvec{q} + \varvec{\Lambda }(\varvec{y}, \varvec{q})^T \frac{\partial \varvec{{\tilde{u}}_T}}{\partial \alpha _k} \\&\quad + \varvec{\delta }^T \left( \textbf{K} \frac{\partial \varvec{{\tilde{u}}_T}}{\partial \alpha _k} + \frac{\partial \textbf{K}}{\partial \alpha _k} \varvec{{\tilde{u}}_T} + \frac{\partial \varvec{{\tilde{f}}_T}}{\partial \alpha _k} \right) . \end{aligned} \end{aligned}$$
(42)

Instead of computing \(\frac{\partial \varvec{{\tilde{u}}_T}}{\partial \alpha _k}\), we solve the adjoint equation

$$\begin{aligned} \textbf{K} \varvec{\delta } = -\varvec{\Lambda }(\varvec{y}, \varvec{q}). \end{aligned}$$
(43)

Hence, Eq. (42) simplifies as

$$\begin{aligned} \begin{aligned} \varvec{y}^T \frac{d\mathbf {{\tilde{K}}_G}}{d\alpha _k} \varvec{q}&= \varvec{y}^T \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial \alpha _k} \varvec{q} \\&\quad + \varvec{\delta }^T \left( \frac{\partial \textbf{K}}{\partial \alpha _k} \varvec{{\tilde{u}}_T} + \frac{\partial \varvec{{\tilde{f}}_T}}{\partial \alpha _k} \right) . \end{aligned} \end{aligned}$$
(44)

Finally, combining Eq. (44) and (39) and rearranging the terms, the sensitivity of \(\omega _T\) is

$$\begin{aligned} \begin{aligned} \frac{\partial \omega _T}{\partial \alpha _k}&= \frac{\partial \omega }{\partial \alpha _k} \left( m_T - \frac{\omega _T}{\omega } \right) \\&\quad + \frac{\phi \varvec{\gamma }^T \frac{\partial \textbf{K}}{\partial \alpha _k} \varvec{q} + \phi \varvec{y}^T \frac{\partial \mathbf {{\tilde{K}}_G}}{\partial \alpha _k} \varvec{q}}{2\omega } \\&\quad + \frac{\phi \varvec{\delta }^T \left( \frac{\partial \textbf{K}}{\partial \alpha _k} \varvec{{\tilde{u}}_T} + \frac{\partial \varvec{{\tilde{f}}_T}}{\partial \alpha _k} \right) }{2\omega }. \end{aligned} \end{aligned}$$
(45)

5 Numerical examples

In this Section, we present the results of the temperature-robust eigenfrequency optimization. To show the validity of the approach, Problem (22) is solved at different temperature conditions (\(\mu\) and \(\sigma\)) with different weights \(w\). After that, we show how to slightly modify the formulation of Problem (22) to design a thermally robust resonator with a specific natural frequency.

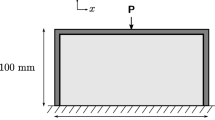
The parameters used in the following examples are reported in Table 1. The material considered is polysilicon, whose mechanical properties as a function of temperature have been intensely studied by Sharpe et al. (2001). The problem settings, the boundary conditions, and the initial layout are shown in Fig. 3.

All the results are obtained using OpenLSTO (Kambampati et al. 2018).

Table 1 Parameters used in the presented numerical examples
Full size table
Fig. 3
figure 3

Problem setting, boundary conditions, and initial layout. In (a) the black region is the proof mass that remains fixed, whereas the gray areas represent the design space which is initially seeded with holes (b)

Full size image

5.1 Thermally robust frequency maximization

The aim of this example is to maximize the natural frequency associated with the oscillation of the proof mass along the y axis (Fig. 3a). The approach is applied to the same problem with different combinations of mean temperature \(\mu\), temperature standard deviation \(\sigma\), and weight \(w\). The numerical results are reported in Table 2, whereas Fig. 4 shows two optimal layouts obtained at the same temperature condition but with two different weights.

By using a value of \(w\) close to 1, the algorithm converges to a solution with stiffer elements, thus increasing the expected natural frequency as well as its variance. On the other hand, if a low value of \(w\) is used, the optimal layout presents more flexible elements that allow the residual thermal stresses to compensate for the frequency variation. This results in a reduction of both its variance and the expected value. When \(w = 1\), there is no control over the frequency variance.

Table 2 Results of Problem (22) for different combinations of \(\mu\), \(\sigma\), and \(w\)
Full size table
Fig. 4
figure 4

Optimal layouts obtained with \(\mu = 100~^\circ C\), \(\sigma = 100~^\circ C\)

Full size image

5.2 Design of a thermally robust resonator

In this Section, we show how the approach presented in Sect. 4 can be used to optimize a MEMS resonator with a prescribed frequency \(\omega _t\) while minimizing its variance. Problem (22) is rewritten as

$$\begin{aligned} \begin{array}{l c l} \min &{} &{} \mathbb {S}^2[\omega ] \\ \mathrm {s.t.}&{} &{} \left( -\omega ^2 \textbf{M} + \phi \textbf{K} + \phi \Delta T\mathbf {{\tilde{K}}_G}\right) \varvec{q} = \varvec{0} \\ &{} &{} \textbf{K} \varvec{{\tilde{u}}_T} = \varvec{{\tilde{f}}_T} \\ &{} &{} \left( \mathbb {E}[\omega ] / \omega _t - 1\right) ^2 \le \varepsilon ^2 \\ &{} &{} A \le A_{\textrm{max}}. \end{array} \end{aligned}$$
(46)

In this formulation, the expected natural frequency is imposed using the third constraint, whereas its variance is minimized through the objective function. We solve this problem for \(\omega _t = 1\) MHz, \(A_{\textrm{max}} = 70\%\), \(\mu = 0~^\circ C\), and \(\sigma = 100~^\circ C\). The desired frequency corresponds to the oscillations of the proof mass along the y axis (Fig. 3).

The results are reported in Fig. 5. This robust solution is compared to a layout obtained through a deterministic approach, i.e. imposing the natural frequency without minimizing its variance. Both solutions exhibit the desired natural frequency of 1 MHz. However, the robust layout presents a much lower variance (4.09 kHz) with respect to the deterministic solution (68.59 kHz). Concerning the TCF value (Sect. 2), the deterministic and the robust designs are characterized respectively by \(-82.83~\textrm{ppm}/^{\circ }\textrm{C}\) and \(-20.22~\textrm{ppm}/^{\circ }\textrm{C}\). In particular, the TCF of the robust design is one-third lower than the typical TCF of silicon resonators (\(-30~\textrm{ppm}/^{\circ }\textrm{C}\)).

Fig. 5
figure 5

Comparison between the deterministic layout (a), obtained with a deterministic level-set optimization, and the robust layout (b), obtained by solving Problem (46)

Full size image

All the layouts in Fig. 5 have been validated using COMSOL Multiphysics\(^{\copyright }\). The geometry is discretized using a body-fitted mesh of triangular elements. The plane stress approximation is used along with a geometrically linear formulation. After enforcing the boundary conditions, the natural frequencies are computed by solving an eigenfrequency step. By following this procedure, we have computed the target natural frequencies (Table 3) at reference temperature (\(\Delta T= 0~^{\circ }\textrm{C}\)). In addition, Fig. 6 shows the target mode shapes of the resonators (eigenmode corresponding to the oscillation of the proof mass along the y axis).

The eigenfrequencies in presence of thermal effects are simulated by coupling the mechanical and thermal domains. Firstly, given a temperature variation \(\Delta T\), Young’s modulus is modified according to Eq.(3). After that, a thermal expansion is applied in the entire domain. Then, a static step is used to compute the residual thermal stresses. Finally, the natural frequencies are computed by solving an eigenfrequency step starting from the results of the previous step. With this procedure, we have computed the TCF values (Table 4) related to the target natural frequencies of the resonators.

The discrepancy between all the numerical results (Table 3) is below 1%, thus confirming the quality of the solutions obtained with OpenLSTO.

Fig. 6
figure 6

Target mode shapes of the resonators shown in Fig. 5

Full size image
Table 3 Target eigenfrequencies of the resonators shown in Fig. 5 at the reference temperature (\(\Delta T= 0~^{\circ }\textrm{C}\)). The values obtained with OpenLSTO are compared to those computed with COMSOL
Full size table
Table 4 TCF values related to the target modes of the resonators shown in Fig. 5. The values obtained with OpenLSTO are compared to those computed with COMSOL
Full size table

5.3 Effects of the boundary conditions

The method proposed in Sect. 4 involves residual thermal stresses, which depend on the boundary conditions. In this Section, we use the same problem formulation presented in Sect. 5.2 (Problem (46)) to show how the optimal solution changes in presence of different boundary conditions. In particular, we consider the two boundary conditions illustrated in Fig. 7.

Fig. 7
figure 7

Different boundary conditions used in Sect. 5.3

Full size image

Figure 8 shows the results obtained with the partial fixed boundary conditions (Fig. 7a), whereas Fig. 9 shows the results obtained with the four corners boundary conditions (Fig. 7b). In all the examples, the target frequency of 1 MHz has been reached. In addition, the robust solutions exhibit lower values of frequency variance and TCF compared to their deterministic counterparts, thus confirming the validity of the proposed approach.

Fig. 8
figure 8

Comparison between the deterministic layout (a), obtained with a deterministic level-set optimization, and the robust layout (b), obtained by solving Problem (46). Solutions obtained with the partial fixed boundary conditions (Fig. 7a)

Full size image
Fig. 9
figure 9

Comparison between the deterministic layout (a), obtained with a deterministic level-set optimization, and the robust layout (b), obtained by solving Problem (46). Solutions obtained with the four corners boundary conditions (Fig. 7b)

Full size image

6 Conclusion

In this work, a novel approach that deals with temperature uncertainties has been described. Statistical analysis was used to obtain analytical expressions for the expected natural frequencies and their variance over temperature. These values were used to formulate the temperature-robust eigenfrequency optimization, which aims at maximizing the expected natural frequency while minimizing its variance due to temperature variations. The optimization problem was solved using a level-set optimization algorithm, and the sensitivities were computed through the adjoint method by exploiting the definition of Static Modal Derivatives (SMD). Even though there exist more accurate approaches for the calculation of modal derivatives, the static approximation was chosen mainly due to its simplicity and computational efficiency. A possible limitation of the proposed approach lies in the first-order approximation of the natural frequencies. While higher-order terms would improve the accuracy of the proposed method, their inclusion would increase the complexity of the formulation, especially that of the statistical and sensitivity analysis. Numerical examples considering different temperature conditions, weights, and boundary conditions were presented to support the effectiveness of the proposed approach, along with an example of a 1 MHz temperature-robust MEMS resonator. The proposed layout, which has been validated using COMSOL, exhibits a TCF coefficient comparable to that of real-world devices. It is worth mentioning that the desired TCF value may not always be achievable. Nonetheless, any attempt aimed at minimizing the TCF will reduce the effort required by other active compensation techniques as well as the amount of energy required by such systems.