1 Introduction

The advent of wireless networks, which was fuelled by breakthroughs in microwave engineering, has revolutionized telecommunication. In the last two decades, the use of wireless and connected home devices, such as cell phones, smart speakers, security cameras, and laptops has increased significantly, resulting in an exponential increase in wireless data traffic. In 2020, global data consumption increased by \(30.4\,\%\) over the previous year, and it is estimated that there will be nearly 30 billion connected devices by 2023 (Cisco 2020; PwC 2021). To accommodate this increase in data traffic, future communication systems and wireless devices need more efficient and improved designs.

Frequency dividing multiplexing (FDM) plays a key role in data transmission for telecommunication (Sakai 1986; Li and Stüber 2006; Snyder et al 2015; Ma et al 2017). It enables a high level of system miniaturization by integrating sub-systems that operate at different frequency bands. On one hand, a frequency dividing multiplexer allows multiple signals of different frequencies to share a single communication channel, such as a waveguide or an antenna. On the other hand, the device divides the frequencies of the communication channel into multiple non-overlapping frequency bands and delivers them to their corresponding output ports. To prevent signal overlapping, sufficient isolation between neighbouring frequency bands is essential. In addition, a sharp roll-off between the adjacent frequency bands is needed to avoid wasting parts of the frequency spectrum. AM and FM broadcasting methods are the most common use of FDM at RF frequencies (Chaparro 2015), and communication satellites (Kharchenko et al 2015), modern radars (Sebt et al 2009), and wireless LAN (Keller and Hanzo 1996) are just a few examples of the application of FDM at microwave frequencies.

In the literature, various concepts are used to design FDM devices (Snyder et al 2015; Cameron and Yu 2007). Two commonly used design concepts of FDM are the cavity-based and the directional-filters approaches. The cavity-based approach relies on the modal field distribution inside a given cavity. The positions of the FDM output ports are properly selected at the boundaries of the cavity to enable efficient signals’ coupling (Yassini and Yu 2015). However, the field distribution inside a loaded cavity changes based on the loading condition, and therefore, the device needs to be redesigned to account for the new loads. On the other hand, FDM based on directional filters rely on loading a transmission line with a series of resonant filters. Each filter stage is designed separately and aims to couple a specified frequency band to an output port (Cameron and Yu 2007). Employing techniques such as adding transmission zeros can improve the transition slope between the neighbouring stages (Sorocki et al 2018). However, the final device becomes bulky, and the overall insertion losses of the device increase significantly.

Topology optimization is an inverse design technique (Bendsøe and Sigmund 2004), which was originally introduced to design linear elastic structures (Bendsøe and Kikuchi 1988). It has since been successfully applied to other disciplines including fluids (Borrvall and Petersson 2002; Gersborg-Hansen et al 2005), acoustics (Wadbro and Berggren 2006; Dühring et al 2008; Lee and Kim 2009; Wadbro 2014; Bokhari et al 2021), and electromagnetics (Aage et al 2010; Hassan et al 2014b, a; Frellsen et al 2016; Wang et al 2017; Hassan et al 2018, 2020). Material-distribution-based topology optimization is the most commonly used approach, where a specified design domain is divided into small elements, and a design variable is assigned to each element to determine presence or absence of material. Typically, gradient-based optimization methods are employed to solve topology optimization problems, where the gradient information can be efficiently evaluated by adjoint-field methods (Giles and Pierce 2000). In this work, we adopt the cavity-based approach to design the FDM. However, here we fix the positions of the output ports and employ the material-distribution-based topology optimization to design a three-port FDM that operates in the X-band (9.0–10.2  GHz). The multiplexing effect is achieved by distributing a metal inside the design domain which splits the input signal frequencies from port-1 into two frequency bands and transmits them to their respective output port (either port-2 or port-3). The design objective is to maximize the transmission of each frequency to its intended output port, minimize reflection to port-1, and limit signal cross-coupling between the adjacent output ports. Previous contributions on the FDMs problems discussed the use of dielectric materials as design materials (Nomura et al 2007; Frellsen et al 2016). In such studies, the interpolation between the design material (dielectric) and the background (void) is also a lossless dielectric material, which entails that the power imposed at the input port would either be reflected back to the same port or transmitted to the output ports.

In the current work, we present a method to design efficient three-port metallic frequency-dividing multiplexers. Here, the design material is a good conductor (copper), which can be treated as a lossless material at microwave frequencies. However, when interpolating between the good conductor (copper) and the void during the optimization procedure, the intermediate materials exhibit ohmic losses. Previous studies on topology optimization of lossy material dealt with one or two port devices, such as antennas and waveguide transitions (Hassan et al 2014b, 2018). For multiport design problems, ohmic losses make the design problem sensitive to the selection of the objective function. The current work features a unique setup to study two main challenges: 1) handling the ohmic losses and 2) selecting a suitable objective function for a multiport design problem. We resolve the first issue by using a non-linear filtering approach coupled with a continuation scheme. In addition, we present a technique to model the material distribution of metal as a good electric conductor against a dielectric background. More precisely, we employ numerical investigations to select suitable values of the electric conductivity for the interpolation function. For the second issue, we devised the power balance of the setup, which we use to formulate a sequence of objective functions. Each objective function includes more information than the preceding one. The results demonstrate that providing useful additional information to the optimizer improves the transmission of the signal to its intended output port.

2 Problem description

Fig. 1
figure 1

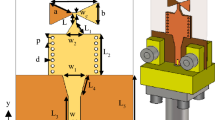
The electric field is polarized normal to the plane. (a) Incoming waves from port–1 should travel to port–2 in frequency band–1 (b) Incoming waves from port–1 should travel to port–3 in frequency band–2. (c) Computational domain for finite element discretization. \(\varGamma _1\), \(\varGamma _2\), and \(\varGamma _3\) indicate the ports of waveguide 1, waveguide 2, and waveguide 3, respectively. The boundary \(\varGamma _\text {PEC}\), denoted by the solid line, is a perfect electric conductor. (d) Local coordinate systems for artificial absorbing boundary conditions

Full size image

Consider the two-dimensional three-port setup illustrated in Fig. 1 (a,b). Port-1 is the waveguide on the left, and port-2 and port-3 are the waveguides on the right. Here, \(\varOmega ^\text {D}\) is our design domain. We denote waves travelling towards \(\varOmega ^\text {D}\) as incoming waves and waves travelling away from \(\varOmega ^\text {D}\) as outgoing waves. In addition, \(\varOmega ^\text {D}\) and the three artificially truncated waveguides constitute the computational domain \(\varOmega\) depicted in Fig. 1 (c). The boundary \(\varGamma _\text {PEC}\) represents a prefect electric conductor, and \(\varGamma _1\), \(\varGamma _2\), and \(\varGamma _3\) are the boundaries of the truncated waveguides. We aim to place metallic material inside \(\varOmega ^\text {D}\) to make this setup serve as a FDM. In other words, we want to optimize this setup in such a way that:

  1. (a)

    For frequency band-1, incoming waves from port-1 only travel to port-2, as illustrated in Fig. 1a.

  2. (b)

    For frequency band-2, incoming waves from port-1 only travel to port-3, as illustrated in Fig. 1b).

The dimensions of this setup are \(l^\text {w} = 50\, \text {mm}\), \(l^\text {D} = 100\, \text {mm}\), \(h^\text {D}= 100\,\text {mm}\), \(h^\text {w} =20 \,\text {mm}\), and \(h^\text {s}= 30 \,\text {mm}\), as illustrated in Fig. 1c.

The electric field \({\mathcal {E}}\) is governed by Maxwell’s equation

$$\begin{aligned} \nabla \times \bigg ( \frac{1}{\mu }\nabla \times {\mathcal {E}}\bigg ) + \epsilon \frac{\partial ^{2}{\mathcal {E}}}{\partial t^{2}} + \sigma \frac{\partial {\mathcal {E}}}{\partial t} = 0 \quad \text {in}\, \varOmega , \end{aligned}$$
(1)

where \(\mu\) is the permeability, \(\sigma\) is the electrical conductivity, and \(\epsilon\) is the permittivity. The permittivity is related to relative permittivity \(\epsilon _r\) by \(\epsilon _r = \epsilon /\epsilon _0\), where \(\epsilon _0\) is the permittivity in free space. Further, we assume that \(\mu \equiv \mu _0\), the permeability in free space. We search for time harmonic solutions by using the ansatz \({\mathcal {E}}(x,t)=\Re \{E(x)e^{\textrm{i}\omega t}\}\), where the angular frequency \(\omega =2\pi f\), f is the frequency, \(\textrm{i}\) is the imaginary unit, and t is the time. This assumption yields that

$$\begin{aligned} \nabla \times \bigg (\nabla \times E\bigg ) - k^2 \bigg (\epsilon _r - \textrm{i} \sqrt{\frac{\mu _0}{\epsilon _0}} \frac{\sigma }{k}\bigg ) E = 0 \quad \text {in}\, \varOmega , \end{aligned}$$
(2)

where \(k=\omega /c\) is the wavenumber, and \(c=(\epsilon _0 \mu _0)^{-1/2}\) denotes the speed of light.

Inside waveguides, the solution of Maxwell’s equations can be decomposed into the transverse electric (TE) and the transverse magnetic (TM) polarizations. Moreover, waveguides are typically dimensioned and used at frequencies where only one mode (namely the dominant mode) is supported at their ports (Pozar 2011). For such cases, it could be numerically more efficient to analyze such waveguide problems by employing 2D symmetry.

We assume that the electric field is polarized normal to the plane. That is, \(E=(0,0,u)\), where u refers to the electric field normal to the plane as demonstrated in Fig. 1. Also, we choose the frequency band of interest so that our waveguide-based FDM only supports the dominant TE\(_{10}\) mode (Pozar 2011). Under these assumptions, Eq. (2) can be reduced to the Helmholtz equation,

$$\begin{aligned} -\varDelta u - k^2\bigg (\epsilon _r - {\textrm{i}} \sqrt{\frac{\mu _0}{\epsilon _0}} \frac{\sigma }{k}\bigg ) u = 0 \quad \text {in} \, \varOmega . \end{aligned}$$
(3)

We assume that the metallic boundaries of device are perfect electric conductors. The boundary condition for the perfect electric conductor is

$$\begin{aligned} u = 0 \quad \text {on}\,\varGamma _\text {PEC}. \end{aligned}$$
(4)

Based on the 20\(\,{\textrm{mm}}\) waveguide width, the waveguide ports only support the first propagating mode between \(7.50\,\textrm{GHz}\) and \(15.0\,\textrm{GHz}\). In this study, we choose frequencies such that all modes except the first are evanescent. The general solution in waveguide m is thus a combination of incoming and outgoing first-mode waves, which can be written as

$$\begin{aligned} u = g_m(y_m)(A_{m}e^{-{\textrm{i}}Kx_{m}} + B_{m}e^{{\textrm{i}}Kx_{m}}) \quad m=1,\,2,\,3, \end{aligned}$$
(5)

where \(A_{m}\) and \(B_{m}\) are the complex amplitudes of incoming and outgoing wave, respectively, at port-m, \(K =\sqrt{k^2 - (\pi /h^\text {w})^{2}}\) is the reduced wavenumber, and

$$\begin{aligned} g_{m} = S_{m} \sin \big (\pi y_m/h^\text {w}\big ), \end{aligned}$$
(6)

in which the scaling factor \(S_m\) is selected such that

$$\begin{aligned} \int _{\varGamma _{m}}g_m g_m=1. \end{aligned}$$
(7)

We use a first-order absorbing boundary condition (Engquist and Majda 1977) to truncate the domain at \(\varGamma _m\). That is,

$$\begin{aligned} \frac{\partial u}{\partial n} + \textrm{i}K u = 2\textrm{i}K g_m A_m \quad \text {on}\,\varGamma _{m} \quad m=1,\,2,\,3. \end{aligned}$$
(8)

The variational form of governing equation (3) with boundary conditions (4) and (8) reads:

$$\begin{aligned}{} & {} \text {Find }u\in {\mathcal {U}},\text { such that}\nonumber \\{} & {} \quad \int _{\varOmega } \nabla u \cdot \nabla v - k^2 \int _{\varOmega } \Bigg (\epsilon _r - \textrm{i} \sqrt{\frac{\mu _0}{\epsilon _0}} \frac{\sigma }{k}\Bigg ) u v + \textrm{i} K \sum _{m=1}^{3}\int _{\varGamma _m} u v \nonumber \\{} & {} \quad = 2 \textrm{i} K \sum _{m=1}^{3}A_m \int _{\varGamma _m}g_m v, \quad \forall \,v\in {\mathcal {U}}. \end{aligned}$$
(9)

where \({\mathcal {U}}=\{v\in H^1(\varOmega ) \mid v = 0 \text {on} \varGamma _\text {PEC} \}\). Having solved the above problem, we compute the complex amplitude of the outgoing waves by using

$$\begin{aligned} B_m = \int _{\varGamma _m} g_m u - A_m, \quad m=1,\,2,\,3. \end{aligned}$$
(10)

3 The power balance and the scattering parameters

We obtain a power balance expression by choosing \(v = {\bar{u}}\) (complex conjugate of u) in Eq. (9), which yields

$$\begin{aligned}{} & {} \int _{\varOmega } \left| \nabla u\right| ^2 - k^2 \int _{\varOmega } \Bigg (\epsilon _r - \textrm{i} \sqrt{\frac{\mu _0}{\epsilon _0}} \frac{\sigma }{k}\Bigg ) \left| u\right| ^2 + \textrm{i} K\sum _{m=1}^{3}\int _{\varGamma _m} \left| u\right| ^2 \nonumber \\{} & {} \quad = 2 \textrm{i} K \sum _{m=1}^{3}A_m\int _{\varGamma _m}g_m {\bar{u}}. \end{aligned}$$
(11)

Taking the imaginary part of the above equation and dividing by K, we have

$$\begin{aligned} \frac{k}{K} \int _{\varOmega } \sqrt{\frac{\mu _0}{\epsilon _0}} \sigma \left| u\right| ^2 + \sum _{m=1}^{3}\int _{\varGamma _m} \Re \{u {\bar{u}} - 2 g_m A_m {\bar{u}} \} = 0. \end{aligned}$$
(12)

The local coordinate systems, as illustrated in Fig. 1 (d), are selected such that \(x_m=0\) on \(\varGamma _m \,\forall \, m\). Thus, by using expression (5), we find

$$\begin{aligned} \begin{aligned}&\text {Re}\{u {\bar{u}} \!-\! 2 g_m A_m {\bar{u}} \} = g_m g_m\,\text {Re}\big \{ (A_m \!+\! B_m) (\overline{A_m+B_m}) \\&\qquad - 2 A_m (\overline{A_m+B_m})\big \} \\&\quad = g_m g_m\,\text {Re}\big \{ A_m{\bar{A}}_m \! +\! B_m{\bar{B}}_m \!+\! {\bar{A}}_m B_m \\&\qquad +\! A_m {\bar{B}}_m \!-\! 2 A_m{\bar{A}}_m \!-\! 2 A_m {\bar{B}}_m\big \}\\&\quad = g_m g_m (\left| B_m\right| ^2 - \left| A_m\right| ^2). \end{aligned} \end{aligned}$$
(13)

Inserting the above expression into Eq. (12) and using that \(\int _{\varGamma _{m}} g_m g_m =1\) yields

$$\begin{aligned} \sum _{m=1}^{3} \left| A_m\right| ^2 = \sum _{m=1}^{3} \left| B_m\right| ^2 + \frac{k}{K} \int _{\varOmega } \sqrt{\frac{\mu _0}{\epsilon _0}} \sigma \left| u\right| ^2, \end{aligned}$$
(14)

where the last term represents the normalized ohmic losses. According to power balance (14), the power of the incoming waves is equal to the sum of the power of outgoing waves plus the ohmic losses.

Furthermore, it is common to use scattering parameters, \(S_\text {mn}\), to define reflection, cross-coupling, and transmission, where m denotes the port of outgoing waves and n denotes the port of incoming waves. The following expression relates the incoming and outgoing wave amplitude to the scattering parameters

$$\begin{aligned} \begin{bmatrix} S_\text {11} &{} S_\text {12} &{} S_\text {13} \\ S_\text {21} &{} S_\text {22} &{} S_\text {23} \\ S_\text {31} &{} S_\text {32} &{} S_\text {33} \\ \end{bmatrix} \begin{bmatrix} A_1 \\ A_2 \\ A_3 \end{bmatrix} = \begin{bmatrix} B_1 \\ B_2 \\ B_3 \end{bmatrix}. \end{aligned}$$
(15)

From power balance (14), we know that the power of an incoming and an outgoing wave is proportional to the square of complex amplitude. That is, we are interested in extremizing \(P_{mn}=\left| S_{mn}\right| ^2\). The following expression computes \(P_{mn}\) under the assumption that the device is only excited at port-n and that the other ports are matched

$$\begin{aligned} \begin{aligned} P_{mn} = \frac{\text {Output power at port}-m}{\text {Input power at port}-n} = \frac{\left| B_m\right| ^2}{\left| A_n\right| ^2}. \end{aligned} \end{aligned}$$
(16)

We want to place a good electric conductor within \(\varOmega ^\text {D}\), so that the three-port setup works as two independent two-port networks. In frequency band-1, we want port-1 to only communicate to port-2, such that

$$\begin{aligned} {\varvec{P}} = \begin{bmatrix} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} P_{33}\\ \end{bmatrix}. \end{aligned}$$
(17)

More precisely, if the incoming waves from port-1 belong to frequency band-1, they are transmitted to port-2, while the incoming waves from port-2 are transmitted to port-1 due to reciprocity.

Furthermore, in frequency band-2, we want port-1 to only communicate to port-3, such that

$$\begin{aligned} {\varvec{P}} = \begin{bmatrix} 0 &{} 0 &{} 1 \\ 0 &{} P_{22} &{} 0 \\ 1 &{} 0 &{} 0 \\ \end{bmatrix}. \end{aligned}$$
(18)

More precisely, if the incoming waves from port-1 belong to frequency band-2, they are transmitted to port-3, while the incoming waves from port-3 are transmitted to port-1 due to reciprocity. Henceforth, we refer to \({\varvec{P}}\) as the power matrix.

4 Discretization, design parameterization, and topology optimization

4.1 Finite element discretization

The finite element method is used to discretize the computational domain \(\varOmega\) into a uniform mesh of square elements. We use basis functions that are continuous and bi-quadratic on each element. These basis functions are denoted by \(\varphi _1,\,\varphi _2,\,\ldots ,\,\varphi _\text {N}\), where N is the number of nodes in the finite element approximation. The complex amplitude function u and the test function v are approximated by \(u^h\in V^h=\text {span}\{\varphi _1,\,\ldots ,\,\varphi _N\}\) and \(v^h\in V^h\), respectively. Further, we approximate the conductivity \(\sigma\) by an elementwise constant function \(\sigma ^h\). We define the \(N^\text {D}\times 1\) vector \(\varvec{\sigma }= \big [\sigma _1,\,\sigma _2,\,\ldots ,\sigma _{N^\text {D}}\big ]^T\) that holds the elementwise values of \(\sigma ^h\) in the design region, where \(N^\text {D}\) denotes the number of elements in \(\varOmega ^\text {D}\). Outside the design region, the conductivity is zero. The discretized version of problem (9) can be expressed in matrix form as

$$\begin{aligned} {\varvec{A}}(\varvec{\sigma }){\varvec{u}} = {\varvec{b}}, \end{aligned}$$
(19)

where the \(N\times 1\) vector \({\varvec{u}}=\big [u_1,\,u_2,\,\ldots ,\,u_N\big ]^T\). Moreover, the \(N\times N\) matrix \({\varvec{A}}\) and the \(N\times 1\) vector \({\varvec{b}}\) have entries

$$\begin{aligned} A_{ij}{} & {} = \int _{\varOmega } \nabla \varphi _i \cdot \nabla \varphi _j - k^2 \int _{\varOmega } \Bigg (\epsilon _r - \textrm{i} \sqrt{\frac{\mu _0}{\epsilon _0}} \frac{\sigma ^h}{k}\Bigg ) \varphi _i \varphi _j \nonumber \\{} & {} \quad +\textrm{i} K \sum _{m=1}^{3} \int _{\varGamma _m} \varphi _i \varphi _j \end{aligned}$$
(20)

and

$$\begin{aligned} b_i = 2\textrm{i} K \sum _{m=1}^{3} A_m \int _{\varGamma _m} \varphi _i \varphi _j g_{m}, \end{aligned}$$
(21)

respectively.

Similarly, Eq. (10) that computes \(B_m\) can be written in matrix form as

$$\begin{aligned} B_m = ({\varvec{c}}_m)^T {\varvec{u}} - A_m, \end{aligned}$$
(22)

where the \(N\times 1\) vector \({\varvec{c}}_m\) has entries

$$\begin{aligned} c_{m_{i}} =\int _{\varGamma _m} g_m \varphi _i. \end{aligned}$$
(23)

4.2 Modeling of a good electric conductor

Fig. 2
figure 2

Left column: For the disk-shaped electric conductor inside \(\varOmega ^\text {D}\), the electrical conductivity \(\sigma\) in the range \([10^{-6},10^{10}]\) is plotted in \(\mathrm {log_{10}}\)-scale against the sum of scattering parameters. Right column: For the triangle-shaped electric conductor inside \(\varOmega ^\text {D}\), the electrical conductivity \(\sigma\) in the range \([10^{-6},10^{10}]\) is plotted in \(\mathrm {log_{10}}\)-scale against the sum of scattering parameters

Full size image

We set the incoming amplitudes \(A_1 =1\) and \(A_2=A_3=0\). Using power balance (14) and the definition (16), we have

$$\begin{aligned} P_{11}+P_{21}+P_{31}+\text {Ohmic losses}=1. \end{aligned}$$
(24)

In the above expression, we have the power output at all the ports and the ohmic losses. We aim to design a lossless device via material-distribution-based topology optimization by placing either a metallic material or free space in each element in \(\varOmega ^\text {D}\) to achieve the multiplexing effect. To obtain a well-performing multiplexer, the device should possess negligible ohmic losses. The perfect electric conductor has \(\sigma =\infty\) and contributes zero ohmic losses. Using a very large value of \(\sigma\), we can model a perfect electric conductor and approximate a zero Dirichlet boundary condition on the metallic boundary inside \(\varOmega ^\text {D}\). However, choosing a very high conductivity value is neither beneficial nor practical. Good electrical conductors, such as silver and copper have finite conductivity of \(\sigma =6.3\times 10^7\,\mathrm {S/m}\) and \(\sigma =5.96\times 10^7\,\mathrm {S/m}\), respectively, at microwave frequencies. For interpolation of material in material-distribution-based topology optimization, we need to select values of conductivity for free space (\(\sigma _\text {min}\)) and good electric conductor (\(\sigma _\text {max}\)) to model the material distribution inside \(\varOmega ^\text {D}\). To find suitable values of \(\sigma _\text {max}\) and \(\sigma _\text {min}\), we conducted numerical tests with a disk and triangle-shaped electric conductor inside \(\varOmega ^\text {D}\), as shown in Fig. 2.

The reason for using different shapes is to experiment with structures that might contribute different amount of losses. The disk and the triangle are simple geometries that possess smooth boundaries and sharp corners, respectively. For both geometries, we vary the conductivity between two extreme values. The graphs in Fig. 2 show that for intermediate values of the conductivity, both geometries exhibit losses and that the amount of losses vary with frequency. That is, the ohmic losses are both frequency and geometry dependent. However, for both geometries, the ohmic losses are negligible for \(\sigma \le 10^{-4}\) and \(\sigma \ge 10^{5}\). This suggests that all the values of \(\sigma \le 10^{-4}\) and \(\sigma \ge 10^{5}\) can model free space and a good electric conductor, respectively, with negligible ohmic losses. Hence, we choose to simulate a good electric conductor using \(\sigma _\text {max}=10^{5}\) and free space using \(\sigma _\text {min}=10^{-4}\). Thus, for \(\sigma \le 10^{-4}\) and \(\sigma \ge 10^{5}\),

$$\begin{aligned} P_{11}+P_{21}+P_{31} \approx 1. \end{aligned}$$
(25)

We tightly choose this range for \(\sigma\) since values outside of it make the problem insensitive during the optimization. Furthermore, numerical tests reveal that the values outside of this range have a negligible impact on the device performance.

4.3 Design definition and filtering

We employ a non-linear filtering approach to relax the problem’s self-penalization issue and impose size control on the design. More precisely, we apply the fW-mean-based filtering framework (Wadbro and Hägg 2015), and harmonic mean-based filters (Svanberg and Svärd 2013) to approximate morphological operators (erode and dilate). Here, we use an extended domain, \(\varOmega ^\text {F}=\varOmega ^\text {D}\cup \varOmega ^\text {M}\cup \varOmega ^\text {W}\), illustrated in Fig. 3, to filter the design variables where \(\varOmega ^\text {M}\) is occupied by material and \(\varOmega ^\text {W}\) is occupied by free space. The material distribution inside \(\varOmega ^\text {F}\) is defined by \(N^\text {F}\times 1\) vector \(\varvec{\zeta }\) in which elements are sorted such that the elements in \(\varOmega ^\text {D}\) come first, the elements in \(\varOmega ^\text {M}\) comes second, and the elements in \(\varOmega ^\text {W}\) come last.

In the discrete setting, the harmonic erode and dilate operators act on \(\varvec{\zeta }\) and are defined as follows:

$$\mathbf{ \varepsilon _{{r,\beta }} (\zeta ) = \textit{f}_{{\varepsilon _{\beta } }}^{{ - 1}} \left[ {W_{r} \textit{f}_{{\mathcal{D}_{\beta } }} (\zeta )} \right]}$$
(26)

and

$$\mathbf{ \mathcal{D}_{{r,\beta }} \left( \zeta \right) = \textit{f}_{{\mathcal{D}_{\beta } }}^{{ - 1}} \left[ {W_{r} \textit{f}_{{\mathcal{D}_{\beta } }} (\zeta )} \right]}$$
(27)

where r is the filter radius, \(\beta > 0\) is a parameter that controls the non-linearity, \(f\varepsilon _{\beta }\) and \({f}_{{\mathcal{D}_{\beta } }}\) have entries

$$f_{{\varepsilon _{\beta } }} \left( \zeta \right) = \left( {\zeta _{i} + \beta } \right)^{{ - 1}} ,\,i = 1,\,2,\,...,\,N^{F}$$
(28)

and

$$f_{{\mathcal{D}_{\beta } }} \left( {\zeta _{i} } \right) = f_{{\varepsilon _{\beta } }} \left( {1 - \zeta _{i} } \right),\,i = 1,\,2,\,...,\,N^{F}$$
(29)

respectively, and \(N^\text {F} \times N^\text {F}\) weight matrix \({\varvec{W}}_r\) implicitly defines neighborhood of element i. More precisely, \({\varvec{W}}_r = {\varvec{D}}^{-1}{\varvec{G}}_r\). In \(N^\text {F} \times N^\text {F}\) matrix \({\varvec{G}}_r\), the entry \(g_{ij}=1\) if the distance between \(x_i\) (centroid of element i) and \(x_j\) (centroid of element j) is less than or equal to r, else \(g_{ij}=0\). In addition, the diagonal matrix \({\varvec{D}}= \text {diag}({\varvec{G}}_r{\varvec{1}}_{N^\text {F}})\), in which all the entries of \(N^\text {F}\times 1\) vector \({\varvec{1}}_{N^\text {F}}\) are equal to 1.

Note that the material distribution inside \(\varOmega ^\text {M}\) and \(\varOmega ^\text {W}\) remains fixed during optimization, while only the material distribution inside \(\varOmega ^\text {D}\) changes. We define a \(N^\text {D}\times 1\) design vector \(\varvec{\alpha }\) for material distribution in \(\varOmega ^\text {D}\). Moreover, we form a harmonic close operator by combining the erode and dilate operators in a series, providing us a size control of radius r on free space. The harmonic close operator, which acts on \(\varvec{\alpha }\), is defined as

$$\begin{aligned}{} & {} {\mathcal {C}}_{r,\beta }(\varvec{\alpha }) = \big [{\varvec{I}}_{N^\text {D}\times N^\text {D}} \quad {\varvec{0}}_{N^\text {D}\times (N^\text {W} + N^\text {M})} \big ]\nonumber \\{} & {} {\mathcal {E}}_{r,\beta }\Bigg ({\mathcal {D}}_{r,\beta }\bigg ( \big [\varvec{\alpha }^T\,{\varvec{0}}^{N^\text {M}}\, {\varvec{1}}^{N^\text {W}}\big ]^T\bigg )\Bigg ), \end{aligned}$$
(30)

where \({\varvec{I}}_{N^\text {D}\times N^\text {D}}\) is an identity matrix, \({\varvec{0}}_{N^\text {D}\times (N^\text {W} + N^\text {M})}\) is a matrix of all zeros, \({\varvec{0}}^{N^\text {M}}\) is a \(1 \times N^\text {M}\) vector of all zeros, \({\varvec{1}}^{N^\text {W}}\) is a \(1\times N^\text {W}\) vector of all ones, and \({\mathcal {C}}_{r,\beta }(\varvec{\alpha })\) provides a filtered version of the design vector \(\varvec{\alpha }\). The element values of conductivity have components

$$\begin{aligned} \sigma _E=10^{\,5-9\,{\mathcal {C}}_{r,\beta }(\varvec{\alpha })_E}, \end{aligned}$$
(31)

where \({\mathcal {C}}_{r,\beta }(\varvec{\alpha })_E=1\) corresponds to \(\sigma _E=10^{-4}\) (free space) and \({\mathcal {C}}_{r,\beta }(\varvec{\alpha })_E=0\) corresponds to \(\sigma _E=10^5\) (good electric conductor).

Fig. 3
figure 3

The filtering domain \(\varOmega ^\text {F}=\varOmega ^\text {D}\cup \varOmega ^\text {M}\cup \varOmega ^\text {W}\)

Full size image

4.4 Objective function

The aim of this study is to design a frequency dividing multiplexer with properties as discussed in Sect. 3. The essential requirement is that the three-port setup should work as two independent two-port networks. That is, in frequency band-1, we want maximal transmission between port-1 and port-2, and in frequency band-2, we want maximal transmission between port-1 and port-3. To this end, we investigate three objective function formulations. Each consecutive objective function includes more information obtained by adding additional terms from power balance expression (24).

In addition, to writing the objective functions in a form inspired by the power balance expression, we also write them in the exact form that we use in the numerical experiments. In the numerical experiments, we use the method of moving asymptotes (MMA) by Svanberg (1987) to solve the optimization problem. MMA provides multiple alternatives for solving an optimization problem, including standard minimization and least square problems. The reason that we provide the exact formulation of the optimization problem that enters the optimizer is that this may significantly affect the performance—both in terms of number of iterations required to find a minimizer, but also in terms of the performance for the optimized design. Henceforth, we denote the formulation we use in MMA as the “MMA formulation” of the optimization problem.

Finally, before stating our three objective functions, we remark that all of these objectives push the power matrix for the optimized design towards form (17) in frequency band-1 and form (18) in frequency band-2. This is further expanded in Remark 2 below.

4.4.1 First optimization problem

For the first objective function, we only optimize with information on transmission. More precisely, the objective is to maximize \(P_{21}\) for frequency band-1 and \(P_{31}\) for frequency band-2. Due to reciprocity, we also implicitly maximize \(P_{12}\) for frequency band-1 and \(P_{13}\) for frequency band-2. For the first study, we formulate the following objective function to be minimized:

$$\begin{aligned} J_1({\mathcal {C}}_{r,\beta }(\varvec{\alpha })){} & {} = \sum _{q=1}^{Q_1} \big (1-P_\text {21}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q)\big ) \nonumber \\{} & {} \quad + \sum _{q=Q_1+1}^{Q_1+Q_2} \big (1-P_\text {31}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q)\big ), \end{aligned}$$
(32)

where \(Q_1\) and \(Q_2\) denote the number of frequencies in frequency band-1 and frequency band-2, respectively.

Remark 1

The reason that we use \(1-P_{21}\) and \(1-P_{31}\) is that the ideal (maximum possible) value for these normalized powers is 1. So each term in the sums above is positive, which paves the way for a straightforward transition to the MMA formulation.

In each iteration of topology optimization, we take the following steps to determine power \(P_{m1}\) for each wavenumber

  1. 1.

    For filtered design vector \({\mathcal {C}}_{r,\beta }(\varvec{\alpha })\), wavenumber \(k_q\), and incoming wave amplitude \(A_1\), solve finite element problem (19) to compute \({\varvec{u}}\).

  2. 2.

    Compute the amplitude of outgoing waves \(B_m\) using Eq. (22).

  3. 3.

    Use expression (16) to compute power \(P_{m1}\), \(m=1,\,2,\,3\).

Here, we aim to minimize \(J_1\) and hence solve the following optimization problem

$$\begin{aligned} \min _{\varvec{\alpha }\in {\mathcal {A}}} J_1({\mathcal {C}}_{r,\beta }(\varvec{\alpha })), \end{aligned}$$
(33)

where \({\mathcal {A}}=\{\varvec{\alpha }\in {\mathbb {R}}^{N^\text {D}} \mid 0 \le \alpha _E \le 1 \, \forall \, E \}\) is the set of admissible designs.

Remark 2

An ideal design for the FDM with objective \(J_1\) has \(P_{21}=1\) in frequency band-1 and \(P_{31}=1\) in frequency band-2. For frequency band-1, \(P_{21}=1\) together with the power balance implies that \(P_{11}=P_{31}=0\), this together with reciprocity implies that \(P_{13}=0\) and \(P_{12}=1\), which (again by a power balance law) implies that \(P_{22}=P_{23}=0\), which by reciprocity implies that \(P_{32}=0\). An analogous argument yields that \(P_{31}=P_{13}=1\) and \(P_{11}=P_{21}=P_{12}=P_{32}=P_{33}=0\) in frequency band-2. Thus, an ideal design that perfectly minimizes \(J_1\) has a power matrix of form (17) in frequency band-1 and of form (18) in frequency band-2.

The standard minimization formulation in MMA is suitable for solving problem (33) where we minimize the difference to maximize \(P_{21}\) and \(P_{31}\). Hence, we do not use the quadratic term provided in the MMA formulation. To solve our optimization problem, we use the following MMA formulation

$$\begin{aligned} \begin{aligned} \min _{\varvec{\alpha },{\varvec{y}}} \quad&\sum _{i=1}^{Q} y_i\\ \text {subject to}\quad&h_i({\mathcal {C}}_{r,\beta }(\varvec{\alpha })) - y_i \le 0,{} & {} \quad i=1,\,\ldots ,\,Q, \\&\varvec{\alpha }\in {\mathcal {A}}, \,\, {\varvec{y}}\ge {\varvec{0}}, \end{aligned} \end{aligned}$$
(34)

where \(Q=Q_1+Q_2\) denotes total number of frequencies,

$$\begin{aligned} \begin{aligned} h_i({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))&= 1 - P_{21}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_i){} & {} i = 1,\,\ldots ,Q_1,\\ h_{i}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))&= 1 - P_{31}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_i){} & {} i = Q_1+1,\,\ldots ,Q, \end{aligned} \end{aligned}$$
(35)

and the \(Q\times 1\) vector \({\varvec{y}}\) represent artificial optimization variable that aids in the formulation of optimization problem. We provide a separate function \(h_i\) to the MMA algorithm for each wavenumber.

4.4.2 Second optimization problem

Only information on transmission is provided to the optimizer in \(J_1\). A possible aid to the objective function would be to provide information on cross-coupling or reflection, which is not present in \(J_1\). After optimizing with \(J_1\), we noticed that the values of cross-coupling are higher than that of reflection. Therefore, we include information on cross-coupling in the second objective function. More precisely, in addition to maximizing transmission, we minimize \(P_{31}\) for frequency band-1 and \(P_{21}\) for frequency band-2. This allows us to control another parameter while also providing the optimizer with additional sensitivities to minimize the cross-coupling. To do so, we formulate the following objective function

$$\begin{aligned} J_2 ({\mathcal {C}}_{r,\beta }(\varvec{\alpha })){} & {} = \sum _{q=1}^{Q_1} \bigg (P_{31}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q) \bigg ) \nonumber \\{} & {} \quad + \sum _{q=Q_1+1}^{Q_1+Q_2} \bigg (P_{21}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q)\bigg ). \end{aligned}$$
(36)

Similarly, due to reciprocity, we implicitly minimize \(P_{13}\) for frequency band-1 as well as \(P_{12}\) for frequency band-2. Hence, we solve the following optimization problem

$$\begin{aligned} \min _{\varvec{\alpha }\in {\mathcal {A}}} J_1({\mathcal {C}}_{r,\beta }(\varvec{\alpha })) + J_2({\mathcal {C}}_{r,\beta }(\varvec{\alpha })). \end{aligned}$$
(37)

To solve optimization problem (37), we obtain the MMA formulation shown below

$$\begin{aligned} \begin{aligned} \min _{\varvec{\alpha },{\varvec{y}}} \quad&\sum _{i=1}^{2Q} y_i\\ \text {subject to}\quad&h_i({\mathcal {C}}_{r,\beta }(\varvec{\alpha })) - y_i \le 0,{} & {} \quad i=1,\,\ldots ,\,2Q, \\&\varvec{\alpha }\in {\mathcal {A}}, \,\, {\varvec{y}}\ge {\varvec{0}}, \end{aligned} \end{aligned}$$
(38)

where the vector \({\varvec{y}}\) is \(2Q\times 1\), which is twice the size of problem formulation (34). Thus, for each wavenumber, we provide the MMA algorithm two \(h_i\), one for maximizing transmission and the other for minimizing cross-coupling. More precisely, we provide \(h_i\) as defined in Eq. (35) for \(i=1,\,\ldots ,\,Q\) and

$$\begin{aligned} \begin{aligned} h_{Q+i}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))&= P_{31}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_i){} & {} i = 1,\,\ldots ,Q_1, \\ h_{Q+i}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))&= P_{21}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_i){} & {} i = Q_1+1,\,\ldots ,\,Q. \end{aligned} \end{aligned}$$
(39)

4.4.3 Third optimization problem

According to Eq. (24), we can also add information about reflection to the objective function, which was not included in the second objective function. Therefore, in the third objective, we also provide information on reflection to the optimizer. More precisely, in addition to maximizing transmission and minimizing cross-coupling, we also minimize \(P_{11}\) for both the frequency bands. To do so, we define the following objective function

$$\begin{aligned} J_3 ({\mathcal {C}}_{r,\beta }(\varvec{\alpha })){} & {} = \sum _{q=1}^{Q_1} \bigg ( P_{11}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q) \bigg ) \nonumber \\{} & {} \quad + \sum _{q=Q_1+1}^{Q_1+Q_2} \bigg (P_{11}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q) \bigg ). \end{aligned}$$
(40)

Hence, we solve the following optimization problem

$$\begin{aligned} \min _{\varvec{\alpha }\in {\mathcal {A}}} J_1({\mathcal {C}}_{r,\beta }(\varvec{\alpha })) + J_2({\mathcal {C}}_{r,\beta }(\varvec{\alpha })) + J_3({\mathcal {C}}_{r,\beta }(\varvec{\alpha })). \end{aligned}$$
(41)

To solve the above optimization problem, we obtain the following MMA formulation

$$\begin{aligned} \begin{aligned} \min _{\varvec{\alpha },{\varvec{y}}} \quad&\sum _{i=1}^{3Q} y_i\\ \text {subject to}\quad&h_i({\mathcal {C}}_{r,\beta }(\varvec{\alpha })) - y_i \le 0,{} & {} \quad i=1,\,\ldots ,\,3Q, \\&\varvec{\alpha }\in {\mathcal {A}}, \,\, {\varvec{y}}\ge {\varvec{0}}, \end{aligned} \end{aligned}$$
(42)

where the vector \({\varvec{y}}\) is \(3Q\times 1\), which is three-times the size of the problem formulation (34). To solve optimization problem (42), we provide \(h_i\) as in Eq. (35) and Eq. (39) for \(i=1,\,\ldots ,\,2Q\), and

$$\begin{aligned} \begin{aligned} h_{2Q+i}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))&= P_{11}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_i){} & {} i = 1,\,\ldots ,Q_1,\\ h_{2Q+i}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))&= P_{11}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_i){} & {} i = Q_1+1,\,\ldots ,\,Q. \end{aligned} \end{aligned}$$
(43)

In this case, we provide the MMA algorithm three \(h_i\) for each wavenumber, first for maximizing transmission, second and third for minimizing cross-coupling and reflection, respectively.

4.4.4 On some relations between the objective functions

Also for the second and third objective, one can make the same argument as that in Remark 2. So, the ideal design for any of the objective functions in this section has a power matrix of form (17) in frequency band-1 and of form (18) in frequency band-2. The key in this argument for all objective functions is that \(P_{21}=1\) in frequency band-1 and \(P_{31}=1\) in frequency band-2. On the other hand, having \(P_{11}=0=P_{31}=0\) in frequency band-1 and \(P_{11}=0=P_{21}=0\) in frequency band-2 does not imply that the design is ideal—it is, for example, possible that all the incoming energy gets burned due to the ohmic losses.

Another, possibly interesting relation between the partial objectives can be found by rearranging power balance (24). It holds that

$$\begin{aligned} J_1=J_2+J_3+\sum _q \text {ohmic losses}. \end{aligned}$$
(44)

Thus, for lossless design the third objective function is a factor 2 times the first objective function. However, for design that exhibit losses, the partial objectives are not perfectly aligned.

4.5 Sensitivity analysis

This study aims to maximize or minimize \(P_{mn}\), which depends upon the complex amplitudes, \(A_m\) and \(B_m\), of the incoming and the outgoing waves, respectively, at \(\varGamma _m\). The values of \(A_m\) are fixed, therefore we can only influence \(B_m\) to optimize \(P_{mn}\). We employ the adjoint-based method for computing the gradient of \(B_m\) with respect to electrical conductivity, \(\sigma _E\).

Let \(\delta \sigma\) be a perturbation of the conductivity. The corresponding first-order perturbation of the outgoing complex amplitude \(B_m\) (22) is

$$\begin{aligned} \delta B_m = ({\varvec{c}}_m)^T \delta {\varvec{u}}, \end{aligned}$$
(45)

where \(\delta {\varvec{u}}\) is the first-order perturbation of \({\varvec{u}}\).

Similarly, since the system matrix \({\varvec{A}}\) is linear in \(\sigma\), the perturbed Eq. (19) yields

$$\begin{aligned} {\varvec{A}}\left( \delta \sigma \right) {\varvec{u}} + {\varvec{A}}\left( \sigma \right) \delta {\varvec{u}} = 0. \end{aligned}$$
(46)

We obtain the following expression by multiplying Eq. (46) by \(N\times 1\) vector \({\varvec{z}}_{m}\),

$$\begin{aligned} ({\varvec{z}}_m)^T {\varvec{A}}\left( \delta \sigma \right) {\varvec{u}} + ({\varvec{z}}_m)^T {\varvec{A}}\left( \sigma \right) \delta {\varvec{u}} = 0. \end{aligned}$$
(47)

Let \({\varvec{z}}_m\) be the solution to the adjoint equation given by

$$\begin{aligned} {\varvec{A}} \,{\varvec{z}}_m = {\varvec{c}}_m. \end{aligned}$$
(48)

Recall that \({\varvec{A}}\) is symmetric which implies that \(({\varvec{z}}_m)^T {\varvec{A}} = ({\varvec{c}}_m)^T\). Substituting this into Eq. (45) provides us

$$\begin{aligned} \delta B_m = ({\varvec{z}}_m)^T {\varvec{A}}(\sigma ) \,\delta {\varvec{u}} = - ({\varvec{z}}_m)^T {\varvec{A}}(\delta \sigma )\, {\varvec{u}}. \end{aligned}$$
(49)

From expression (49), we identify the derivative of \(B_m\) with respect to \(\sigma _E\)

$$\begin{aligned} \frac{\partial B_m}{\partial \sigma _E} = -({\varvec{z}}_{m})^T_E \, \Bigg (\textrm{i}k\sqrt{\frac{\mu _0}{\epsilon _0}} {\varvec{M}}_E \Bigg ) {\varvec{u}}_E, \end{aligned}$$
(50)

where \({\varvec{M}}_E\) is a mass matrix of element \(\varOmega _E\) in \(\varOmega ^\text {D}\) and has entries

$$\begin{aligned} m_{ij} = \int _{\varOmega _E} \varphi _i \varphi _j, \end{aligned}$$
(51)

\({\varvec{u}}_E\) and \(({\varvec{z}}_m)_E\) are sub-vectors of \({\varvec{u}}\) and \({\varvec{z}}_m\), respectively, which correspond to nodal values in element \(\varOmega _E\).

By differentiating Eq. (31) and using the chain rule, we obtain the gradient of \(B_m\) with respect to design variable \(\alpha _E\), as presented by Hägg and Wadbro Hägg and Wadbro (2017).

4.6 Continuation approach

Previous studies by Hassan et al (2014b, 2015) have shown that the problem of designing a metallic antenna to maximize transmission is self-penalized. Based on power matrices of form (17) and (18), we choose to maximize transmissions \(P_{21}\) for frequency band-1 and \(P_{31}\) for frequency band-2, respectively. Maximizing the transmission implicitly minimizes the ohmic losses, which makes the optimization problem self penalized. Thus, no explicit penalty is required to suppress the intermediate values of design variables. As stated earlier, to solve this issue, we employ a continuation approach for the filtering of the design variables. That is, we solve a sequence of optimization problems, each starting with the previously optimized solution as initial guess. At each continuation step, we decrease the non-linearity parameter \(\beta\) when the residual norm of the KKT (or the first-order optimality) condition is smaller than \(10^{-3}\). More specifically, we use \(\beta = 10^{2-\frac{n}{2}}\) where \(n=0,\,1,\,\ldots ,12\). As we decrease \(\beta\), the filter’s non-linearity increases. The blurring caused by the filtering implicitly imposes losses. The non-linearity of the filter increases with each successive step, which is associated with and negatively correlated to the amount of induced losses. Thus, in this case, the non-linearity of filter reduces blurring in the design in addition to providing size control and mesh-independent design.

5 Numerical results

We use a set of 11 frequencies in each band for the topology optimization of the three port setup. More precisely, in frequency band-1, we use the frequencies \(9.0,\,9.02,\,\ldots ,\,9.2\,\textrm{GHz}\), while in frequency band-2, we use the frequencies \(10.0,\,10.02,\,\ldots ,\,10.2\,\textrm{GHz}\). Using the definition of wavenumber k and angular frequency w, we compute \(k_q\) for each frequency in both bands. The design domain \(\varOmega ^\text {D}\) is discretized into \(320 \times 320\) elements. The wave propagation here is well resolved, with \(\lambda /\varDelta x\approx 106\) elements per wavelength at the lowest frequency \(9.0\,\textrm{GHz}\) and \(\lambda /\varDelta x\approx 94\) elements per wavelength at the highest frequency \(10.2\,\textrm{GHz}\), where \(\lambda\) is the wavelength and \(\varDelta x\) is the element size of finite element discretization. The mesh resolution in this case is determined by the desired design resolution in \(\varOmega ^\text {D}\) and not by the wave propagation.

For all experiments, the final optimized designs are evaluated using a real electric conductor copper with \(\sigma =5.96\times 10^7\mathrm {S/m}\) over the frequency range 8.8–10.4\(\,\textrm{GHz}\) with an increment of \(0.01\,\textrm{GHz}\). Recall that the first objective function measures the transmission for both the frequency bands. Therefore, we evaluate \(J_1\) to compare all the optimized designs. As a reference value, \(J_1=12.2225\) for the free space (empty cavity) initial design. That is, \({\mathcal {C}}_{r,\beta }(\varvec{\alpha })_E=1\), \(\forall \,E\) in \(\varOmega ^\text {D}\).

5.1 Maximizing transmission

Fig. 4
figure 4

The optimized design (left) along with the frequency response (right) for the first objective function

Full size image

For the first study, we employ our basic objective function \(J_1\) formulated in Eq. (32). This objective function maximizes the transmission \(P_{21}\) for frequency band-1 and \(P_{31}\) for frequency band-2. The optimized design and frequency response are shown in Fig. 4. Within frequency band-1, more than \(93.5\%\) of the power is transmitted to port-2, with an average transmission of more than \(95.1\%\). In addition, the reflection and the cross-coupling are less than \(3.2\%\) and \(4.4\%\), respectively, for all frequencies in the range 9.0\(-\)9.2\(\,\textrm{GHz}\). Similarly, within frequency band-2, more than \(92.5\%\) of the power is transmitted to port-3, with the average transmission to port-3 is more than \(93.9\%\). In addition, the reflection and the cross-coupling are less than \(0.7\%\) and \(7\%\), respectively, for all frequencies in the range 10.0\(-\)10.2\(\,\textrm{GHz}\). Furthermore, \(J_1=1.1987\) at the end of optimization implies that the transmission can further be improved by minimizing the cross-coupling and the reflection terms. At the completion of optimization, the element entries of filtered design vector \({\mathcal {C}}_{r,\beta }(\varvec{\alpha })\) are nearly binary. More precisely, we employ the measure of non-discreteness (\(\text {M}_{nd}\)) proposed by Sigmund (2007), which is

$$\begin{aligned} \text {M}_{nd}=400\,({\mathcal {C}}_{r,\beta }(\varvec{\alpha })^T\left( {\mathcal {C}}_{r,\beta }(\varvec{\alpha }) -1 \right) /N^\text {D}) \,\%. \end{aligned}$$
(52)

For this measure, \(\text {M}_{nd}=0\,\%\) means that the element values of the filtered design vector are binary (either 0 or 1), whereas \(\text {M}_{nd}=100\,\%\) means that the design is totally gray and all the element values are 0.5. \(\text {M}_{nd}=0.0213\,\%\) for the design presented in Fig. 4, which indicates that the optimized design is essentially lossless. Power balance states that sum of power is always equal to 1. Here, we verify that the design is essentially lossless by summing the outgoing powers \(P_{11}+P_{21}+P_{31}\). This holds for all the numerical results presented in this work.

5.2 Maximizing transmission and minimizing cross-coupling

Fig. 5
figure 5

The optimized design (left) along with the frequency response (right) for the second objective function

Full size image

As stated previously, the coupling values are higher than that of reflection in the first study. Therefore, in the second study, we maximize transmission as well as minimize cross-coupling by employing the second objective function defined in expression (37). The optimized design along with its frequency response is shown in Fig. 5. Within frequency band-1, more than \(93.7\%\) of the power is transmitted to port-2, with an average transmission of more than \(96.1\%\). Furthermore, the reflection and the cross-coupling is less than \(1.7\%\) and \(4.1\%\), respectively, for all frequencies in the range 9.0\(-\)9.2 \(\,\textrm{GHz}\). Similarly, within frequency band-2, more than \(94.4\%\) of the power is transmitted to port-3, with an average transmission of more than \(95.2\%\). Furthermore, the reflection and the cross-coupling are less than \(0.9\%\) and \(2.3\%\), respectively, for all frequencies in the range 10.0\(-\)10.2 \(\,\textrm{GHz}\). As compared to the first study, the transmission is higher and the cross-coupling is lower for both the frequency bands. In addition, the optimized design exhibits a value \(J_1=0.9583\), which indicates that the second objective function is better than the first objective function, and hence the design provides a better multiplexing effect. Furthermore, as shown in the frequency response (Fig. 5), the multiplexing effect extends well beyond the target frequency bands, with more than 90% of power transmission to port-2 for frequencies in the range 8.9\(-\)9.4 \(\,\textrm{GHz}\) and more than 88% of power transmission to port-3 for frequencies in the range 9.9\(-\)10.3 \(\,\textrm{GHz}\).

5.3 Maximizing transmission, minimizing cross-coupling, and minimizing reflection

Fig. 6
figure 6

The optimized design (left) along with the frequency response (right) for the third objective function

Full size image

Along with optimizing transmission and cross-coupling, the third objective function formulated in expression (41) also aims to minimize the reflection term \(P_{11}\) for both frequency bands. The optimized design along with its frequency response is shown in Fig. 6. The optimized design obtained from the second and third objective function are almost identical. Similarly, the frequency responses are quantitatively similar. In addition, \(J_1=0.9524\) for the third study. This is comparable to the second study, implying that adding the reflection term to the objective does not provide a significant benefit in this case. However, previous studies have shown that including the reflection information to the objective function can be beneficial in some cases (Hassan et al 2018).

5.4 Validation of results

Fig. 7
figure 7

Electric field distribution \(\text {Re}(u)\) is plotted: (a) at 9.0 \(\textrm{GHz}\) where the incoming waves from port-1 travel to port-2 and (b) at 10 \(\textrm{GHz}\) where the incoming waves from port-1 travels to port-3. Design validation: (c) Frequency response computed by our algorithm implemented using MATLAB compared to frequency response computed using COMSOL Multiphysics

Full size image

We use COMSOL Multiphysics to validate the results of our numerical experiments. For the validation, we select the final design from the second objective function depicted in Fig. 5. A MATLAB code that generates the coordinates was used to trace the boundaries of optimized design. Using these coordinates, the optimized design was created in COMSOL Multiphysics. We use triangular elements with a maximum side length of \(1\,\textrm{mm}\) for the discretization in COMSOL Multiphysics. The frequency response computed by our algorithm in MATLAB is compared to the frequency response computed in COMSOL Multiphysics. The two computations exhibit a perfect match over the simulated frequency band and thus validate our results, as shown in Fig. 7(c). In addition, we show in Fig. 7(a,b) the electric field distribution \(\text {Re}(u)\) at 9.0 and 10.0\(\,\textrm{GHz}\) to demonstrate the multiplexing effect of the optimized device.

5.5 Sensitivity to initial design

Fig. 8
figure 8

Left column: Objective function versus the number of iterations together with some snapshots showing the development of the design when using free space, circle-shaped, triangle-shaped initial designs. Right column: The performance of the corresponding final optimized designs, shown on the left

Full size image

For the designs presented in Figs. 4, 5, and 6, we initiate the optimization process with free space inside \(\varOmega ^\text {D}\), and the optimizer only places material close to the boundary walls, with no material in the center of \(\varOmega ^\text {D}\). Therefore, it is reasonable to investigate the optimization problem with different initial designs. To study this further, we perform two more numerical experiments with different initial distribution of material inside \(\varOmega ^\text {D}\). In the first experiment, we use a circle-shaped initial design, and in the second, we use a triangle-shaped, as illustrated in Fig. 8. We use both the second and third objective functions in these numerical experiments. However, the value of \(J_1\) is comparable for both the objective functions, which indicates that for this problem setup, adding information on reflection does not significantly improve the multiplexing effect. Therefore, in this section, we only present the results with the second objective function.

Figure 8 shows the optimization results using free space, circle-shaped and triangle-shaped initial designs. For the case with free space initial design, the optimization algorithm initially places gray material close to the boundaries of \(\varOmega ^\text {D}\) but not in the middle. Moreover, the final design we acquire has no material in the middle of \(\varOmega ^\text {D}\). For cases with circle-shaped and triangle-shaped initial designs, we obtain gray material close to the boundaries and the center of \(\varOmega ^\text {D}\). The material in the middle changes shape but does not disappear during the optimization process in both cases. This investigation highlights how the problem is affected by the initial design. Within frequency band-1, we obtain more than \(90\%\) transmission to port-2 for all three initial designs, with the circle-shaped initial design providing a flat response and nearly \(100\%\) transmission to port-2. Moreover, the difference between \(J_1=0.5370\) for circle-shaped initial design and \(J_1=1.5570\) for triangle-shaped initial design suggests that the former provides a much better multiplexing effect. However, for some frequencies in frequency band-2, the transmission to port-3 falls below \(90\%\) for circle-shaped and triangle-shaped initial designs.

6 Discussion

In section 4.4, we present three MMA formulations for our optimization problems, and explain how we increase the number of functions \(h_i\) for each objective function. We can, however, decrease the number of functions provided to the algorithm, which affects the design and its performance. We decreased the number of functions by using the same problem formulation as in (34), where instead of providing one \(h_i\) for each term to the algorithm, we just provide two, one for each frequency band. More precisely, for the first objective function, we use the following MMA formulation

$$\begin{aligned} \begin{aligned} \min _{\varvec{\alpha },{\varvec{y}}} \quad&y_1+y_2\\ \text {subject to}\quad&\underbrace{\sum _{q=1}^{Q_1}\bigg ( 1 - P_{21}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q) \bigg )}_{ h_1({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))} - y_1 \le 0, \\&\underbrace{\sum _{q=Q_1+1}^{Q_1+Q_2}\bigg ( 1 - P_{31}({\mathcal {C}}_{r,\beta }(\varvec{\alpha }),k_q) \bigg )}_{ h_2({\mathcal {C}}_{r,\beta }(\varvec{\alpha }))} - y_2 \le 0, \\&\varvec{\alpha }\in {\mathcal {A}}, \,\, {\varvec{y}}\ge {\varvec{0}}. \end{aligned} \end{aligned}$$
(53)

Similarly, we provide only two \(h_i\) for the second and third objective function as well. With only two \(h_i\) provided to the MMA, \(J_1=1.3952\), 1.0545, and 1.0235 for the first, second, and third objective function, respectively, with free space initial design. Providing information on cross-coupling and reflection also improves multiplexing in this case. Moreover, with the second objective function, \(J_1 = 7.9185\) and 3.0855 for the circle and triangle-shaped initial designs, respectively, by supplying only two \(h_i\) to the MMA. These designs are inferior compared to the designs presented in section 5. In short, we want to highlight two key points from these numerical experiments. First, the results suggest that in this case, providing more information (cross coupling and reflection terms, as well as their gradients) aids the optimizer in finding a better solution, resulting in an improved multiplexing effect. Second, providing information to the optimizer as separate functions—as is the standard practice for least squares problems, where specialized algorithms, such as Gauss–Newton and Levenberg–Marquardt, make use of this information—yields better performing optimized designs.

In all three objective functions, we use an explicit term to maximize the transmission because the minimization of the reflection and cross-coupling terms does not imply the maximization of the transmission term. This is due to ohmic losses, which can be seen in Eq. (24). According to the system power balance, a possible solution to minimize the reflection and the cross-coupling is to increase ohmic losses. As a result, in a wave propagation problem with losses, an explicit term is required to maximize transmission. Maximizing transmission makes the optimization problem self-penalized and the final designs are essentially black and white without using an explicit penalty. More precisely, the maximum measure of non-discreteness (\(\text {M}_{nd}\)) for all optimized designs in this paper is \(0.0223\,\%\). In a lossless case, however, we can implicitly maximize transmission by minimizing cross-coupling and reflection (Wadbro 2014; Bokhari et al 2021).

We experimented with numerous initial designs in this study, including square-shaped initial designs, various sizes of circles, and triangular forms. We also experimented with different values of gray material initial designs. The results show that many good designs are possible with various initial designs and there are multiple good local minima. Here, we present three initial designs to optimize our three-port setup, all of them provide different designs and produce a good multiplexing effect. However, we only achieve a flat response with nearly 100\(\%\) transmission in frequency band-1 for the circle-shaped initial design. This demonstrates that the initial design has an impact on the final optimized design, and we typically end up at a local minimum.

7 Conclusions

FDM plays a crucial role in data transmission for communication systems. Because of the complexity of the design task, the design of FDM devices is typically carried out manually by highly experienced engineers. To automate the design procedure, we present a topology optimization method relying on an accurate numerical solutions of the wave propagation. Using metals as design materials in topology optimization of electromgentic problems results in ohmic losses associated with intermediate designs. The ohmic losses and the multiport features of the FDM’s setup make the optimization problem sensitive to the formulation of the objective function and the solution strategy. The sole use of the maximization of power transmission, as an objective function, reveals a self-penalization of such formulation: the maximization of the transmitted power could be easily achieved by minimizing the ohmic losses in the design domain. The filtering method relaxes the self-penalization issue during the design process by controlling the ohmic losses which enables the optimization procedure to converge to satisfying solutions. The power balance of the setup, however, reveals that other factors can provide additional useful information which, when included in the objective function formulation, can result in better solutions. In other words, the system power (or energy) balance is essential to guide the formulation of objective function. Also, in designing metallic multiport electromagnetic devices, the design problem is likely to be formulated as a multiobjective optimization problem that combines various power (or energy) measures.