Finding globally optimal arrangements of multiple point loads in structural design using a single FEA

Abstract

Many structures around us are designed to carry point loads. Such structures are typically sensitive to load arrangements, including load locations, magnitudes, and directions; a slight change in these ingredients could significantly affect the structural response. Therefore, knowing the extremal load arrangements to achieve the best and worst structural performance holds great potential to maximize structural efficiency and avoid structural failure, respectively. Existing studies have attempted to optimize load conditions using iterative optimization algorithms. However, they cannot always guarantee to find the global optimum and may instead obtain the local optima. In this study, we propose a new method, the single FEA method, that can effectively and efficiently find the extremal load conditions of a given structure. The new method considers all possible arrangements of prescribed loads without needing to create and analyze the corresponding finite element models. This is achieved by utilizing a single finite element analysis (FEA) with multiple load cases, where each load case has a unit load applied at one of the candidate load locations. Using the proposed method, we can quickly obtain the extremal load arrangements of the structure to produce the best and worst stiffness performance. A variety of 2D and 3D examples are presented to demonstrate the effectiveness and wide applicability of the new method.

1 Introduction

In structural design, a point load represents an established load applied at a specific, concentrated point on a supporting structure. Many structures around us are designed to carry one or multiple point loads, such as bridges, buildings, and structural components. To examine the performance of such structures under different load conditions, engineers usually need to perform a series of structural analyses by modifying the arrangement of point loads on structures considering load locations, magnitudes, and directions (Li et al 2005; Lee and Martins 2012). If engineers wish to find the optimal arrangements of point loads so that the given structure can perform at its best, using the trial-and-error approach may be inefficient, and the results can be far from the optimum (Lee and Xie 2022).

It is worth pointing out that a slight change in the arrangements of point loads, including load locations, magnitudes, and directions, may significantly affect the structural response (Vollum and Fang 2014). Knowing the optimal arrangement of point loads thus can best utilize the given structure and avoid structural failure. Besides, the structure can exhibit the highest and lowest performance if the loads are arranged on the ‘sweet spots’ (Cross 1998) and ‘weak spots’ (Lahti et al 2020), respectively. However, finding such extremal (i.e., globally optimal) arrangements of point loads in a complex structure is very challenging.

Structural optimization is an effective strategy to automatically achieve specific objectives while satisfying certain constraints. Many optimization techniques have been developed with applied loads that change during the course of the optimization (Lee et al 2012; Alacoque et al 2021). However, these techniques aim to create lightweight and high-performance structures instead of improving the structural performance of given structures, with resulting designs assumed to be loaded with the predetermined condition. For example, optimal structural topologies can be designed based on multiple load cases to accommodate different load conditions (Zhou and Li 2006; Zhuang et al 2007). Some topology optimization techniques account for uncertain load conditions, where the load locations and directions can vary continuously throughout the optimization process (Dunning et al 2011; Zhao and Wang 2014).

There are a limited number of studies in the literature concerning load condition optimization in structural design. In fact, considering load conditions as design variables in the optimization formulation is against the conventional thinking of structural design, as the structure’s purpose may be changed. However, for structures that do not have a clearly defined function or ‘mode of operation’, the load conditions can be adjusted significantly. Recent studies show that treating load locations and directions as design variables in the optimization formulation is an effective strategy to enhance the performance of a structure. Alacoque and James (2022) have obtained improved 2D topology optimization results using a higher-order or super-Gaussian projection method. Lee and Xie (2022) have achieved significant improvement in the structural performance of a variety of complex 2D and 3D structures using the optimality criteria method. Although both methods can produce good results and meet the respective optimization criteria, they cannot guarantee to find the global optimum every time. Finding the globally optimal load conditions of complex structures is an exceptional challenge and remains completely unexplored. Actually, obtaining the global optimum using optimization methods is an extremely difficult task in most structural design problems (Stolpe and Bendsøe 2011).

This paper presents a new method to effectively and efficiently find globally optimal arrangements of point loads to obtain the best and worst stiffness performance of a complex structure. The proposed method requires only a single finite element analysis (FEA) with a few load cases and without needing optimization algorithms. Hence, we can inexpensively find the global optimum and avoid testing a large number of possible finite element models. Section 2 describes the details of the new method. Section 3 demonstrates the implementation and verification of the new method. Section 4 uses a series of examples to explore the capabilities of the new method. Section 5 gives a technical discussion on the new method, followed by a conclusion in Sect. 6.

Fig. 1

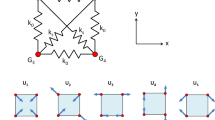
The procedure to obtain extremal load conditions of a given structure to achieve its worst and best stiffness performance using the proposed single FEA method. a Initial set-up with allowable load conditions considering load direction, quantity, sign, and magnitude. b Left: load cases of a single FEA performed based on the specification of allowable load direction and candidate load locations. Right: a list of all possible load conditions obtained based on the specification of prescribed loads. c Calculation method and exhaustive search results

Fig. 2

Demonstration of implementing the proposed single FEA method. A python script controls the FEA software (Abaqus) to solve multiple load cases, with the displacement results recorded in a single matrix. Next, we can utilize this matrix to calculate the mean compliance for many possible load conditions. If all possible load conditions are considered, we can use the maximum and minimum functions to find the extremal load conditions

Fig. 3

Detailed demonstration of the proposed single FEA method using one allowable load direction. a The initial set-up of the design problem, where prescribed loads are allowed only in the y direction. b Left: constructing the D matrix based on the single FEA with multiple load cases. Right: listing all possible load conditions F. c Calculation example using Condition 1. d Demonstration of the exhaustive search method to obtain the maximum and minimum mean compliance and the corresponding extremal load conditions

Fig. 4

Detailed demonstration of the proposed single FEA method using two allowable load directions. a The initial set-up of the design problem, where prescribed loads are allowed in x and y directions. b Left: constructing the D matrix based on the single FEA with multiple load cases. Right: listing all possible load conditions F. c Demonstration of the exhaustive search method to obtain the maximum and minimum mean compliance and the corresponding extremal load conditions

2 Finding optimal arrangements of point loads

2.1 Method overview

Inspired by the well-known virtual work method (or unit-load method) developed in 1717 by Johann Bernoulli (Oden and Reddy 2012), here we propose the ‘single FEA method’ that applies a positive unit load at each point of interest (i.e., candidate load location) in order to obtain the stiffness performance of a given structure carrying multiple point loads without testing all possible finite element models. Figure 1 shows the summary of the proposed single FEA method using a simple 2D tree example. Here, we are searching for the best and worst arrangements for two loads among four branch tips. It should be noted that the performance of a structure usually depends on its geometry, material properties, support conditions, and load conditions. The proposed method begins by prescribing the first three ingredients, with the load conditions remaining undetermined. As shown in Fig. 1a, we specify (i) the allowable load direction (e.g., y) and (ii) prescribed loads considering the load quantity, sign, and magnitude (e.g., $2 \times -F$).

• Task 1: Subsequently, a single FEA with multiple load cases is performed to obtain displacements about candidate load locations, where each load case is imparted with a positive unit load (i.e., $+1$) parallel to the direction specified in (i) at one of the candidate locations, as shown in Fig. 1b.

• Task 2: Meanwhile, the information specified in (ii) is sufficient to explicitly generate all possible load conditions using numerical descriptions, as shown in Fig. 1b.

• Task 3: Combining the displacement results of the single FEA (from Task 1) with each possible load condition (from Task 2) gives a list of values representing the stiffness performance of the structure under different load conditions.

• Task 4: Finally, we perform an ‘exhaustive search’ based on the calculated values to quickly find the extremal load conditions, as shown in Fig. 1c. Specifically, we use simple ‘maximum’ and ‘minimum’ functions to find the largest and smallest values of a list containing all values of compliance corresponding to different load conditions.

Note that the proposed method avoids performing all six possible FEA with different load conditions, as listed in Fig. 1b. The implementation of the proposed single FEA method is demonstrated more clearly in Fig. 2, with implementation details described later in Sect. 3.1.

2.2 Objective function

In structural design, stiffness is one of the key factors that must be taken into account. The mean compliance, C, the inverse measure of the overall stiffness of a structure, is commonly considered, where low and high C imply stiff and flexible structures, respectively. Many efficient structural designs in the literature are achieved by minimizing the mean compliance (Huang and Xie 2010; Stolpe and Bendsøe 2011; Lee and Xie 2022), with the following objective function typically used:

$$\begin{aligned} C = \frac{1}{2}{{\textbf {f}}}^{T}{{\textbf {u}}} \end{aligned},$$

(1)

where f and u are the global force vector and displacement vector, respectively. To ensure the equilibrium of the overall structural system, the relationship between f and u is as follows:

$$\begin{aligned} {\textbf {Ku}}={\textbf {f}} \end{aligned},$$

(2)

where K is the global stiffness matrix.

Instead of using global operation, the mean compliance can also be calculated based on the information about candidate load locations, requiring Eq. 1 to be simplified as follows:

$$\begin{aligned} C = \frac{1}{2}{{\textbf {u}}}^{T}{{\textbf {f}}} = \frac{1}{2}{{\textbf {U}}}^{T}{{\textbf {F}}} \end{aligned},$$

(3)

where U and F are the displacement vector and force vector about candidate load locations, respectively. The relationship between U and F is given below, derived based on Eq. 2, with details described in Sect. 2.5.1.

$$\begin{aligned} {{\textbf {U}}}^{T} = {{\textbf {F}}}^{T}{{\textbf {D}}} \end{aligned},$$

(4)

where D is a matrix combining the displacement results about candidate load locations based on the single FEA performed with multiple load cases.

Finally, substituting Eq. 4 into Eq. 3 gives

$$\begin{aligned} C = \frac{1}{2}{{\textbf {F}}}^{T}{{\textbf {D}}}{{\textbf {F}}} \end{aligned}.$$

(5)

Using Eq. 5, we can mathematically calculate the mean compliance of a given structure based purely on D and F, where D combines the results of the single FEA and F is the prescribed load condition defined by the user. Hence, we do not need to perform an FEA carrying F. That is to say, the mean compliance can be calculated without knowing the actual displacements about candidate locations U caused by F (see Eq. 3).

2.3 Single FEA with multiple load cases

In the proposed method, the number of load cases, M, required in the single FEA is

$$\begin{aligned} M = \rho N \end{aligned},$$

(6)

where $\rho$ is the number of allowable load directions, and N is the number of candidate load locations. Note that, in this study, the allowable load direction, V, considers only x, y, and z. If we allow one load direction (e.g., $V=y$), then $\rho =1$, so $M=N$ (see Fig. 1). If we allow two load directions (e.g., $V=x$ and z), then $\rho =2$, so $M=2N$ (see Fig. 8).

In each load case of the single FEA, a positive unit load parallel to V is applied at one of the candidate load locations. Next, we solve the FEA for all load cases and record the resultant displacements about all candidate locations in the ${\textbf {D}}$ matrix. If two load directions are considered, each load case records the displacements of both directions about all candidate load locations. In doing so, each load case generates M displacement data. Combining the displacement data of all (M) load cases gives the ${\textbf {D}}$ matrix required for Eq. 5, which has a size of $M \times M$. Details on constructing the ${\textbf {D}}$ matrix considering one and two allowable load directions are fully described in Sect. 2.5.2.

2.4 Possible load conditions

To calculate C using Eq. 5, the D matrix is first obtained by solving all load cases in the single FEA, then the user needs to specify a list of F (each F has a size of $M \times 1$), corresponding to different arrangements of point loads, as shown in Fig. 1b. The number of total possible arrangements of prescribed loads (i.e., the length of the list) can be obtained using Eqs. 7–9 based on the specified load quantity, sign, and magnitude.

If prescribed loads all have the same sign and magnitude (see Figs. 6 and 7), the number of total possible arrangements, $P_{\rm C}$, can be calculated using the following ‘combination’ equation:

$$\begin{aligned} P_{\rm C} = \frac{M!}{(M-k)!k!} \end{aligned},$$

(7)

where k is the quantity of prescribed loads (i.e., the number of point loads applied in the structural design).

If prescribed loads include multiple sets of repeating numbers (see Fig. 8), the number of total possible arrangements, $P_{\rm R}$, can be calculated using the following ‘permutation with repetition’ equation:

$$\begin{aligned} P_{\rm R} = \frac{M!}{x_1!x_2!...x_n!} \end{aligned},$$

(8)

where $x_n$ is the number of times a number is repeated in F.

If prescribed loads are different numbers (see Fig. 9), the number of total possible arrangements, $P_{\rm P}$, can be calculated using the following ‘permutation’ equation:

$$\begin{aligned} P_{\rm P} = \frac{M!}{(M-k)!} \end{aligned}.$$

(9)

Note that the number of total non-zero values in F is represented as k in Eqs. 7 and 9.

According to Eq. 5, the number of total possible arrangements of prescribed loads is equal to the number of total possible mean compliance results. It should be noted that $P_{\rm C}$, $P_{\rm R}$, and $P_{\rm P}$ can easily become very large numbers because of the M! term (see Eqs. 7–9). Due to this, it is extremely challenging and almost impossible to perform a large number of FEA based on all possible load arrangements. The proposed single FEA method offers a robust solution to quickly obtain all possible mean compliance values corresponding to different arrangements of prescribed loads. This allows us to perform an exhaustive search at a low computational cost based purely on a list of calculated C values. Hence, we can easily find the extremal load conditions (F) of the given structure, as shown in Fig. 1c.

2.5 Components of the proposed single FEA method

2.5.1 Derivation of local matrices

While performing the single FEA with multiple load cases, the global equilibrium equation (see Eq. 2) can be modified as follows:

$$\begin{aligned} {\textbf {Ku}}_j={\textbf {f}}_j \end{aligned},$$

(10)

where ${\textbf {f}}_j$ is a global force vector with a unit load applied at the j-th location, and $u_j$ is the corresponding displacement vector.

Here, we set the global force vector, f, equals to the summation of f multiplied by load factors $\lambda _j$:

$$\begin{aligned} {\textbf {f}}=\sum _{j} \lambda _j {\textbf {f}}_j \end{aligned}.$$

(11)

Combining Eq. 10 with Eq. 11 gives

$$\begin{aligned} {\textbf {f}}={\textbf {K}} \sum _{j} \lambda _j {\textbf {u}}_j \end{aligned}.$$

(12)

Subsequently, we substitute Eq. 2 in Eq. 12 to obtain the global displacement vector, u:

$$\begin{aligned} {\textbf {u}} = \sum _{j} \lambda _j {\textbf {u}}_j \end{aligned}.$$

(13)

Converting Eq. 13 into the vector form gives

$$\begin{aligned} {\textbf {u}}^T = \varvec{\lambda }^T {\textbf {d}} = {\textbf {f}}^T{\textbf {d}} \end{aligned},$$

(14)

where d contains the displacement results (${\textbf {u}}_j$) of the single FEA, which can be represented as ${\textbf {d}}^T=[{\textbf {u}}_1, {\textbf {u}}_2, {\textbf {u}}_3,..., {\textbf {u}}_N]$. Besides, $\varvec{\lambda }^T = [\lambda _1, \lambda _2, \lambda _3,..., \lambda _N]$, and $\lambda _j = {\textbf {f}}/{\textbf {f}}_j$, where ${\textbf {f}}_j$ contains a unit load, thus $\varvec{\lambda }^T = {\textbf {f}}^T$.

Finally, by selecting u, f, and d about candidate load locations in Eq. 14, we get ${{\textbf {U}}}^{T} = {{\textbf {F}}}^{T}{{\textbf {D}}}$, which is Eq. 4, containing only local matrices.

2.5.2 Construction of the local displacement matrix

After solving each load case of the single FEA, we record the displacements, $D^{m,j}_{V,i}$, of all candidate locations to construct D, where $D^{m,j}_{V,i}$ represents the displacement about the i-th candidate load location in direction V, with the unit load applied at the j-th location in the single FEA of Case m. This is demonstrated more clearly in Figs. 3 and 4, corresponding to one and two allowable load directions, respectively.

2.5.3 Matrix sizes

Equation 5 is the key equation of the proposed single FEA method, which includes four symbols (C, ${\textbf {F}}^T$, D, and F) representing one scalar and three matrices of different sizes. D is the collection of displacement results of the single FEA with M load cases. Hence, the size of D is $M \times M$, determined by the number of allowable load directions and locations (see Eq. 6). ${\textbf {F}}$ represents one possible arrangement of prescribed loads, which has M entries for loads specified at allowable load directions and locations, where 0 is used to represent disabled load directions and locations. ${\textbf {F}}^T$ is the transpose of F. The sizes of F and ${\textbf {F}}^T$ are $M \times 1$ and $1 \times M$, respectively. It should be noted that the values used in F can be altered, corresponding to a different load condition and resulting in a different C. Many combinations of F can be tested, which requires repeating the calculation of Eq. 5, leading to a list of calculated C. If all possible load conditions are considered, the list size of calculated C will be $P_{\rm C}$, $P_{\rm R}$, or $P_{\rm P}$ depending on the specified load quantity, sign and magnitude, as described in Sect. 2.4.

2.5.4 Detailed demonstrations

Two detailed demonstrations of the proposed single FEA method are given in Figs. 3 and 4 using the simple 2D tree. Here, we are searching for the extremal arrangements of two vertical loads among four branch tips to obtain the worst and best stiffness performance of the structure. The overall size of the tree is 1,406 mm tall and 930 mm wide. All branches have a width of 30 mm. The entire structure is discretized with triangular shell elements (S3) that have a mesh size of 3 mm and a thickness of 1 mm. The material is assumed to be linearly elastic and isotropic, with Young’s modulus of 100 GPa and Poisson’s ratio of 0.3. A fixed boundary condition is assigned at the base of the trunk. Four candidate load locations are assigned at the tips of all branches, meaning $N = 4$. Prescribed loads are $-\,50$ N and $-\,100$ N, meaning $k = 2$. In Fig. 3, prescribed loads are allowed only in the y direction, meaning $\rho = 1$ and $M = 1\times N = 4$. Hence, $P_{\rm P} = 4!/(4-2)! = 12$. In Fig. 4, prescribed loads are allowed in x and y directions, meaning $\rho = 2$ and $M = 2\times N = 8$. Hence, $P_{\rm P} = 8!/(8-2)! = 56$.

Fig. 5

The computational workflow to implement and verify the proposed single FEA method

3 Numerical analysis

3.1 Method

A computational workflow for numerical analysis has been developed to verify the proposed single FEA method, as shown in Fig. 5. It requires the utilization of three software. First, we use the Rhino 7 Grasshopper software to generate computer-aided design (CAD) models and visualize the results. Second, the CAD models are imported into the commercial FEA software Abaqus 2018 to create finite element models and perform structural analysis. Note that the structural equilibrium stated in Eq. 2 is ensured by using the implicit static analysis method in Abaqus; we do not need to have access to or alter the global stiffness matrix K in the FEA codes. Last, we have written a Python 2.7 script to automatically modify the finite element models and calculate the results, controlled by the Spyder 3.3.3 software. All codes in this computational workflow are developed based on shell elements, enabling us to conveniently investigate 2D plane structures and 3D shell structures. Details of the proposed computational workflow are summarized as follows.

In preparation, CAD models are created as .sat files and then processed by Abaqus to generate finite element models. Here, the finite element models are assigned with candidate load locations, support conditions, material properties, and meshes, with the load conditions remaining undefined. We export the ‘half-finished’ finite element models as .inp files, which are the input files for Abaqus representing the finite element models in a text format.

To perform the proposed single FEA method, we first use the Spyder software to modify the given half-finished .inp file to automatically generate all required load cases (i.e., load conditions) based on the details described in Sect. 2.3, thereby completing a ‘proper’ .inp file. The modified .inp file is then analyzed by Abaqus to generate the displacement data about candidate load locations, resulting in the D matrix. At the same time, we use the Python iterator, ‘itertools’, to automatically generate a list of all possible F (see Sect. 2.4). Combining D and F gives C (see Eq. 5), enabling us to perform an exhaustive search to find the extremal load arrangements based on the rank of calculated C values. Finally, we use the Grasshopper software to better visualize the results in geometric descriptions, as the calculated results are only numerical representations.

It is worth pointing out that, using the proposed single FEA method, the calculated C caused by the selected F does not have a corresponding finite element model created yet. To this end, we use the selected F to complete the half-finished finite element model in order to perform structural analysis for verification. In theory (see Sect. 2.2), for the same structural system, the calculated C obtained from the proposed single FEA method should be exactly the same as the C generated from the finite element model, examined further below.

Fig. 6

Finding the arrangements of five vertical loads among 36 branch tips to achieve the extremal load conditions of a 2D potted plant, where there are 376,992 possible load arrangements. a From left to right: lowest stiffness, highest stiffness, and three manually selected results obtained using the single FEA method. b Verification results obtained using finite element models

3.2 Results and verifications

The proposed single FEA method is first tested using a 2D potted plant example, as shown in Fig. 6. Here, we are searching for the extremal arrangements of five vertical loads among 36 branch tips to obtain the worst and best stiffness performance of the structure. The overall size of the potted plant is 1,557 mm tall and 740 mm wide. It includes two tree-like structures with a uniform branch width designed to be 6 mm, and a pot that is 300 mm tall and 200 mm wide. The entire structure is discretized with triangular shell elements (S3) that have a mesh size of 4 mm and a thickness of 1 mm. The material is assumed to be linearly elastic and isotropic, with Young’s modulus of 100 GPa and Poisson’s ratio of 0.3. A fixed boundary condition is assigned at the base of the pot. Thirty-six candidate load locations are assigned at the tips of all branches, meaning $N = 36$. Prescribed loads are $5 \times (-100$) N, meaning $k = 5$, which are allowed only in the y direction, meaning $\rho = 1$. Hence, the number of load cases required in the single FEA is $M = 1\times N = 36$. Together, the number of total possible arrangements of prescribed loads is $P_{\rm C} = 36!/(31!5!) = 376,992$.

Figure 6a shows the results obtained from the proposed single FEA method. It can be seen that extremal results have the highest and lowest C, corresponding to the load locations with the lowest and highest stiffness, respectively. In fact, finding these globally optimal solutions using the trial-and-error approach is almost impossible, as there are 376,992 possible FEA to be analyzed. Hence, the proposed single FEA method is demonstrated to be highly efficient, as we only need to perform a single FEA with 36 load cases to obtain the global optimum. Note that this example is solved in less than two minutes on an ordinary personal computer. Using a fine mesh, the single FEA is completed in approximately one minute to construct D using multiple load case analysis; using the equivalent multiple step analysis to solve the same single FEA needs approximately seven minutes, discussed later in Sect. 5. The total computation time on generating all possible F, calculating the corresponding C, and finding the extremal results are completed in less than a minute. In the previous study (Lee and Xie 2022), solving a similar design problem using optimization algorithms requires approximately 30 min and 100 iterations (corresponding to 100 finite element analyses). Hence, the proposed single FEA method is confirmed to be relatively inexpensive in terms of computational cost.

The accuracy of the proposed single FEA method is confirmed using finite element models imparted with selected load conditions, as shown in Fig. 6b. We find that the calculated C values obtained from the proposed single FEA method are exactly the same as the C generated from the corresponding finite element models, where double precision numbers are used in both methods. Actually, this verification proves that both sides of Eq. 3 to calculate C are equal ($\frac{1}{2}{{\textbf {u}}}^{T}{{\textbf {f}}} = \frac{1}{2}{{\textbf {U}}}^{T}{{\textbf {F}}}$). In detail, the $\frac{1}{2}{{\textbf {u}}}^{T}{{\textbf {f}}}$ part is handled by the FEA software, where C is directly obtained as the summation of strain energy of all elements; the $\frac{1}{2}{{\textbf {U}}}^{T}{{\textbf {F}}}$ part considers candidate load locations only, where C is calculated using the proposed single FEA method. Together, this example confirms that by using the proposed single FEA method, we can automatically, quickly, inexpensively, and accurately find the extremal load conditions of a complex structure from many potential load arrangements.

Fig. 7

Finding the arrangements of five vertical loads among 37 candidate locations to achieve the extremal load conditions of a 3D structure possessing a doubly-curved roof, where there are 435,897 possible load arrangements. a The initial set-up of the design problem. b From left to right: lowest stiffness, highest stiffness, and three manually selected results obtained using the single FEA method

4 Test examples

In this section, we use a series of examples to explore the capabilities of the proposed single FEA method. Note that the material used in the following examples is the same as in the 2D potted plant example (see Sect. 3.2). Moreover, all results presented in this section have been verified using their corresponding finite element models.

Fig. 8

Results of finding the arrangements of six vertical loads among 10 candidate locations to achieve the extremal load conditions of a complex 2D frame with curved members, where there are 37,800 possible load arrangements. Note that prescribed loads include positive and negative repeated values. From top to bottom: the first two rows include two maximum and two minimum results, and the last row includes two manually selected results

4.1 3D applications

Figure 7 investigates the potential practical applications of the proposed single FEA method using a complex 3D example. This example represents a prototype of a pavilion design, which includes a doubly-curved roof, a flat base, and three hollow columns, resulting in a continuous piece of geometry created using the surface bridging technique, demonstrated more clearly in Fig. 7a. Here, we are searching for the extremal arrangements of five vertical loads among 37 candidate locations to obtain the worst and best stiffness performance of the structure. The design problem can be understood in a different way, that is, finding the most dangerous and safest standing locations on the curved roof carrying five people of the same weight simultaneously.

In detail, the bounding dimensions of the 3D structure are approximately 500 mm × 500 mm × 259 mm, corresponding to width × length × height, respectively. The structure is discretized with quadrangle shell elements (S4R) that have a mesh size of 5 mm and a thickness of 1 mm. A fixed boundary condition is assigned behind the whole base surface. Thirty-seven candidate load locations are assigned on the rooftop, meaning $N=37$. Prescribed loads are $5 \times (-100)$ N, meaning $k=5$, which are allowed only in the z direction, meaning $\rho = 1$. Hence, the number of load cases required in the single FEA is $M = 1\times N = 37$. Together, the number of total possible arrangements of prescribed loads is $P_{\rm C} = 37!/(32!5!) = 435,897$.

Figure 7b shows the calculation results of the 3D structure. It is reasonable to observe that the five load locations to achieve the maximum C are gathered around the roof edge, corresponding to the most dangerous standing locations. On the other hand, in order to achieve the minimum C, it can be seen that three loads on the rooftop should be arranged around the shortest column, and the remaining two loads should be arranged on the ‘mountain’ region of the rooftop between the two long columns, corresponding to the safest five standing locations. Interestingly, as shown in Fig. 7b, changing the arrangement of load locations can significantly affect the stiffness performance of the structure, where there are 435,897 possible arrangements. However, we only need to perform a single FEA with 37 load cases without testing all possible FEA. Hence, the present results clearly demonstrate that the proposed single FEA method can be effectively adopted for 3D practical applications to obtain their extremal load conditions. Although we here use a small-scale prototype to look at the structural design problem, the proposed single FEA method can be readily used on any scale. Besides, the proposed single FEA method could work for multi-material structures, commonly seen in real structural designs, without any modification because we do not need to deal with the global stiffness matrix ${\textbf {K}}$ that controls the material properties.

Fig. 9

Finding the arrangements of five loads among five candidate locations to achieve the extremal load conditions of a 3D curved ladder, where there are 30,240 possible load arrangements. Note that prescribed loads are of different magnitudes and are allowed in two load directions. a The initial set-up of the design problem. b Results of the single FEA method. c Simplified visualization of the results

4.2 Multiple load signs and magnitudes

In previous examples (see Figs. 6 and 7), the structures are designed to carry identical loads. However, some structures may instead carry loads with different signs and magnitudes, making the extremal load conditions more difficult to predict. Figure 8 explores the capability of the proposed single FEA method to handle such cases using a complex 2D frame example. Here, we are searching for the extremal arrangements of six vertical loads among ten candidate locations to obtain the worst and best stiffness performance of the structure, where prescribed loads include positive and negative repeated values. It should be noted that although the frame is symmetric, we still model the full frame instead of half of the structure due to the consideration of non-symmetric load conditions, corresponding to a bigger search space. The design parameters are detailed as follows.

The frame is designed to be 615 mm wide and 110 mm tall, with curved members that have maximum and minimum widths of 10 mm and 4 mm, respectively. The structure is discretized with triangular shell elements (S3) that have a mesh size of 2 mm and a thickness of 1 mm. Pinned and roller boundary conditions are assigned on the left and right bottom corners, respectively. A total of ten candidate load locations are assigned on the top and bottom edges, meaning $N=10$. Prescribed loads are 100 N, $-100$ N, $2 \times 50$ N, and $2 \times (-50)$ N. According to Eq. 8, $x_1 = 2$, $x_2 = 2$, and $x_3 = 4$, corresponding to the number of times 50 N, $-50$ N, and 0 N repeated in ${\textbf {F}}$, respectively. The loads are allowed only in the y direction, meaning $\rho = 1$. Hence, the number of load cases required in the single FEA is $M = 1\times N = 10$. Together, the number of total possible arrangements of prescribed loads is $P_{\rm R} = 10!/(2!2!4!) = 37,800$.

Figure 8 shows the calculation results of the frame example. It can be seen that there are two maximum and two minimum solutions. However, it is not surprising to obtain multiple global optimums due to the use of symmetric geometry and the prescribed loads being symmetric number sets possessing different signs (i.e., (50, 50, 100, 50, 50) and $(-50, -50, -100, -50, -50)$). In order to generate the maximum C, the loads are arranged similarly to twisting the frame around its center, meaning loads of identical signs are gathered on the same side. It should be noted that the two maximum solutions are generated due to opposite twisting directions, where the sign can be changed, but the load locations and magnitudes are unchanged. Separately, to achieve the minimum C, the largest loads should be arranged at the middle locations, with the small loads arranged at their neighboring locations. The load signs can change completely, leading to the two minimum solutions corresponding to stretching and compressing the frame with the same load magnitudes, respectively. Besides, non-symmetric load arrangements may occur in real applications, and our method can conveniently calculate the corresponding compliance values. Together, this example confirms that the proposed single FEA method can effectively obtain extremal load conditions with loads of different signs and magnitudes. More significantly, this example clearly shows that multiple global optimums may occur, and our method is capable of finding all of them from many possible solutions at a low computational cost.

4.3 Multiple allowable load directions

As mentioned in Sect. 2.3, the proposed single FEA method can consider multiple load directions, demonstrated using a prototype of a 3D curved ladder design (see Fig. 9). Here, we are searching for the extremal arrangements of five loads among five candidate locations to obtain the worst and best stiffness performance of the structure, where we allow prescribed loads of different magnitudes in two load directions. The design parameters of the ladder are given as follows.

The bounding dimensions of the ladder are approximately 299 mm × 161 mm × 405 mm, corresponding to x × y × z, respectively. The ladder is curved and tapered, with members possessing an approximately 15 mm wide and 10 mm deep ‘C’ profile, as highlighted in Fig. 9a. The structure is discretized with quadrangle shell elements (S4R) that have a mesh size of 2 mm and a thickness of 1 mm. Pinned boundary conditions are assigned on four end edges. Five candidate load locations are assigned on midpoints of intermediate members, meaning $N=5$. Prescribed loads are $-100$ N, $-80$ N, $-60$ N, $-40$ N, and $-20$ N, meaning $k=5$. They are allowed in x and z directions, meaning $\rho = 2$. Hence, the number of load cases required in the single FEA is $M = 2\times N = 10$. Together, the number of total possible arrangements of prescribed loads is $P_{\rm P} = 10!/5! = 30,240$.

Figure 9b shows the calculation results of the 3D ladder. It can be seen that some load locations may carry two loads in different directions. Although there are five candidate load locations and five prescribed loads, it is not necessary to impart loads at all candidate locations, as each load location can carry up to two loads of different directions due to the specification of $\rho =2$. In order to achieve the maximum C, prescribed loads are seen to be gathered on the top part of the ladder, where the remaining candidate locations are not carrying any loads. On the other hand, to achieve the minimum C, it is reasonable to observe that loads are arranged around both support regions, with most loads gathered on the bottom part (stronger part) of the ladder.

It is worth pointing out that the proposed single FEA method does not aim to optimize the load directions. Optimization of load directions in structural design has been developed previously by the authors (Lee and Xie 2022). In this example, it can be understood that we are finding the extremal arrangements of prescribed ‘force components’. Suppose one load location is imparted with two force components. In that case, the force components must be in different directions, which can be combined into an inclined load not aligning with the allowable directions, as shown in Fig. 9c. Moreover, it can be seen that the stiffness performance is highly sensitive to the load locations and directions, as shown in the significant change in compliance. Together, this example clearly shows that allowing multiple load directions in the proposed single FEA method offers new opportunities to significantly improve specific design objectives (e.g., compliance maximization and minimization) based on the arrangements of prescribed force components.

5 Discussion

The proposed single FEA method is demonstrated to successfully find extremal load arrangements on various examples. It is worth pointing out that the proposed method is considered efficient if the possible loaded degrees of freedom are significantly fewer than the total degrees of freedom of the FE model. In detail, the possible loaded degrees of freedom are equal to M, determined by the number of allowable load directions, $\rho$, and locations, N (see Eq. 6); it makes the size of the ${\textbf {D}}$ matrix to be $M \times M$. The total degrees of freedom of the FE model are controlled by $\rho$ and the number of nodes used in the whole model (n), represented as $\rho \times n$. The proposed single FEA method is highly efficient when $\rho \times N$ is much smaller than $\rho \times n$; it becomes inefficient when $N \approx n$. If $N=n$, the number of load cases required in the single FEA is $\rho \times n$, meaning multiple load cases are created by applying a positive unit load at every node of the FE model in allowable directions. Thus, not suitable for complex structural designs that must be modeled using a large number of fine meshes (corresponding to many nodes), potentially causing a high computational cost to solve all load cases, and possibly leading to a brute-force search to find the extremal load arrangements.

The success of the proposed single FEA method also relies on the multiple load case analysis used in the FEA software. In this study, all examples are linear static. We use a direct solver considering factorization of the stiffness matrix in the Abaqus software to solve multiple load cases of the single FEA. Typically, a non-zero scale factor is used in the solver to scale the structural responses linearly to represent the actual load condition, controlled by scaling the values in the global stiffness matrix. Here, we assign the scale factor to be 1, meaning the unit loads used in all load cases has a magnitude of 1 N in the positive allowable directions. The actual load condition is considered later using the ${\textbf {F}}$ matrix. It should be noted that the global stiffness matrix factorization consumes the majority of the total computation time of the FEA. However, it is done only once, as the stiffness matrix is exactly the same for all load cases. Therefore, a multiple load case analysis is generally much more efficient than the equivalent multiple step analysis. For example, solving one load case of the simple tree example shown in Fig. 1b requires approximately 15 s; the computation time to solve four load cases using multiple step analysis is approximately 60 s, and using multiple load case analysis needs approximately 18 s only.

Finally, as the proposed single FEA method has a low computational cost nature, it could potentially be combined with topology optimization techniques to inexpensively create efficient structures while searching for extremal load arrangements. This is feasible because we can perform the proposed single FEA method to find the ‘best’ load condition of the current structural topology and use the obtained load condition in the next iteration to create a new structural topology. Repeating this process can iteratively generate optimal structural topologies and load conditions. Ultimately, the final structural topology can best meet user-defined objectives and constraints. Note that simultaneous optimization of the load conditions and structural topology has been developed previously by the authors (Lee and Xie 2022). Here, the proposed extension of the single FEA method comes from a different perspective, aiming to improve computational efficiency. However, it will face two technical challenges. First, as discussed in Sect. 4.2, multiple best load arrangements could occur in the current structural design, and selecting the ‘most appropriate’ one for the next iteration can be difficult, which may require subjective preferences. Second, the proposed single FEA method is only guaranteed to find the globally optimal load arrangements in the current design. Still, topology optimization techniques typically find the local optima, so this combination cannot ensure a global optimum.

6 Conclusions

This study has presented a new method, the single FEA method, to find the extremal load conditions of a given complex structure to achieve its worst and best stiffness performance. The new method is developed based on the objective function typically used in topology optimization and a single FEA of multiple load cases. We find that this combination can efficiently calculate the mean compliance (the inverse measure of stiffness) caused by specified load conditions without needing to create and analyze the corresponding finite element models. Due to this, we have successfully found the extremal load conditions of various structures at a low computational cost by avoiding testing a large number of possible finite element models. Specifically, we achieve this using the exhaustive search method based on the calculated mean compliance values; manual verifications have been carried out to confirm the calculation results.

Numerous exciting findings have been observed. First, it is found that the proposed single FEA method can be effectively and readily adopted for both 2D and 3D applications. Second, multiple globally optimal load conditions may occur, but we show that the proposed method is capable of finding all of them. Finally, we find by allowing multiple load directions in the proposed method, the stiffness performance of the structure becomes highly sensitive, corresponding to new opportunities to achieve significantly improved structural performance. We believe the techniques presented in this study will enable the development of a wide range of efficient structures and improve structural safety by avoiding dangerous load arrangements. Future research may extend the single FEA method to a new technique that treats load conditions as design variables to generate maximum or minimum displacements on selected points, or to consider other static or dynamic structural responses.