1 Introduction

The aim of this work is to extend existing feature-mapping methods, with a focus on the optimal design layout for continuous fiber-reinforced polymers (CFRP). We first give a brief overview about current approaches for continuous fiber design to motivate our feature-mapping approach.

Owing to their large stiffness to weight ratio, the past decades have seen a vast amount of works considering the optimization of composite materials. A first area of focus was the design of fiber directions within a fixed geometric configuration, such as beams or plates (see, e.g., (Nikbakt et al. 2018; Venkataraman and Haftka 1999) and the references therein). More recent composite manufacturing techniques have allowed for the steering of fiber paths, however introducing additional manufacturing constraints. The most significant from an optimal design perspective start with a prescribed minimum turning radius of the fibers, which is needed to prevent process-induced defects. Additionally, gaps and overlaps between fiber paths should be avoided, meaning that fiber paths should be close to parallel. Lastly, it is not possible to lay the fibers in a controlled manner if their length is shorter than a certain value called minimum cut length. For a comprehensive review on modeling and design considerations for fiber-steered composite laminates, see (Aragh et al. 2021) and the references therein.

Within the framework of layout optimization for composite structures with curved fiber paths, one major approach has been the so-called continuous fiber angle optimization (CFAO), in which the fiber orientations are continuous design variables that can vary throughout the structure. These field-based approaches may be seen as a direct extension of the greatly successful density-based topology optimization (see Bendsøe and Sigmund 2003) for anisotropic element densities with local optimal material orientation. While these methods provide good results, they also lead to a couple of inherent difficulties. Firstly, due to the existence of local minima of the strain energy with respect to material orientation, angle optimization is rather susceptible to local optima, which is well analyzed in Stegmann and Lund (2005). Secondly, the angle formulation is \(2\pi\)-periodic, meaning that, e.g., both 0 and \(2\pi\) represent the same orientation. While this drawback is largely remedied by the formulation in Nomura et al. (2015) using Cartesian instead of polar coordinates and by Smith and Norato (2022) using quaternions, in linear elasticity the material parameters are still subject to a \(\pi\)-periodicity as well. A solution to this would be to formulate design filtering directly for the material tensor as done in Jantos et al. (2020) or averaging the material tensors as in Smith and Norato (2021, 2022). However, this has the disadvantage of requiring a recovery step in order to obtain a material orientation angle again. Lastly, it is quite challenging to implement manufacturing constraints in the CFAO framework, with a couple of works trying to tackle this issue. To restrict the maximum curvature, slope constraints as well as convolution filters can be used, as shown in Greifenstein and Stingl (2016). Nevertheless, CFAO results can be still quite far away from fiber printing paths, with a number of publications studying different post-processing techniques to obtain continuous fiber paths from orientation fields (see Papapetrou et al. 2020; Boddeti et al. 2020; Fedulov et al. 2021; Fernandes et al. 2021). Another notable method to introduce manufacturing constraints into CFAO is detailed in Tian et al. (2019), which uses angular constraints similar to slope constraints to mimic gap overlap and curvature constraints for tow-steered composite panels. Furthermore, Fernandez et al. (2019) suggest a formulation including manufacturing constraints for direct ink writing which is able to provide toolpaths, however without optimizing the topology.

The goal of this work will be to develop a formulation, which allows for a more direct consideration of manufacturing constraints than CFAO, while at the same time reducing the gap between optimization result and interpretation as fiber paths. Even though we will not go all the way to a manufacturable structure yet, the advances in this article can still be seen as an important intermediate step in this direction. The basic idea of this work is the optimization of a set of parallel fiber bundles with a prescribed maximum curvature. For the numerical evaluation, these sets of parallel fiber bundles will be mapped to a pseudo-density field, leading to the class of feature-mapping methods.

Feature-mapping methods share the elegance of optimizing explicitly parametrized objects (typically primitives like circles and bars), thus allowing for close control on the designs. On the other hand, mapping the features to a fixed pseudo-density discretized on a fixed grid allows to benefit from sensitivity analysis as known in density-based topology optimization and helps avoid/handle issues like remeshing and topological changes arising in classical shape optimization. The mapping is performed by integrating for each finite element the signed distance function to the boundary of the geometrical object subject to a nonlinear boundary function. This requires the exact distance (and its sensitivity) for each integration point. Not all geometrical models take care for a strict differentiability of the distance function. This sketched hybrid approach of analytical objects with late discretization has been presented in recent years by several authors with individual terminology, we refer to the review article (Wein et al. 2020). In density-based topology optimization, a specific approach needs decisions in kind and parametrization of regularization, penalization, and used optimization solver. Similarly, a specific feature-mapping optimization needs decisions on the determination of the signed distance field, shape boundary smoothing, combination of features, numerical integration, and elimination of superfluous design elements. Our contribution is focused on the signed distance field and combination of features issues. For the other topics, we apply default variants but refer to more sophisticated solutions, e.g., with respect to object elimination.

A formulation of a feature-mapping method has already been successfully applied for the optimization of fiber-reinforced composites in Smith and Norato (2021). There, in contrast to our work, the fibers are modeled by a set of individual straight bars, while we will model long, curved fiber objects. This will also give us control of the fiber length following the curved path. We note, however, that an accurate representation of minimum cut length constraints would further require the rounded shapes to stay entirely within the domain, which can be achieved using constraints as suggested in Zhang et al. (2018).

In principle, splines, B-splines, and Bézier curves (we summarize them as splines here) are a very natural class of objects to be applied for feature-mapping, starting with Garcia and Gonzalez (2004) (but there without sensitivities). However, they generally suffer from an expensive evaluation of a finely resolved signed distance field, as no closed analytical distance formula exists for general splines and Bézier curves. In Zhu et al. (2021), Bézier curves are used in a feature-mapping approach, but the distance needs to be computed by an iterative search for every point in space. In Guo et al. (2016), curved analytical geometries are mapped with X-FEM (among other geometries); however, no closed distance function can be given either. In order to obtain an efficient and differentiable signed distance field, we choose similar to Wein and Stingl (2018) a first-order (piecewise linear) spline where the closest distance from arbitrary points within the whole spacial domain is trivial to obtain. To still generate a sufficiently smooth curvature, in the mentioned paper, the first-order spline is parametrized using a large number of design parameters. In the present approach, we use a small number of parameters, but insert arcs in between the straight linear objects to smooth the design objects. This allows us to obtain full differentiability of the signed distance field while keeping the numerical efficiency provided by the linear spline formulation. As a side effect, we gain control on the minimum turning radius of the fibers demanded from manufacturing.

We chose to term our parametrized design objects spaghetti (spaghetto for singular). Alternative formulations like feature, design object, or spline object appear in our context rather unspecific and generic. Furthermore, we find the association suitable of long, slim flexible objects which can be aligned and possibly stick against each other.

In Sec. 2, we present the modified spline model and derive the corresponding derivatives in Sec. 3. In Sec. 4, we apply a standard feature-mapping interface smoothing. Thereafter, we state both a classical isotropic and an adapted anisotropic material formulation in Sec. 5. For the combination of multiple spaghetti, we restate in Sec. 6 classical combination techniques for the isotropic material formulation and propose a novel approach for the combination of oriented anisotropic material. The proposed geometry is described by continuous, mesh-independent functions until here and we derive the associated mapping to a fixed grid in Sec. 7. Finally we present the compliance problem formulation in Sec. 8 and a numerical benchmark example in Sec. 9.

The full source code of the presented approach is publicly available as part of the academic finite element simulation and optimization package openCFS.

2 Curved feature construction

In this section, we describe the construction of the curved feature from a first-order spline. We start out by defining a straight line between two design points P and Q in \(\mathbb {R}^2\). In order to get more design flexibility of a single feature, we split the line into \(m\in \mathbb {N}\) equidistant sections. For these sections, we then define additional design parameters \(a^i\in \mathbb {R},\,i=1,\ldots ,m-1\) representing a vertical deflection from the straight line \(\overline{PQ}\) and obtain a piecewise linear spline. For the purpose of differentiability and to obtain a smoother design appearance, we round out the corners between sections using circular arcs. The arcs have a fixed prescribed radius r and are fitted to match the tangents of the piecewise linear line feature. Finally, for a profile width parameter \(p\in \mathbb {R}\), the smoothed piecewise line will be dilated by p/2 in all directions from the center line, resulting in rounded ends. This means also that we have half circles at the ends, in order to obtain a fully differentiable signed distance field. Although this issue is neglected in many publications, it is addressed in similar fashion by Norato et al. (2015) and other authors. As we will see in the following, this construction will allow for an efficient distance evaluation to the spaghetti. An illustration of the construction idea is shown in Fig. 1.

Fig. 1
figure 1

Illustration of a single spaghetto

Full size image

For the more technical construction of the exact shape, we define a number of quantities derived from the design parameters \(P,Q,a^i,i=1,\ldots ,m-1\) and p, which are also depicted in Fig. 1, with their definitions detailed within the next paragraphs. Furthermore, in order to check which points are part of the dilated spaghetto and to obtain design gradients, we will need to derive a formula for the distance from the center line.

To this end, we start by introducing a local coordinate system \(\varvec{u_0},\varvec{u_0^\bot }\) in longitudinal and vertical directions of the shape:

$$\begin{aligned}&\varvec{u}:=Q-P=\begin{pmatrix} Q_x-P_x \\ Q_y-P_y \end{pmatrix}, \qquad \varvec{u_0} := \frac{1}{\Vert \varvec{u}\Vert }\varvec{u},\\&\varvec{u_0^\bot } := \frac{1}{\Vert \varvec{u}\Vert }\begin{pmatrix} P_y-Q_y \\ Q_x-P_x \end{pmatrix} \end{aligned}$$

With this, the summit points \(H^i,i=1,\ldots ,m-1\) can be written as

$$\begin{aligned} H^i = P + \frac{i}{m}\varvec{u}+a^i\varvec{u_0^\bot }. \end{aligned}$$

Note that, letting \(a^0=a^m:=0\), this formula also yields \(H^0=P\) and \(H^m=Q\).

Further, we define the normalized vectors \(\varvec{t}^i,i=1,\ldots m\) in tangential direction of the straight shape segments

$$\begin{aligned} \varvec{t}^i:=&\frac{1}{\Vert H^i-H^{i-1}\Vert }(H^i-H^{i-1})\\ =&\frac{\frac{1}{m}\varvec{u}+(a^{i}-a^{i-1})\varvec{u_0^\bot }}{\Vert \frac{1}{m}\varvec{u}+(a^{i}-a^{i-1})\varvec{u_0^\bot }\Vert }. \end{aligned}$$
Fig. 2
figure 2

Computation of \(C^i\)

Full size image

For the computation of the center points of the circular sections \(C^i\), we first calculate the distance from \(H^i\) to \(C^i\) by calculating the angle \(\alpha ^i\) in the triangle marked in light blue in Fig. 2:

$$\begin{aligned} \alpha ^i=\frac{1}{2}\arccos \left( \varvec{-t^i}\cdot \varvec{t}^{i+1}\right) ,\quad i=1,\ldots ,m-1 \end{aligned}$$

where \(\cdot\) denotes the scalar product. Using trigonometric identities in the same triangle, we get

$$\begin{aligned} \sin (\alpha ^i)=\frac{r}{\Vert C^i-H^i \Vert }. \end{aligned}$$

Lastly, we know that \(C^i\) lies on the bisecting line between \(\varvec{t}^i\) and \(\varvec{t}^{i+1}\). The vector \(\varvec{t}^{i+1}-\varvec{t}^i\) is showing in the direction we need, as long as \(\varvec{t}^{i+1}\ne \varvec{t}^i\). Thus, we obtain

$$\begin{aligned} C^i&=H^i+\Vert C^i-H^i \Vert \frac{\varvec{t}^{i+1}-\varvec{t}^i}{\Vert \varvec{t}^{i+1}-\varvec{t}^i\Vert }\\&=H^i+\frac{r}{\sin (\alpha ^i)} \frac{\varvec{t}^{i+1}-\varvec{t}^i}{\Vert \varvec{t}^{i+1}-\varvec{t}^i\Vert }. \end{aligned}$$

Even though \(C^i\) is not well defined for the case of \(\varvec{t}^{i+1}=\varvec{t}^i\), the spaghetto still is, as we have a straight line of segments and the arc vanished. Although for this case \(C^i\) makes a jump from one side of the spaghetto to the other when \(a^i\) changes sign, the distance function remains continuous. Using \(C^i\), for any point \({x}\in {\mathbb {R}}^2\) within the circular sector around \(C^i\) containing the arc segment of the spaghetto, i.e., for

$$\begin{aligned} ({x}-C^i)\cdot \varvec{t}^i< 0 \qquad \text { and }\qquad ({x}-C^i) \cdot \varvec{t}^{i+1}> 0, \end{aligned}$$

we can compute the distance to the center line of the spaghetto as

$$\begin{aligned} d({x}) = |\Vert {x}-C^i \Vert - r |. \end{aligned}$$

As with the previous definitions of \(E^i\) and \(H^i\), we extend the definition of \(C^i\) using

$$\begin{aligned} C^0:=P,\qquad C^m:=Q. \end{aligned}$$

Finally, the distance of a point x to the beginning and endpoint of the spaghetti is

$$\begin{aligned} d({x}) = \Vert {x} - P \Vert ,\qquad d({x}) = \Vert {x}-Q \Vert , \end{aligned}$$

respectively.

In order to compute the distance to the straight line segments, we first define the corresponding normal vectors to each segment as

$$\begin{aligned} \varvec{n^i}:=\begin{pmatrix} -t^i_y \\ t^i_x \end{pmatrix}. \end{aligned}$$

This allows us to easily compute the distance d from any point x to the line linking \(H^i\) and \(H^{i-1}\) as

$$\begin{aligned} d({x}) = |({x}-H^i)\cdot \varvec{n_i}|. \end{aligned}$$

However, \(H^i\) and \(H^{i-1}\) are not actually part of the spaghetto’s center line as can be seen in 1. This means this distance formula to a segment i only holds if the point x lies in between the lines perpendicular to \(\varvec{t}^i\) passing through \(C^{i-1}\) and \(C^i\), respectively. This condition can be expressed as

$$\begin{aligned} ({x}-C^i) \cdot \varvec{t}^i \le 0 \qquad \text { and } \qquad ({x}-C^{i-1}) \cdot \varvec{t}^i \ge 0. \end{aligned}$$

Putting things together, we get as formula for the distance of a point x to the center line of a spaghetto

$$\begin{aligned} d({x}) = \min \Bigg \{&\min _{ \begin{array}{c} i=1,\ldots ,m: \\ \scriptstyle ({x}-C^i) \cdot \varvec{t}^i \le 0 \\ \scriptstyle ({x}-C^{i-1}) \cdot \varvec{t}^i \ge 0 \end{array} } |( {x}-H^i) \cdot \varvec{n^i} |, \nonumber \\&\min _{ \begin{array}{c} i=1,\ldots ,m-1: \\ \scriptstyle ({x}-C^i)\cdot \varvec{t}^i< 0 \\ \scriptstyle ({x}-C^i) \cdot \varvec{t}^{i+1}> 0 \end{array} } |\Vert {x}-C^i \Vert - r |, \nonumber \\&\quad \Vert {x} - P \Vert , \Vert {x}-Q \Vert \Bigg \}. \end{aligned}$$
(1)

Finally, we need another constraint to ensure that the formulation given above cannot degenerate. While the maximum curvature of the center line is prescribed by the radius, it might happen that the control polygon oscillates so much that the straight line segments disappear and the arc elements overlap. Fig. 3 is an example, in which the first two straight segments basically disappear. For the limiting case, in which a straight segment i exactly vanishes (i.e., it has length 0), we know that the circles around the adjacent \(C^{i-1}\) and \(C^i\) touch the line \(\overline{H^{i-1}H^i}\) at the same point. Consequently, \((C^i-C^{i-1})\) is vertical to \((H^i-H^{i-1})\), i.e., \((C^i-C^{i-1})\cdot (H^i-H^{i-1})=0\). This can be seen quite nicely in Fig. 3. If the straight segment now has positive length, we can see that \((C^i-C^{i-1})\) tilts further in the direction of \((H^i-H^{i-1})\), i.e., the scalar product \((C^i-C^{i-1})\cdot (H^i-H^{i-1})\) becomes positive. Hence, we can set up a constraint for the non-degeneration as

$$\begin{aligned} (C^i-C^{i-1})\cdot (H^i-H^{i-1})\ge 0, \qquad i=1,\ldots ,m. \end{aligned}$$
Fig. 3
figure 3

Potential degeneration of the center line, when control points oscillate strongly and arcs start touching or even overlapping. The straight line segment disappears

Full size image

Note that as we defined \(C^0:=P\) and \(C^m:=Q\), the inequality may be written this exact same way for the first and last segment.

3 Differentiability and derivatives

The first goal is to differentiate the distance function w. r. t. the control variables of the spaghetti spline. In order to get there, we start with the derivatives of the different quantities appearing either directly or indirectly in the distance formula. Firstly, we have stated the primitive derivatives in Table 1, which will later be reused in the derivatives of the more complex quantities in order to keep them simpler.

Table 1 Derivatives of different quantities used in spaghetti definition
Full size table

In continuation, it is easily seen that

$$\begin{aligned} \Vert H^i-H^{i-1}\Vert =\sqrt{\frac{\Vert \varvec{u}\Vert ^2}{m^2}+(a^i-a^{i-1})}. \end{aligned}$$

Using these primitives, we can compute the derivatives of the more complex expressions. For the segment vectors \(t_i\) we have

$$\begin{aligned} \frac{\partial \varvec{t}^i}{\partial \,\cdot }=&\frac{\frac{1}{m}\frac{\partial \varvec{u}}{\partial \,\cdot }+(a^i-a^{i-1})\frac{\partial \varvec{u_0}^\bot }{\partial \,\cdot } }{\Vert H^i-H^{i-1}\Vert }\\&-\frac{ (H^i-H^{i-1})\frac{\Vert \varvec{u}\Vert }{m^2\Vert H^i-H^{i-1}\Vert }\frac{\partial \Vert \varvec{u}\Vert }{\partial \,\cdot }}{\Vert H^i-H^{i-1}\Vert ^2} \end{aligned}$$

as derivatives w. r. t. the control point variables \(P_x,P_y,Q_x\) and \(Q_y\). W. r. t. \(a^i\), the non-zero values are

$$\begin{aligned} \frac{\partial \varvec{t}^i}{\partial a^{i-1}}=&\frac{-\varvec{u_0}^\bot \Vert H^i-H^{i-1}\Vert +(H^i-H^{i-1})\frac{a^i-a^{i-1}}{\Vert H^i-H^{i-1}\Vert }}{\Vert H^i-H^{i-1}\Vert ^2}\\ \frac{\partial \varvec{t}^i}{\partial a^{i}}=&\frac{\varvec{u_0}^\bot \Vert H^i-H^{i-1}\Vert -(H^i-H^{i-1})\frac{a^i-a^{i-1}}{\Vert H^i-H^{i-1}\Vert }}{\Vert H^i-H^{i-1}\Vert ^2}. \end{aligned}$$

By definition, we have

$$\begin{aligned} \frac{\partial n^i_x}{\partial \,\cdot }&=\frac{-\partial t^i_y}{\partial \,\cdot }, \qquad \frac{\partial n^i_y}{\partial \,\cdot }=\frac{\partial t^i_x}{\partial \,\cdot }. \end{aligned}$$

Lastly, the derivatives of \(\alpha ^i\) and \(C^i\) are all defined for \(i=1,\ldots ,m-1\) using the previous quantities:

$$\begin{aligned} \frac{\partial \alpha ^i}{\partial \,\cdot }=&\frac{\varvec{t}^i\cdot \frac{\partial \varvec{t}^{i+1}}{\partial \,\cdot }+\varvec{t}^{i+1}\cdot \frac{\partial \varvec{t}^i}{\partial \,\cdot }}{2\sqrt{1-(\varvec{t}^{i+1}\cdot \varvec{t}^i)^2}}\\ \frac{\partial C^i}{\partial \,\cdot }=&\frac{\partial H^i}{\partial \,\cdot } +\frac{r\left( \frac{\partial \varvec{t}^{i+1}}{\partial \,\cdot }-\frac{\partial \varvec{t}^i}{\partial \,\cdot } \right) }{\sin {\alpha ^i}\Vert \varvec{t}^{i+1}-\varvec{t}^i\Vert }\\&-\frac{r\cos {\alpha ^i}}{(\sin {\alpha ^i})^2} \frac{\partial \alpha ^i}{\partial \,\cdot }\frac{\varvec{t}^{i+1}-\varvec{t}^i}{\Vert \varvec{t}^{i+1}-\varvec{t}^i\Vert } \\&-\frac{r\left( \varvec{t}^{i+1}-\varvec{t}^i\right) \cdot \left( \frac{\partial \varvec{t}^{i+1}}{\partial \,\cdot }-\frac{\partial \varvec{t}^i}{\partial \,\cdot } \right) }{\sin {\alpha ^i}\Vert \varvec{t}^{i+1}-\varvec{t}^i\Vert ^3}\left( \varvec{t}^{i+1}-\varvec{t}^i\right). \end{aligned}$$

Note that both \(\frac{\partial \alpha ^i}{\partial a^j}\) and \(\frac{\partial C^i}{\partial a^j}\) are only non-zero for \(j\in \{i-1,i,i+1\}\).

These prerequisites now finally allow us to state the derivatives of the distance function to the spaghetti’s center line, which has the following piecewise form depending on the position of x:

$$\begin{aligned} \frac{\partial d}{\partial \,\cdot }={\left\{ \begin{array}{ll} {\text {sign}}\left( ({x}-H^i)\cdot \varvec{n}^i\right) \left[ ({x}-H^i)\cdot \frac{\partial \varvec{n}^i}{\partial \,\cdot } - \frac{\partial H^i}{\partial \,\cdot }\cdot \varvec{n}^i \right] &{} {x} \text { closest to line segment } \overline{H^{i-1}H^i} \\ {\text {sign}}\left( \Vert {x}-C^i\Vert -r\right) \frac{(C^i-{x})\cdot \frac{\partial C^i}{\partial \,\cdot }}{\Vert {x}-C^i\Vert } &{} {x} \text { closest to arc segment around } C^i\\ \frac{(P-{x})\cdot \frac{\partial P}{\partial \,\cdot }}{\Vert {x}-P\Vert } &{} {x} \text { closest to endpoint } P\\ \frac{(Q-{x})\cdot \frac{\partial Q}{\partial \,\cdot }}{\Vert {x}-Q\Vert } &{} {x} \text { closest to endpoint } Q \end{array}\right. } \end{aligned}$$
(2)

Although we have stated a lot of different sensitivities for the constructed properties \(C, H, \varvec{t}, \varvec{n}\), they need to be precomputed only once per iteration and can then be inserted into the sensitivity formula of the distance function, which is evaluated for each integration point and hence much more often.

4 Smooth boundary transition

Up to here, we have described an exact geometry, which would have material inside the dilated spaghetti and void outside. In order to obtain a differentiable formulation, we change this shift from full material (pseudo-density 1) to void (pseudo-density 0) to a smooth transition introducing a transition length h and a polynomial boundary function as interpolation as suggested in Wein et al. (2020) (Fig. 4):

$$\begin{aligned} \sigma _{\text {poly}}(d({x}))=&{\left\{ \begin{array}{ll} 1\\ \frac{3}{4}\left( \frac{d({x})-p/2}{h}-\frac{(d({x})-p/2)^3}{3h^3} \right) +0.5\\ 0 \end{array}\right. }\\&\qquad {\left\{ \begin{array}{ll} \text { if } 0\le d({x}) \le p/2-h \\ \text { if } p/2-h\le d({x}) \le p/2+h\\ \text { if } d({x})>p/2+h \end{array}\right. } \end{aligned}$$

with the corresponding derivative

$$\begin{aligned} \frac{\partial \sigma _{\text {poly}}(d({x}))}{\partial d}={\left\{ \begin{array}{ll} 0\qquad \text { if } 0\le d({x}) \le p/2-h \\ \frac{3}{4}\left( \frac{1}{h}-\frac{(d({x})-p/2)^2}{h^3} \right) \qquad \text { else}\\ 0\qquad \text { if } d({x})>p/2+h. \end{array}\right. } \end{aligned}$$
Fig. 4
figure 4

Illustration of the smooth boundary transition

Full size image

The effective pseudo-density \(\rho\) can then be defined directly as \(\sigma _{\text {poly}}(d({x}))\) or an additional penalty function can be used in order to further discourage overlapping boundary regions. For the results in this work, we use the so-called RAMP scheme, i.e.,

$$\begin{aligned} \rho ({x}):=\frac{\sigma _{\text {poly}}(d({x}))}{1+q(1-\sigma _{\text {poly}}(d({x})))} \end{aligned}$$

with penalty parameter \(q=3\). In classical density-based topology optimization, for the static case almost any penalizing interpolation function results in a distinct topology – the only requirement is the avoidance of the non-physical linear weight to density relationship. To approximately model the physical relationship, RAMP fits much better than the common power law, see (Bendsøe and Sigmund 1999) and Wein et al. (2020). However, the impact on the final design is minor.

5 Material formulation

We consider both isotropic as well as anisotropic material properties. In the simpler case of isotropic material, the effective elasticity tensor generated by our shapes is

$$\begin{aligned} \varvec{C}({x}) = \varvec{C}^\text {void}+\rho ({x})\varvec{C}^\text {iso} \end{aligned}$$

for some given isotropic elasticity tensor \(\varvec{C}^\text {iso}\).

Furthermore, we would like to use an anisotropic material motivated by carbon fiber-reinforced polymers (CFRP). For this material, we would like to prescribe the carbon fiber reinforcement to be aligned with the direction of the center line of our spaghetto. Hence, for CFRP, we assume a transversely isotropic elasticity tensor, which we will rotate using tensor rotation matrices s.t. the fiber directions align with the shape. For a point x within or closest to an arc section i of the spaghetti, this means the fiber direction is vertical to the vector \(x-C^i\), otherwise the direction is parallel to the closest segment. Consequently, the fiber direction for a shape s is chosen in the direction of

$$\begin{aligned} {\left\{ \begin{array}{ll} H^i-H^{i-1} &{} {x} \text { in or closest to segment }i\\ \text {vertical to }{x}-C^i &{} {x} \text { in or closest to arc }i\\ H^1-P &{} {x} \text { closest to }P \\ H^m-H^{m-1} &{} {x} \text { closest to }Q. \end{array}\right. } \end{aligned}$$

In our approach, we represent this by rotating a given transversely isotropic CFRP tensor \(\varvec{C}^\text {CFRP}\) with fiber direction in the \(x-\)direction as

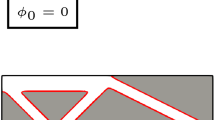
$$\begin{aligned} \varvec{C}({x}) =\varvec{C}^\text {void}+ \Phi (\phi ({x}))^\top \rho ({x})\varvec{C}^\text {CFRP}\Phi (\phi ({x})), \end{aligned}$$

where \(\Phi (\phi )\) are rotation matrices (counterclockwise) for 2D elasticity tensors in Voigt notation given as

$$\begin{aligned} \Phi (\phi )&= \begin{pmatrix} \cos (\phi )^2 &{} \sin (\phi )^2 &{} -\sin (2\phi ) \\ \sin (\phi )^2 &{} \cos (\phi )^2 &{} \sin (2\phi ) \\ \frac{\sin (2\phi )}{2} &{} -\frac{\sin (2\phi )}{2} &{} \cos (2\phi ) \end{pmatrix}. \end{aligned}$$

\(\phi ({x})\) is computed as

$$\phi({x}) = \begin{cases} \operatorname{atan2}(H^i_y-H^{i-1}_y,H^i_x-H^{i-1}_x) & x \text{ in or closest to seg. }i \\ \operatorname{atan2}(C_y^i-x_y,x_x-C_x^i) & x\text{ in or closest to arc }i\\ \operatorname{atan2}(H^1_y-P_y,H^1_x-P_x) & x\text{ closest to } P \\ \operatorname{atan2}(H^m_y-H^{m-1}_y,H^m_x-H^{m-1}_x) & x\text{ closest to }Q. \end{cases}$$

6 Multiple spaghetti and shape combination

6.1 Combining pseudo-densities

We now consider a set of multiple spaghetti denoted by a subscript s and constructed in the same way as previously described. More precisely, the set of spaghetti is determined by \(\left\{ P_s,Q_s,p_s,a_s^i,i=1,\ldots ,m_s-1\right\}\) and results in a number of effective pseudo-densities

$$\begin{aligned} \rho _s({x}):=\sigma _{\text {poly}}(d_s({x})), \end{aligned}$$

where \(d_s\) denotes the distance function to shape s. In order to obtain a single global pseudo-density, we subsequently combine the different shapes using a smooth approximate maximum function (map-then-combine approach):

$$\begin{aligned} \bar{\rho }({x}) = \overline{\max _s}\rho _s({x}) \end{aligned}$$

Commonly used types for this smooth maximum include the p-norm and the Kreisselmeier–Steinhauser (KS) function

$$\begin{aligned} \overline{\max _s}^p \rho _s({x}):= \left( \sum _s \rho _s({x})^p \right) ^\frac{1}{p} \\ \overline{\max _s}^\text {KS} \rho _s({x}):= \frac{1}{p}\log \sum _s e^{p\rho _s({x})} \end{aligned}$$

as well as the softmax function (Goodfellow et al. 2016; Smith and Norato 2021)

$$\begin{aligned} \overline{\max _s}^\text {sm} \rho _s({x}):= \frac{\sum _s \rho _s({x}) e^{p\rho _s({x})}}{\sum _s e^{p\rho _s({x})}}. \end{aligned}$$

For the results presented in this work, we chose to use the softmax as smooth maximum with \(p=8\). The value of p determines the sharpness of the interpolation between primitives in overlapping boundary regions.

6.2 Anisotropy for multiple shapes

Using a smooth maximum function for the angle \(\phi\) to determine a dominant material direction is unfortunately less straightforward than it is for the pseudo-density \(\rho\). Specifically, the challenge of averaging orientation angles of linear elastic material is that the material tensors are invariant to \(180^\circ\) rotations. Effective material properties would be the same for \(0^\circ\) as for \(180^\circ\), while a direct averaging of these two angles would result in a \(90^\circ\) angle.

One way to circumvent this problem is to average the coefficients of the material tensor directly instead of the orientation angles. However, to do this without changing the effective material stiffness, a smooth maximum function is required which provides weights forming a convex combination, effectively leaving only the softmax. In fact, in Smith and Norato (2021) the softmax function is used and the elasticity tensors produced by the different shapes are averaged using their respective softmax weights. Apart from the restricted choice of the smooth maximum function, after averaging the elasticity tensors, a directional variable is not directly available anymore to be used for interpretation as fiber printing paths. Note that for a strongly anisotropic CFRP tensor, this direction might be recovered retroactively. However, this would require a separate post-processing step searching for the maximum directional stiffness of the effective elasticity tensor as described in Jantos et al. (2020) for filtered tensor coefficients. This is why we chose to investigate a different method, which is able to directly provide an effective directional variable throughout the optimization process.

To achieve this, at a point x we start by considering the angle variables as vectors

$$\begin{aligned} v(\rho _s({x}),\phi _s({x}))=\begin{pmatrix} \rho _s \cos {\phi _s} \\ \rho _s \sin {\phi _s} \end{pmatrix}. \end{aligned}$$

A \(180^\circ\) change in material orientation angle, which would result in identical material properties, now leads to a vector flipped in the opposite direction in this polar coordinate system:

$$\begin{aligned} v(\rho _s({x}),\phi _s({x})+\pi ) = \begin{pmatrix} -\rho _s \cos {\phi _s} \\ -\rho _s \sin {\phi _s} \end{pmatrix}. \end{aligned}$$

Consequently, when trying to find the average angle coinciding best with overlapping shape’s material orientation independent of \(180^\circ\) rotations, we can consider the sum of all combinations of (un)flipped vectors \(\sum _s \pm v(\rho _s({x}),\phi _s({x}))\) and look for the maximum norm (i.e., the smallest cancelation when considering flipped orientations as equivalent). An illustration of this method is shown in Fig. 5. Using this approach, the formula for the average angle for a number of shapes is

$$\begin{aligned} \bar{\phi }:= {\text {atan2}}\left( \underset{\pm }{{\text {argmax}}} \Vert \sum _s \pm v(\rho _s({x}),\phi _s({x})) \Vert \right) \end{aligned}$$
(3)
Fig. 5
figure 5

Illustration of weighted angle average for two overlapping shapes with \(v_1:=v(\rho _1,\phi _1)\) and \(v_2:=v(\rho _2,\phi _2)\). As \(\Vert v_1-v_2\Vert >\Vert v_1+v_2\Vert\), we get \(\bar{\phi }={\text {atan2}}(v(\rho _1,\phi _1)-v(\rho _2,\phi _2))\)

Full size image

Note that the scaling by \(\rho _s\) not only weighs the angles but also ensures that only angle variables inside the shape and its transition zone are considered, as \(\rho _s({x})=0\) for \(d_s({x}) > p/2+h\). Hence, it suffices to consider active shapes when determining the maximum sum. We further note that this formula is not strictly differentiable, as an average of \(0^\circ\) and \(90^\circ\) can either be \(45^\circ\) or \(-45^\circ\) because \(90^\circ\) is equivalent to \(-90^\circ\). This discontinuity may lead to a finite difference gradient check failing at times. However, as the analytical derivatives always remain bounded and will be summed up for the whole shape with most derivatives being well defined, the effects of this should be marginal. As discussed in Sect. 6.2, averaging the material tensors of the different shapes instead of the angles would lead to a rigorously differentiable formulation. Nevertheless, we chose to investigate this novel angle combination in order to keep a material orientation available without post-processing steps and in fact could not observe any problems during optimization.

If we want to be even closer to the physical importance of the respective shape’s angle variables, we can also define the vectors as

$$\begin{aligned} v(\rho _s({x}),\phi _s({x}))=\begin{pmatrix} w(\rho _s) \cos {\phi _s} \\ w(\rho _s) \sin {\phi _s} \end{pmatrix}, \end{aligned}$$

where \(w(\cdot )\) weighs the angles according to the corresponding pseudo-density. Choosing \(w(\rho _s)=\rho _s\) would match the previous definition, while another suitable formulation would be choosing the weights corresponding to the shape’s fraction in the used smooth maximum formula:

$$\begin{aligned} w^p(\rho _s)=\rho _s^p,\quad \text {or} \quad w^\text {sm}(\rho _s)=\rho _s e^{p\rho _s}. \end{aligned}$$

Note that this works quite nicely not only for the softmax function but also for the p-norm. While for the KS smooth maximum this could be done in principle as well, the drawback here is that the angle average would become global due to the associated weights \(w^\text {KS}(\rho _s)=e^{p\rho _s}\) not vanishing for \(\rho _s=0\), potentially leading to a drastically increased computational cost for computing the angle average.

Putting things together, the final formula for the parametrization can be written as

$$\begin{aligned} \varvec{C}({x}) =\varvec{C}^\text {void}+ \Phi (\bar{\phi }({x}))^\top \overline{\max _s}\rho _s({x})\varvec{C}^\text {CFRP}\Phi (\bar{\phi }({x})). \end{aligned}$$

7 Geometry mapping to a fixed grid

Up to here we have defined the high-level geometry using a pseudo-density approach in a continuous setting. For the numerical analysis, we will now project this continuous feature onto a fixed finite element mesh. We do this by integration and assign each element a constant pseudo-density and material orientation angle. For the integration, oftentimes a simple midpoint evaluation is used. However, in Wein et al. (2020) it is shown that this low integration precision may lead to problems in accurately approximating the compliance of the geometry. Because our transition function \(\sigma _{\text {poly}}\) is only piecewise polynomial, we use a simple average of evenly distributed function values for integration instead of weighted quadrature rules. Specifically, the domain is partitioned into finite elements \(e\in {\mathscr {E}}\), where \({\mathscr {E}}\) is the set of element numbers. Then for each element e,

$$\begin{aligned} \bar{\rho }^e = \frac{1}{N_{\text {ip}}}\sum _{i=1}^{N_{\text {ip}}} \overline{\max _s}\rho _s({x}_e^i), \end{aligned}$$

where \({x}_e^i\) are the integration points and \(N_{\text {ip}}\) denotes their total. For this work, we used \(5\times 5\) evenly distributed integration points.

As the continuous orientation angle \(\phi ({x})\) does not change as quickly as the pseudo-density, in this case we use the computed element pseudo-density as input for the angle average (3), but evaluate the formula only at the midpoint in order to improve computational efficiency, i.e.,

$$\begin{aligned} \bar{\phi }^e= {\text {atan2}}\left( \underset{\pm }{{\text {argmax}}} \Vert \sum _s \pm v(\rho ^e_s,\phi _s({x}_C)) \Vert \right) , \end{aligned}$$
(4)

where \({x}_C\) denotes the center point of element e. The effective material tensor in the discretized setting hence is

$$\begin{aligned} \varvec{C}^e = \varvec{C}^\text {void}+\bar{\rho }^e\varvec{C}^\text {iso} \end{aligned}$$
(5)

in the isotropic case and

$$\begin{aligned} \varvec{C}^e =\varvec{C}^\text {void}+ \Phi (\bar{\phi }^e)^\top \bar{\rho }^e\varvec{C}^\text {CFRP}\Phi (\bar{\phi }^e) \end{aligned}$$
(6)

for anisotropic material.

8 Discretized optimization problem

The full, discretized optimization setting is denoted as

$$\begin{aligned}&\min _{\left\{ P_s,Q_s,p_s,a_s^i,i=0,\ldots ,m_s\right\} }c=L^\top U \nonumber \\ \text {s.t.: }&KU=F\nonumber \\&\frac{\sum _e \bar{\rho }_e V_e}{\sum _e V_e} \le \bar{v}\nonumber \\&(C_s^i-C_s^{i-1})\cdot (H_s^i-H_s^{i-1})\ge 0, \ i=1,\ldots ,m_s \end{aligned}$$
(7)

where F and U are the global force and displacement vectors, L is the output vector in mechanism design and \(L=F\) for compliance, K is the global stiffness matrix, \(V_e\) the volume of element e, and \(\bar{v}\) is the prescribed upper limit on the volume fraction. The last constraints ensure that the single spaghetti sections do not overlap. Simple box constraints are not explicitly stated, but can be easily added to the problem formulation. Furthermore, approximate length constraints may be defined on \(\overline{P_s Q_s}\) or along the linear spline and even accurate length constraints along the center line may be considered. We note, however, that a rigorous implementation of length constraints would further require constraints ensuring the entire primitives stay within the design domain. A possibility to achieve this is given by Zhang et al. (2018), where a ghost layer around the domain is introduced, for which the mapped density field is restricted to zero values.

9 Numerical case study

In comparison to a pure pseudo-density optimization, for feature-mapping methods it is not as straightforward to choose a starting value. Intuitively, simply distributing a large number of features comes to mind. While this works well w. r. t. obtaining a good compliance value, this approach can also lead to numerous regions with multiple overlapping spaghetti. Consequently, the advantage of deliberately chosen features more easily interpretable as fiber paths is diminished, as can be observed in the results of the second example in Sect. 9.2. In the first example, we will therefore follow a different methodology. Specifically, for a given loading scenario we will first optimize the setting using an established CFAO algorithm. More precisely, we use the formulation given in Greifenstein and Stingl (2016) optimizing topology and material angle for a given anisotropic material. We will then loosely match the resulting topology with a suitable number of spaghetti shapes. Lastly, using this starting value we solve problem 7.

9.1 Bridge

Fig. 6
figure 6

Bridge design region (\(2\times 1\) meter, 200\(\times\)100 finite elements). Support and loading scenario. A minimum of material is prescribed along the top edge. For the anisotropic material settings, the fiber angles are aligned with the edge. In light gray, the starting value of the spaghetti optimization based upon a CFAO result (see Fig. 7) is shown

Full size image

As first numerical example, we choose a setting that is known for a good performance advantage using strongly anisotropic material, as was shown in Smith and Norato (2021). Specifically, we study the loading scenario of a bridge with a distributed load and an aspect ratio of 1:4. Since the problem is symmetric, we only model the left half of the domain. The geometry is detailed in Fig. 6. As described in the last paragraph, we start by solving a CFAO problem with density filter for this problem. The resulting optimal topology and angle design is shown in Fig. 7. Next, this topology is loosely interpreted using five spaghetti shapes as depicted in Fig. 6. The resulting interpretation has a total of 35 optimization variables. Using this starting value, we run a number of different material scenarios. We start by running the full anisotropic model using the CFRP material constants (Figs. 9 and 10). For the tensor CFRP, we use the same values as in Smith and Norato (2021) and a transversely isotropic material model (equivalent to orthotropic material in 2D). Secondly, we perform the optimization using two different fictitious isotropic materials to obtain a baseline performance as comparison. One has the same overall stiffness (i.e., the same trace of the elasticity tensor / trace of the Voigt tensor with the shear modulus values weighted double) and the other has the same Young’s modulus as the fiber direction modulus of CFRP (maximum stiffness). For the concrete engineering coefficients, see Table 2.

Table 2 Material coefficients used in numerical examples
Full size table

Finally, for the result of the isotropic optimization (Fig. 8), we replace the material with the CFRP tensor to see whether there is a noticeable performance advantage in using the more complex anisotropic model as compared with simply orienting the fibers along the features optimized in the isotropic setting. The problems in this section were solved using a volume fraction of 0.4 and equal parameters for transition zone and void. All problems were solved using the SQP algorithm SNOPT (Gill et al. 2005) with the forces being scaled such that the objective values are in a numerically reasonable range. The compliance values for the numerical experiments can be found in Table 3 and the convergence history in Fig. 11.

Fig. 7
figure 7

Optimal topology (CFAO result)

Full size image
Fig. 8
figure 8

Isotropic spaghetti optimization result

Full size image
Fig. 9
figure 9

Anisotropic spaghetti optimization result

Full size image
Fig. 10
figure 10

Visualization of fiber orientations for anisotropic spaghetti optimization result

Full size image
Table 3 Optimal compliance results for different settings
Full size table
Fig. 11
figure 11

Convergence plot for bridge design problem

Full size image

When comparing the results, we first note the big gap between the compliance of the CFRP optimization and the isotropic result with the same overall material stiffness. Having the stiffness directed almost entirely along the principal spaghetti direction proves to be greatly beneficial in this case. Even the compliance for the isotropic case with stiffness equal to the fiber stiffness but in all directions shows only a 30% advantage compared to CFRP, despite the drastically larger overall material stiffness. Lastly, evaluating the isotropic optimal design using CFRP material aligned with the spaghetti shows a 28% worse performance than the actual anisotropic design, even though the two topologies appear largely similar. Consequently, performing the optimization using the anisotropic model proves clearly advantageous. Furthermore, the result satisfies the parallelism of fiber orientations and minimum curvature in most of the domain, even though in intersecting regions with overlapping shapes these manufacturing constraints might still be violated.

9.2 MBB beam

Next, we apply the method using a generic starting value and the design of a Messerschmitt–Bölkow–Blohm (MBB) beam and anisotropic material as in Table 2. The setting is given in Fig. 12, the results in Figs. 13 and 14, and the convergence plot in Fig. 15. Even though this is not the use case we devised the method for, it still yields reasonable results. As the primitives can only become very small but not disappear in the current formulation, they can only be moved on top of each other in order to not use up volume though. One feature actually remains surrounded fully by void without information in which direction to hide. Here, we can see the general susceptibility of feature-mapping methods to local minima. One possibility to improve the convergence of the method for the use of a generic starting value would be to introduce a size variable as in Smith and Norato (2021), which allows the shapes to vanish in place. We further see that the primitives are aligned as straight bars, which is expected for this type of problem. Finally, we note that with these many shapes the desired properties of the underlying primitives are lost in large parts of the composite structure, hence further complicating a possible interpretation to fiber paths.

Fig. 12
figure 12

MBB beam design region (\(2\times 1\) meter, 100\(\times\)50 finite elements). In light gray, the starting value is shown

Full size image
Fig. 13
figure 13

Optimal result of MBB beam design problem

Full size image
Fig. 14
figure 14

Visualization of fiber orientations for MBB beam result

Full size image
Fig. 15
figure 15

Convergence plot for MBB beam design problem

Full size image

9.3 Force inverter

As last example, we consider the design of a compliant mechanism. We again use the anisotropic material parameters as in Table 2. For this design problem, using a generic starting value easily leads to getting stuck in local minima for which the design does not connect input force and output, which shows close to zero output. Consequently, we use a starting value roughly resembling the common SIMP result, which already exhibits a negative output. The setting and starting value are given in Fig. 16, the results in Fig. 17, and the convergence plot in Fig. 18. However, in order to prevent the formation of hinges, we start with a single shape connecting support and output. For the springs, we use equal values of \(k_{\text {in}}=k_{\text {out}}=50\).

Fig. 16
figure 16

Support and loading scenario for compliant mechanism (force inverter). \(100\times 100\) elements. In light gray, the starting value is shown

Full size image
Fig. 17
figure 17

Optimal result of force inverter design problem

Full size image
Fig. 18
figure 18

Convergence plot for force inverter design problem

Full size image

We observe that slightly rounded shapes appear again to be optimal for this example.

10 Conclusion and future work

We presented a feature-mapping approach to optimize a design suitable for carbon fiber-reinforced filament printing. The design parametrization can serve as a blueprint for final printing path generation. The proposed method advances existing feature-mapping methods by introducing a curved geometric primitive, which still allows for a closed-form calculation of the signed distance to a boundary and hence an efficient evaluation. Furthermore, a number of critical manufacturing constraints in carbon fiber-reinforced filament printing are addressed, namely parallelism of fibers and minimum turning radius, even though this still cannot be guaranteed in intersecting regions. Additionally, minimum cut length constraints may also be characterized more accurately.

Nevertheless, the current work can clearly only constitute an intermediate step toward manufacturability. An open problem of the proposed method is that the fiber orientation field may violate the manufacturing constraints in intersecting areas. This would hamper a direct interpretation to printing paths in carbon fiber-reinforced printing. A solution to this would be to prevent overlaps, e.g., applying the formulation given in Smith and Norato (2022). However, we postpone this problem to a three-dimensional extension of the model, where structures are able to bypass each other without overlapping. Furthermore, feedback from manufacturers suggests that for best performance it might actually be preferable to have different carbon fibers continuing across all directions of an intersection.