Abstract
This paper presents a new topology optimization framework in which the design decisions are made by humans and machines in collaboration. The new Human-Informed Topology Optimization approach eases the accessibility of topology optimization tools and enables improved design identification for the so-called ‘everyday’ and ‘in-the-field’ design situations. The new framework is based on standard density-based compliance minimization. However, the design engineer is enabled to actively use their experience and expertise to locally alter the minimum feature size requirements. This is done by conducting a short initial solution and prompting the design engineer to evaluate the quality. The user can identify potential areas of concern based on the initial material distribution. In these areas, the minimum feature size requirement can be altered as deemed necessary by the user. The algorithm rigorously resolves the compliance problem using the updated filtering map, resulting in solutions that eliminate, merge, or thicken topological members of concern. The new framework is demonstrated on 2D benchmark examples and the extension to 3D is shown. Its ability to achieve performance improvement with few computational resources are demonstrated on buckling and stress concentration examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Topology-optimized designs have the ability to leverage new rapidly developing fabrication possibilities. They do not rely on a preconceived notion of the final layout and have therefore be shown to lead to new and surprising solutions that typically outperform conventional low-weight design (Bendsøe and Sigmund 2003). Most existing topology optimization frameworks are fully automated such that the design generation and evolution are driven exclusively by a machine. Input by a human design engineer is only needed to initialize the design and judge the quality of the final output.
The human designer initiates the design by defining a design domain with relevant loads and boundary conditions. Additionally, they must cast the design task as a formal optimization problem. The most popular design task is to find a material distribution that maximizes the structural stiffness using a specified amount of material. It is most often assumed that the performance can be evaluated by a simple linear elastic mechanics model.
It is well documented that deviations from the exact design scenario, either by differences in the operating conditions or to ease manufacturing, may be detrimental for the physical performance of a topology-optimized design (see, e.g., experimental investigation in Jewett and Carstensen (2019)). A prominent research trend is therefore to cast more realistic design problems by increasing the complexity of the mechanics model and/or constraints. Recent examples include designing with complex nonlinear mechanics (Lawry and Maute 2015; Wallin et al. 2016; Russ and Waisman 2020; Carstensen et al. 2022), and the literature is rich on topology optimization with buckling (Lund 2009; Gao and Ma 2015; Ferrari and Sigmund 2019; Dalklint et al. 2021) or stress constraints (Duysinx and Bendsøe 1998; Le et al. 2010; Holmberg et al. 2013; Picelli et al. 2018; Kambampati et al. 2021).
The cost of increasing the complexity in a fully automated framework is the introduction of new design parameters that require tuning with many associated restarts. Moreover, the computational time also increases with the complexity of the problem formulation and/or finite element model.
As a complex design problem is often nontrivial to set up, significant training can be needed before initiating a topology optimization design task that may take many engineering hours to conduct.
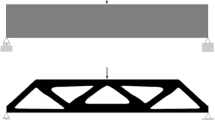
It is herein stipulated that the combined demand on engineering hours and computational resources prohibits the use of topology optimization for a large range of engineering applications. Examples include the so-called ‘every-day’ and ‘in-the-field’ design situations. These refer to design scenarios where a good or improved solution must be obtained quickly on a laptop. Examples include design for architecture and civil engineering, small manufacturing (mom-and-pop) shops with restricted cluster or cloud computing capabilities, and design in austere environments with limited or unreliable network or internet access (e.g., war zones). Moreover, currently a design engineer facing any type of design task can choose between a manual design approach that makes use of design principles Fu et al. (2016) or to generate the design by fully automated topology optimization. The two options are illustrated in Fig. 1a and will typically result in different design solutions. Whereas, the drawback of topology optimization is the resource requirement, heavily relying on design principles can cause fixation on what the design should be. This has been shown to negatively impact design outcomes if pronounced in the exploratory or conceptual design generation stage (Moreno et al. 2016).
a Illustration of how design engineers currently have two options when faced with a design problem. They can either use their pre-existing knowledge and/or available design guidelines or formulate the design problem such that it can be solved by fully automated topology optimization. b Envisioned human-informed topology optimization framework that combines the exploratory power of fully automated topology with the knowledge and intuition of skilled human designers
This work proposes a new free-form design framework that combines the exploratory powers of fully automated topology optimization with the expertise of human design engineers (Fig. 1b). The new framework is intended to expand the use of topology optimization to industry applications that currently sees the time and computational requirements as prohibitively large. The new approach will integrate the two key components needed for successful free-form design Lynch et al. (2019): (i) the automated machine discovery and (ii) the experienced human perception of a satisfactory design quality. The herein proposed Human-Informed Topology Optimization (hitop) algorithm uses an interactive scheme where the design decisions are guided by humans and machines in collaboration.
Enabling human interaction in optimization-driven design frameworks is not a new idea. Evolutionary approaches have been suggested for truss design (Mueller and Ochsendorf 2015) and continuum topology optimization (Yang et al. 2019). In these, multiple designs with similar performance are generated, allowing the designer to select their esthetic favorite. In contrast, the herein proposed framework will leverage the human expertise to develop a single design. The new hitop approach uses standard density-based (Bendsøe 1989; Rozvany et al. 1992) compliance optimization as the backbone of the algorithm. To allow for fast computations, the underlying mechanics model uses a homogeneous, linear elastic material and small deformation assumptions. The initial exploratory design iterations are performed using a standard fully automated mathematical program. After a set number of initial iterations, the program is interrupted. The design engineer is prompted to judge the quality of the design and can raise the need for the modifications. In the herein proposed approach, the design engineer can interactively change the minimum feature size requirements in different regions of the design domain.
Interactively changing the minimum feature size requirement (often referred to as minimum length scale control) is chosen for two reasons. Firstly, the effect of local feature sizes on a design can in many cases be intuitive to evaluate. Figure 2 gives examples of how intuitively modifying the local feature sizes improves the buckling performance (Fig 2a, b) and can limit stress concentrations (Fig. 2c, d). Secondly, the implementation of minimum feature size control in density-based topology optimization is a well-studied field (see, e.g., review by Lazarov et al. 2016). Feature size control can, for example, be implemented implicitly through the filtering operations, e.g., using Heaviside projection (Guest et al. 2004; Xu et al. 2010), morphology (Sigmund 2007) or robust (Wang et al. 2011) filtering techniques.
Most existing works use a single and constant minimum feature size control for the entire design. Extensions have been suggested to allow control of the minimum feature size of multiple phases (typically solid and void) (Guest 2009; Wang et al. 2011; Zhou et al. 2015; Lazarov and Wang 2017; Carstensen and Guest 2018; Fernández et al. 2020). The multi-phase controls generally allow for different sizes to be imposed on each phase. However, to the best of the authors’ knowledge, all literature examples apply constant limits throughout the design domain.
Recently, some works have explored the idea of varying the minimum size requirement across the design domain. Amir and Lazarov (2018) propose methods for density-based topology optimization that automatically manipulate the minimum feature size to bound the maximum stress. Liu (2019) suggest a level-set approach that applies piece-wise minimum feature size control in a dynamic and fully automated fashion. Related is also the work by Schmidt et al. (2019) on generating and controlling infill design for additive manufacturing through the application of local volume constraints that are non-uniform in size. In addition to presenting fully automated approaches as in Amir and Lazarov (2018), Liu (2019), Schmidt et al. (2019) also includes an option that allows the user to manually prescribe non-uniformity of the local volume constraint (and thus where infill should be included) when initially setting up the design problem.
This work differs significantly in that the decisions on the minimum feature sizes are interactively imposed by the design engineer. A recently published interactive tool for architectural design by Yan et al. (2022) builds on the same idea. Here esthetic preferences are interactively implemented in a Bi-Directional Evolutionary Structural Optimization (BESO) framework. In contrast, this work aims at improving complex performance requirements by leveraging intuition and past experience while rigorously solving a density-based topology optimization problem.
Prior to detailing the human interaction, this paper will for completeness give a brief introduction to density-based compliance optimization in Section 2. For a more in-depth description, the reader is referred to Bendsøe and Sigmund (2003); Andreassen et al. (2011) or to Wang et al. (2021) for an overview of available educational papers. Section 3 will demonstrate how modifying the minimum feature size requirements affects the resulting designs, and the human interaction is enabled and demonstrated in Sections 5-6.
2 Compliance minimization
The classic topology optimization problem that minimizes compliance seeks to find a distribution of material that creates a stiff structure under the applied loads. To evaluate the performance, the design domain is discretized with finite elements. In density-based topology optimization, the material distribution is defined by the density \(\bar{\pmb {x}}\) of the finite elements. Element e will be considered a solid element if \({\bar{x}}_{\text{e}}=1\) and a void element when \({\bar{x}}_{\text{e}}=0\).
The design problem is cast as the following formal optimization problem:
Here, \(\pmb {x}\) is the vector of design variables that are bounded by 0 and 1 and controls the element densities \(\bar{\pmb {x}}\). The objective is to minimize the compliance c that is calculated using the \(\pmb {U}\) global displacement vector and the global stiffness matrix \(\pmb {K}\). The designed structure must fulfill static equilibrium (\(\pmb {K}\pmb {U}=\pmb {F}\)), where \(\pmb {F}\) is the global force vector. In addition, a volume fraction f is prescribed to limit the use of material. The volume fraction is defined as the ratio of used material volume \(V(\pmb {x})\) to the volume of the design domain \(V_{0}\).
The compliance objective in Eq. (1) can conveniently be computed as the sum of the element compliances for all N elements within the design domain:
where \(\pmb {u}_{\text{e}}\) is the element displacement vector. The element stiffness matrix \(\pmb {k}_{0e}\) denotes a solid element, calculated with Young’s modulus equal to 1.
In the density-based approach to topology optimization, the discrete 0–1 restriction on the element densities \(\bar{\pmb {x}}\) is relaxed to allow the design problem to be solved by gradient-based optimizers. A penalization scheme is used to guide the final solution toward a 0–1 design. This work uses the Solid Isotropic Material Penalization (SIMP) method (Bendsøe 1989; Rozvany et al. 1992), and the element stiffness \(E_{\text{e}}({\bar{x}}_{\text{e}})\) is thus taken as follows:
Here, p is the SIMP penalty exponent and \(E_{0}\) is the stiffness of the structural material. This work applies continuation to the SIMP exponent throughout, raising it from \(p=3\) to \(p=10\) every 50 iterations with \(\Delta p =1.\) A small stiffness \(E_{{\text{min}}}\) is assigned to void elements to circumvent numerical instabilities. This work uses \(E_{{\text{min}}} = 1^{-9}\).
2.1 Filtering and feature size control
It is well established that a direct relation between the design variables \(\pmb {x}\) and the element densities \(\bar{\pmb {x}}\) results in numerical instabilities (Diaz and Sigmund 1995; Sigmund and Petersson 1998; Borrvall 2001). Density-based topology optimization therefore requires a filtering operation that relates \(\pmb {x}\) to \(\bar{\pmb {x}}\). This works uses the Heaviside projection method (Guest et al. 2004) as it implicitly enforces a minimum feature size control. Although not tested herein, the proposed framework should conceptually work with other filtering methods that enforce feature size control, such as Xu et al. (2010); Sigmund (2007); and Wang et al. (2011).
The filter is implemented by defining a neighborhood \(N_{\text{e}}\) of element e. This neighborhood contains all elements i with center \({\textbf {x}}_{i}\) within a radius \(r_{\text{min}}\):
The design variables are averaged within the neighborhood using the following function (Bruns and Tortorelli 2001; Bourdin 2001):
Here, \(H_{{\text{e}}i}\) is the weight factor on element e from element i. It is defined as \(H_{{\text{e}}i}=\max (0,r_{\text{min}}-\Delta (e,i))\). As \(H_{{\text{e}}i}\) remains constant during the design iterations, it can conveniently be computed before the optimization loop is started.
When filtering using the Heaviside projection method (Guest et al. 2004), the element densities are obtained by passing the averaged design variables \(\pmb {\tilde{x}}\) through a Heaviside function:
The parameter \(\beta\) controls the smoothness of the approximation. This work uses a constant \(\beta = 25\) unless otherwise specified.
Filtering using Eqs (4-6) implicitly gives the design engineer control over the minimum size of the solid topological features. An active design variable (\(x_{\text{e}}=1\)) will create a solid circular feature with radius \(r_{\text{min}}\). When the design engineer selects \(r_{\text{min}}\), they select how large the circle of elements with density \({\bar{x}}_{\text{e}}=1\) will be. The influence of \(r_{\text{min}}\) on the size of the solid feature is illustrated in Fig. 3.
2.2 Sensitivities
All design problems in this work are solved using the Method of Moving Asymptotes (MMA) (Svanberg 1987) as the gradient-based optimizer. Solving Eq. (1) using a gradient-based optimizer requires calculation of the design sensitivities. The sensitivity calculation makes use of the chain rule. For the compliance objective this means
Using the adjoint method, the sensitivity of the penalized compliance (Eqs. (2-3)) with respect to the element densities can be described by the following:
The sensitivity of the averaged design variables with respect to the design variables \(\frac{\partial \tilde{x}_{\text{e}}}{\partial x_{j}}\) is found by differentiation of Eq. (5).
Differentiation of Eq. (6) gives the sensitivity of the element densities with respect to the averaged design variables:
The sensitivity of the volume constraint is also required. It is again calculated using the chain rule:
where
Here, \(v_{\text{e}}\) is the volume of element e.
3 Non-uniform feature size control
As mentioned, most topology optimization is performed using a minimum feature size that is constant throughout the design domain. However, the feature size control can easily be varied by specifying a non-uniform \(r_{\text{min}}\) map. The \(r_{\text{min}}\) map contains the minimum feature size control that is relevant to consider for each element within the design domain.
To illustrate the effect of pre-selecting a non-uniform \(r_{\text{min}}\) map, the classic MBB benchmark example in Fig. 4 is considered. Herein the dimensions of the MBB beam are taken as \(H= 80\) and \(L = 480\) and the external load magnitude is \(P=1\). The volume fraction is set to \(f = 0.50\). The symmetry of the design domain is utilized such that only half the domain is modeled. The Young’s modulus and Poisson’s ratio for the solid material are \(E_0 = 2\) and \(\nu = 0.3\). The design problem in Eq. (1) is herein solved using the 88 line code (Andreassen et al. 2011) in MATLAB (MATLAB 2020b) with the modifications specified in Section 2. All designs are obtained with unit-sized elements.
If a designer knows a priori that different minimum feature size controls should be imposed at specified locations, the \(r_{\text{min}}\) map can be set up accordingly. Figure 5 shows how changes in the \(r_{\text{min}}\) map affect the design solution. The figure gives design solutions for half the MBB beam in Fig. 4, solved with the same parameter settings, varying only the \(r_{\text{min}}\) map. The obtained compliance is reported for all cases. Maps with constant \(r_{\text{min}}\) values of \(r_{{\text{min}}1}=3.2\) and \(r_{{\text{min}}2}=9.6\) are shown in (a) and (g) and their corresponding design solutions are given in (b) and (h), respectively. In (c), the \(r_{\text{min}}\) map contains two distinct regions: a region with a small \(r_{{\text{min}}1}\) near the center of the span and regions with large \(r_{{\text{min}}2}\) that are located within L/4 from each of the supports. The \(r_{\text{min}}\) map in (e) is similar, but instead of having a discrete difference in the map at L/4, the value of the prescribed \(r_{\text{min}}\) varies linearly between the supports and the mid span.
Results of half the MBB beam with different pre-specified \(r_{\text{min}}\) maps. (a,c, e, g) gives the \(r_{\text{min}}\) distribution across the design domain and the resulting designs are shown in (a, d, f, h), where constant values are prescribed in (a, b) as \(r_{{\text{min}}1} = 3.2\) and in (g-h) \(r_{{\text{min}}2} = 9.6\). In (c-f) non-uniform \(r_{\text{min}}\) maps varying between the two extremes in (a) and (g) are prescribed where (a, a) has a discrete transition vertically at L/4 and (e, f) transitions linearly
The results in Fig. 5 shows that the obtained designs fulfill the minimum feature sizes specified in the \(r_{\text{min}}\) maps. As expected, the design that has the ability to use the smallest \(r_{\text{min}}\) value throughout the domain (Fig. 5a, b) achieves the lowest compliance. In turn, the largest compliance is obtained when requiring a constant large minimum feature size (Fig. 5g, h). The compliances obtained with the two varying \(r_{\text{min}}\) maps fall in between the two extremes, with the discrete map (Fig. 5c, d) performing better than the linear (Fig. 5e, f). The design obtained with the discontinuous \(r_{\text{min}}\) map has a noticeable sudden change in the topological features at the discrete boundary (Fig. 5d). In contrast, the linear transition results in more smooth gradual variation of the feature sizes (Fig. 5h). When proceeding to manufacture, the sharp corners may give rise to valid concerns that they potentially will lead to residual stress or stress concentrations.
A nonlinear grading scheme is herein suggested to resolve the transition boundary issue without excessively sacrificing performance.
The following nonlinear function is used when grading the \(r_{\text{min}}\) map along the length of beam:
where \(\lambda\) is a user-specified parameter that controls the steepness of the nonlinear function and i1 runs from 1 to the number of elements along the beam length. Figure 6 plots the nonlinear function and illustrates the influence of the steepness parameter. Note that this equation provides a mesh-dependent transition. This is due to the fact that \(r_{\text{min}}\) will be distributed among the elements in the discretization. To limit the introduction of new parameters, the herein presented framework uses the same discretization for the \(r_{\text{min}}\) field as for the finite elements.
MBB results obtained with nonlinear grading of the \(r_{\text{min}}\) map are shown in Fig. 7. All designs are obtained with maps that separate the design domain in the same two distinct regions as in Fig. 5c; a small \(r_{{\text{min}}1}=3.2\) is applied near the center of the span and a large \(r_{{\text{min}}2}=9.6\) is specified close to the supports. Different values are taken for the steepness parameters \(\lambda\). It is seen that using the nonlinear grading in Eq. (12) preserves the feature size distinction on both sides of the transition boundary. In addition, a smoother feature size transition is observed than in Fig. 5d. The extent of the smoothness is influenced by \(\lambda\), where larger values of \(\lambda\) grades the transition over a longer distance. However, the length of the transition only has a minor influence on the final compliance. As such, the steepness parameter should be chosen based on the following two metrics: (1) the difference between two filtering radii and (2) the distance over which the transition is desired to occur. It should be noted that the choice of \(\lambda\) does not significantly influence the required computational resources.
MBB beam results designed with nonlinear \(r_{\text{min}}\) maps, pre-specified using Eq. (12). (a, c, e) gives the \(r_{\text{min}}\) distribution across the design domain and the resulting designs are shown in (b, d, f). All maps have a minimum \(r_{\text{min}}\) value of \(r_{{\text{min}}1} = 3.2\) and a maximum value of \(r_{{\text{min}}2} = 9.6\) and the steepness factor is set to (a, b) \(\lambda =3\), (c, d) \(\lambda =10\), and (e, f) \(\lambda =20\)
4 Selecting the feature size control in a Region of Interest (ROI)
As will be detailed in Section 5, the new hitop framework enables the design engineer to alter the minimum feature size in local regions around topological members of concern. Such a local region is herein defined as a Region of Interest (ROI).
For 2D design problems, this work suggests defining ROIs of elliptical shape. The implementation of hitop herein uses the 88 line code (Andreassen et al. 2011) as the backbone of the algorithm. In the 88 line code, the material distribution within the design domain is continuously plotted as the design evolves. The image resolution of each of these plots is \(nelx \times nely\). In this work, a ROI is defined by interactively drawing on top of an image of the material distribution. After drawing the ellipse, the elements with centroids inside the ROI are identified by a simple search. The ROI is herein drawn using the MATLAB Image Processing Toolbox (MATLAB 2020b) by defining the center \(x_{\text{c}}\), rotation angle \(\theta\), and 2 semi-axes (a, b). An illustrative example detailing the defining parameters of a 2D ROI is shown in Fig. 8.
Once a ROI has been defined, a different minimum feature size control can be prescribed within it. When selecting a single ROI this results in the \(r_{\text{min}}\) map having two distinct regions; \(r_{{\text{min}}1}\) that defines the minimum feature size control in the majority of the design domain and \(r_{{\text{min}}2}\) that is the updated size limit within the selected ellipse.
To avoid the issues with sharp transitions of the topological features reported in Section 3, this work applies a nonlinear grading scheme within the ROI. The grading scheme is based on Eq. (12), but is discretized with a user-specified \(n_{\text{c}}\) number of contours. When defining a ROI, the design engineer thus has to select the nonlinear transition degree \(\lambda\) and the number of contours \(n_{\text{c}}\). If the user selects \(n_{\text{c}}=0\), the nonlinear grading is not applied and the transition between the two \(r_{\text{min}}\) regions becomes discrete. Selecting \(n_{\text{c}} \ge 1\) herein defines a transition zone. The transition zone is illustrated in Fig. 9a and determines the number of elements over which the nonlinear function in Eq. (12) changes from \(r_{{\text{min}}1}\) to \(r_{{\text{min}}2}\). In this work, the transition zone is initiated and terminated when the change in the function values is \(\Delta r_{\text{min}} > 0.01\). The transition zone is subsequently divided into \(n_{\text{c}}\) intervals with equal numbers of elements. Each interval will be associated with the \(r_{\text{min}}\) value at its initiation.
When applying the transition zone to the \(r_{\text{min}}\) map, an additional \(n_{\text{c}}\) number of contour ellipses are drawn inside the ROI. Figure 9b shows how a ROI with \(\lambda = 3\) and \(n_{\text{c}} = 2\) makes two internal ellipses on the \(r_{\text{min}}\) map. The contour ellipses have the same center and rotational angle as the ROI. The contour spacing is such that the semi-axes are 3 pixels apart. The inner most ellipse defines the region with \(r_{\text{min}}=r_{{\text{min}}2}\). The \(n_{\text{c}}\) concentric regions between the inner contour and the ROI are prescribed the intermediate \(r_{\text{min}}\) values associated with each of the intervals.
Example of the nonlinear transition from \(r_{{\text{min}}1}\) to \(r_{{\text{min}}2}\), discretized by \(n_{\text{c}}\) number of contours here with \(\lambda = 3\) and \(n_{\text{c}}=2\). In a the transition zone and its division into \(n_{\text{c}}\) intervals are shown on the nonlinear grading function from Eq. (12), and b illustrates how the \(r_{\text{min}}\) map has \(n_{\text{c}}\)+2 zones with corresponding prescribed values
5 Human-Informed Topology Optimization
The new hitop framework consists of the following three steps:
-
(i)
An initial standard compliance minimization that solves Eq. (1) for a limited number of iterations with a uniform \(r_{\text{min}}\) map.
-
(ii)
A prompt asking the user to judge the quality of the design. If desired, the user can select one or more ROIs that change the \(r_{\text{min}}\) map locally.
-
(iii)
Equation (1) is resolved with the updated \(r_{\text{min}}\) map.
Steps (i-iii) can be repeated as necessary.
The initial standard compliance minimization in step (i) ensures that hitop has the ability to leverage the power of fully automated computational design exploration. In step (ii), the user has the ability to enrich the automatic design generation with their pre-existing knowledge. This is done by allowing the user to identify potential problematic design features and highlight these areas of concern. If, for example, selecting an ROI around a thin topological member and assigning a large \(r_{{\text{min}}2}\), the algorithm must respond in step (iii) by either placing more material within the ROI or removing the member of concern.
From the authors’ experimentation, it has been found that letting step (i) run for 50 iterations with \(p = 3\) and \(\beta =25\) is typically sufficient to generate a design solution that is reasonable for a user to judge. Additionally, \(\lambda = 3\) has been found to work well for all cases. This allows for a noticeable distinction between inside and outside of the ROI while maintaining a smooth transition between filtering radii.
For the examples herein, it has been found that 50 iterations within step (i) generally work well across design scenarios. All examples herein have been conducted with standard settings of the move limits within MMA. However, it should be noted that 50 iterations may not be sufficient if changing the move limits, designing with a very large reference \(r_{\text{min}}\), or different settings of p and/or \(\beta\).
In step (iii), the design is restarted from a uniform material distribution and continuation is applied to the SIMP exponent. The experimentation around step (iii) has included resuming the optimization with the new \(r_{\text{min}}\) map rather than restarting it. However, resuming the optimization was not found to work well. When the features are distinct enough for the user to identify areas of concern, the objective function has already narrowed in on a local minimum. When resuming with the new \(r_min\) map, the MMA optimizer used herein has generally not been able to navigate away from this local solution.
5.1 Numerical examples
The hitop framework is demonstrated on 2D benchmark problems. The example problems include the MBB beam from Fig. 4 and the medium cantilever beam that is illustrated in Fig. 1. The material properties and load magnitude are in both cases as taken as specified in Sect. 3. All examples presented use the same volume fraction in hitop and reference cases.
5.1.1 MBB beam
Figure 10 shows the hitop steps and result on an MBB example on one half of the \(L = 480\) and \(H = 80\) domain. The initial uniform \(r_{\text{min}}\) map is set to \(r_{{\text{min}}1}=3.2\).
Once the topology starts to take shape, the user selects a ROI around a thin member as indicated in Fig. 10a. The minimum feature size in this region is selected as \(r_{{\text{min}}2}=6.4\). The steepness of the nonlinear grading is set as \(\lambda = 3\) and \(n_{\text{c}}=3\) contours are chosen. Figure 10b reflects the changes that this imposes on the \(r_{\text{min}}\) map.
The design problem is resolved with the new \(r_{\text{min}}\) map and the final design result is shown in Fig. 10c. The user input is seen to have had a significant impact on the design. The specification of a larger \(r_{{\text{min}}2}\) within the ROI has made it uneconomical to place material here. The topological member of potential concern in Fig. 10a has therefore been eliminated, allowing more density to be allocated to the previously partial member.
MBB beam designed with hitop. (a) gives the initial density distribution that is presented to the design engineer for input. The user-selected ROI with \(n_{\text{c}}=3\) contours is indicated in white. In (b) the \(r_{\text{min}}\) map is updated based on the user input, and (c) gives the final density distribution. For replication purposes, the selected ROI can be described by the following parameters: \(x_{\text{c}}=(113.3,43.5)\), \((a,b)=(14.8,9.1)\), and \(\theta =306.7^\circ\)
5.2 Medium cantilever
Results obtained when using hitop to design medium cantilever beams are shown in Fig. 11. The designs are obtained on a \(192 \times 120\) mesh with a volume fraction of \(f=0.3\). Two different minimum feature size controls are imposed through the initial uniform maps, namely with \(r_{{\text{min}}1}=4.8\) (Fig. 11a–c) and \(r_{{\text{min}}1}=2.4\) (Fig. 11d–f). As expected, this results in the user being presented with two slightly different topologies after the initial 50 design iterations.
Design steps and results with hitop for a medium cantilever beam. The initial designs after 50 iterations with uniform feature size control are shown in (a, d), the update to the \(r_{\text{min}}\) map based on the user input is given in (b, e), and (c, f) shows the final designs. The initial \(r_{\text{min}}\) map is (a–c) \(r_{{\text{min}}1}=4.8\) and (d–f) \(r_{{\text{min}}1}=2.4\). The geometric parameters for the selected ROIs are (a–c) \(x_{\text{c}} = (96.3, 33.4)\), \((a,b)=(26,8, 16.6)\), \(\theta =62.5^\circ\) and (d–f) \(x_{\text{c}}=(102.0, 88.7)\), \((a,b)=(25.5, 19.6)\), and \(\theta =301.7^\circ\)
The user-selected ROIs are indicated in Fig. 11a and d.
For the design case in Fig. 11a–c, the user chooses to increase the minimum feature size in the ROI to \(r_{{\text{min}}2}=12.8\). The steepness of the nonlinear grading is set to \(\lambda = 3\) and the number of contours are chosen as \(n_{\text{c}} = 5\). This is seen to result in an increase in thickness of the member of concern. To accommodate the thickening of the member in the ROI while respecting the volume constraint, thinning of the rest of the topology is necessary. However, the thinning is in this case not found to visually change the overall topology.
The user selection also affects the result for the design case with smaller initial feature size control in Fig. 11d–f. Here, the user increases the minimum feature size in the ROI to \(r_{{\text{min}}2}=6.4\), while choosing \(\lambda = 3\) and \(n_{\text{c}} = 4\). The algorithm responds to the human input by fusing the two thin topological members within the ROI, creating a single-thicker member.
Medium cantilever beam designed with hitop where the user selects multiple ROIs. The design uses the same initial minimum feature size requirements as in Fig. 11c-f. The initial design solution after 50 iterations is shown in a that also indicates the four user-specified ROIs. In b the updated \(r_{{\text{min}}}\) map reflects the user-imposed changes to the minimum feature size controls and c gives the final design
The new hitop framework is not limited to the selection of a single ROI. A user can select as many ROIs as desired and prescribe different feature size controls within them. Figure 12 gives the same cantilever beam example as in Fig. 11c–f. However, here the user selects all the compressive members, in total four ROIs, as shown in Fig. 12a. Within the four regions, different feature size controls are imposed as revealed by the updated \(r_{{\text{min}}}\) map (Fig. 12b). The design algorithm can easily handle this complex \(r_{{\text{min}}}\) map and responds by providing a solution that has both fused and thickened topological members.
As expected, the compliance increases when the user imposes further design restrictions. This can be seen by comparison of the design solutions in Figs. 11f and 12c. For the shown examples with the same initial design requirements, the final compliance is 30.9% higher when selecting multiple ROIs.
6 Improving performance properties through human input
As mentioned in Section 1, changing the feature sizes of a design can sometimes be an intuitive way to improve certain mechanical properties. To demonstrate this notion, the current section presents examples where hitop is used to improve the buckling performance and limit a stress concentration.
6.1 Increasing the buckling load
The buckling benchmark problem of a short cantilever beam is considered (Fig. 13a). The domain is herein discretized with \(90 \times 210\) elements and the initial feature size control is defined uniformly by \(r_{{\text{min}}1}=2\). The applied load is taken as \(P =1\), and the volume fraction is taken as \(f = 0.15\).
Figure 13b shows the design results obtained when minimizing the compliance by solving Eq. (1).
Figure 13c gives the design solution obtained when maximizing the buckling load factor BLF. The result is obtained using the 250-line code (Ferrari et al. 2021) with the design in 13b as the initial guess. The compliance and buckling load factor are reported for both solutions. Running the 250-line code demands definition of additional parameters. The reader is referred to Ferrari et al. (2021) for a thorough explanation of these. They are herein taken as the standard settings, namely \(\texttt {ftBC} = \texttt {'N'}\), \(\texttt {eta} = 0.5\), \(\texttt {beta} = 6\), \(\texttt {ocPar} = [0.1,0.7,1.2]\), \(\texttt {penalG}=3\), \(\texttt {nEig}=12\), \(\texttt {pAgg}=160\), \(\texttt {prSel}=[\texttt {'B'},\texttt {'C'},\texttt {'V'}]\), and [1.2, 0.15]. Note here that the 250-line code uses the Heaviside filtering from Wang et al. (2011) rather than Guest et al. (2004). For ease of reproducibility and to avoid parameter tuning, the 250-line code is executed with its inbuilt Heaviside filter and recommended parameter settings.
The compliance design in Fig. 13b consists of two topological members that are equally sized. In contrast, the maximized buckling load design in Fig. 13c is more complex and places more material in the lower half of the design domain where compression dominates. This is seen to have a small negative impact on the compliance that is increased by 2.2%. However, the buckling load factor is approximately reduced by a factor of 5.
In Fig. 14, the same design problem is solved using hitop. The design engineer uses their experience to identify the compressive topological member as a ROI. The minimum feature size is increased locally to \(r_{{\text{min}}2}=15\) with a nonlinear steepness factor of \(\lambda = 6\) and \(n_{\text{c}} = 8\) contours. The obtained hitop design is shown in Fig. 14c. As expected, the user input negatively affects the compliance. However, the resulting buckling load factor is 2 times higher than for the compliance design in Fig. 13b.
As expected, using hitop does not permit reaching the same performance levels as when directly and rigorously optimizing the buckling load. However, it does allow the design engineer to improve upon a design in a simple and fast manner. In addition having significantly less input parameters, the computational requirement is smaller. For the simple examples in Figs. 13 and 14, hitop is able to double the buckling load in a matter of 20 minutes on a regular laptop. In contrast, 420 minutes are needed to achieve the performance improvement that is possible only with the 250-line code. Note that the solution time reported here for directly maximizing the buckling load does not account for the time associated with potentially needed parameter tuning.
Short cantilever from Fig. 13 designed with hitop; a gives the initial material distribution and indicates the selected ROI, b shows the updated \(r_{{\text{min}}}\), and c provides the final design solution
6.2 Limiting stress concentrations
To demonstrate hitop’s ability to limit stress concentrations, the benchmark L-bracket problem in Fig. 15a is considered. The load \(P=1\) is distributed over 8 nodes to eliminate singularities. The overall design domain (including the top right void region of size \(0.6L \times 0.6H\)) is discretized using a \(150 \times 150\) mesh and the volume fraction is selected as \(f=0.23\).
For the current example, the minimum feature size control is applied to the void phase of the design. The reader is referred to Guest (2009) for details on how to change from solid to void feature size control. The minimum feature size is initially set uniformly to \(r_{{\text{min}}1}=2\). The design problem is modified slightly to give human engineer control over the fillet size at the entrant corner. This is done by letting 3 design variables on each side be prescribed to zero. Similarly, 7 solid elements are prescribed under the loaded tip.
Figure 15 shows the hitop workflow and solution. After 50 iterations, the user identifies the entrant corner as a region of concern for a potential stress concentration. In response, a ROI is defined as shown in Fig. 15d and a local fillet radius of \(r_{{\text{min}}2}=4\) is selected. The transition from \(r_{{\text{min}}1}\) to \(r_{{\text{min}}2}\) is chosen to have \(n_{{\text{c}}}=4\) contours and steepness \(\lambda =3\). The optimized design in Fig. 15e responds by having a larger fillet. The stress distributions with a uniform \(r_{{\text{min}}}\) map and after the change are shown in Fig. 15c and f. These refer to the stress distributions for fully converged designs. It is evident that the simple change of the the local fillet radius does not eliminate the stress concentration. However, making the corner fillet larger does reduce the von Mises stress by 10.8%.
L-Bracket designed with hitop where the minimum feature size control is prescribed to the void phase of the design. a shows the design domain, loading, and boundary conditions of the problem. The initial design solution after 50 iterations and the selected ROI are shown in b. In d the updated \(r_{{\text{min}}}\) map reflects the user-imposed changes to the minimum feature size controls and e gives the final design. The von Mises stress distributions obtained with a constant \(r_{{\text{min}}}=r_{{\text{min}}1}\) map for (e) are given in c and f, respectively
7 Extension to 3D
The new hitop framework is straight forward to extend to 3D. To demonstrate this notion, the cantilever problem in Fig. 16 is considered. The dimensions of the design domain are taken as \(L=48\), \(H=96\), and \(D=96\), and the applied load is \(P=10\). The volume faction of the desired design is \(f=0.1\). The initial minimum feature size for the solid features is uniformly set to \(r_{{\text{min}}1}=1.5\). The extension to 3D is herein done using the 3D Multi Grid Conjugate Gradient (MGCG) MATLAB code from Amir et al. (2014), modified as described in Section 2. The parameters associated with the MGCG code are set at default: nl=4, cgtol=1e-10, and cgmax=100.
The workflow and obtained design are shown in Fig. 17. The design at 50 iterations and the selected ROI are shown in Fig. 17a. To simplify the presentation of the results, a cuboid-shaped ROI that contains almost the entire lower half of the design domain is selected.
The minimum feature size in the ROI is user-specified as \(r_{{\text{min}}2}=6\), with \(\lambda =3\) and \(n_{{\text{c}}}=4\) (Fig. 17b, e).
Prior to receiving the user input, the top and bottom members have the same cross-section. This is illustrated in Fig. 17d that give a 2D slice of the design at L/2. As clearly visible in the final solution in Fig. 17c, the user input thickens the lower topological members. Interestingly, the diameter of the top members also increase. However, as revealed by the slice in Fig. 17f, the top members are designed with internal voids such that they have a lower material consumption than the bottom members.
3D cantilever designed with hitop where the user selects a cuboid-shaped ROI. The initial design solution after 50 iterations and selected ROI are shown in a. In b the updated \(r_{{\text{min}}}\) map reflects the user-imposed changes to the minimum feature size controls and c gives the final design. 2D slices at L/2 of the the plots in a–c are provided where d gives the initial design, e shows the updated \(r_{{\text{min}}}\) map, and f gives the final design
8 Conclusion
This work has presented a new topology optimization framework that allows human input during the design process. With the aim of obtaining designs that address multiple or complex performance and/or manufacturing requirements using simple compliance minimization, the user is given the ability to update the minimum feature size controls locally in the design domain. The new framework allows the design engineer to access the exploratory power of topology-optimized designs while actively using their expertise and previous experience. It is stipulated that the low resources requirements of hitop (computational and engineering hours for training and design set-up) will enable the use of topology optimization tools for a wide range of applications where it is currently perceived as inaccessible. Examples include the so-called ’every-day’ and ’in-the-field’ design situations. It should be emphasized that using hitop does not allow the user to reach the same levels of superior performance that are possible with more complex topology optimization schemes. If access and resources are available for high-performance computing, complex problem formulation, and tuning, such an approach should be the preference. This notion has been demonstrated herein through the buckling load example in Section 6. However, the new framework is not intended to supplant existing rigorous approaches, but rather aimed at obtaining performance improvement in cases where these frameworks cannot be used.
Enabling human input does not come without risks for the design outcome. If the design engineer does not provide quality input, the performance of the final design may deteriorate rather than improve. In experimenting with the presented framework, the authors have found that identifying a suitable ROI that improves the structural performance is not always a trivial task. This is especially the case for more complex designs. A recommendation for future implementations of hitop is therefore to provide the design engineer with additional information when prompted to judge the design. This could, for example, include the stress distribution, buckling shape, or simulation results that asses the manufacturability of the design.
References
Amir O, Lazarov BS (2018) Achieving stress-constrained topological design via length scale control. Struct Multidisc Optim 58(5):2053–2071
Amir O, Aage N, Lazarov BS (2014) On multigrid-cg for efficient topology optimization. Struct Multidisc Optim 49(5):815–829
Andreassen E, Clausen A, Schevenels M, Lazarov BS, Sigmund O (2011) Efficient topology optimization in matlab using 88 lines of code. Struct Multidisc Optim 43(1):1–16
Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):193–202
Bendsøe MP, Sigmund O (2003) Topology optimization: theory, methods and applications, 1st edn. Springer-Verlag, Berlin
Borrvall T (2001) Topology optimization of elastic continua using restriction. Arch Comput Method Eng 8(4):351–385
Bourdin B (2001) Filters in topology optimization. Int J Numer Method Eng 50(9):2143–2158
Bruns TE, Tortorelli DA (2001) Topology optimization of non-linear elastic structures and compliant mechanisms. Comput Method Appl Mech Eng 190(26):3443–3459
Carstensen JV, Guest JK (2018) Projection-based two-phase minimum and maximum length scale control in topology optimization. Struct Multidisc Optim 58(5):1845–1860
Carstensen JV, Lotfi R, Chen W, Szyniszewski S, Gaitanaros S, Schroers J, Guest JK (2022) Topology-optimized bulk metallic glass cellular materials for energy absorption. Scripta Mater 208:114361
Dalklint A, Wallin M, Tortorelli DA (2021) Structural stability and artificial buckling modes in topology optimization. Struct Multidisc Optim 64(4):1751–1763
Diaz A, Sigmund O (1995) Checkerboard patterns in layout optimization. Struct Multidisc Optim 10(1):40–45
Duysinx P, Bendsøe MP (1998) Topology optimization of continuum structures with local stress constraints. Int J Numer Method Eng 43(8):1453–1478
Fernández E, Yang K-K, Koppen S, Alarcón P, Bauduin S, Duysinx P (2020) Imposing minimum and maximum member size, minimum cavity size, and minimum separation distance between solid members in topology optimization. Comput Method Appl Mech Eng 368:113157
Ferrari F, Sigmund O (2019) Revisiting topology optimization with buckling constraints. Struct Multidisc Optim 59(5):1401–1415
Ferrari F, Sigmund O, Guest JK (2021) Topology optimization with linearized buckling criteria in 250 lines of matlab. Struct Multidisc Optim 63(6):3045–3066
K. K. Fu, M. C. Yang, K. L. Wood (2016) Design principles: literature review, analysis, and future directions, J Mech Design 138(10): 101103
Gao X, Ma H (2015) Topology optimization of continuum structures under buckling constraints. Comput Struct 157:142–152
Guest JK (2009) Topology optimization with multiple phase projection. Comput Method Appl Mech Eng 199(1):123–135
Guest JK (2009) Imposing maximum length scale in topology optimization. Struct Multidisc Optim 37(5):463–473
Guest JK, Prévost JH, Belytschko T (2004) Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int J Numer Method Eng 61(2):238–254
Holmberg E, Torstenfelt B, Klarbring A (2013) Stress constrained topology optimization. Struct Multidisc Optim 48(1):33–47
Jewett JL, Carstensen JV (2019) Topology-optimized design, construction and experimental evaluation of concrete beams. Automat Constr 102:59–67
Kambampati S, Chung H, Kim HA (2021) A discrete adjoint based level set topology optimization method for stress constraints. Comput Method Appl Mech Eng 377:113563
Lawry M, Maute K (2015) Level set topology optimization of structural problems with interface cohesion. Struct Multidisc Optim 52(6):1107–1119
Lazarov BS, Wang F (2017) Maximum length scale in density based topology optimization. Comput Method Appl Mech Eng 318:826–844
Lazarov BS, Wang F, Sigmund O (2016) Length scale and manufacturability in density-based topology optimization. Arch Appl Mech 86(1):189–218
Le C, Norato J, Bruns T, Ha C, Tortorelli D (2010) Stress-based topology optimization for continua. Struct Multidisc Optim 41(4):605–620
Liu J (2019) Piecewise length scale control for topology optimization with an irregular design domain. Comput Method Appl Mech Eng 351:744–765
Lund E (2009) Buckling topology optimization of laminated multi-material composite shell structures. Compos Struct 91(2):158–167
M. E. Lynch, S. Sarkar, K. Maute (2019) Machine learning to aid tuning of numerical parameters in topology optimization. J Mech Design 138(10):114502
MATLAB, version (2020b) The MathWorks Inc., Natick, Massachusetts
Moreno DP, Blessing LT, Yang MC, Hernández AA, Wood KL (2016) Overcoming design fixation: design by analogy studies and nonintuitive findings. Artif Intell Eng Design Anal Manuf 30(2):185–199
Mueller CT, Ochsendorf JA (2015) Combining structural performance and designer preferences in evolutionary design space exploration. Automat Constr 52:70–82
Picelli R, Townsend S, Brampton C, Norato J, Kim HA (2018) Stress-based shape and topology optimization with the level set method. Comput Method Appl Mech Eng 329:1–23
Rozvany GIN, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Optim 4(3–4):250–252
Russ JB, Waisman H (2020) A novel topology optimization formulation for enhancing fracture resistance with a single quasi-brittle material. Int J Numer Method Eng 121(13):2827–2856
Schmidt M-P, Pedersen CB, Gout C (2019) On structural topology optimization using graded porosity control. Struct Multidisc Optim 60(4):1437–1453
Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidisc Optim 33(4–5):401–424
Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Multidisc Optim 16(1):68–75
Svanberg K (1987) The method of moving asymptotes: A new method for structural optimization. Int J Numer Method Eng 24(2):359–373
Wallin M, Jönsson V, Wingren E (2016) Topology optimization based on finite strain plasticity. Struct Multidisc Optim 54(4):783–793
Wang F, Lazarov BS, Sigmund O (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidisc Optim 43(6):767–784
Wang C, Zhao Z, Zhou M, Sigmund O, Zhang XS (2021) A comprehensive review of educational articles on structural and multidisciplinary optimization. Struct Multidisc Optim 64(5):2827–2880
Xu S, Cai Y, Cheng G (2010) Volume preserving nonlinear density filter based on heaviside functions. Struct Multidisc Optim 41(4):495–505
Yan X, Bao D, Zhou Y, Xie Y, Cui T (2022) Detail control strategies for topology optimization in architectural design and development. Front Architect Res 11(2):340–356
Yang K, Zhao Z-L, He Y, Zhou S, Zhou Q, Huang W, Xie YM (2019) Simple and effective strategies for achieving diverse and competitive structural designs. Extreme Mech Lett 30:100481
Zhou M, Lazarov BS, Wang F, Sigmund O (2015) Minimum length scale in topology optimization by geometric constraints. Comput Method Appl Mech Eng 293:266–282
Acknowledgements
No funding was received for the current research.
Funding
Open Access funding provided by the MIT Libraries.
Author information
Authors and Affiliations
Contributions
Dat Ha and Josephine Carstensen contributed equally to this work.
Corresponding author
Ethics declarations
Conflict of interest
The authors did not receive support from any organization for the submitted work. The authors have no competing interests to declare that are relevant to the content of this article.
Replication of results
Sufficient information is provided within the paper to reproduce the results presented in Figs. 5, 6, 7, 10, 11, and 13. Additional information regarding the other examples can be made available upon request.
Supplementary Information
The MATLAB version of the 2D MBB beam of Fig. 10 in this article can be accessed online via the following link: https://github.com/datquocha/CarstensenGroup_Public.
Additional information
Responsible Editor: Xiaojia Shelly Zhang
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ha, D.Q., Carstensen, J.V. Human-Informed Topology Optimization: interactive application of feature size controls. Struct Multidisc Optim 66, 59 (2023). https://doi.org/10.1007/s00158-023-03512-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-023-03512-0