Expedited surrogate-based quantification of engineering tolerances using a modified polynomial regression

Abstract

Statistical analysis is frequently used to determine how manufacturing tolerances or operating condition uncertainties affect system performance. Surrogate is one of the accelerating ways in engineering tolerance quantification to analyze uncertainty with an acceptable computational burden rather than costly traditional methods such as Monte Carlo simulation. Compared with more complicated surrogates such as the Gaussian process, or Radial Basis Function (RBF), the Polynomial Regression (PR) provides simpler formulations yet acceptable outcomes. However, PR with the common least-squares method needs to be more accurate and flexible for approximating nonlinear and nonconvex models. In this study, a new approach is proposed to enhance the accuracy and approximation power of PR in dealing with uncertainty quantification in engineering tolerances. For this purpose, first, by computing the differences between training sample points and a reference point (e.g., nominal design), we employ certain linear and exponential basis functions to transform an original variable design into new transformed variables. A second adjustment is made to calculate the bias between the true simulation model and the surrogate’s approximated response. To demonstrate the effectiveness of the proposed PR approach, we provide comparison results between conventional and proposed surrogates employing four practical problems with geometric fabrication tolerances such as three-bar truss design, welded beam design, and trajectory planning of two-link and three-link (two and three degrees of freedom) robot manipulator. The obtained results prove the preference of the proposed approach over conventional PR by improving the approximation accuracy of the model with significantly lower prediction errors.

1 Introduction

The identification and modeling of uncertainty sources are critical steps in solving any uncertainty quantification problem. Each uncertain model parameter can be represented in a probabilistic setting by a random variable and a corresponding probability density function (PDF) of the form $X\sim {f}_{X}(x)$ (Lataniotis et al. 2015). Manufacturing tolerances, particularly those relating to geometry parameters, can have a significant impact on the performance of engineering designs. To account for these, geometric tolerance analysis or uncertainty quantification is required (Du et al. 2019). Uncertainty quantification is becoming an increasingly important field in the majority of modern engineering contexts (and in applied sciences in general). To account for the uncertainty in physical processes and measurements, deterministic scenario-based predictive modeling is gradually being replaced by stochastic modeling. This rapid transition, however, comes at the cost of dealing with significantly increased amounts of data (e.g., when Monte Carlo simulation is used), frequently necessitating repeated expensive computational model evaluations (Marelli et al. 2014).

One of the major challenges in statistical analysis for uncertainty quantification is the computational requirement of the simulation (mathematical) model used to evaluate the large-scale engineering problems at hand (Dutta and Gandomi 2020). By replacing costly-to-evaluate computational models, surrogate modeling (also known as metamodeling) tries to counterbalance the additional costs associated with stochastic modeling (e.g., finite element analysis) for less expensive-to-evaluate surrogates (Amaran et al. 2016; Kleijnen et al. Aug. 2005; Simpson et al. 2001). Because of their improved versatility, nonlinear interpolating functions of surrogates, such as RBF and Kriging, have received a lot of attention in a variety of engineering design applications, including optimization, what-if analysis, and sensitivity analysis, and have been used most recently in engineering robust design and uncertainty management, see (Chatterjee et al. 2019; Parnianifard et al. 2019a, 2018). These models, however, frequently involve more parameters and nonlinear, nonconvex terms that are difficult to optimize globally (Boukouvala and Floudas 2017; Kim and Boukouvala 2019). Yet, it is common to employ reputable surrogates such as ANN, Kriging (also called Gaussian process), RBF, and polynomial chaos expansion, as their fitting functionality has been confirmed in the literature (Amaran et al. 2016; Miriyala et al. 2016), probably the most widely used methods are different-order polynomial regression techniques because of simpler formulation (Myers et al. 2016), however, it is less flexible and inaccurate (Parnianifard et al. 2019; Gano et al. 2006; Kleijnen 2017; Jin et al. 2003). The main purpose of the current study is to improve the performance of conservative polynomial regression and assess the compression results between the conventional approach and the proposed promising method using the different case studies and engineering problems in the statistical analysis of manufacturing tolerances.

The application of transforming of model’s variables has been highlighted when the variance of the original observations tends to be constant for all values of the response vector, so transformations may stabilize the situation, see (Tibshirani 1988; Myers et al. 2012). Generally, employing the transformation of the response variables instead of the original model’s responses has been employed for three main purposes: stabilizing the variance, making the distribution of the variable closer to the normal distribution, and improving the fit of the model to the data. This last objective could include model simplification, say by eliminating interaction, or higher-order polynomial terms, see (Myers et al. 2016). Here we are interested to study the variability of a model in the vicinity of the nominal design (uncertainty quantification), so transformation which magnifies the differences between perturbed designs and nominal design can allow a better fit for the different-order polynomial model than the original metric. In other words, the model can fit small changes in perturbed designs compared with nominal designs. Also, in such cases, the effect of the transformed design variables on the response is more underlined compared with the original variables (Breiman and Friedman 1985; Montgomery et al. 2021; Hoeting et al. 2002).

On the other side, bias correction can be done for smoothing by minimizing coverage error and increasing robustness to tuning parameter choice (Neumann 1997; Calonico et al. 2018). Bias reduction can provide a smoother local prediction in different orders of polynomial regression, see (Xia 1998; Karson 1970). In (Khuri and Mukhopadhyay 2010), it was shown that more reduction in the variance of linear regression was possible by introducing a little bias. In the current paper, we are interested in bias estimation for data-driven polynomial regression, while we reveal it can reduce the over and lower fitting due to variability in the model by manufacturing tolerances. Notably, the quality of surrogate construction also strongly depends on the distribution of training points, sample size, and optimally adjustments of hyperparameters of the surrogate. Hyperparameter optimization along with control on a number of expensive simulations keeping in mind the model doesn’t get overfitted has been performed in the literature (Kiran Inapakurthi 2022). There are new studies in the literature has been proposed the trade-off between model accuracy and sample size, with optimization of the surrogate’s hyperparameters for surrogate model development, see (Miriyala et al. 2018; Inapakurthi et al. 2021).

In this paper, we aim at proposing a promising approach named Modified Polynomial Regression (MPR) to improve the performance (accuracy and robustness) of Ordinary Polynomial Regression (OPR) in engineering tolerance design that deals with uncertainty quantification. The traditional formulation in OPR produces an inaccurate model because it cannot capture the nonlinearity of the actual function. While more complex surrogates like Kriging produce a rather accurate model, their functional form is complex (i.e., the number of terms is equal to the number of samples used). Therefore, the proposed MPR attempts to bridge the gap between model accuracy, computational complexity, and interpretability. To construct MPR, we first employ a particular basis function (linear or exponential) to transform an original design of variables into new transformed variables by computing the differences between training sample points with a reference point (e.g., a center of design space under study as a location of the nominal point). The differential evolution (DE) is applied to compute the optimal hyperparameters to estimate the bias function to correct the prediction error by MPR (i.e., other evolutionary algorithms like Genetic algorithm, or particle swarm also can be used instead of DE; however, in this study DE is used due to efficiency, applicability, and simplicity formulation). In each iteration of the DE optimizer, we compute the sum square error by the leave-one-out cross-validation approach as a fitness function of the DE optimizer.

The major contributions of this study can be highlighted as (i) a simple, and yet reliable surrogate method is proposed by enhancing the conventional PR, (ii) a comprehensive comparison is provided to study the performance of the MPR technique for surrogate modeling with the OPR technique in the same platforms of uncertainty quantifications and geometric tolerance analysis of different practical engineering design problems, (iii) the proposed approach can modify different degrees of PR (e.g., linear, quadratic, cubic, etc.).

The rest of this paper is organized as follows. The recent developments regarding the subject of the current paper in the literature are concisely reviewed in Sect. 2. Section 3 provides more descriptions regarding the overall framework for a geometric tolerance analysis in engineering design problems, ordinary (conventional) PR, and the measurement indexes that we used in this paper to compare the performances of both conventional and proposed MPR. In Sect. 4, the proposed approach is elaborated in detail. The comparison results between ordinary and modified PR for uncertainty quantifications of different practical engineering and robotic problems are discussed in Sect. 5. Finally, this paper is concluded in Sect. 6.

2 Related works

Engineering design includes the quantification of uncertainty as a key component. In actuality, the uncertainty of numerous kinds could have an unfavorable impact on how the system functions. Therefore, determining whether the system is likely to meet the required performance standards may depend on how appropriately they are quantified (Pietrenko-Dabrowska et al. 2020). Given that manufacturing tolerances often take the shape of probability distributions and are stochastic, quantifying calls for statistical analysis (Polini 2011). In the manufacturing process, items are put together from parts or components that have been produced or processed using various methods or equipment. Due to the inherent variability imposed by the machines, tools, raw materials, and human–machine interface, differences in the quality attributes (length, diameter, thicknesses, tensile strength, etc.) will always exist (Chandra 2001). The existence of unwanted variation and the requirement for interchangeability necessitate the specification of some limits for the fluctuation of any quality feature. Tolerances are used to describe these permissible deviations (Jeang 2001; Walter et al. 2014). Only if the variation of the production attribute obtained through parameter design is unsatisfactory, tolerance design is implemented. In general, statistical analysis techniques used in uncertainty quantification can be classified to:

• (i) Model-based or simulation-based design using Monte Carlo experiments (Papadopoulos and Yeung 2001; Janssen 2013), robust design (Choi 2005; Du and Chen 2002), Bayesian inference method (Li and Wang 2020; Chandra et al. 2019), Taguchi parameter design (Parnianifard et al. 2019b; Díaz and Hernández 2010), reliability-based design optimization (António and Hoffbauer 2017; Alyanak et al. 2008), etc. (Abdar et al. 2021; Lalléchère et al. 2019).

• (ii) Surrogate-based stochastic design using polynomial chaos expansion (Crestaux et al. 2009; Hariri-Ardebili and Sudret 2020), PR (also called response surface methodology) (Prasad et al. 2016; Dellino et al. 2010), Gaussian process (also called Kriging) (Rohit and Ganguli 2021; Li and Wang 2019), etc. (Keane and Voutchkov 2020; Sudret et al. 2017).

Due to the necessity of doing neighborhood assessments of each solution to calculate the configuration errors and reliability, the computing component of standard uncertainty quantification can frequently become computationally costly. Uncertainty quantification with the aid of surrogates (also known as metamodels) is one of the effective solutions to this problem of computational expense (Soares do Amaral 2020; Bhosekar and Ierapetritou 2018). A surrogate model is a precise approximation of the input–output information from the simulation. After a surrogate is trained employing input–output data, analytical approximations of the constraints and the goal of a black-box problem become available, and these are computationally less expensive to analyze and compute derivatives for (Bhosekar and Ierapetritou 2018). There are two types of surrogate models now available: interpolating and noninterpolating (Wang et al. 2014). Interpolating algorithms like Kriging (Kleijnen 2017) and RBF (Jakobsson et al. 2010) have more versatility since they incorporate multiple basis functions (or kernels) that are created to precisely anticipate the training points (Jin et al. 2003; Li et al. 2010; Hussain et al. 2002). Models have been effectively employed in a variety of fields, including steady-state flowsheet simulation (Palmer and Realff 2002), pharmaceutical process modeling (Boukouvala et al. 2011), Geostatistics and environmental science (Li and Heap 2011), and aerospace and aerodynamic design challenges (Yondo et al. 2018; Jeong et al. 2005) in particular. These models, however, frequently involve more parameters and nonconvex, highly nonlinear components that are difficult to optimize globally (Boukouvala and Floudas 2017; Gano et al. 2006).

Non-interpolating regression models may result in simple and understandable functional forms, such as different orders of polynomial regression (Angün et al. 2009), which seek to lower the sum of squared errors between a predetermined conceptual model and the data points gathered. To detect highly nonlinear interactions, nonetheless, they are not adaptable enough (Jones 2001). The traditional PR of Box and Wilson (Box and Wilson 1992) searches for the set of continuous inputs that reduces the single output of a real-world system (or maximizes that output). In comprehensive surveys in the literature, such as (Khuri and Mukhopadhyay 2010; Kleijnen 2008; Myers et al. 2004), numerous applications of PR are discussed. (Kleijnen 2015) and (Myers et al. 2016) are two recent full textbooks in public relations. Studies of Angün et al. (2009); Kleijnen 2008), and (Angun 2004) show how PR has been used in simulation-based optimization in actual engineering design. To identify the uncertain inputs that have the greatest effect on the variability of the model output, uncertainty quantification is a crucial step that can be sped up via PR (Sudret 1203; Victor et al. 2022; Allen and Camberos 2009).

3 Problem statement

In many real-world engineering difficulties, complicated computer simulations are utilized to obtain more accurate and high-fidelity information about complex, multiscale, multiphase, and/or distributed systems. However, they usually employ proprietary codes, if–then operators, or numerical integrators to depict phenomena that cannot be accurately captured by physics-based algebraic equations (Boukouvala and Floudas 2017). The system cannot be immediately improved using derivative-based optimization techniques since the algebraic model and derivatives are either absent or too challenging to get. These issues are referred to as “black-box” systems since the constraints and objective(s) of the problem cannot be stated as closed-form equations (Amaran et al. 2016; Hong and Zhang 2021). In this study, we particularly address the following black-box problem (Eq. (1)), in which the explicit forms of the constraints ${{g}_{j}}\left(x\right)$ and the objective ${f}\left(x\right)$ are both unknown.

$$Minor\,Max:f\left( x \right), \ldots x \in \mathbb{R}^{n}$$

$$Subject\,to:g_{j} \left( x \right) \le 0,j = {\text{1}},{\text{2}}, \ldots ,J$$

(1)

In Eq. (1), $J$ denotes the number of constraints. An optimization issue that is not a black box because restrictions and/or the objective can be expressed algebraically is referred to as a gray box or hybrid optimization problem. These formulas can be used in a variety of engineering design situations, see (Yondo et al. 2018; Deb 2012; Parkinson et al. 2013; Parnianifard et al. 2019c, 2020).

3.1 Analysis of manufacturing tolerances

In practical engineering optimal designs, statistical analysis is used to account for changes in geometry and material properties brought on by production tolerances. These are measured using the presupposed probability distributions, which are commonly uniform or Gaussian. Let ${f}_{ }\left(x\right)$ stand for the output of the simulation model (or algebraically mathematical model) under design ${\varvec{x}}={\left[{x}_{1},{x}_{2},\cdots ,{x}_{m}\right]}^{T}\in X$ is a vector of adjustable variables. Typically, the parameter space $X$ is defined by the lower and upper bounds ${\varvec{l}}={\left[{l}_{1}\dots {l}_{m}\right]}^{T}$ and ${\varvec{u}}={\left[{u}_{1}\dots {u}_{m}\right]}^{T}$ so that ${l}_{k}\le {x}_{k}\le {u}_{k}$, $k=1,\dots ,m$. Given the scalar merit function $U$ quantifying the design utility, the optimization task can be defined as:

$$x^{*} = \left\{ {arg\,\mathop {{\text{min}}}\limits_{{x \in X}} U(f(x))|\begin{array}{*{20}c} {g_{j} \left( {x^{*} } \right) \le 0,} \\ {forj = {\text{1}},{\text{2}}, \ldots ,J} \\ \end{array} } \right\}$$

(2)

Let ${{\varvec{x}}}^{*}$ to be called nominal (optimal) design. By considering manufacturing tolerance, the perturbed designs in the vicinity of the nominal design of the size ${\varvec{d}}= {[{d}_{1},. . ., {d}_{m}]}^{T}$ (i.e., the interval$\left[{{\varvec{x}}}^{*}-{\varvec{d}},{{\varvec{x}}}^{*}+{\varvec{d}}\right]$) are characterized as:

$${\Delta {\varvec{x}}}^{*}={\left[{x}_{1}^{*}+{\delta }_{1},\dots ,{x}_{k}^{*}+{\delta }_{k},\dots ,{x}_{m}^{*}+{\delta }_{m}\right]}^{T}$$

(3)

where ${\delta }_{k}$ ($1\le k\le m$) is the $k$ th parameter’s random departure from its nominal value. Due to manufacturing inaccuracies (geometric tolerances), it is supposed that ${\Delta {\varvec{x}}}^{*}$ is defined by a specific probability distribution (such as a Gaussian distribution with zero mean and a specific standard deviation or a uniform distribution with a specific lower and upper bound, e.g., ${\delta }_{k}\in \left[-{d}_{\mathrm{k}},{+d}_{\mathrm{k}}\right]$). After performing optimization and obtaining nominal design, it is interesting to carry out the required statistical analysis considering tolerances centered on predefined nominal design.

3.2 Surrogate-based polynomial regression

The computational requirements of the simulation (numerical) model that is used to analyze the sizable engineering problems under consideration represent one of the major challenges for statistical analysis when attempting to quantify the effects of uncertainty resulting from manufacturing tolerances. To get around this problem, replacement models known as surrogate models are frequently utilized in place of high-fidelity simulation models (Pietrenko-Dabrowska et al. 2020; Koziel 2015). One of the surrogates commonly employed for analysis of uncertainty in engineering designs is a different order of PR, see (Kleijnen 2017; Victor et al. 2022; Roderick et al. 2010). The primary goal of PR is typically the approximate determination of the underlying response function using the Taylor series expansion centered on a set of design points. The first-order PR model’s broad overview is displayed as:

$$y=f\left(X\right)={\widehat{\beta }}_{0}+\sum_{i=1}^{m}{\widehat{\beta }}_{i}{x}_{i}+\varepsilon$$

(4)

where $m$ denotes the number of design variables, ${\widehat{\beta }}_{0}$ and ${\widehat{\beta }}_{i}$ show regression coefficients, and the expression $\varepsilon$ is the random error (noise) element. In a multiple linear regression model, the regression coefficients are commonly estimated using the method of least squares. Assume that $n>m$ statements on the response variable are available, named ${y}_{1}, {y}_{2},\dots , {y}_{n}$. In conjunction with each stated response${y}_{i}$, observations will be made for each regressor variable. Let ${x}_{ij}$ refer to the $i$ th level of variable (observation)${x}_{j}$. It is assumed that the error phrase $\varepsilon$ in the model specified by $E(\varepsilon )=0$ and Var ($\varepsilon$) = ${\sigma }^{2}$ and that the $\{ {\varepsilon }_{i} \}$ are uncorrelated random variables. It is simpler to solve the least-squares model in a matrix notation. The model in terms of the observations, for example for the linear form of the model in Eq. (4), in matrix notation is expressed as:

$$y\, = \,X\beta \, + \,\varepsilon$$

(5)

where

$${\varvec{y}}=\left[\begin{array}{c}{y}_{1}\\ \begin{array}{c}{y}_{2}\\ \vdots \end{array}\\ {y}_{n}\end{array}\right], {\varvec{X}}=\left[\begin{array}{c}\begin{array}{ccc}1& {x}_{11}& {x}_{12}\\ 1& {x}_{21}& {x}_{22}\\ \vdots & \vdots & \vdots \end{array}\\ \begin{array}{ccc}1& {x}_{n1}& {x}_{n2}\end{array}\end{array} \begin{array}{c}\begin{array}{cc}\dots & {x}_{1m}\\ \dots & {x}_{2m}\\ & \vdots \end{array}\\ \begin{array}{cc}\dots & {x}_{nm}\end{array}\end{array}\right],{\varvec{\beta}}=\left[\begin{array}{c}{\beta }_{1}\\ \begin{array}{c}{\beta }_{2}\\ \vdots \end{array}\\ {\beta }_{n}\end{array}\right],{\varvec{\varepsilon}}=\left[\begin{array}{c}{\varepsilon }_{1}\\ \begin{array}{c}{\varepsilon }_{2}\\ \vdots \end{array}\\ {\varepsilon }_{n}\end{array}\right]$$

As a whole, $y$ is an $n\times 1$ vector of the responses (train points), and the $n\times p$ matrix of $X$ is created by the levels of the independent variables that are expanded into model form, $\beta$ and $\varepsilon$ are $p\times 1$ vector of the regression coefficients and $n\times 1$ vector of random errors, respectively. Observe that $X$ is made up of the independent variable’s column(s) plus a column of $1s$ to represent the model’s intercept term. Finding the least-squares estimator vector that minimizes:

$$L=\sum_{i=1}^{n}{{\varepsilon }_{i}}^{2}$$

(6)

The estimators of least squares are required to satisfy $\frac{\partial L}{\partial \beta }$, and thus the least-squares estimator of $\beta$ is obtained by:

$$\beta ={\left({X}^{^{\prime}}X\right)}^{-1}{X}^{^{\prime}}y$$

(7)

In most cases, the response surface’s curvature is greater than the first model’s ability to approximate it, even with the interaction terms; therefore, a higher-order regression model (such as a quadratic or cubic model) can be used. For instance, a second-order (quadratic) model is shown as:

$$y=f\left(X\right)={\widehat{\beta }}_{0}+\sum_{i=1}^{k}{\widehat{\beta }}_{i}{x}_{i}+\sum_{i=1}^{k}{\widehat{\beta }}_{ii}{x}_{i}^{2}+\sum_{i=1}^{k}\sum_{i<j=2}^{k}{\widehat{\beta }}_{i\mathrm{j}}{x}_{i}{x}_{j}+ \varepsilon$$

(8)

where ${\widehat{\beta }}_{0}, {\widehat{\beta }}_{i}, {\widehat{\beta }}_{ii}$ and ${\widehat{\beta }}_{ij}$ are unknown regression coefficients. The method of least squares is used as well to estimate the unknown regression coefficients. Regarding solving the model of least-squares error using matrix notations for regressors estimation, refer to Myers et al. (2016).

4 Proposed methodology

4.1 Modified polynomial regression

The OPR has been commonly used as a regression-based surrogate that led to simpler formulations, but it is less flexible and inaccurate compared to more complex surrogates such as the Gaussian process and RBF (Parnianifard et al. 2019; Victor et al. 2022). Here, a promising approach is proposed to improve the performance (accuracy and robustness) of the common framework of PR applied in engineering tolerance design. Different orders of PR including linear, quadratic, cubic, and higher orders are targeted by the proposed approach. Overall, the operation of the proposed approach can be outlined in two aspects of PR, (i) performing a basis function (linear or exponential) to transform an original design of variables into new transformed variables by computing the differences between training sample points with a reference point (e.g., a center of design space under study as a location of the nominal point), and (ii) estimating the bias function to correct the prediction error by MPR using the DE optimizer by computing the sum square error of the leave-one-out cross-validation as a fitness function. Let’s rewrite Eq. (5) with the proposed modification as below:

$${\varvec{y}}={{\varvec{X}}}^{{\varvec{E}}}{{\varvec{\beta}}}^{{\varvec{U}}}+{\varvec{\varepsilon}}+Bias$$

(9)

where ${{\varvec{X}}}^{{\varvec{E}}}$ displays the matrix of transported design variables using a basis function (linear or exponential), ${{\varvec{\beta}}}^{{\varvec{U}}}$ indicates vector of regression coefficients regarding the matrix of ${{\varvec{X}}}^{{\varvec{E}}\boldsymbol{ }}$ obtained with the common method of least-squares error, thus ${{\varvec{\beta}}}^{{\varvec{E}}}={\left({{{\varvec{X}}}^{{\varvec{E}}}}^{\boldsymbol{^{\prime}}}{{\varvec{X}}}^{{\varvec{E}}}\right)}^{-1}{{{\varvec{X}}}^{{\varvec{E}}}}^{\boldsymbol{^{\prime}}}{\varvec{y}}$. So, we fit the PR model over transformed train points using the transformation function. The $n\times p$ model matrix of ${{\varvec{X}}}^{{\varvec{E}}}$ in Eq. (9) consisting of the levels of the transformed independent variables can be defined as:

$${{\varvec{X}}}^{{\varvec{E}}}=\left[\begin{array}{c}\begin{array}{ccc}1& {x}_{11}^{E}& {x}_{12}^{E}\\ 1& {x}_{21}^{E}& {x}_{22}^{E}\\ \vdots & \vdots & \vdots \end{array}\\ \begin{array}{ccc}1& {x}_{n1}^{E}& {x}_{n2}^{E}\end{array}\end{array} \begin{array}{c}\begin{array}{cc}\dots & {x}_{1m}^{E}\\ \dots & {x}_{2m}^{E}\\ & \vdots \end{array}\\ \begin{array}{cc}\dots & {x}_{nm}^{E}\end{array}\end{array}\right]$$

(10)

Let assume ${{\varvec{x}}}^{\boldsymbol{*}}= {[{x}_{1}^{*},. . ., {x}_{m}^{*}]}^{T}$ and ${\varvec{x}}= {[{x}_{1},. . ., {x}_{m}]}^{T}$ show the nominal design and any arbitrary train point, respectively, so that we obtain each component of the matrix ${{\varvec{X}}}^{{\varvec{E}}}$ and as below:

$${{\varvec{x}}}^{{\varvec{E}}}=\left\{\begin{array}{c}{\left[\gamma .\sum_{j=1}^{m}\left({x}_{j}-{x}_{j}^{*}\right)\right]}^{T} , Linear transform \\ {\left[\gamma .\sum_{j=1}^{m}exp\left({x}_{j}-{x}_{j}^{*}\right)\right]}^{T} , Exponential transform\end{array}\right.$$

(11)

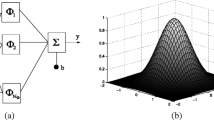
where $\gamma$ is the scale parameter that controls the growth of the basis function and is defined optimally among the proposed approach (the relevant procedure will be explained through Algorithm 2). In general, the points which are closer and farther to the nominal design obtain different merit by the transformation in Eq. (11) for computing regression coefficients in PR, see Fig. 1a.

Fig. 1

Schematic representation of proposed approach to modify approximation results in MPR (a) Transforming training points over nominal design using exponential basis function, and (b) Bias prediction using function of residuals of $k$ nearest points to new sample point ${x}^{0}$

On the other side, we assume the prediction error of PR can be reduced by employing a residual error of all or a part of existing training sample points. In another mean, to estimate the response $\widehat{f}({x}^{0})$ of any new sample point (${x}^{0}$) in a design space using MPR, the bias to reduce prediction error can be calculated as a function of residuals of nearest sample points surrounding ${x}^{0}$, see Fig. 1b. So, the bias expression can be obtained as a multiple of the sum of the residuals of $k$ nearest points to each arbitrary new sample point according to Euclidean distance in design space:

$$Bias\left({x}^{0}\right)=\alpha .\sum_{i=1}^{k}{\left(\frac{{d}_{i}^{0}}{{D}^{0}}\right).R}_{i}^{0} , \alpha \in \left[{\alpha }_{l},{\alpha }_{u}\right]$$

(12)

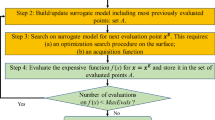
where ${d}_{i}^{0}=\Vert {x}_{i}-{x}_{0}\Vert$ and ${D}^{0}=\sum_{i=1}^{k}\Vert {x}_{i}-{x}_{0}\Vert$ are the second norm (Euclidean distance) between ith nearest point to ${x}^{0}$ and total distances of k nearest points to ${x}^{0}$, respectively. ${R}_{i}^{0}$ depicts the least-squares residual for ith nearest point to ${x}^{0}$. Three optimal values for hyperparameters of $\gamma$, $\alpha ,$ and $k$ in Eqs. (11) and (12) are optimally obtained by the DE optimizer using the mean square error (MSE) of the leave-one-out cross-validation approach as a fitness function of the optimizer. The expression $R$ indicates the relevant least-squares residual error. Thereupon, the framework of the proposed modification approach is outlined in Fig. 2. The operating algorithmic steps in pseudocode according to the proposed approach are outlined in Algorithm 1. The algorithmic steps to optimally define hyperparameters of $\gamma$, $\alpha$, and $k$ in Eqs. (11) and (12) are provided in Algorithm 2 using hybrid DE optimizer and leave-one-out cross-validation methodologies.

Fig. 2

Flowchart diagram including operated steps for the proposed PR approach compare with ordinary PR

4.2 Accuracy and performance measurement

Here to evaluate the prediction performance of each predictor (surrogate), e.g., MPR compared with OPR, for each test problem in engineering design, we define and employ three different performance measures including relative prediction error, coefficient of determination (R-square) and reliability performance index (RMI). Note that most practical engineering problems are described by constraint function(s) besides objective function(s). Let ${\varvec{R}} ={\left[f,{g}_{1},{g}_{2},\cdots ,{g}_{J}\right]}^{T}$ is the vector of objective and constraint functions, so the relative prediction error can be computed by:

$$Pred.Error = \Vert {\varvec{R}}-\widehat{{\varvec{R}}}\Vert$$

(13)

where $R$ and $\widehat{R}$ represent true simulation output and PR surrogate prediction respectively.

${R}^{2}$ is a measure of the goodness of fit of a model. In regression, the ${R}^{2}$ coefficient of determination is a statistical measure of how well the regression predictions approximate the real data points. An ${R}^{2}$ of $1$ indicates that the regression predictions perfectly fit the data. The ${R}^{2}$ the coefficient can be obtained by:

$${R}^{2}=1-\frac{\sum_{i=1}^{n}{\left({y}_{i}-\widehat{{y}_{i}}\right)}^{2}}{\sum_{i=1}^{n}{\left({y}_{i}-\overline{{y }_{i}}\right)}^{2}}$$

(14)

where $\overline{{y }_{i}}$ is the mean of observed values (${y}_{i}$) and $\widehat{{y}_{i}}$ is corresponding predicted values.

The third performance measure, i.e., RMI for the reliability of the model is defined to consider the existence of constraint functions in the problem. Such formulation is inspired by the merit function used frequently in yield-driven design for analyzing tolerance in electromagnetic engineering models, see (Pietrenko-Dabrowska et al. 2020; Koziel and Bandler 2015). The performance of each surrogate to predict the feasibility or infeasibility of the problem can be evaluated by:

$$RMI=\frac{1}{Nt}\sum_{t=1}^{Nt}H({x}_{t})$$

(15)

where $Nt$ is the total number of test points, i.e., here a large number of test points are generated randomly using Monte Carlo (MC) simulation to evaluate both measurement indexes in Eq. (13) and Eq. (15). In Eq. (15), an auxiliary function $H(x)$ is defined by:

$$H(x)=\left\{\begin{array}{c}1, if \left\{{ g}_{j}\left(x\right)\le 0 \forall j=\mathrm{1,2},\dots ,J\right\}\\ 0, else.\end{array}\right.$$

(16)

According to Eq. (16), for each random design (test point), if the model meets the problem’s requirements, e.g., satisfies all constraints, the auxiliary function $H(x)$ takes one, else it takes zero.

5 Demonstration case studies

In this section, four engineering design problems are solved in the following sections. The first two problems are classical engineering design problems named three-bar truss design and welded beam design problems. The next two problems are selected from the practical robotic engineering called trajectory control of two-link planar and three-link robot manipulators to compare the performances of both ordinary polynomial regression and the proposed modified approach (OPR vs MPR) in tolerance analysis. For this purpose, uncertainty due to manufacturing geometric tolerances is assumed for all test problems. Here, the training sample points are designed using a common space-filling sampling design named Latin Hypercube Sampling (LHS) (Viana 2016). Inspired by Jin et al. (2001), we employ 100 training data points (experimental designs) for test problems with two design variables and 125 training sample points for problems with three and four design variables. Here, 1,000 data test points are used for validation as well as employing the same data points for Monte Carlo simulation results. In this paper, we train PR with three orders including linear, quadratic, and cubic orders of polynomials. We employ the MC to generate a large set of test points, e.g., here we use 1,000 MC random designs for each problem. Three hyperparameters of $\gamma$, $\alpha$ and $k$ in Eqs. (11) and (12) optimally investigated in intervals $\gamma =[\mathrm{0,0.5}]$, $\alpha =[-\mathrm{2,2}]$ and $k=[\mathrm{0,10}]$. Notably, to make comparison results more reliable, the evaluation procedure for each problem is done with five separate repetitions over two scenarios considering types of probability distribution for uncertainty (manufacturing tolerances) in models including i) first scenario (SN. 1) by assuming Gaussian probability distribution, and ii) the second scenario (SN. 2) by assuming uniform probability distribution for uncertainty. The MATALB®/R2022a program is used to simulate models and quantification of uncertainty in each test problem.

5.1 Three-bar truss design

In the subject of civil engineering, this problem is a structural optimization model. Due to its severely limited search space, this problem is frequently used for the case of studies in the literature (Mirjalili et al. 2017; Saremi et al. 2017). Two parameters must be optimally specified, as seen in Fig. 3, to attain the least weight while adhering to stress, deflection, and buckling limits. The mathematical formulation of this issue is as follows:

Fig. 3

Schematic overview of three-bar truss design problem

$$Consider \overrightarrow{x}=\left[{x}_{1}, {x}_{2}\right]=[{A}_{1},{A}_{2}]$$

$$Minimize f\left(\overrightarrow{x}\right)=\left(2\sqrt{2}{x}_{1}+{x}_{2}\right)*l$$

$$Subject to:$$

$${c}_{1}\left(\overrightarrow{x}\right)=\frac{\sqrt{2}{x}_{1}+{x}_{2}}{\sqrt{2}{x}_{1}^{2}+2{x}_{1}{x}_{2}}P-\sigma \le 0,{c}_{2}\left(\overrightarrow{x}\right)=\frac{{x}_{2}}{\sqrt{2}{x}_{1}^{2}+2{x}_{1}{x}_{2}}P-\sigma \le 0,$$

$${c}_{3}\left(\overrightarrow{x}\right)=\frac{1}{\sqrt{2}{x}_{2}+{x}_{1}}P-\sigma \le 0,Variable range: 0\le {x}_{1}\le 1, 0\le {x}_{2}\le 1,$$

$$where l=100 cm, p=2 KN/{cm}^{2}, \sigma =2 KN/{cm}^{2}$$

(17)

Uncertainty due to fabrication tolerances is assumed in two dimensions ${A}_{1}$ and ${A}_{2}$. The nominal design and tolerances for two parameters are considered as:

$${{\varvec{x}}}^{\mathbf{*}}={[0.789, 0.408]}^{T}, {\varvec{d}}{\varvec{x}}={[\pm 0.05, \pm 0.05]}^{T}$$

The objective function and three constraints are trained separately by both OPR and MPR. Geometric tolerances in both dimensions are causes of variability in objective and constraint functions. For the schematic instance, Fig. 4 represents the MC analysis displaying the variability of nominal design due to a fabrication tolerance with a uniform probability distribution in the three-bar truss design problem. The proposed approach according to the algorithmic procedure in Sect. 4.1 is derived. The DE optimizer combining the leave-one-out approach regarding Algorithm 2 is run to obtain optimal hyperparameters $\gamma$, $\alpha ,$ and $k$ in Eqs. (11) and (12) (relevant statistical results are provided in Appendix 1). We train objective and constraint functions using designed training points by LHS for each of the two scenarios mentioned in the previous section and for three different orders of PR including linear, quadratic, and cubic orders. Three performance measurements of relative prediction errors, ${R}^{2}$, and RMI are obtained using all random test points generated by the MC method. The prediction errors obtained by each method are shown in Fig. 5 for five repetitions. Table 1 illustrates the average of five repetitions for prediction error, ${R}^{2}$ and RMI criteria. Note that the true RMI was obtained from the simulation model using MC random designs (see Sect. 4.2). The percentage improvements for both prediction error and ${R}^{2}$ obtained by the proposed approach than OPR are revealed in Fig. 6. As can be seen, the proposed MPR approach using both linear and exponential transformations provide a significant improvement in prediction error and ${R}^{2}$ measures. Also, the proposed approach presents lower differences between SM-based (true) and approximated RMI compared with the conventional OPR method.

Fig. 4

Monte Carlo simulation random designs (1000 points) with uniform probability distribution is analyzed and show for an objective and first constraint function of three-bar truss design problem. Uncertainty as a source of variability is existed in the model due to fabrication geometric tolerances

Fig. 5

Comparison of prediction errors for MPR (linear and exponential transformation) vs OPR in three-bar truss design problem for two scenarios, orders of polynomials, and five separate repetitions

Table 1 Average relative prediction error, ${R}^{2}$ and RMI over five repetitions, two scenarios of uncertainty and comparison of results for methods of MPR with linear and exponential transformation vs OPR in three-bar truss design problem

Fig. 6

Percent improvement of prediction errors and ${R}^{2}$ for MPR (linear and exponential transformation) vs OPR in three-bar truss design problem for two scenarios, and orders of polynomials

5.2 Welded beam design

This problem is modeled to minimize the cost of fabrication considering the model’s constraints including shear stress ($\tau$), bending stress in the beam ($\theta$), buckling load on the bar (${P}_{c}$), end deflection of the beam ($\delta$), and side constraints (Coello Coello 2000). Four design variables need to be optimized as shown in Fig. 7 consisting of the thickness of the weld ($h$), the length of the clamped bar ($l$), the height of the bar ($t$), and the thickness of the bar ($b$). The mathematical formulation of this constrained optimization problem is as follows:

Fig. 7

Schematic overview of welded beam design problem

$$Consider \overrightarrow{x}=\left[{x}_{1}, {x}_{2},{x}_{3},{x}_{4}\right]=[h,l,t,b]$$

$$Minimize f\left(\overrightarrow{x}\right)={1.10471x}_{1}^{2}{x}_{2}+0.04811{x}_{3}{x}_{4}(14.0+{x}_{2})$$

$$Subject to:$$

$${c}_{1}\left(\overrightarrow{x}\right)=\tau \left(\overrightarrow{x}\right)-{\tau }_{max}\le 0, {c}_{2}\left(\overrightarrow{x}\right)=\sigma \left(\overrightarrow{x}\right)-{\sigma }_{max}\le 0,$$

$${c}_{3}\left(\overrightarrow{x}\right)={x}_{1}-{x}_{4}\le 0,$$

$${c}_{4}\left(\overrightarrow{x}\right)=0.10471{x}_{1}^{2}+0.04811{x}_{3}{x}_{4}\left(14.0+{x}_{2}\right)-0.5\le 0,$$

$${c}_{5}\left(\overrightarrow{x}\right)=0.125-{x}_{1}\le 0, {c}_{6}\left(\overrightarrow{x}\right)=\delta \left(\overrightarrow{x}\right)-{\delta }_{max}\le 0, {c}_{7}\left(\overrightarrow{x}\right)=P-{P}_{c}\left(\overrightarrow{x}\right)\le 0,$$

$$Variable range: 0.1\le {x}_{1}\le 2, 0.1\le {x}_{2}\le 10, 0.1\le {x}_{3}\le 10, 0.1\le {x}_{4}\le 2$$

$$where$$

$$\tau \left(\overrightarrow{x}\right)=\sqrt{{\left({\tau }^{\mathrm{^{\prime}}}\right)}^{2}+2{\tau }^{\mathrm{^{\prime}}}{\tau }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\frac{{x}_{2}}{2R}+{\left({\tau }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\right)}^{2}}, {\tau }^{\mathrm{^{\prime}}}=\frac{P}{\sqrt{2}{x}_{1}{x}_{2}}, {\tau }^{\mathrm{^{\prime}}}=\frac{MR}{J}, M=\left(L+\frac{{x}_{2}}{2}\right), R=\sqrt{\frac{{x}_{2}^{2}}{4}+{(\frac{{x}_{1}+{x}_{3}}{2})}^{2}}, J=2\left\{\sqrt{2}{x}_{1}{x}_{2}\left[\frac{{x}_{2}^{2}}{12}+{(\frac{{x}_{1}+{x}_{3}}{2})}^{2}\right]\right\}$$

$$\sigma \left(\overrightarrow{x}\right)=\frac{6PL}{{x}_{4}{x}_{3}^{2}}, \delta \left(\overrightarrow{x}\right)=\frac{4P{L}^{3}}{E{x}_{3}^{3}{x}_{4}}, {P}_{c}\left(\overrightarrow{x}\right)=\frac{4.013E\sqrt{\frac{{x}_{3}^{2}{x}_{4}^{6}}{36}}}{{L}^{2}}\left(-\frac{{x}_{3}}{2L}\sqrt{\frac{E}{4G}} \right)$$

$$P=6000 lb, L=14 in,$$

$$E=30\times {10}^{6} psi, G=12\times {10}^{6} psi$$

$${\tau }_{max}=\mathrm{13,600 }psi,$$

$${\sigma }_{max}=\mathrm{30,000 }psi, {\delta }_{max}=0.25 in$$

(18)

All four geometric dimensions are assumed to vary due to fabrication tolerances. Let nominal design and maximum variation by tolerances considered to be:

$${{\varvec{x}}}^{\mathbf{*}}={[0.206, 3.478, 9.037, 0.206]}^{T},$$

$${\varvec{d}}{\varvec{x}}={[\pm 0.05, \pm 0.1, \pm 0.1, \pm 0.1]}^{T}$$

Uncertainty due to tolerance provides a source of variability in the model for objective and all constraint functions, see Fig. 8. Analysis of uncertainty with the MC method required a large number of simulation experiments, e.g., 1,000 experiments, while using a PR surrogate can smooth this computation burden while training PR by much smaller sample points, e.g., 125 sample points in the current example with four design variables. The proposed MPR approach is implemented using the procedure elaborated in Sect. 4.1. The hyperparameters $\gamma$, $\alpha ,$ and $k$ in Eqs. (11) and (12) are optimally computed by following steps in Algorithm 2 (as statistical results revealed in Appendix 2). The same as other test problems, 1,000 MC random points are used to calculate three performance measures of the relative prediction error, ${R}^{2}$, and RMI for both OPR and MPR (linear and exponential transformations) which are fitted for both scenarios separately. The results for relative prediction error over five separate repetitions are shown in Fig. 9, and the average of errors, ${R}^{2}$ and RMI values also are depicted in Table 2. Considering these results, Fig. 10 reveals the percent improvement provided by the proposed approach compared with the conventional OPR method. Except in the third order of polynomial (cubic) using exponential transformation, these results further support the superiority of the proposed MPR (both linear and exponential transformation) approach compared with the conventional OPR method in training and approximating the model.

Fig. 8

Monte Carlo simulation random designs (1000 points) with uniform probability distribution is analyzed and show for an objective and first constraint function of welded beam design problem. Uncertainty as a source of variability is existed in the model due to fabrication geometric tolerances

Fig. 9

Comparison of prediction errors for MPR (linear and exponential transformation) vs OPR in welded beam design problem for two scenarios, orders of polynomials, and five separate repetitions

Table 2 Average relative prediction error, ${R}^{2}$ and RMI over five repetitions, two scenarios of uncertainty and comparison of results for methods of MPR with linear and exponential transformation vs OPR in welded beam design problem

Fig. 10

Percent improvement of prediction errors and ${R}^{2}$ for MPR (linear and exponential transformation) vs OPR in welded beam design problem for two scenarios, and orders of polynomials

5.3 Two-link robot manipulator (trajectory control)

Figure 11 depicts a two-link manipulator (Spong et al. 2020; Farooq et al. 2013) with two rotary degrees of freedom (DOF) in the same plane. The trajectory planning of the manipulator’s end-effector (tip) is of particular relevance in the kinematic analysis of this system. We must first establish the end-connections effectors with the joint angles, namely ${\theta }_{1}$ and ${\theta }_{2}$, to move it from its initial Cartesian position to any given point in Cartesian space. There are two ways to do this: using forward or inverse kinematics. In this instance, we investigate the robot’s forward kinematics. The issue of calculating the Cartesian position of the manipulator’s end-effector in terms of joint angles is known as the forward kinematics approach. Due to the existence of several coordinate frames, i.e., $({x}_{0}, {y}_{0})$, $({x}_{1}, {y}_{1})$ and $({x}_{2}, {y}_{2})$, this is a difficult undertaking. This problem is typically solved by creating a fixed coordinate system, commonly referred to as the world or base frame, from which the manipulator and any other objects can be referenced. Typically, the origin of the manipulator is the base coordinate frame. Now, using this coordinate system, the end effector’s Cartesian coordinates $(x, y)$ can be written as:

$$x={l}_{1}\mathrm{cos}{\theta }_{1}+{l}_{2}\mathrm{cos}\left({\theta }_{1}+{\theta }_{2}\right)$$

$$y={l}_{1}\mathrm{sin}{\theta }_{1}+{l}_{2}\mathrm{sin}\left({\theta }_{1}+{\theta }_{2}\right)$$

(19)

where ${l}_{1}$ and ${l}_{2}$ are the lengths of the two links, respectively. Uncertainty due to fabrication tolerances can be assumed in both links. To plan the path of the manipulator and control the position of the end-effector, we must first understand its dynamic properties (angular velocities of the links, and acceleration) by calculating the amount of force needed to move it: Using too little or too much force can make the manipulator slow to react or cause the arm to move around or crash against objects. Here, we employ the common dynamics equations of the two-link manipulator, refer to Spong et al. (2020). Let ${\left(x,y\right)}_{t}$ represent the position of end-effector in time slot $t$. To evaluate the prediction performance of surrogates, we compute the Euclidean distance between real position obtained by the true model in Eq. (19) at time slot $t$ with the predicted position by MPR and OPR.

Fig. 11

Schematic kinematic diagram a two-link planar manipulator

$${\left\{error\right\}}_{t}= \Vert {\left(x,y\right)}_{t}^{simulation}-{\left(x,y\right)}_{t}^{surrogate}\Vert$$

(20)

Here, the simulation is modeled in time interval $T=\left[\mathrm{0,3}\right]$ with step time 0.1. So, 30 positions of end-effectors planned in the workspace. It should also be emphasized that to simplify the modeling process and reduce the computational time, we compute the error Eq. (20) for a smaller number of positions as feature points. Figure 12 represents the path planning of the end-effector in the simulated time domain, and the position of feature points, i.e., here four feature points are selected. Let the nominal design and tolerances for geometric links of the manipulator be assumed to be:

Fig. 12

Path planning and the position of feature points in workspace simulated in time domain [0, 3]

$${{\varvec{x}}}^{\mathbf{*}}={[15, 10]}^{T}, {\varvec{d}}{\varvec{x}}={[\pm 0.1, \pm 0.1]}^{T}$$

The variability in properties of the manipulator is estimated by MC random designs as schematically shown in Fig. 13. Both conventional and proposed PR approaches are trained using the same comparative procedure with other test problems in this study. The optimal hyperparameters $\gamma$, $\alpha ,$ and $k$ in Eqs. (11) and (12) for the current problem are optimally obtained using the procedure in Algorithm 2 (see the relevant statistical results in Appendix 3). The positions of feature points are approximated, and the prediction error is computed for five separate repetitions considering two scenarios of probability distributions, and different orders of polynomials. The comparison prediction errors are provided in Fig. 14. To determine the RMI measure, we define the constraint function as below:

$$\prod_{f=1}^{F}\Vert {\left(x,y\right)}_{f}^{nominal}-{\left(x,y\right)}_{f}^{MC}\Vert \le \varepsilon$$

(21)

where $F$ denotes the number of feature points, and index $f$ is to specify each feature point. The function in Eq. (21) is defined to count the number of MC random designs in which the Euclidean differences between nominal design and related MC design for all feature points are less than threshold $\varepsilon$, e.g., $\varepsilon =0.05$ in the current case. The SM-based RMI are estimated using all MC random designs and are computed using a true simulation model as well approximation by both OPR and MPR surrogates. The average results over five separate repetitions are provided in Table 3. As well as the percent improvement for prediction error and ${R}^{2}$ are shown in Fig. 15. These results also clearly indicate the superiority of the proposed MPR approach either using linear or exponential transformation compared with the ordinary PR approach in approximation and interpolation of the simulation model for engineering tolerance problems under study.

Fig. 13

Fabrication tolerances as a source of variability in dynamic parameters of two-link robot manipulator. The variability simulated using 1000 MC random designs with uniform probability distribution

Fig. 14

Comparison of prediction errors for MPR (linear and exponential transformation) vs OPR in trajectory control of two-link robot manipulator for two scenarios, orders of polynomials, and five separate repetitions

Table 3 Average relative prediction error, ${R}^{2}$ and RMI over five repetitions, two scenarios of uncertainty and comparison of results for methods of MPR with linear and exponential transformation vs OPR in trajectory control of two-link manipulator

Fig. 15

Percent improvement of prediction errors and ${R}^{2}$ for MPR (linear and exponential transformation) vs OPR in trajectory control of two-link robot manipulator for two scenarios, and orders of polynomials

5.4 Three-link robot manipulator (trajectory control)

A schematic kinematic diagram of a three-link planar robot manipulator is shown in Fig. 16. Compared with the two-link planner in the previous problem, this manipulator includes one more joint and arm linked to the second arm, so it provides three degrees of freedom (3DOF). Regarding the forward kinematics of the 3DOF robot manipulator, the end effector’s Cartesian coordinates $(x, y)$ can be computed by Spong et al. (2020):

Fig. 16

Schematic kinematic diagram a three-link (3DOF) planar robot manipulator

$$x={l}_{1}\mathrm{cos}{\theta }_{1}+{l}_{2}\mathrm{cos}\left({\theta }_{1}+{\theta }_{2}\right)+{l}_{3}\mathrm{cos}\left({\theta }_{1}+{\theta }_{2}+{\theta }_{3}\right)$$

$$y={l}_{1}\mathrm{sin}{\theta }_{1}+{l}_{2}\mathrm{sin}\left({\theta }_{1}+{\theta }_{2}\right)+{l}_{3}\mathrm{sin}\left({\theta }_{1}+{\theta }_{2}+{\theta }_{3}\right)$$

(22)

Uncertainty due to manufacturing tolerances is expected in all three geometric parameters of (${l}_{1}, {l}_{2},$ and ${l}_{3}$) as:

$${{\varvec{x}}}^{\mathbf{*}}={[15, 10, 10]}^{T},$$

$${\varvec{d}}{\varvec{x}}={[\pm 0.1, \pm 0.1, \pm 0.1]}^{T}$$

All model parameters are adjusted the same as mentioned in the previous section for the two-link planner. The model for four considered feature points (as illustrated in Fig. 17) was trained by MPR (linear and exponential transformation) and OPR separately using 125 experimental samples designed by LHS. Two scenarios according to the Gaussian and uniform probability distribution are assumed for uncertainty in the model. Fabrication tolerances are a source of variability in the dynamic parameters of the three-link robot manipulator. For instance, Fig. 18 illustrates the simulated variability due to uncertainty using 1000 MC random designs with a uniform probability distribution. To construct MPR, the optimal hyperparameters of $\gamma$, $\alpha ,$ and $k$ in Eqs. (11) and (12) are computed according to Algorithm 2 (the relevant statistical results are provided in Appendix 4). The relative prediction errors regarding each scenario and each order of polynomial for five separate repetitions are computed as shown in Fig. 19. Additionally, the ${R}^{2}$ and RMI criterion are approximated using trained PR surrogates and the average of results over five repetitions are presented in Table 4. The percentage of improvement which is achieved using the proposed approach compared with the conventional OPR approach is depicted in Fig. 20. It is apparent from the obtained results that the proposed MPR approach overcomes OPR with a much smaller prediction error, and a larger coefficient of determination (${R}^{2}$), and closer RMI to SM-based magnitude.

Fig. 17

Path planning and the position of feature points in workspace simulated in time domain [0, 3] for trajectory control of three-link (3DOF) planar robot manipulator

Fig. 18

Fabrication tolerances as a source of variability in dynamic parameters of three-link robot manipulator. The variability simulated using 1000 MC random designs with uniform probability distribution

Fig. 19

Comparison of prediction errors for MPR (linear and exponential transformation) vs OPR in trajectory control of three-link (3DOF) robot manipulator for two scenarios, orders of polynomials, and five separate repetitions

Table 4 Average relative prediction error, ${R}^{2}$ and RMI over five repetitions, two scenarios of uncertainty and comparison of results for methods of MPR with linear and exponential transformation vs OPR in trajectory control of three-link manipulator

Fig. 20

Percent improvement of prediction errors and ${R}^{2}$ for MPR (linear and exponential transformation) vs OPR in trajectory control of three-link (3DOF) robot manipulator for two scenarios, and orders of polynomials

6 Conclusion

This paper presented a novel algorithm named MPR for improving the approximation power of conventional polynomial regression with the common least-squares method. Two main modifications were done; first, we use a specific basis function (linear and exponential) to transform an original variable design into new transformed variables by computing the differences between training sample points and a reference point (e.g., a center of design space under study as a location of the nominal point). The second modification was done to estimate the bias between approximated responses by surrogate with a true simulation model. To investigate this, we compute the sum square error as a fitness function of the DE optimizer in each iteration using the leave-one-out cross-validation approach aiming to compute the optimal hyperparameter used in estimating bias. The bias function is formed based on a coefficient of the sum of the remainders in $k$ nearest points to each arbitrary sample point. The comparison results between the conventional PR method and the proposed approach over four engineering design problems demonstrate the superiority and effectiveness of the proposed algorithm in analyzing geometric manufacturing tolerances and approximating the real simulation model even with a small number of computational costs. Considerably more work will need to be done to evaluate the performance of the proposed MPR approach, particularly in comparison with famous surrogates such as the Kriging (Gaussian process), RBF, and polynomial chaos expansion in the same platforms. Also, further development of the proposed approach applied for such surrogate methods can be the subject of future research. The application of U-space transformation and a GP-based bias term which are common in reliability-based models have also been suggested for further remarks in the future.

Appendix

See Figs. 21, 22, 23, 24.

Fig. 21

Boxplot for optimal hyperparameters $\gamma$, $\alpha$ and $k$ applied in Eqs. (11) and (12) concerning the proposed procedure in Algorithm 2 for three-bar truss design problem. Data are collected for five separate repetitions over each scenario.

Fig. 22

Boxplot for optimal hyperparameters $\gamma$, $\alpha$ and $k$ applied in Eqs. (11) and (12) concerning the proposed procedure in Algorithm 2 for welded beam design problem. Data are collected for five separate repetitions over each scenario.

Fig. 23

Boxplot for optimal hyperparameters $\gamma$, $\alpha$ and $k$ applied in Eqs. (11) and (12) concerning the proposed procedure in Algorithm 2 for trajectory control of two-link robot manipulator. Data are collected for five separate repetitions over each scenario.

Fig. 24

Boxplot for optimal hyperparameters $\gamma$, $\alpha$ and $k$ applied in Eqs. (11) and (12) concerning the proposed procedure in Algorithm 2 for trajectory control of three-link (3DOF) robot manipulator. Data are collected for five separate repetitions over each scenario.