Abstract
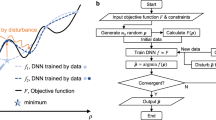
Topology optimization (TO) provides a systematic approach for obtaining structure design with optimum performance of interest. However, the process requires the numerical evaluation of the objective function and constraints at each iteration, which is computationally expensive, especially for large-scale designs. Deep learning-based models have been developed to accelerate the process either by acting as surrogate models replacing the simulation process, or completely replacing the optimization process. However, most of them require a large set of labelled training data, which is generated mostly through simulations. The data generation time scales rapidly with the design size, decreasing the efficiency of the method itself. Another major issue is the weak generalizability of deep learning models. Most models are trained to work with the design problem similar to that used for data generation and require retraining if the design problem changes. In this work an adaptive, scalable deep learning-based model-order-reduction method is proposed to accelerate large-scale TO process, by utilizing MapNet, a neural network which maps the field of interest from coarse-scale to fine-scale. The proposed method allows for each simulation of the TO process to be performed at a coarser mesh, thereby greatly reducing the total computational time. More importantly, a crucial element, domain fragmentation, is introduced and integrated into the method, which greatly improves the transferability and scalability of the method. It has been demonstrated that the MapNet trained using data from one cantilever beam design with a specific loading condition can be directly applied to other structure design problems with different domain shapes, sizes, boundary and loading conditions.

























Similar content being viewed by others
References
Aage N, Andreassen E, Lazarov BS, Sigmund O (2017) Giga-voxel computational morphogenesis for structural design. Nature 550(7674):84–86
Ates GC, Gorguluarslan RM (2021) Two-stage convolutional encoder-decoder network to improve the performance and reliability of deep learning models for topology optimization. Struct Multidisc Optim 63(4):1927–1950
Baandrup M, Sigmund O, Polk H, Aage N (2020) Closing the gap towards super-long suspension bridges using computational morphogenesis. Nat Commun 11(1):1–7
Bendsoe MP, Sigmund O (2003) Topology optimization: theory, methods, and applications. Springer, Berlin
Benner P, Gugercin S, Willcox K (2015) A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev 57(4):483–531
Boyaval S (2008) Reduced-basis approach for homogenization beyond the periodic setting. Multiscale Model Simul 7(1):466–494
Chi H, Zhang Y, Tang TLE, Mirabella L, Dalloro L, Song L, Paulino GH (2021) Universal machine learning for topology optimization. Comput Methods Appl Mech Eng 375:112739
Cremonesi M, Néron D, Guidault P, Ladevèze P (2013) A PGD-based homogenization technique for the resolution of nonlinear multiscale problems. Comput Methods Appl Mech Eng 267:275–292
Hernández JA, Oliver J, Huespe AE, Caicedo MA, Cante J (2014) High-performance model reduction techniques in computational multiscale homogenization. Comput Methods Appl Mech Eng 276:149–189
Huang X, Xie YM (2007) Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem Anal Des 43(14):1039–1049
Kalina KA, Linden L, Brummund J, Metsch P, Kästner M (2022) Automated constitutive modeling of isotropic hyperelasticity based on artificial neural networks. Comput Mech 69:213–232
Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint. https://arxiv.org/abs/1412.6980
Kollmann HT, Abueidda DW, Koric S, Guleryuz E, Sobh NA (2020) Deep learning for topology optimization of 2D metamaterials. Mater Des 196:109098
Lee S, Kim H, Lieu QX, Lee J (2020) CNN-based image recognition for topology optimization. Knowl Based Syst 198:105887
Lu L, Meng X, Mao Z, George EK (2020) DeepXDE: a deep learning library for solving differential equations. SIAM Rev 63(1):208–228
Monteiro E, Yvonnet J, He Q (2008) Computational homogenization for nonlinear conduction in heterogeneous materials using model reduction. Comput Mater Sci 42(4):704–712
Nguyen NC (2008) A multiscale reduced-basis method for parametrized elliptic partial differential equations with multiple scales. J Comput Phys 227(23):9807–9822
Nie Z, Jiang H, Kara LB (2020) Stress field prediction in cantilevered structures using convolutional neural networks. J Comput Inf Sci Eng 20(1):011002
Qian C, Ye W (2021) Accelerating gradient-based topology optimization design with dual-model artificial neural networks. Struct Multidisc Optim 63(4):1687–1707
Raissi M, Karniadakis GE (2018) Hidden physics models: machine learning of nonlinear partial differential equations. J Comput Phys 357:125–141
Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707
Raissi M, Yazdani A, Karniadakis GE (2020) Hidden fluid mechanics: learning velocity and pressure fields from flow visualizations. Science 367(6481):1026–1030
Ronneberger O, Fischer P, Brox T (2015) U-net: convolutional networks for biomedical image segmentation. In: International conference on medical image computing and computer-assisted intervention. pp 234–241
Sosnovik I, Oseledets I (2019) Neural networks for topology optimization. Russ J Numer Anal Math Model 34(4):215–223
Tan RK, Zhang NL, Ye W (2020) A deep learning-based method for the design of microstructural materials. Struct Multidisc Optim 61(4):1417–1438
Tan RK, Qian C, Wang M, Ye W (2022) An efficient data generation method for ANN-based surrogate models. Struct Multidisc Optim 65(3):1–22
Wang D, Xiang C, Pan Y, Chen A, Zhou X, Zhang Y (2021) A deep convolutional neural network for topology optimization with perceptible generalization ability. Eng Optim. https://doi.org/10.1080/0305215X.2020.1846031
White DA, Arrighi W, Kudo JJ, Watts SE (2019) Multiscale topology optimization using neural network surrogate models. Comput Methods Appl Mech Eng 346:1118–1135
Yu Y, Hur T, Jung J, Jang IG (2019) Deep learning for determining a near-optimal topological design without any iteration. Struct Multidisc Optim 59(3):787–799
Yvonnet J, He Q (2007) The reduced model multiscale method (R3M) for the non-linear homogenization of hyperelastic media at finite strains. J Comput Phys 223(1):341–368
Funding
This work is supported by the Hong Kong Research Grants Council under Competitive Earmarked Research Grant No. 16206320.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Replication of results
The code and data used for the implementation of the proposed method can be provided up on request.
Additional information
Responsible Editor: Seonho Cho
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Tan, R.K., Qian, C., Li, K. et al. An adaptive and scalable artificial neural network-based model-order-reduction method for large-scale topology optimization designs. Struct Multidisc Optim 65, 348 (2022). https://doi.org/10.1007/s00158-022-03456-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-022-03456-x