A stress-based criterion to identify and control intersections in 2D compliance minimization topology optimization

Abstract

Topology optimization typically generates designs that exhibit significant geometrical complexity, which can pose difficulties for manufacturing and assembly. The number of occurrences of an important design feature, in particular intersections, increases with geometrical complexity. Intersections are essential for load transfer in many engineering structures. For certain upcoming manufacturing processes, such as direct metal deposition, the size of an intersection plays a role. During metal deposition, slim intersections are more prone to manufacturing defects than bulkier ones. In this study, a computationally tractable methodology is proposed to both control occurrence and size of intersections in topology optimization. To identify intersections, a stress-based quantity is proposed, denoted as Intersection Indicator. This quantity is based on the local degree of multi-axiality of the stress state, and identifies material points at intersections. The proposed intersection indicator can identify intersections in both single as well as multi-load case problems. To detect the relative size of intersections, the average density in the vicinity of an intersection is used to penalize or promote intersection sizes of interest. The corresponding sensitivity analysis involves solving a set of adjoint equations for each load case. Numerical 2D experiments demonstrate a controllable reduction of penalized slim intersections compared to the designs obtained from conventional compliance minimization. The overall geometrical complexity of the design is reduced due to the promotion of bulkier intersections which leads to an increase in compliance. The designs obtained are more suitable for manufacturing processes such as direct metal deposition.

1 Introduction

Topology Optimization (TO) is an effective method to generate early phase designs in a variety of engineering applications such as aerospace, biomedical, optics and maritime (Bendsoe and Sigmund 2013). Designs obtained by TO, although having a superior mechanical performance, can be difficult or impossible to manufacture due to their geometrical complexity (Lazarov et al. 2016). Additional manufacturing constraints are hence usually integrated into TO to generate designs which are suitable for processes such as casting  (Xia et al. 2010; Zhou and Zhang 2019), machining  (Sigmund 2009; Langelaar 2019) and Additive Manufacturing (AM) (Langelaar 2016; Gaynor and Guest 2016; Van de Ven et al. 2020). Many other studies have also provided methods to specifically reduce the geometrical complexity of TO designs. For instance, controlling minimum length scale in material and void regions. Length scale control can be achieved by filters or projection methods (Bourdin 2001; Guest et al. 2004; Zhou et al. 2015) and skeleton-based methods  (Zhang et al. 2014; Xia and Shi 2015; Zhang et al. 2016, 2017a). Moreover, geometrical complexity can also be controlled by restricting the number of structural components, in, e.g., the moving morphable component framework (Zhang et al. 2017b; Wein et al. 2020). In all mentioned methods a certain amount of mechanical performance is typically sacrificed in order to achieve a manufacturable design.

Here we focus on generating designs by TO while controlling an important geometrical aspect of a structural design, namely intersections. The number of occurrences of intersections increase with the increase in geometrical complexity. Intersections are critical from both a performance and manufacturing point of view. However, how to explicitly control intersections is an open question in the literature. An intersection is a connection between two or more structural members in a design where a major change in the stress state occurs (Ambrozkiewicz and Kriegesmann 2018). Consequently, a multi-axial stress state is encountered at intersections (Bendsøe and Haber 1993). Intersections can be susceptible to failure due to stress multi-axiality  (Clausmeyer et al. 1991). Moreover, from a manufacturing perspective, intersections can be associated with high cost. For structures produced by assembly operations, intersections may imply joining through riveting, bolting or welding operations  (Megson 2019). Consequently, reducing the number of intersections in designs will lead to less joining operations, and lower cost. Intersections also pose a problem in certain AM methods. A prominent example is Direct Metal Deposition (DMD). DMD is a metal AM variant which is rapidly maturing and used currently to produce large functional structures such as ship propellers and aircraft components  (Lockett et al. 2017). In DMD, simultaneous material melting and deposition occurs along the deposition lines. It is difficult to avoid overlapping of the deposition paths at intersections. This leads to extra material deposition at intersections which in turn cause geometrical deviations (Mehnen et al. 2014). However, when the size of an intersection is sufficiently large, overlapping of the deposition paths can be avoided. Hence, it is of interest to control not only the number but also the size of intersections.

Intersection detection in density based TO problem has been investigated through an image-based method (Gamache et al. 2018) and a stress-based method (Ambrozkiewicz and Kriegesmann 2018). In the image-based method, the skeleton of the structure is used to identify the structural members intersecting at nodes. These nodes are considered as intersections. However, the algorithm used for detection is not differentiable and therefore design sensitivities can not be calculated. This poses a problem in using this approach in gradient-based optimization (Gamache et al. 2018). Detection of intersections through a stress-based parameter provides a possibility for design sensitivity calculation. Stresses and sensitivities of stress-based quantities are readily computable for mechanical TO problems. Ambrozkiewicz and Kriegesmann (2018) used principal stress ratios to detect intersections and straight members connected to it, in order to evaluate the load path in the design. However, specific control on intersections during optimization was not performed and the use of these ratios was limited to detection in single load case problem.

In this paper, the control of intersections is studied using stress-state information in the context of the classical density based TO problem of compliance minimization (Bendsøe 1989). Controlling the number and/or size of intersections that are typically generated in TO may lead to major topological changes. To illustrate this, consider the schematic of a structural baseline design, shown in Fig. 1a. The intersections are marked by red dashed circles. The designs shown in Fig. 1b and c have the same material volume as the baseline design, but the intersections are larger and fewer. A significant reduction in the geometrical complexity is observed from Fig. 1a to b and from Fig. 1b to c. The aim of this paper is to present a computationally tractable approach for identifying and controlling intersections as a function of their size, in 2D density-based compliance minimization for single and multi load case problems. 2D problems are relevant for industrial DMD applications, because most of the structural components produced by DMD are manufactured by stacking 2D layers on top of each other. A discussion on challenges to extend the method to 3D is given at the end of the paper. Note that controlling intersections is shown for compliance minimization TO problems, however, the stress multi-axiality at intersections can also be used in many other applications.

Fig. 1

Schematic representation : a Complex baseline design with marked intersections (red dashed circles). b Design modification with reduced geometrical complexity and relatively thicker intersections than the baseline design. c Design modification with further reduced geometrical complexity and an even thicker intersection than in (b)

In order to achieve the above mentioned aim, a mathematical formulation is developed to identify the intersections in the density based minimum compliance TO. There are two aspects to consider: detection and discriminating intersections depending on their relative size. In order to detect intersections, the stress state generated in the design due to the applied loads and boundary conditions is evaluated. The key idea is that at an intersection, the stress state exhibits an higher level of multi-axiality compared to uniaxially loaded design features. Therefore, a stress-based parameter is defined to measure the local degree of stress multi-axiality, making use of the principal stress ratios. An absolute value of this ratio close to 1 indicates a multi-axial state that occurs typically in the vicinity of an intersection. The stress-based parameter is selected because the sensitivity with respect to the design variables can be calculated easily. The mathematical description of the proposed Intersection Indicator is given for both single load and multi load problems. The latter is more challenging, because stress fields produced in response to each load system are different.

Once the intersections can be identified, a further step is to control the occurrence as a function of the relative size of the intersections. In order to identify relative size, the average density in a local circular domain at the location of an intersection is used as a measure of the size of the intersection. Consequently, intersections slimmer (or bulkier) in size can be penalized more, whereas bulkier (or slimmer) can be allowed in the design domain using a weight function. To illustrate how these measures can be combined, we propose an objective function aiming to minimize relatively slim intersections, as this is of particular interest for the DMD process.

During optimization, if the objective is dominated equally by compliance and intersection reduction, then black and white design will be realized. However, if the objective is dominated by intersection minimization, designs with considerable gray regions may result. This problem arises because, the intersection identification is indifferent to the magnitude of the local stress but solely depends on the local principal stress ratio. For this, a threshold stress level is introduced to distinguish between elements with similar principal stress ratios but different stress levels. Moreover, since the intersection indicator is a function of the principal stress ratio, if one or both principal stresses vanish during optimization the intersection indicator will be ill-defined. By introducing the threshold stresses into the formulation, this problem is also resolved. In general for stress-based TO, problems related to the local nature of the stresses and possible stress singularity are of concern  (Kirsch 1990; Duysinx and Bendsøe 1998; Bruggi 2008). However, these problems are encountered when the stresses are constrained in the design domain. In our case, no constraints are imposed on the stresses, hence, reported problems are not encountered in our work. The effectiveness of our formulation is demonstrated, and the influence of various numerical parameters is studied based on several 2D compliance minimization problems.

The remainder of the paper is organized as follows: Sect. 2 presents the formulation of the Intersection Indicator, influence of threshold stress levels and intersection size estimation. The topology optimization problem formulation to minimize slim intersections and influence of threshold stress during optimization are presented in Sect. 3. Description of the numerical examples and resulting optimized designs and discussion are given in Sect. 4. A brief discussion on challenges to extend the method to 3D problems are outlined in Sect. 5. Finally, Sect. 6 provides the final conclusions.

2 Intersection Indicator

Table 1 Default Parameters for the optimization

Fig. 2

Load case Cantilever Beam : a design domain with dimensions discretized with $300 \times 100$ quadrilateral finite elements, loading and boundary conditions indicated, b design ($\tilde{\rho }_e$) obtained upon solving the standard compliance minimization problem c vector plot of dominant principal stress directions scaled with the magnitude dominant principal stress. Red and Blue are the representation of principal stresses $\sigma _I$ and $\sigma _{II}$, respectively. d Intersection indicator ($\xi _e$) field of the corresponding design which indicates biaxiality of the stress state within the structure when it is approximately one (red regions)

2.1 Optimization problem

For completeness, we briefly summarize the optimization problem considered:

$$\begin{aligned} \underset{\varvec{\rho }}{\min }&\quad c = \sum ^N_{e=1} E_e(\tilde{\rho }_e)\mathbf {u}_e^\text {T}\mathbf {k}_0\mathbf {u}_e, \end{aligned}$$

(1)

$$\begin{aligned} \text {where}&\quad \tilde{\rho }_e = \dfrac{\sum _{i \in \varOmega ^{\text {min}}_e}t_i(\mathbf {x}_i)v_i \rho _i}{\sum _{i \in \varOmega ^{\text {min}}_e}t_i(\mathbf {x}_i)v_i}, \end{aligned}$$

(2)

$$\begin{aligned}&\quad t_i(\mathbf {x}_i) = r_{\text {min}} - ||\mathbf {x}_i - \mathbf {x}_e||. \end{aligned}$$

(3)

$$\begin{aligned} \text {s.t.}&\quad \mathbf {Ku =f}. \end{aligned}$$

(4)

$$\begin{aligned}&\quad g = \dfrac{\sum _{\varOmega _N}v_e\tilde{\rho }_e}{V_0} - 1 \le 0. \end{aligned}$$

(5)

$$\begin{aligned}&\quad 0 \le \rho _e \le 1, \quad \forall e \in \varOmega _N. \end{aligned}$$

(6)

In Eq. (1), c is the structural compliance, $\mathbf {u}_e$ represents the element nodal degrees of freedom, $\mathbf {k_0}$ is the element stiffness matrix, and $E_e$ is the Young’s modulus which is scaled using the filtered density $\tilde{\rho }_e$ as

$$\begin{aligned} E_e(\tilde{\rho }_e) = E_{\text {min}} + \tilde{\rho }_e^p (E_0 - E_{\text {min}}). \end{aligned}$$

(7)

$E_0$ and $E_{\text {min}}$ are the Young’s modulus of material and void, respectively, p is the SIMP penalization exponent and N is the total number of elements in design domain $\varOmega _N$. Eq. (2) defines the density filter applied to the design variable $\rho _e$ at position $\mathbf {x_e}$ with element volume $v_e$ (Bruns and Tortorelli 2001). Eq. (3) represents the weight ($t_i$) calculation for the density filter. $\varOmega ^{\text {min}}_e$ is the local circular region in which the filter is effective with a radius $r_{\text {min}}$. Eq. (4) is the linear elastic state equation, where $\mathbf {K}$ is the global stiffness matrix and, $\mathbf {u}$ and $\mathbf {f}$ are the global nodal degrees of freedom and nodal loads, respectively. Eq. (5) represents the volume constraint, and Eq. (6) bounds the density variable for all elements in the design domain $\varOmega _N$. The 2D problem is solved using gradient-based optimization  (Svanberg 1987) following the nested analysis and design approach (Amir et al. 2010).

2.2 Intersection detection

2.2.1 Single load case

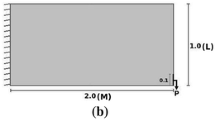
In order to identify intersections in compliance minimization TO, multi-axiality of the stress state is exploited. In compliance optimization the TO generates structural features typically under uniaxial stress to bear the load, such that the principal stress direction align in accordance with the orientation of a member  (Bendsøe and Haber 1993; Ambrozkiewicz and Kriegesmann 2018). Since an intersection is where members with different orientation meet, the stress tensor should exhibit a multi-axial characteristic for single load case. This notion is illustrated using an optimized cantilever beam layout shown in Fig. 2. The optimization is carried out using the default parameters shown in  Table 1, for the design domain depicted in Fig. 2a along with loading and boundary conditions. For the design obtained by standard compliance minimization, as depicted in Fig. 2b, two principal stresses $\sigma _I$ and $\sigma _{II}$ are calculated and the directions of the dominant principal stresses, i.e. either $\sigma _I$ or $\sigma _{II}$, for the material region are realized by line segments in Fig. 2c. The length of the line segments in Fig. 2c are scaled with the magnitude of the principal stresses. As expected, the stress state is primarily uniaxial in the members except at the intersections.

It remains to quantify stress multi-axiality in a design. The stresses in each element can be computed as follows:

$$\begin{aligned} \varvec{\sigma }_e = \tilde{\rho }_e^p \mathbf {D}_e\mathbf {B}_e\mathbf {u}_e. \end{aligned}$$

(8)

Note that the displacement field is already calculated in each optimization iteration. Stresses can therefore be obtained for a low computational cost. Here, $\varvec{\sigma }_e$ is the stress state of element e calculated at its centroid, $\mathbf {B}_e$ is the strain-displacement matrix and $\mathbf {D}_e$ is the constant constitutive matrix for isotropic linear elasticity. A plane stress condition is considered, i.e. $\varvec{\sigma }_e$ is given by $[\sigma _{xx}, \sigma _{yy}, \tau _{xy}]^T$ using Voigt notation. Next, the principal stresses for element e are calculated using:

$$\begin{aligned} \begin{aligned} \sigma _{I}&= \dfrac{\sigma _{xx} + \sigma _{yy}}{2} + \sqrt{\bigg (\dfrac{\sigma _{xx} - \sigma _{yy}}{2}\bigg )^2 + \tau _{xy}^2},\\ \sigma _{II}&= \dfrac{\sigma _{xx} + \sigma _{yy}}{2} - \sqrt{\bigg (\dfrac{\sigma _{xx} - \sigma _{yy}}{2}\bigg )^2 + \tau _{xy}^2}. \end{aligned} \end{aligned}$$

(9)

To measure stress biaxiality, we introduce a quantity $R_e$ composed of the ratios of these principal stresses

$$\begin{aligned} R_e = \dfrac{\sigma _{I}^2}{\sigma _{II}^2}+\dfrac{\sigma _{II}^2}{\sigma _{I}^2}. \end{aligned}$$

(10)

The above function is chosen because it involves both ratios $\sigma _{I}/\sigma _{II}$ and $\sigma _{II}/\sigma _{I}$. The stresses are squared because principal stresses could be both negative as well as positive and here we are only interested in the magnitude of stresses. For a biaxial stress state with principal stresses of roughly equal magnitude we obtain $R_e \approx 2$. In cases where the magnitude of the principal stresses differ significantly, including uniaxial stress states, it follows that $R_ e>> 2$. In the void regions, where the magnitude of the principal stresses is relatively small, $R_e$ may give false positives. Therefore, the filtered design variables $\tilde{\rho }_e$ can be used to avoid incorrect intersection detection in void regions. Thus, an Intersection Indicator ($\xi _e$) is proposed as:

$$\begin{aligned} \xi _e = \dfrac{\tilde{\rho }^p_e}{\log _2\big (R_e\big )}. \end{aligned}$$

(11)

The operation $1/\log _2(.)$ is applied on $R_e$ to map the value of $\xi _e$ between 0 and 1. As a result, three distinct settings can be identified: biaxial stress states in the solid ($\xi _e \approx 1$), uniaxial stress states in the solid ($0<\xi _e\ll 1$) and void regions ($\xi _e\approx 0$). Contours of this Intersection Indicator of the cantilever beam presented in Fig. 2b, are shown in Fig. 2d. It is clearly visible that the indicator reaches values near unity at intersections and does not lead to false positive in void regions. Thus, through exploiting biaxiality of the stress state intersections can be accurately identified.

Fig. 3

The effect of the threshold stress on the multi-axiality criterion. The x-axis represent the stress ratios assuming $|\sigma _{II}|\le |\sigma _I|$, and y-axis represent the corresponding value of the multi-axiality criterion. The multi-axiality criterion is plotted for various ratios of threshold stress and first principal stress

Fig. 4

Effect of the threshold stresses : a, b and c shows the effect on multiaxiality criterion ($1/\log _2(H_e)$) and, d, e and f shows the effect on Intersection Indicator $I_e$ for $\sigma _0 = 0~\mathrm MPa, 10~MPa$ and $100~\mathrm MPa$, respectively. The average and maximum value of $|\sigma _I|$ and $|\sigma _{II}|$ in the domain are $25.05~\mathrm MPa$ and $618.16~\mathrm MPa$, respectively

2.2.2 Influence of threshold stress on Intersection Indicator

As mentioned previously, $\xi _e$ is the intersection indicator which is a function of filtered density variable $\tilde{\rho }_e$ and stress multiaxiality measure $R_e$. The intersection indicator is used for optimization but when the design focus is primarily on intersection reduction, gray regions in mildly stressed regions remain. This is because the multi-axiality criterion $R_e$ is indifferent to stress levels. Therefore, the optimizer tends to reduce the multi-axiality of the local stress state instead of reducing the density of the element. Two elements which are at different stress levels but with comparable principal stress ratios will give a similar value of $R_e$. Therefore, it is desirable to distinguish between elements at different stress levels during optimization. Although void regions that are not load bearing are filtered out by the $\tilde{\rho }_e$ dependence of Eq. (11), the indifference of stress multi-axiality to differing stress levels can result in gray densities remaining in the design.

We introduce a threshold stress to distinguish between points at different stress levels to mitigate the complications discussed above. Moreover, to define intersection indicator for the cases where principal stresses may vanish, i.e., $\sigma _I \approx 0$ or $\sigma _{II} \approx 0$ or both, the threshold stress is used. The multi-axiality criterion, $R_e$, is thus modified to account for multi-axiality of the stress state only above a threshold stress level $\sigma _0$:

$$\begin{aligned} H_e = \dfrac{\sigma _{I}^2 + \sigma _{0}^2}{\sigma _{II}^2 + \sigma _{0}^2}+\dfrac{\sigma _{II}^2 + \sigma _{0}^2}{\sigma _{I}^2+ \sigma _{0}^2}. \end{aligned}$$

(12)

For $\sigma _0 = 0$, $H_e$ is equal to $R_e$. The effect of threshold stresses on the multi-axiality criterion is shown in Fig. 3. For a non-zero $\sigma _0$, the multi-axiality criterion will behave almost identical for points in the domain where stress levels are significantly above $\sigma _0$ (compare cases $|\sigma _0/\sigma _I|=0.05$ and $|\sigma _0/\sigma _I|=0$). However, regions where both principal stresses are significantly smaller than the threshold stress level (see for example the case $|\sigma _0/\sigma _I|=10$) will be considered artificially as biaxially stressed regions even when $|\sigma _{II}|$ is very different from $|\sigma _{I}|$. Consequently, for mildly stressed areas the multi-axiality criterion becomes insensitive to the modification of the stress state. Replacing $R_e$ with $H_e$ in Eq. (11) provides the modified Intersection Indicator ($I_e$):

$$\begin{aligned} I_e = \dfrac{\tilde{\rho }^p_e}{\log _2\big (H_e\big )}. \end{aligned}$$

(13)

The effect of $\sigma _0$ is demonstrated in Fig. 4. In this figure, $1 / \log _2{(H_e)}$ and $I_e$ are plotted for values of threshold stresses equal to 0, $10~\mathrm MPa$ and $100~\mathrm MPa$ for the design shown in Fig. 2b. The average and maximum value of both $|\sigma _I|$ and $|\sigma _{II}|$ in the domain are $25~\mathrm MPa$ and $618~\mathrm MPa$, respectively. For $\sigma _0 = 0$, in Fig. 4a it can be seen that the low-stressed regions, which are the void regions, exhibit both uniaxiality as well as biaxiality of the stress state. Since the stress levels are insignificant in these regions, the notion of multi-axiality of the stress state does not signify presence of any relevant design features at these locations. However, in the solid region the multiaxiality parameter clearly identifies the straight members and intersections via an uniaxial or biaxial stress state, respectively. Note that the magnitude of principal stresses in the void areas are orders of magnitude smaller than those in the solid area, but still the multiaxiality criterion does not differentiate between them. Scaling the multiaxiality criterion with the local density yields the intersection indicator shown in Fig. 4d. For the case $\sigma _0 = 10~\mathrm MPa$, the multiaxiality criterion is shown in Fig. 4b. It can be observed that the void regions in which the stress levels are negligible are now artificially identified as being in the biaxial stress state. Scaling with the filtered design variable removes these artificial biaxial regions. The resulting intersection indicator plot shown in Fig. 4e, shows no sign of artificial biaxial regions and no effect in the material regions. Hence, through the introduction of the threshold stresses, for mildly stressed regions multi-axiality becomes constant and thus cannot be influenced by the optimizer. The effect of threshold stress during optimization for intersection minimization of the same problem is discussed in detail in  Section 3.2. More importantly, most solid regions experience stress levels far above the threshold stress levels, thus the effect of the threshold stress is not visible in the solid region. This observation will be used in Section 3.2 to select the threshold stress for different considered problems. A higher threshold stress value, like $\sigma _0 = 100~\mathrm MPa$, affects both the multiaxiality criterion and the intersection indicator, such that the material regions are also considered in the artificial biaxial stress state as shown in Fig. 4c and f, which should be avoided. Therefore, threshold stresses should be lower than the principal stresses in the solid region.

Fig. 5

Multi-load case Cantilever Beam : a design domain with specified size, loading and boundary conditions, b design ($\tilde{\rho }_e$) obtained by solving standard topology optimization compliance minimization problem, c and d represents the biaxiality criterion ($1/\log _2{(H_e^{(m)})}$) for each load $P_1$ and $P_2$, respectively. e and f shows the Intersection Indicator ($I_e^{(m)}$) field of the corresponding design considering load case $P_1$ and $P_2$, respectively. (g) represents the aggregated biaxiality criterion ($1/\log _2{(H_e)}$). $H_e$ is calculated using Eq. (16). (h) is the corresponding intersection indicator field obtained by aggregating the biaxiality of the stress state experienced by the structure by load $P_1$ and $P_2$

2.2.3 Multi-load case

The Intersection Indicator defined above can be easily extended to multi-load case problems. First, a slight modification in notation is required for a multi-load case problem. Analogous to Eq. (10), for a total of M load cases with $m=1 \ldots M$, biaxiality in the design due to the $m^\text {th}$ load case is determined via

$$\begin{aligned} R^{(m)}_e = \dfrac{\big (\sigma ^{(m)}_{I}\big )^2 }{\big (\sigma ^{(m)}_{II}\big )^2}+\dfrac{\big (\sigma ^{(m)}_{II}\big )^2 }{\big (\sigma ^{(m)}_{I}\big )^2}. \end{aligned}$$

(14)

Substituting, $R_e^{(m)}$ in Eq. (11) provides the intersection indicator for the $m^{th}$ load case, denoted as $\xi _e^{(m)}$.

Multiple threshold stress values should be selected, one $\sigma _0^{(m)}$ corresponding to each load case m because loads can be of differing magnitude. Therefore, Eq. (14) becomes

$$\begin{aligned} H^{(m)}_e = \dfrac{\big (\sigma ^{(m)}_{I}\big )^2 + \big (\sigma ^{(m)}_{0}\big )^2}{\big (\sigma ^{(m)}_{II}\big )^2 + \big (\sigma ^{(m)}_{0}\big )^2}+\dfrac{\big (\sigma ^{(m)}_{II}\big )^2 + \big (\sigma ^{(m)}_{0}\big )^2}{\big (\sigma ^{(m)}_{I}\big )^2 + \big (\sigma ^{(m)}_{0}\big )^2}. \end{aligned}$$

(15)

Substituting $H_e^{(m)}$ in Eq. (13) gives the intersection indicator ($I_e^{(m)}$) corresponding to the $m^{th}$ load case. Fig. 5a shows the design domain of a cantilever beam with prescribed boundary and loading conditions. Note that, $P_1$ and $P_2$ are applied as separate load cases, corresponding to $m = 1$ and $m=2$, respectively. Through standard topology optimization for multi-load case problem, the design shown in Fig. 5b is obtained. The default parameters used for optimization are given in  Table 1. The average $|\sigma _I|$ and $|\sigma _{II}|$ in the domain corresponding to only load $P_1$ are $26~\mathrm MPa$ and $24~\mathrm MPa$, respectively, and corresponding to only load $P_2$ are $9~\mathrm MPa$ and $7~\mathrm MPa$, respectively. Therefore, the threshold stresses $\sigma _0^{(m)}$ corresponding to only load $P_1$ and $P_2$ are selected as $10~\mathrm MPa$ and $3~\mathrm MPa$, respectively, which are lower than both average principal stress values. The biaxiality criterion $1/\log _2(H_e^{(m)})$ for load case $m=1$ and 2 are shown in Fig. 5c and d, respectively. The corresponding intersection indicator $I_e^{(m)}$ for load case $m=1$ and 2 are shown in Fig. 5e and f, respectively. It is evident that through $I_e^{(1)}$ all intersections of the design can be identified. However, $I_e^{(2)}$ shows several false positives in the structural members (for example, Point $d_2$ in Fig. 5f). This is due to the fact that part of the structure on the right side of the load $P_2$ is not load-bearing for the load case with $P_2$ only. Therefore, the stresses generated on the right side are negligible. Thus, false multi-axiality is detected in the unloaded part of the structure. To account for all the load cases and mitigate false positives, an aggregation scheme is applied considering the following statements:

• If an Element e has an uniaxial stress state and is load bearing in all load cases, then for all load cases, $|\sigma ^{(m)}_{I}| \gg |\sigma ^{(m)}_{II}|$ or vice versa, leading to high $H_e^{(m)}$ values in each case. In the example problem depicted in Fig. 5, Point $d_1$ is load bearing for both load $P_1$ and $P_2$. The values of $H_e^{(m)}$ for Point $d_1$ in both load cases are considerably higher than 2 which can be inferred by Fig. 5c–d. Another case would be an Element e loaded in a uniaxial stress state for several loadcases which is not load bearing in other loadcases. Then, for loadcases in which it is load bearing $|\sigma ^{(m)}_{I}| \gg |\sigma ^{(m)}_{II}|$ or vice versa, again leading to high $H_e^{(m)}$ values in each case. However, for loadcases in which it is not loaded $|\sigma ^{(m)}_{I}| \approx |\sigma ^{(m)}_{II}| \approx 0$. Therefore, $H_e^{(m)}$ will be approximately equal to 2. In the example problem, Point $d_2$ is uniaxially loaded for loadcase $P_1$ but is not loaded for $P_2$. Therefore, the value of $H_e^{(1)}$ is high and $H_e^{(2)}\approx 2$ as shown in Fig. 5c–d. Thus, all Elements e which are uniaxially loaded in at least one loadcase will exhibit at least one $H_e^{(m)}$ which is $\gg 2$. It implies that aggregating the individual $H_e^{(m)}$ for an uniaxially loaded element across all loadcases will result into values $\gg 2$.

• Similarly, if an Element e is biaxially loaded and is load bearing in all load cases then $|\sigma ^{(m)}_{I}| \approx |\sigma ^{(m)}_{II}|$. In the example problem, Point $d_4$ is biaxially load-bearing for both loads $P_1$ and $P_2$. The $H_e^{(m)}$ values for both loadcases is approximately 2. Another case occurs when Element e is biaxially loaded in certain load cases and not loaded in other cases. Then for load cases in which the Element is biaxially loaded, $|\sigma ^{(m)}_{I}| \approx |\sigma ^{(m)}_{II}|$. However, for the case in which it is not loaded, $|\sigma ^{(m)}_{I}| \approx |\sigma ^{(m)}_{II}| \approx 0$. Note, for both sets, $H_e^{(m)} \approx 2$ is obtained. Point $d_3$ is biaxially load-bearing for load $P_1$ only but not load-bearing for $P_2$. The values of $H_e^{(m)}$ in both load cases are approximately 2 which can be inferred by Fig. 5c–d. Thus, for elements which are biaxially loaded in at least one load case and not load bearing in other cases results with $H_e^{(m)}$ approximately 2 for all load cases. Aggregating $H_e^{(m)}$ over all the loadcases will hence result into a value approximately equal to 2M.

Motivated by above observations to formulate the intersection indicator for multi load case problems, the biaxiality in the structure is aggregated as follows:

$$\begin{aligned} H_e = \dfrac{1}{M}\sum _{m=1}^MH_e^{(m)}. \end{aligned}$$

(16)

Through this definition the uniaxially loaded elements in at least one loadcase will exhibit value of $H_e\gg 2$. Moreover, the biaxially loaded elements at least in one loadcase will exhibit value of $H_e\approx 2$. Now, substituting Eq. (16) in Eq. (13) provides intersection indicator ($I_e$) for the multi-load case problem. For the example problem, the plot of $1/\log _2{(H_e)}$ and corresponding intersection indicator is shown in Fig. 5g and h, respectively. It can be observed in Fig. 5g that through aggregation the uniaxially and biaxially loaded elements in the solid are clearly identified. The void regions are considered in artificially biaxial state which are then filtered out through filtered density as shown in corresponding intersection indicator plot Fig. 5h. This formulation is also applied to problems with more than 2 load cases to check the scope of the approach. It is observed that through proposed aggregation, intersections can be detected in multi-load case problems with more than two load cases. We note in passing, for $M=1$, Eq. (16) reduces to Eq. (12).

Fig. 6

Schematic illustration of various design features such as a a slim intersection b a bulky intersection c a slim intersection with extra material around and d a straight member

2.3 Intersection Size

As discussed in the Introduction, in certain applications one may require to control the occurrence of intersections depending on their sizes. Consider the two intersections, shown in Fig. 6a and b. To evaluate the intersection size, assume a circular domain, $\varOmega ^{\text {int}}_e$, centered at Element e (indicated by a red dot in Fig. 6). Averaging the filtered densities in this local domain provides information on the size of the intersection at Element e. For a relatively bulky intersection, shown in Fig. 6b, the average filtered density is higher than in case of a relatively slim intersection, shown in Fig. 6a. However, the intersection shown in Fig. 6c, which happens to be an intersection as slim as the intersection depicted in Fig. 6a, has a higher average density in the local region $\varOmega _e^{\text {int}}$ compared to that of the intersection shown in Fig. 6a. Note that, the farther the material is located from the center of the circular domain at Element e, the lower the probability this material is part of the intersection. To account for this, a weighted averaging scheme is proposed, such that the contribution of the filtered density of a particular element to the local averaged density at a point of interest depends on the distance between the element and the point of interest. The weighted density filter  (Bruns and Tortorelli 2001) is used to calculate the local weighted average of the filtered density$(\hat{\tilde{\rho }}_e)$:

$$\begin{aligned}&\hat{\tilde{\rho }}_e = \dfrac{\sum _{i \in \varOmega ^{\text {int}}_e}w_i(\mathbf {x}_i) v_i\tilde{\rho }_i}{\sum _{i \in \varOmega ^{\text {int}}_e}w_i(\mathbf {x}_i) v_i},\\&\quad w_i(\mathbf {x}_i) = r_{\text {int}} - ||\mathbf {x}_i - \mathbf {x}_e||.\\ \end{aligned}$$

(17)

Here, $r_{\text {int}}$ is the radius of the local circular domain $\varOmega ^\text {int}$.

A straight member, as shown in Fig. 6d, has values of $\hat{\tilde{\rho }}_e$ equivalent to that of a bulky intersection. To distinguish between a straight member and an intersection, this size measure $\hat{\tilde{\rho }}_e$ must be combined with the Intersection Indicator $(I_e)$.

Inspired by the requirements in the DMD process, we consider the case of allowing bulky intersections, while suppressing slim ones. Thus, to penalize slim intersections, weight factors are calculated as function of intersection size

$$\begin{aligned} \hat{s}_e&= 1 - \hat{\tilde{\rho }}_e, \end{aligned}$$

(18)

$$\begin{aligned} S_e&= \hat{s}_eI_e. \end{aligned}$$

(19)

Here, $\hat{s}_e$ is the weight assigned to the intersections at Element e and $S_e$ is the weighted intersection indicator that is higher for slim intersections in a design. These weights are chosen as an example for the DMD application, however, the weights can be chosen in other ways to target different intersection sizes for other applications.

Recall that the minimum member size in TO is set to be $2r_\text {min}$ therefore, the minimum intersection size is $2\sqrt{2}r_\text {min}$. Thus, to detect the size of an intersection, we require $r_{\text {int}} > \sqrt{2}r_\text {min}$. Consequently, intersections larger than the chosen value $r_\text {int}$ are not detected. To illustrate this with an example, we revisit the cantilever problem shown in Fig. 2. The filter given in Eq. (17) is applied to the filtered density field shown in Fig. 2b for three different $\beta$ values, where $\beta = r_{int}/r_{min}$, as shown in Fig. 7. The chosen values of $\beta$ are 2, 4 and 6. As observed from Fig. 7a–c, increasing the radius increases $\hat{s}_e$ in entire domain, and thus, a greater number of thin intersections are identified below the domain size $\varOmega ^{\text {int}}_e$. This is evident from Fig. 7d–f. Note that the weighted averaging in the local domain provides a relative size measure which can distinguish between bulky and slim intersections.

Fig. 7

Load case Cantilever Beam : a, b and c show the intersection weight factors, $\hat{s}_e$, for $\beta = r_{int}/r_{min} = 2$, 4 and 6, respectively. d, e and f represent the corresponding weighted intersection indicator $S_e = \hat{s}_eI_e$ representing the intersections smaller than the threshold defined by $r_{\text {int}}$. The red and black circles represent the size of the $r_\text {min}$ and $r_\text {int}$, respectively. As radius $r_\text {int}$ increases more number of intersecting features are identified

3 Problem Description and Threshold Stress Selection

3.1 Multi-Objective Formulation : Compliance and Intersection Objective

So far it has been established that the presence of intersections can be identified and their relative size can be determined. It remains to control the occurence of intersections in TO. The intersection indicator defined in the previous section only gives an indication of intersection presence. It does not provide insight on the actual number of intersections. Moreover, as stated in the Introduction, intersections facilitate load transfer, therefore their presence is paramount for mechanical performance. However, from a manufacturing point of view, such as for DMD, slim intersections are problematic. Therefore, the number of slim intersections should be restricted to improve manufacturability of through DMD. Therefore, there is a trade off between performance and manufacturability. Consequently, for optimization we adopt a multi-objective approach where a total objective function is defined as a combination of compliance of the structure and a function suppressing slim intersections.

Firstly, we define the function that will be minimized to achieve fewer slim intersections for DMD application. The proposed function which is also termed as intersection objective I is defined as:

$$\begin{aligned} I = \dfrac{\sum _{\varOmega _N}S_e}{\dfrac{1}{V_0}{\sum _{\varOmega _N}v_e\tilde{\rho }_e}}. \end{aligned}$$

(20)

The numerator of the intersection objective I is the summation of the weighted intersection indicator $S_e$ over the entire domain. Given Eq. (18), the contribution from relatively slim intersections will be higher, whereas bulky intersections and straight members will only contribute marginally. Thus, minimizing the numerator will minimize thin intersections and promote bulky intersections or straight members in a design. The denominator of the intersection objective is the design volume normalized by the allowed volume in the design domain $V_0$. Upon omitting the term, the optimizer removes material from the intersection location and the optimization tends towards a trivial solution of no material. Therefore, the denominator term promotes material in the design domain.

Finally, the standard compliance minimization problem, given in Eq. (1)–(6) is extended to a multi-objective problem as described below:

$$\begin{aligned} \underset{\rho }{\min }&\quad O = \dfrac{1}{\mu }\Bigg (\theta \dfrac{c}{c^*} + (1-\theta ) \dfrac{I}{I^*}\Bigg ). \end{aligned}$$

(21)

$$\begin{aligned} \text {s.t.}&\quad \mathbf {Ku =f}. \end{aligned}$$

(22)

$$\begin{aligned}&\quad g = \dfrac{\sum _{\varOmega _N}v_e\tilde{\rho }_e}{V_0} - 1 \le 0. \end{aligned}$$

(23)

$$\begin{aligned}&\quad 0 \le \rho _e \le 1, \quad \forall e \in \varOmega _N. \end{aligned}$$

(24)

In Eq. (21), O is the total objective function, $\theta$ is the weight assigned to the compliance objective, consequently, $(1-\theta )$ is the weight assigned to the intersection objective. The parameter $\theta$ is a tuning parameter which can be reduced to emphasis on manufacturability of the design through DMD. Both the objectives are normalized by their respective values of the compliance ($c^*$) and intersection ($I^*$) calculated for the design obtained by the standard compliance minimization problem. Superscripts $(*)$ are used to indicate values that are calculated on the converged standard compliance minimization design. The constant factor $\mu$ is introduced to scale the value of the objective such that it ranges between 1 and 100 for the stability of the MMA optimizer, see (Svanberg 1987). The sensitivity analysis of the objective and constraint functions are determined using the adjoint method and detailed in Appendix A.

Fig. 8

Effect of threshold stress levels on intersection minimization results for Problem 1: a Design at $100^{th}$ iteration for $\sigma _0=0~\mathrm MPa$. b is the corresponding multi-axiality criterion $1/\log _2(H_e)$. c and d Design and corresponding multi-axiality criteria at $100^{th}$ iteration step for $\sigma _0=10~\mathrm MPa$. The threshold stress is selected from the reference compliance minimization design shown in Fig. 2b. For the reference case, the average and maximum value of both $|\sigma _I|$ and $|\sigma _{II}|$ in the domain are $25~\mathrm MPa$ and $618~\mathrm MPa$. The threhold stress, $\sigma _0=10~\mathrm MPa$, is below the average stress value in the reference case

3.2 Effect of threshold stress levels on Intersection Minimization and Selection Strategy

As mentioned in Section 2.2.2, the effect of the chosen threshold stress during optimization is crucial. To demonstrate its effect, initially the threshold stress is assumed to be zero ($\sigma _0 = 0$). The multi-objective formulation is applied to Problem 1 with $\theta = 0.2$, i.e, the contribution of intersection objective I is dominant. The pure compliance minimization design previously shown in Fig. 2b is chosen as the reference case for the calculation of $c^*$ and $I^*$. The value of $\beta = 6$ is chosen because it targets every intersection in a compliance minimization design, shown in Fig. 7f. The results obtained after 100 iterations are presented in Fig. 8. In the design shown in Fig. 8a, it can be observed gray regions are present at locations which experience low stress levels, such as Region 1 and 2 (indicated by red circles) and an arch shaped design feature is observed with high material density in Region 3. The corresponding objective values are $c / c^* = 2.01$, $I / I^* = 0.44$ and $O / O^* = 0.75$, see Eq. (21). It shows that the intersection objective and total objective have reduced, as desired. However, the obtained result does not represent a desired, manufacturable geometry. The features formed in the low stresses regions demonstrate that the effect of reducing the local multi-axial stress state dominates removal of local densities in these regions, as shown in Fig. 8b, leading to the depicted undesired result. In order to facilitate only removal of local densities from low stresses regions, the effect of reducing local multi-axial stress state should be nullified.

To avoid generation of the design features in regions where the stress is negligible during optimization, the threshold stress, mentioned in Section 2.2.2, is introduced. The stress response from the pure compliance minimization reference design is used to aid in the selecting the threshold stress level. Recalling that for the compliance minimization design in Fig. 2b average and maximum value of both $|\sigma _I|$ and $|\sigma _{II}|$ in the domain are $25~\mathrm MPa$ and $618~\mathrm MPa$, respectively. Also, it is shown previously that for $\sigma _0 = 10~\mathrm MPa$, which is below the average stress value, does not affect the intersection indicator of the converged compliance design (see Fig. 4d and e). Therefore, for the intersection minimization problem, $\sigma _0 = 10~\mathrm MPa$ is selected because in the reference compliance minimization case, the stresses in the solid region are significantly above $10~\mathrm MPa$. The result of intersection minimization after 100 optimization iterations considering $\sigma _0 =10~\mathrm MPa$ is shown in Fig. 8c. The design does not contain gray design features in the lowly stressed region, as they are artificially considered in the biaxial stress state which can be observed in Fig. 8d. Since, there is no possibility to reduce the local multi-axial stress state in the low stressed region, the intersection objective is reduced by removing the local densities in these regions, which promotes convergence to a manufacturable designs. The corresponding objective values are $c / c^* = 1.34$, $I / I^* = 0.35$ and $O / O^* = 0.55$.

It remains to determine the value of the threshold stress for general cases. The key aspect is that low-stressed regions should be discouraged to affect the detection of stress multi-axiality. Since the intersection minimization problem is solved simultaneously with the compliance minimization problem, the stress levels found in the solid regions of the compliance minimization design are considered as representative. Therefore, the threshold stress value should be selected such that it is smaller than the stress levels present in the solid regions of the compliance minimization design. Now, the stress levels in the solid regions are either dictated by $\sigma _{I}$, $\sigma _{II}$ or both. Thus, the measure of stress levels should be combination of the individual principal stress components. This motivates the selection of Von Mises stresses as a measure of stress levels in solid regions and the threshold stress should be smaller than the Von Mises stress field in the solid regions of compliance minimization design.

The compliance minimization design consists of void (white) and material (black) regions separated by interface (gray) regions. The stress levels experienced by interface (gray) regions fall between those in void and material regions. In this paper, the following procedure is adopted to select the threshold stresses for single and multi loadcase problems:

• 1. Apply the load and boundary conditions to the converged design obtained from the standard compliance minimization problem and determine the principal stresses at each element in the domain using Eq. (8) and Eq. (9).

• 2. Calculate the Von Mises stress ($\sigma _\text {(vm)}$) at each element in the domain using $\sqrt{\sigma _{I}^2 - \sigma _{I}\sigma _{II} + \sigma _{II}^2}$.

• 3. To identify the Von Mises stress in the gray regions, stresses which corresponds to filtered design variables $0.1<\tilde{\rho }_e < 0.5$ are selected. Due to SIMP penalization, the stress levels corresponding to the value of $\tilde{\rho }_e = 0.1$ and $\tilde{\rho }_e = 0.5$ will be in the order of $0.1\%$ and $12.5\%$ compared to the stress levels in the solid region ($\tilde{\rho }_e = 1$), respectively. Therefore, the stress levels in the selected range will be significantly lower than the stresses in the solid region.

• 4. To select the threshold stresses as low as possible, sort the Von Mises stresses of the selected filtered density range in ascending order. Pick the stress value found at an index closest to $90\%$ of the length of the array. The $90\%$ value is selected as threshold so that most of the lowly stressed regions in a design are artificially considered in biaxial stress state.

The proposed algorithm used to systematically select threshold stresses presented a good performance distinguishing between the lowly and significantly stressed regions during optimization for all problems discussed in this paper. Nevertheless, note that the proposed algorithm is only one option and choosing the best algorithm is beyond the scope of this work.

Fig. 9

Test problems: a Cantilever beam; b MBB Beam; c Cantilever beam with a hole; d Multi load case beam problem with equal loads e Multi load case beam problem with different loading. The dimensions of the design domain of all the test problems are $300~{\mathrm{mm}} \times 100~{\mathrm{mm}}$

4 Results

In this section, results obtained by applying the proposed multi-objective formulation on various single and multi load problems are presented. The design domains and boundary conditions of the 5 considered test problems are given in Fig. 9. Each problem is labeled with a problem number for reference. All the design domains have equal dimensions. Recall that the default optimization settings are given in Table 1. Optimization results of all the problems and effect of different parameters on the designs are shown in Section 4.1. An overall discussion is given in Section 4.2.

4.1 Designs

4.1.1 Effect of $\theta$

The designs obtained for all of the test problems defined in Fig. 9 are shown in Fig. 10. Results obtained for $\beta = 6$ are shown. Here, $r_\text {int}$ is chosen to be sufficiently large to target every intersection in the respective compliance minimization design, further effects of $r_\text {int}$ on the design are discussed in Section 4.1.2. Converged designs obtained for different values of $\theta$ and their corresponding intersection and compliance objective values are shown in Fig. 10. Designs for $\theta =1.0$ correspond to standard compliance minimization, the reference design for each of the problems. It is evident from the designs that, as the weight on the intersection objective increases, the number of intersections reduces in the design. Consistently the compliance objective is increasing while the intersection objective is decreasing. In all the problems, it is observed that the minimization of intersections comes at the cost of inferior stiffness performance.

Fig. 10

Designs obtained after applying compliance and intersection minimization for considered problems. Arrows indicate designs for the corresponding data point. The parameter $\theta$ associated to a design is given below the design. In all the test problems, as the weight on the intersection objective increases slim intersections are reduced and bulky intersections are preferred, consequently, geometrical complexity is reduced

4.1.2 Effect of $r_\text {min}$ and $r_\text {int}$

Recall that the proposed method utilizes two local circular domains, determined by the radii, $r_\text {min}$ and $r_\text {int}$, that are anticipated to affect the optimized design. Increasing $r_\text {min}$ leads to an increase in the minimum member size and, thus, leading to fewer intersections. In order to isolate the effect of $r_\text {int}$, $r_\text {min}$ is kept constant and $r_\text {int}$ is varied. In Fig. 11, designs for Problem 1 are illustrated for three selected values of $\beta = r_\text {int}/r_\text {min}$ equal to 2 ,4 and 6, while keeping $r_\text {min}= 2.5~\mathrm mm$ and $\theta = 0.6$. The values of compliance and intersection objective given in Fig. 11 are normalized by the reference design shown in Fig. 2b. For all the designs, the intersections are clearly identified by the intersection indicator as shown in the corresponding plot of $I_e$, see Fig. 11.

During optimization, if an intersection size reaches the size of the local domain with radius $r_\text {int}$, then the contribution of that intersection to the intersection objective will be negligible and therefore, the intersection will not be reduced. This effect is clearly visible in the design for $\beta = 2$, as shown in Fig. 11. The weights $\hat{s}_e$, which is inversely proportional to intersection size (see Eq. (18)), corresponding to each intersection are close to 0. It suggests that the intersection size is equivalent to the local domain with radius $r_\text {int}$. Also the contribution of the intersections in the intersection objective is close to 0 as evident from the $S_e$ plots.

As $r_\text {int}$ increases, bulkier intersections are preferred which can be seen in the design for $\beta = 4$, see Fig. 11. The weight $\hat{s}_e$ corresponding to the bulky intersection is close to 0 as can be seen in the $\hat{s}_e$ plots. Furthermore, the contribution from bulky intersections to the intersection objective is also close to 0 as shown in the $S_e$ plots.

Further increasing $r_\text {int}$, i.e. for $\beta = 6$, relatively thicker intersections are observed than for $\beta = 2$. However, a slim intersection is also observed which is not removed during optimization. Plot of weight $\hat{s}_e$ shows that the bulky intersection has relatively lower value of $\hat{s}_e$ than the slim intersection. The contribution from slim intersection to the intersection objective is also higher as shown in $S_e$ plot. It means that the slim intersections are detected, however, it is not removed during optimization. This happens because, firstly, the slim intersections are minimized which does not mean that slim intersections can not exist in a design. Secondly, using $\theta =0.6$ means that the compliance objective function has a greater influence, therefore, the slim feature is not removed completely.

Fig. 11

Effect of $r_\text {int}$ on Problem 1 : Cantilever Beam. The red and black circles indicate the size of the local circular domain with radius $r_\text {min}$ and $r_\text {int}$, respectively. As the radius $r_\text {int}$ increases the size of the intersections promoted in the design domain increases. Therefore, the size of the intersections also increases in the converged designs with increase of $r_\text {int}$

4.2 Discussions on Results

The results show that by minimizing the slim intersections, the topology of the compliance minimization design has been simplified. Moreover, calculation of the intersection indicator is computationally efficient because at every iteration step displacement information is available, and calculation of stresses based on this requires only element level linear operations (see Eq. (8)). However, for minimizing the intersection objective an additional set of adjoint equations has to be solved which increases its computational cost. For the multi-load case problem, the number of adjoint equations scales with the number of load cases in a single problem because stress fields from different load cases are aggregated together. The convergence behavior of normalized compliance and intersection objective with respect to iteration step of Problem 1 with $\beta = 6$ are shown in Figs. 12 and 13, respectively. The convergence plots show smooth convergence. However, the number of iterations required was quite high compared to standard compliance minimization problem. This is due to the fact that the sensitivity of the compliance minimization problem is always negative with respect to every design variable, but for the intersection objective it is not the case, thus the convergence gets slower compared to compliance minimization.

Fig. 12

Convergence of compliance objective of cantilever beam (Problem 1)

Fig. 13

Convergence of intersection objective of cantilever beam (Problem 1)

5 Extension to 3D Problems

For 3D problems, again there are two aspects to be considered, identification and control of 3D intersections. In contrast to the 2D problems, it was observed, by examining 3D TO results, one may identify following types of intersections:

• Straight beams intersecting with each other.

• Straight beams intersecting with a plate type structure.

• Two or more plate like structures intersecting with each other.

To identify above mentioned 3D intersections certain ‘signatures’ in terms of principal stress ratios have been recognized. However, defining an indicator, similar to the 2D case, to reliably identify these features proves more challenging due to the larger variety of intersection types. Further investigation is needed to develop an intersection indicator for 3D problems.

Moreover, controlling 3D intersections to generate designs for certain manufacturing process such as DMD have two important aspects. Firstly, 3D intersections need not be problematic for the DMD process because mostly the production happens in a layer-by-layer manner. Thus, it is possible that within the deposition layer intersections are not encountered and the part could be produced easily. A rather challenging problem left for future research is to identify the intersections within the deposition layers and then minimize them for DMD related applications. This could be achieved by projecting the stress components to the plane of deposition. Secondly, for DMD processes, designs with high geometric complexity could also pose a problem during manufacturing. Hence, once a reliable 3D intersection indicator is developed, then, based on their relative size, intersections can be controlled to achieve minimal geometric complexity, similar to the 2D case.

6 Conclusions

In this study a novel approach to reduce geometric complexity of designs in 2D compliance minimization topology optimization is presented. The reduction in the geometric complexity is attained through identifying and controlling intersections by means of the local stress state for single and multi load case problems. The reduction of geometric complexity of a design improves manufacturability through both conventional as well as additive manufacturing processes, such as DMD.

The proposed Intersection Indicator is a function of the ratio of local principal stresses. Therefore, the design sensitivities of the indicator can be easily evaluated by solving a set of adjoint equations per loadcase. This renders the indicator suitable for gradient-based optimization. To prevent convergence problems due to spurious stress ratios in low-stressed regions, a threshold stress is introduced as well as a procedure to select an appropriate value. To control intersections, a multi-objective formulation is proposed comprising of a compliance and intersection objective. A provision to emphasize intersections according to their size has also been presented, and demonstrated in the context of the DMD process, where slim intersections are to be avoided. Controlled by the relative weight of the intersection objective, different levels of design simplification are achieved, both for single as well as multi-load problems. As expected, increasing restrictions on design complexity leads to increased compliance.

Smooth convergence is observed without a continuation scheme. However, the number of iterations required for convergence increases when the relative weight of the intersection objective increases. Implementing the proposed formulation in an existing topology optimization framework, such as the 88-line MATLAB TO code presented by Andreassen et al. (2011), is straightforward. It involves calculation of principal stresses, threshold stresses and sensitivities of intersection objective.

Although the proposed approach proved effective in various test problems, it has limitations. First, it does not provide control on the exact number of intersections. Second, the stress-based indicator relies on characteristics of optimal designs obtained in compliance minimization. Its extension to other problems such as compliant mechanism or thermal optimization will require developing a relation between geometrical aspects of intersections and the ‘physics’ observed at intersections. Currently, the presented intersection indicator is therefore restricted to 2D compliance minimization problems. Extension to a 3D setting is a topic for future work, where stress-based recognition of the variety of intersection types that can occur in 3D is the main challenge.

Appendix A: Sensitivity Analysis

1.1 A.1 Sensitivity Analysis

The sensitivity calculation of the compliance objective and volume constraint is well known (Bendsoe and Sigmund 2013) and given as follows:

$$\begin{aligned} \dfrac{\partial c}{\partial \tilde{\rho }_j}&= - p(E_0-E_{min})\tilde{\rho }_j^{p-1}\mathbf {u}_j^T\mathbf {k_0}\mathbf {u}_j. \end{aligned}$$

(25)

$$\begin{aligned} \dfrac{\partial g}{\partial \tilde{\rho }_j}&= \dfrac{v_j}{V_0}. \end{aligned}$$

(26)

The sensitivity of the intersection objective is calculated by applying the quotient, product and chain rules of derivatives. The sensitivity calculation is shown for a single loadcase problem for clarity and it can be extended to multi loadcase problem with minor modification. Firstly, design differentiation of Eq. (20),yields:

$$\begin{aligned} \dfrac{\partial I}{\partial \tilde{\rho }_j} = -V_0\dfrac{\sum _{\varOmega _N}\hat{s}_eI_e}{(\sum _{\varOmega _N}\tilde{\rho }_ev_e)^2} \sum _{\varOmega _N}\dfrac{\partial \tilde{\rho }_e}{\partial \tilde{\rho }_j}v_e + \dfrac{V_0}{(\sum _{\varOmega _N}\tilde{\rho }_ev_e)} \sum _{\varOmega _N}\dfrac{\partial (\hat{s}_eI_e)}{\partial \tilde{\rho }_j}. \end{aligned}$$

(27)

The term $\dfrac{\partial \tilde{\rho }_e}{\partial \tilde{\rho }_j} = \delta _{ej}$, where $\delta _{ej}$ is the Kronecker delta function, thus the above equation reduces to:

$$\begin{aligned} \dfrac{\partial I}{\partial \tilde{\rho }_j} = -V_0v_j\dfrac{\sum _{\varOmega _N}\hat{s}_eI_e}{(\sum _{\varOmega _N}\tilde{\rho }_ev_e)^2} +\dfrac{V_0}{(\sum _{\varOmega _N}\tilde{\rho }_ev_e)}\sum _{\varOmega _N}\dfrac{\partial (\hat{s}_eI_e)}{\partial \tilde{\rho }_j}. \end{aligned}$$

(28)

Now the product rule is applied to the later part of the above equation using Eq. (18), as shown below:

$$\begin{aligned} \sum _{\varOmega _N}\dfrac{\partial (\hat{s}_eI_e)}{\partial \tilde{\rho }_j} = \sum _{\varOmega _N}\Bigg (-I_e\dfrac{\partial \hat{\tilde{\rho }}_e}{\partial \tilde{\rho }_j} + (1-\hat{\tilde{\rho }}_e)\dfrac{\partial I_e}{\partial \tilde{\rho }_j}\Bigg ). \end{aligned}$$

(29)

In the above equation, the term $\dfrac{\partial \hat{\tilde{\rho }}_e}{\partial \tilde{\rho }_j}$, can be derived from Eq. (17) as shown below:

$$\begin{aligned} \sum _{\varOmega _N}-I_e\dfrac{\partial \hat{\tilde{\rho }}_e}{\partial \tilde{\rho }_j} = \sum _{\varOmega _N}-I_e\dfrac{\sum _{\varOmega ^{\text {int}}_e}w_i v_i\dfrac{\partial \tilde{\rho }_i}{\partial \tilde{\rho }_j}}{\sum _{\varOmega ^{\text {int}}_e}w_i v_i}. \end{aligned}$$

(30)

Now, since filtered densities are independent variables thus, the above equation can be written as:

$$\begin{aligned} \dfrac{\partial \hat{\tilde{\rho }}_e}{\partial \tilde{\rho }_j} = {\left\{ \begin{array}{ll} \dfrac{w_j v_j}{\sum _{\varOmega ^{\text {int}}_e}w_i v_i} \quad &{}\text {if,}\;i=j,\\ 0 \quad &{}\text {if,}\;i\ne j. \end{array}\right. } \end{aligned}$$

(31)

To calculate the term with $\dfrac{\partial I_e}{\partial \tilde{\rho }_j}$ in Eq. (29), the product rule is applied to Eq. (13). With some simplifications and using Eq. (8), Eq. (9), Eq. (12) and Eq. (13) the term can be reduced to the following form:

$$\begin{aligned}&\sum _{\varOmega _N}(1-\hat{\tilde{\rho }}_e)\dfrac{\partial I_e}{\partial \tilde{\rho }_j} = \dfrac{p\tilde{\rho }_j^{p-1}(1-\hat{\tilde{\rho }}_j)}{\log _2(H_j)} \nonumber \\&\quad - \dfrac{p\tilde{\rho }_j^{2p-1} (1-\hat{\tilde{\rho }}_j)}{\ln (2)(\log _2(H_j))^2}\Bigg [\dfrac{\partial H_j}{\partial \sigma _{p}}\Bigg ] \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _{j}}\Bigg ] \mathbf {D}_j\mathbf {B}_j\mathbf {u}_j \nonumber \\&\quad - \sum _{\varOmega _N}\dfrac{\tilde{\rho }_e^{2p} (1-\hat{\tilde{\rho }}_e)}{\ln (2)(\log _2(H_e))^2}\Bigg [\dfrac{\partial H_e}{\partial \sigma _{p}}\Bigg ] \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _e}\Bigg ] \mathbf {D}_e\mathbf {B}_e\dfrac{\partial \mathbf {u}_e}{\partial \tilde{\rho }_j}. \end{aligned}$$

(32)

where,

$$\begin{aligned} \Bigg [\dfrac{\partial H_e}{\partial \sigma _{p}}\Bigg ]= & {} \begin{bmatrix} \dfrac{\partial H_e}{\partial \sigma _{I}} \;&{} \dfrac{\partial H_e}{\partial \sigma _{II}}\\ \end{bmatrix}, \end{aligned}$$

(33)

$$\begin{aligned} \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _e}\Bigg ]= & {} \begin{bmatrix} \dfrac{\partial \sigma _{I}}{\partial \sigma _{xx}} \;&{} \dfrac{\partial \sigma _{I}}{\partial \sigma _{yy}} \;&{} \dfrac{\partial \sigma _{I}}{\partial \tau _{xy}}\\ \\ \dfrac{\partial \sigma _{II}}{\partial \sigma _{xx}} \;&{} \dfrac{\partial \sigma _{II}}{\partial \sigma _{yy}} \;&{} \dfrac{\partial \sigma _{II}}{\partial \tau _{xy}}\\ \end{bmatrix}, \end{aligned}$$

(34)

$$\begin{aligned} \Bigg [\dfrac{\partial \sigma _e}{\partial \tilde{\rho }_j}\Bigg ]= & {} \begin{bmatrix} \dfrac{\partial \sigma _{xx}}{\partial \tilde{\rho }_j} \; &{} \dfrac{\partial \sigma _{yy}}{\partial \tilde{\rho }_j} \;&{} \dfrac{\partial \tau _{xy}}{\partial \tilde{\rho }_j}\\ \end{bmatrix}^T. \end{aligned}$$

(35)

The sensitivity calculation of individual terms is given subsequently as

$$\begin{aligned} \Bigg [\dfrac{\partial H_e}{\partial \sigma _{p}}\Bigg ] = \begin{bmatrix} \dfrac{\partial H_e}{\partial \sigma _{I}} \;&{} \dfrac{\partial H_e}{\partial \sigma _{II}}\\ \end{bmatrix} \end{aligned}$$

(36)

where,

$$\begin{aligned} \dfrac{\partial H_e}{\partial \sigma _{I}}&= \dfrac{2\sigma _{I}}{\sigma _{II}^2 +\sigma _0^2} - \dfrac{2\sigma _{I}(\sigma _{II}^2 +\sigma _0^2)}{(\sigma _{I}^2 +\sigma _0^2)^2} \end{aligned}$$

(37)

$$\begin{aligned} \dfrac{\partial H_e}{\partial \sigma _{II}}&= \dfrac{2\sigma _{II}}{\sigma _{I}^2 +\sigma _0^2} - \dfrac{2\sigma _{II}(\sigma _{I}^2 +\sigma _0^2)}{(\sigma _{II}^2 +\sigma _0^2)^2} \end{aligned}$$

(38)

$$\begin{aligned} \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _e}\Bigg ]&= \begin{bmatrix} \dfrac{\partial \sigma _{I}}{\partial \sigma _{xx}} \;&{} \dfrac{\partial \sigma _{I}}{\partial \sigma _{yy}} \;&{} \dfrac{\partial \sigma _{I}}{\partial \tau _{xy}}\\ \\ \dfrac{\partial \sigma _{II}}{\partial \sigma _{xx}} \;&{} \dfrac{\partial \sigma _{II}}{\partial \sigma _{yy}} \;&{} \dfrac{\partial \sigma _{II}}{\partial \tau _{xy}}\\ \end{bmatrix} \end{aligned}$$

(39)

where,

$$\begin{aligned} \dfrac{\partial \sigma _{I}}{\partial \sigma _{xx}}&= \dfrac{1}{2} + \dfrac{1}{4}\;\dfrac{\sigma _{xx} - \sigma _{yy}}{\sqrt{\dfrac{(\sigma _{xx}-\sigma _{yy})^2}{4}+\tau _{xy}^2}} \end{aligned}$$

(40)

$$\begin{aligned} \dfrac{\partial \sigma _{I}}{\partial \sigma _{yy}}&= \dfrac{1}{2} - \dfrac{1}{4}\;\dfrac{\sigma _{xx} - \sigma _{yy}}{\sqrt{\dfrac{(\sigma _{xx}-\sigma _{yy})^2}{4}+\tau _{xy}^2}} \end{aligned}$$

(41)

$$\begin{aligned} \dfrac{\partial \sigma _{I}}{\partial \tau _{xy}}&= \dfrac{\tau {xy}}{\sqrt{\dfrac{(\sigma _{xx} -\sigma _{yy})^2}{4}+\tau _{xy}^2}} \end{aligned}$$

(42)

$$\begin{aligned} \dfrac{\partial \sigma _{II}}{\partial \sigma _{xx}}&= \dfrac{1}{2} - \dfrac{1}{4}\;\dfrac{\sigma _{xx} - \sigma _{yy}}{\sqrt{\dfrac{(\sigma _{xx}-\sigma _{yy})^2}{4}+\tau _{xy}^2}} \end{aligned}$$

(43)

$$\begin{aligned} \dfrac{\partial \sigma _{II}}{\partial \sigma _{yy}}&= \dfrac{1}{2} + \dfrac{1}{4}\;\dfrac{\sigma _{xx} - \sigma _{yy}}{\sqrt{\dfrac{(\sigma _{xx}-\sigma _{yy})^2}{4}+\tau _{xy}^2}} \end{aligned}$$

(44)

$$\begin{aligned} \dfrac{\partial \sigma _{II}}{\partial \tau _{xy}}&=\dfrac{-\tau {xy}}{\sqrt{\dfrac{(\sigma _{xx}-\sigma _{yy})^2}{4}+\tau _{xy}^2}} \end{aligned}$$

(45)

Now, in order to calculate the last term of Eq. (32), the adjoint method is used by adding the sensitivity of the state equation, given in Eq. (22) with Lagrange multiplier ($\varvec{\lambda }$) to above equation. This leads to following equation:

$$\begin{aligned} \sum _{\varOmega _N}(1-\hat{\tilde{\rho }}_e)\dfrac{\partial I_e}{\partial \tilde{\rho }_j}&= \dfrac{p\tilde{\rho }_j^{p-1}(1-\hat{\tilde{\rho }}_j)}{\log _2(H_j)} \nonumber \\&- \dfrac{p\tilde{\rho }_j^{2p-1} (1-\hat{\tilde{\rho }}_j)}{\ln (2)(\log _2(H_j))^2} \Bigg [\dfrac{\partial H_j}{\partial \sigma _{p}}\Bigg ] \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _{j}}\Bigg ] \mathbf {D}_j\mathbf {B}_j\mathbf {u}_j \nonumber \\&- \sum _{\varOmega _N}\dfrac{\tilde{\rho }_e^{2p} (1-\hat{\tilde{\rho }}_e)}{\ln (2)(\log _2(H_e))^2} \Bigg [\dfrac{\partial H_e}{\partial \sigma _{p}}\Bigg ] \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _e}\Bigg ] \mathbf {D}_e\mathbf {B}_e\dfrac{\partial \mathbf {u}_e}{\partial \tilde{\rho }_j} \nonumber \\&+ \varvec{\lambda }^T\Bigg (\dfrac{\partial \mathbf {K}}{\partial \tilde{\rho }_j}\mathbf {u} + \mathbf {K}\dfrac{\partial \mathbf {u}}{\partial \tilde{\rho }_j}\Bigg ). \end{aligned}$$

(46)

The Lagrange multiplier can be chosen such that the state sensitivity terms vanish. To this end the following adjoint equation can be solved:

$$\begin{aligned} \mathbf {K}\varvec{\lambda } = \sum _{\varOmega _N}\dfrac{\tilde{\rho }_e^{2p} (1-\hat{\tilde{\rho }}_e)}{\ln (2) (\log _2(H_e))^2}\mathbf {B}_e^T \mathbf {D}_e^T \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _e}\Bigg ]^T \Bigg [\dfrac{\partial H_e}{\partial \sigma _{p}}\Bigg ]^T. \end{aligned}$$

(47)

Finally, Eq. (46) is evaluated as follows:

$$\begin{aligned} \sum _{\varOmega _N}(1-\hat{\tilde{\rho }}_e)\dfrac{\partial I_e}{\partial \tilde{\rho }_j}&= \dfrac{p\tilde{\rho }^{p-1}_j(1-\hat{\tilde{\rho }}_j)}{\log _2(H_j)} \nonumber \\&- \dfrac{p\tilde{\rho }_j^{2p-1} (1-\hat{\tilde{\rho }}_j)}{\ln (2)(\log _2(H_j))^2} \Bigg [\dfrac{\partial H_j}{\partial \sigma _{p}}\Bigg ] \Bigg [\dfrac{\partial \sigma _{p}}{\partial \sigma _{j}}\Bigg ] \mathbf {D}_j\mathbf {B}_j\mathbf {u}_j \nonumber \\&+ \varvec{\lambda }^T\dfrac{\partial \mathbf {K}}{\partial \tilde{\rho }_j}\mathbf {u}. \end{aligned}$$

(48)

The sensitivity analysis shown above is for the single load case. For multiple loadcases, the main differences are using the $H_e$ term expressed in Eq. (16), and that multiple state equations must be used for the adjoint method and thus, multiple adjoint equations have to be solved to calculate the Lagrange multipliers associated to each state equation. The process of calculating the Lagrange multiplier is the same as shown in this section.