Skip to main content
SpringerLink
Log in

Topology optimization under microscale uncertainty using stochastic gradients

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

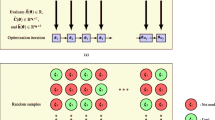
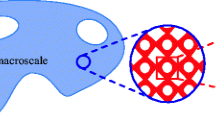
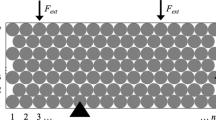
This paper considers the design of structures made of engineered materials, accounting for uncertainty in material properties. We present a topology optimization approach that optimizes the structural shape and topology at the macroscale assuming design-independent uncertain microstructures. The structural geometry at the macroscale is described by an explicit level set approach, and the macroscopic structural response is predicted by the eXtended Finite Element Method (XFEM). We describe the microscopic layout by either an analytic geometric model with uncertain parameters or a level-cut from a Gaussian random field. The macroscale properties of the microstructured material are predicted by homogenization. Considering the large number of possible microscale configurations, one of the main challenges of solving such topology optimization problems is the computational cost of estimating the statistical moments of the cost and constraint functions and their gradients with respect to the design variables. Methods for predicting these moments, such as Monte Carlo sampling, and Taylor series and polynomial chaos expansions often require a large number of random samples resulting in an impractical computation. To reduce this cost, we propose an approach wherein, at every design iteration, we only use a small number of microstructure configurations to generate an independent, stochastic approximation of the gradients. These gradients are then used either with a gradient descent algorithm, namely Adaptive Moment (Adam), or the globally convergent method of moving asymptotes (GCMMA). Three numerical examples from structural mechanics are used to show that the proposed approach provides a computationally efficient way for macroscale topology optimization in the presence of microstructural uncertainty and enables the designers to consider a new class of problems that are out of reach today with conventional tools.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24

Similar content being viewed by others

References

  • Aboulkhair NT, Everitt NM, Ashcroft I, Tuck C (2014) Reducing porosity in AlSi10Mg parts processed by selective laser melting. Addit Manuf 1:77–86

    Google Scholar 

  • Alvarez F, Carrasco M (2005) Minimization of the expected compliance as an alternative approach to multiload truss optimization. Struct Multidisc Optim 29(6):470–476

    MATH  Google Scholar 

  • Asadpoure A, Tootkaboni M, Guest JK (2011) Robust topology optimization of structures with uncertainties in stiffness—application to truss structures. Comput Struct 89(11–12):1131–1141

    Google Scholar 

  • Bae K-R, Wang S (2002) Reliability-based topology optimization. In: 9th AIAA/ISSMO symposium on multidisciplinary analysis and optimization, p 5542

  • Barrera JL, Maute K (2020) Ambiguous phase assignment of discretized 3D geometries in topology optimization. Comput Methods Appl Mech Eng 369:113201

    MATH  Google Scholar 

  • Barrera JL, Geiss MJ, Maute K (2020) Hole seeding in level set topology optimization via density fields. Struct Multidisc Optim 61(4):1319–1343

    Google Scholar 

  • Bendsoe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224

    MATH  Google Scholar 

  • Benveniste Y (1987) A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech Mater 6(2):147–157

    Google Scholar 

  • Beuth J, Klingbeil N (2001) The role of process variables in laser-based direct metal solid freeform fabrication. J Manuf 53(9):36–39

    Google Scholar 

  • Beyer H-G, Sendhoff B (2007) Robust optimization—a comprehensive survey. Comput Methods Appl Mech Eng 196(33–34):3190–3218

    MATH  Google Scholar 

  • Blatman G, Sudret B (2008) Sparse polynomial chaos expansions and adaptive stochastic finite elements using a regression approach. Comptes Rendus Mécanique 336(6):518–523

    MATH  Google Scholar 

  • Böhm HJ (2004) A short introduction to continuum micromechanics. In: Mechanics of microstructured materials. Springer, pp 1–40

  • Bottou L, Curtis FE, Nocedal J (2018) Optimization methods for large-scale machine learning. SIAM Rev 60(2):223–311

    MATH  Google Scholar 

  • Budarapu PR, Zhuang X, Rabczuk T, Bordas SP (2019) Multiscale modeling of material failure: theory and computational methods. Adv Cryst Elast Metamater 52(1):1–103

    Google Scholar 

  • Burman E, Hansbo P (2012) Fictitious domain finite element methods using cut elements: II. A stabilized Nitsche method. Appl Numer Math 62(4):328–341

    MATH  Google Scholar 

  • Burman E, Hansbo P (2014) Fictitious domain methods using cut elements: III. A stabilized Nitsche method for Stokes’ problem. ESAIM : Mathematical Modelling and Numerical Analysis 48(3):859–874

    MATH  Google Scholar 

  • Chatterjee T, Chakraborty S, Goswami S, Adhikari S, Friswell MI (2021) Robust topological designs for extreme metamaterial micro-structures. Sci Rep 11:15221

    Google Scholar 

  • Chen S, Chen W (2011) A new level-set based approach to shape and topology optimization under geometric uncertainty. Struct Multidisc Optim 44(1):1–18

    MATH  Google Scholar 

  • Chen S, Chen W, Lee S (2010) Level set based robust shape and topology optimization under random field uncertainties. Struct Multidisc Optim 41(4):507–524

    MATH  Google Scholar 

  • Coelho PG, Fernandes PR, Guedes JM, Rodrigues HC (2008) A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct Multidisc Optim 35(2):107–115

    Google Scholar 

  • Collet M, Noël L, Bruggi M, Duysinx P (2018) Topology optimization for microstructural design under stress constraints. Struct Multidisc Optim 58(6):2677–2695

    Google Scholar 

  • Conti S, Held H, Pach M, Rumpf M, Schultz R (2009) Shape optimization under uncertainty—a stochastic programming perspective. SIAM J Optim 19(4):1610–1632

    MATH  Google Scholar 

  • De S, Wojtkiewicz SF, Johnson EA (2017) Efficient optimal design and design-under-uncertainty of passive control devices with application to a cable-stayed bridge. Struct Control Health Monit 24(2):e1846

    Google Scholar 

  • De S, Hampton J, Maute K, Doostan A (2020a) Topology optimization under uncertainty using a stochastic gradient-based approach. Struct Multidisc Optim 62(5):2255–2278

    Google Scholar 

  • De S, Maute K, Doostan A (2020b) Bi-fidelity stochastic gradient descent for structural optimization under uncertainty. Comput Mech 66(4):745–771

    MATH  Google Scholar 

  • De S, Maute K, Doostan A (2021) Reliability-based topology optimization using stochastic gradients.Struct Multidisc Optim 64: 3089–3108

    Google Scholar 

  • Deaton JD, Grandhi RV (2014) A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct Multidisc Optim 49(1):1–38

    Google Scholar 

  • Diaz A, Bendsøe M (1992) Shape optimization of structures for multiple loading conditions using a homogenization method. Struct Optim 4(1):17–22

    Google Scholar 

  • Diwekar UM (2020) Optimization under uncertainty. Springer, Cham, pp 151–215

    Google Scholar 

  • Dong G, Tang Y, Zhao YF (2017) A survey of modeling of lattice structures fabricated by additive manufacturing. J Mech Des 139(10):100906

    Google Scholar 

  • Doostan A, Owhadi H (2011) A non-adapted sparse approximation of PDEs with stochastic inputs. J Comput Phys 230(8):3015–3034

    MATH  Google Scholar 

  • Doostan A, Ghanem RG, Red-Horse J (2007) Stochastic model reduction for chaos representations. Comput Methods Appl Mech Eng 196(37–40):3951–3966

    MATH  Google Scholar 

  • Du Z, Zhou X-Y, Picelli R, Kim HA (2018) Connecting microstructures for multiscale topology optimization with connectivity index constraints. J Mech Des 140(11):111417

    Google Scholar 

  • Eom Y-S, Yoo K-S, Park J-Y, Han S-Y (2011) Reliability-based topology optimization using a standard response surface method for three-dimensional structures. Struct Multidisc Optim 43(2):287–295

    MATH  Google Scholar 

  • Eschenauer HA, Olhoff N (2001) Topology optimization of continuum structures: a review. Appl Mech Rev 54(4):331–390

    Google Scholar 

  • Eshelby JD (1957) The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond Ser A 241(1226):376–396

    MATH  Google Scholar 

  • Geiss MJ, Boddeti N, Weeger O, Maute K, Dunn ML (2019) Combined level-set-XFEM-density topology optimization of four-dimensional printed structures undergoing large deformation. J Mech Des 141(5)

  • Ghanem RG, Spanos PD (2003) Stochastic finite elements: a spectral approach. Courier Corporation, North Chelmsford

    MATH  Google Scholar 

  • Guest JK, Igusa T (2008) Structural optimization under uncertain loads and nodal locations. Comput Methods Appl Mech Eng 198(1):116–124

    MATH  Google Scholar 

  • Haldar A, Mahadevan S (2000) Probability, reliability, and statistical methods in engineering design, 1st edn. Wiley, New York

    Google Scholar 

  • Jung H-S, Cho S (2004) Reliability-based topology optimization of geometrically nonlinear structures with loading and material uncertainties. Finite Elem Anal Des 41(3):311–331

    Google Scholar 

  • Keshavarzzadeh V, Fernandez F, Tortorelli DA (2017) Topology optimization under uncertainty via non-intrusive polynomial chaos expansion. Comput Methods Appl Mech Eng 318:120–147

    MATH  Google Scholar 

  • Kharmanda G, Olhoff N, Mohamed A, Lemaire M (2004) Reliability-based topology optimization. Struct Multidisc Optim 26(5):295–307

    Google Scholar 

  • Kim C, Wang S, Rae K-R, Moon H, Choi KK (2006) Reliability-based topology optimization with uncertainties. J Mech Sci Technol 20(4):494

    Google Scholar 

  • Kingma DP, Ba J (2014) Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980

  • Kreissl S, Maute K (2012) Levelset based fluid topology optimization using the extended finite element method. Struct Multidisc Optim 46(3):311–326

    MATH  Google Scholar 

  • Li W, Zhang XS (2020) Momentum-based accelerated mirror descent stochastic approximation for robust topology optimization under stochastic loads. Int J Numer Methods Eng

  • Lipton R, Stuebner M (2007) Optimal design of composite structures for strength and stiffness: an inverse homogenization approach. Struct Multidisc Optim 33(4):351–362

    MATH  Google Scholar 

  • Liu S, Shin YC (2019) Additive manufacturing of Ti6Al4V alloy: a review. Mater Des 164:107552

    Google Scholar 

  • Marmarelis MG, Ghanem RG (2020) Data-driven stochastic optimization on manifolds for additive manufacturing. Comput Mater Sci 181:109750

    Google Scholar 

  • Maute K (2014) Topology optimization under uncertainty. In: Topology optimization in structural and continuum mechanics. Springer, New York, pp 457–471

  • Maute K, Frangopol DM (2003) Reliability-based design of MEMS mechanisms by topology optimization. Comput Struct 81(8–11):813–824

    Google Scholar 

  • Michel J-C, Moulinec H, Suquet P (1999) Effective properties of composite materials with periodic microstructure: a computational approach. Comput Methods Appl Mech Eng 172(1–4):109–143

    MATH  Google Scholar 

  • Mogami K, Nishiwaki S, Izui K, Yoshimura M, Kogiso N (2006) Reliability-based structural optimization of frame structures for multiple failure criteria using topology optimization techniques. Struct Multidisc Optim 32(4):299–311

    Google Scholar 

  • Moon H, Kim C, Wang S (2004) Reliability-based topology optimization of thermal systems considering convection heat transfer. In: 10th AIAA/ISSMO multidisciplinary analysis and optimization conference, p 4410

  • Mori T, Tanaka K (1973) Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall 21(5):571–574

    Google Scholar 

  • Nitsche J (1971) On a variational principle for the solution of dirichlet problems under the use of subspaces which are subject to no boundary conditions. In: Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, vol 36, pp 9–15

  • Noël L, Duysinx P (2017) Shape optimization of microstructural designs subject to local stress constraints within an xfem-level set framework. Struct Multidisc Optim 55(6):2323–2338

    Google Scholar 

  • Parry L, Ashcroft I, Wildman RD (2016) Understanding the effect of laser scan strategy on residual stress in selective laser melting through thermo-mechanical simulation. Addit Manuf 12:1–15

    Google Scholar 

  • Pasini D, Guest JK (2019) Imperfect architected materials: Mechanics and topology optimization. MRS Bull 44(10):766–772

    Google Scholar 

  • Roberts AP, Teubner M (1995) Transport properties of heterogeneous materials derived from Gaussian random fields: bounds and simulation. Phys Rev E 51(5):4141

    Google Scholar 

  • Rodrigues H, Guedes JM, Bendsoe M (2002) Hierarchical optimization of material and structure. Struct Multidisc Optim 24(1):1–10

    Google Scholar 

  • Ruder S (2016) An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747

  • Schmitt O, Friederich J, Riehl S, Steinmann P (2016) On the formulation and implementation of geometric and manufacturing constraints in node-based shape optimization. Struct Multidisc Optim 53(4):881–892

    Google Scholar 

  • Schott B, Rasthofer U, Gravemeier V, Wall WA (2015) A face-oriented stabilized Nitsche-type extended variational multiscale method for incompressible two-phase flow. Int J Numer Methods Eng 104(7):721–748

    MATH  Google Scholar 

  • Schury F, Stingl M, Wein F (2012) Efficient two-scale optimization of manufacturable graded structures. SIAM J Sci Comput 34(6):B711–B733

    MATH  Google Scholar 

  • Sharma A, Villanueva H, Maute K (2017) On shape sensitivities with heaviside-enriched XFEM. Struct Multidisc Optim 55(2):385–408

    Google Scholar 

  • Sigmund O (1994) Materials with prescribed constitutive parameters: an inverse homogenization problem. Int J Solids Struct 31(17):2313–2329

    MATH  Google Scholar 

  • Sigmund O (1995) Tailoring materials with prescribed elastic properties. Mech Mater 20(4):351–368

    Google Scholar 

  • Sigmund O, Maute K (2013) Topology optimization approaches: a comparative review. Struct Multidisc Optim 48(6):1031–1055

    Google Scholar 

  • Sivapuram R, Dunning PD, Kim HA (2016) Simultaneous material and structural optimization by multiscale topology optimization. Struct Multidisc Optim 54(5):1267–1281

    Google Scholar 

  • Suzuki K, Kikuchi N (1991) A homogenization method for shape and topology optimization. Comput Methods Appl Mech Eng 93(3):291–318

    MATH  Google Scholar 

  • Svanberg K (2002) A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J Optim 12(2):555–573

    MATH  Google Scholar 

  • Tootkaboni M, Asadpoure A, Guest JK (2012) Topology optimization of continuum structures under uncertainty—a polynomial chaos approach. Comput Methods Appl Mech Eng 201:263–275

    MATH  Google Scholar 

  • Tran VP, Brisard S, Guilleminot J, Sab K (2018) Mori-Tanaka estimates of the effective elastic properties of stress-gradient composites. Int J Solids Struct 146:55–68

    Google Scholar 

  • Villanueva CH, Maute K (2014) Density and level set-XFEM schemes for topology optimization of 3-D structures. Comput Mech 54(1):133–150

    MATH  Google Scholar 

  • Xia L (2016) Multiscale structural topology optimization. Elsevier, Amsterdam

    Google Scholar 

  • Xia L, Breitkopf P (2014) Concurrent topology optimization design of material and structure within FE\(^2\) nonlinear multiscale analysis framework. Comput Methods Appl Mech Eng 278:524–542

    MATH  Google Scholar 

  • Xia L, Breitkopf P (2017) Recent advances on topology optimization of multiscale nonlinear structures. Arch Comput Methods Eng 24(2):227–249

    MATH  Google Scholar 

  • Zaoui A (2002) Continuum micromechanics: survey. J Eng Mech 128(8):808–816

    Google Scholar 

Download references

Acknowledgements

The authors acknowledge the support of the Defense Advanced Research Projects Agency (DARPA) under the TRADES program (agreement HR0011-17-2-0022). The opinions and conclusions presented in this paper are those of the authors and do not necessarily reflect the views of DARPA. AD also acknowledges partial support from AFOSR grant FA9550-20-1-0138.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Northern Arizona University, Flagstaff, AZ, 86011, USA

    Subhayan De

  2. Smead Aerospace Engineering Sciences Department, University of Colorado, Boulder, CO, 80303, USA

    Kurt Maute & Alireza Doostan

Authors
  1. Subhayan De
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kurt Maute
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alireza Doostan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alireza Doostan.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Replication of results

The stochastic gradient-based optimization algorithms used to generate results in Sect. 4 have been implemented in MATLAB and will be uploaded to the GitHub page https://github.com/CU-UQ/TOuU once the paper is published. The TO and XFEM calculations were performed using an in-house solver that is not at the stage of being publicly available. However, the MATLAB codes used in this study can interface with other TO and XFEM codes.

Additional information

Responsible Editor: Josephine Voigt Carstensen

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Topical Collection: 14th World Congress of Structural and Multidisciplinary Optimization.

Guest Editors: Y. Noh, E. Acar, J. Carstensen, J. Guest, J. Norato, and P. Ramu

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

De, S., Maute, K. & Doostan, A. Topology optimization under microscale uncertainty using stochastic gradients. Struct Multidisc Optim 66, 17 (2023). https://doi.org/10.1007/s00158-022-03417-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00158-022-03417-4

Keywords

Search

Navigation