Abstract
Presented herein is a novel design framework for obtaining the optimal design of functionally graded lattice (FGL) structures that involve using a physical discrete structural model called the Hencky bar-grid model (HBM) and topology optimization (TO). The continuous FGL structure is discretized by HBM comprising rigid bars, frictionless hinges, frictionless pulleys, elastic primary and secondary axial springs, and torsional springs. A penalty function is introduced to each of the HBM spring’s stiffnesses to model non-uniform material properties. The gradient-based TO method is applied to find the stiffest structure via minimizing the compliance or elastic strain energy by adjusting the HBM spring stiffnesses subjected to prescribed design constraints. The optimal design of FGL structures is constructed based on the optimal spring stiffnesses of the HBM. The proposed design framework is simple to implement and for obtaining optimal FGL structures as it involves a relatively small number of design variables such as the spring stiffnesses of each grid cell. As illustration of the HBM-TO method, some optimization problems of FGL structures are considered and their optimal solutions obtained. The solutions are shown to converge after a small number of iterations. A Python code is given in the Appendix for interested readers who wish to reproduce the results.
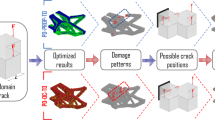
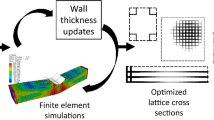
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Additive manufacturing opens up new opportunities to fabricate as-designed functionally graded lattice (FGL) structures by building up material layer-by-layer (Maconachie et al. 2019). Lattice structures (also referred to as cellular structures) have a clear network feature comprising basic elements like solid struts or plates (Gibson 1989). Properly designed FGL structures can achieve high performance with great control in stiffness and strength, weight, energy absorption, heat exchange and acoustic insulation (Zhang et al. 2015; Ferro et al. 2022). Generally, elastic structures with minimum compliance or minimum elastic strain energy are the stiffest (Hassani and Hinton 1999; Kaveh et al. 2008; Zhang et al. 2014). Topology optimization (TO) method is commonly adopted to minimize the compliance or elastic strain energy of FGL structures by iteratively updating the material distribution subjected to loading, boundary conditions and prescribed deflection or stress constraints (Panesar et al. 2018; Liu et al. 2018; Li et al. 2018; Zhu et al. 2021).
Many design strategies have been proposed for obtaining optimal designs of FGL structures with prescribed mechanical properties. Most of the existing strategies may be grouped into two categories. One category is the greyscale density mapping (GDM) strategy. This design strategy first uses standard TO algorithms such as the solid isotropic material with penalization (SIMP) method (Bendsøe 1989; Zhou and Rozvany 1991; Mlejnek 1992; Sigmund 2001; Andreassen et al. 2011; Wang et al. 2022), the evolutionary structural optimization method (Querin et al. 1998, 2000; Huang and Xie 2007), or the level set method (Wang et al. 2003; Challis and Guest 2009; Challis 2010; van Dijk et al. 2013; Azari Nejat et al. 2022; Lin et al. 2022) with finite element discretization or Isogeometric Analysis (Guerder et al. 2022) to determine a greyscale density solution of material distribution. Next, FGL structures with a selected type-based unit cell are established according to the obtained material distribution. The other category is the ground structure optimization (GSO) strategy. In this strategy, physical structures such as trusses, beams or frames are used to represent the FGL structures. Gradient-based and derivative free methods have been used to optimize the cross-section dimensions, node positions and the structural topology (or element connectivity) of truss, beam and frame subjected to prescribed design requirements such as volume ratio, deflection and stress (Miguel et al. 2013; Nguyen et al. 2013; Zhang et al. 2015; Han and Lu 2018). By comparing these two main strategies, GDM is more efficient because it needs to optimize a smaller number of design variables associated with each structural element. In contrast, GSO requires the optimization of a much larger number of design variables including material properties, node positions and the structure topology (or element connectivity) (Miguel et al. 2013). However, the GSO strategy provides a clearer physical structural configuration without the need of designing the internal structure and the connectivity for each lattice unit cell (Panesar et al. 2018).
In this paper, we propose a new strategy for the optimal design of FGL structures. This new strategy involves using a recently proposed lattice structure model called the Hencky bar-grid model (HBM) (Zhang et al. 2021a, b, 2022). A Hencky bar model is a type of bar-spring structural model that was pioneered by Hencky (1921). Owing to its simple and clear physical representation and great flexibility, it had been recently revisited and expanded to study various static, buckling and dynamic problems of different structural types (Wang et al. 2017, 2020; Zhang et al. 2018c, b, a, d, 2019a, b, 2022). HBM comprises bars and springs whose stiffnesses may be adjusted to allow for different material property distributions. The optimization of the spring stiffnesses is performed by using a gradient-based TO method to minimize the compliance while satisfying required constraints. The proposed design framework combines the advantages of both GDM and GSO strategies. Firstly, HBM is easy to couple with standard TO algorithms such as SIMP to efficiently obtain optimal designs involving a smaller number of design variables such as the spring stiffnesses of each grid cell. Secondly, HBM is a simple bar-spring model which does not need detail design to the internal structure and connectivity for every lattice unit cells.
The layout of this paper is as follows: Sect. 2 presents the optimization problem definition. The new version of the HBM is presented in Sect. 3. Section 4 explains how to select the value of the HBM spring stiffnesses for solving a linear elasticity problem. The implementation of the HBM for TO is described in Sect. 5. Section 6 illustrates examples of an FGL beam and an FGL plate that are optimally designed through the proposed HBM-TO method. Section 7 shows a summary of the proposed HBM-TO method and Sect. 8 gives the concluding remarks. Appendix A contains a simple python code that was used to obtain the optimal solutions presented in Sect. 6.
2 Problem definition
Consider an elastic FGL structure with length \(\alpha L\), width \(L\) , and a uniform thickness \(h\), which is illustrated in Fig. 1. A non-uniform Young's modulus \(E(x,y)\) and a constant Poisson’s ratio \(\overline{\nu }\) are assumed. The FGL structure is simply supported along its longitudinal edges and is subjected to a central line load \(P\). Body forces are not considered.
The problem at hand is to determine the optimal design of the cross-section of FGL structures composed by either large or small lattice units for maximum stiffness (Kaveh et al. 2008), i.e. having minimum compliance (Hassani and Hinton 1999) and then design a structure made by functionally graded material based on the material distribution given by the optimal FGL structures. Figure 1b and c illustrates optimal design examples that differ in terms of lattice cell size. Figure 1d illustrates an optimal design example of a functionally graded solid structure.
3 Hencky bar-grid model
Hencky (1921) proposed a discrete structural model comprising rigid bars connected by frictionless hinges and elastic rotational springs for solving the elastic buckling problem of columns under a compressive axial load. Since then, there has been much work done on the so-called Hencky bar-chain/net/grid model (HBM) for analysis of all kinds of structural forms from beams to frames to arches to plates (Wang et al., 2020). Recently, Zhang et al. (2021b) extended the HBM for solving plane elasticity problems which has the ability to model 2D structures for the full range of Poisson’s ratio. In contrast, some previous lattice models such as the models formulated by Born and Karman (1912) and Hrennikoff (1941) can only model 2D structures for Poisson’s ratio less than 1/3 (Zhang et al. 2021a; Challamel et al. 2022).
In this study, we develop a slightly different version of HBM. A comparison of the new version of HBM and its predecessor reported in Zhang et al. (2021b) is given in Fig. 2. The main difference between the newly proposed HBM and its predecessor is the construction of the internal (i.e. not at the edge or corner) rigid bars. The new HBM has twice the number of rigid bars and springs. This change is essential, as it allows the determination of local stiffness matrix for each HBM grid cell (see Eq. (27)) which will be required by the topology optimization algorithm developed for the adoption of HBM.
Figure 3 shows the structure representation, a unit rigid bar-grid representation and a lattice structure representation of the new HBM. As shown in Fig. 3a, the new version of HBM discretize a continuum plane structure into a rigid bar-grid system with a cell size \(\mathcal{l}\) that are connected by frictionless hinges. Within a grid cell, four primary axial springs connect two rigid bars placed at each side of the grid cell with stiffnesses \({\overline{k} }^{xx}\) and \({\overline{k} }^{yy}\) in the x- and y- directions, respectively, as shown in Fig. 3b. Four secondary axial springs are employed to model the Poisson effect with stiffnesses \({k}^{xy}\) and \({k}^{yx}\) in the y- and x- directions, respectively, as shown in Fig. 3b. Four torsional springs are installed at the four corners with stiffnesses \({k}^{S}\) as shown in Fig. 3b. While primary and secondary springs model the axial stiffness and the Poisson effect, respectively, torsional springs are employed to resist in-plane shear forces. A lattice structure representation related to HBM is shown in Fig. 3c. It is worth noting that the secondary axial springs of HBM are represented by some curved bars. It is possible to use other structures to represent the secondary axial springs.
For the sake of clarity, we shall demonstrate the topology optimization of HBM by using the lattice structures comprising basic lattice cell as shown in Fig. 3c. For a lattice cell whose centre is located at \(\frac{x}{\ell } = i + \frac{1}{2}\) and \(\frac{y}{\ell } = j + \frac{1}{2}\), its horizontal and vertical axial bars have stiffnesses of \(\overline{k}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{xx}\) and \(\overline{k}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{yy}\), respectively. Likewise, its curved bars located at the corners and middle of the cell have stiffnesses of \(k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{S}\) and \(k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{xy} \left( {{\text{or }} k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{yx} } \right)\), respectively. We assume that the bars in all lattice cells have a constant elastic modulus \(\tilde{E}\) and a constant density \(\tilde{\rho }\) but a varying cross-section area \(\ A_{{i + \frac{1}{2}, \, j + \frac{1}{2}}}\). Therefore, an HBM grid with stiffer springs results in a lattice cell with a greater mass as shown in Fig. 3d.
When a bar-grid cell as shown in Fig. 3b is stretched or shortened, the resulting axial forces \(f^{x} ,{ }f^{y}\) are resisted by both primary axial springs and secondary axial springs, i.e.
where u, v are the in-plane displacements in the x- and y- directions at the joints, respectively. The subscripts i and j indicate the location of corresponding joints in the model.
When the new version HBM cell undergoes in-plane shearing, the elastic torsional springs are deformed due to the change of angles at each corner. In this way, the lumped torque TS for one bar-grid cell is given by
where θ is the change of angle at each corner of the bar-grid cell. The superscripts a, b, c, and d denote the corner points at the bar-grid cell (see Fig. 3b).
Based on small angle approximation, θ may be expressed in terms of the in-plane displacements u, v as
The elastic strain energy \(\overline{U}_{{i + \frac{1}{2},j + \frac{1}{2}}}\) including the contribution of the torsional energy stored in the deformed springs for a bar-grid cell is
In view of Eqs. (1)–(13) the elastic strain energy \(\overline{U}_{{i + \frac{1}{2},j + \frac{1}{2}}}\) can be reformulated in terms of in-plane displacements u, v,
Next, the work done by in-plane axial forces \({F}^{xx}\), \({F}^{yy}\), in-plane shear force \({F}^{xy}\) and the in-plane body forces \({b}^{x}\) and \({b}^{y}\) lumped on the joints of each HBM cell as shown in Fig. 3b are given by
The total potential energy function is given by
where \({\Omega }\) is a set contains all the indexes of the bar-grid cells for the HBM.
Now, the local stiffness matrix of an HBM cell is obtained through a variational formulation, by taking
Based on Eq. (14), the discrete equations of the derivative of the elastic strain energy \({\overline{\text{U}}}_{{i + \frac{1}{2},j + \frac{1}{2}}}\) for an HBM cell (\(i + \frac{1}{2},j + \frac{1}{2}\)) are given by
and
Likewise, the discrete equations of the derivative of the external work \({\overline{\text{W}}}_{{i + \frac{1}{2},j + \frac{1}{2}}}\) for an HBM cell (\(i + \frac{1}{2},j + \frac{1}{2}\)) are given by
From Eqs. (18)–(29), the local stiffness matrix for a bar-grid cell of the HBM is given by
where
with
and \(\overline{k}^{xy} = \frac{1}{2}\left( {k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{xy} + k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{yx} } \right)\);
In view of Eqs. (18)–(38) and by assembling the expressions for all nodes in the system, the following linear system of equation can be derived
where
and
The in-plane displacements of each joint \(u_{i,j}\) and \(v_{i,j}\) can be calculated by solving Eq. (39). Next the axial forces \(f_{{i + \frac{1}{2},j}}^{x}\) and \(f_{{i,j + \frac{1}{2}}}^{y}\) and the torque \(T_{{1 + \frac{1}{2},1 + \frac{1}{2}}}^{S}\) are computed via the obtained in-plane displacements \(u_{i,j}\) and \(v_{i,j}\) using Eqs. (1)–(8).
4 Determination of HBM spring stiffness
In this section, we shall determine the spring stiffnesses of HBM. For simplicity, it is assumed that each individual HBM grid cell is homogeneous and isotropic. The inhomogeneous material properties of the structure are captured by varying the material properties of different HBM cells. A general version of the continuum equations of elastodynamics (or Navier’s equations of elastodynamics) considering inhomogeneous material properties and plane-strain can be written as (Gurtin 1973)
and
By considering the local homogeneous properties within the area of each HBM grid cell, i.e. \(x \in \left[ {\left( {i - \frac{1}{2}} \right)\ell ,\left( {i + \frac{1}{2}} \right)\ell } \right],{ }y \in \left[ {\left( {j - \frac{1}{2}} \right)\ell ,\left( {j + \frac{1}{2}} \right)\ell } \right]\)
the general continuum equations of elastodynamics can be simplified to
and
By expanding Eqs. (18) and (19) using Taylor’s series following the procedures used in (Zhang et al. 2019c), we obtain
and
By assuming the case of quasi-static, neglecting higher order terms and comparing Eqs. (48) and (49) to the continuum equation of motion Eqs. (46) and (47), it follows that
A first-order central finite difference (FD) discretization of Eqs. (43) and (44) results in
The difference equation in y- direction is obtained from Eq. (54) by swapping variables u, v and indices i, j. Now, if we assemble four adjacent HBM grid cells like Fig. 3b, the difference equation of the middle node can be obtained based on Eqs. (18)–(25) as follows:
The difference equation in y- direction is Eq. (55) by swapping variables u, v and indices i, j. In view of Eqs. (50)–(55), it can be seen that solving the linear algebraic system given by the HBM proposed in this work is equivalent to solving an inhomogeneous two-dimensional elasticity problem using FD method.
Noting that the new HBM coincides with the old one (Zhang et al. 2021b) when modelling homogeneous structures. So, it is possible to use the old HBM to model inhomogeneous structures, but the resulting energy functions could not be readily applied to derive the local stiffness matrix for each grid cell.
5 Topology optimization
The SIMP method is employed to optimize the HBM formulated herein. The spring stiffnesses of each grid cell is formulated as
where \(\overline{k}_{0}^{xx} , \overline{k}_{0}^{yy} , k_{0}^{xy} , k_{0}^{yx}\) and \(k_{0}^{S}\) are the starting values of spring stiffnesses for TO, \(\hat{\rho }\) is a non-dimensional variable introduced for HBM-TO and \(m\) is the exponent for penalization. In order to avoid singularity issues when solving the linear system given in Eq. (39), all HBM spring stiffnesses are constrained to have a minimum value of \(\phi_{{{\text{min}}}} \overline{k}_{0}\) at the void areas. In view of Eqs. (56)–(61) and Eq. (14), the elastic strain energy of a grid cell may be expressed as
where the starting value of elastic strain energy \({\overline{\text{U}}}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{0}\) is given by
In view of Eqs. (63) and (16), the total strain energy is
The TO problem for HBM can be posed as
where \(V_{f}\) is the prescribed volume fraction and \(V\left( {\hat{\rho }} \right)\) and \(V_{0}\) are the material volume and design volume, respectively. There are various methods for solving the aforementioned optimization problem such as Optimality Criteria (OC) (Yin and Yang 2001), Sequential Linear Programming (Dunning and Kim 2015), and Method of Moving Asymptotes (Svanberg 1987). The OC method is adopted herein due to its efficiency in solving optimization problems with a single objective function (Sigmund 1997).
Following the works of Bendsøe (1989), Sigmund (1997) and Sigmund and Petersson (1998) and assuming a constant change of design volume, the design variable \(\hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}}\) is updated as follows:
If \(\max \left( {0,\hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}} - \delta } \right) \ge \hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}} \hat{D}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{\gamma }\)
if \(\max \left( {0,\hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}} - \delta } \right) < \hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}} \hat{D}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{\gamma } \le \min \left( {1,\hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}} + \delta } \right)\)
if \(\hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}} \hat{D}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{\gamma } > \min \left( {1,\hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}} + \delta } \right)\)
where δ is a positive value to limit the change of design variable \(\hat{\rho }_{{i + \frac{1}{2},j + \frac{1}{2}}}\) between two successive iterations and γ is a numerical damping exponent. These parameters are introduced to avoid drastic change of density between adjacent cells that are impractical (i.e. porous structures). \(\hat{D}_{{i + \frac{1}{2},j + \frac{1}{2}}}\) is an auxiliary variable defined as
where λ is a Lagrangian multiplier which can be obtained through the bisection method. In view of Eq. (64), the HBM grid cell sensitivity matrices \(\hat{c}\) can be written as follows
In order to avoid potential “chess board patterns”, a simple filtering technique formulated by Andreassen et al. (2011) is adopted by replacing the HBM grid cell sensitivity matrices \(\hat{c}_{{i + \frac{1}{2} + j + \frac{1}{2}}}\) with
where \(\hat{\varphi }\left( {i,j,k,l} \right)\) is a weight factor defined as
The k and l indicate the location of corresponding joints in the model. Equations (71) and (72) indicate that the filter is a local averaging operator whereby the HBM grid cell sensitivity matrices \(\hat{c}_{{i + \frac{1}{2} + j + \frac{1}{2}}}\) take on an average value of all \(\hat{c}\) weighted by \(\hat{\varphi }\) within a radius \(\hat{r}\). The filtered HBM grid cell sensitivity matrices obtained through Eqs. (71) and (72) are used when updating \(\hat{D}_{{i + \frac{1}{2},j + \frac{1}{2}}}\) in Eq. (69).
6 Results and discussions
In this section, we first validate the proposed HBM through modeling continuous functionally graded structures. We then apply the HBM-TO to determine the optimal design of a beam and a plate FGL structures subjected to central line loading. The considered boundary conditions include loads and prescribed displacements. In the following example problems, we assume the material has Poisson’s ratio of 0.3 and set the starting value for the elastic modulus \(E_{0}\) as 1.
6.1 Validation of HBM for functionally graded plane bodies
In this section, plane-stress and plane-strain elasticity problems are considered that are confined in a square design domain under the loading and displacements boundary conditions illustrated in Fig. 1. The functionally graded Young’s modulus is assumed to be
The accuracy of the proposed HBM is assessed by comparing the predicted in-plane displacements u, v, with results obtained through the direct stiffness matrix method (Rao 2005). A general form of the local stiffness matrix for a unit square FEM plane element and a square HBM cell with unit bar length, can be expressed using Eq. (31). We assume isotropic material properties within individual FEM elements and HBM cells. The coefficients of the local stiffness matrix are for plane-stress:
for plane-strain:
The abovementioned coefficients of the local FEM stiffness matrix can be derived as detailed in Rao (2005). For the plane-stress case, the coefficients of local HBM stiffness matrix are obtained using the HBM spring stiffnesses expression given by Zhang et al. (2021b). For the plane-strain case, the coefficients of local HBM stiffness matrix are computed by using Eqs. (50)–(53). It is interesting to note that FEM and HBM have identical values for the coefficients b and d which indicate that both FEM and HBM have a similar physical interpretation of the Poisson effect.
In investigating the performance of HBM, several simulations were run by adopting grid/mesh size \(\ell = L/100\). For each test, we only change the local stiffness matrix based on the choice of FEM/HBM or plane-stress/plane-strain. Figure 4a and b presents the horizontal displacement u fields predicted by FEM and HBM, respectively, for the plane-stress problem under a central point load. Figure 4c and d present the corresponding vertical displacement v fields. Figure 5a–d presents the in-plane displacements for the plane-strain problem under a central line load. Based on the results shown in Figs. 4 and 5, it can be seen that the in-plane displacements given by HBM agree well with those obtained through FEM for both the plane-stress and plane-strain problems. These results show that the proposed HBM is a simple and robust physical structural model that handle well elasticity problems for functionally graded structures.
6.2 Optimal design of FGL beams subjected to a central line load
The HBM-TO is first applied to the optimal design of an FGL beam with a square cross-section (\(\alpha = 1\)) under a central line load. The bottom edges are fixed in y- direction. The geometry and boundary conditions are shown in Fig. 6.
The HBM-TO is carried out as follows.
-
1.
Set the prescribed volume fraction \(V_{f} = 0.4\) by initializing all HBM design variable \(\hat{\rho }\) as 0.4;
-
2.
Set parameters \(\delta = 0.1\), \(\phi_{{{\text{min}}}} = 0.01\), \(\hat{r} = 2\) and \(\gamma = 0.5\);
-
3.
Set the size of HBM grid \(\ell\) as \(L/10\), \(L/20\) or \(L/30\);
-
4.
Select the exponent for penalization \(m\) as 0.5, 1 or 2;
-
5.
Solve optimization problem defined by Eq. (65) and using Eqs. (66)–(72);
-
6.
The optimization process will stop when the change of elastic strain energy \(\Delta \overline{U}\) is smaller than 0.01;
-
7.
Finally, construct the FGL beam cross-section based on the optimal \(\hat{\chi }\).
Noting that the variation of the elastic modulus changes the stiffness of the springs, thus the cell mass changes accordingly. In actual design of FGL structures, the cross-section area \(\tilde{A}\), the elastic modulus \(\tilde{E}\) and the density \(\tilde{\rho }\) of lattice bars are dependent on the applied material.
Figure 7 shows the optimal cross-section designs of FGL structures obtained by HBM-TO. It can be seen that the solutions are significantly affected by the size of the HBM grid cell \(\ell\) and the penalty exponent \(m\). The cross-section mass is more concentrated when \(\ell\) is smaller and \(m\) is larger. In contrast, the mass of cross-section becomes more distributed when \(\ell\) is larger and \(m\) is smaller. It can be seen from Fig. 8 that the elastic strain energy converges after 25 iterations and the solutions converge faster when \(m\) is smaller. The converged elastic strain energy tends to be lower when \({ }m\) is smaller.
The optimally designed FGL beams can be classified into two groups: “distributed” and “defined”; see also Fig. 9. The first group suggests the beams could be designed with functionally graded properties such as a graded elastic modulus. The second group suggests that the beams could be designed with a defined geometry. The observed results from Fig. 9 show that the “distributed” FGL beams are stiffer than the “defined” FGL beams. The former ones have a smoother transition of mass which could help in preventing failure initiations (Wang 1983; Mahamood et al. 2012). However, the latter ones could be manufactured more readily.
Based on Eqs. (56)-(60), the variable \(\hat{\chi }\) describes the distribution of the elastic modulus of the FGL beams. By least-squares fitting \(\hat{\chi }\) from HBM-TO FGL beams using \(\ell = \frac{L}{20}, \, m = 0.5\); and \(\ell = \frac{L}{30}, \, m = 0.5\), one finds the following elastic modulus distribution function, i.e.
where
A contour plot showing the distribution given in Eq. (86) is presented in Fig. 10.
The functionally graded beams subjected to a central line load with elastic modulus varying in x- and y-directions (as shown in Figs. 1d and 6) could be designed following the distribution function given in Eq. (86) as follows
6.3 Optimal design of FGL plate subjected to a central line load
For the second example, we apply HBM-TO to design the cross-section of an FGL plate with a rectangular cross-section under a central line load. The bottom edges are fixed in the y- direction. The geometry and boundary conditions are presented in Fig. 11. In this example, the same parameters of the previous example are used except \(\ell = \frac{L}{10}\) or \(\frac{L}{20}\) in this example.
Figure 12 presents the optimal cross-section designs of the FGL plates obtained from HBM-TO. Similar to what observed in the previous example, results show that the mass is more concentrated; thus, resulting in a more defined geometry when \(\ell\) is smaller and \(m\) is larger. It can be seen from Fig. 13 that the elastic strain energy converges after 80 iterations and the solutions with smaller \(m\) converge faster. Similar to the HBM-TO designed FGL beams, the converged elastic strain energy is lower when \({ }m\) is smaller. The results of optimally designed FGL plates can be classified into two groups. The first group suggests the FGL plates could be designed with a more distributed elastic modulus and a smoother transition of mass which could help in preventing failure initiations (Wang 1983; Mahamood et al. 2012) as shown in Fig. 14a, while the other group (Fig. 14b) suggests the plates could be designed with a specific shape which could be manufactured more readily.
By least-squares fitting \(\hat{\chi }\) from HBM-TO FGL plates using \(\ell = \frac{L}{10}, \, m = 0.5\); and \(\ell = \frac{L}{20}, \, m = 0.5\), one finds the following elastic modulus distribution function, i.e.
where
A contour plot showing the distribution given in Eq. (89) is presented in Fig. 15.
The functionally graded plates subjected to a central line load with elastic modulus varying along x- and y-directions (as shown in Figs. 1d and 11) could be designed following the distribution function given in Eq. (89) as follows
7 Summary
Developed herein is a novel strategy to obtain optimal designs of FGL structures. It involves the use of the Hencky bar-grid model and topology optimization. The HBM formulated herein extends a previous model with twice the number of internal rigid bars and springs as shown in Fig. 2. The new HBM enables the determination of the local stiffness matrix for each HBM grid cell by using the expressions of the stiffnesses of elastic primary axial springs, elastic secondary axial springs and torsional springs that are employed to connect the rigid bars. A TO with filtering processes is presented based on the obtained local stiffness matrices for optimizing HBM. The objective is to minimize the strain energy of an HBM subjected to boundary conditions and equilibrium and compatibility constraints by varying spring stiffnesses within each grid cell. The obtained HBM with optimal material property distribution is then used to build FGL structures (see Fig. 3c and d, for example). We assume that the horizontal and vertical axial bars have the stiffnesses of \(\overline{k}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{xx}\) and \(\overline{k}_{{i + \frac{1}{2},j + \frac{1}{2}}}^{yy}\), respectively. Likewise, its curved bars located at the corners and middle of the cell have the stiffnesses \(k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{S}\) and \(k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{xy} \left( {{\text{or}} k_{{i + \frac{1}{2},j + \frac{1}{2}}}^{yx} } \right)\), respectively. The bars in all lattice cells have a constant elastic modulus \(\tilde{E}\) and a constant density \(\tilde{\rho }\) but a varying cross-section area \(\tilde{A}_{{i + \frac{1}{2},j + \frac{1}{2}}}\). Therefore, HBM grid cells with larger spring stiffnesses corresponds to lattice structures with thicker bars and thus more mass.
8 Concluding remarks
Based on the HBM-TO optimal designs of an FGL beam and an FGL plate under a central line load, the following observations may be drawn:
-
1.
HBM-TO can efficiently find optimal FGL structures by optimizing a small number of design variables such as the spring stiffness of each grid cell;
-
2.
HBM-TO does not need to perform extra optimization for the structure and connectivity of each lattice unit cell;
-
3.
All optimal FGL structures studied herein can be effectively obtained by HBM-TO with fewer than 80 iterations;
-
4.
The designed cross-section has more concentrated mass and a more “defined” shape when using a smaller grid cell size or a larger penalty exponent;
-
5.
The “distributed” solutions are generally stiffer than the “defined” ones and with a smoother transition of mass;
-
6.
Polynomial functions that approximate the elastic modulus distribution for the optimal designed FGL beams (Eqs. (88)) and FGL plates (Eqs. (91)) are presented for the first time. These functions could be useful for fabrication, buckling and vibration analysis of these FGL structures as shown in Fig. 1d.
In this study, we only consider one type of lattice representation as shown in Fig. 3c. A more rigorous investigation of the HBM lattice representation such as the effect of the shape of the curved bars and the relation between the HBM spring stiffness and the geometry of the unit lattice structure could be performed in a future study (Cheng et al. 2019).
Owing to its physical representation, the HBM-TO can account for local damage and local stiffening constrains (Wang et al. 2009; Cui et al. 2011) as well as advanced material constitutive behaviour (O’Brien 2008) by simply adjusting the spring stiffnesses. Moreover, as a physical model-based optimization framework, HBM-TO can be applied to optimize micro- and nano-structures by setting the grid length to the characteristic length of the intended scale. Due to HBM having similar governing equations as the ones given by standard FD method, the efficient alternating direction implicit method could be applied for dynamic problems (Zhang et al. 2016, 2017). The proposed design framework can be used for other lattice models (Wieghardt 1906; Born and Karman 1912; Hrennikoff 1941; McHenry 1943; Gazis et al. 1960; Suiker et al. 2001).
Abbreviations
- FGL:
-
Functionally graded lattice
- HBM:
-
Hencky bar-grid model
- TO:
-
Topology optimization
- GDM:
-
Greyscale density mapping
- SIMP:
-
Solid isotropic material with penalization
- GSO:
-
Ground structure optimization
- OC:
-
Optimality criteria
- FD:
-
Finite difference
References
Aage N, Johansen VE (2013) Topology optimization codes written in Python
Andreassen E, Clausen A, Schevenels M, Lazarov BS, Sigmund O (2011) Efficient topology optimization in MATLAB using 88 lines of code. Struct Multidisc Optim 43:1–16. https://doi.org/10.1007/s00158-010-0594-7
Azari Nejat A, Held A, Trekel N, Seifried R (2022) A modified level set method for topology optimization of sparsely-filled and slender structures. Struct Multidisc Optim 65:85. https://doi.org/10.1007/s00158-022-03184-2
Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1:193–202. https://doi.org/10.1007/BF01650949
Born M, Karman TV (1912) Über schwingungen in raumgittern. Phys Zeit 8:297–309
Challamel N, Zhang YP, Wang CM, Ruta G, dell’Isola F (2022) Discrete and continuous models of linear elasticity: history and connections. Contin Mech Thermodyn, Under Review
Challis VJ (2010) A discrete level-set topology optimization code written in Matlab. Struct Multidisc Optim 41:453–464. https://doi.org/10.1007/s00158-009-0430-0
Challis VJ, Guest JK (2009) Level set topology optimization of fluids in Stokes flow. Int J Numer Methods Eng 79:1284–1308. https://doi.org/10.1002/nme.2616
Cheng L, Bai J, To AC (2019) Functionally graded lattice structure topology optimization for the design of additive manufactured components with stress constraints. Comput Methods Appl Mech Eng 344:334–359. https://doi.org/10.1016/j.cma.2018.10.010
Cui X, Xue Z, Pei Y, Fang D (2011) Preliminary study on ductile fracture of imperfect lattice materials. Int J Solids Struct 48:3453–3461. https://doi.org/10.1016/j.ijsolstr.2011.08.013
Dunning PD, Kim HA (2015) Introducing the sequential linear programming level-set method for topology optimization. Struct Multidisc Optim 51:631–643. https://doi.org/10.1007/s00158-014-1174-z
Ferro N, Perotto S, Bianchi D, Ferrante R, Mannisi M (2022) Design of cellular materials for multiscale topology optimization: application to patient-specific orthopedic devices. Struct Multidisc Optim 65:79. https://doi.org/10.1007/s00158-021-03163-z
Gazis DC, Herman R, Wallis RF (1960) Surface elastic waves in cubic crystals. Phys Rev 119:533–544. https://doi.org/10.1103/PhysRev.119.533
Gibson LJ (1989) Modelling the mechanical behavior of cellular materials. Mater Sci and Engg: A, 110:1-36. https://doi.org/10.1016/0921-5093(89)90154-8
Guerder M, Duval A, Elguedj T, Feliot P, Touzeau J (2022) Isogeometric shape optimisation of volumetric blades for aircraft engines. Struct Multidisc Optim 65:86. https://doi.org/10.1007/s00158-021-03090-z
Gurtin ME (1973) The linear theory of elasticity. Linear theories of elasticity and thermoelasticity. Springer, Berlin, Heidelberg, pp 1–295
Han Y, Lu WF (2018) A novel design method for nonuniform lattice structures based on topology optimization. J Mech Des. https://doi.org/10.1115/1.4040546
Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ, Kern R, Picus M, Hoyer S, van Kerkwijk MH, Brett M, Haldane A, del Río JF, Wiebe M, Peterson P, Gérard-Marchant P, Sheppard K, Reddy T, Weckesser W, Abbasi H, Gohlke C, Oliphant TE (2020) Array programming with NumPy. Nature 585:357–362. https://doi.org/10.1038/s41586-020-2649-2
Hassani B, Hinton E (1999) Homogenization and structural topology optimization. Springer, London
Hencky H (1921) Über die angenäherte Lösung von Stabilitätsproblemen im Raum mittels der elastischen Gelenkkette. Der Eisenbau 11:437–452
Hrennikoff A (1941) Solution of problems of elasticity by framework method. ASME J Appl Mech 8:A169–A175
Huang X, Xie YM (2007) Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem Anal Des 43:1039–1049. https://doi.org/10.1016/j.finel.2007.06.006
Hunter JD (2007) Matplotlib: A 2D graphics environment. Comput Sci Eng 9:90–95. https://doi.org/10.1109/MCSE.2007.55
Kaveh A, Hassani B, Shojaee S, Tavakkoli SM (2008) Structural topology optimization using ant colony methodology. Eng Struct 30:2559–2565. https://doi.org/10.1016/j.engstruct.2008.02.012
Li D, Liao W, Dai N, Dong G, Tang Y, Minxie Y (2018) Optimal design and modeling of gyroid-based functionally graded cellular structures for additive manufacturing. Comput Des 104:87–99. https://doi.org/10.1016/j.cad.2018.06.003
Lin Y, Zhu W, Li J, Ke Y (2022) A distance regularization scheme for topology optimization with parametric level sets using cut elements. Struct Multidisc Optim 65:88. https://doi.org/10.1007/s00158-021-03098-5
Liu J, Gaynor AT, Chen S, Kang Z, Suresh K, Takezawa A, Li L, Kato J, Tang J, Wang CCL, Cheng L, Liang X, To AC (2018) Current and future trends in topology optimization for additive manufacturing. Struct Multidisc Optim 57:2457–2483. https://doi.org/10.1007/s00158-018-1994-3
Maconachie T, Leary M, Lozanovski B, Zhang X, Qian M, Faruque O, Brand M (2019) SLM lattice structures: Properties, performance, applications and challenges. Mater Des 183:108137. https://doi.org/10.1016/j.matdes.2019.108137
Mahamood RM, Akinlabi ET, Shukla M, Pityana S (2012) Functionally graded material: an overview. In: Proceedings of the World Congress on Engineering 2012, Vol III (WCE). London
McHenry D (1943) A lattice analogy for the solution of stress problems. J Inst Civ Eng 2:59–82
Miguel LFF, Lopez RH, Miguel LFF (2013) Multimodal size, shape, and topology optimisation of truss structures using the Firefly algorithm. Adv Eng Softw 56:23–37. https://doi.org/10.1016/j.advengsoft.2012.11.006
Mlejnek HP (1992) Some aspects of the genesis of structures. Struct Optim 5:64–69. https://doi.org/10.1007/BF01744697
Nguyen J, Park S, Rosen D (2013) Heuristic optimization method for cellular structure design of light weight components. Int J Precis Eng Manuf 14:1071–1078. https://doi.org/10.1007/s12541-013-0144-5
O’Brien GS (2008) Discrete visco-elastic lattice methods for seismic wave propagation. Geophys Res Lett 35:L02302. https://doi.org/10.1029/2007GL032214
Panesar A, Abdi M, Hickman D, Ashcroft I (2018) Strategies for functionally graded lattice structures derived using topology optimisation for Additive Manufacturing. Addit Manuf 19:81–94. https://doi.org/10.1016/j.addma.2017.11.008
Querin OM, Steven GP, Xie YM (1998) Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Eng Comput 15:1031–1048. https://doi.org/10.1108/02644409810244129
Querin OM, Young V, Steven GP, Xie YM (2000) Computational efficiency and validation of bi-directional evolutionary structural optimisation. Comput Methods Appl Mech Eng 189:559–573. https://doi.org/10.1016/S0045-7825(99)00309-6
Rao SS (2005) The finite element method in engineering. Elsevier
Sigmund O (1997) On the design of compliant mechanisms using topology optimization*. Mech Struct Mach 25:493–524. https://doi.org/10.1080/08905459708945415
Sigmund O (2001) A 99 line topology optimization code written in Matlab. Struct Multidiscip Optim 21:120–127. https://doi.org/10.1007/s001580050176
Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Optim 16:68–75. https://doi.org/10.1007/BF01214002
Suiker ASJ, Metrikine AV, De Borst R (2001) Dynamic behaviour of a layer of discrete particles, part 1: analysis of body waves and eigenmodes. J Sound Vib 240:1–18. https://doi.org/10.1006/jsvi.2000.3202
Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24:359–373. https://doi.org/10.1002/nme.1620240207
van Dijk NP, Maute K, Langelaar M, van Keulen F (2013) Level-set methods for structural topology optimization: a review. Struct Multidisc Optim 48:437–472. https://doi.org/10.1007/s00158-013-0912-y
Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, van der Walt SJ, Brett M, Wilson J, Millman KJ, Mayorov N, Nelson ARJ, Jones E, Kern R, Larson E, Carey CJ, Polat İ, Feng Y, Moore EW, VanderPlas J, Laxalde D, Perktold J, Cimrman R, Henriksen I, Quintero EA, Harris CR, Archibald AM, Ribeiro AH, Pedregosa F, van Mulbregt P, Vijaykumar A, Bardelli AP, Rothberg A, Hilboll A, Kloeckner A, Scopatz A, Lee A, Rokem A, Woods CN, Fulton C, Masson C, Häggström C, Fitzgerald C, Nicholson DA, Hagen DR, Pasechnik DV, Olivetti E, Martin E, Wieser E, Silva F, Lenders F, Wilhelm F, Young G, Price GA, Ingold G-L, Allen GE, Lee GR, Audren H, Probst I, Dietrich JP, Silterra J, Webber JT, Slavič J, Nothman J, Buchner J, Kulick J, Schönberger JL, de MirandaCardoso JV, Reimer J, Harrington J, Rodríguez JLC, Nunez-Iglesias J, Kuczynski J, Tritz K, Thoma M, Newville M, Kümmerer M, Bolingbroke M, Tartre M, Pak M, Smith NJ, Nowaczyk N, Shebanov N, Pavlyk O, Brodtkorb PA, Lee P, McGibbon RT, Feldbauer R, Lewis S, Tygier S, Sievert S, Vigna S, Peterson S, More S, Pudlik T, Oshima T, Pingel TJ, Robitaille TP, Spura T, Jones TR, Cera T, Leslie T, Zito T, Krauss T, Upadhyay U, Halchenko YO, Vázquez-Baeza Y (2020) SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17:261–272. https://doi.org/10.1038/s41592-019-0686-2
Wang SS (1983) Fracture mechanics for delamination problems in composite materials. J Compos Mater 17:210–223. https://doi.org/10.1177/002199838301700302
Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192:227–246. https://doi.org/10.1016/S0045-7825(02)00559-5
Wang G, Al-Ostaz A, Cheng AH-D, Mantena PR (2009) Hybrid lattice particle modeling: theoretical considerations for a 2D elastic spring network for dynamic fracture simulations. Comput Mater Sci 44:1126–1134. https://doi.org/10.1016/j.commatsci.2008.07.032
Wang CM, Zhang YP, Pedroso DM (2017) Hencky bar-net model for plate buckling. Eng Struct 150:947–954. https://doi.org/10.1016/j.engstruct.2017.07.080
Wang CM, Zhang H, Challamel N, Pan WH (2020) Hencky bar-chain/net for structural analysis. World Scientific, Europe
Wang J, Wu J, Westermann R (2022) Stress topology analysis for porous infill optimization. Struct Multidiscip Optim 65:92. https://doi.org/10.1007/s00158-022-03186-0
Wieghardt K (1906) Über einen Grenzübergang der Elastizitätslehre und seine Anwendung auf die Statik hochgradig statisch unbestimmter Fachwerke. Verhandtlungen Des Vereinz z Beförderung Des Gewerbefleisses Abhandlungen 85:139–176
Yin L, Yang W (2001) Optimality criteria method for topology optimization under multiple constraints. Comput Struct 79:1839–1850. https://doi.org/10.1016/S0045-7949(01)00126-2
Zhang W, Yang J, Xu Y, Gao T (2014) Topology optimization of thermoelastic structures: mean compliance minimization or elastic strain energy minimization. Struct Multidisc Optim 49:417–429. https://doi.org/10.1007/s00158-013-0991-9
Zhang P, Toman J, Yu Y, Biyikli E, Kirca M, Chmielus M, To AC (2015) Efficient design-optimization of variable-density hexagonal cellular structure by additive manufacturing: theory and validation. J Manuf Sci Eng. https://doi.org/10.1115/1.4028724
Zhang YP, Pedroso DM, Li L (2016) FDM and FEM solutions to linear dynamics of porous media: stabilised, monolithic and fractional schemes. Int J Numer Methods Eng 108:614–645. https://doi.org/10.1002/nme.5231
Zhang YP, Pedroso DM, Li L, Ehlers W (2017) FDM solutions to linear dynamics of porous media: efficiency, stability, and parallel solution strategy. Int J Numer Methods Eng 112:1539–1563. https://doi.org/10.1002/nme.5568
Zhang H, Wang CM, Challamel N, Zhang YP (2018a) Uncovering the finite difference model equivalent to Hencky bar-net model for axisymmetric bending of circular and annular plates. Appl Math Model 61:300–315. https://doi.org/10.1016/j.apm.2018.04.019
Zhang H, Zhang YP, Wang CM (2018b) Hencky bar-net model for vibration of rectangular plates with mixed boundary conditions and point supports. Int J Struct Stab Dyn 18:1850046. https://doi.org/10.1142/S0219455418500463
Zhang YP, Wang CM, Pedroso DM (2018c) Hencky bar-net model for buckling analysis of plates under non-uniform stress distribution. Thin-Walled Struct 122:344–358. https://doi.org/10.1016/j.tws.2017.10.039
Zhang YP, Wang CM, Pedroso DM, Zhang H (2018d) Extension of Hencky bar-net model for vibration analysis of rectangular plates with rectangular cutouts. J Sound Vib 432:65–87. https://doi.org/10.1016/j.jsv.2018.06.029
Zhang H, Challamel N, Wang CM, Zhang YP (2019a) Buckling of multiply connected bar-chain and its associated continualized nonlocal model. Int J Mech Sci 150:168–175. https://doi.org/10.1016/j.ijmecsci.2018.10.015
Zhang H, Challamel N, Wang CM, Zhang YP (2019b) Exact and nonlocal solutions for vibration of multiply connected bar-chain system with direct and indirect neighbouring interactions. J Sound Vib 443:63–73. https://doi.org/10.1016/j.jsv.2018.11.037
Zhang YP, Challamel N, Wang CM, Zhang H (2019c) Comparison of nano-plate bending behaviour by Eringen nonlocal plate, Hencky bar-net and continualised nonlocal plate models. Acta Mech 230:885–907. https://doi.org/10.1007/s00707-018-2326-9
Zhang YP, Challamel N, Wang CM (2021a) Elasticity solutions for nano-plane structures under body forces using lattice elasticity, continualised nonlocal model and Eringen nonlocal model. Contin Mech Thermodyn 33:2453–2480. https://doi.org/10.1007/s00161-021-01031-1
Zhang YP, Wang CM, Pedroso DM, Zhang H (2021b) Hencky bar-grid model for plane stress elasticity problems. J Eng Mech 147:04021021. https://doi.org/10.1061/(asce)em.1943-7889.0001931
Zhang YP, Wang CM, Pedroso DM, Zhang H (2022) Hencky bar-grid model and Hencky bar-net model for buckling analysis of rectangular plates. In: Analysis and design of plated structures. Elsevier, pp 75–107
Zhou M, Rozvany GIN (1991) The COC algorithm, part II: topological, geometrical and generalized shape optimization. Comput Methods Appl Mech Eng 89:309–336. https://doi.org/10.1016/0045-7825(91)90046-9
Zhu J, Zhou H, Wang C, Zhou L, Yuan S, Zhang W (2021) A review of topology optimization for additive manufacturing: Status and challenges. Chinese J Aeronaut 34:91–110. https://doi.org/10.1016/j.cja.2020.09.020
Acknowledgements
The authors wish to thank the review editor and the two anonymous reviewers for their insightful suggestions and comments that help to improve the paper.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Replication of results
All important details have been presented in the paper. The results obtained in this paper can be reproduced by using the python code given in Appendix A.
Additional information
Responsible Editor: Seonho Cho
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
A Python 3 code is presented for solving the problems as articulated in Sects. 6.2 and 6.3. This code is highly inspired by an open source code from Aage and Johansen (2013). The open source libraries “numpy” (Harris et al. 2020), “scipy” (Virtanen et al. 2020) and “matplotlib” (Hunter 2007) are adopted in the following code.


Disclaimer: The authors do not guarantee that the code is free from errors, and they shall not be liable in any event caused by the use of the code.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Y.P., Wang, C.M., Challamel, N. et al. Optimal design of functionally graded lattice structures using Hencky bar-grid model and topology optimization. Struct Multidisc Optim 65, 276 (2022). https://doi.org/10.1007/s00158-022-03368-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-022-03368-w