Topology optimization using difference-based equivalent static loads

Abstract

Topology optimization of crash-related problems usually involves a huge number of design variables as well as nonlinearities in geometry, material, and contact. The Equivalent Static Load (ESL) method provides an approach to solve such problems. This method has recently been extended under the name Difference-based Equivalent Static Load (DiESL) method to employ a set of Finite Element models, each describing the deformed geometry at an individual time step. Only sizing optimization problems were considered so far. In this paper, the DiESL method is extended to topology optimization utilizing a Solid Isotropic Material with Penalization approach (SIMP). The method is tested using an example of a rigid pole colliding with a simple beam, where the intrusion of the pole is minimized. The initial velocity of the pole is varied in order to examine the influence of inertia effects on the optimized structures. It is shown that the results differ significantly depending on the chosen initial velocity and, consequently, that they exhibit inertia effects. This cannot be seen in the results derived by the standard ESL method. Consequently, the results of the DiESL method’s show a considerable improvement compared to those of the standard ESL method.

1 Introduction

Topology optimization strives to find the optimal distribution of material within a discretized design domain under specified load cases, constraints, and objectives (Bendsøe 1989). For linear static response topology optimization, several approaches are available, enabling an efficient application during the design process in many fields of industry. The most common methods are summarized below: the homogenization method (Bendsøe and Kikuchi 1988), which utilizes a material model corresponding to a periodic microstructure consisting of infinitely small square cells with rectangular holes. Through numerical homogenization, the macroscopic material properties of the micro cells can be obtained, depending on certain parameters describing the size and orientation of holes in the microcells. These parameters are then optimized to maximize the performance of the structure. The resulting multi-scale structures are often hard to interpret due to manufacturability problems, although advances in additive manufacturing technologies are pushing the boundaries nowadays. These difficulties do not arise if the Solid Isotropic Material with Penalization (SIMP) approach is applied, where the distribution of a homogenous isotropic material is optimized (Bendsøe 1989; Zhou and Rozvany 1991; Bendsøe and Sigmund 1999). Here, only one design variable per element is used—the normalized density—which is related to the element’s stiffness. This density-based approach is the most prominent, and many commercial codes such as MSC NASTRAN, Altair OptiStruct, or VRAND GENESIS are utilizing it. Furthermore, approaches like Soft Kill Option (SKO) (Baumgartner et al. 1992; Harzheim and Graf 2005), Evolutionary Structural Optimization (ESO) (Xie and Steven 1993; Huang et al. 2010), the Phase Field method (Bourdin and Chambolle 2003), and the Level Set method (Wang et al. 2003; Allaire et al. 2004) are to be mentioned. Unfortunately, none of these approaches is applicable directly when it comes to nonlinear dynamic response optimization like crashworthiness optimization, where a transient problem including nonlinearities in geometry, material, and contact has to be solved. In this case, sensitivity information is either very expensive or not even available.

Nevertheless, efforts are made toward an applicable and efficient calculation of sensitivities for highly nonlinear problems: Weider et al. (2018, 2019) are computing the topological derivatives using adjoint sensitivity analysis considering nonlinearities in material and geometry. Ivarsson et al. (2018) are employing the adjoint sensitivity analysis involving a transient finite strain material model. The gradients are used to maximize the absorbed viscoplastic energy of structures subjected to impact. Both efforts have in common that an adjoint terminal value problem has to be solved, which needs to be integrated backwards in time after the original nonlinear dynamic problem has been analyzed. To decrease the computational effort of this procedure, usually implicit time integration schemes are utilized due to their capability of handling larger time steps. Furthermore, matrices like the factorized tangent stiffness can be stored during the analysis of the original problem and be reused during the backward integration to further decrease the computational costs. However, this can be very storage demanding especially for large-scale automotive models. The major drawback affects problems where multiple contacts are the dominant nonlinearity: Here, the time step size is limited to a small value even for implicit time integration schemes in order to resolve each contact. Additionally, implicit integration schemes may fail for complex contact problems such as crash. For this reason, explicit integration schemes are typically used for crash analysis in automotive industry. Thus, the usage of adjoint sensitivity analysis for nonlinear dynamic response optimization may be limited to problems in which contact has no major influence.

Alternative approaches circumventing the calculation of sensitivities comprise the following: The Graph and Heuristic-based Topology optimization (GHT) has been introduced to optimize the cross-section of profiles (Ortmann and Schumacher 2013) and has been extended by Beyer et al. (2020) to three-dimensional structures. Here, the topology of the structure is alternately changed according to heuristic rules based on expert knowledge and then optimized in terms of size and shape. Furthermore, Patel (2009) introduced Hybrid Cellular Automata (HCA) to crashworthiness optimization. The main idea here is to find a topology with uniform internal strain energy at the final state by a heuristic update-approach. The normalized density of each cell is updated as a function of the internal strain energy. Here, the internal strain energies are filtered by using a von Neumann neighborhood in the cellular automata paradigm. The material properties of each element are related to the density by using an extended SIMP approach for elasto-plastic materials.

Another prominent approach to circumvent the sensitivity problem is to define linear auxiliary load cases enabling linear static response optimization. The nonlinear dynamic optimization problem then is split into an analysis domain where nonlinear dynamic analysis is performed and a design domain where a set of linear static response optimization subproblems is solved afterward. A well-known method to compute such auxiliary load cases is the Equivalent Static Load (ESL) method. There are many examples for a successful application in sizing, shape, free sizing, and topology optimization (Choi and Park 2002; Park et al. 2005; Shin et al. 2007; Jeong et al. 2008; Kim and Park 2010; Park 2011; Lee et al. 2013, 2015; Lee and Park 2015; Choi et al. 2018; Karev et al. 2018). Nevertheless, the ESL method has some limitations and drawbacks. This can largely be attributed to the fact that the ESLs are always calculated based on the undeformed initial geometry. To overcome this disadvantage, a difference-based approach—the DiESL method—has been introduced for sizing optimization (Triller et al. 2021). It has been shown that the DiESL method provides a significant increase in approximation quality of structural responses such as displacements and strains from nonlinear dynamic problems while at the same time accelerating convergence. It was shown that the DiESL method succeeded in finding the optimum of a nonlinear problem where the ESL method failed. Furthermore, it has been shown how an appropriate selection of ESL times in each cycle can further increase the approximation quality of the DiESL method (Triller et al. 2022). Additionally, it has been demonstrated that local stiffness adaption could improve the result if the elements neither in the elastic nor in the plastic range are dominating the structure’s behavior. As a next step, the DiESL method is extended to topology optimization and is presented in this paper, which is structured in the following way: In Sect. 2, the ESL and the DiESL methods are explained. Furthermore, all necessary extensions for topology optimization are elaborated. In Sect. 3, the method is tested numerically using a simple beam structure subjected to an impact, and results are compared to results of the ESL method. In order to examine the influence of inertia effects on the resulting structure, the initial velocity and mass of the impactor are varied. This includes a linear static load case representing zero impactor velocity. Finally, a conclusion and an outlook are worked out.

2 The DiESL (Difference-based Equivalent Static Loads) method for topology optimization

The setup of the DiESL method is very similar to the ESL method introduced by Choi and Park (2002), which has been extended to nonlinear dynamic response topology optimization by Lee and Park (2015). The basic idea of the ESL method is to create linear auxiliary load cases for nonlinear dynamic response optimization problems, which are then used as approximation of the nonlinear system in optimization. The user has to select ${n}_{\mathrm{T}}$ time steps ${t}_{i}$ corresponding to the number of auxiliary load cases. For each linear auxiliary load case, so-called equivalent static loads ${\mathbf{f}}_{\mathrm{ESL}}^{i}$ are calculated in the linear static system by

$${\mathbf{K}}^{i} {\mathbf{u}}\left( {t_{i} } \right) = {\mathbf{f}}_{{{\text{ESL}}}}^{i} { };{ }i = 0,{ } \ldots ,{ }n_{{\text{T}}} - 1.$$

(1)

Here, $\mathbf{u}({t}_{i})$ is the solution of the nonlinear dynamic analysis for the selected time steps ${t}_{i}$

$${\mathbf{M}}_{{{\text{NL}}}} {\mathbf{\ddot{u}}}\left( {t_{i} } \right) + {\mathbf{C}}_{{{\text{NL}}}} {\dot{\mathbf{u}}}\left( {t_{i} } \right) + {\mathbf{K}}_{{{\text{NL}}}} {\mathbf{u}}\left( {t_{i} } \right) = {\mathbf{f}}\left( {t_{i} } \right)$$

(2)

where $\mathbf{f}(t)$, ${\mathbf{M}}_{\mathrm{NL}}$, ${\mathbf{C}}_{\mathrm{NL}}$, and ${\mathbf{K}}_{\mathrm{NL}}$ are the external dynamic force, the mass, the damping, and the stiffness matrix, respectively. Consequently, each equivalent static load ${\mathbf{f}}_{\mathrm{ESL}}^{i}$ yields the same displacement vector $\mathbf{u}({t}_{i})$ in linear statics as those obtained in the nonlinear dynamic system. In other words, the loads ${\mathbf{f}}_{\mathrm{ESL}}^{i}$ received are equivalent in the sense that they lead to same displacement fields.

The basic procedure is thus the following: in the analysis domain, the nonlinear system is simulated, and afterward, the system is optimized in the design domain (inner optimization loop) based on linear static auxiliary load cases. Because the linear approximation is not perfect, this procedure is iterated (outer loop). Note that the displacements in the linear and nonlinear system are only identical at the beginning of each inner loop.

This approach is advantageous for many reasons: Firstly, the missing sensitivity problem for highly nonlinear problems is addressed. Secondly, well-developed commercial software systems can be used for analysis and optimization and no development of an own sensitivity analysis and optimization algorithm is necessary.

The original nonlinear dynamic response optimization problem can be stated as

$$\min f\left( {{\mathbf{x}},{\mathbf{u}}\left( {{\mathbf{x}},t} \right)} \right)$$

(3a)

$${\text{s}}.{\text{t}}.{\kern 1pt} \quad g_{j} \left( {{\mathbf{x}},{\mathbf{u}}\left( {{\mathbf{x}},t} \right)} \right) \le 0;\quad j = 1, \ldots , m$$

(3b)

$$x_{i}^{L} \le x_{i} \le x_{i}^{U} ;\quad i = 1, \ldots ,n_{{\text{D}}} .$$

(3c)

Here, $f$, $m$, and ${n}_{\text{D}}$ are the objective function, the number of constraints ${g}_{j}$, and the number of design variables ${x}_{i}$, respectively. The latter has lower and upper bound ${x}_{i}^{\mathrm{L}}$ and ${x}_{i}^{\mathrm{U}}$, respectively. The displacement vector ${\mathbf{u}}^{T}\left(\mathbf{x},t\right)$ is the solution of (1).

2.1 Comparison of ESL and DiESL

The basic difference between ESL and DiESL is depicted in Fig. 1: consider the displacement path of an arbitrary node, i.e., its coordinates $\mathbf{r}\left(t\right)$ as obtained by a nonlinear dynamic simulation (Fig. 1, left). Results are given at discrete times ${t}^{0}, \ldots , {t}^{i}$. The standard ESL method uses the undeformed geometry (i.e., at time ${t}^{0}$) to assemble the stiffness matrix. The loads ${\mathbf{f}}_{\mathrm{ESL}}^{i}$ to derive the nodal displacements $\mathbf{u}({t}^{i})$ are calculated using one subcase for each given time ${t}^{i}$ (Fig. 1, middle). Consequently, it falls short of following the given nonlinear displacement path (Fig. 1, left). In contrast, DiESL is designed to follow the nonlinear displacement path by splitting it into linear increments (Fig. 1, right) and by using linear submodels with the corresponding deformed geometry at each time ${t}^{i}$. Consequently, the DiESL approach requires ${n}_{\mathrm{T}}$ linear submodels, one for each time step ${t}^{i}$, $i=0,\ldots ,{n}_{\mathrm{T}}-1$. We call such a Linear Submodel at time ${t}^{i}$ ${\mathrm{LSM}}^{i}$ in the following. The $i$ ^th ${\mathrm{LSM}}^{i}$ is defined by the coordinates of all nodes at time step ${t}^{i}$ which can be combined in the vector

Fig. 1

Displacement path of an arbitrary node during the deformation of a structure (left) and the corresponding displacement $\mathbf{u}({t}^{i})$ (middle) and $\Delta \mathbf{u}\left({t}^{i}\right)$ (right) used for the computation of the ESLs and DiESLs at time steps ${t}^{i}$, respectively.

$${\mathbf{r}}^{T}\left({t}^{i}\right)= \left({\mathbf{r}}_{1}^{T}\left({t}^{i}\right), {\mathbf{r}}_{2}^{T}\left({t}^{i}\right), \ldots ,{\mathbf{r}}_{{n}_{\mathrm{N}}}^{T}\left({t}^{i}\right)\right)$$

(4)

containing the coordinates ${\mathbf{r}}_{j}\left({t}^{i}\right)$ of all ${n}_{\mathrm{N}}$ nodes of the FE-model. Accordingly, $\mathbf{r}\left({t}^{0}\right)$ describes the coordinates of all nodes of the undeformed model. All ${\mathrm{LSM}}^{i}$ have the same mesh topology and they differ only in the coordinates $\mathbf{r}({t}^{i})$. The coordinates of a linear submodel ${\mathrm{LSM}}^{i}$ describing the deformed geometry at time ${t}^{i}$ can therefore be calculated by

$$\mathbf{r}\left({t}^{i}\right)=\mathbf{r}\left({t}^{0}\right)+\mathbf{u}({t}^{i})$$

(5)

where displacement field $\mathbf{u}({t}^{i})$

$${\mathbf{u}}^{T}\left({\mathrm{t}}^{i}\right)= \left({\mathbf{u}}_{1}^{T}\left({t}^{i}\right), {\mathbf{u}}_{2}^{T}\left({t}^{i}\right), \ldots ,{\mathbf{u}}_{{n}_{\mathrm{N}}}^{T}\left({t}^{i}\right)\right)$$

(6)

is the solution of (1) at time ${t}_{i}$ containing the displacements of all ${n}_{\mathrm{N}}$ nodes at time ${t}^{i}$.

In contrast to ESL, which requires only a single FE-model representing the undeformed structure of the initial model with the coordinates $\mathbf{r}\left({t}^{0}\right)$, DiESL requires the computation of incremental equivalent static loads ${\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i}$ in each linear submodel ${\mathrm{LSM}}^{i}$,

$${\mathbf{K}}^{i}\Delta \mathbf{u}\left({t}^{i}\right)={\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i} ;\quad i=0, \ldots , {n}_{\mathrm{T}}-1 .$$

(7)

where the linear statics stiffness matrix ${\mathbf{K}}^{i}=\mathbf{K}(\mathbf{x},\mathbf{r}\left({t}^{i}\right))$ depends on the design variables $\mathbf{x}$ and the nodal coordinates $\mathbf{r}\left({t}^{i}\right)$ of ${\mathrm{LSM}}^{i}$. The incremental nonlinear displacements $\Delta \mathbf{u}\left({t}^{i}\right)$ leading from $\mathbf{r}\left({t}^{i}\right)$ to $\mathbf{r}\left({t}^{i+1}\right)$ are calculated by

$$\Delta \mathbf{u}\left({t}^{i}\right)=\mathbf{u}\left({t}^{i+1}\right)-\mathbf{u}\left({t}^{i}\right)=\mathbf{r}\left({t}^{i+1}\right)-\mathbf{r}\left({t}^{i}\right)$$

(8)

For optimization, multimodel optimization (MMO) has to be applied where multiple FE-models are taken into account simultaneously in one linear static response optimization run.

2.2 DiESL procedure for topology optimization

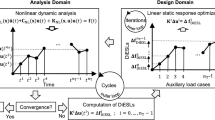
The general procedure of the DiESL method for nonlinear dynamic responses optimization is the following (Fig. 2): First, a nonlinear dynamic analysis is performed and the displacement fields $\mathbf{u}({t}^{i})$ are obtained for all specified time steps ${t}^{i}$, $i=1, \ldots , {n}_{\mathrm{T}}$. Based on the nonlinear displacement fields $\mathbf{u}({t}^{i})$ or the deformed mesh coordinates $\mathbf{r}({t}^{i})$, the incremental displacements $\Delta \mathbf{u}\left({t}^{i}\right)$ can be calculated using (8).

Fig. 2

General optimization process of the DiESL method for nonlinear dynamic response optimization

In each ${\mathrm{LSM}}^{i}$, we then calculate the loads ${\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i}$ according to Eq. (7). Using the incremental equivalent static loads ${\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i}$, gradient-based linear static response multimodel optimization (inner loop) can now be performed. Since the linear auxiliary load cases are only an approximation of the nonlinear behavior of the system, the linear static and the nonlinear dynamic responses no longer match at the end of the inner loop. Consequently, nonlinear dynamic analysis has to be applied again using the updated design variables. Then response differences to the previous cycle can be calculated. If the difference is too high, the process is iterated (outer loop) until the difference is small enough and additional termination criteria are fulfilled (Shin et al. 2007; Jeong et al. 2010; Kim and Park 2010; Park 2011; Lee and Park 2015).

The difference between the linear and nonlinear dynamic responses is expected to increase with the length of the inner loop optimization path, i.e., with the amount of design change. If this difference is too high, the update in the outer loop may result in significant changes in the search directions causing convergence to be slowed down or even unachievable. For this reason, commercial ESL codes, such as VRAND ESLDYNA, limit the number of iterations in the inner loop and offer the application of move limits to restrict the length of the optimization path in each cycle. For sizing and shape optimization, the transfer of the optimized design from design domain to analysis domain can be done without problems for both ESL and DiESL approach. This is not true for topology optimization employing the SIMP approach where the design variables are the normalized densities of ${n}_{\mathrm{E}}$ elements. Here, the resulting densities have to be interpreted after each optimization, and nonlinear dynamic analysis is executed using the interpreted model.

A detailed explanation of this interpretation process is given in the next section.

2.2.1 Density interpretation

In contrast to sizing and shape optimization, topology optimization generally does not provide a final optimized design but only a design proposal. Consequently, an interpretation of the proposal and a conversion into a detailed engineering component is always necessary. Whereas such conversion can be done manually after an ordinary linear static response topology optimization, an automatic procedure is required in each DiESL cycle for transforming the density-based design proposal into a nonlinear model. The easiest approach seems to be transferring the optimized density field ${\mathbf{x}}^{*}$ resulting of the inner loop optimization directly to the analysis domain. However, it is well known that low-density elements with corresponding low stiffness may cause mesh distortion problems in the nonlinear model due to excessive deformations of these elements. This is a severe issue because it may terminate the nonlinear simulation run and hence the entire optimization process.

The mesh distortion problem has been addressed by Lee and Park (2015) and others (Bai et al. 2019; Lu et al. 2021).To prevent the problem, they generate a zero–one design after each linear static response optimization using a threshold ${\varepsilon }_{\mathrm{vf}}$. Densities equal or below ${\varepsilon }_{\mathrm{vf}}$ are interpreted as voids and all densities above are interpreted as solids. Lee and Park recommend to use the value of the volume fraction constraint for ${\varepsilon }_{\mathrm{vf}}$. However, they also state that this procedure “does not always work well” (Lee and Park 2015) and further research is required in order to find a technique to determine the threshold ${\varepsilon }_{\mathrm{vf}}$.

We propose an alternative approach here: Only elements with densities smaller than a low threshold value ${\varepsilon }_{\mathrm{v}}$ are interpreted as voids and densities above a high threshold ${\varepsilon }_{\mathrm{s}}$ are interpreted as solids. Void elements are deleted, solid elements are assigned to the original solid material. All remaining densities between ${\varepsilon }_{\mathrm{v}}$ and ${\varepsilon }_{\mathrm{s}}$ are carried over to the analysis domain as-is. This is done by introducing a transformation variable ${\chi }_{i}$ for each element $i$ defined as

$${\chi }_{i}=\left\{\begin{array}{l}0\quad if\quad {x}_{i}\le {\varepsilon }_{v} \\ {x}_{i}\quad if\quad {\varepsilon }_{v}<{x}_{i}\le {\varepsilon }_{s} \\ 1\quad if\quad {x}_{i}>{\varepsilon }_{s} \end{array}\right.; \quad i=1,\ldots ,{n}_{\mathrm{E}} .$$

(9)

In the nonlinear model, we assign the density ${\chi }_{i}$ to element $i$ if ${\chi }_{i}>0$ whereas ${\chi }_{i}=0$ means that element $i$ has to be deleted. In the following, we refer to the resulting nonlinear model as container model.¹ Note that this works only if the meshes in the linear statics and nonlinear model are congruent. This is the case for the example presented in this publication. If the meshes are not congruent, then a mapping of the density values is required from one mesh to the other and (9) has to be applied to the mapped densities.

As a consequence, islands of unconnected elements may develop. They need to be identified and deleted automatically since they do not contribute to the structure’s stiffness. This is accomplished using the “connectivity” tool of the pre-processor ANSA, which groups interconnected elements. Islands of unconnected elements can then be distinguished from the main structure based on their low mass and can be deleted. The overall procedure is visualized in Fig. 3. Note that in Fig. 3, the borders of the deleted void elements are still shown for illustration purposes. In the nonlinear simulation model, all unconnected nodes are also deleted.

Fig. 3

Interpretation of densities resulting from linear static response optimization (inner loop) for usage in subsequent nonlinear dynamic analysis

We propose to use ${\varepsilon }_{\mathrm{v}}$=0.1 and ${\varepsilon }_{\mathrm{s}}$=0.9. This ensures to keep continuity in material distribution from cycle to cycle and thus enables the topology to evolve in a smooth way. The continuity is seen as an advantage over the zero–one design approach as presented by Lee and Park (2015). It is beneficial especially in early stages of the DiESL procedure, after all densities have been initialized with a uniform value, and while a discrete structure has not evolved yet. In these early stages, the choice of one threshold ${\varepsilon }_{\mathrm{vf}}$ would be of major influence on the result of the subsequent nonlinear dynamic analysis. In the extreme case that the densities of all elements are smaller than ${\varepsilon }_{\mathrm{vf}}$, all elements would be deleted. The other extreme case is that the densities of all elements are larger than ${\varepsilon }_{\mathrm{vf}}$, thus no element would be deleted. These extreme cases show that generally either too many or too few elements are deleted, depending on the choice of ${\varepsilon }_{\mathrm{vf}}$. Hence, the mass of the nonlinear dynamic model significantly depends on ${\varepsilon }_{\mathrm{vf}}$. In the approach presented here, intermediate densities are transferred and the number of deleted elements is kept low by using a relatively small ${\varepsilon }_{\mathrm{v}}$.

As in the design domain, the densities ${\varvec{\upchi}}$ of the nonlinear dynamic simulation model need to be related to material properties. We use an extended SIMP approach for the elasto-plastic properties of a piecewise linear plastic material—the physical density, the Young’s modulus $E$, the yield stress ${\sigma }_{Y}$, and the strain hardening modulus $H$:

$$E\left(\chi \right)={\chi }^{{p}_{\mathrm{NL}}} {E}_{0}$$

(10a)

$${\sigma }_{Y}\left(\chi \right)={\chi }^{{p}_{\mathrm{NL}}}{ \sigma }_{Y,0}$$

(10b)

$${H}_{i}\left(\chi \right)={\chi }^{{p}_{\mathrm{NL}}} {H}_{i,0}$$

(10c)

where ${E}_{0}$, ${\sigma }_{Y,0}$, and ${H}_{i,0}$ are the values of the respective original solid material (Fig. 4). This approach is similar to the one used in (Patel 2007; Patel et al. 2009) with the difference that a common exponent ${p}_{\mathrm{NL}}$ is used here. Note that ${p}_{\mathrm{NL}}$ should not have the same value as in the SIMP approach of the linear statics model where we used a penalty exponent of$p=3$. Problems are to be expected in the nonlinear system for such a value because elements with $0<\chi <0.4$ would obtain very low stiffness$E<0.064 {E}_{0}$. This can cause mesh distortion problems in the analysis domain during simulation, as described above. In Fig. 5, these problems are exemplified using the SIMP penalty exponent ${p}_{\mathrm{NL}}=3$ in Eqs. (10). For areas with low densities, plasticized areas of excessive deformation and the so-called hedgehog effect can occur (Karev et al. 2018). The latter can be observed in impact zones, where individual nodes are flying away in the nonlinear dynamic simulation. This can be attributed to the high mass/stiffness ratio of elements with small densities. An element’s mass is proportional to its density, but according to Eq. (10a) its stiffness is proportional to the density raised to the power${p}_{\mathrm{NL}}=3$. Therefore, small density elements suffer from extremely small stiffness and may not be able to retain their nodes in place if they are located in the impact zone where they are subjected to high contact forces. According to Fig. 6, left, a threshold ${\varepsilon }_{\mathrm{v}}\approx 0.4$ would be necessary for $p=3$ in order to resolve this issue completely by deleting all affected elements. However, this would negate the benefits of using the container approach described above.

Fig. 4

Elasto-plastic piecewise linear material model for different densities $\chi$ using SIMP with ${p}_{\mathrm{NL}}=1$

Fig. 5

Mesh distortion problems during nonlinear dynamic analysis using SIMP approach with ${p}_{\mathrm{NL}}=3$ and non-binary density distribution: hedgehog effect (left), excessive deformation (right)

Fig. 6

Relation between normalized density and normalized stiffness in the design and analysis domain (left) and difference between normalized stiffness in design domain and analysis domain using a container model and a zero–one interpretation with ${\varepsilon }_{\mathrm{vf}}=0.2$ (right)

To circumvent this, the SIMP penalty exponent ${p}_{\mathrm{NL}}$ used in the design domain is reduced in order to decrease the mass/stiffness ratio of elements with small densities. Using a penalty exponent ${p}_{\mathrm{NL}}=1$ in the analysis domain prevents mesh distortion entirely. For this benefit, an inconsistency in stiffness between analysis and design domain is tolerated. This inconsistency is illustrated in Fig. 6. On the left side, the normalized stiffness of elements in the design domain ${\xi }_{i}=E({x}_{i})/{E}_{0}$ and in the analysis domain ${\xi }_{i,\mathrm{NL}}=E({\chi }_{i})/{E}_{0}$ is plotted over the density ${x}_{i}$ and ${\chi }_{i}$, respectively. On the right hand side, the difference $\Delta \xi ={\xi }_{\mathrm{NL}}-\xi$ between both is given employing the container model as well as the zero–one interpretation according to (Lee and Park 2015). It can be seen that this inconsistency is worse for the zero–one interpretation. However, it should be noted that the inconsistency of both interpretations decreases with progressing optimization, since the SIMP approach penalizes intermediate densities in the linear static response optimization and strives toward a zero–one design.

2.2.2 Reconstruction of the LSM mesh coordinates

As previously explained in Sect. 2.1, the linear static optimization in DiESL utilizes the deformed geometry from the analysis domain at given times ${t}^{i}$ to derive the LSMs. At this point, a problem arises that is specific to topology optimization: The nonlinear model employed in the analysis domain is incomplete in the sense that it is not capable of providing the complete deformation field in the entire design space. This is because all elements considered void are deleted during interpretation of the design densities (see previous section). This includes deletion of any free node that is no longer connected to an element. Furthermore, all nodes and elements in isolated areas are deleted. Hence, the displacements of the deleted nodes are not available after nonlinear analysis and the corresponding coordinates cannot be computed in the LSMs as illustrated in Fig. 7 for an incomplete FE mesh (top left) with deformation results (top right).

Fig. 7

Workaround for calculating the deformed mesh coordinates of the nodes deleted in the nonlinear dynamic analysis

We propose the following method to reconstruct the missing coordinates: A dedicated reconstruction FE analysis is executed in the design domain. This FE analysis uses the complete undeformed geometry in the design space to constitute the model. For each ESL time ${t}^{i}$, a subcase is created to solve the following problem:

$${\mathbf{K}}^{0}\widetilde{\mathbf{u}}\left({t}^{i}\right)={\mathbf{f}}^{{\varvec{i}}} ;\quad i=0, \ldots , {n}_{\mathrm{T}}-1$$

(11)

The vector $\widetilde{\mathbf{u}}\left({t}^{i}\right)$ contains both the known deformations transferred from the analysis domain and the missing coordinates of the deleted void nodes. This means the known displacements are applied as SPCs (prescribed displacements) in a linear static analysis (Fig. 7, bottom left). As a result, the remaining nodes are dragged along and plainly follow the prescribed deformation of the surrounding mesh (Fig. 7, bottom right). This way, all missing displacements can be computed in a single FE analysis where each ESL time ${t}^{i}$ is covered in a separate subcase. Note that the reconstruction FE run is executed as a topology optimization restart-run with 0 iterations using the densities of the previous cycle of all elements (see the coloring scheme in Fig. 7).

3 Summary of the DiESL approach for nonlinear dynamic response Topology Optimization

Summarizing, the DiESL approach solves the following surrogate optimization problem in each cycle:

$$\mathrm{min}\quad f(\mathbf{x},\Delta {\mathbf{u}}^{0}\left(\mathbf{x}\right), \ldots ,\Delta {\mathbf{u}}^{{n}_{\mathrm{T}}-1}\left(\mathbf{x}\right))$$

(12a)

$${\text{s}}.{\text{t}}.\quad g_{j} \left( {{\mathbf{x}},{\Delta }{\mathbf{u}}^{0} \left( {\mathbf{x}} \right), \ldots , {\Delta }{\mathbf{u}}^{{n_{{\text{T}}} - 1}} \left( {\mathbf{x}} \right)} \right) \le 0;\quad j = 1, \ldots , m$$

(12b)

$${\mathbf{x}}^{{\text{L}}} \le {\mathbf{x}} \le {\mathbf{x}}^{{\text{U}}} ;\quad {\mathbf{x}} \in {\mathbb{R}}^{n}$$

(12c)

where $\Delta {\mathbf{u}}^{i}$ is the solution of the FE equation of linear statics in ${\mathrm{LSM}}^{i}$:

$$\mathbf{K}(\mathbf{x},\mathbf{r}\left({t}^{i}\right))\Delta {\mathbf{u}}^{i}= {\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i} ;\quad i=0, \ldots , {n}_{\mathrm{T}}-1 .$$

(12d)

The difference-based equivalent static loads $\Delta {\mathbf{f}}_{\mathrm{DiESL}}^{i}$ are computed from the same equation using the given deformation fields from the analysis domain $\Delta \widetilde{\mathbf{u}}\left({t}^{i}\right)$ after reconstruction of the missing nodes:

$${\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i}=\mathbf{K}(\mathbf{x},\mathbf{r}\left({t}^{i}\right))\Delta \widetilde{\mathbf{u}}\left({t}^{i}\right) ;\quad i=0, \ldots , {n}_{\mathrm{T}}-1.$$

(12e)

The prescribed deformations $\Delta \widetilde{\mathbf{u}}\left({t}^{i}\right)=\widetilde{\mathbf{u}}\left({t}^{i+1}\right)-\widetilde{\mathbf{u}}\left({t}^{i}\right)$ are computed as the incremental deformation from time ${t}^{i}$ to time ${t}^{i+1}$. Here, $\widetilde{\mathbf{u}}\left({t}^{i}\right)$ contains two portions of displacements: Firstly, the solution of the nonlinear simulation in the analysis domain given by

$${\mathbf{M}}_{{{\text{NL}}}} \left( {{\varvec{\upchi}}} \right){\mathbf{\ddot{u}}}\left( t \right) + {\mathbf{C}}_{{{\text{NL}}}} \left( {{\varvec{\upchi}}} \right){\dot{\mathbf{u}}}\left( t \right) + {\mathbf{K}}_{{{\text{NL}}}} \left( {{{\varvec{\upchi}}},{ }{\mathbf{u}}\left( t \right)} \right){\mathbf{u}}\left( t \right) = {\mathbf{f}}\left( t \right);\quad \chi_{i} = \left\{ {\begin{array}{ll} 0 & {if\quad x_{i} \le \varepsilon_{{\text{v}}} } \\ {x_{i} } & {if\quad \varepsilon_{{\text{v}}} < x_{i} \le \varepsilon_{{\text{s}}} } \\ 1 & {if\quad x_{i} > \varepsilon_{{\text{s}}} } \\ \end{array} } \right.$$

(12f)

for the selected time steps ${t}^{i}$. Secondly, the displacements of all missing nodes approximated by the reconstruction analysis

$${\mathbf{K}}^{0}\widetilde{\mathbf{u}}\left({t}^{i}\right)=\mathbf{f};\quad i=0, \ldots , {n}_{\mathrm{T}}-1 .$$

(12g)

The vector $\widetilde{\mathbf{u}}\left({t}^{i}\right)$ therefore contains both the known deformations transferred from the analysis domain $\mathbf{u}\left({t}^{i}\right)$ as well as the missing coordinates of the deleted void nodes. This results in the overall procedure illustrated in Fig. 8 involving all necessary extensions of the DiESL procedure for topology optimization elaborated above.

Fig. 8

General optimization process of the DiESL method for nonlinear dynamic response topology optimization

3.1 Computation of displacement

During optimization of all LSMs using MMO, each LSM analysis yields incremental displacements $\Delta {\mathbf{u}}^{i}$. The total linear displacement of a node at time ${t}^{i}$ is used as an approximation of the respective nonlinear displacement. It can be computed recursively as

$${\mathbf{u}}^{i}={\mathbf{u}}^{i-1}+\Delta {\mathbf{u}}^{i-1}$$

(13)

where $\Delta {\mathbf{u}}^{i-1}$ is the solution of (12d) for ${\mathrm{LSM}}^{i-1}$. Accordingly, the cumulated displacements can be calculated as

$${\mathbf{u}}^{i}= {\mathbf{u}}^{0}+\sum_{j=0}^{i-1}\Delta {\mathbf{u}}^{j} .$$

(14)

In general, ${\mathbf{u}}^{0}=0$ applies because the undeformed geometry has not seen any deformations by definition. The accumulation is processed by the MMO, which administers all LSMs and accumulates their solutions $\Delta {\mathbf{u}}^{i}$ according to Eq. (14).

3.2 Implementation

The DiESL method’s overall program flow has been implemented in Python. It employs the commercial solver LS-DYNA (LSTC 2015) for nonlinear dynamic analysis in the analysis domain and OptiStruct (HyperWorks 2021) for linear static response optimization in the design domain. Because the linear static subproblem only approximates the actual problem, the optimized responses in the design domain often differ from those in the analysis domain. Thus, the convergence check has to be performed after the nonlinear dynamic analysis. Here, a small constraint violation is tolerated.

Three termination criteria have been used. The first criterion is that the design has to be feasible. This is implemented by the requirement that the maximum normalized constraint violation ${g}_{\mathrm{max}}$ has to be smaller than a specified limit ${\upvarepsilon }_{\mathrm{g}}>0$:

$${g}_{\mathrm{max}} \le {\upvarepsilon }_{\mathrm{g}} .$$

(15)

For all calculations ${\upvarepsilon }_{\mathrm{g}}=0.01$ has been used, which is sufficiently small such that all converged designs still can be considered feasible.

The second criterion is that the relative change of the objective function between two subsequent cycles $k-1$ and $k$ has to be smaller than or equal to a given value ${\varepsilon }_{\mathrm{f}}$:

$$\frac{\left|f({\mathbf{x}}^{\left(k\right)})-f({\mathbf{x}}^{(k-1)})\right|}{\left|f({\mathbf{x}}^{(k)})\right|}\le {\varepsilon }_{\mathrm{f}} .$$

(16)

Again, for all calculations, the value ${\varepsilon }_{\mathrm{f}}=0.01$ has been used. If this criterion is satisfied, the objective hardly changes and continuing the optimization is not worthwhile in most cases.

The third criterion is that the relative change of discreteness of the structure has to be smaller than a given value ${\varepsilon }_{\mathrm{d}}:$

$$\frac{\left|D({\mathbf{x}}^{\left(k\right)})-D({\mathbf{x}}^{(k-1)})\right|}{\left|D({\mathbf{x}}^{(k)})\right|}\le {\varepsilon }_{\mathrm{d}}$$

(17)

The discreteness index $D$ reported by OptiStruct is the mass fraction of all elements with a density above or equal 0.9 relative to the whole mass of the structure (HyperWorks 2021):

$$D\left(\mathbf{x}\right)=\frac{\sum_{i}^{{\mathrm{n}}_{\mathrm{E}}}{x}_{i}{V}_{i}, if \, 0.9\le {x}_{i}\le 1.0}{\sum_{i}^{{\mathrm{n}}_{\mathrm{E}}}{x}_{i}{V}_{i},}$$

(18)

where ${\mathrm{n}}_{\mathrm{E}}$ is the number of all elements in the design space and ${V}_{i}$ is the volume of the $i$th element. Here, $D=1$ corresponds to a zero–one design. For all calculations, the value ${\varepsilon }_{\mathrm{d}}=0.02$ has been used.

To account for the fact that the linear static subproblem is only an approximation of the actual nonlinear dynamic response optimization problem, the length of each inner loop optimization path is limited by introducing move limits. These are used to constrain the change of each design variable per iteration:

$$\begin{gathered} \hat{x}_{j}^{{{\text{U}},\left( l \right)}} = {\text{min}}\left( {x_{j}^{{\text{U}}} ,{ }x_{j}^{{\left( {l - 1} \right)}} + \vartheta^{\left( l \right)} \left| {x_{j}^{{\left( {l - 1} \right)}} } \right|} \right) \hfill \\ \hat{x}_{j}^{{{\text{L}},\left( l \right)}} = {\text{max}}\left( {x_{j}^{{\text{L}}} ,{ }x_{j}^{{\left( {l - 1} \right)}} - \vartheta^{\left( l \right)} \left| {x_{j}^{{\left( {l - 1} \right)}} } \right|} \right);\quad \vartheta \in \left[ {0,{ }1} \right]. \hfill \\ \end{gathered}$$

(19)

Parameter ${\vartheta }^{\left(l\right)}$ controls the size of the current move limits in iteration $l$. The initial value of $\vartheta$ in (19) is defined by the parameter ${\vartheta }_{\mathrm{ini}}$

$${\vartheta }^{(1)}={\vartheta }_{\mathrm{ini}} .$$

(20)

The value $\vartheta$ changes in each iteration. In OptiStruct, it cannot be further specified how $\vartheta$ is changing, since this is handled internally and no detailed explanation is given in the manual. At the start of a new cycle, the value $\vartheta$ is initialized from the value at the end of previous cycle. In this publication, the parameter ${\vartheta }_{\mathrm{ini}}=0.2$ has been used in all test problems. Since the move limits only limit the length of the optimization path per iteration, a second restriction is needed. The second parameter ${max}_{\mathrm{iter}}$ defines the maximum number of iterations (inner loop) per cycle (outer loop). For all examples shown below, the parameter $ma{x}_{\mathrm{iter}}=4$ has been used. This means, each cycle contains 4 iterations (unless the linear static response optimization converges before reaching 4 iterations).

Because DiESL does not start from a single undeformed initial model but from deformed structures related to the different ESL times ${t}_{i}$, it may happen that the linear static response optimization does not pass the initial element quality check due to excessively deformed elements and thus poor element quality. In order to realize a robust application of DiESL, an automated repair mechanism for the mesh of the affected $\mathrm{LSM}$s has been developed by deleting the distorted elements. This elements deletion is not permanent but is applied to the affected $\mathrm{LSM}$s in the current cycle only. Every new cycle starts with all elements in all $\mathrm{LSM}$s.

Note that time dependent responses (e.g., intrusions) are only checked at the selected ESL times. Consequently, it is essential here to define an adequate number ${n}_{\mathrm{T}}$ of ESL times to avoid inaccuracy due to insufficient time resolution. However, because each ESL time corresponds to an LSM, and each LSM increases the computational effort in the design domain, the number of ESL times should be limited (inner loop).² To address this balancing act, the positions of all ${n}_{\mathrm{T}}$ ESL times ${t}^{i}$ are selected adaptively in each cycle such that an appropriate response curve is fitted by a polygonal line, where the ESL times are the breakpoints. This way the ESL times should be placed at points in time at which nonlinearities are dominant. In this paper, a beam structure subjected to an impact is examined. The contact–force curve between impactor and beam was chosen as response curve to determine the ESL times because it is considered a good indicator for the occurrence of nonlinearities. For a more detailed description of the procedure, refer to Triller et al. (2022).

The overall flow scheme explained before is implemented as follows:

Step 1:	Set initial design variables and parameters: $k=0$,${{\varvec{\upchi}}}^{\left(k\right)}={\mathbf{x}}^{\left(k\right)}$,${\varepsilon }_{\mathrm{v}}$,${\varepsilon }_{\mathrm{s}}$,${\upvarepsilon }_{\mathrm{g}}$,${\varepsilon }_{\mathrm{f}}$,${\varepsilon }_{\mathrm{d}}$,${\vartheta }_{\mathrm{ini}}$,$ma{x}_{\mathrm{iter}}$,${n}_{\mathrm{T}}$
Step 2: Step 3:	Perform nonlinear dynamic analysis with ${{\varvec{\upchi}}}^{(k)}$ Determine the position of all ESL times by fitting an appropriate response, e.g., contact force
Step 4:	If $k>0$, check convergence criteria: If Eqs. (15), (16), (17) are satisfied then terminate the process
Step 5:	If $k>0,$ reconstruct missing coordinates by calculating the displacement field $\widetilde{\mathbf{u}}\left({t}^{i}\right)$ including all nodes for all selected time steps ${t}^{i}$
Step 6:	Calculate the incremental displacements $\Delta \widetilde{\mathbf{u}}\left({t}^{i}\right)$ and the node coordinates $\mathbf{r}\left({t}^{i}\right)$ of all LSMs for all selected time steps ${t}^{i}$
Step 7:	Check the element-quality of each LSM FE mesh. If check was not successful, delete distorted elements in respective LSM
Step 8:	Calculate the incremental equivalent static loads ${\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i}$
Step 9:	Solve the linear static response optimization problem with the incremental equivalent static loads ${\Delta \mathbf{f}}_{\mathrm{DiESL}}^{i}$
Step 10:	Interpret the resulting design variables ${\mathbf{x}}^{\mathbf{*}(\mathrm{k})}$ and update the design variables ${{\varvec{\upchi}}}^{(k)}$ in the analysis domain, increment $k$ by 1 and go to step 2

4 Test problem

In this section, the previously described approach for topology optimization is tested using a simple beam structure subjected to an impact. As illustrated in Fig. 9, the beam structure is clamped at both ends in all 6 degrees of freedom using single-point constraints (SPC). A cylindrical rigid pole impacts the structure in the middle with the initial velocity ${v}_{0}$. The impactor’s translational degrees of freedom in $x$- and $z$-direction as well as all its rotations are locked. In order to decrease computational costs, symmetry conditions are applied and only a quarter of the original beam is used in the simulation. This problem is similar to one used by Patel to verify the HCA optimization scheme (Patel 2007). Three parameter sets’ initial velocity ${v}_{0}$ and mass ${m}_{i}$ of the impactor are studied for the purpose of examining the influence of inertia effects:${(v}_{0},{m}_{i})=\left\{(10 \frac{\mathrm{m}}{\mathrm{s}}, 65.7\mathrm{ kg});(40 \frac{\mathrm{m}}{\mathrm{s}}, 65.7\mathrm{ kg});(150\frac{\mathrm{m}}{\mathrm{s}}, 4.69\mathrm{ kg})\right\}$. For the last set, the impactor’s mass is reduced in order to keep its kinetic energy the same compared to the set with ${v}_{0}=40\frac{\mathrm{m}}{\mathrm{s}}$. Both surface contact between the beam structure and the impactor and self-contact for the beam are defined in LS-DYNA. In the LSMs, no contact is defined because this leads to reduced numerical stability. Hence, the impactor is not present in the linear static models and the impactor’s intrusion in OptiStruct has to be approximated. This is done by averaging the displacements in y-direction of one column of structural nodes in the impact zone (i.e., along z-direction in the middle of the whole beam). The beam structure is made of aluminum (Young’s modulus $E=70 \mathrm{GPa}$, density $\rho =2700 \mathrm{kg}/{\mathrm{m}}^{3}$, number of nodes = 9664), and piecewise linear material behavior is applied (Fig. 9 right). Twenty ESL times are used resulting in 20 different FE-models. When performing multimodel topology optimization with OptiStruct, minimum member size control is used by default and cannot be turned off. Here, the default value of 3 times the average element size is used (30 mm).

Fig. 9

Nonlinear FE model of the beam exposed to an impact (left); piecewise linear material model (right)

The objective of the optimization problem is to minimize the intrusion of the pole in y-direction $d\left(\mathbf{x}\right)$ while constraining the mass ${m}_{b}$ of the beam structure. Mathematically, the problem can be written as:

$${\text{min }}f\left( {\mathbf{x}} \right) = d\left( {\mathbf{x}} \right)$$

$${\text{s}}.{\text{t}}.\quad m_{b} \left( {\mathbf{x}} \right) \le 4.33{\text{ kg}}$$

The optimizer is initialized using a homogeneous density distribution of ${x}_{i}=0.2$ such that the mass constraint is active (i.e.${m}_{b}\left({\mathbf{x}}^{0}\right)=4.33\mathrm{ kg}$). The optimization problem is solved for each of the given sets of initial velocity and impactor mass ${m}_{i}$ individually. Afterward, the results are compared both visually and by means of a cross validation, where each optimal structure is exposed to the remaining other load cases, in order to check the plausibility of the results.

The history of optimization and subsequent interpretation is exemplified for ${v}_{0}=40\frac{\text{m}}{{\text{s}}}$. In Fig. 10, the optimization history is shown. The objective function and the maximum normalized constraint violation are plotted in the left diagrams as function of iterations. Blue circles show the values of each linear static response optimization per iteration and red circles mark values obtained from the nonlinear analysis in each cycle. In the right plot of Fig. 10, the convergence criteria are plotted over cycles. The overall convergence behavior is relatively smooth, and all three convergence criteria are fulfilled after 26 cycles. Note that the constraint violation is zero at the start and at the end of the optimization. It increases to a maximum of 12% in cycle 3 and then gradually reduces. This behavior is a side effect of using the TOPDISC parameter in OptiStruct.

Fig. 10

Objective function and maximum relative constraint violation over iterations (left) and convergence criteria over cycles (right) using DiESL and ${v}_{0}=40\frac{\text{m}}{{\text{s}}}$

Figure 11, left, illustrates the container model as obtained by the optimization. As the final discreteness value does not reach 100% (see Fig. 10, right bottom), the container model still contains elements with intermediate densities, most prominently a connection between the front part of the structure’s impact zone and the rear part (see Fig. 10, left top, dashed ellipse). In order to identify a zero–one structure with similar performance as the container model, two different strategies were tested. For both strategies, a 0–1 design is created and any intermediate densities are eliminated by setting the density thresholds ${\varepsilon }_{\mathrm{v}}={\varepsilon }_{\mathrm{s}}$. In the next step, we use bisection to determine the value of the single variable $\varepsilon ={\varepsilon }_{\mathrm{v}}={\varepsilon }_{\mathrm{s}}$ by postulating that one of the two conditions is fulfilled:

• 1. The value of the objective functions of the 0–1 model and the container model must be equal

• 2. The mass constraint of the 0–1 model and the container model must be equal

Fig. 11

Container model of converged cycle 26 for ${v}_{0}=40\frac{\text{m}}{{\text{s}}}$ (left) as isometric (top) and top view (bottom); corresponding zero–one interpretations (right) using “same objective” (top) and “same constraint” (bottom) strategies

The reason for this procedure is that it is usually not possible to find a unique $\varepsilon$ value for a design that fulfills both conditions. In this sense, our procedure leads to designs on the extremes of possible solutions. If both designs are identical in a topological way then it is a hint that the solution is unique and robust. This is the case for the resulting zero–one designs that are illustrated in Fig. 11 right and denoted in Table 1. The appearance and performance of both interpretations are very similar and no significant tradeoff between the interpretations has to be made. This also holds for the other two parameter sets of initial velocity ${v}_{0}$ and mass ${m}_{i}$.

Table 1 Optimization results using DiESL and corresponding interpretations

Table 1 lists the optimization results for all three parameters sets and for all three optimal designs for each set (container model as well as zero–one interpretations by “same objective” and “same constraint” strategies). Due to the interpretation process described in Sect. 2.2.2 and the deletion of elements smaller than ${\varepsilon }_{\mathrm{v}}$, the mass of the container models is considerably smaller than the defined upper bound. Column $D\left({\mathbf{x}}^{\mathbf{*}}\right)$ reports the discreteness calculated by OptiStruct for the container model, and it is set to 1 for the zero–one interpretations by definition. From the examples tested, we conclude that the introduced procedure for topology optimization yields zero–one designs that can easily be interpreted. In the following, we will use the container models in illustrations and comparisons because their performance is extremely similar to their respective zero–one interpretations.

Table 2 shows the results of the cross validation of the derived optimal structures. In this study, we evaluated the performance of each optimal container model when loaded under the other remaining initial velocity and mass conditions. It can be seen that each container model performs best for its respective load case (bold), e.g., for the initial velocity $v_{0} = 10 \frac{{\text{m}}}{{\text{s}}}$, the design that has been obtained for this velocity has the lowest intrusion 13.2 mm compared to the other two designs that were obtained for other initial velocities.

Table 2 Cross validation: resulting intrusions $d\left( {{{\varvec{\upchi}}}^{*} } \right)$ for the three optimal structures (container models) shown in Fig. 13 subjected to each of three initial velocities and masses

In the following, the optimal structures of all three load cases are discussed and compared visually. For comparison, the results of a linear static load case are shown additionally. As shown in Fig. 12, the pole is removed and replaced by a static force that is imposed on the middle of the original contact zone (blue line). Furthermore, rigid elements (RBE2) are defined in the contact zone to distribute the loading force across the entire zone (red area). Based on this load case, the linear static response optimization problem is solved according to the previously defined optimization problem but without employing the ESL algorithm. Figure 13 illustrates the results of the linear and all nonlinear dynamic load cases as an iso-surface visualization of the container models. Each result is displayed as reconstructed full model in an isometric view (left) as well as three projections viewed from front, top, and bottom (right, top to bottom). The linear static result mainly consists of compression-loaded diagonal connections between the impact zone and the rear end of the clamping (see Fig. 13, upper left, dashed ellipse). The nonlinear dynamic load cases can be interpreted as evolutions from this design: with increasing impactor velocity, these compression-loaded connections first become smaller and then vanish for $v_{0} = 40\frac{{\text{m}}}{{\text{s}}}$ and $v_{0} = 150\frac{{\text{m}}}{{\text{s}}}$. In contrast, the tension-loaded diagonal connection between the rear end of the impact zone and the front of the clamping (see Fig. 13, lower right, dotted ellipse) seems to become increasingly more important. Furthermore, it can be seen that for $v_{0} = 150\frac{{\text{m}}}{{\text{s}}}$, more mass is distributed in the center of the structure and in the impact zone. This can possibly be explained by the increasing influence of inertia effects using $v_{0} = 150\frac{{\text{m}}}{{\text{s}}}$. With increasing mass in the contact zone, the structure’s tendency to resist accelerations increases. A similar trend has been observed by Ivarsson et al. (2018) optimizing a 2D structure by employing the adjoint method. However, the computational effort for this significantly exceeds that of the DiESL method.

Fig. 12

Linear static load case for comparison of DiESL and ESL results for nonlinear dynamic response optimization

Fig. 13

Resulting container model in iso-surface visualization ($\chi_{iso} = 0.4)$ for linear static load case (upper left) and using DiESL: $v_{0} = 10\frac{{\text{m}}}{{\text{s}}}$ (upper right), $v_{0} = 40\frac{{\text{m}}}{{\text{s}}}$ (lower left), and $v_{0} = 150\frac{{\text{m}}}{{\text{s}}}$ (lower right)

For comparison, the standard ESL method is applied to some of the load cases discussed before. The same container approach is employed in the analysis domain. As described before, ESL uses the undeformed mesh geometry for each auxiliary load case. Therefore, no MMO has to be performed. For the same reason, the missing coordinates of nodes in a deformed mesh geometry in the analysis domain do not have to be reconstructed according to Sect. 2.2.2.

The iso-surface visualization of the container models obtained with the ESL method is given in Fig. 14, and the final objective values are listed in Table 3. Generally, it can be seen that ESL needs fewer cycles to converge in comparison with DiESL. However, the discreteness of the derived designs is lower for both load cases compared to DiESL.

Fig. 14

Resulting container model in iso-surface visualization ($\chi_{iso} = 0.4)$ using ESL for $v_{0} = 10\frac{{\text{m}}}{{\text{s}}}$ (left) and $v_{0} = 40\frac{{\text{m}}}{{\text{s}}}$ (right)

Table 3 Optimization results using ESL

Both ESL results are dominated by the previously described compression-loaded connection of the linear static load case. Thus, the difference to DiESL for $v_{0} = 10\frac{{\text{m}}}{{\text{s}}}$ is comparably small. This is also reflected by the resulting objective value, which is only slightly better than for DiESL. Since the impactor’s intrusion and therefore the beam’s deflection are relatively small for this load case, DiESL obviously cannot draw a benefit from using the deformed mesh and from following the displacement path incrementally. This is different for a higher velocity ($v_{0} = 40\frac{{\text{m}}}{{\text{s}}}$) where the amount of deformation is increased. In this case, the intrusion of the ESL result is almost double the corresponding DiESL result (Fig. 15) because the compression-loaded members buckle. Obviously, ESL is not able to handle highly nonlinear problems and related inertia effects in a proper way whereas DiESL is able.

Fig. 15

Deformed container model in iso-surface visualization ($\chi_{iso} = 0.4)$ using ESL (left) and DiESL (right) for $v_{0} = 40\frac{{\text{m}}}{{\text{s}}}$

5 Conclusions and outlook

In this paper, a novel procedure for nonlinear dynamic response topology optimization has been presented. The DiESL method has been extended to topology optimization. For this purpose, the SIMP approach is utilized to relate the design variables to all relevant properties of an elasto-plastic material, like Young’s modulus, yield stress, and strain hardening modulus. To prevent mesh distortion problems, a smaller penalty exponent has been used in the analysis domain than in the design domain. Furthermore, intermediate densities derived in the design domain are transferred unchanged to the analysis domain, in order to enable a continuous and smooth change of designs from cycle to cycle.

The proposed method has been tested using a simple beam structure impacted by a rigid pole. The pole’s initial velocity and mass have been varied in order to examine their influence on the resulting optimized structures. For all load cases, the DiESL method yields discrete and thus easy to interpret designs. A cross validation of the optimized structures, where each optimal structure is exposed to the remaining other load cases, has been conducted. Each optimized structure performs best for its respective load case, which confirms the plausibility of each result. Additionally, the resulting structures have been compared and discussed visually. For that purpose, the results of a linear static load case have been presented as well. It turns out that the linear static result is most similar to the optimized structure of the nonlinear dynamic problem for the smallest initial velocity. The optimal structure changes significantly if the initial velocity is increased. For the highest velocity, mass is accumulated in the impact zone, reflecting the increasing influence of inertia effects. We therefore conclude that the DiESL method is able to handle inertia effects.

Moreover, the standard ESL method has been applied to some of the load cases. For both small and high velocities, the resulting structures are dominated by the characteristics of the result of the linear static load case. This indicates that ESL is not capable of handling inertia effects. For high velocities, the DiESL result outperforms the ESL result by far. Furthermore, DiESL outperforms ESL in terms of discreteness of the optimized designs and thus yields easier to interpret the structures.

For future investigations, further practice-relevant examples should be examined, involving other crash relevant responses like accelerations or contact forces. For the latter, a reliable approach must be developed to handle contact forces in combination with DiESL.