Latest developments in node-based shape optimization using Vertex Morphing parameterization

Abstract

The latest updates on the Vertex Morphing technique for large optimization problems are shown in this work. Discussions about the challenges of node-based shape optimization in academic and industrial applications are included. The adaptive Vertex Morphing technique is demonstrated, which is easy to use in practice and allows the full exploitation of the potential of node-based shape optimization to find new designs in large-scale applications. We also show an efficient optimization method to handle different physical responses with many geometrical constraints. A state-of-the-art example of industrial importance supports the work.

1 Introduction

In many industrial applications, adjoint-based shape optimization application with response functions, computed by computational fluid dynamics (CFD) analysis, has become an important analysis tool in the design process of the products (Papoutsis-Kiachagias and Giannakoglou 2014; Müller et al. 2021). In shape optimization, the aim is to find an optimal shape of the model regarding a physical quantity, for instance, drag force.

The choice of the design parameters (parameterization) plays a key role in successful results in realistic optimization problems. There are different methods and strategies to parameterize the design space of large problems. There are two major groups of parameterization techniques: CAD and CAD-free (or parameter-free) methods. CAD methods control the position of “many” surface points based on “few” CAD parameters(Xu et al. 2014; Agarwal et al. 2018). In contrast, CAD-free methods use the surface nodes directly as the design parameters (Firl and Bletzinger 2012; Stück and Rung 2013; Bletzinger 2017; L. A. G and Guillaume 2018). CAD-free methods have difficulties attaining the final shape without rough/noisy boundaries (Stück and Rung 2011). In this regard, several techniques are proposed to increase the regularity of the shape update (Stavropoulou et al. 2014; Kröger and Rung 2015).

Vertex Morphing is a successful CAD-free technique introduced by Hojjat et al. (2014) and Bletzinger (2014), Bletzinger (2017). The main characteristics of the technique are as follows:

• 1. The method uses the filtering operation to generate smooth design updates and control the surface mesh quality.

• 2. No extra optimization model is needed. The Finite Element (FE) model is used directly. The Vertex Morphing parameterization is easy to set up for complex models and geometries, and it is a good alternative to well-known parameterization strategies (Baumgärtner et al. 2016);

• 3. The Vertex Morphing method can be successfully integrated into the multi-disciplinary optimization framework. An example of such implementation can be found in Ghantasala et al. (2021), Baumgärtner (2020);

• 4. Vertex Morphing parameterization provides a rich design space, allowing new solutions to be explored. (Bletzinger 2017);

• 5. Different design constraints, such as symmetry, axis-symmetry, or damped (non-design) zones, can be consistently integrated into the parameterization. This ensures the satisfaction of the given requirements without using advanced constrained optimization algorithms (Najian Asl 2019).

The main parameter to adjust Vertex Morphing is a filter radius (“filtering intensity”). It is an additional design parameter to modify generated shape update modes and define shape features of the initial geometry that will be preserved. In the work of Hojjat et al. (2014), it has been shown that the optimizer converges to different target local optimums by adjusting the filtering radius. The role of the filtering radius can be defined as follows:

• 1. The optimizer is driven to a certain local minimum by choice of the filter radius;

• 2. The filter radius directly controls the final shape (smoothness, wavelength);

• 3. All the initial features of the geometry which are smaller than the filter radius are preserved;

• 4. A priori the “good” size of the filter radius is unknown;

• 5. During the optimization process, the large deformations of the design surface can change the surface mesh size dramatically. Therefore, the filter radius can become too small concerning surface mesh size, and it will cover only a few layers of the elements. As a result, the consequential following shape updates are not smooth anymore. In contrast, the filter radius may become too large if the model shrinks. Hence, the big parts of the model move as a rigid body.

The adaptive Vertex Morphing is proposed to address the challenges mentioned above. The adaptive Vertex Morphing method computes the smallest radius required for appropriate filtering on each node. As a result, adaptive Vertex Morphing can be used without any user’s input, or it can correct the given user’s input. Additionally, in contrast to the initial method, in adaptive Vertex Morphing, the user can provide not only “global” radius size but also “local” sizes. In this paper, CFD shape optimization problems are solved using the adaptive Vertex Morphing technique.

Structural optimization problems with Vertex Morphing parameterization require robust and efficient optimization methods to handle many design variables and different physical and geometric constraints. Also, the efficient line search strategy can improve the computation of descent improvement of the objective function and keep the design feasible. Typically, a structural optimization problem with Vertex Morphing has the following properties:

• 1. A large number of design variables. The “usual” number is $1e4 - 1e6$. Therefore, the sensitivities of the response functions have to be computed using adjoint sensitivity analysis (Najian Asl 2019);

• 2. For typical engineering optimization tasks, computing the response values of the objective and constraint functions requires numerically expensive CFD (or structural) analysis. Therefore, optimization methods must be robust and efficient to reduce the number of evaluations of response values as much as possible;

• 3. The objective and constraints functions are typically highly non-linear (Firl and Bletzinger 2012);

• 4. The sensitivities of the response functions have to be scaled due to the different physical units (m, kg, N, etc.). Therefore the information regarding the magnitude of the raw sensitivities can be lost;

• 5. Due to a large number of design variables, geometric constraints and design bounds lead to a large number of constraints. An efficient aggregation method may be required (Geiser et al. 2021);

• 6. Line search techniques can be numerically expensive or non-accurate for highly non-linear functions. In practical application, a constant step size may be preferred.

Generally, a constraint shape optimization problem is formulated as follows:

$$\begin{aligned} \begin{aligned} \mathbf{minimize} : f(\varvec{x}) \\ \textbf{design variables}: \varvec{x} \\ \textbf{subject to}: \\ g_j(\varvec{x}) \le 0 \text {, where } j = 1..n_g \\ h_k(\varvec{x}) = 0 \text {, where } k = 1..n_h \\ \end{aligned} \end{aligned}$$

(1)

where $\varvec{x}$ represents design parameters that define the design surface, $n_g$ and $n_h$ are numbers of inequality ($g(\varvec{x}) \le 0$) and equality ($h(\varvec{x}) = 0$) constraints.

The algorithms that have been successfully used with Vertex Morphing parameterization are gradient projection (Najian Asl et al. 2017; Ertl 2020), the relaxed gradient projection (RGP) method (Antonau et al. 2021), and the modified search direction method (Chen et al. 2019; Chen 2021). All methods are first-order direct optimization methods that can find good search directions to improve the objective functions and handle constraints.

In the mentioned works, a constant step size has been used. However, the good step size is an unknown a priori and may lead to poor performance or higher computational cost. There are various methods to calculate the exact or approximate step length to find a minimum of the objective function or sufficient reduction along the descent search direction. For instance, Cauchy methods may require calculating the Hessian matrix, which is not always available or very expensive to compute (Zhou et al. 2006). Besides, Armijo’s backtracking schemes try several step sizes until the acceptance criteria are satisfied (Ahookhosh and Ghaderi 2017). In large CFD optimization problems, additional functional evaluation may excessively increase the computational cost of each optimization iteration.

On the other hand, the Barzilai–Borwein (BB) method (Barzilai and Borwein 1988) attracts many research groups because of its simplicity and surprising efficiency in unconstrained optimization problems. The method’s main advantage is that it does not require any costly computational operations to approximate the step size. There are various modifications of the technique: Projected Barzilai–Borwein method (Dai and Fletcher 2005), Adaptive Barzilai–Borwein method (Zhou et al. 2006), Stabilized Barzilai–Borwein method (Oleg Burdakov and Dai 2019), and accelerated Barzilai–Borwein method (Huang et al. 2022).

The Quasi-Newton Barzilai–Borwein (QN–BB) method is introduced in this work. In contrast to the original and modified versions, the QN–BB method computes each design variable’s step size independently. Therefore, each design parameter has its step size based on the local sensitivity information. The QN–BB method has been coupled with the relaxed gradient projection method (QN–BB–RGP). The QN–BB–RGP algorithm uses a linear approximation of the constraints to compute feasible design updates. It allows for solving efficiently large optimization problems with localized constraints. Additionally, in this work, the maximum-value aggregation technique is introduced. It combines a large number of nodal constraints into one, where each node has an individual correction based on the nodal constraint value. The QN–BB method was first time shown at Eccomas Congress 2020 & 14th WCCM; the record of the presentation talk can be found under the link (https://slideslive.com/38944933).

The paper is structured as follows: First, the Vertex Morphing method is reviewed, and the proposed adaptive Vertex Morphing is introduced. Then the QN–BB–RGP method is described with all its components: QN–BB, RGP, and the max-value aggregation technique. The following sections describe the academic and industrial optimization problems and show a detailed analysis of the performance of the proposed methods. Finally, conclusions are drawn from the work.

2 Vertex Morphing

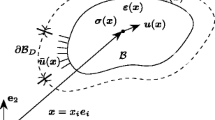
Without appropriate regularization measures, node-based shape optimization produces high-frequency, noisy geometries. Therefore, one means of choice is to subject the raw geometry to smoothing using filters. In the context of Vertex Morphing, thus, the structural geometry $\varvec{x}$ is indirectly controlled by a control field $\varvec{s}$ and a kernel or filter function A, for example, on the surface $\varGamma$ with surface coordinates ($\xi , \eta , \zeta$):

$$\begin{aligned} \varvec{x}(\xi _0, \eta _0, \zeta _0) = \int _{\varGamma } {A} (\xi - \xi _0, \eta - \eta _0, \zeta - \zeta _0)\varvec{s}(\xi , \eta , \zeta ) d\varGamma \end{aligned}.$$

(2)

Vertex Morphing belongs to the direct filtering techniques as opposed to the indirect ones, such as Sobolev smoothing (Jameson 1988, 1995; Pironneau 1974), where the filter is applied to the actual geometry $\varvec{x}$. There is great freedom to choose kernel functions. For the choice of simple polynomials on compact support (including a piecewise linear hat function and splines), it is shown that Vertex Morphing is identical to a generalized CAD-based approach with indirectly defined spline base functions (Bletzinger 2017). When taking the Gauss bell-shaped distribution function, the technique has additional equivalent properties compared to indirect smoothing (Stück and Rung 2011).

After discretization of the structural geometry $\varvec{x} = [x_1^x, x_1^y, x_1^z, ..., x_n^x, x_n^y, x_n^z]$ and control function $\varvec{s} = [s_1^x, s_1^y, s_1^z, ..., s_m^x, s_m^y, s_m^z]$ by standard techniques as the finite element method, Vertex Morphing appears as follows:

$$\begin{aligned} \varvec{x} = \varvec{A} \varvec{s} \end{aligned},$$

(3)

where $\varvec{x}$ is the vector of coordinates of nodes where the spatial coordinates in $x-$, $y-$, and $z-$ direction of a node are arranged sequentially. $\varvec{A}$ is the filter operator matrix, and $\varvec{s}$ is the vector of discrete control field parameters, again arranged sequentially. The most straightforward approach is to add control parameters to every node, i.e., vertex, of the finite element model, which motivates the term “Vertex Morphing.”

The entries ${A}_{ij}$ of $\varvec{A}$ reflect the filter effect as the interaction between two different nodes i and j, their spatial position vectors $x_i$ and $x_j$, and their Euclidean distance $\left|x_i - x_j\right|$. For the case of the Gauss distribution as kernel and approximating integration by summation it holds:

$$\begin{aligned} \begin{aligned} A_{ij} = \frac{F(x_i, x_j)}{sum} \\ sum = \sum _j F(x_i, x_j) \end{aligned} \end{aligned},$$

(4)

where

$$\begin{aligned} F(x_i, x_j) = {\left\{ \begin{array}{ll} \exp \left\| {(- \left|x_i - x_j\right|^2 / 2 r^2)} \right\|&{} \left|x_i - x_j\right| < r \\ 0.0 &{} \left\| {x_i - x_j} \right\| \ge r \end{array}\right. } \end{aligned}$$

(5)

and r is the filter radius. Different from the initial version of Vertex Morphing (Hojjat et al. 2014), the same filter operations are applied of any item assigned to a discrete node, which are in particular each component of the spatial coordinates. As a consequence, the entries $\varvec{A}_{ij}$ appear as scalar matrices in $\varvec{A}$:

$$\begin{aligned} \begin{aligned} \varvec{A}_{ij} = A_{ij} * \varvec{I} \\ \varvec{A}=\begin{bmatrix} \varvec{A}_{11} &{} \dots &{} \varvec{A}_{n1}\\ \vdots &{} \ddots &{} \vdots \\ \varvec{A}_{1m} &{} \dots &{} \varvec{A}_{nm} \\ \end{bmatrix} \end{aligned} \end{aligned},$$

(6)

where I is an identity matrix 3 by 3. This technique is equivalent to the finite element method interpolating every nodal coordinate by the same shape function assigned to the individual node. Consequently, Vertex Morphing simultaneously controls the shape growth in normal surface direction and the mesh adaptation tangential to the surface without further considerations.

3 Adaptive Vertex Morphing

This section introduces the AVM technique and its properties: computation of radius field, smoothing process, and radius control by the user.

3.1 Radius field computation

The size of the radius plays a crucial role in the filtering process. If the radius does not cover enough elements, the final design may not be smooth and have kinks and poor quality surface mesh. Even if we choose a suitable radius size for the initial model, after n optimization iterations, the model can be deformed dramatically, and the radius size becomes inappropriate. Therefore, it is essential to check if the radius has a proper size during optimization. The adaptive Vertex Morphing computes the minimum required radius for every node during the optimization process. Consequently, it can adapt the radius size for each node to keep the filtering property. The required radius for node k is computed based on the distances to the neighboring nodes j as follows:

$$\begin{aligned} r_k = C \cdot \max _j(d_j) \end{aligned},$$

(7)

where $d_j = \left\| \varvec{x}_k - \varvec{x}_j \right\|$ is a distance between node k and j. The constant C can be understood as a number of element layers the filtering includes. From various numerical experiments, the good values for C are in the range [4, 10] (Firl et al. 2012; Hojjat et al. 2014; Stavropoulou et al. 2014).

Firl et al. (2012) show that any filtering introduces the filtering error: the gap between the optimal shape and the “true” optimum. The error disappears, when $r \rightarrow 0$. The adaptive Vertex Morphing method allows finding the solution with the smallest possible radius for the given mesh. Hence, it generates the smallest filtering error. Figure 1 shows the computed radii (radius field) by eq. (7) with $C = 7$ as a field, where the value refers to the filter radius at the node.

Fig. 1

Individual radii for each node of the mesh, orange—radius of the big element, blue—radius of the small element

3.2 Radius field smoothing process

In the above-computed radius field, the radii size at neighboring nodes varies a lot because the plate has an unstructured mesh. As it is shown in Geiser (2017), the Vertex Morphing generates a gap in the shape update on the border between two different radii. The proposed solution is to have a smooth transition in space from one radius size to another. The adaptive Vertex Morphing method smoothens the computed radius field from eq. 7 so that the radii at the neighboring nodes have similar radii (smooth transition). In this work, an adaptive Vertex Morphing mapping operator $\varvec{A}$ with linear kernel function and local radius size has been applied to smooth the radius field, Algorithm 1.

In the smoothing process, it is required to do multiple filtering iterations because the initial radius field is discrete. The number of smoothing iterations can vary for different examples. Figure 2 compares the raw and smoothed radii for different $N_{iter}$ numbers. The results can be summarized as follows:

• 1. In case $N_{iter} = 0$, there is no smoothing of the radius field, Fig. 2a, b;

• 2. In case $N_{iter} = 1$, the radius field is non-smooth in the region with higher radius values, Fig. 2c;

• 3. In case $N_{iter} = [2, 10]$, the radius field is smooth. If the $N_{iter}$ number increases, the high radius values diffuse into the regions with low radius values, Fig. 2d, e;

• 4. In case $N_{iter} = 100$, the radius field has very small changes in the values [0.54, 0.6], almost a constant field, Fig. 2f. If $N_{iter} \rightarrow \inf$, the radius fields converges to a constant field.

Fig. 2

Radius field comparison with respect to $N_{iter}$ smoothing iterations

3.3 Local and global radius control

In the initial and adaptive Vertex Morphing methods, the filtering radius size is considered as an additional design parameter that strongly affects the final shape. Minimal required radii computed by the adaptive Vertex Morphing method are not always the best choice. Due to manufacturing limitations, weak performance, or unaesthetic design, one may need to change the radius size to find a new design in the next optimization process. The adaptive Vertex Morphing technique allows setting a global or local minimum radius. Hence, equation 7 is modified as follows:

$$\begin{aligned} r_k = \max (C \cdot \max _j(d_j), r_{min, k}) \end{aligned},$$

(8)

where the $r_{min, k}$ is a given minimal radius for a node k. Figure 3 shows how the “minimum radius” ($r_{min, k} = 0.3$) modifies the resulting radius field.

Fig. 3

Comparison of radius fields: left—original, right—with minimum required radius, ($r_{min, k} = 0.3, N_{iter} = 10, C =7$)

The modification in equation (8) extends the design features of the adaptive Vertex Morphing method. On one side, the adaptive Vertex Morphing method is straightforward to use, and on the other side, it is very powerful and flexible parameterization. The workflow with adaptive Vertex Morphing parameterization with a new unknown model is as follows:

• 1. Run the first cycle of the optimization using only the computed radius field without any additional input for the filter radius.

• 2. Based on the outcoming results from the first run, adjust the sizes of the filtering radius in the regions where the final shape modes are not suitable or lead to bad performing design.

The adaptive Vertex Morphing method increases the mesh dependency of the parameterization because if the finite element model is discretized with a new mesh, the minimum required radii will also change (see eq. 7). If the optimization problem is convex, the final shape will always converge to an unique solution, independent of the filter radius constant or variable sizes. In contrast, if the optimization problem is non-convex, the choice of the filter radius will guide the optimizer to the different local optima; hence, the adaptive Vertex Morphing method may find different local minima for different discretizations. The interested reader is referred to Firl et al. (2012), Hojjat et al. (2014) to peruse mesh-independency in FE-based parameterizations.

3.4 Simple 3D plate example

The 3D plate example is prepared to demonstrate the influence of the computed radius field on the design surface’s quality. The discrete sensitivity field has been computed and used as a sensitivity field on the plate geometry (Fig. 1). 10 optimization iterations of the steepest descent algorithm with constant step size have been applied to find the deformed plate. The sensitivity field is defined as follows:

$$\begin{aligned} \nabla f(x_i) = \varvec{n}_i A_{i} \end{aligned},$$

(9)

where $n_i$ and $A_i$ are the nodal normal and area, respectively. The steepest descent shape update is computed as follows:

$$\begin{aligned} \varDelta \varvec{x} = \varvec{A} \left(\frac{\alpha }{\left||\varvec{s}\right|| } \varvec{s}\right) \end{aligned},$$

(10)

where $\varvec{A}$ is an adaptive Vertex Morphing filtering matrix, which is computed using the smoothed radius field.

In Figs. 4 and 5, the deformed plate is shown with respect to different values of C and $N_{iter}$. If $N_{iter} = [0,1]$, the radius field is non-smooth and the deformed plate has rough surface with kinks. In contrast, if $N_{iter} \ge 2$, the radius field is smooth, and the deformed plate has a smooth surface. These results correlate with the statements from Geiser (2017). Similarly, if $C<4$, the filter radius size covers only a few elements; hence the adaptive Vertex Morphing does not compute smooth shape change.

Fig. 4

Deformed plate with respect to different $N_{iter}$ numbers

Fig. 5

Deformed plate with respect to different C constant

4 Quasi-Newton relaxed gradient projection method

This section introduces the Quasi-Newton Barzilai–Borwein and Quasi-Newton relaxed gradient projection methods and max-value aggregation techniques.

4.1 Relaxed gradient projection method

The relaxed gradient projection method (RGP method) is a modification of a well-known Rosen’s gradient projection method (Rosen 1960, 1961). The main idea of the RGP algorithm is to use information regarding the values of the constraints from previous optimization iterations to compute a buffer (critical) zone around the constraint boundary and keep the constraint active if the value is inside the buffer zone. For convenience, the basic formulas are presented below. For more details, the reader should refer to Antonau et al. (2021).

The buffer coefficient $\omega ^{(i)}_{j}$ can be computed based on the constraint value $g_j(\varvec{x}^{(i)})$ and the buffer size $BS^{(i)}_j$:

$$\begin{aligned} \begin{aligned} \omega ^{(i)}_{j} = \frac{g_j(\varvec{x}^{(i)}) - LBV^{(i)}_j}{BS^{(i)}_j} \\ LBV^{(i)}_j = CBV^{(i)}_j - BS^{(i)}_j \end{aligned} \end{aligned}$$

(11)

or for equality constraints ($h_j(\varvec{x}_i) = 0$):

$$\begin{aligned} \begin{aligned} \omega ^{(i)}_{j} = 1 + \frac{abs[g_j(\varvec{x}^{(i)}) - LV_j]}{BS^{(i)}_j} \end{aligned} \end{aligned},$$

(12)

where $LBV^{(i)}_j$ (“lower buffer value”) is a lower boundary of the buffer zone, $BS^{(i)}_j$ (“buffer size”) is a size of the buffer zone, $CBV^{(i)}_j$ (“central buffer value”) is a value of buffer zone’s center, and $LV_j$ is a constraint limit value. The buffer size BS is based on constraints values from previous iterations:

$$\begin{aligned} \begin{aligned} BS^{(i)}_j = BSF^{(i)} \cdot \max _{k}(\varDelta g_{j}(\varvec{x}^{(k)})) \\ \varDelta g^{(i)}_{j} = abs(g_j(\varvec{x}^{(i)}) - g_j(\varvec{x}^{(i-1)})) \end{aligned} \end{aligned},$$

(13)

where $BSF^{(i)}$ can be adjusted by the buffer adaptation functions (Antonau et al. 2021). The buffer coefficient can be separated into two components: “relaxation” and “correction” coefficient. The first part, “relaxation,” is calculated as follows:

$$\begin{aligned} \omega ^{r,(i)}_{j} = {\left\{ \begin{array}{ll} \omega ^{(i)}_{j}, &{} \text {if } \omega ^{(i)}_{j} \le 1.0 \\ 1, &{} \text {if } \omega ^{(i)}_{j} > 1.0 \end{array}\right. } \end{aligned}$$

(14)

If the constraint is equality, the relaxation coefficient is always equal to one, $\omega ^{r,(i)}_{j} = 1.0$. The second component, “correction,” $\omega ^{c,(i)}_{j}$ is

$$\begin{aligned} \omega ^{c,(i)}_{j} = {\left\{ \begin{array}{ll} BSF^{(0)}(\omega ^{(i)}_{j} - 1), &{} \text {if } 1.0<\omega ^{(i)}_{j}<\omega ^{max} \\ 0, &{} \text {if } \omega ^{(i)}_{j} \le 1.0 \\ BSF^{(0)}(\omega ^{max}-1), &{} \text {if } \omega ^{(i)}_{j} \ge \omega ^{max} \\ \end{array}\right. } \end{aligned},$$

(15)

where the factor $BSF^{(0)} = 2$ is the initial buffer size factor, and $\omega ^{max}$ is the maximum correction coefficient. If the problem starts from an infeasible domain, the correction coefficient can be very high and may cause numerical issues. The $\omega ^{max} = 2$ limits the correction coefficient to the values inside the buffer zone and works in most cases. The search direction can be defined as follows:

$$\begin{aligned} \begin{aligned} \varvec{p}^{(i)} = -[\varvec{I}-\varvec{N} \varvec{\omega }^{r,(i)} (\varvec{N}^T \varvec{N})^{-1} \varvec{N}^T]\nabla f^{(i)} \\ \hat{\varvec{s}}^{(i)} = \varvec{p}^{(i)} - \varvec{N} \varvec{\omega }^{c,(i)} \\ \varvec{s}^{(i)} = \frac{\hat{\varvec{s}}^{(i)}}{||\hat{\varvec{s}}^{(i)}||_{max}} \end{aligned} \end{aligned}$$

(16)

The last equation scales the search direction using the max norm and can be skipped if the line search method works with an unscaled search direction. However, max scaling is required in the practical optimization application, where the shape can be changed by a certain amount (constant or limited).

4.2 Barzilai–Borwein method

The Barzilai–Borwein method (BB method) suggests a step size approximation using current and previous sensitivity information. The Barzilai–Borwein method computes a new step size as follows:

$$\begin{aligned} \alpha ^{(i)} = \frac{\varvec{y}^{(i),T} \varvec{d}^{(i-1)}}{\varvec{y}^{(i),T} \varvec{y}^{(i)}} \end{aligned}$$

(17)

or

$$\begin{aligned} \alpha ^{(i)} = \frac{\varvec{d}^{(i-1),T} \varvec{d}^{(i-1)}}{\varvec{d}^{(i-1),T} \varvec{y}^{(i)}} \end{aligned},$$

(18)

where $\boldsymbol{y}^{(i)} = \nabla f(\boldsymbol{x}^{(i)}) - \nabla f(\boldsymbol{x}^{(i-1)})$ is a change in the sensitivities of the objective function and $\varvec{d}^{(i-1)} = \varvec{x}^{(i)} - \varvec{x}^{(i-1)}$ is the previous update of the design variables. Therefore, if $\varvec{s}^{(i)}$ is a search direction at iteration i, the design update is

$$\begin{aligned} \varDelta \varvec{x}^{(i)} = \alpha ^{(i)} \cdot \varvec{s}^{(i)} \end{aligned}$$

(19)

A modification to the original Barzilai–Borwein method is introduced in this work, the Quasi-Newton Barzilai–Borwein method (QN–BB). The main idea of our modification is to compute the step size for each design variable instead of one step size for the full search direction vector. The design update can be found as follows:

$$\begin{aligned} \varvec{H}^{(i)}&= [\alpha _{k}^{(i)}] \end{aligned}$$

(20)

$$\begin{aligned} \alpha _{k}^{(i)}&= \min \left(abs \left [ \frac{\varvec{y}_{k}^{(i),T} \varvec{d}_{k}^{(i-1)}}{\varvec{y}_{k}^{(i),T} \varvec{y}_{k}^{(i)}} \right ], \alpha _{k, max}^{(i)}\right) \end{aligned}$$

(21)

$$\boldsymbol{y}_k^{(i)} =\boldsymbol{s}_k^{(i-1)} - \boldsymbol{s}_k^{(i)} $$

(22)

$$\begin{aligned} \varDelta \varvec{x}^{(i)}&= \varvec{H}^{(i)} \cdot \varvec{s}^{(i)} \end{aligned}$$

(23)

where $\varvec{s}^{(i)}$ is a search direction computed by the relaxed gradient projection method at iteration i and $\alpha _{k, max}^{(i)}$ is a maximum allowed step size at node k. If $\varvec{s}^{(i)}$ is normalized by equation (16), $\alpha _{k, max}^{(i)} = r_k^{(i)} / 5$.

4.3 Quasi-Newton relaxed gradient projection method

The Quasi-Newton relaxed gradient projection method combines the Quasi-Newton Barzilai–Borwein method and the relaxed gradient projection method. Linear approximation of the constraints is used to improve the constraint handling. In Fig. 6, the Quasi-Newton relaxed gradient projection method is shown. The QN–BB–RGP method is performed as follows:

• 1. Compute response values at the current design state: $f(x^{(i)})$, $g(x^{(i)})$;

• 2. Compute gradients of the objective function and active constraints: $\nabla \varvec{f}(x^{(i)})$, $\nabla \varvec{g}(x^{(i)})$;

• 3. Find shape update $\varDelta \varvec{x}^{(i)}$:

  • (a) Compute search direction $\varvec{s}^{(i)}$, eq. (16);

  • (b) Compute shape update $\varDelta \varvec{x}^{(i)}$, eq. (23);

  • (c) Compute linear approximation to response function for the computed shape update: $\tilde{g}(\varvec{x}^{(i+1)})$, $\tilde{h}(\varvec{x}^{(i+1)})$;

  • (d) If $\tilde{g}(\varvec{x}^{(i+1)}) <= 0$ and $\tilde{h}(\varvec{x}^{(i+1)}) = 0$, then the feasible shape update is found. The inner loop is converged;

  • (e) If $\tilde{g}(\varvec{x}^{(i+1)}) > 0$ and $\tilde{h}(\varvec{x}^{(i+1)}) != 0$, then the feasible shape update is not found. Update the buffer coefficients $\omega _j^{(i)} += 0.02$ and repeat the inner loop process;

• 4. Save current $\varDelta \varvec{x}^{(i)}$, $\varvec{s}^{(i)}$;

• 5. Check if the optimization algorithm has converged. If not, go to Step 1.

The constant to increase the $\omega _j^{(i)}$ is based on the numerical experiments, and it shows a good compromise between accuracy and cost. It has no effect on $\omega _j^{(i+1)}$.

Fig. 6

Flowchart of the Quasi-Newton relaxed gradient projection method

4.4 Maximum-value constraint aggregation technique

The RGP and QN–BB–RGP methods compute the buffer coefficient based on the constraint value and buffer size using equation (11). For the nodal constraints, the buffer coefficients are computed for each node. For constraint $g_{j}(x_k^{(i)})$ of node k at the optimization iteration i, the buffer coefficient is computed as follows:

$$\begin{aligned} w_{j,k}^{(i)} = \frac{g_{j}(x_k^{(i)}) - LBV_j^{(i)}}{BS_j^{(i)}} \end{aligned}$$

(24)

If $\nabla g_j(x_k^{(i)})$ is a gradient vector of the constraint for node k, the aggregated constraint can be formulated as follows:

$$\begin{aligned} \begin{aligned} g_j(x^{(i)}) = \max _k(g_{j}(x_k^{(i)})) \\ \nabla g(x^{(i)}) = \sum _k w_{j,k}^{(i)} \cdot \nabla g_{j}(x_k^{(i)}) \\ w_j^{(i)} = \max _k(w_{j,k}^{(i)}) \end{aligned} \end{aligned}.$$

(25)

Linear approximation to a constraint function at the new design point $x_k^{(i+1)}$ is

$$\begin{aligned} \tilde{g}(x_k^{(i+1)}) = g(x_k^{(i)}) + \nabla g_{j}(x_k^{(i)} \varDelta \varvec{x}^{(i)}) \end{aligned}.$$

(26)

If the approximated value $\tilde{g}(x_k^{(i+1)}) > 0$, the QN–BB–RGP method increases the $w_{j,k}^{(i)}$ to modify the computed search direction $\varvec{s}^{(i)}$, equation (16).

5 Academic experiment

This numerical investigation is designed to illustrate the applicability of the methods above in a highly non-linear shape optimization problem. Reynolds-averaged Navier–Stokes (RANS) equations are used to solve for flow variables in the fluid domain utilizing the $k-\omega -sst$ two-equation turbulence model. The reader is referred to Warnakulasuriya (2021) for more information on the specific implementations of the two-equations turbulence model in a Finite Element (FE) context.

5.1 Experimental set-up

The fluid domain $\varOmega = (-24.5D, 24.5D)\times (-16D, 16D) \subset {R}^2$ chosen after a domain size study is illustrated in Fig. 7, where $D = 0.1\,m$. The inlet (i.e., $\varGamma _{inlet}$) is applied with a constant velocity (i.e., $u_{inlet}$), and turbulence quantities are determined using a turbulence intensity of $5\%$ and a turbulent mixing length of 45D. The Reynolds number is $Re = 10e5$. The outlet (i.e., $\varGamma _{outlet}$) is applied with a $0\,Pa$ Dirichlet boundary condition for P, zero gradient boundary conditions for variables $u, k, \epsilon , \omega$. The slip condition (i.e., $\varGamma _{far}$) is applied on the top and bottom slip boundary for variable u, and all other variables are applied with a zero gradient boundary condition. Linear-log law wall functions developed by Launder and Spalding (1983) are used on the aerofoil boundary (i.e., $\varGamma _s$) to accommodate a wide range of meshes with $y^+\in [0, 300]$ in the first element near the wall boundary.

Fig. 7

Aerofoil problem configuration used in RANS in 2D

Figure 8 illustrates the overall mesh (refer to Fig. 8a) and enlarged view of the same mesh near the initial aerofoil geometry (refer fig. 8b) consisting of 20, 183 triangle elements.

Fig. 8

Initial mesh for a 2D aerofoil optimization problem

5.2 Optimization procedure

Drag and lift forces are the interested scalar QOI in this numerical experiment because the aerofoil’s usefulness depends on having maximum lift with minimum drag force. Equation (26) describes the optimization problem of interest.

$$\begin{aligned} \begin{aligned} \min _{\varvec{s}} \quad&J_{drag}\left( \varvec{w}(\varvec{s}), \varvec{s}\right) \\ \text {subjected to} \\&\varvec{R}_{\phi } = \varvec{0} \quad \forall \phi \in \left\{ u,v,w,p, k,\omega \right\} \\&G_{centroid}\left( \varvec{s}\right) = 0 \\&J_{lift}\left( \varvec{w}(\varvec{s}), \varvec{s}\right) - J_{lift}\left( \varvec{w}(\varvec{s}_{initial}), \varvec{s}_{initial}\right) \ge 0.0 \\ \end{aligned} \end{aligned},$$

(27)

where $J_{lift}\left( \varvec{w}(\varvec{s}_{initial}), \varvec{s}_{initial}\right) = 0.89$ in all experiments.

$G_{centroid}$ is computed by averaging all nodal coordinates along the aerofoil boundary as illustrated in equation (27) where N represents the number of nodes in $\varGamma _s$. It is applied to constrain aerofoil geometry to be present at the center of $\varOmega$ for all design iterations. AVM is used to smooth the noisy sensitivity field on the aerofoil boundary, and QN–BB–RGP is used to obtain the next aerofoil boundary for the optimization problem

$$\begin{aligned} G_{centroid} = \left\Vert \frac{1}{N}\sum _{i=1}^{N} (\varvec{x}_{current, i} - \varvec{x}_{\varOmega _{center}})\right\Vert ^2_2 \end{aligned},$$

(28)

where $\varvec{x}_{\varOmega _{center}}$ is the center of $\varOmega$.

5.3 Results

The results of the academic experiment are presented hereafter. The academic experiment is carried out with adaptive Vertex Morphing (AVM) and different radius set-ups: adaptive radius ($C=7$), $20\,mm$ and $50\,mm$. The QN–BB–RGP algorithm is used in all experiments to solve the optimization problems. The focus of this experiment is to show the importance of the filtering radius. All experiments have done 500 optimization iterations without further convergence criteria.

Fig. 9

Drag force variation with optimization design iterations

Figure 9 illustrates drag force variation with each design iteration. The experiment with constant Vertex Morphing radii of $50\,mm$ shows oscillations and does not depict an overall improvement in the drag force reduction. However, the experiments with adaptive and $20\,mm$ radii show improvement over the design iterations where $20\,mm$ radius set-up finds the best performing design.

Fig. 10

Geometric constraint variation with optimization design iterations

Geometric constraint variations with respect to optimization iterations are illustrated in Fig. 10. It depicts that all the proposed designs satisfy the geometric constraint, which enforces keeping the aerofoil design in the center of the fluid domain.

Fig. 11

Lift constraint variation with optimization design iterations

However, the lift constraint as depicted in Fig. 11 shows oscillating behavior, thus with constraint violations. The QN–BB–RGP method cannot precisely predict the constraint value of the non-linear constraints such as lift by using a linear approximation. However, the QN–BB–RGP can correct the violated constraint values in all experiments. Hence, there are improved feasible designs during the optimization process. Table 1 summarizes the results of the experiments and shows the performance of the last and the best-feasible designs. Table 2 summarizes the computational time.

Table 1 Optimization results of the aerofoil, in red—best-feasible designs

Table 2 Computation time

Fig. 12

Optimized aerofoil design, on left—velocity $[ms^{-1}]$ and on right—pressure [Pa] distributions

To further investigate the final design from each experiment, Fig. 12 illustrates the velocity and pressure distributions of the optimized designs. It can be observed that the experiments with adaptive and constant Vertex Morphing radii of $20\,mm$ try to reduce the frontal area to reduce drag force acting upon the aerofoil. The optimized design obtained by the experiment with radii of $50\,mm$ does not significantly reduce the frontal area, and it is due to restricting sensitivity information by having higher constant Vertex Morphing radii. In all experiments, the final designs have smooth boundaries. In the case of adaptive radius, the final design has smaller local changes on the lower surface and the trailing edge, see Fig. 12.

Figure 13 illustrates the effect of the filtering radii on the generated shape update. At iteration 1, in all experiments, the raw drag sensitivities are identical, as well as the steepest descent step ($\varDelta \varvec{x}^{(1)} = - \alpha ^{(1)} \cdot \nabla \varvec{f}^{(1)}$). It can be observed that the radius of $20\,mm$ smoothens the non-accurate sensitivity on the trailing edge (flow separation point) better than a smaller (adaptive) radius ($7\,mm$ at the point). Therefore, the large filter helps to reduce the local error of the sensitivities and generates shape update changes that modify the aerofoil profile more “globally.” As a result, the optimizer finds a better-performing design with a $20\,mm$ radius. In contrast, the optimizer finds a weak design with a radius of $50\,mm$ due to high filtering error. As it is discussed in Firl et al. (2012), the filtering intensity is always a compromise between filtering error and smoothing of sensitivity error.

Fig. 13

Drag sensitivities and shape updates at the wing’s tip, iteration 1

6 Large industrial example

An industrial CFD optimization problem is solved to demonstrate the full potential and flexibility of the adaptive Vertex Morphing technique and the robustness of the QN–BB–RGP algorithm. The goal of the optimization is to reduce the drag force of the BMW M4 GT4 car, while the downforce has to be equal to or larger than an initial value. The example has been prepared in cooperation with BMW Group, Motorsport division. All methods above are implemented in the optimization framework “ShapeModule” (BMW Group). Siemens STAR-CCM+$^\text {TM}$ software (Version 2020.2) is used to do primal and sensitivity analysis of the numerical model.

6.1 Problem description

Table 3 summarizes the properties of the CFD model/analysis, optimization problem, and parameterization. All geometrical constraints are aggregated into one, as shown in Section 4.4. The details of the turbulence models, solvers, and adjoint analysis can be found in the documentation of the Siemens STAR-CCM+^TM.

Table 3 Optimization problem description

Figure 14 shows the CFD model of the full car, where the design surface is highlighted in blue. The car’s exterior surface is chosen as a design surface: front flaps, front splitter, and rear wing. All these features have different physical and mesh sizes. Hence, they require different radius sizes. Figure 15 shows the radius field over the design surface and Table 3 gives the radius sizes.

Fig. 14

Geometry of the CFD model: design surface—blue, non-design parts—light gray

Fig. 15

Radius field over the design surface

The CFD model is highly detailed, and it contains a lot of non-design parts on the exterior surface and inside the car as well. For instance, non-design parts are the door handles, radiator, mirrors, lights, engine, suspension, gearbox, etc. Therefore, the geometrical constraints are needed to avoid the penetration between design and non-design parts. Figure 16 shows the design surface, where the geometrical constraints are applied.

Fig. 16

Geometrical constraint: constrained zone—red, free design surface—blue, non-design parts—light gray

6.2 Results and discussions

The QN–BB–RGP method solves this problem successfully without any parameter tuning of the optimization algorithm. It is an important point because finding suitable parameters is a very expensive and time-consuming process. The simulation is run on a 12-node HPC cluster, where each node has 2 x AMD 24-Core EPYC 7402 with 252 GB RAM. In total, simulation takes 210 hours or 120960 CPUh. Figure 17 shows the response values change during the optimization process. The optimization process is stopped by a maximum number of iterations due to the time limit. From the results given in Table 4, the most consuming operation is primal and adjoint CFD analysis. Finding the search direction takes around 1 hour, which is less than other operations: mesh motion, file saving, etc. One inner iteration takes approximately 3 min, where computing the search direction takes around 0.2 s, the shape update – 4.3 s, and mapping the shape update takes the rest. Figure 17e shows the number of iterations required to converge the inner loop. The most needed number of iterations is at optimization iterations 3 when the geometric constraint gets active.

Figure 17b shows that the lift constraint is not active at the final design. However, if the downforce constraint is not included, the optimizer chooses another local optimum and dramatically reduces the downforce. Figure 17c shows the performance of the optimization algorithm to hold the geometric constraint. As described in Section 4.3 and 4.4, the geometric constraints are aggregated and accurately handled during optimization. The design stays just in 0.04 mm distance from the limit value (limit value: 5 mm, max design value: 4.96 mm), while the design update in the whole model is up to 10 mm (see Fig. 19d).

The optimization results are shown in Figs. 18 and 19. One can see that the most shape changes happened on the rear wing, trunk lid, front flaps, and front splitter. The middle section of the rear wing, trunk lid, and frontal flaps has been deformed to generate less drag. In contrast, side sections of the rear wing and front splitter generate more lift, this explains why our final design has improved both aerodynamic characteristics. Suppose the design surface is not so large and includes only the rear wing and front splitter, in that case, the final results will not be so impressive, just $4\%$ drag reduction (the results have been shown at ISSMO-14th World Congress of Structural and Multidisciplinary Optimization, “Quasi-Newton Relaxed Gradient Projection method in large constrained node-based shape optimization problems”).

In Figure 19d, one can see the difference on the final shape update with different radii. The rear wing has a radius of 5 mm, while the trunk lid is – 20 mm. The final shape of the trunk lid is very smooth, and the wavelength of shape change is large. In contrast, the shape change of the rear wing is locally detailed, but it is smooth. Due to manufacturing limitations or unaesthetic design, one can change the radii to find a new design in the next optimization process.

Fig. 17

Optimization results: response function evaluations & size of shape updates

Table 4 Computation time [hour]

Fig. 18

Optimization results: shape change on top & bottom view

Fig. 19

Optimization results: optimized design—blue, initial design—transparent yellow, non-design parts—light gray

7 Conclusions

Adaptive Vertex Morphing extends Vertex Morphing parameterization to solve large-scale optimization problems with local control on the final shape. It allows reasonable control of the final form and finds various solutions. The QN–BB–RGP method shows good potential as an acceleration and stabilization technique for gradient descent methods with many design variables and expensive response functions. The proposed QN–BB–RGP method, in combination with the maximum value aggregation technique, solves large optimization problems with a huge amount of geometric constraints. Linear approximation is not accurate for highly non-linear constraints, but still, the method can handle such constraints and find feasible solutions. In future work, modifications of the Barzilai–Borwein method can be studied to improve the QN–BB method, and adaptive Vertex Morphing can be extended to solve multi-disciplinary optimization problems with non-matching meshes.