Robust feasibility verification and region inner-point detection algorithms for geometric shape objects applied to electric machine optimization workflow

Abstract

In most cases, the search for the optimal design of an electrical machine is closely related to its 2D radial cross section. When optimizing a 2D cross section, special attention must be paid to the geometry and to the definition of the parameters along with their boundaries. Even if properly bounded, complex geometries generated by optimization algorithms can lead to geometrically infeasible candidates. These cannot be manufactured because they contain generally undesirable geometric relationships between air, magnets, and steel. Different commercial and open-source finite element analysis (FEA) design tools treat the infeasible designs differently. The results vary from simulation stop to successful FEA calculation of the infeasible candidate, which wastes time by producing useless data. To prevent the infeasible designs from entering the optimization competition and possibly appearing incorrectly as optimal solutions, and to reduce optimization time, it is important to capture the infeasible designs during optimization. Moreover, the FEA tool requires a precisely determined interior point to assign the material to each closed region (air, steel, epoxy, magnet...). This can be very challenging for complex geometries. To avoid creating geometry or material regions that are not valid, this paper proposes a novel robust methods for checking feasibility and determining interior points on geometric shape objects. In this paper, the proposed method is applied to the optimization of electrical machines.

1 Motivation

Our research group is involved in the state-of-the-art design of electrical machines based on mathematical optimization. The presented methods have been proven in industrial applications and can be applied to any similar problem that can be defined with geometric shapes following the procedure described in the last sections of the paper. Considering the fact that this paper deals with a complex problem and proposes a solution that is relatively simple to implement, the reader is gradually introduced to several topics: electric machine optimization workflow, geometric feasibility, standard feasibility detection, region inner-point detection issues, and finally, the proposed robust set of solutions.

2 Introduction

The electrification of the transportation sector will be one of the biggest disruptions to market dynamics over the next two decades. This will create significant winners and notable losers among vehicle original equipment manufacturers (OEMs) (International Energy Agency 2020).

All the major OEMs have launched their electric vehicles (EVs) to the market. Despite many advantages, EVs are not cost competitive as conventional vehicles, which is the main requirement for large-scale market penetration (Sarlioglu et al. 2017; De La Parra et al. 2009). For this to become a reality, continuous research is required to develop optimized and cost-effective technologies in three main areas: battery, inverter, and electric machine.

In the design of an electrical machine, the objective is to reduce component cost while maintaining sufficient efficiency and torque density. Since these requirements are in conflict, modern electrical machine design techniques require a kind of mathematical optimization procedure (Bråmå and Enblom 1996; Zhao and Schofield 2020; Lee et al. 2021). This is particularly evident in the problem of increasing efficiency through global legislative initiatives (EU 2009; European Environment Agency 2016).

In most cases, the search for the optimal design of an electrical machine is closely related to its 2D radial cross-section. The increase in parametric complexity correlates with an increase in the performance of the optimal design, but also with a longer optimization time (Pellegrino et al. 2015; Lu et al. 2017) and a higher probability of producing a geometrically infeasible design. In addition, some FEA tools require a precisely determined interior point to assign the material to each closed region (air, steel, magnet...), which can be difficult to determine for complex geometries.

The paper provides a novel solution to both problems through a novel robust feasibility verification procedure and inner-point detection using Matlab polyshape objects. The generality of approach is demonstrated through a set of simple, but extremely robust algorithms. The approach elevates geometric design analysis from geometric primitives (points, lines and arcs) to the level of objects (shapes), applicable to any type of machine geometry as an upgrade to existing code.

3 Optimization methodology

Most of the requirements for the design of electric machines are in conflict with each other (reduction of volume or mass, increase of efficiency, etc.). Therefore, a manual design that satisfies all constraints can be an overwhelming task due to a large number of coupled parameters that affect the performance and quality of the machine. The solution is in the use of mathematical optimization.

Optimization algorithms can be divided into gradient based methods and stochastic or metaheuristic methods. Gradient-based methods converge quickly but have difficulty with global optima.

Usually they require feasible starting point which can be a problematic task in complex problems (Quasi Newton method (Kamper et al. 1996). Stochastic methods are heavily used in electrical machine optimization (Powell’s method (Kamper et al. 1996). The disadvantage is that convergence can take days and the global optimum cannot be mathematically proven. On the other hand, from the engineer’s point of view, these methods can find a satisfactory global result. Popular metaheuristic methods are based on natural behaviour (Genetic algorithm, Differential evolution (Lampinen 2002; Zarko et al. 2017), Particle swarm (Bramerdorfer et al. 2016), but they can also be iterative (Lee et al. 2010), or based on approximation (Lee and Jang 2021).

All methods are generally set to solve a multi-objective problem, which is mathematically defined as follows: find the vector of parameters (1), subject to D parameter boundary constraints (2) and subject to m inequality constraint functions (3), that will minimize (or maximize) n objective functions (4). A vector $\vec {x}$ of D variables specifies dimensions, dimensionless ratios, current densities, material types used, etc. The goal of design optimization is to have a chosen objective function $f(\vec {x})$ reach its minimum or maximum value while keeping other engineering indices within an acceptable range.

$$\begin{aligned} \vec {x}&=[x_1,x_2,\ldots ,x_D],\quad&\vec {x}\in R^D \end{aligned}$$

(1)

$$\begin{aligned} x_i^{(L)}&\le x_i\le x_i^{(U)},&i=1,\ldots ,D \end{aligned}$$

(2)

$$\begin{aligned} g_j(\vec {x})&\le 0,&j=1,\ldots ,m \end{aligned}$$

(3)

$$\begin{aligned} min(f_k(\vec {x})&),&k=1,\ldots ,n \end{aligned}$$

(4)

3.1 Cross section parametrization

Each machine geometry is described by a set of parameters. The most influential design parameters that make up the vector $\vec {x}$ are usually identified using a sensitivity analysis tool. All parameters are bounded in predefined intervals, called boundary constraints, which define the search space or the design space.

Some authors use model parameters (stator bore diameter, stator slot depth, etc.) directly as optimization variables, while other authors use ratios of model parameters as optimization variables (Žarko et al. 2005; Zarko et al. 2017). A better approach (which can improve the efficiency of gradient-based algorithms) is to choose variables given as dimensionless ratios of related geometric parameters, e.g. ratio of stator inner diameter to stator outer diameter, ratio of tooth (or slot) width to slot pitch, magnet pole arc relative to pole pitch, etc.

Some parameters can just be considered as optimization variables directly within the given interval (stator outer diameter, stack length, slot current density). On the other hand, some parameters have practical limitations and should not be normalized. E.g. minimum permanent magnet width is tied to the magnet manufacturing process. Finally, a designer might choose a combination of normalized and model parameters which might create geometrical feasibility issues.

3.2 Optimization workflow

A typical optimization workflow is a series of computations consisting of: optimization algorithm that generates optimization variables according to the given parameter boundaries, geometry generation block that passes the design to the selected FEA tool for performance calculations, and finally post-processing block that returns the computed data to the optimization algorithm for further evaluation (Fig. 1, black). Additionally, a geometric feasibility checking (FC) block can be part of the optimization workflow (Fig. 1, red).

3.3 Geometric feasibility

The term feasibility usually refers to the solution and means that the solution satisfies all given constraints. In other words, the region enclosed by $\forall g_j(\vec {x}) = 0$ is called a feasible region. This paper concentrates on another type of feasibility called geometric or model feasibility. Geometrically feasible model is valid for solving if there are no overlapping edges or non-conventional geometric relations. Infeasible candidate is the one that cannot be produced as a real machine because there are overlapping magnets, non-rectangular shaped magnets, air pockets overlapping magnets etc. Infeasible candidates should not be evaluated for performance because theoretically they can falsely appear as optimal solutions but can never be considered for manufacturing/production. It is important to note that geometric feasibility checking methods from the following sections are intended to be used only as an optimization procedure add-on (Fig. 1).

Fig. 1

FC as an optimization workflow add-on feature

Fig. 2

Infeasible geometry (a) and forced feasibility (b)

3.3.1 Optim. workflow without FC

If the optimization software does not include a feasibility check (FC), two different scenarios may occur during the FEA calculation (depending on the selected FEA tool).

In the first case, the FEA tool detects that the design is erroneous and throws an error. In this case, the designer must implement a try-catch procedure which will capture the event, otherwise the optimization procedure will fail (try-catch adds $t_{\text {extra}}\ge 4$s per design evaluation). In the second case, the FEA tool does not detect the infeasibility and a full FEA calculation is performed. This is the worst case scenario which will produce useless results and cause significant increase of optimization time (e.g., detailed transient electromagnetic simulations can take $t_{\text {extra}}\ge 15$min).

3.3.2 Optimization workflow with FC

However, if the optimization software includes a feasibility detection procedure, the designer can either attempt to correct the problematic instance or skip it. There are two typical ways to correct the optimization candidate prior to performance evaluation (passing it to the FEA calculation).

First, the entire set of optimization variables for that candidate is reinitialized randomly within the specified parameter bounds until geometric feasibility is achieved. This is a brute-force approach, but it is mandatory since evolutionary optimization algorithms (e.g. Genetic Algorithm, Differential Evolution) must have the same number of members in each population of optimization candidates. This is due to the fact that the each generation must be equal or better than the previous as the algorithm advances towards the optimum.

The alternative is forced feasibility, where each infeasible design is subjected to minimal parameter modification until feasibility is reached (e.g., the magnetic layer angle $\alpha _V$ is modified until $w_{\text {min}}$ is reached, Fig. 2b). This approach can be complicated and requires an advanced parameterization with minimal feasibility constraints (Ban et al. , 2021).

Depending on the complexity of the design, both methods may increase execution time ($t_{\text {extra}}= 2-15$s). On the other hand, detecting and skipping the infeasible design actually does not impact execution time ($t_{\text {extra}}= 0$).

4 Standard approach for feasibility detection

The standard approach to feasibility detection is specific to each parameterized template, which typically requires immense programming/development resources for research groups engaged in electric machine design optimization. Not only are top-level differences between templates relevant, e.g., a single-layer V-shape geometry compared to spoke interior permanent magnet machine (IPM), but also peculiarities such as air-pockets around magnets and curvature of posts and bridges have a significant impact on potential geometric feasibility. Modern high performance machines, especially in automotive traction, are all about these subtle design features. This means that an extensive study of the mathematical geometry dependencies has to be performed between arcs and lines that are either adjacent or have the possibility to touch or intersect during optimization process. All geometry primitives such as points, lines, arcs must be mathematically defined through coordinates or equations, ideally in both polar and Cartesian coordinate systems.

Depending on the definition of the optimization variables, this process can be fairly simple in some cases. For example, if the optimization variable for stator bore is defined as ratio of stator bore diameter to stator outer diameter

$$\begin{aligned} 0.55< D_{bore}/D_{outer} < 0.75 \end{aligned}$$

(5)

then it is assured that the stator bore is always, as it should be, within the outer dimensions of the stator. A similar approach can be used for the height of the stator yoke - it must be shorter than the height of the stator annulus because both the slot and back iron must fit inside the stator. Therefore, this optimization variable is also defined as a ratio:

$$\begin{aligned} 0.2< 2h_{yoke}/(D_{outer}-D_{bore}) < 0.6 \end{aligned}$$

(6)

Finally, the slot width or the tooth width, depending on the choice of stator slot type must be smaller than stator slot pitch in order to fit in the slot + the tooth inside one slot pitch.

However, when it comes to IPM rotors, especially multi-layered configurations as in Fig. 3, the mathematical description is much more complicated and, more importantly, it needs to be refined after each intervention in the template change. This is often the case in modern high performance automotive traction motors.

Fig. 3

Example of 2-layer V-shape IPM: a feasible case, b barrier definition point crossing polar lines, c barrier arc crossing polar lines, d barrier collision

Typically, a single-layer, V-shape IPM rotor is described with a large number of rotor variables. The complexity can vary between different software packages or user defined templates in general-purpose FEA tools. In the case of commercial design tools, the minimum number of parameters to describe a layer is approximately 11. For multi-layer configurations, it increases linearly, so that a typical 2-layer V-shaped IPM traction motor (rotor shown in Fig. 3a) requires 22 variables just for magnets and barriers. If such a geometry is subjected to an optimization process to explore its full potential, or in other words, if the limits of the optimization parameters are set wide enough, there can be a large number of possible overlaps between air pockets, flux barriers, and magnets of a given layer or between different layers (Figs. 2, 3b–d).

The first step in the the standard approach would be to check whether any point (object vertex) is outside the rotor boundary: towards the stator and airgap, or inside the shaft. This is most easily achieved by checking the radial polar coordinates: any point with a radius greater than the outer radius of the rotor, or with a radius smaller than the inner radius of the rotor, means that the geometry is not feasible. A similar test exists to check if any point (object vertex) can be found outside the boundaries of each rotor pole (Fig. 3b). This is easily achieved by checking the angular polar coordinates: The angular coordinates should be within one pole. However, other tests, such as checking that barrier-limit arcs do not cross the interpolar line (Fig. 3c) and checking that there is no possible intersection between two layers (Fig. 3d), require hard-coding more complicated mathematical dependencies.

All of these calculations need to be changed, or at least reviewed, if the geometry slightly changes. The exact math can become considerably more complicated if barrier air pockets take stress relief shapes in the form of successive tangential arcs and ellipses, or if cooling channels and mass reduction holes are present in the geometry.

The procedures for feasibility verification are specific and different for each different geometry. The pseudocode for a 2-layer V-shape IPM is shown in Algorithm 1. It is difficult to tackle all possible geometry failure cases so sometimes the algorithm can let the infeasible geometry further down the optimization pipeline. Then it is up to the wrapper of the FEA solver to try and catch the error and ignore the solution. This invalid geometry can be examined later and the feasibility checking function can be further improved.

It can be seen that this method is not robust and needs to be modified even for small changes in the geometry features of the topology under study. Therefore, a novel feasibility handling algorithm is presented in the next chapter.

5 Robust feasibility detection

For optimization purposes, the cross-sectional geometry of the stator and rotor of the machine can be reduced to 2D Euclidean space. Geometry parameterization is performed in either Cartesian or polar coordinates, specifying all geometric primitives: Points, Lines, Arcs, and Polylines, which are sets of multiple lines that model a complex curve (polyline can be approximated with series of arcs and lines before sending a drawing .dxf to FEA solver). A set of connected primitives forms an object as a shape, such as a rotor barrier, which has mathematical properties: Area, Perimeter, Centroid etc. If the entire machine geometry can be defined by shapes - software objects, it would be very convenient to have some sort of functional tool to determine the correlation between different shapes. Correlations include Boolean functions, intersections, areas etc. This novel approach is made possible by the Matlab Polyshape class (Mathworks 2020), which enables elevation of primitives to an object (shape) level. Once created, the shape objects can be organized in the form of a vector. The polyshape functionality allows a quick analysis of vectorized shape objects. One of the functions is Intersection, which returns information when there is an intersection between members of the shape vector. This provides a robust feasibility check regardless of parameter boundaries and regardless of the complexity of the geometry shape. Considering that any electric machine topology can be reduced to geometric primitives, the proposed method can be implemented on all types of geometries as an upgrade of pre-existing code.

The main advantage of this approach is moving away from strict mathematical feasibility verification to shape object level which allows great design freedom, instead of relying on the rather complicated procedure described in the previous chapter (all functionality has been verified on Matlab releases after 2019b). Currently, there is no open-source code in Python or other interesting scripting languages that can provide the same functionality as Matlab polyshapes. Hovewer, this does not limit the presented novel approach. Considering the outlined benefits, open-source community will close this gap soon.

5.1 Polyshape function - details

Polyshape function creates a polygon defined by 2-D vertices and returns a polyshape object with properties describing its vertices, solid regions, and holes (Mathworks 2020). Essentially, polyshape is a structure that defines all vertices and holes within the 2-D shape. The syntax breakdown is given below (detailed variable description in Table 3).

$$\begin{aligned} P_{x,y}&= \textit{Point} (x_p,y_p) \end{aligned}$$

(7)

$$\begin{aligned} L_{x,y}&= \textit{Line} (P_{1}, P_{2}) \end{aligned}$$

(8)

$$\begin{aligned} A_{x,y}&= \textit{Arc} (P_{Or}, P_{1}, P_{2}) \end{aligned}$$

(9)

$$\begin{aligned} M_{\text {dxf}}&= \begin{pmatrix} L_{1} &{} L_{2} &{} \cdots &{} L_{n} \\ A_{1} &{} A_{2} &{} \cdots &{} A_{m} \end{pmatrix} \end{aligned}$$

(10)

$$\begin{aligned} \vec {x}_s&=[A_{3x},L_{1x},L_{3x}, A_{1x} \ldots ] \end{aligned}$$

(11)

$$\begin{aligned} \vec {y}_s&=[A_{3y},L_{1y},L_{3y}, A_{1y} \ldots ] \end{aligned}$$

(12)

$$\begin{aligned} \text {poly}&= \textit{polyshape}(\vec {x}_s,\vec {y}_s) \end{aligned}$$

(13)

$$\begin{aligned} \text {polyvec}&= [\text {poly}_1, \text {poly}_2,\ldots ] \end{aligned}$$

(14)

$$\begin{aligned} C_{x,y}&= \textit{Centroid} (\text {poly}) \end{aligned}$$

(15)

Fig. 4

All geometry points, lines and arcs (a); Machinecross section with all polyshapes (b)

Some of the predefined functions for manipulating polyshape structures are listed in Table 1. For better understanding, a pseudocode formulation is used in this paper, the functional source code is available in the (Ban 2021).

Table 1 List of used primitives and polyshape functions

5.2 Geometry polyshape definition

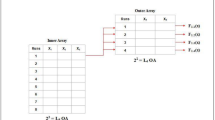
The automated geometry parameterization (Fig. 4a) defines all rotor and stator point objects (7). Line objects are defined by two points (8), while arc objects are defined by origin, start and end points (9). When generated, line and arc objects contain corresponding vertex data. Shape $\vec {x}_s,\vec {y}_s$ vertex vectors are constructed by concatenating line and arc vertices in user-defined order (11), (12). Finally, $\vec {x}_s,\vec {y}_s$ are the arguments to the polyshape construction function (13). If there are multiple shapes (e.g., rotor of an electric machine), they can be vectorized (14), Fig. 4b.

All adjacent shapes are built from the same set of polygons with a high number of vertices, which means that there will be no resolution problems in detecting intersections. It is important to note that when exporting the validated design for FEA calculation, the arcs do not consist of many polylines, but of .dxf primitives, so that the selected FEA software can optimise the arc meshing and speed up the calculation process. On the other hand, when assigning values to polyshapes, the arc and line vertices are passed as discrete vectors (11), (12). This means that the matrix of line and arc primitives (10), and the polyshape vector (14) are stored and processed separately.

5.3 Convex and concave shapes

All electromagnetic FEA tools require that a certain material is assigned to every closed region, except when boundary conditions handle holes in the model. In automated optimization procedures it is therefore necessary to define the shape region precisely, which can be a problem. The problem is even greater when complex geometries are used in the optimization of high performance machines.

In general, a generated shape can be either convex or concave (by default, shapes with holes are not allowed). A shape is said to be convex if, for any two points in the shape, the straight line segment between them lies entirely within the shape. Convex polygon centroid is always within the vertex envelope (Fig. 5a), which need not be the case for concave shapes (Fig. 5c–e). A typical example of a strictly convex shape is the permanent magnet rectangle (Fig. 5a), while the general shape may have “dents” (Fig. 5b).

Fig. 5

Convex (a), general (b) and concave shapes (c, d, e)

On the other hand, air barriers are inherently concave because permanent magnets (PM’s) are glued to the barrier surface and form separate shapes, thus creating a concave air pocket with an outer centroid (Fig. 5d). Furthermore, synchronous reluctance machine (SyRM) barriers are always concave, and depending on the curvature can have outer centroid. In the example of Fig. 5e, the centroid is within the shape limits, but very close to the edge, which can lead to problems in FEA calculations.

Overall, closed region inner-point detection by assigning the centroid point works well for convex shapes, but is unreliable for concave shapes.

5.4 Region inner-point detection

A robust region detection algorithm (Algorithm 2) was developed in combination with the existing polyshape functions and applied to all objects within the polyshape vector except magnets. Magnets are convex by default and require a specific magnetization direction determined by the GetMagnetAngle function (Algorithm 3).

GetRegion function argument is polyshape structure $\hbox {poly}_\mathrm{in}$ (Fig. 6a green). $\hbox {poly}_\mathrm{in}$ $\vec {x}_s,\vec {y}_s$ vertex limits are extracted resulting in a 4x4 vectorized polyshape rectangle mesh (Algorithm 2:ln:6–7, Fig.6b). Each rectangle is intersected with $\hbox {poly}_\mathrm{in}$ to form an output vector of intersection points (Algorithm 2:ln:9, Fig.6b).The intersection element with the largest area is identified with the (Algorithm 2:ln:10, Fig.6c).

The next step is to compute the temporary inner-point calculation (Algorithm 2:ln:11). The point $C_{x,y}$ is checked to be inside the original $\hbox {poly}_\mathrm{in}$ with boolean function (Algorithm 2:ln:12). Finally, if $C_{x,y}$ is inside of the shape, it is returned as a region interior point, otherwise the procedure is repeated recursively on $\hbox {poly}_\mathrm{big}$ (Alg. 2:ln:15).

The proposed algorithm basically searches for a convex sector of the initial polyshape. Brute-force tests of the presented method prove that the inner-point of the region is always found within the shape boundaries, regardless of the generated geometry.

Fig. 6

Concave shapes robust region detection meshing example (a–d), functionality of Polybuffer function (e)

Polyshape mesh can be set to any rectangular dimension. Considering that the function execution time is proportional to the number of used mesh shapes, it is important to set the optimal mesh size. Different combinations of mesh sizes were tested on randomly generated concave shapes. In case of 2 × 2 mesh, there is a 40% probability that the inner region of concave shape is found in the first function iteration (e.g. Fig 7a). The second iteration (e.g. Fig 7b) captures the inner region in 90% cases and sets the total number of mesh shapes to 2 × 2 + 2 × 2 = 8 ($1^{\mathrm{st}}$ plus $2^{\mathrm{nd}}$ iteration). On the other hand, when tested with 4 × 4 mesh, the inner region was in 90% cases found in the first iteration resulting in a total of 4 × 4 = 16 mesh shapes (e.g. Fig 7c).

Finally, 8 × 8 mesh finds the inner region in the first iteration in 98% cases, but with the expense of 8 × 8 = 64 shapes (e.g. Fig 7d). Compared with previous alternatives, the shape number is high and can potentially be doubled in $^{\mathrm{nd}}$ iteration. Considering that 4 × 4 mesh has a rather high probability of finding the inner region in the first function iteration, 4 × 4 was selected as the optimal number of mesh shapes.

Fig. 7

Example of region detection mesh sizing

5.5 Magnetization direction

In addition to region inner-point, permanent magnets have magnetization direction (Fig. 8). The procedure for custom magnet shapes must be implemented individually. In this section, the procedure for V-shape rotor designs (Alg. 3) is explained. The magnet shape with the magnet angle parameter $\alpha _V$ and the pole step constant $\tau =\pi /p$ where p is the number of pole pairs, is passed to the function GetMagnetAngle. The function computes magnet centroid region point $C_{x,y}$ (Algorithm 3:ln:2) and the magnetization angle $\alpha _M$. Algorithm 3:ln:6-12 and Fig.8 show the $\alpha _M$ calculation procedure which works when $\alpha _V \ge 180^{\circ }$, and even in the case of square-shaped magnets.

Fig. 8

Determining magnetization direction

Fig. 9

Feasible (a, b) and infeasible geometry (c, d)

5.6 Feasibility check

The complete machine cross section with all polyshapes and assigned material regions including the rectangular mesh intersections is shown in Fig. 9a. In this example, a total of 15 polyshapes are stored in a vector form (14). The polyshape vector is passed to the overlaps function which returns overlaps matrix $M_{ovl}$ (Alg. 4:ln:3). If $M_{ovl}$ is a unitary matrix (Algorithm 4:ln:4), the design is feasible and there are no overlaps (Fig.9a, b), otherwise the generated design is infeasible (Fig. 9c, d). If the user wants to include a limit on the distance between certain shapes (useful for detecting material elements that are too thin to be manufactured), the Polybuffer function can temporarily increase the borders of the shape during feasibility check (Algorithm4:ln:2, Fig. 6e). Additionally, the same function is used to avoid geometrical conflicts (11), (12) in borderline cases (e.g. two shapes are touching).

5.7 Impact on total execution time

The feasibility and region detection procedure is performed only once during geometry generation, with a typical duration of 0.5–2 s. The transient calculation of a single operating point in ANSYS Motor-CAD for a two-layer IPM machine geometry typically takes between 30–60 s. If additional calculations are performed during the design evaluation (thermal transients, drive cycle analysis, etc.), the cumulative time can increase to 10–15 min.

Table 2 FC impact on total optimization time

As an experiment, a sensitivity analysis with 4 consecutive runs of 1000 iterations was performed for a well-defined two-layer V-shape rotor geometry with 44 parameters (Table 2). The design space has been specified by defining upper and lower bounds of all design parameters. A set of parameters for each design has been generated by scanning the multidimensional space via Space filling Latin Hypercube sampling method using Ansys OptiSLang surrogate modelling tool. The average design evaluation time is 300 s (5 min). Using try-catch adds 4 s (304 s per design evaluation), while using feasibility check adds 2 s (302 s per design evaluation).

Let us first consider the worst-case scenario without try-catch or FC (FEA tool runs the entire simulation). This approach leads to a maximum duration of 83.3 h per run. On the other hand, the try-catch procedure detects all possible errors, leading to an average execution time of 63.1 h (here we assume the scenario where the FEA tool outputs an error for each infeasible design). Finally, using FC results in an average execution time of 62.6 h.

As expected, the try-catch and FC procedures result in virtually the same execution time and a significant overall time savings (25% or 20 h shorter execution time). The conclusion is that the use of FC has no impact on the total execution time. Unlike the try-catch procedure, FC can provide the information about the colliding regions and parameters that can be exploited in surrogate (metamodel) optimization, or tools such as Ansys OptiSLang (Riviere et al. 2019, 2020).

6 Conclusion

Optimization is an important and inevitable part of the modern electric machine design process. When properly applied, optimization leads to a design that satisfies all imposed requirements.

Even when properly constrained, complex geometries generated by optimization algorithm can lead to infeasible designs that in worst case increase optimization time or propagate non-manufacturable candidates. In addition, the accurate detection of interior points for each closed region in order to assign material can be a serious challenge.

The standard procedure for solving these issues is based on hard coding of simple or complex mathematical relationships between geometric elements. This method tends to be inflexible to any major changes and leads to a complex geometry code. The paper provides a solution to both problems through a novel robust feasibility verification procedure and inner-point detection using Matlab polyshape objects. The generality of the approach allows application in any other script language. The polyshape approach elevates geometric design analysis from geometric primitives (points, lines and arcs) to the level of objects (shapes), applicable to any type of machine geometry as an upgrade to existing code. In addition to geometrical properties (vertex coordinates), elevation to shapes allows severely simplified surface, mass and Boolean calculations. When implemented, the method represents a paradigm shift in electric machine design.

The main benefits of robust feasibility checking are: preventing infeasible (non-manufacturable) candidates to be propagated or to win in the optimization competition, gathering information about which shapes and parameters cause problems and finally, greater freedom in defining geometry parameter boundaries when describing complex geometries.

Appendix

See Tables 3 and 4.

Table 3 Complete list of variables and functions

Table 4 List of abbreviations