1 Introduction

Thermal radiation is a physical phenomenon affecting the design of many aerospace systems including hypersonic vehicles and spacecraft. The need to design lightweight, efficient structural elements within these systems has driven the development of many design optimization tools. Topology optimization has grown to become a popular method for light-weighting structural elements due to its ability to modify an existing design in a free-form manner.

Topology optimization methods identify an optimal material layout within a fixed design domain subject to a set of boundary conditions and other constraints to minimize a cost functional. While other structural optimization methods handle a fixed set of design variables such as the lengths, thicknesses, and other relevant dimensions of predetermined features, topology optimization allows for variation in the overall shape and connectivity of the structure (2014). This procedure is typically more advantageous in earlier design stages where a variety of geometries can be explored. Several papers provide overviews of the various topology optimization methods and current areas of research (Eschenauer and Olhoff 2001; Rozvany 2009; Sigmund and Maute 2013; Deaton and Grandhi 2014).

Much research has been done on optimizing thermally conductive structures using topology optimization methods (Dbouk 2017), including heat exchanger design applications with convective boundary conditions (Coffin and Maute 2016; Kambampati and Kim 2020), and transient thermal problems (Hyun and Kim 2021). However, less attention has been given to solving problems incorporating a radiative boundary condition. Two recent works include Castro et al. (2015) and Munk et al. (2017). Castro et al. (2015) investigated the design of radiative enclosures by redistributing reflective material using a solid isotropic material with penalization (SIMP)-based approach. The 2D element density variables were used to interpolate surface reflectivity within the enclosure and subsequently determine the temperature and heat flux fields. Munk et al. (2017) used an evolutionary structural topology optimization approach on a three-dimensional panel model of a hypersonic aircraft wing incorporating aerothermoelastic effects. The evolutionary optimization method was a hard-kill bi-directional method; element densities were integer variables and void elements were excluded from the finite element and radiation analysis altogether. The objective was to minimize weight and stress.

In the approach used by Castro et al. (2015), the radiating surface does not change topologically, and in Munk et al. (2017), the radiative heat transfer was not included in either the objective or constraint functions. A level set method approach which explicitly incorporates the radiative heat transfer in the optimization problem would be advantageous for two reasons: (1) a design-dependent load problem, such as those involving structures subjected to hydrostatic pressure loads (Neofytou et al. 2020), would be easier to formulate since the structural boundaries are implicitly defined by the level set function and (2) the designer could manipulate the radiative capabilities of the final design more easily.

The remainder of this paper is organized as follows: Sect. 2 provides some background on level set methods and reviews how they implicitly represent structural boundaries. Section 3 presents a two-dimensional single-objective, single-constraint optimization problem to design a thermally efficient radiating structure. In Sect. 4, a level set-based topology optimization approach is defined using an augmented Lagrangian method. We then derive the shape sensitivity in Sect. 5 for maximizing thermal heat power radiated. In Sect. 6, we demonstrate the proposed methodology on a 2D radiating aluminum plate problem with varied initial material configurations to illustrate how the method is identifying locally optimal solutions. We also present several candidate designs to illustrate that using a thermal compliance objective function is insufficient for this class of problems. Finally in Sect. 7, we provide a summary of the contributions presented in this paper and discuss future work.

2 Background

Topology optimization offers the designer flexibility in the geometric shape of the structure under consideration. Typically, a finite element model is employed to evaluate the objective and constraint functions, in addition to any sensitivities needed for implementing a gradient-based optimizer. A density value is assigned to each element of the mesh which interpolates the stiffness, conductivity, or other relevant material property throughout the design domain. Because the number of design variables in topology optimization problems scales directly with the number of nodes or elements in the finite element model, they tend to be much larger in dimension than parametric design problems. However, topology optimization offers much greater design freedom since a nearly limitless number of shapes can be obtained.

Boundary variation methods are a subset of topology optimization routines which employ an implicit representation of the structure’s boundaries rather than an explicit parameterization of the design domain (Deaton and Grandhi 2014). Several methods fall under this category including level set method (LSMs) and phase-field methods. Both utilize an implicit function \( \phi \) to define the structural boundary as well as an evolution equation used to update \( \phi \) between optimization iterations. Compared to the level set approach, phase-field methods tend to exhibit higher numerical instability and are computationally more expensive when tested on similar design problems Hua et al. (2014). Therefore, they have not been widely employed for topology optimization problems and the reader is referred to Takezawa et al. (2010), Choi et al. (2011), Jeong et al. (2014) for more information. In addition, Sobolev gradient flows such as the H1 and L2 gradient flows are other methods of representing and evolving shapes in a topology optimization framework (Burger 2003; Sundaramoorthi et al. 2007; Henning and Peterseim 2020).

In level set methods, \( \phi \) is defined as the level set function and implicitly defines the boundary of the structure through the following conditions:

$$\begin{aligned} \begin{aligned} \phi (x)<0&\qquad x\in \varOmega \\ \phi (x)=0&\qquad x\in \partial \varOmega \\ \phi (x)>0&\qquad x\in {\mathscr {D}}\setminus \varOmega \end{aligned} \end{aligned}$$
(1)

where \( \varOmega \) is the structure domain, \( \partial \varOmega \) is the structure boundary and \( {\mathscr {D}} \) is the design domain. Note that \( {\mathscr {D}} \) defines the physical limitations of how large the structure can become, and in all cases \( \varOmega \subset D \). Figure 1 illustrates an example level set function and the zero level set which identifies \( \varOmega \) and \( \partial \varOmega \) defined in Eq. (1).

Fig. 1
figure 1

Implicit boundary representation by the level set function

Full size image

The level set method was developed by Osher and Sethian (1988) for modeling moving boundaries encountered in many applications including combustion, computer vision, and path planning (Sethian 1999). Sethian and Wiegmann (2000) introduced a topology optimization routine where the structural boundary is defined by a level set function and updated using a stress-based heuristic criteria. A complete review of level set methods can be found in (Osher and Fedkiw 2001; van Dijk et al. 2013). The traditional algorithm requires solving the Hamilton Jacobi equation (HJE) to update \( \phi \) using a numerical procedure such as an upwind finite difference scheme. The HJE is written as follows:

$$\begin{aligned} \frac{\partial \phi (x,t)}{\partial t}+v_n\cdot \nabla \phi (x,t)=0 \end{aligned}$$
(2)

where t is a fictitious time and \( v_n \) represents a velocity field normal to the structural boundary defined on \( x\in \partial \varOmega \). Many techniques have been implemented to extend the normal velocity field such that it is redefined on the entire design domain \( x\in {\mathscr {D}} \) (Burger 2003). The velocity field is constructed using a shape sensitivity analysis to drive the design toward a local optimum Allaire et al. (2004). As the solution converges, the velocity field on the structural boundary will converge to zero, and the boundaries will stagnate.

3 Problem statement

While a substantial amount of research has been devoted to optimizing thermally conductive structures, relatively little attention has been given to problems where the boundary conditions are nonlinear. In Sect. 3.1, we introduce the nonlinear phenomenology of thermal radiation. Subsequently, we define a 2D, single-objective, single-constraint example optimization problem in Sect. 3.2.

3.1 Thermal radiation

Thermal radiation is a nonlinear mode of heat transfer where the heat power radiated is directly proportional to the fourth power of the surface temperature. The Stefan–Boltzmann equation quantifies the heat power radiated from a surface across all wavelengths in the electromagnetic spectrum.

$$\begin{aligned} Q_{\text {rad}}=\varepsilon \varUpsilon \theta _{\text {surf}}^4 \end{aligned}$$
(3)

In Eq. (3), \( Q_{\text {rad}} \) is the heat power flux radiated in units of \( \hbox {W}\,\hbox {m}^{-2} \), \( \varepsilon \) is the emissivity, \( \varUpsilon \) is the Stefan–Boltzmann constant \( 5.670\times 10^{-8} \hbox {W}\,\hbox {m}^{-2}{\hbox {K}^{-4}} \), and \( \theta _{\text {surf}} \) is the temperature field of the radiating surface. The emissivity \( \varepsilon \) varies between 0 and 1 and accounts for the fact that real surfaces do not absorb or emit as much energy as a blackbody (\( \varepsilon =1 \)). While the emissivity of real surfaces is also a function of wavelength, analysts oftentimes assume it to be constant as an approximation.

3.2 2D single-objective thermal radiation problems

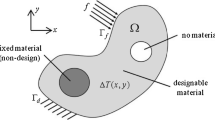
We consider 2D problems where a surface is radiating solely to an ambient environment and a fixed temperature boundary condition is enforced. A Dirichlet boundary condition is applied to an edge segment on the structural boundary and the radiating surface is defined as a fixed subdomain. Recall the notation defined in Sect. 2 which is used to describe the geometry. Figure 2 illustrates the design domain \( {\mathscr {D}} \), structure domain \( \varOmega \), radiating subdomain \( \varOmega _{\text {rad}} \) , and structure boundary \( \partial \varOmega \).

Fig. 2
figure 2

Structural domains and boundaries for 2D thermal radiation problem

Full size image

The structural boundary consists of two disjoint parts: the Dirichlet \( \Gamma _{D,\theta } \) and insulating \( \Gamma _{0,\theta } \) boundaries.

$$\begin{aligned} \partial \varOmega =\Gamma _{D,\theta }\cup \Gamma _{0,\theta } \end{aligned}$$
(4)

The structure domain always remains a subset of the design domain (\( \varOmega \subset D \)) as does the radiating subdomain always remain a subset of the structure domain (\(\varOmega _{\text {rad}}\subset \varOmega \)). These relations are illustrated in Fig. 2. While our approach would be capable of solving 3D problems, the added dimension significantly increases computational cost and complexity. We consider only 2D problems here in order to validate our gradient-based approach, rather than optimize the methodology for large and computationally expensive problems.

In this paper, we define a thermally efficient radiating structure as one that can exchange as much heat power between itself and its surroundings as possible provided some restriction on material or weight. The total heat power radiated (in units of watts \( \hbox {W} \)) is calculated by integrating the Stefan–Boltzmann law from Eq. (3) over the radiating surface \( \varOmega _{\text {rad}} \). The heat power radiated functional \( J(\varOmega _{\text {rad}},\theta ) \) is written as follows:

$$\begin{aligned} J(\varOmega _{\text {rad}},\theta )=\int _{\varOmega _{\text {rad}}}^{}\varepsilon \varUpsilon \theta ^{4}\,dA \end{aligned}$$
(5)

where \( \theta =\theta (x) \) is the temperature field within the design domain \( x\in {\mathscr {D}} \). Since \( \varOmega _{\text {rad}}\subset \varOmega \), the objective function \( J(\varOmega _{\text {rad}},\theta ) \) can also be defined without loss of generality as follows:

$$\begin{aligned} J(\varOmega ,\theta )=\int _{\varOmega }^{}\chi \varepsilon \varUpsilon \theta ^{4}\,dA \end{aligned}$$
(6)

where \( \chi \) is a domain flag defined in Eq. (7).

$$\begin{aligned} \chi ={\left\{ \begin{array}{ll} 1\qquad \text {for }\,x\in \varOmega _{\text {rad}}\\ 0\qquad \text {for }\,x\in {\mathscr {D}}\setminus \varOmega _{\text {rad}} \end{array}\right. } \end{aligned}$$
(7)

The reason why the objective is transformed in this way will be apparent when the notion of shape derivatives are introduced in Sect. 5.

To limit the amount of material that can be used to design the structure, a volume fraction equality constraint is enforced. The volume fraction is defined as the volume of the structure domain \( \varOmega \) normalized by the volume of the design domain \( {\mathscr {D}} \). Thus, the equality constraint function is written as follows:

$$\begin{aligned} h(\varOmega ) = \frac{\int _{\varOmega }^{}\,dV - V_{\text {req}}}{\int _{{\mathscr {D}}}^{}\,dV} \end{aligned}$$
(8)

where \( V_{\text {req}} \) is the required material volume. The integrals in the numerator and denominator represent the material and total design domain volumes, respectively. Finally, the governing partial differential equation (PDE) defined by Fourier’s law of conduction coupled with the Dirichlet boundary and radiation conditions is written in Eq. (9).

$$\begin{aligned} \begin{aligned} \text {div}\left( \kappa \nabla \theta \right)&=\varepsilon \varUpsilon \theta ^4&\quad&\text {in}\quad \varOmega _{\text {rad}} \\ \text {div}\left( \kappa \nabla \theta \right)&=0&\quad&\text {in}\quad \varOmega \setminus \varOmega _{\text {rad}} \\ \left( \kappa \nabla \theta \right) \cdot n&=0&\quad&\text {on}\quad \Gamma _{0,\theta }\\ \theta&=\theta _0&\quad&\text {on}\quad \Gamma _{D,\theta } \\ \end{aligned} \end{aligned}$$
(9)

In Eq. (9), \( \kappa \) is the second-order thermal conductivity tensor, and \( \theta _0 \) is the prescribed temperature on the Dirichlet boundary \( \Gamma _{D,\theta } \). We assume that the 2D elements have a uniform thickness of 1 and thus the radiating term \( \varepsilon \varUpsilon \theta ^4 \) on the first line of Eq. (9) is in units of \( \hbox {W}\,\hbox {m}^{-3} \). For isotropic materials, the thermal conductivity tensor reduces to a single term \( \varrho \) defined in units of \( \hbox {W}\,\hbox {m}^{-1}\,\hbox {K}^{-1} \) and also assumed to be invariant with temperature.

The above objective and constraint functions along with the governing PDE can now be formally written as the following optimization problem (SP):

$$\begin{aligned} \begin{array}{lrrlll} {\mathrm{(SP):}} &{} \max _{\varOmega } &{} {\int _{\varOmega }^{}\chi \varepsilon \varUpsilon \theta ^{4}\,dA} \\ &{} \text {subject to} &{} \frac{\int _{\varOmega }^{}\,dV - V_{\mathrm{req}}}{\int _{D}^{}\,dV} &{} = &{} 0 \\ &{} &{}\text {div}\left( \kappa \nabla \theta \right) &{} = &{} \varepsilon \varUpsilon \theta ^4 &{}\text {in}\quad \varOmega _{\mathrm{rad}} \\ &{} &{}\text {div}\left( \kappa \nabla \theta \right) &{} = &{} 0 &{}\text {in}\quad \varOmega \setminus \varOmega _{\mathrm{rad}} \\ &{} &{}\left( \kappa \nabla \theta \right) \cdot n&{} = &{} 0 &{}\text {on}\quad \Gamma _{0,\theta }\\ &{} &{}\theta &{} = &{}\theta _0 &{}\text {on}\quad \Gamma _{D,\theta } \\ \end{array} \end{aligned}$$

The volume fraction equality constraint is added to formulate a well-posed topology optimization problem. Without this constraint, the optimizer would select a fully filled material design domain to maximize the radiated heat power. While the volume fraction could also be posed as an inequality constraint, any solution with an inactive volume fraction inequality constraint could be improved by the addition of material to further increase the thermal conductivity of the structure.

4 Methodology

In order to solve optimization problem (SP), we employ an augmented Lagrangian method to handle the volume constraint. This method is detailed in Sect. 4.1. In addition, our level set method requires an explicit definition of the level set function over the design domain. This definition is detailed in Sect. 4.2. Section 4.3 provides an explanation of how the material properties are interpolated across the entire design domain using the Ersatz material approach. And finally Sect. 4.4 describes how the HJE is solved numerically at each step of the optimizer.

4.1 Augmented Lagrangian method

A common way to solve constrained optimization problems is to replace the original problem by a series of unconstrained subproblems which are iteratively solved until a converged solution is achieved. Each subproblem seeks to minimize a single equation constructed by adding terms derived from the constraint functions to the original objective function (Nocedal and Wright 2006). Example methods which uniquely define these subproblems include penalty methods, interior point methods, method of Lagrange multipliers, and augmented Lagrangian methods.

We select an augmented Lagrangian method to solve optimization problem (SP). The augmented Lagrangian combines both the Lagrangian function and a penalty function derived from the equality constraint. Equation (10) defines the augmented Lagrangian:

$$\begin{aligned} L(\varOmega ,\theta ,\lambda ,\mu )=J(\varOmega ,\theta )+\lambda h(\varOmega )+\frac{\mu }{2}\left[ h(\varOmega )\right] ^{2} \end{aligned}$$
(10)

where \( J(\varOmega ,\theta ) \) is the original objective function found in Eq. (6), \( h(\varOmega ) \) is the equality constraint function found in Eq. (8), \( \lambda \) is the Lagrange multiplier estimate, and \( \mu \) is the penalty parameter. The unconstrained subproblem to be solved at every iteration k during the optimization routine is then:

$$\begin{aligned} \underset{\varOmega }{{\text {arg}}\,{\text {min}}}\;L(\varOmega ,\theta (\varOmega ),\lambda ^k,\mu ^k) \end{aligned}$$
(11)

where the superscript k denotes the current iteration. Recall that the optimizer is changing the structural boundaries via updates to the level set function. However, for simplicity, we indicate \( \varOmega \) as the design variable describing the structural shape. Also, we have defined the temperature field as a function of the structural domain \( \theta =\theta (\varOmega ) \) since at every iteration, the finite element model is updated and solved using the current shape \( \varOmega \). More details on this step are provided in Sect. 4.3. The Lagrange multiplier estimate and penalty parameter are also iteratively updated to drive the design toward a feasible solution where \( \lambda \) approaches the Lagrange multiplier \( \lambda ^*\) that satisfies the Karush–Kuhn–Tucker (KKT) conditions. Our approach for updating these parameters follows that of Nocedal and Wright (2006).

4.2 Defining the level set function

The level set function \( \phi =\phi (x) \) is a scalar valued function defined on the design domain \( x\in {\mathscr {D}} \) illustrated in Fig. 2. Equation (1) defines the structure domain \( \varOmega \) where an isotropic material exists and the void domain \( {\mathscr {D}}\setminus \varOmega \) where no material exists. The boundary \( \partial \varOmega \) between the material and void domains can be calculated using a variety of interpolation techniques employing an approximate Heaviside function (van Dijk et al. 2013). In our approach, however, the level set function is interpolated within each element e via the shape functions \( N^e_i \) from the finite element mesh used to analyze the structure:

$$\begin{aligned} \phi (x)=\sum _{i=1}^{\ell }N^e_i(x)\phi ^e_i\qquad \text {for }x\in {\mathscr {T}}_e \end{aligned}$$
(12)

In Eq. (12) \( i=\lbrace {1,2,...,\ell }\rbrace \) where \( \ell \) is the total number of shape functions in element e, \( \phi ^e_i \) is the ith nodal value of the level set function in element e, and \( {\mathscr {T}}_e \) is the domain of element e. For our approach, we use the finite element model to define the level set function. Thus, the structure boundary \( \partial \varOmega \) is defined within each element cut by \( \phi =0 \) by solving the following equation for x:

$$\begin{aligned} \sum _{i=1}^{\ell }N^e_i(x)\phi ^e_i=0 \end{aligned}$$
(13)

For quadratic and higher order elements, a Heaviside function is a useful approximation for determining the structural boundary \( x\in \partial \varOmega \) within each element. However, this approximation will introduce numerical errors and care must be taken to devise a suitable function which balances numerical error and smoothness (since the Heaviside function itself is non-differentiable). For the example problem presented here, we use only linear finite elements and thus the structural boundary is piecewise linear and hence straightforward to calculate.

4.3 Ersatz material technique

Two strategies for handling elements cut by the zero level set \( \phi =0 \) are (1) the Eulerian approach and (2) the Lagrangian approach. In this paper, we adopt an Eulerian approach where the mesh for the design domain \( {\mathscr {D}} \) is kept fixed for the entirety of the optimization procedure. The Ersatz material technique then dictates that elements cut by \( \phi =0 \) are assigned an interpolated value for the material thermal conductivity. In the Lagrangian approach, the structural domain \( \varOmega \) is re-meshed at each iteration in the optimizer such that all elements are either solid material or completely void. Void elements are removed entirely from the finite element model. Both Dapogny et al. (2014) and Allaire et al. (2014) have shown that Lagrangian methods improve accuracy but suffer from the added computational effort needed to perform a meshing operation at every iteration. Using the Ersatz material approach, a density value \( \rho _e \) is assigned to each element e similar to the design variables used in a SIMP-based approach. These values are used to interpolate the thermal conductivity within cut elements and are calculated based on the volume fraction within element e lying inside the structure domain according to Eq. (14):

$$\begin{aligned} \rho _e=\frac{\left| \varOmega _e\right| }{\left| {\mathscr {T}}_e\right| } \end{aligned}$$
(14)

where \( \varOmega _e \) is the material subdomain of element e defined as \( \varOmega _e:=\left\{ x \mid x\in \varOmega \cap {\mathscr {T}}_e\right\} \), \( \left| \varOmega _e\right| \) is the area of \( \varOmega _e \), and \( \left| {\mathscr {T}}_e\right| \) is the total element area since the elements are two-dimensional. In the case of a 3D problem, the areas described above would be defined as volumes.

Equation (13) provides an analytic expression for defining the zero level set using the element shape functions. Subsequently, it is straightforward to calculate the element density using Eq. (14). Elements not intersected by the boundary \( \partial \varOmega \) are either void (\( \rho _e=0 \)) if all level set nodal values are all positive, or completely solid (\( \rho _e=1 \)) if the nodal values are all non-positive.

The densities \( \rho _e \) linearly interpolate the element thermal conductivity matrices \( {\mathbf {L}}_e \). The global thermal conductivity matrix is then assembled according to the following equation:

$$\begin{aligned} {\mathbf {L}}=\sum _{e=1}^{m}\max \left( \delta ,\frac{\left| \varOmega _e\right| }{\left| {\mathscr {T}}_e\right| }\right) {\mathbf {L}}_e \end{aligned}$$
(15)

where \( \delta \) is a small positive number and m is the total number of elements in the mesh. If an element density lies in the range \( 0\le \rho _e\le \delta \), then the element matrix is multiplied by \( \delta \) to avoid ill-conditioning or generating a singular global matrix. The analyst must make a judicious choice for \( \delta \) which balances numerical stability and model accuracy.

4.4 Solving the Hamilton Jacobi equation

The level set function is updated at each optimization iteration by solving the Hamilton–Jacobi equation found in Eq. (2). We initialize the level set function as a signed distance function, reproduced from Dapogny and Frey (2012) and presented in Eq. (16) below:

$$\begin{aligned} \begin{aligned} D_s(x)={\left\{ \begin{array}{ll}-d(x,\partial \varOmega )&{}\qquad \text {if}\quad x\in \varOmega \\ 0&{}\qquad \text {if}\quad x\in \partial \varOmega \\ d(x,\partial \varOmega )&{}\qquad \text {if}\quad x\in {\mathscr {D}}\setminus \varOmega \end{array}\right. } \end{aligned} \end{aligned}$$
(16)

where \( d(x,\partial \varOmega ) \) is the shortest distance between the point x and the boundary \( \partial \varOmega \). From this distance function, several metrics can be computed such as the boundary normal \( n={\nabla \phi }\big /{\left| \nabla \phi \right| } \) and curvature \( H=\text {div}\left( {\nabla \phi }\big /{\left| \nabla \phi \right| }\right) \). The normal advection velocity \( v_n \) can therefore be rewritten as a vector with magnitude v and direction n:

$$\begin{aligned} v_n=v\frac{\nabla \phi }{\left| \nabla \phi \right| } \end{aligned}$$
(17)

Equation (17) is substituted into Eq. (2) to yield the following form of the HJE.

$$\begin{aligned} \frac{\partial \phi }{\partial t}+v|\nabla \phi |=0 \end{aligned}$$
(18)

We periodically reinitialize the level set function to a signed distance function in order to accurately calculate the boundary normal n(x) and curvature H(x) for \( x\in {\mathscr {D}} \) (Allaire et al. 2004; Wang et al. 2004; van Dijk et al. 2013). These fields are a necessary ingredient to constructing the velocity field discussed later in this paper. We accomplish these reinitializations by solving the Eikonal equation (Dapogny and Frey 2012), a boundary value problem stated below:

$$\begin{aligned} \begin{aligned} \left| \nabla \phi (x)\right|&=1\\ \phi (x)&=0\qquad \forall x\in \partial \varOmega \end{aligned} \end{aligned}$$
(19)

A method for solving Eq. (19) was introduced by Sethian (1999) known as the fast marching method. We employ this method to reinitialize the level set function periodically because it is significantly faster than iterative algorithms. Since the level set function needs to be reinitialized often, this advantage will play an important role in speeding up our level set-based approach.

Equation (18) can be solved using a variety of upwind finite difference schemes for structured meshes (Sethian 1999; Allaire et al. 2004; Carlini et al. 2005) as well as for unstructured meshes (Sethian 1999; Zhu and Qiu 2013) and more recently using the method of characteristics (Allaire et al. 2014). We choose a second-order upwind scheme to solve Eq. (18) on a structured Cartesian grid. Details regarding this scheme can be found in Sethian’s book (1999). Neumann type boundary conditions are implemented and written as follows:

$$\begin{aligned} \frac{\partial \phi }{\partial n}=0\qquad \text {on}\qquad \partial {\mathscr {D}} \end{aligned}$$
(20)

where \( \partial {\mathscr {D}} \) is the boundary of the design domain. While there is no clear correct choice for the level set function boundary conditions, the Neumann type seems to be the most natural and most common (Allaire and Jouve 2005; van Dijk et al. 2013). This boundary condition alleviates any artificial effect that the design domain boundary would have on the structural boundary.

The velocity field v in Eq. (18) is constructed to minimize the augmented Lagrangian stated in Eq. (10). Recall in optimization problem (SP) that the design variable is the structural shape \( \varOmega \). In order to employ a gradient-based optimizer, we require sensitivity information of the augmented Lagrangian to perturbations in the structural boundary. This sensitivity information is commonly referred to as a shape derivative. In order to improve convergence and stability, the velocity field is also regularized. We accomplish this by projecting the velocity onto the Hilbert inner product space presented by Gournay (De Gournay 2006).

5 Shape sensitivity analysis

A shape sensitivity analysis is performed on the radiated heat power objective functional defined in Eq. (6) and restated below:

$$\begin{aligned} J(\varOmega ,\theta )=-\int _{\varOmega }^{}\chi \varepsilon \varUpsilon \theta ^{4}\,dA \end{aligned}$$
(21)

We negate the function found in Eq. (6) since our goal is to maximize the heat power radiated. We also restate the governing PDE here for reference:

$$\begin{aligned} \begin{aligned} \text {div}\left( \kappa \nabla \theta \right)&=\chi \varepsilon \varUpsilon \theta ^4&\quad&\text {in}\quad \varOmega \\ \left( \kappa \nabla \theta \right) \cdot n&=0&\quad&\text {on}\quad \Gamma _{0,\theta }\\ \theta&=\theta _0&\quad&\text {on}\quad \Gamma _{D,\theta } \\ \end{aligned} \end{aligned}$$
(22)

where the domain flag \( \chi \) is a Boolean operator used to specify the radiating (\( \chi =1 \)) and non-radiating (\( \chi =0 \)) domains explicitly written in Eq. (9). The derivation presented here closely follows that found in Allaire et al. (2004) which the authors credit to Murat and Simon (1975) and Simon (1980). The interested reader should refer to (Pironneau 2012) and (Sokołowski and Zolésio 1992) for a more detailed review of shape derivatives.

We use the adjoint method to perform the necessary shape sensitivity analysis. The adjoint method allows for efficient calculation of sensitivities for large dimensional problems oftentimes encountered in PDE constrained optimization. This process is enumerated in the following steps:

  1. 1.

    Define the Lagrangian \( {\mathscr {L}}(\varOmega ,\theta ,q) \) from the objective function in (21), governing PDE in (22) and corresponding Lagrange multiplier q.

  2. 2.

    Find the stationary point \( \left( \theta ^{*},q^{*}\right) \) of the Lagrangian by setting the derivatives with respect to the Lagrange multiplier q and solution \( \theta \) to zero. These equations define the optimality conditions for minimizing the Lagrangian.

  3. 3.

    Calculate the shape derivative of the Lagrangian at the stationary point \( {\mathscr {L}}(\varOmega ,\theta ^{*},q^{*}) \), where \( q^* \) is the adjoint state vector.

Beginning with step (1), the Lagrangian is defined as follows:

$$\begin{aligned} \begin{aligned} {\mathscr {L}}(\varOmega ,\theta ,q)=&-\int _{\varOmega }^{}\chi \varepsilon \varUpsilon \theta ^{4}\,dV\\&+\int _{\varOmega }^{}q\cdot \left( \text {div}\left( \kappa \nabla \theta \right) -\chi \varepsilon \varUpsilon \theta ^{4}\right) dV\\&+\int _{\Gamma _{D,\theta }}^{}\left( (\kappa \nabla q)\cdot n\right) \left( \theta -\theta _0\right) ds\\&+\int _{\Gamma _{0,\theta }}^{}q\cdot \left( -\left( \kappa \nabla \theta \right) \cdot n\right) ds \end{aligned} \end{aligned}$$
(23)

In Eq. (23), an insulating boundary condition on \( \Gamma _{0,\theta } \) has been imposed. Recall that the boundary \( \partial \varOmega \) is composed of both the Dirichlet and insulating boundaries according to Fig. 2:

$$\begin{aligned} \partial \varOmega =\Gamma _{D,\theta }\cup \Gamma _{0,\theta } \end{aligned}$$
(24)

After applying Green’s first identity and grouping terms, the Lagrangian is transformed into Eq. (25).

$$\begin{aligned} \begin{aligned} {\mathscr {L}}(\varOmega ,\theta ,q)=&-\int _{\varOmega }^{}\chi \varepsilon \varUpsilon \theta ^{4}\,dV-\int _{\varOmega }^{}\left( \nabla q\cdot \kappa \nabla \theta \right) dV\\&-\int _{\varOmega }^{}q\cdot \chi \varepsilon \varUpsilon \theta ^{4}\,dV \\&+\int _{\Gamma _{D,\theta }}^{}\left[ q\cdot \left( (\kappa \nabla \theta )\cdot n\right) \right. \\&\left. +\left( \theta -\theta _0\right) \left( (\kappa \nabla q)\cdot n\right) \right] ds \end{aligned} \end{aligned}$$
(25)

In step (2), we find the stationary point \( (\theta ^*,q^*) \) where the partial derivatives of the Lagrangian with respect to q and \( \theta \) are set equal to zero. The derivative of the Lagrangian with respect to q in the direction \( \zeta \in H^1(\varOmega ) \), where \( H^1(\varOmega ) \) is the Sobolev space whose functions and first-order weak derivatives are both Lebesgue square-integrable, is given below:

$$\begin{aligned} \begin{aligned} \left\langle \frac{\partial {\mathscr {L}}}{\partial q}\left( \varOmega ,\theta ^*,q^*\right) ,\zeta \right\rangle =&-\int _{\varOmega }^{}\left( \nabla \zeta \cdot \kappa \nabla \theta ^*\right) dV\\&-\int _{\varOmega }^{}\zeta \cdot \chi \varepsilon \varUpsilon \theta ^{*4}\,dV\\&+\int _{\Gamma _{D,\theta }}^{}\zeta \cdot \left( (\kappa \nabla \theta ^*)\cdot n\right) ds\\&+\int _{\Gamma _{D,\theta }}^{}\left( \theta ^{*}-\theta _0\right) \left( \left( \kappa \nabla \zeta \right) \cdot n\right) ds \end{aligned} \end{aligned}$$
(26)

Using Green’s first identity again to rewrite the first integral and collecting terms on the Dirichlet and insulating boundaries, Eq. (26) is transformed as follows:

$$\begin{aligned} \begin{aligned} \left\langle \frac{\partial {\mathscr {L}}}{\partial q}\left( \varOmega ,\theta ^*,q^*\right) ,\zeta \right\rangle =&\int _{\varOmega }^{}\zeta \cdot \left( \text {div}(\kappa \nabla \theta ^*)-\chi \varepsilon \varUpsilon \theta ^{*4}\right) dV \\&+\int _{\Gamma _{0,\theta }}^{}\zeta \cdot \left( -(\kappa \nabla \theta ^*)\cdot n\right) ds\\&+\int _{\Gamma _{D,\theta }}^{}\left( \theta ^{*}-\theta _0\right) \left( \left( \kappa \nabla \zeta \right) \cdot n\right) ds \end{aligned} \end{aligned}$$
(27)

Setting Eq. (27) equal to zero yields the original state equation and boundary conditions found in Eq. (22). The first integral gives the state equation for any \( \zeta \) with compact support in \( \varOmega \). Varying the trace function \( \zeta \) on \( \Gamma _{0,\theta } \) gives the insulating boundary condition and by varying \( (\kappa \nabla \zeta )\cdot n \) on \( \Gamma _{D,\theta } \) gives the Dirichlet boundary condition.

Next the derivative of the Lagrangian with respect to the state variable \( \theta \) is used to define the adjoint equations.

$$\begin{aligned} \begin{aligned} \left\langle \frac{\partial {\mathscr {L}}}{\partial \theta }\left( \varOmega ,\theta ^*,q^*\right) ,\zeta \right\rangle =&-\int _{\varOmega }^{}\zeta \cdot 4\chi \varepsilon \varUpsilon \theta ^{*3}\,dV\\&-\int _{\varOmega }^{}\left( \nabla q^*\cdot \kappa \nabla \zeta \right) dV\\&-\int _{\varOmega }^{}\zeta \cdot \left( q^*\cdot 4\chi \varepsilon \varUpsilon \theta ^{*3}\right) dV\\&+\int _{\Gamma _{D,\theta }}^{}q^*\cdot \left( (\kappa \nabla \zeta )\cdot n\right) ds\\&+\int _{\Gamma _{D,\theta }}^{}\zeta \cdot \left( (\kappa \nabla q^*)\cdot n\right) ds \end{aligned} \end{aligned}$$
(28)

Again by using Green’s first identity and grouping terms on the Dirichlet and insulating boundary conditions, Eq. (28) is transformed as follows:

$$\begin{aligned} \begin{aligned} \left\langle \frac{\partial {\mathscr {L}}}{\partial \theta }\left( \varOmega ,\theta ^*,q^*\right) ,\zeta \right\rangle =&\int _{\varOmega }^{}\zeta \cdot \left( \text {div}(\kappa \nabla q^*)-4\chi \varepsilon \varUpsilon \theta ^{*3}-q^*\right. \\&\left. \cdot 4\chi \varepsilon \varUpsilon \theta ^{*3}\right) dV \\&+\int _{\Gamma _{0,\theta }}^{}\zeta \cdot \left( -(\kappa \nabla q^*)\cdot n\right) ds\\&+\int _{\Gamma _{D,\theta }}^{}q^*\cdot \left( (\kappa \nabla \zeta )\cdot n\right) ds \end{aligned} \end{aligned}$$
(29)

Setting Eq. (29) equal to zero yields the adjoint state equations. The first integral gives the adjoint state equation for any \( \zeta \) with compact support in \( \varOmega \):

$$\begin{aligned} \text {div}(\kappa \nabla q^*)-4\chi \varepsilon \varUpsilon \theta ^{*3}-4q^*\cdot \chi \varepsilon \varUpsilon \theta ^{*3}=0\qquad \text {in}\quad \varOmega \end{aligned}$$
(30)

Similarly, the insulating boundary condition is given by varying the trace function \( \zeta \) on the boundary \( \Gamma _{0,\theta } \):

$$\begin{aligned} -(\kappa \nabla q^*)\cdot n=0\qquad \text {on}\quad \Gamma _{0,\theta } \end{aligned}$$
(31)

Finally, the Dirichlet boundary condition is given by varying \( \kappa \nabla \zeta \) on the boundary \( \Gamma _{D,\theta } \):

$$\begin{aligned} q^*=0\qquad \text {on}\quad \Gamma _{D,\theta } \end{aligned}$$
(32)

Note that \( q^* \) is the adjoint state vector. In summary, the adjoint state is defined by the following set of equations:

$$\begin{aligned} \begin{aligned} \text {div}\left( \kappa \nabla q^*\right) -4\chi \varepsilon \varUpsilon \theta ^{*3}-4q^*\cdot \chi \varepsilon \varUpsilon \theta ^{*3}&=0&\quad&\text {in}\quad \varOmega \\ \left( \kappa \nabla q^*\right) \cdot n&=0&\quad&\text {on}\quad \Gamma _{0,\theta }\\ q^*&=0&\quad&\text {on}\quad \Gamma _{D,\theta } \\ \end{aligned} \end{aligned}$$
(33)

While the thermal radiation problem is shown to be well posed, it is not self-adjoint (i.e., \( q^*\ne \theta \)). In order to calculate the shape derivative, we need to first solve the original governing PDE in Eq. (22). Next, the solution \( \theta \) is substituted into Eq. (33) as \( \theta ^* \) and the equation is solved for \( q^* \). We use the finite element method to solve both PDEs numerically.

Finally, the shape derivative of the Lagrangian defined in Eq. (25) at the stationary point \( \left( \theta ^{*},q^*\right) \) is calculated. Allaire et al. (2004) provide the general forms of shape derivatives for domain and boundary integral functionals which are used to construct the following:

$$\begin{aligned} \begin{aligned} D{\mathscr {L}}(\varOmega )(\xi )=&\int _{\partial \varOmega }^{}\xi \cdot n\left( -\chi \varepsilon \varUpsilon \theta ^{*4}-\nabla q^*\cdot \kappa \nabla \theta ^*-q\cdot \chi \varepsilon \varUpsilon \theta ^{*4}\right) ds\\&+\int _{\Gamma _{D,\theta }}^{}\xi \cdot n\left( \frac{\partial \bigg (q^*\cdot \left( (\kappa \nabla \theta ^*)\cdot n\right) \bigg )}{\partial n}\right) ds\\&+\int _{\Gamma _{D,\theta }}^{}\xi \cdot n\left( \frac{\partial \bigg (\left( \theta ^*-\theta _0\right) \left( (\kappa \nabla q)\cdot n\right) \bigg )}{\partial n}\right) ds\\&+\int _{\Gamma _{D,\theta }}^{}\xi \cdot n\bigg (H\left[ q^*\cdot \left( (\kappa \nabla \theta ^*)\cdot n\right) \right. \\&\left. +\left( \theta ^*-\theta _0\right) \left( (\kappa \nabla q)\cdot n\right) \right] \bigg )ds \end{aligned} \end{aligned}$$
(34)

Splitting terms into the Dirichlet and insulating boundaries, and using Eqs. (22) and (33) to enforce \( {{\theta }}^*-\theta _0=0 \) and \( q^*=0 \) on the boundary \( \Gamma _{D,\theta } \), the above equation is simplified as follows:

$$\begin{aligned} \begin{aligned}&D{\mathscr {L}}(\varOmega )(\xi )\\&\quad =\int _{\Gamma _{0,\theta }}^{}\xi \cdot n\left( -\chi \varepsilon \varUpsilon \theta ^{*4}-\nabla q^*\cdot \kappa \nabla \theta ^*-q^*\cdot \chi \varepsilon \varUpsilon \theta ^{*4}\right) ds\\&\quad \quad +\int _{\Gamma _{D,\theta }}^{}\xi \cdot n\left( -\chi \varepsilon \varUpsilon \theta ^{*4}-\nabla q^*\cdot \kappa \nabla \theta ^*\right) ds \end{aligned} \end{aligned}$$
(35)

In practice, additional simplifications are made to shorten Eq. (35). First, the optimizer should not be removing material from the Dirichlet boundaries since this area is the source of the heat power being radiated by the structure. Isolating or removing material in this region would cause the temperature on the radiating subdomain to drop, causing the radiated heat power to decrease. Therefore, on \( \Gamma _{D,\theta } \) , the optimizer is forced to retain the structural boundary and the dot product \( \xi \cdot n \) goes to zero, eliminating the second integral in Eq. (35).

Using a similar reasoning, the radiation flag \( \chi \) is only active (\( \chi =1 \)) on the subdomain \( \varOmega _{\text {rad}} \). This subdomain should also remain fixed since removing radiating material will reduce the radiated heat power. As such, the optimizer is only affecting regions with \( \chi (x)=0 \) where there is no thermal radiation. Note that regions and boundaries that are not able to be modified by the optimizer are termed “non-design,” meaning they are not subject to the removal or addition of material. By enforcing these practices, Eq. (35) is reduced to the following single term:

$$\begin{aligned} D{\mathscr {L}}(\varOmega )(\xi )=\int _{\Gamma _{0,\theta }}^{}\xi \cdot n\left( -\nabla q^*\cdot \kappa \nabla \theta \right) ds \end{aligned}$$
(36)

As previously mentioned, solutions for both \( \theta ^* \) and \( q^* \) are required to calculate the shape derivative. These solutions are found numerically using the finite element method.

The sensitivity field for the radiating heat power functional defined in Eq. (36) is also calculated using the finite element method according to Eq. (37):

$$\begin{aligned} D{\mathscr {L}}(\varOmega )(\xi )_e=-\frac{1}{|{\mathscr {T}}_e|}{\mathbf {q}}_{e}^{T}{\mathbf {L}}_e\varvec{\theta }_e \end{aligned}$$
(37)

where the subscript e identifies the local element, \( {\mathbf {q}}_e \) is the element adjoint vector, and \( \varvec{\theta }_e \) is the element nodal temperatures. Equation (37) is normalized by the element area \( |{\mathscr {T}}_e|\) due to the fact that the finite element equations are written in the weak form, and hence the term \( {\mathbf {q}}_{e}^{T}{\mathbf {L}}_e\varvec{\theta }_e \) is an integral over the element volume.

$$\begin{aligned} {\mathbf {q}}_{e}^{T}{\mathbf {L}}_e\varvec{\theta }_e={\mathbf {q}}_{e}^{T}\left[ \int _{{\mathscr {T}}_e}^{}{\mathbf {B}}^{T}{\mathbf {D}}{\mathbf {B}} \ \text {det}\left( {\mathbf {J}}_e\right) dV\right] \varvec{\theta }_e \end{aligned}$$
(38)

where B is the strain matrix of shape function derivatives, D is the constitutive matrix, and Je is the element Jacobian matrix. Equation (38) must be normalized by \( |{\mathscr {T}}_e|\) to arrive at the shape sensitivity at the element centroid.

6 2D case study

We present a 2D problem to demonstrate that the optimizer is converging to locally optimal solutions and validate that the shape sensitivity is correct. Modeling, analysis, and optimization are all performed within the MATLAB®environment. All numerical analyses are performed and timed on a Dell laptop equipped with an Intel® Core\(^{\mathrm{TM}}\) i7-4700MQ processor running at \( {2.40}\,\hbox {GHz} \), and \( {16.0}\,\hbox {GB} \) of DDR3 SDRAM. All codes were compiled and run using MATLAB®version 8.6 (R2015b). Section 6.1 defines the problem geometry, boundary conditions, and material properties. Section 6.2 provides an overview of the finite element model used to evaluate the structural performance and sensitivities. Then in Sect. 6.3, we illustrate several candidate solutions, demonstrating that the thermal compliance objective function is insufficient for solving this class of problems.

6.1 Problem definition

The problem analyzes a thin square plate with dimensions \( {100}\,\hbox {cm}\times {100}\,\hbox {cm} \) and thickness \( {1}\,\hbox {cm} \). A Dirichlet boundary condition is enforced on a \( {20}\,\hbox {cm} \) segment along the center of the left edge where the temperature is fixed at \( {300}\,\hbox {K}\). The plate rejects heat via thermal radiation on a domain of size \( {4}\,\hbox {cm}\times {100}\,\hbox {cm} \) located on the right side of the square plate. This subdomain \(\varOmega _{\text {rad}} \) is the only region where heat is being radiated. Thermal radiation is emitted from the surface of this subdomain rather than the edges, accounting for a total of \( {800}\,\hbox {cm}^{2} \) when considering both front (out of the page) and back (into the page) surfaces. For simplicity, the radiating surface is modeled as a perfect blackbody, meaning the emissivity \( \varepsilon =1 \) and the plate does not absorb any energy from the surrounding environment (assumes that the mean ambient temperature is \({0}\,\hbox {K}\)). Figure 3 illustrates the problem geometry.

Fig. 3
figure 3

Geometry, boundary conditions, and subdomain definitions of 2D thermally radiating plate

Full size image

In Fig. 3, the gray region indicates the radiating subdomain \( \varOmega _{\text {rad}} \) as well as the non-design subdomain (i.e., the radiating material is fixed during the optimization and cannot change shape). This is a common tactic used in the topology optimization community to enforce a design-independent load condition. Some authors have also considered design-dependent load conditions where the boundary conditions are affected by the structural shape (Bourdin and Chambolle 2003; Allaire et al. 2004; Iga et al. 2009; Yamada et al. 2011). However, design-dependent load conditions are computationally challenging to implement and are not necessary for the purposes of verifying the thermal heat-radiated sensitivity analysis.

The plate is made from an isotropic material (aluminum alloy) whose physical properties are listed in Table 1.

Table 1 Aluminum alloy material properties
Full size table

Note that the material properties are identical for both the design and non-design domains.

6.2 Finite element model

A finite element model is used to solve the governing PDE from Eq. (9) for the 2D radiating plate problem illustrated in Fig. 3. For an in-depth review of finite element methods, the interested reader is referred to Bathe (2014). We employ MATLAB®’s Partial Differential Equation Toolbox to handle finite element modeling and analysis. A structured mesh is generated using 5000 linear triangle elements including 2601 nodes.

The finite element program solves the following global linear system of equations:

$$\begin{aligned} {\mathbf {L}}\varvec{\theta }={\mathbf {g}} \end{aligned}$$
(39)

where \( {\mathbf {L}} \) is the \( p\times p \) global thermal conductivity matrix, \( \varvec{\theta } \) is the \( p\times 1 \) temperature vector, and \( {\mathbf {g}} \) is the \( p\times 1 \) heat load vector. The dimension p is the number of nodes (and degrees of freedom) in the finite element model. MATLAB®’s PDE Toolbox implements a Gauss–Newton solver since the heat load vector \( {\mathbf {g}} \) is a nonlinear function of the temperature according to the Stefan–Boltzmann law. The global conductivity matrix is assembled from the elemental conductivity matrices according to Eq. (15). The heat power radiated is calculated using Gauss quadrature to integrate the fourth power of the temperature in each radiating element.

6.3 Efficient thermal design using a compliance objective function

Various other researchers, while not tackling problems that incorporate thermally radiating boundary conditions in particular, have investigated the design of efficient thermally conductive structures (Gao et al. 2008; Iga et al. 2009; Burger et al. 2013; Liu and Tovar 2014; Zhu et al. 2016). The common objective function used in these problems is a thermal compliance function written as follows:

$$\begin{aligned} J=\int _{\varOmega }^{}\left( \nabla \theta \cdot \kappa \nabla \theta \right) dA \end{aligned}$$
(40)

where \( \nabla \theta \) is the temperature gradient vector field. Equation (40) is analogous to the structural compliance objective where \( \nabla \theta \) and \( \kappa \) are replaced, respectively, by the second-order strain tensor and fourth-order elasticity tensor (Allaire et al. 2002). The thermal compliance functional is a measure of how well the structure conducts heat. By minimizing the thermal compliance, the optimizer is minimizing the temperature gradients and hence keeping the structure as isothermal as possible. Thus, the goal of these problems is to design for thermal efficiency since a limited amount of material is allocated to minimize thermal resistance and hence transport heat as effectively as possible.

Table 2 Thermal compliance vs. radiated heat power objective function comparison for three structural designs
Full size table

A classic example is the 2D design of a thermal heat sink in a square design domain. This problem has been solved using both SIMP (Bendsøe and Sigmund 2004; Maute 2014) and level set methods (Yamada et al. 2011). In this problem, a uniformly distributed heat load is imparted on the design domain, with a fixed temperature on a segment of one edge. The solution is a symmetric branched tree structure which attempts to capture as much of the distributed heat load and transfer it to the Dirichlet boundary. This classic problem has also been solved in 3D by Burger et al. (2013).

We find that minimizing the thermal compliance of a thermally radiating structure does not necessarily maximize the heat power radiated. If these two objective functions were negatively correlated, we could pose the optimization problem using a thermal compliance objective function. However, we demonstrate a counterexample where the two objective functions are instead positively correlated. Consider the three test designs illustrated in Table 2, each with a volume fraction of 0.5, along with their corresponding finite element solutions. The boundary conditions and material properties are the same as those presented in Sect. 6.1. Each design is evaluated for thermal compliance and heat power radiated.

The material and void domains in the illustrated shapes are designated by the cyan and white colors, respectively. The radiating strip is shown in gray on the right side of the design domain as was depicted in Fig. 3. Note that although the third design (bottom row in Table 2) completely disconnects the material domain from the radiating domain, the structure is still able to radiate some heat. Using the Ersatz material approach described in Sect. 4.3, the void domain retains a small nonzero thermal conductivity. The thermal conductivity of the void region is \( 10^{3} \) times smaller than the nominal material conductivity.

It is clear from Table 2 that there is a positive rather than negative correlation between the thermal compliance and heat power radiated functions of the three test designs. The designs in Table 2, which exhibit lower thermal compliance also have a reduced capacity to radiate heat. This finding debunks our hypothesis that these two objective functions are strictly negatively correlated, such that a lower thermal compliance design would always be radiating a larger amount of heat. While there are possible cases in which these two objectives do negatively correlate, it is clear from the above counterexamples that this is not always guaranteed. As such, it is crucial to develop a topology optimization framework which specifically defines a radiated heat power objective function and its corresponding shape derivative.

6.4 Numerical results

A finite element analysis is first performed on the plate with all of the design domain filled by material. The results of the finite element analysis are shown in Fig. 4. The temperature on the Dirichlet boundary is fixed at \( {300}\,\hbox {K}\) and heat flows from this boundary to the radiating domain, where it is then radiated out to the ambient surroundings. The average temperature of the radiating boundary is approximately \( {278}\,\hbox {K} \) and the total heat power radiated from this surface is \( {27.25}\,\hbox {W} \).

Fig. 4
figure 4

Finite element solution of 2D thermally radiating plate

Full size image

We also evaluate two designs each with a volume fraction of 0.5 to serve as baselines to compare with those generated by the topology optimization method. They are shown in Fig. 5. Test Design 1 and Test Design 2 have total radiated heat powers of \( {22.58}\,\hbox {W} \) and \( {22.90}\,\hbox {W} \) , respectively. Because the boundary conditions are symmetric about the horizontal mid-line of the design domain, both design shapes also exhibit this symmetry. The intuition leading to these design shapes is that thermal conduction is a linear phenomenon, and the goal is to maximize the radiated heat power by designing a structure with minimal thermal gradients between the Dirichlet boundary and radiating subdomain. As such, keeping the thermal pathways as direct (i.e., as short) as possible to the radiating subdomain should yield a well-performing structure. Again these two designs will be revisited later to compare to the results from the topology optimization method.

Fig. 5
figure 5

Baseline test designs for optimization problem (SP)

Full size image

The topology optimization problem (SP) is solved with a volume fraction equality constraint of 0.5. The first case is initiated with a fully filled design domain, and a Lagrange multiplier estimate and penalty parameter of \( \lambda ^0=1 \) and \( \mu ^0=10 \) , respectively. The initial and final shapes are illustrated in Fig. 6. The optimal shape radiates \( {24.1}\,\hbox {W} \) of heat power. Thus, the structural weight is reduced by \( 50\% \) while the heat rejected drops by \( 11.5\% \) from the fully filled design. The optimal design is analyzed to show the temperature and heat flow fields in Fig. 7.

Fig. 6
figure 6

Initial and optimal shapes for optimization problem (SP)

Full size image
Fig. 7
figure 7

Finite element solution of optimal design for optimization problem (SP)

Full size image

The objective, constraint and augmented Lagrangian histories are given next in Fig. 8. From Fig. 8b, the shape converges after approximately 45 iterations.

Fig. 8
figure 8

Objective, constraint, augmented Lagrangian, and Lagrange multiplier estimate histories for optimization problem (SP)

Full size image

The prior oscillations are due to several factors including that (1) the initial design is infeasible (\( h(\varOmega )\ne 0 \)), (2) the Lagrange multiplier estimate is updated at each iteration using a monotonically increasing penalty parameter, and (3) the iterative updates to the structural boundary allow for a small increase in the augmented Lagrangian up until iteration 50. Allowing the augmented Lagrangian to increase in the first few iterations allows the optimizer to find a locally optimal solution that is sufficiently far, or topologically different, from the initial design. The number of iterations in which the augmented Lagrangian is allowed to increase is a heuristic parameter. Allaire et al. (2004) mention that different choices of this parameter can yield different locally optimal solutions.

In the above analysis, we implement a backtracking line search method to speed convergence. Our backtracking routine iteratively reduces the number of time steps T and step size \( \varDelta t \) to advance the level set function until the updated augmented Lagrangian is reduced. If the optimizer selects an update corresponding to the maximum number of time steps \( T=T_{\text {max}} \), the next optimization iteration will attempt to advance the level set function by a larger number of time steps. Conversely, if the optimizer selects a single time step, \( T=1 \), the next iteration will use a smaller time step. This technique is similar to the trust region methods discussed in Nocedal and Wright (2006). The time step size is constrained by the Courant–Friedrichs–Lewy (CFL) condition since we are using an explicit time integration scheme to solve the HJE.

For a converged solution, the gradient of the augmented Lagrangian should be approximately zero. This criterion is used in augmented Lagrangian methods to determine that a KKT point has been reached. Because the velocity field is constructed from the derivative of the augmented Lagrangian with respect to a perturbation in the normal direction of the boundary, we expect the velocity at the boundary of the shape to approach zero (Allaire et al. 2004). Figure 9 illustrates several metrics of the velocity field on the structural boundary over the optimization history.

Fig. 9
figure 9

Convergence history using boundary velocity metrics for optimization problem (SP)

Full size image

In Fig. 9a, the metrics labeled as “Min(\(v_{\partial \varOmega }\))” and “Max(\(v_{\partial \varOmega }\))” refer to the minimum and maximum value of the velocity on the boundary, respectively. The normed metrics are defined using Eq. (41) for the \( L_1 \) norm and (42) for the \( L_2 \) norm:

$$\begin{aligned}&\left| \left| v_{\partial \varOmega }\right| \right| _{1}=\frac{\int _{\partial \varOmega }^{}|v|\,ds}{\left| \partial \varOmega \right| } \end{aligned}$$
(41)
$$\begin{aligned}&\left| \left| v_{\partial \varOmega }\right| \right| _{2}=\frac{\left[ \int _{\partial \varOmega }^{}|v|^2\,ds\right] ^{1/2}}{\left| \partial \varOmega \right| } \end{aligned}$$
(42)

where \( \left| \partial \varOmega \right| \) is the perimeter of the structural boundary \( \partial \varOmega \). Intuitively, as the velocity field approaches zero on the boundary \( \partial \varOmega \), updates to the level set function from solving the Hamilton–Jacobi equations will cause smaller changes in the shape. Therefore, the structure domain \( \varOmega \) will ultimately converge.

From the plots in Fig. 9b, it is clear that a converged solution has been achieved since the velocity field norms are asymptotically becoming smaller. Note that the velocity fields will never achieve zero due to numerical errors inherent in the level set method. One of the primary errors arises from interpolating the shape sensitivity field from the center of each mesh element to the node points (Dijk et al. (2012)). The interpolated sensitivity field is then used to construct the velocity field. Additionally, the reinitialization of the level set function using the fast marching method is not a volume-preserving procedure, meaning that the structural boundary will shift by some small amount. In the analyses considered here, the level set function is reinitialized every other time step taken by the HJE solver.

Since a gradient-based optimization method is employed, the solution shown in Fig. 6 is only guaranteed to be a local optimum. Two additional analyses are now presented, each with different initial conditions. Specifically, \( 2\times 2 \) and \( 4\times 4 \) arrays of circular holes are introduced in the interior of the material domain to allow for voids in the final design solution. Because the step sizes for our explicit HJE solver must be limited by the CFL condition coupled with the frequent reinitializations of the level set function, it is impossible to nucleate new holes in the interior of a material domain (Allaire et al. 2004). By initiating the level set function with voids in the interior, locally optimal solutions not achievable with a fully filled initial design domain can now be reached. We choose symmetric hole patterns for the initial material configurations since the boundary conditions and previous optimal design exhibit a line of symmetry at the horizontal mid-line of the design domain.

The optimal shape for the initial design containing a \( 2\times 2 \) array of holes is illustrated in Fig. 10. The corresponding finite element solution for the temperature field and heat flux of the optimal design are also presented in Fig. 11. The optimal solution retains several voids from the initial design. These voids align with the direction of heat flow and place material farther from the horizontal axis of symmetry. Although the complexity of this design has increased, the heat power radiated has also increased by \( {0.18}\,\hbox {W} \) from the optimal solution found using an initial fully filled design domain.

Fig. 10
figure 10

Initial and optimal shapes for optimization problem (SP) with initial material configuration of \( 2\times 2 \) array of equally spaced circular holes

Full size image
Fig. 11
figure 11

Finite element solution of optimal design for optimization problem (SP) with initial material configuration of \( 2\times 2 \) array of equally spaced circular holes

Full size image

The objective, constraint, and augmented Lagrangian histories are plotted in Fig. 12. These histories show that after approximately 15 iterations, the design converges. The same velocity field metrics previously introduced are also tracked to illustrate that convergence has been reached. Figure 13 plots the histories of these metrics and demonstrates that the velocity approaches zero on the structural boundaries.

Fig. 12
figure 12

Objective, constraint, augmented Lagrangian, and Lagrange multiplier estimate histories for optimization problem (SP) with initial material configuration of \( 2\times 2 \) array of equally spaced circular holes

Full size image
Fig. 13
figure 13

Convergence history using boundary velocity metrics for optimization problem (SP) with initial material configuration of \( 2\times 2 \) array of equally spaced circular holes

Full size image

Next the results for the initial material configuration containing a \( 4\times 4 \) array of holes are displayed in Figs. 14, 15, 16, and 17. Our method converges to a final design which again retains some of the voids from the initial shape. Having increased the number of holes in the initial shape has resulted in more voids in the final design and more intricate structural features near the radiating surface.

Fig. 14
figure 14

Initial and optimal shapes for optimization problem (SP) with initial material configuration of \( 4\times 4 \) array of holes

Full size image
Fig. 15
figure 15

Finite element solution of optimal design for optimization problem (SP) with initial material configuration of \( 4\times 4 \) array of holes

Full size image
Fig. 16
figure 16

Objective, constraint, augmented Lagrangian, and Lagrange multiplier estimate histories for optimization problem (SP) with initial material configuration of \( 4\times 4 \) array of equally spaced circular holes

Full size image
Fig. 17
figure 17

Convergence history using boundary velocity metrics for optimization problem (SP) with initial material configuration of \( 4\times 4 \) equally spaced circular array of holes

Full size image

A summary of the two test design shapes along with the three topologically optimized solutions, designated as “Design A,” “Design B,” and “Design C,” is provided in Table 3.

Table 3 Comparison of test designs with locally optimal solutions for optimization problem (SP)
Full size table

All of the topologically optimized designs outperformed the two test designs presented earlier. Design A achieved a \( 3.5\% \) and \( 2.2\% \) improvement in radiated thermal heat power from Test Designs 1 and 2, respectively. Likewise, both Designs B and C achieved a \( 4.3\% \) and \( 2.9\% \) improvement in performance over Test Designs 1 and 2, respectively.

Another important finding here is that the added topological complexity in Design B and C offer only a \( 0.8\% \) improvement in performance (in terms of radiated heat power) over Design A. Additionally, both Designs B and C are iso-performing, meaning they both radiate the same heat power. Therefore, the additional geometric complexity found in Design C compared to Design B in no way improves the performance. This finding suggests that design problems exist where too much geometric complexity could stunt or even degrade performance. Whether or not added geometric complexity affords better performing designs is problem-dependent.

7 Conclusions

In this paper, we presented a level set-based topology optimization method to maximize thermally radiated heat power. Using the adjoint method, we derived a shape derivative for this class of problems which was necessary for our gradient-based solver. The topology optimization method was then demonstrated on an example 2D problem of an aluminum plate radiating heat to the surrounding environment. The problem was well posed by including a single volume fraction constraint. We solved this problem using three different initial material configurations, each yielding a distinct locally optimal design. Our method was shown to converge smoothly by tracking the iteration histories of the objective, constraint, augmented Lagrangian, and Lagrange multiplier. The \( L_1 \) and \( L_2 \) norms of the boundary velocity also indicated that the solutions had converged. The resulting locally optimal geometries indicated that adding geometric complexity, in the form of voids and branching features, can in fact improve the performance. However, the performance benefit gained by increasing topological complexity can also stagnate. Because of these findings, it is important that we consider methodologies to explore the design tradespace in order to not only identify new unintuitive topological features, but also better understand their cost-benefit between geometric complexity and performance.