1 Introduction

The civil aviation industry aims to build more environmentally friendly aircraft. Structural mechanics play a significant role as lighter aircraft need less lift, which reduces drag and consequently require less power and fuel. An efficient way of obtaining more lightweight wings is load alleviation, which is the focus of current research. According to certification specification CS 25.337 (EASA 2021), civil passenger aircraft must be designed to withstand forces to a load factor of \(n_z=2.5\) times the gravity acceleration g. Although such high load scenarios are rare events, they require additional material in the wing structure for sufficient strength, making the design less weight-efficient. Load alleviation reduces the peak forces during rare high load scenarios, allowing for a more weight-efficient design.

The lift produced by a wing or airfoil rises with the airspeed, air density, and angle between the upstream airflow and the chord line of the airfoil. This angle is called the angle of attack. At a given airspeed and density, the relation between lift and angle of attack is linear until a critical angle of attack is reached, after which the airflow detaches from the wing and less lift is produced. This is called a stall. For non-accelerated flights like cruise, the total lift is equal to the aircraft weight, which corresponds to a load factor of \(n_z=1\).

Load reduction can be achieved by shifting the lift distribution inwards, which reduces the bending moment at the wing root, while sustaining the total lift. Even more weight reduction can be achieved if the maximum possible load factor is reduced below the threshold value of \(n_z=2.5\). In this case, the certification specification CS 25.337(d) allows using the maximum possible load factor as the design load factor. A similar approach is used with low airspeeds, during which the airfoil cannot produce such a high lift without stalling. In the case of load alleviation, this limit is not the critical angle of attack but rather the combination of deformation and the subsequent lift. Load alleviation can also reduce dynamic gust loads, which do not always reach the maximum stationary load. However, it still has a positive effect on the fatigue behavior of the wing components.

To make use of load alleviation, the wing needs to deform into a shape at high loads, reducing the effective angle of attack and hence lift. Load alleviation techniques can be grouped into passive and active approaches. Active load alleviation uses actuators, such as a piezoelectric actuator, to morph the wing into the desired shape (Henry et al 2019). Piezoelectric actuators show promising experimental results for the use of gust load alleviation on an idealized wing (Versiani et al 2019). Passive load alleviation does not rely on actuators to morph the wing’s shape. Instead, the wing is designed such that a load deforms the wing in the desired way. Exploiting directional stiffness for this purpose is called aeroelastic tailoring (Shirk et al 1986). Research by Handojo et al (2018) shows that passive load alleviation efficiently reduces the wing’s weight: a weight reduction by 24% was achieved by tailoring the composite layup. Geometric nonlinearities of the wing bending have an increasing influence on the aeroelastic calculation of high aspect ratio wings (Afonso et al 2017) and are considered in recent aeroelastic tailoring studies (Krüger et al 2019).

As well as taking into account nonlinearities, new approaches for passive load alleviation also aim to exploit stronger nonlinearities for progressive load alleviation. Arrieta et al (2014) placed bistable elements at the trailing edge of the wing. These bistable elements buckled under load, which lowered their stiffness. The wing’s trailing edge bends upwards, reducing the lift and consequently the aerodynamic forces. Hahn and Haupt (2020) used a similar approach, exploiting the nonlinear anisotropic response of a tailored composite layup for wing box segments to achieve progressive bending-torsion coupling. The bending moment results in a twisting deformation of the wing. This lowers the angle of attack in the outer wing sections, thus reducing the impact of the the aerodynamic forces. One advantage of using bending-torsion coupling of the wing box is that it permits the use of wing attachments such as ailerons and flaps. This is not possible if the inner wing structure buckles at the trailing edge, where these attachments are mounted (Arrieta et al 2014; Cavens et al 2021). Fig. 1 outlines the working mechanism of nonlinear load alleviation. The illustration shows only angles below the stall angle of attack, so the aerodynamic load increases linearly with the effective angle of attack. The upstream flow angle can be changed by a gust or by the pilot initiating maneuvers. Nonlinear deformation starts at the critical load in the form of torsion, reducing the effective angle of attack compared to the upstream flow angle. This decreases the aerodynamic load for a given upstream flow angle compared to a rigid case, where the upstream flow angle is equal to the effective angle of attack. In Fig. 1, the deformation behavior appears to be primarily linear, becoming nonlinear after the critical load point. However, this is not mandatory, provided the deformation progresses in nonlinear fashion.

Fig. 1
figure 1

Working mechanism of the nonlinear load alleviation through nonlinear deformation behavior in response to the upstream flow angle

Full size image

The research mentioned earlier requires a priori knowledge of design techniques to achieve the desired nonlinear behavior. One way of overcoming this is topology optimization, and this paper presents a methodology making use of geometric nonlinearities for passive load alleviation. Our research uses a progressive bending-torsion coupling approach similar to that used by Hahn and Haupt (2020). However, our material model remains isotropic, enabling us to better understand the topology’s deformation behavior without the interference of anisotropic material effects. While the topology optimization methodologies used by Sigmund (2001) and Andreassen et al (2011) form the basis of many subsequent studies their finite element analysis (FEA) is linear. Since our goal is to exploit geometric nonlinearities, a suitable FEA is required, which incorporates this behavior. There are several studies on topology optimization with large displacements: Buhl et al (2000) applied a geometric nonlinear FEA to compliance optimization and investigated different objective functions. Their FEA is based on the St. Venant-Kirchhoff material model. To mitigate the convergence issue of FEA, they ignored low-density elements in the solution process for the equilibrium. Pedersen et al (2001) used geometric nonlinear topology optimization based on the same material model to generate topologies that will follow a predetermined path under load. They used counter loads, applied orthogonally and in opposite direction to the desired path to obtain a well-posed optimization problem. Klarbring and Strömberg (2013) compared the stiffness optimization results of linear and geometric nonlinear FEA and showed that the resulting designs are dependent on whether linear or nonlinear FEA is used. Additionally, they analyzed the numerical performance of different hyperelastic material models, including the St. Venant-Kirchhoff model. Xia and Shi (2016) incorporated large displacements into the level-set approach for topology optimization using the St. Venant-Kirchhoff model. They compared different stiffness measures and their results. Recently, Lee et al (2020) presented a methodology for altering the inherent nonlinearity of the initial topology using slope constraints. The resulting topologies followed a predefined force displacement curve, describing softening (stiffness decreases under load) or hardening (stiffness increases under load) behavior. Lee et al (2020) also used the St. Venant-Kirchhoff model.

2 Methodology

The aim of our methodology is to find a design for the inner wing structure, which twists under a high bending load (bending-torsion coupling). The twisting deformation of the wing lowers the angle of attack, consequently reducing lift and, therefore, the aerodynamic forces. However, the aerodynamic properties of the aircraft must not be significantly altered if it operates in its normal flight envelope and two force levels are thus analyzed: until the lower force level \({\mathbf {f}}_1\) is reached, the wing should only bend. At the higher load level \({\mathbf {f}}_2\), the bending-torsion coupling should be at its maximum. This nonlinear behavior is illustrated in Fig. 2.

Fig. 2
figure 2

The airfoil of a wing at different load levels. At \({\mathbf {f}}_0\), the airfoil is not loaded. If \({\mathbf {f}}_1\) is applied, the leading edge (LE) and trailing edge (TE) of the airfoil deform equally. At \({\mathbf {f}}_2\), the bending–torsion coupling is at its maximum, and the airfoil twists downwards, thus lowering the angle of attack

Full size image

2.1 Optimization problem

The optimization problem (Eq. (1)) aims to find a possible topology candidate with a high bending–torsion coupling at loads above \({\mathbf {f}}_1\). The objective function c (Eq. (1a)) minimizes the difference between the deformation of the leading edge (LE) \({\mathbf {l}}_{\text {LE}}^{T}\,{\mathbf {u}}\) and the trailing edge (TE) \({\mathbf {l}}_{\text {TE}}^{T}\,{\mathbf {u}}\) at the force level \({\mathbf {f}}_2\), which in turn maximizes the desired twisting deformation. Here, the vector \({\mathbf {l}}\) filters the displacement vector \({\mathbf {u}}\) with respect to the desired degree of freedom (DOF). The corresponding force-displacement curve is shown in Fig. 3.

$$\begin{aligned}&\!\min _{{\mathbf {x}}} c({\bar{\tilde{\mathbf{x }}}}, \, i) = \left[ {\mathbf {l}}_{\text {LE}}^{T}\,{\mathbf {u}}({\mathbf {f}}_{2}, \,{\bar{\tilde{\mathbf{x }}}}) - {\mathbf {l}}_{\text {TE}}^{T}\,{\mathbf {u}}({\mathbf {f}}_{2},\,{\bar{\tilde{\mathbf{x }}}}) \right] + w({\bar{\tilde{\mathbf{x }}}}, \, i) \end{aligned}$$
(1a)
$$\begin{aligned}&\text {s.t.} \ {\mathbf {x}}_{\text {min}}\,\le \,{\mathbf {x}}\,\le \,{\mathbf {x}}_{\text {max}} \end{aligned}$$
(1b)
$$\begin{aligned}&{\mathbf {r}} = {\mathbf {0}} \end{aligned}$$
(1c)
$$\begin{aligned}&\vert {\mathbf {l}}_{\text {LE}}^{T}\,{\mathbf {u}}({\mathbf {f}}_{1}, \,{\bar{\tilde{\mathbf{x }}}}) - {\mathbf {l}}_{\text {TE}}^{T}\,{\mathbf {u}}({\mathbf {f}}_{1},\,{\bar{\tilde{\mathbf{x }}}}) \vert \le g \end{aligned}$$
(1d)
$$\begin{aligned}&\dfrac{V({\bar{\tilde{\mathbf{x }}}})}{V_0} \le V_{\text {max}} \end{aligned}$$
(1e)

The design domain is discretized by a uniform mesh with m elements. Each element has a physical density \(\bar{\tilde{x}}_e\). An optimum is reached by varying the vector of the design variables \({\mathbf {x}}\). The design variables are subject to boundaries (Eq. (1b)): \(0\le x_e \le 1\) applies to the set of active elements \({\mathbf {x}}_{{\mathcal {A}}}\). The densities of solid and void passive elements are set to \(x_{e,\,s} = 1\) and \(x_{e,\,v}=0\) respectively.

Fig. 3
figure 3

Idealized force-displacement curve of LE and TE of an airfoil with bending-torsion coupling

Full size image

To ensure that the wing does not (significantly) twist during the standard flight envelope, the absolute value of the difference between LE and TE needs to be smaller than a threshold g (see Eq. (1d)). A volume constraint is also applied (Eq. (1e)).

The second part w of the objective function c represents a compliance minimization problem with a decaying weight (CMDW):

$$\begin{aligned} w({\bar{\tilde{\mathbf{x }}}}, \, i) = \left( r\left( 1-\gamma \left( \frac{i}{i_{\max }}\right) \right) + s \right) \sum _k \left( {\mathbf {f}}_{k}^{T}{\mathbf {u}}({\bar{\tilde{\mathbf{x }}}})\right) ^2 \,. \end{aligned}$$
(2)

The number of the current iteration i needs to be normalized by the maximum number of iterations \(i_{\max }\). It can then be used with the smoothed Heaviside function (Wang et al 2011)

$$\begin{aligned} \gamma (x)= \dfrac{\tanh \left( {\beta \eta }\right) + \tanh {\left( \beta \left( x-\eta \right) \right) }}{\tanh \left( {\beta \eta }\right) + \tanh {\left( \beta \left( 1-\eta \right) \right) }}\, \end{aligned}$$
(3)

with the steepness parameter \(\beta\) and the threshold \(\eta\). Adding w to the objective function is necessary because otherwise only the deformation of the TE will be maximized. Large displacements can lead to an unstable FEA, where no equilibrium with \({\mathbf {r}} = {\mathbf {0}}\) can be found (violating condition (1c)). The influence of the CMDW is high at the beginning of the optimization process and stiff structures are therefore favored. These stiff structures are necessary to ensure the existence of a convergent FEA. As the optimization progresses, the CMDW decays, and the focus shifts towards the maximization of the bending-torsion coupling.

The parameter r scales the CMDW at the start of the optimization. At the later stages of the optimization process, the parameter s sets the floor of the CMDW to ensure that excessive deformation is still penalized. The higher the parameters r and s, the higher the structure’s compliance’s impact on the objective function’s value. The course of the CMDW and the effect of parameters r and s are visualized in Fig. 4. Squaring the compliance \(({\mathbf {f}}^T{\mathbf {u}})^2\) helps with convergence at the later stages, because more significant deformations have a disproportionately larger influence on the value of the objective function than the linear compliance formulation \({\mathbf {f}}^T{\mathbf {u}}\). In Sect. 4.2, we will elaborate on the effects of CMDW on the optimization history and the resulting topologies and discuss different settings for the CMDW parameters.

Fig. 4
figure 4

CMDW with its scaling parameters r and s

Full size image

2.2 Filtering and projection

Topology optimization can produce material distributions with a checkerboard pattern and be dependent on the mesh’s resolution. Another common problem is the presence of many local minima, where the optimizer can get stuck (Bruns and Tortorelli 2001). A widely used technique to mitigate these problems is density filtering (Bendsøe and Sigmund 2004; Bruns and Tortorelli 2001)), which averages the weighted densities of neighboring elements. The density filter function is defined for the virtual density x of an element e as

$$\begin{aligned} \tilde{x}_e = \dfrac{\sum _{j\in {\mathcal {N}}_e} h_{e,\, j}\,v_j\,x_j}{\sum _{j\in {\mathcal {N}}_e} h_{e,\, j}\,v_j} \quad \forall x_e,x_j \in {\mathbf {x}}_{\mathcal {A}} \end{aligned}$$
(4)

with the volume of an element v. Excluding densities of the passive elements from both the considered \(x_e\) and the neighboring elements \(x_j\) prevents changes the the volume fraction by the filter. The set of indices for elements in the neighborhood of the considered element \({\mathcal {N}}_e\) is given by

$$\begin{aligned} {\mathcal {N}}_e = \left\{ j : \text {dist}(e,j)\le R\right\} \, , \end{aligned}$$
(5)

with the distance \(\text {dist}(e,j)\) between the centers of the elements e and j and the filter radius R. The weight factor \(h_{e,\, j}\) is defined as

$$\begin{aligned} h_{e,\, j} = \max (0,\; R - \text {dist}(e,j)) \, . \end{aligned}$$
(6)

In this work, we used the threshold projection by Xu et al (2010) to reduce grayness by projecting gray elements to either void or solid. Threshold projection reuses the smoothed Heaviside function from Eq. (3):

$$\begin{aligned} {\bar{\tilde{\mathbf{x }}}} = \gamma ({\tilde{\mathbf{x }}}) \end{aligned}$$
(7)

The parameters \(\beta\) and \(\eta\) do not have to be constant during optimization. A continuation scheme is possible (Wang et al 2011). \(\beta\) doubles after 30 iterations, whereas \(\eta\) changes in every iteration to make the projection method volume-preserving (Li and Khandelwal 2015), making the optimization more efficient (Ferrari and Sigmund 2020). The difference between the volume of the virtual densities \({\mathbf {x}}\) and the physical densities \({\bar{\tilde{\mathbf{x }}}}\) is minimized using the Newton method to find the optimal, volume-preserving threshold \(\eta ^*\)

$$\begin{aligned} \eta ^*\rightarrow \min \limits _{\eta \in [0,1]} \vert V(\mathbf{x} ) - V(\bar{\tilde{\mathbf{x }}})\vert \end{aligned}$$
(8)

with the sensitivity of the smoothed Heaviside function (Eq. (3)) with respect to \(\eta\)

$$\begin{aligned} \frac{\partial V({\tilde{{\mathbf {x}}}})}{\partial \eta } = -2\beta \sum \limits _{i \in {\mathcal {A}}} \frac{\left( e^{\beta (1-{\tilde{x_i}})}-e^{\beta ({\tilde{x_i}}-1)}\right) \left( e^{\beta x_i }-e^{\beta {\tilde{x_i}}}\right) }{\left( e^{\beta }-e^{-\beta }\right) \left( e^{\beta (\tilde{x_i}-\eta )}+e^{\beta (\eta -\tilde{x_i})}\right) ^2} \, . \end{aligned}$$
(9)

2.3 Finite element method

The proposed topology optimization methodology aims to exploit geometric nonlinearities. Consequently, large displacements are allowed, but it is assumed that the strain remains small. Such large displacements are taken into account by the Green-Lagrange strain tensor \(\varvec{\mathsf {E}}\) in the definition of the second Piola-Kirchhoff stress tensor

$$\begin{aligned} \varvec{\mathsf {S}} = \varvec{\mathsf {D}} : \varvec{\mathsf {E}}\,. \end{aligned}$$
(10)

We assume small strains to permit the use of the linear isotropic St. Venant-Kirchhoff material model. Wallin et al (2021) have pointed out that this material model does not require the third-order derivative of the strain energy in the sensitivity analysis. This simplicity makes the St. Venant-Kirchhoff material model a common choice for topology optimization. Since main focus of this research is the optimization strategy, we exploited this simplicity. The assumption of small strains and the well-known problems of the St. Venant-Kirchhoff material model during compression loads (Raoult 1986; Klarbring and Strömberg 2013) are discussed in Sect. 4.4. The constitutive relation of St. Venant-Kirchhoff is

$$\begin{aligned} \varvec{\mathsf {D}} = \lambda \varvec{\mathsf {I}}\otimes \varvec{\mathsf {I}} + 2\mu \varvec{\mathsf {I}} \end{aligned}$$
(11)

with the Lamé constants \(\lambda = \frac{\nu E}{(1+\nu )(1-2\nu )}\) and \(\mu = \frac{E}{2(1+\nu )}\) and the identity tensor \(\varvec{\mathsf {I}}\). To penalize gray material, Young’s Modulus E is calculated using the SIMP (Solid Isotropic Material with Penalization) material model (Bendsøe and Sigmund 1999)

$$\begin{aligned} E_e = \bar{\tilde{x}}_e^p(E_1 - E_{\min }) + E_{\min } \end{aligned}$$
(12)

with Young’s modulus of solid and void elements \(E_1\) and \(E_{\min }\), respectively, and the SIMP parameter p. \(E_{\min }\) needs to be much smaller than \(E_1\), therefore \(E_{\min } = 10^-9 E_1\). The Green-Lagrange strain tensor is defined by

$$\begin{aligned} \varvec{\mathsf {E}} = \frac{1}{2}(\varvec{\mathsf {F}}^T\varvec{\mathsf {F}}-\varvec{\mathsf {I}}) \end{aligned}$$
(13)

with the deformation gradient \(\varvec{\mathsf {F}}\). A total Lagrangian formulation is used.

The proposed optimization methodology encourages large displacements, which can lead to mesh distortion, especially in void—and therefore low stiffness—elements. The energy interpolation scheme proposed by Wang et al (2014) reduces mesh distortion, which helps with the convergence of the FEA. This method interpolates the elastic strain energy density \(\Phi\) of gray elements and reuses the smoothed Heaviside function of Eq. (3):

$$\begin{aligned} \Phi ({\mathbf {u}}_e) = \left[ \Phi _{NL}(\gamma (\bar{\tilde{x_e}}^{\,p}){\mathbf {u}}_e) - \Phi _{L}(\gamma (\bar{\tilde{x_e}}^{\,p}){\mathbf {u}}_e)+\Phi _{L}({\mathbf {u}}_e)\right] E_e \end{aligned}$$
(14)

Solid elements use the nonlinear elastic strain energy density \(\Phi _{NL}=\frac{1}{2}\varvec{\mathsf {E}}:\varvec{\mathsf {D}}:\varvec{\mathsf {E}}\), and void elements use the linear counterpart \(\Phi _{L}=\frac{1}{2}\varvec{\mathsf {\epsilon }}:\varvec{\mathsf {D}}:\varvec{\mathsf {\epsilon }}\) with the linear strain tensor \(\varvec{\mathsf {\epsilon }}\). As recommended by Wang et al (2014) \(\beta =500\) and \(\eta =0.01\) is used for the energy interpolation.

The internal force vector is defined as

$$\begin{aligned} {\mathbf {f}}^{\,\text {int}}_e = \frac{\partial \!\int _{V_e}\Phi _e({\mathbf {u}}_e)\;\mathrm {d}V}{\partial {\mathbf {u}}_e}\;. \end{aligned}$$
(15)

The equilibrium equation

$$\begin{aligned} {\mathbf {r}} = {\mathbf {f}}^{\,\text {ext}}-{\mathbf {f}}^{\,\text {int}}={\mathbf {0}} \end{aligned}$$
(16)

is solved iteratively using the Newton method, which requires the tangent stiffness matrix

$$\begin{aligned} {\mathbf {K}}_T= - \frac{\partial {\mathbf {r}}}{\partial {\mathbf {u}}} \,. \end{aligned}$$
(17)

Kim (2015) describes in more detail the finite element formulation used.

2.4 Sensitivity analysis

The filtering and projection are applied directly to the design variables \({\mathbf {x}}\). Thus, the sensitivity of a function of the optimization problem \(q({\mathbf {x}})\) follows as

$$\begin{aligned} \frac{\mathrm {d}q}{\mathrm {d}x_e} = \frac{\mathrm {d}q}{\mathrm {d}\bar{\tilde{x_e}}}\frac{\partial \bar{\tilde{x_e}}}{\tilde{x_e}}\frac{\partial \tilde{x_e}}{\partial x_e} \end{aligned}$$
(18)

with the sensitivity of the projection

$$\begin{aligned} \dfrac{\partial \bar{\tilde{x}}_e}{\partial \tilde{x}_e} = \frac{\partial \gamma (x)}{\partial x} = \dfrac{\beta \,\text {sech}^2\left( \beta \left( \tilde{x}_e-\eta \right) \right) }{\tanh \left( {\beta \eta }\right) + \tanh {\left( \beta \left( 1-\eta \right) \right) }} \end{aligned}$$
(19)

and the sensitivity of the density filter

$$\begin{aligned} \dfrac{\partial \tilde{x}_e}{\partial x_e} = \dfrac{h_{e}\,v_e}{\sum _{j\in {\mathcal {N}}_e} h_{e,\, j}\,v_j}\,. \end{aligned}$$
(20)

The optimization problem consists of two basic components: \(q_{\text {lin}}\) has a linear relationship with the deformation vector \({\mathbf {u}}\) [e.g. first part of \(c_1\) in Eq. (1a) and the torsion constraints in Eq. (1d)], and \(q_{\text {qaud}}\) has a quadratic relationship with \({\mathbf {u}}\) [the CMDW in Eq. (2)]. The adjoint method is used to compute the sensitivities. It is given by Buhl et al (2000) as

$$\begin{aligned} \frac{\mathrm {d}q}{\mathrm {d}\bar{\tilde{x}}_e} = \varvec{\lambda }^T\frac{\partial {\mathbf {r}}}{\partial \bar{\tilde{x}}_e} \end{aligned}$$
(21)

with the adjoint problem for \(q_{\text {lin}}\)

$$\begin{aligned} {\mathbf {K}}_T\varvec{\lambda }_{\text {lin}}={\mathbf {l}}\,. \end{aligned}$$
(22)

The sensitivity of \(q_{\text {quad}}\) only requires substitution of \(\varvec{\lambda }_{\text {lin}}\) with

$$\begin{aligned} {\varvec{\lambda }}_{\text {quad}} = 2({\mathbf {l}}^T{\mathbf {u}}-u_{\text {pre, k}})\varvec{\lambda } \,. \end{aligned}$$
(23)

The sensitivity of the equilibrium equation is given by Wang et al (2014) as

$$\begin{aligned} \frac{\partial {\mathbf {r}}}{\partial \bar{\tilde{x}}_e} = \frac{\partial {\mathbf {f}}_{\text {int}}}{\partial \bar{\tilde{x}}_e} + \frac{\partial {\mathbf {f}}_{\text {int}}}{\partial \gamma }\frac{\partial \gamma (\bar{\tilde{x}}^p)}{\partial \bar{\tilde{x}}_e} \,. \end{aligned}$$
(24)

3 Implementation

The methodology is implemented using Matlab. The topology optimization problem uses the Method of Moving Asymptotes optimizer by Svanberg (1987). As recommended by Svanberg (1987), the constraints functions are scaled to satisfy \(1\le g_{\max } \le 100\). The first part of the objective function \(c_1\) is multiplied by 1000.

The assembly of \({\mathbf {K}}_T\) and \({\mathbf {f}}_{\text {int}}\) requires many matrix multiplications. In order to reduce the computational cost, we implemented a vectorized approach, which multiplies the pages of 4-dimensional arrays. We recommend the use of pagemtimes by Matlab2020b or newer. Older systems can use ndfun.c by Vistalab and Stanford University (2021). If the Newton method of the FEA fails to converge after a certain number of iterations or if \(\vert {\mathbf {r}}\vert _{\max }\) becomes too large, the current load step is bisected, in which case, a sensitivity analysis is not necessary. A bisection of the load steps improves the convergence of the FEA despite the large deformation of some elements. If the FEA fails to converge, the optimization process terminates.

Both the Newton method and the adjoint problem of the sensitivity analysis use \({\mathbf {K}}_T\) to solve a linear equation system. Consequently, it is useful to cache the decomposition of \({\mathbf {K}}_T\) during the Newton process and reuse it in the sensitivity analysis after the equilibrium is reached. Although caching reduces computational costs, it increases the RAM requirements. A reasonably sized test problem with \(150 \times 75 \times 30 = 337500\) elements uses approximately 250GB RAM. We performed the optimizations on compute nodes with two Intel Xeon E5-2640v4 with up to 512GB RAM. This test problem takes on average 1.4h per optimization iteration on this system.

4 Case studies

4.1 Definition of test cases

This study focuses on the wing box, the main structural part of a wing, specifically a section between two ribs. There are two reasons for this: Firstly, topology optimization typically uses a cuboid design space. Optimizing the whole wing section, including LE and TE, would require adding void passive elements above and below the airfoil, which would increase the computational cost. Secondly, since we use a uniform mesh, the representation of the wing’s curvature has only two infeasible solutions (see Fig. 5). The curved airfoil surface would be discretized by placing several layers of solid elements in a stepped structure. These layers could either overlap (see Fig. 5a), which would add thickness and, therefore, localized stiffness, or the would be diagonally opposite to each other (see Fig. 5b), introducing a hinge-like behavior into the wing’s skin. With today’s computer hardware, it is not feasible to increase the mesh resolution to a level where the effect of the overlapping layers could be neglected.

Fig. 5
figure 5

An airfoil with its main structural component, the wing box (marked in bold), and two possibilities of representing the curves in a uniform mesh. Representation a adds additional thickness at the transition step; representation b has a hinge-like behavior at the transition step

Full size image

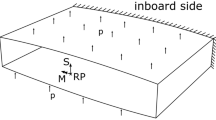
Since the wing box still has a slight curvature, we have idealized it with a cuboid (see Fig. 6). Both the upper and the lower skins and the free rib consist of solid passive elements. The DOFs at coordinate \(x=0\) are locked. Karpuk and Elham (2021) provide a spanwise shear force and bending moment distribution at \(n_z=1\) calculated by the preliminary aircraft design process, which we used to derive our load cases. Since the study aims to evaluate the optimization methodology and the effect of the resulting design features on the bending-torsion coupling, it is expedient to consider a load case with low complexity. We therefore selected a wing box section positioned near the wingtip at 93.7% of the wingspan, which allowed us to neglect the bending moment. We analyzed two different test cases, T1 and T2, with two different lengths a between the ribs: in T1 \(a =0.5 m\), and in T2 \(a = 1.0 m\). The width (x-direction) was 1 m for both test cases. The forces applied to the wing box section were extracted from this data set and scaled to \(n_z=2.5\). The shear force at the location of the free rib was applied to this rib. The force difference between the free and the fixed rib was applied to the wing box skin. Two thirds of this force were distributed across the upper skin, whereas one third was applied to the lower skin. All forces act only in z-direction They do not change under deformation and should therefore be considered as mechanical rather than aerodynamic loads. This idealization is justified because this paper aims to present a new optimization methodology for achieving passive load alleviation through nonlinear bending-torsion coupling. Since the application of the loads is symmetric and only in z-direction, all bending-torsion coupling comes from the structure itself.

Fig. 6
figure 6

Dimensions of the test case. The solid passive elements, i.e. the wing box skin and the free rib, are marked in dark gray. The active elements are marked in light gray. The hatched surface is fixed. The loads \({\mathbf {f}}_a\) and \({\mathbf {f}}_b\) are distributed across the respective skin; \({\mathbf {f}}_c\) is distributed across the free rib

Full size image

The general optimization parameters are given in Table 1 and the parameters specific to each test case in Table 2. Since the minimum element size of 6.7 mm is much bigger than the skin thickness of a typical aluminum wing box close to the wingtip [2 mm to 3 mm, Handojo et al (2018)], the test cases would be much stiffer and geometric nonlinear behavior would therefore not be possible. Hence, we lowered Young's modulus to a level where geometric nonlinearities occur during topology optimization (c.f. Table 2). The evaluation points for the displacement of LE and TE are located at the free rib and have the coordinates \((0 m, a, 0.1 m)_{\text {LE}}\) and \((1 m, a, 0.1 m)_{\text {TE}}\).

Table 1 General parameters valid for both wing box test cases
Full size table
Table 2 Test case parameters
Full size table

4.2 Results

4.2.1 Test Case T1

The parameters of the CMDW and the displacement constraint have a significant impact on the optimization history, which is worth analyzing. The optimization history of the short wing box test case T1 is depicted in Fig. 7. The value of the objective function steadily declines until iteration 48. This development can be attributed to two effects. The first, steeper decline until iteration 15 results directly from compliance minimization (c.f. Fig. 7b). The compliance stagnates after 15 iterations, and choosing \(i_{\text {crit}} = 30\) for the CMDW is therefore justified. No great additional improvements would result from increasing the parameter \(i_{\text {crit}}\) and further optimizing the wing box’s compliance. Since our goal was not to find the stiffest possible wing box section, a higher \(i_{\text {crit}}\) would waste computational resources.

Fig. 7
figure 7

Optimization history of test case T1. The best feasible design is marked with a dashed line

Full size image

The second decline after 15 iterations corresponds to the decrease of the CMDW, which reduces the value of the objective function. While the wing box section twists with this decline of the CMDW, structural response remains linear. This can be seen in Figs. 7c and d. From iterations 20 to 48, the difference between LE and TE stays at 0.5 mm and 1 mm at force levels \({\mathbf {f}}_1\) and \({\mathbf {f}}_2\), respectively. The topologies of these iterations have linear bending-torsion coupling.

From iteration 49, the structural response becomes nonlinear. This corresponds to the CMDW reaching its lower floor level, which is controlled by the parameter s. These nonlinearities and higher deformation introduce instabilities into the optimization process. The objective function no longer declines steadily, and the displacement constraint of Eq. (1d) is violated (c.f. Fig. 7d; the displacement curve enters the red area). Despite the instability, the optimizer continues to find designs that meet the constraint. Furthermore, the displacement difference at \({\mathbf {f}}_2\) is clearly rising, whereas the compliance does not increase except for some spikes.

However, the optimization is prematurely terminated after 105 iterations, because the design of iteration 106 does not have a convergent FEA. Consequently, the objective and constraint functions and their sensitivities, are not computed, and the optimization cannot continue. One option would be to increase the CMDW parameter s, since a higher s would favor stiffer and, therefore, more stable structures, and the optimization would continue. In fact, we tested this hypothesis and increased s from \(2 \times 10^{-5}\) to \(3 \times 10^{-5}\). But while optimization did continue, the performance concerning our primary goal, designing a wing box segment with maximal torsion at \({\mathbf {f}}_2\), was worse than in the presented test case. The maximum displacement difference (with satisfied displacement constraint) reached only 7.96 mm compared with 16.1 mm in the presented optimization. This was expected because, the torsion maximization is less favored with a higher s.

The best design for T1 is the topology of iteration 101. This iteration is marked with a dashed line in Fig. 7. The displacement difference between LE and TE is 16.1 mm at \({\mathbf {f}}_2\), which is equivalent to a torsion angle of 0.92\(^\circ\), and 0.31 mm at \({\mathbf {f}}_1\), equivalent to a torsion angle of 0.018\(^\circ\). This design is discussed in more detail below.

The force-displacement curve of this design is depicted in Fig. 8. During the optimization, the displacement was only analyzed at \({\mathbf {f}}_1\) and \({\mathbf {f}}_2\). permit a better analysis of the mechanical behavior, the resolution of the force-displacement curve is increased to 20 load steps. This shows that the structural response of the wing box segment remains linear until \({\mathbf {f}}_1\) is reached. Both LE and TE have the same deformation. This is the ideal behavior for our proposed use case: as shown by Skinn et al (1999), maneuvering loads barely exceed a load factor of \(n_z=1.25\) (corresponds to \({\mathbf {f}}_1\)) during normal operation of passenger aircraft. Consequently, this design will not interfere with the maneuvering capabilities of the aircraft. Once the common maneuver load is surpassed, the passive load alleviation begins, and this effect increases with higher loads. The maneuver loads are therefore not entirely capped at \(n_z=1.25\). Between \({\mathbf {f}}_1\) and \({\mathbf {f}}_2\), the wing box section shows a softening mechanical behavior, i.e., a disproportionate increase in the displacement of both LE and TE. Nevertheless, both the linear and nonlinear structural responses meet the goals of our use case, which clearly shows the potential and effectiveness of the proposed optimization methodology

Fig. 8
figure 8

Force-displacement curve of short wing box test case T1

Full size image

The optimal short wing box design still follows a classical approach with a front and rear spar (see Fig. 9 for the voxel representation and Fig. 10 for the iso-volume representation). Based on the force-displacement curve in Fig. 8, there are only minor differences between the load-free (Fig. 9 a. and b.) and the \({\mathbf {f}}_1\)-loaded geometries. At \({\mathbf {f}}_2\), the rear spar buckles, and the upper skin has a distinctive bulge. The rear spar consists of two struts separated by a low-density element group (marked with \(\text {H}_4\)), which has a hinge-like behavior. The rear spar is mounted on the lower and upper skins with hinges \(\text {H}_3\) and \(\text {H}_5\). This three-hinge design allows the rear spar to buckle, such that \(\text {H}_4\) moves downwards and the two struts rotate around \(\text {H}_3\) and \(\text {H}_5\). The buckled rear spar has less stiffness, which introduces the desired twisting motion to the wing box section.

Fig. 9
figure 9

Deformed topology of the short wing box test case T1 at different force levels; hinges (H) in orange, defects (D) in blue; density cutoff at \(x=0.3\). All elements with a density below the cutoff threshold are hidden to visualize the topology better

Full size image
Fig. 10
figure 10

Deformed topology of the short wing box test case T1 at \({\mathbf {f}}_2\) using an iso-volume representation

Full size image

The front spar is a two-hinge design that cannot buckle. It is connected at \(\text {H}_2\) with an eccentric U-shaped mounting on the upper skin. The front spar uses the eccentricity of the U-mounting as a lever and rotates the mounting. The rotation in turn applies a bending moment to the upper skin, which introduces the bulge. The bending of the skin then introduces tensile forces on the LE side of the free rib, which reduces its upward displacement.

Unfortunately, there are still some defects (marked in blue and with \(\text {D}\) in Fig. 9) in the topology. Neither \(\text {D}_1\) nor \(\text {D}_2\) are connected to other parts of the geometry at both end. Consequently, they should have no impact on the structural response of the wing box section. Since the optimization terminated early, the presented topology did not fully converge. It can be expected that these defects would disappear in later stages of the optimization and they should therefore not be seen as inherited problems of the optimization methodology.

4.2.2 Test Case T2

The optimization history of the long wing box test case T2 is depicted in Fig. 11. It is similar to test case T1. The compliance (see Fig. 11b) reaches a minimum after 20 iterations and stagnates until iteration 60. As outlined earlier, this validateschoosing \(i_{\text {crit}}=30\) and \(\beta =16\) as parameters for the CMDW. Since the same values are successful in both test cases, these values are reasonable initial guesses for possible applications of the proposed optimization methodology.

Fig. 11
figure 11

Optimization history of test case T2. The optimal design is marked with a dashed line

Full size image

Compared to T1, the linear bending-torsion coupling commences at a later stage of the iteration. Until iteration 40, the topologies only have bending deformation. The later start of nonlinear deformation at iteration 62 (compared to iteration 48 for T1) is therefore hardly surprising. There are two possible explanations. A higher value of the parameter s would favor compliance optimization rather than torsion maximization. However, with \(s= 6 \times 10^-6\) in T2 and \(s= 2 \times 10^-5\) in T1, this is not the case. This explanation is not feasible even if the higher compliance value \(({\mathbf {f}}^T{\mathbf {u}})^2\) of T2 is factored in: the minimal compliance of T2 is only 2.7 times higher than the compliance of T1, which does not account for the different values for s.

The other explanation is the parameter r, which is higher in T2 and controls the initial influence of the compliance minimization. This indicates that a higher value of r impacts the duration until the torsion-bending coupling commences. It would therefore be preferable to use a low value for r, due to the high computational cost of T1/T2. However, lowering r introduces instability in the later optimization stages. Finding the optimal value for r therefore requires considerable effort, as a single optimization can take several days. That is why we suggest using higher values for r.

The optimization was terminated early after 86 iterations due to time constraints. The best design was computed in iteration 83 (marked with a dashed line in Fig. 11). The displacement difference between LE and TE is 24.3 mm at \({\mathbf {f}}_2\), which is equivalent to a torsion angle of 1.37\(^\circ\), and 0.69 mm at \({\mathbf {f}}_1\), equivalent to a torsion angle of 0.039\(^\circ\). The design violates the displacement constraint at \({\mathbf {f}}_1\) but considering that this wing box section is twice as long as the wing box section in T1, it can still be regarded as feasible for our use case as the inner wing structure for passive load alleviation. The following discussion focuses on this T2 design.

Figure 12 shows the force-displacement curve of this design. A comparison with T1 shows that the displacements of LE and TE diverge at a higher force level. While the T1 force-displacement curves start to diverge at \({\mathbf {f}}_1\), the T2 curves start to move apart at 17kN. This does not interfere with our goal of not wanting to change flight properties during normal operation. However, the load alleviation would start at higher loads, which is, of course, not ideal. Similar to T1, this design experiences softening, but with a more substantial effect than T1.

Fig. 12
figure 12

Force-displacement curve of long wing box test case T2

Full size image

The optimal T2 design is depicted in Fig. 13(voxel representation) and Fig. 14(iso-volume representation). It is again a classical design with front and rear spars. The spars have a framework-like structure with several diagonal struts connecting the upper and lower skins. This framework structure originates from compliance minimization (c.f. the results from Buhl et al (2000); Wang et al (2014); Chen et al (2019)). Without the CMDW and its early focus on compliance minimization, it would not be possible to achieve such a framework structure. The resulting topology would then have too much deformation for application as a wing box.

Fig. 13
figure 13

Deformed topology of the long wing box test case T2 at different force levels; hinges (H) in orange, defects (D) in blue, contact between elements (C) in red; density cutoff at \(x=0.3\)

Full size image
Fig. 14
figure 14

Deformed topology of the long wing box test case T2 at \({\mathbf {f}}_2\) using an iso-volume representation

Full size image

The upper skin buckles on both the LE and TE sides, with buckling starting at \({\mathbf {f}}_1\) and becoming severe at \({\mathbf {f}}_2\). Similar to the LE spar in T1, the hinge \(\text {H}_3\) at the TE of T2 is eccentrically mounted to the upper skin. Looking from the TE, this mounting point rotates clockwise, which bends the skin upwards on the side of the fixed rib. At the LE, by contrast, the mounting near \(\text {H}_1\) bends the skin downwards in the direction of the fixed rib. These bending moments introduce imperfections into the skin, which then initialize skin buckling. Due to the different buckling directions, the bulges are oriented diagonally over the wing box segment. The diagonal buckling mode creates directional stiffness and acts like a tilted hinge, which leads to the desired twisting deformation. This effect is similar to the results discussed by Hahn and Haupt (2020).

The topology has defects, which are evidence of the early termination of the optimization. For example, defect D (marked in blue in Fig. 13) has created an additional connection between the upper and lower skins in the compliance-dominated part of the optimization process, which was broken as the CMDW decayed and the focus of the optimization shifted. It is then only connected to the upper skin and has no longer an impact on the structural response.

At the front spar, the upper skin submerges into one of the struts. This contact area is marked in red in Fig. 13. Contact is not modeled in the used FE formulation, and therefore it does not affect the deformation. Adding a contact formulation to the FEA is a good starting point for further research, as it can be the source of the desired nonlinear behavior.

4.3 Comparison of the test cases

Both test cases show that the proposed optimization methodology can produce topologies from which design ideas can be derived, such as where to place the struts, where and how to mount them, and where to place hinges. These design ideas are an ideal starting point for further design refinements.

A significant difference between the T1 and T2 geometries lies in the introduction of the nonlinear structural response. T2 has only struts with at most two hinges. Consequently, the spars do not buckle and have a constant stiffness. The nonlinearity of T2 originates in the buckling of the skin, whereas with T1, it is the three-hinged rear spar that buckles. The buckling mode of T1 is preferred because extensive buckling of the wing box skin, as in T2, might lead to undesired aerodynamic effects.

Additionally, the performance of T1 is better than that of T2. Using two T1 design wing box segments in sequence would be equal in length to a wing box segment of 1m, the same as T2. The dual-T1 configuration would have a total torsion angle at \({\mathbf {f}}_2\) of 1.84\(^\circ\) (single T2: 1.37\(^\circ\)) and a torsion angle at \({\mathbf {f}}_1\) of only 0.036\(^\circ\) (single T2: 0.039\(^\circ\)). Paired with the ideal starting point of the nonlinear bending-torsion coupling directly after \({\mathbf {f}}_1\), the T1 wing box design is superior. Furthermore, T1 uses fewer elements, which either reduces computation time or provides an opportunity to look at a finer mesh on the same hardware.

4.4 Discussion of the numerical results

The FEA of this research is based on the St. Venant-Kirchhoff material model, which assumes that the strain remains small despite large displacements. It is known from Klarbring and Strömberg (2013) that this material model has limitations under large strains, especially if compressed. They showed that the St. Venant-Kirchhoff material softens under compression (\(\epsilon <0\)) compared to material models that consider higher-order terms of the strain energy density.

The strain distribution can be analyzed to investigate whether the small strain assumption holds true. The histogram of the relative principal strain distribution is shown in Fig. 15. Like Wang et al (2014), we have considered relevant only elements with a higher physical density than \(\bar{\tilde{x}}>0.5\) because the SIMP method reduces Young’s modulus of gray elements. Therefore, the possible erroneous response of elements with \(\bar{\tilde{x}}<0.5\) can be neglected. Wang et al (2014) compared the topologies of optimizations using the St. Venant-Kirchhoff model and the modified neo-Hookean model. They concluded that topologies with a strain distribution between \(-0.2 \le \epsilon \le 0.2\) for elements \(\bar{\tilde{x}}>0.5\) are not significantly affected by the choice of the material model. Figure 15 clearly shows that the vast majority of elements in the presented test cases experience strain levels of \(\epsilon \in [-0.06,0.17]\), which are acceptable in the context of topology optimization. Furthermore, the strain distribution is shifted towards stretching (\(\epsilon >0\)), where the St. Venant-Kirchhoff model performs better than under compression. Based on these points, our small strain assumption appears reasonable.

Fig. 15
figure 15

Relative principal strain distribution (strain defined as \(\epsilon = (l-l_0)/l_0\)) of elements with a higher physical density than \(\bar{\tilde{x}}>0.5\)

Full size image

Klarbring and Strömberg (2013) also pointed out that topologies with the St. Venant-Kirchhoff material model need more iterations in the Newton method to converge to the equilibrium than other material models. We observed a similar behavior: the test cases were terminated, because too many attempts of the Newton method were needed to find an equilibrium The energy interpolation scheme used, which is based on the work of Wang et al (2014), helps with convergence. It reduces the excessive deformation of low-density elements using the linear instead of the nonlinear strain energy density, which in turn improves convergence. However, it does not entirely solve the convexity issues of the St. Venant-Kirchhoff model, which is based on a non-convex strain energy density (Raoult 1986). The interpolation only suppresses the ill-posedness for low-density elements. Although the linear strain energy density, which is used for the void elements, is convex, the interpolated energy density is not necessarily convex as well. Convexity can only be assumed for elements with a density \(\bar{\tilde{x}}\) below the interpolation threshold of \(\eta =0.01\). The nonconvex strain energy density governs elements with a higher density.

To further improve the numerical performance, it could be helpful to explore different material models such as the neo-Hookean, which implies a poly-convex strain energy density (Lahuerta et al 2013). The stabilization approach of Ortigosa et al (2020) is another technique for improving the convergence of topology optimizations with large deformations/strains. With improved numerical performance and stability, the optimization could run more robustly, which would reduce the number of defects in the topology as the optimization would converge further.

5 Conclusions and outlook

The proposed methodology shows excellent potential for maximizing passive load alleviation of the idealized inner wing structures. The resulting geometries have distinctive features, for instance, hinges, struts, and eccentrical mounting points, from which new design ideas can be deduced. The force-displacement curves show that these geometries maximize load alleviation at high force levels without interfering in normal maneuvering during low load scenarios. Unlike other methods, such as optimizing a topology to hit predefined force-displacement points (Lee et al 2020; Saxena and Ananthasuresh 2001), our approach does not make any assumption regarding the mechanical response of the design domain. It is therefore ideal for exploring what is possible by exploiting geometric nonlinearities.

The core of our methodology is the CMDW. It adds a compliance term with a decaying weight to the optimization problem. The decaying weight ensures that this penalization of large displacements is large at the beginning of the optimization and small at the end. Consequently, the topology optimization yields stiff structures, which are then optimized to exhibit the desired nonlinearity. Without the CMDW, maximizing the difference between LE and TE, and thus maximizing total displacement, would inevitably result in an unstable FEA after a few optimization iterations. Although this paper only applies this optimization methodology to maximizing the bending-torsion coupling of a wing box, the scope of the CMDW is not limited to the proposed use case. It can stabilize any topology optimization, where the objective function maximizes some displacement. The proposed methodology therefore makes a new class of optimization problems possible.

The distinct design features introduce buckling into the wing box skin and the spars. However, our nonlinear FEA does not directly solve a buckling problem with an eigenvalue analysis. Lindgaard and Dahl (2013) presented a methodology to include a nonlinear buckling analysis into topology optimization. Together with a more complex material model (such as neo-Hookean), a geometric nonlinear FEA with buckling might yield a more physical mechanical response of our topology.

The research by Hahn and Haupt (2020) shows promising results by exploiting anisotropic material responses to achieve bending-torsion coupling. Kim et al (2020) proposed a topology optimization methodology to optimize anisotropic material distribution and the fiber layout simultaneously. However, Kim et al (2020) optimized the structure’s stiffness and used not only the SIMP method but also a homogenization design method to find the fiber orientation. Incorporating anisotropic materials into the presented methodology might increase the passive load alleviation potential even more, but further research is necessary to adapt the methods of Kim et al (2020) to the approach presented here.

The question of how to find the optimal parameters for the CMDW remains. Especially the parameter s, which controls how much influence compliance minimization has at the later stages of the optimization, has a significant impact on the stability and performance of the optimization. Automated hyperparameter tuning using Bayesian optimization (Snoek et al 2012) or other algorithms (Yu and Zhu 2020) is not feasible. As one topology optimization with the required amount of elements takes several days, the automated hyperparameter tuning would take weeks or even months. That is why further research should be conducted on a continuation scheme for the CMDW parameter s, similar to the continuation of eta proposed by Ferrari and Sigmund (2020). If load steps of the FEA are bisected more often, s should increase to push the optimizer to stiffer topologies with more stable FEAs. If the FEA continues to be stable, s needs to decrease to shift the focus towards maximizing the bending-torsion coupling.