A pointwise ensemble of surrogates with adaptive function and heuristic formulation

Abstract

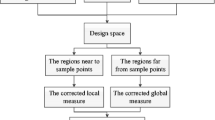
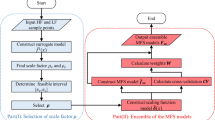
Due to the advantages of easy implementation and high efficiency, surrogate models have been widely used in designing complex engineering systems. In general, a stand-alone surrogate model cannot perform well for all engineering design problems, and the performance of a surrogate model is not known in advance. Ensembles of surrogates that combine various stand-alone surrogates have been developed to improve the robustness of stand-alone surrogate models. Inspired by the previous research on using the heuristic formulation to calculate weights of stand-alone surrogate models, we propose a pointwise ensemble of surrogates with adaptive function and heuristic formulation (PEAH) in this paper. The adaptive function presented in this paper contains the local accuracy and prediction uncertainty information around a prediction point. Thus, the adaptive function can adapt to the local characteristics of the prediction point. Various analytical test functions and two engineering design problems have been selected to test PEAH, and existing well-known ensembles of surrogates are employed to compare with the proposed pointwise ensemble model. The test results indicate that PEAH performs better in those problems with a better balance between accuracy and robustness.

Appendix: Explicit functions of of PRS, RBF and Kriging

PRS

PRS model (Box et al. 1978) has been widely applied for estimating the output response in engineering systems. A second-order PRS model can be expressed as:

$$\begin{aligned} {\hat{y}} = {\beta _0} + \sum \nolimits _{i = 1}^d {{\beta _d}{x_i}} + \sum \limits _{i = 1}^d {{\beta _{ii}}x_i^2} + \sum \limits _i {\sum \limits _j {{\beta _{ij}}{x_i}{x_j}} } \end{aligned}$$

(40)

where ${\hat{y}}$ and x represent the predicted response and the input variable vector, respectively. $\beta$ indicates the coefficient vector of the PRS model and d refers to the dimension of the input variable vector.

RBF

RBF (Hardy 1971) has been developed for approximating the relationship between input variables and the output response. The RBF model utilizes combinations of a radially symmetric function based on Euclidean distance or other such metrics to approximate the response function (Jin et al. 2001). The radial basis function can be expressed as:

$$\begin{aligned} {\hat{y}} = \sum \nolimits _{k = 1}^N {{\beta _k}\phi (\left\| {x - {x^{(k)}}} \right\| } ) \end{aligned}$$

(41)

where N refers to the number of training points in the training set. $\phi$ is the the basis function and $\beta$ is the coefficient vector of the basis function. $\left\| {x - {x^{(k)}}} \right\|$ represents the Euclidean distance between the prediction point x and the kth training point ${x^{(k)}}$.

Kriging

The Kriging model (Sacks et al. 1989) postulates that the output response at a prediction point can be expressed as a linear combination of the output responses of the training points in the neighborhood of the prediction point. The Kriging model can be expressed as:

$$\begin{aligned} {\hat{y}} = \sum \nolimits _{k = 1}^N {{\beta _k}{f_k}(x) + Z(x)} \end{aligned}$$

(42)

where ${f_k}(x)$ is the output response at the kth training point. Z(x) is assumed to be the realization of a stochastic process with mean zero and spatial correlation function (Jin et al. 2001), given by:

$$\begin{aligned} {\mathop {\mathrm{cov}}} [Z({x_i}),Z({x_j})] = {\delta ^2}R({x_i},{x_j}) \end{aligned}$$

(43)

where ${\delta ^2}$ indicates the process variance, and $R({x_i},{x_j})$ refers to the correlation function.