A modified level set method for topology optimization of sparsely-filled and slender structures

Abstract

In structural optimization, the level set method is known as a well-established approach for shape and topology optimization. However, special care must be taken, if the design domains are sparsely-filled and slender. Using steepest descent-type level set methods, slender structure topology optimizations tend to instabilities and loss of structural cohesion. A sole step size control or a selection of more complex initial designs only help occasionally to overcome these issues and do not describe a universal solution. In this paper, instead of updating the level set function by solving a Hamilton–Jacobi partial differential equation, an adapted algorithm for the update of the level set function is utilized, which allows an efficient and stable topology optimization of slender structures. Including different adaptations, this algorithm replaces unacceptable designs by modifying both the pseudo-time step size and the Lagrange multiplier. Besides, adjustments are incorporated in the normal velocity formulation to avoid instabilities and achieve a smoother optimization convergence. Furthermore, adding filtering-like adaptation terms to the update scheme, even in case of very slender structures, the algorithm is able to perform topology optimization with an appropriate convergence speed. This procedure is applied for compliance minimization problems of slender structures. The stability of the optimization process is shown by 2D numerical examples. The solid isotropic material with penalization (SIMP) method is used as an alternative approach to validate the result quality of the presented method. Finally, the simple extension to 3D optimization problems is addressed, and a 3D optimization example is briefly discussed.

1 Introduction

The topology optimization of solid structures is one of the most challenging areas in structural optimization. Thereby, the size, shape and connectivity of the structure are not prescribed, and due to the possibility of topological changes, the initial design does not necessarily have to be a close-to-optimal design. Hence, its influence on the final design is alleviated, see Bendsoe and Sigmund (2013). Over the past decades, a diverse range of topology optimization methods has been developed and reached a convincing maturity. Among a wide variety of approaches, density and level set methods are used most frequently. In Sigmund and Maute (2013), an overview of the topology optimization methods along with a critical comparison and discussion of their strengths and weaknesses is given. In the current work, a level set-based topology optimization is considered.

The level set method is an implicit boundary-based geometry method, which has originally been developed by Osher and Sethian (1988) for following fronts propagation in surface motion problems, see also Osher and Fedkiw (2005) and Sethian (1999). In this approach, the moving surfaces, also referred to as moving interfaces or free boundaries, are represented implicitly as the zero isosurface of a higher-dimensional scalar level set function $\phi$. By this, topological complexities and changes can be captured naturally (Osher and Sethian 1988), and the evolving boundaries can break up, merge or disappear for instance based on the laws of physics (Tsai and Osher 2003).

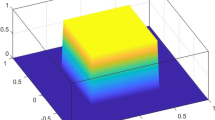
In a level set-based topology optimization, a level set function $\phi$ is defined over the design domain D. Depending on the level set function value at each arbitrary point of D with the position vector $\varvec{r}$, this point can then be assigned to the interior [$\phi (\varvec{r})>0$], exterior [$\phi (\varvec{r})<0$] or free boundaries [$\phi (\varvec{r})=0$] of the structural design. In Fig. 1, this implicit representation is depicted by a 2D example, where the level set function $\phi$ is defined over a rectangular design domain D and creates due to its negative value in the middle region, a design with a central elliptical void.

Fig. 1

Definition (a) of a level set function $\phi$ over the design domain D and the resulting design (b)

In conventional level set methods for structural optimization such as Allaire et al. (2004) and Wang et al. (2003), the design evolution is based on the solution of the Hamilton–Jacobi partial differential equation

$$\frac{\partial \phi }{\partial {{\tilde{t}}}}-V_{\text {n}}\cdot |\nabla \phi |=0, \quad \phi (\varvec{r},0)=\phi _{0}(\varvec{r}) .$$

(1)

Thereby, ${{\tilde{t}}}$ is the pseudo-time in the optimization process and $V_{\text {n}}$ the normal velocity. Besides, $\nabla \phi$ describes the spatial derivative of $\phi$ with $|\nabla \phi |=\sqrt{\nabla \phi \cdot \nabla \phi }$ and $\phi _{0}$ is the initial level set function.

For the conventional solution of the Hamilton–Jacobi equation (1), in literature auspicious methods with a convincing accuracy and robustness are introduced, such as explicit upwind schemes, see also Jiang and Peng (2000), Osher and Sethian (1988) and Osher and Shu (1991). However, these methods lead to some difficulties in the structural optimization, see van Dijk et al. (2013) and Luo et al. (2007). Among others, in case of explicit time-marching schemes, a stability limit based on the Courant–Friedrichs–Lewy (CFL) condition, see Osher and Fedkiw (2005), has to be considered for the pseudo-time step size, which reduces the efficiency. Furthermore, often a signed-distance reinitialization, see Osher and Fedkiw (2005) and Sethian (1999), is utilized to prevent the level set function from becoming too flat or too steep. This is necessary to avoid deteriorating approximation errors, see Allaire and Jouve (2005). Nevertheless, maintaining the regularity of the level set function by a classical reinitialization, in the conventional level set methods a hole creation in the interior of the design is not possible. Hence, additional procedures, such as topological derivatives are required to enable a hole nucleation, see Allaire et al. (2005) and Burger et al. (2004).

To circumvent the mentioned drawbacks of the conventional level set methods, alternative approaches have been developed, see for instance the well-established concepts proposed in Luo et al. (2008), Wang et al. (2007), Wang and Wang (2006a, b), Wei et al. (2018) and Yamada et al. (2010). In these variants, other evolution techniques rather than the explicit update schemes are used, which help to dispose of the stability limit imposed by the CFL condition. Besides, these approaches do not include a signed-distance reinitialization. In this way, a hole creation is not hindered, and more complex topologies can be created during the optimization process, for instance, based on a natural velocity extension, see Allaire et al. (2004) and van Dijk et al. (2013). Following this path of alternative approaches, here an approximate level set method is utilized, which basically updates the nodal level set function values by a forward Euler scheme, and includes an approximate reinitialization. The main steps of this procedure are adopted from the work proposed by Wei et al. (2018).

Even if alternative approaches avoid the mentioned issues of the conventional level set methods, in literature both conventional and alternative level set methods are typically studied for topology optimization of structures with a moderate width/length ratio, e.g., 1/2 or 1/3 for a 2D cantilever beam. To the best knowledge of the authors, there is a gap regarding the level set-based topology optimization of sparsely-filled and slender structures, e.g., 2D cantilever beams with a width/length ratio $\ll$ 1/3. At least in case of steepest decent-type level set methods, the optimization process of slender structures is not successful, and tends to instabilities and loss of structural cohesion. Thereby, even common adaptations, such as a pseudo-time step size control or the use of more complex initial designs can only help occasionally and do not describe a universal solution.

To resolve the mentioned issues, in the current work a set of algorithmic and numerical as well as filtering-like adaptations are developed and included into the approximate level set method. The modified algorithm is then successfully tested for the compliance minimization problem of sparsely-filled and slender structures. Besides, in order to validate the optimization results, a comparison is made with a solid isotropic material with penalization (SIMP) optimization, which is performed by the method of moving asymptotes (MMAs), see Svanberg (1987). Moreover, the extension of the adapted algorithm to 3D examples is shortly addressed.

The remainder of this paper is organized as follows: In Sect. 2, the approximate level set method for a compliance minimization problem is shortly reviewed. In addition, the functionality of the algorithm and also issues regarding the topology optimization of sparsely-filled and slender structures are shown by demonstration examples. In Sect. 3, the algorithmic and numerical adaptations are presented, and their contributions are illustrated by further examples. In Sect. 4, the filtering-like adaptations are described, and the final level set algorithm including all adaptations is applied for topology optimization of examples with different volume limits. Section 5 presents a short description of the SIMP method and subsequently a comparison of results obtained with both the modified level set algorithm and the SIMP method. After that, the 3D extension of the level set algorithm is shortly described, and the optimization results for a 3D cantilever beam are included. In the end, Sect. 6 provides a summary and conclusion.

2 Approximate level set method

In this work, an approximate level set method is utilized, which is mainly adopted from the work proposed by Wei et al. (2018). In the following, first the fundamental steps of the procedure are addressed. Afterward, the considered compliance minimization problem is introduced. Then, the numerical implementation of the normal velocity $V_{\text {n}}$ for the compliance minimization problem is described. Subsequently, the optimization algorithm is illustrated. After all, demonstration examples are presented and numerical limitations of the approximate level set method are pointed out.

2.1 Basic steps of the method

For the discretization of the level set function $\phi$ in space, a typical sampling on a fixed Cartesian grid is considered. The nodal level set function variables $\{{\phi }_{1},\ldots ,{\phi }_{n}\}$ at the n grid nodes with position vectors $\{\varvec{r}_{1},\ldots ,\varvec{r}_{n}\}$ are then directly used as the design variables of the optimization problem, see also Wang et al. (2003). In other words, the update of the continuous level set function $\phi$ is replaced by an update of the discretized level set function $\varvec{\phi }=[\phi _{1},\ldots ,\phi _{n}]^{\top }$. In the approximate level set method, $\varvec{\phi }$ is updated by a forward Euler scheme as

$$\varvec{\phi }({{\tilde{t}}}_{k+1})={\varvec{\phi }}({{\tilde{t}}}_{k})+\varDelta {{\tilde{t}}}\, \hat{\varvec{B}}({{\tilde{t}}}_{k}),$$

(2)

where ${{\tilde{t}}}_{k}$ is the k-th time step, ${{\tilde{t}}}_{k+1}$ the subsequent one, and $\varDelta {{\tilde{t}}}$ the corresponding pseudo-time step size. Furthermore, the augmented velocity vector $\hat{\varvec{B}}$ is defined as

$$\begin{aligned}&\hat{\varvec{B}}({{\tilde{t}}}_{k}) \\&\quad =[V_{\text {n}}(\varvec{r}_{1},{{\tilde{t}}}_{k})\cdot {{\hat{\delta }}}(\phi (\varvec{r}_{1},{{\tilde{t}}}_{k})),\ldots , V_{\text {n}}(\varvec{r}_{n},{{\tilde{t}}}_{k})\cdot {{\hat{\delta }}}(\phi (\varvec{r}_{n},{{\tilde{t}}}_{k}))]^{\top }. \end{aligned}$$

(3)

In this formulation, the normal velocity $V_{\text {n}}$ at each node is multiplied with a distribution function

$$\begin{aligned} {{\hat{\delta }}}(\phi )=\left\{ \begin{array}{ll} 0,&{}\phi >\varDelta ,\\ 1-\dfrac{\phi ^{2}}{\varDelta ^{2}},&{} -\varDelta \le \phi \le \varDelta ,\\ 0,&{}\phi <-\varDelta , \end{array}\right. \end{aligned}$$

(4)

where $\varDelta$ is the distribution half-width, see also Wang et al. (2003) and Wei et al. (2018). In this work $\varDelta =10$ is chosen. As it is shown in Fig. 2, depending on the value of $\phi$, ${{\hat{\delta }}}$ gives a smoothing factor between 1 for $\phi =0$ and 0 for $|\phi |\ge \varDelta$. The modification of the normal velocity by the distribution function ${{\hat{\delta }}}$ hinders, among others, a limitless growth of the level set function $\phi$ in areas with a high value of normal velocity $V_{\text {n}}$ and, thus, helps to avoid the corresponding convergence issues. Compared to the original Hamilton–Jacobi equation (1), it can be argued that here the spatial derivative value $|\nabla \phi |$ is replaced by the distribution function ${{\hat{\delta }}}(\phi )$, see also Wang and Wei (2005). Hence, the approximate update scheme (2) applied in this work can be interpreted as a relaxed variant, see also Sigmund and Maute (2013) for more details.

Fig. 2

Definition of the distribution function ${{\hat{\delta }}}(\phi )$

Moreover, to maintain the regularity of the discretized level set function $\varvec{\phi }$, an approximate reinitialization procedure is used, see Wei et al. (2018). Thereby, it is only tried to hold the spatial derivative value around the zero-level set in a range close to 1, so that a hole creation is not prevented. For this purpose, the discretized level set function $\varvec{\phi }$ can be divided by the average of the spatial derivative values at m selected nodes around the zero-level set as

$${\varvec{\phi }}=\dfrac{\varvec{\phi }}{\texttt {mean}(|\nabla \phi _{1}^{0} |,\, |\nabla \phi _{2}^{0} |,\ldots ,|\nabla \phi _{m}^{0}|)}.$$

(5)

Here, $|\nabla \phi _{j}^{0}|$ denotes the spatial derivative value at node j, which belongs to the neighborhood of the zero-level set, and the function ${\texttt {mean}(\cdot )}$ gives the average of included values. This reinitialization can be considered either after each update or periodically. Unlike a signed-distance reinitialization, the spatial derivative values after approximate reinitialization are not equal to 1, but distributed around it. Nevertheless, from a numerical point of view, this manipulation is useful and enough to retain the regularity of the level set function around the zero-level set.

Undisturbed from a global reinitialization and based on a naturally extended velocity, see Allaire et al. (2004) and van Dijk et al. (2013), the approximate update scheme (2) can develop the level set function over the entire design domain D. Thereby, a hole creation in the interior of the design is not suppressed. This decreases the influence of a selected initial design on the optimization results, and allows a simultaneous shape and topology optimization. Furthermore, the presented scheme alleviates the necessity of significantly fine grids and the CFL condition. Accordingly, the space and time discretization can be performed based on the requirements of the studied optimization problem rather than the numerical considerations of conventional level set methods. In this way, higher efficiency and convergence speeds can be reached, see also Wang et al. (2007).

2.2 Compliance minimization problem

In the current work, the well-studied problem of compliance minimization for a statically loaded linear elastic structure is considered. In Allaire et al. (2004) and Wang et al. (2003), details on the classical level set-based notion of the compliance minimization problem are given. In case of a FE-discretized mechanical model, the compliance $\psi$ of the structure can be formulated as the sum of element compliances $\psi _{\ell }$. It follows

(6)

where $n_{\text {e}}$ is the number of FE-elements, $\varvec{u}_{{\ell }}$ the nodal displacement vector and $\varvec{K}_{\ell }$ the stiffness matrix of element $\ell$. Depending on the element fill volume $v_{\ell }^{\text {e}}$, here the element stiffness matrix $\varvec{K}_{\ell }$ is parametrized linearly as

$$\varvec{K}_{\ell }=\big (\epsilon +(1-\epsilon )\,v^{\text {e}}_{\ell }\big )\varvec{K}_{0},$$

(7)

see also Norato et al. (2004). Thereby, $\varvec{K}_{0}$ is the stiffness matrix of a completely filled reference element. Besides, $\epsilon$ is a weak material density, which is included to avoid numerical difficulties due to singular structural problems, see also Allaire et al. (2004). Here $\epsilon =10^{-9}$ is chosen. It should also be mentioned that in the considered parametrization, the element fill volumes depend on the discretized level set function, i.e., $v^{\text {e}}_{\ell }=v^{\text {e}}_{\ell }(\varvec{\phi })$. These can be calculated, for instance, based on level set function values interpolated on a refined mesh grid over the elements, see Wei et al. (2018).

Furthermore, the vector $\varvec{u}_{{\ell }}$ of nodal displacements for element $\ell$ results from the finite element static equilibrium equation

$$\overline{\varvec{K}}\,\overline{\varvec{U}}-\overline{\varvec{F}}=0,$$

(8)

where $\overline{\varvec{K}}$ is the global stiffness matrix, $\overline{\varvec{U}}$ the global vector of nodal displacements, and $\overline{\varvec{F}}$ the global force vector. Considering Eqs. (6)–(8), the level set-based compliance minimization problem of a structural model under static loads can be defined as

$$\begin{aligned}&\underset{{\varvec{\phi }\in {{\mathbb {R}}}^{n}}}{{\text{minimize}}}\,\, \psi (\varvec{\phi }) =\sum _{\ell =1}^{n_{\text {e}}}{ \big (\epsilon +(1-\epsilon )v^{\text {e}}_{\ell }\big ) \varvec{u}_{\ell }^\top \varvec{K}_{0}\,\varvec{u}_{\ell } }\end{aligned}$$

(9a)

$$\begin{aligned}&\text {subject to} \,\, \left\{ \begin{array}{l}\overline{\varvec{K}}\,\overline{\varvec{U}}-\overline{\varvec{F}}=0\\ h(\varvec{\phi })=v(\varvec{\phi })-v_{\text {max}}= 0 \end{array}\right. \end{aligned}$$

(9b)

Here, the constraint equation $h(\varvec{\phi })=0$ imposes a limit of $v_{\text {max}}$ to the volume fraction v of the structural design. Thus, it can be stated that the goal of the optimization problem (9) is to find a discretized level set function $\varvec{\phi }$, which implicitly describes a close-to-optimal design with a minimized compliance and a prescribed material use.

2.3 Formulation of the normal velocity $V_{\text {n}}$

A common approach to obtain the normal velocity $V_{\text {n}}$ in a level set-based optimization problem stems from the classical shape sensitivity analysis, see, for instance, the references Pironneau (1982) and Sokolowski and Zolésio (1992). In this context, Allaire et al. (2004) proposed the shape derivative in the framework of level set-based structural optimization. In the presented compliance minimization problem, this approach with the steepest descent direction provides the normal velocity $V_{\text {n}}$ of each node on the free boundary by the local energy density obtained from a FE-analysis and a single Lagrange multiplier $\lambda$, which corresponds to the volume constraint. Using a natural velocity extension, see Allaire et al. (2004) and van Dijk et al. (2013), the normal velocity can then be extended to the entire design domain D.

In this work, the fixed uniform Cartesian grid of the level set function coincides with the underlying FE-mesh, see also Wei et al. (2018, 2021). Unlike a classical density-based topology optimization with element-wise design variables, here the nodal variables $[\phi _{1},\ldots ,\phi _{n}]$ of the discretized level set function $\varvec{\phi }$ are updated as design variables. Hence, the element compliances $\psi _{\ell }$ should be mapped to the FE-nodes. In each pseudo-time step ${{\tilde{t}}}_{k}$, the normal velocity $V_{\text {n}}(\varvec{r}_{i},{{\tilde{t}}}_{k})$ of each node i with the position vector $\varvec{r}_{i}$ is then constructed by the nodal energy density ${{\overline{\psi }}}_{i}$, which is the average compliance of the surrounding elements, a scaling factor c, and the current value $\lambda _{k}$ of the Lagrange multiplier as

(10)

Thereby, $n_{\text {s}}$ is the number of surrounding FE-elements of node i. It should be mentioned that the use of average element compliances ${{\overline{\psi }}}_{i}$ in the formulation of normal velocity has a filtering and smoothing effect, and helps to avoid checkerboard instabilities (Sigmund and Maute 2013). Moreover, the included scaling factor c serves as a normalization of the incorporated compliance values, which helps to keep the optimization process independent of absolute FE-analysis results. Similar to Wei et al. (2018), here this factor is selected as the median of element compliances in each iteration k. Nevertheless, further normalization variants, for instance by the average of element compliance values, are also possible, which can influence the optimization convergence depending on the studied example (Wei et al. 2018).

Furthermore, an appropriate selection of the Lagrange multiplier in the optimization process is of great importance. It has a decisive influence on the satisfaction of the volume constraint, the numerical stability and convergence speed. In literature, the bi-sectioning algorithm (Sigmund 2001; Wang et al. 2007; Wang and Wang 2006b) and the augmented Lagrangian method (Belytschko et al. 2003; Luo et al. 2008; Wei et al. 2018; Wei and Wang 2006) are mostly used to update the Lagrange multiplier $\lambda$. Unlike bi-sectioning algorithm, in the augmented Lagrangian method, no abrupt correction of the volume fraction is considered, and the constraint violation is increased gradually. In the current work, the augmented Lagrange update scheme suggested by Wei et al. (2018) is considered. This scheme consists of two stages: an early stage up to a selected number $n_{\text {E}}$ of iterations and after that a convergence stage. For the $(k\,{+}\,1)$-th pseudo-time step, it follows

$$\lambda _{k+1}= \left\{ \begin{array}{ll} \mu \,{{\hat{h}}}_{k} &{} k\le n_{\text {E}},\\ \lambda _{k}+\gamma _{k}h_{k} &{} k> n_{\text {E}}.\\ \end{array}\right.$$

(11)

In the early stage, the Lagrange multiplier is chosen as the multiplication of a selected factor $\mu$ and a relaxed volume constraint ${{\hat{h}}}_{k}$ defined as

$${{\hat{h}}}_{k}= v_{k}-\left[ v_{0}-\dfrac{k}{n_{\text {E}}}\left( v_{0}-{v}_{\text {max}}\right) \right] , \quad \text {with} \,\, k\le n_{\text {E}}.$$

(12)

This choice makes it possible to start with an initial volume $v_{0}$ far away from the prescribed volume limit $v_{\text {max}}$ and moves the designs within $n_{\text {E}}$ steps gradually into the direction of smaller constraint violations. Subsequently, in the convergence stage, the Lagrange multiplier is adapted from step to step by the current value of the volume constraint $\,h_{k}=v_{k}-v_{\text {max}}\,$ multiplied with a process parameter $\gamma$, which is in turn updated as

$$\gamma _{k+1}= {\text {min}}(\gamma _{k}+\varDelta \gamma ,\gamma _{\text {max}}), \quad \text {with} \,\, k> n_{\text {E}}.$$

(13)

For this update, an initial value $\gamma _{0}$, the increment $\varDelta \gamma$ and the upper limit $\gamma _{\text {max}}$ are required. Similar to the pseudo-time step size $\varDelta {{\tilde{t}}}$, the introduced process parameters influence the stability, convergence, and results of the optimization process. Hence, they should be selected carefully.

2.4 Optimization algorithm

The algorithmic representation of the approximate level set method can be seen in Fig. 3. In this optimization algorithm, first the initial vector $\varvec{\phi }_{0}$ of the discretized level set function is defined, which captures the initial design. After that, the FE-analysis is prepared and performed. Subsequently, the optimization loop starts with the update of the Lagrange multiplier $\lambda$. Using the calculated element compliances $\psi _{\ell }$ and $\lambda$, the normal velocity $V_{\text {n}}$ is constructed. In the next step, the discretized level set function $\varvec{\phi }$ is developed by the update scheme (2). For the resulting design, which belongs to the iteration $k{+}1$, the FE-analysis is performed. Then, the optimization loop is repeated until a prescribed iteration number $n_{\text {I}}$ is reached.

Fig. 3

Flow diagram of the optimization process

It is worth mentioning that the simple stopping criterion utilized in this work allows to observe the optimization histories and potential stability issues in a desired number $n_{\text {I}}$ of iterations, which is preferred here. Nevertheless, in practical terms, it is more convenient to use an improved stopping criterion, which terminates the optimization process based on compliance changes and the volume fraction v, see for instance Wei et al. (2018).

The optimization algorithms presented in this work are all implemented using Matlab, and the corresponding calculations are performed on a personal computer equipped with a $3.80\,\hbox {GHz}\, \texttt {Intel}{\circledR }\,\texttt {Xeon}{\circledR }\,{\text {E}}3{\text {-}}1270 \,{\text {v}}6$ processor and $\hbox {64}{}$ GB RAM.

2.5 Demonstration examples and numerical limitations

In order to demonstrate the possibilities and limits of the level set method described above, three 2D optimization examples are presented, namely a short cantilever beam with a moderate volume limit $v_{\text {max}}=0.5$ (example 1-A), a second one with the same size and a lower volume limit $v_{\text {max}}=0.35$ (example 1-B), and a slender cantilever beam again with $v_{\text {max}}=0.5$ (example 1-C). The problem definitions and optimization results of the three examples are summarized in Table 1.

Table 1 Problem definitions and optimization results of demonstration examples in Sect. 2

All 2D cantilever beams presented here and also in the next sections are discretized using bilinear unit square finite elements. Thereby, a Young’s modulus $E_{0}=1\,{\text {Pa}}$ and a Poisson ratio $\nu =0.3$ are considered to formulate the stiffness matrix $\varvec{K}_{0}$ of the completely filled reference element. These material properties are adopted from the reference implementations provided in Sigmund (2001) and Wei et al. (2018).

In Fig. 4, the discretized model of a 2D cantilever beam is shown, which has a length of $l_{{x}}$ and a width of $l_{{y}}$. In all studied examples, the left end of the cantilever beam is in both x- and y-direction fixed and the structure is loaded by a single force $F=1\,{\text {N}}$ at the middle node of the right end.

Fig. 4

Discretized model of a cantilever beam

In example 1-A, the short cantilever beam is discretized by $20\times 40$ elements. For a level set-based topology optimization, the update scheme (2) with a pseudo-time step size $\varDelta {{\tilde{t}}}=0.5$ and the process parameters $n_{\text {E}}=20$, $\mu =5$, $\gamma _{0}=0.1$, $\varDelta \gamma =0.1$, $\gamma _{\text {max}}=5$ is applied. Thereby, a simple initial level set function $\{\forall i\in \,1(1)n:\phi (\varvec{r}_{i},0)=1\cdot 10^{-3}\}$ is selected, which leads to a completely filled initial design. However, the approximate reinitialization (5) does not work for such a simple design without free boundaries. Hence, this reinitialization method is switched on later, where a lower volume fraction such as $v=0.9$ is reached, and free boundaries are available. It is worth mentioning that the same process parameters and initial design are used for all further demonstration examples, unless explicit changes are noticed. As mentioned before, the volume limit in example 1-A is set to $v_{\text {max}}=0.5$, and the design is developed within a chosen number $n_{\text {I}}=100$ of optimization iterations.

In Fig. 5a, the final level set function $\phi _{\text {end}}$ of example 1-A after 100 optimization iterations is shown. The corresponding final design can then be described by the zero-level contour, see Fig. 5b. This plot is created by the function surf in Matlab. The final level set function has a relatively high value at the edges of the fixed side and in the location of the load point. This is in accord with the high strain energy density in these areas. Nevertheless, due to the included distribution function ${{\hat{\delta }}}$, the growth of the level set function $\phi$ is controlled by the introduced limit $\varDelta =10$.

Fig. 5

Final level set function (a) and topology (b) of example 1-A

The optimization histories of example 1-A are shown in Fig. 6. It is obvious that the completely filled initial design has the highest stiffness and the lowest compliance. Reducing the material volume, the compliance rises and reaches a maximum $\psi _{\text {max}}=62.5\,{\text {Nm}}$ at $k=34$. However, in this iteration, the design has a volume fraction $v=0.478$ below the prescribed volume limit $v_{\text {max}}=0.5$. This is due to an overshoot of the Lagrange multiplier $\lambda$. The update scheme (11) with the introduced process parameters turns the volume fraction v gradually back to $v_{\text {max}}=0.5$. At $k=100$, a final design with compliance $\psi _{\text {end}}=59.7\,{\text {Nm}}$ and volume fraction $v_{\text {end}}=0.501$ is reached.

Fig. 6

Optimization histories of examples 1-A and 1-B

Assuming that an appropriate set of process parameters is used, the update scheme (2) with the developed normal velocity $V_{\text {n}}$ from Eq. (10) can provide meaningful optimization results for a wide range of benchmark examples as before, see also Wei et al. (2018). However, it is obvious that the presented implementation with a single Lagrange multiplier $\lambda$ and a constant pseudo-time step size $\varDelta {{\tilde{t}}}$ cannot always guarantee the numerical stability. Consequently, in critical cases such as topology optimization with low volume limits or slender structures, convergence issues, significant oscillations, and in the worst case loss of structural cohesion can be observed. For instance, setting the desired volume limit $v_{\text {max}}$ to 0.35, the optimization process of the short cantilever beam with $20\times 40$ elements (example 1-B) becomes instable. Accordingly, inappropriate design updates result. For this example, the jagged instable optimization histories are shown in Fig. 6. Besides, the inappropriate design updates of the iterations 53 to 56 can be seen in Fig. 7.

Fig. 7

Example 1-B: termination of optimization due to numerical instability

For slender structures, instabilities arise even much earlier in the very first iterations. In case of a completely filled cantilever beam with $20\times 200$ elements (example 1-C), the update scheme (2) with the volume limit $v_{\text {max}}=0.5$ and the same process parameters as before results directly in a disjointed design update in iteration 2, see Fig. 8. For sure, a more careful combination of process parameters or an initial design of a higher complexity are intuitive possibilities to increase the stability of a single topology optimization example. However, experiences from numerous numerical examples show that even these changes cannot completely solve the stability problem in the critical cases. Hence, in this work it is intended to overcome the mentioned issues for slender and sparsely-filled structures by further adaptations of the update scheme. These are described in the following sections.

Fig. 8

Example 1-C: termination of optimization due to tear off of material

3 Algorithmic and numerical adaptations

The goal of this work is to improve the stability of the optimization process so that it becomes applicable for sparsely-filled and slender design domains. To this end, different adaptations are introduced into the optimization algorithm, see Fig. 9. The adaptations can be roughly divided into two types: algorithmic and numerical as well as filtering-like. While the former (adaptations I–III) are presented in this section, the latter (adaptations IV–V) are discussed in Sect. 4. For both adaptation types, further demonstration examples are used to show the influence and functionality of the individual changes.

Fig. 9

Flow diagram of the optimization process including adaptations

3.1 Adaptation I: reconstruction of the load path

The loss of structural cohesion in the demonstration example 1-C is catastrophic. The associated break of the load path leads in the subsequent iteration to a corrupted FE-analysis and a disruptive normal velocity $V_{\text {n}}$. The main reason for the loss of structural cohesion is an inappropriate change of the Lagrange multiplier $\lambda$. To reconstruct the load path, it is therefore decided to adjust the Lagrange multiplier $\lambda$ (adaptation I). Using a pseudo-code, this adaptation is presented in Algorithm 1. In each iteration k, after the level set function is updated, it is checked, whether a prescribed connection condition is fulfilled. A simple way to check the connection is to pass the density-based material distribution of each design to the Matlab function bwlabel, which labels connected components in a matrix.

Comparing the label of elements around the load point with the label of elements including fixed nodes, broken load paths can be detected. If the connectivity condition is not fulfilled, a small term $\varepsilon _{1}=0.01$ is subtracted from the Lagrange multiplier and the level set function update is renewed with the adjusted Lagrange multiplier. This iteration is repeated until a solid load path is reconstructed. Alternatively, it is possible to reconstruct the load path by an iterative adjustment of the pseudo-time step size $\varDelta {{\tilde{t}}}$. However, since the loss of structural cohesion is mainly caused by an inappropriately fast update of the Lagrange multiplier $\lambda$, the use of a pseudo-time step size adaptation is in this connection ineffective and, thus, it is not considered.

To test the utility of adaptation I, first, only this step is added to the approximate level set method and applied for the topology optimization of the completely filled slender cantilever beam with $20\times 200$ elements and a volume limit $v_{\text {max}}=0.5$ within 200 iterations (example 2-A). Table 2 contains the problem definitions and optimization results of the current and further examples, which are discussed later in this section. In Fig. 10, the important optimization histories are included, and the final designs are shown in Fig. 11.

Table 2 Problem definitions and optimization results of demonstration examples in Sect. 3

Fig. 10

Optimization histories of examples 2-A, 2-B, and 2-C

Fig. 11

Final designs of examples in Sect. 3

In example 2-A, the Lagrange multiplier adaptation is only necessary once in the beginning. In Fig. 10c, the adapted Lagrange multiplier $\lambda _{1}$ is marked by an asterisk. Moreover, the corresponding compliance history in Fig. 10a shows some huge jumps. These arise after the reconstruction of the load path or due to some numerical reasons, such as the normalization of the compliance values by their median in the formulation of the normal velocity $V_{\text {n}}$ from Eq. (10) or the chosen discretization. The large compliance changes are an indicator for a distorted optimization process. It can, for instance, be observed that the jump of the compliance in iteration $k=44$ is followed by an undesired increase of the volume fraction v, see the magnified section of the volume history of example 2-A in Fig. 10b. This leads to a delay in the optimization convergence. To control undesired compliance changes, the adaptation II is introduced in the following.

Despite the mentioned issues in example 2-A, after 200 iterations a meaningful final design with $\psi _{\text {end}}= 4.75\cdot 10^{3}\,{\text {Nm}}$ and $v_{\text {end}}=0.500$ is obtained, see Fig. 11. It should be noticed that the thin broken connections included in the final design are due to the relatively coarse discretization and the utilized zero-level contour representation. They indicate only that the elements of the underlying FE-mesh in these areas are not completely filled. In case of slender structures, such patterns are not uncommon. However, a coarse discretization combined with an inappropriate set of process parameters leads to oscillations around these thin struts, similar to those observed in Fig. 7. The following adaptations II–V are a remedy to reduce such oscillations, and to provide a stable optimization process despite a coarse discretization.

3.2 Adaptation II: control of the compliance change

To avoid a large increase of the compliance $\psi$ from one step to another, and to relax contaminating oscillations, adaptation II is considered. With that, a combination of two different step size control schemes is incorporated into the optimization process. These are shown in Algorithms 2 and 3, respectively.

By Algorithm 2, it is checked, whether a prescribed compliance change limit $\varDelta \psi _{\text {max}}$ is exceeded. As long as this is the case, the current pseudo-time step size $\varDelta {{\tilde{t}}}_{k}$ is iteratively reduced by a factor $\tau _{1}$. Here $\varDelta \psi _{\text {max}}=0.05$ and $\tau _{1}=0.8$ are used. Subsequently, the level set function update and the FE-analysis are repeated. It is obvious that a high number of iterations in Algorithm 2 leads to a high number of FE-calculations, which makes the optimization process inefficient. Hence, the limit $\varDelta \psi _{\text {max}}$ should not be set too low. The Algorithm 2 is only appropriate to avoid some sporadic compliance peaks, and its frequent use is rather an indicator for the fact that some process parameters or optimization steps should be reviewed.

In a further part, Algorithm 3 provides another step size control based on the compliance history. Thereby, the sign of two successive compliance changes are compared. In case of non-conformity, the pseudo-time step size $\varDelta {{\tilde{t}}}_{k+1}$ for the next step is reduced by the parameter $\tau _{2}$. Moreover, if no compliance oscillation is detected, and Algorithm 2 is also not used in the current iteration, then an increase of $\varDelta {{\tilde{t}}}_{k+1}$ by $\tau _{3}$ up to a prescribed limit $\varDelta {{\tilde{t}}}_{\text {max}}$ is made. Here $\tau _{2}=0.8$, $\tau _{3}=1.1$, $\varDelta {{\tilde{t}}}_{\text {max}}=0.5$ are chosen, and the optimization process starts with $\varDelta {{\tilde{t}}}_{1}=0.5$. Using Algorithm 3, oscillations, which arise, for instance, around thin connections, can be alleviated, and it helps to develop these connections better. Nevertheless, again, instead of too many step size adaptations by Algorithm 3, it is more convenient to change the process parameters, such as using a lower limit $\varDelta {{\tilde{t}}}_{\text {max}}$.

Considering both adaptations I and II, here the topology optimization of the completely filled slender cantilever beam with $20\times 200$ elements is repeated (example 2-B). Thereby, a sharp jump of the compliance $\psi$ is avoided, see Fig. 10a, though in the exchange of an inefficient reduction of the pseudo-time step size $\varDelta {{\tilde{t}}}$ by Algorithm 2. In Fig. 10d, the pseudo-time step size $\varDelta {{\tilde{t}}}$ over the iteration number k is shown, where the adaptations by Algorithm 2 are marked with asterisks. It can be seen that a high number of step size adaptations in the first 50 iterations are performed, which emphasizes that the applied normal velocity $V_{\text {n}}$ for the design evolution is not completely appropriate. Besides, it is obvious that the dramatic reduction of $\varDelta {{\tilde{t}}}$ simultaneously with the increase of the Lagrange multiplier $\lambda$ results in an overshoot of $\lambda$, see Fig. 10c, and a meaningless ascent and descent in the compliance progression, see Fig. 10a. This overshoot causes also an oscillation of the volume around the prescribed volume limit $v_{\text {max}}$, see the magnified section of the volume history of example 2-B in Fig. 10b. Adaptation III is intended to counter these issues.

It is clear that in example 2-B, the iterations between $k=10$ and 80 are performed with inefficiently small pseudo-time step sizes $\varDelta {{\tilde{t}}}$, see Fig. 10d. Nevertheless, after raising $\varDelta {{\tilde{t}}}$ gradually by Algorithm 3, a meaningful design evolution follows. Moreover, in the part between $k=140$ and 200, the compliance changes are insignificantly small, which indicates that a close-to-optimal design is almost reached at $k=140$. In this stage, the sign of compliance changes from one step to the other can switch frequently. Consequently, the pseudo-time step size is pushed down by Algorithm 3. In this way, only small design changes in the last iterations are allowed, which leads in case of permanent compliance oscillations to a type of stop criterion with $\varDelta {{\tilde{t}}}_{k} \rightarrow 0$. In Fig. 11, the final design of example 2-B after 200 iterations is shown, which has a compliance $\psi _{\text {end}}=4.84\cdot 10^{3}\,{\text {Nm}}$ and a volume fraction $v_{\text {end}}=0.500$. The final compliance is about $2\%$ higher compared to example 2-A.

The applied algorithmic adaptations I and II are both reasonable and contribute to the stability of the optimization process. However, to achieve a more convenient optimization progression further adaptations of the approximate level set method are required, which are discussed in the following.

3.3 Adaptation III: further numerical modifications

As mentioned before, in the formulation of the normal velocity $V_{\text {n}}$ from Eq. (10), the nodal strain energy densities are normalized by the factor c, which is the median of the element compliances in each iteration k, see also Wei et al. (2018). This type of normalization or similar ones based on an evolving term can help to increase the convergence speed. However, such a factor can become itself a source of instability and oscillation. For this reason, here a constant normalization is used for each structural model under prescribed loads, which is formulated with the maximum $\psi ^{\text {e}}_{\text {max},{0}}$ and minimum $\psi ^{\text {e}}_{\text {min},0}$ element compliance of the initial design, and in addition a factor d. The normal velocity $V_{\text {n}}$ can be rewritten as

(14)

In this way, the difference between minimum and maximum value of the normal velocity $V_{\text {n}}$ for the initial design is normalized to a prescribed factor d. Here $d=10$ is chosen. This knowledge about the range of the initial normal velocity can also help to choose more appropriate process parameters.

Moreover, as it is observed in example 2-B, inappropriately fast updates of the Lagrange multiplier $\lambda$ can lead to a large overshoot and also oscillations of $\lambda$. To tackle this issue, the update of the process parameter $\gamma$ is adjusted. Therefore, instead of Eq. (13), $\gamma$ is updated as

$$\begin{aligned} \gamma _{k+1}=\,&\gamma _{k}+\varDelta \gamma \cdot \,\exp (\,\ln {| v_{k}-v_{\text {max}}| }\cdot {v_{\text {max}}}), \\ {}&\quad \text {with} \, k> n_{\text {E}}. \end{aligned}$$

(15)

Here, the initial value $\gamma _{0}$ and the increment $\varDelta \gamma$ are selected as before. The upper limit $\gamma _{\text {max}}$ is not included anymore. Though, the empirical term $\exp (\,\ln {| v_{k}-v_{\text {max}}| }\cdot {v_{\text {max}}})$ is considered to slow the update of $\gamma$, and accordingly, the Lagrange multiplier update, when volumes closer to the volume limit $v_{\text {max}}$ are reached. In this way, the mentioned issues can be alleviated.

Including the adaptations I, II and III, the topology optimization of the slender cantilever beam with $20\times 200$ elements is repeated (example 2-C). The corresponding optimization histories are shown in Fig. 10. Compared to examples 2-A and 2-B, here the compliance and volume progression are smoother. This is due to the change of the normalization factor in the formulation of the normal velocity $V_{\text {n}}$ from Eq. (14). Besides, the Lagrange multiplier $\lambda$ is increased slower, which is linked to the included term $\exp (\,\ln {| v_{k}-v_{\text {max}}| }\cdot {v_{\text {max}}})$ in the update of $\gamma$ by Eq. (15).

After 200 steps, a final design with a compliance $\psi _{\text {end}}=4.80\cdot {10^{3}}\,{\text {Nm}}$ and a volume fraction $v_{\text {end}}=0.500$ results, see Fig. 11. Here, the final compliance is around $1\%$ higher than example 2-A and $1\%$ lower than example 2-B. It can be stated that the final designs of examples 2-A, 2-B and 2-C are all in the same quality range. However, considering the optimization histories in Fig. 10, for sure, the approximate level set method with all three adaptations is more convenient, and is used in the following. Nevertheless, a remaining issue is the large influence of the selected process parameters on the success of the optimization process. For instance, setting the volume limit in the last example equal to $v_{\text {max}}=0.3$ (example 2-D), the optimization algorithm with presented adaptations I, II and III does not perform well and gets stuck on the path. At iteration $k=81$, a design with an unsuitable load path and a high compliance $\psi _{\text {end}}=6.44\cdot {10^{3}}\,{\text {Nm}}$ results, whereas the volume fraction is still too high, $v_{\text {end}}=0.755$, see also Fig. 11. For sure, it can be tried to find an appropriate set of process parameters. Though, as it is mentioned in Sigmund and Maute (2013), the success of the optimization process for a wide range of problems with fixed process parameters is desired. To follow this idea, it is decided to include additional filtering-like terms, which lead, among others, to a higher stability and applicability of the approximate level set method. In Sect. 4, these modifications are presented.

4 Filtering-like adaptations

To sustain the optimization stability, and decrease the influence of the process parameters on the success of the topology optimization, in the current work, further modifications of the normal velocity $V_{\text {n}}$ from Eq. (14) and the update scheme (2) by additional filtering-like distribution functions ${{\check{\delta }}}$ (adaptation IV) and ${{\tilde{\delta }}}$ (adaptation V) are considered. In the following, these adaptations are described. Subsequently, a new update scheme including the mentioned adaptations is formulated and used for the topology optimization of the presented slender cantilever beam with different volume limits.

4.1 Adaptation IV: introduction of the distribution function ${{\check{\delta }}}$

From a practical point of view, a fast update of the Lagrange multiplier $\lambda$ can help to reach higher convergence speeds. However, it normally reduces the design complexity, and leads specially in case of slender structures to the loss of structural cohesion. This is due to the rash omission of connections. In general, areas with a high amount of material can comply better with a fast increase of $\lambda$ and a resulting large material removal. To maintain the design complexity and structural cohesion despite an appropriate convergence speed, here it is decided to adapt the normal velocity for each node i based on the material distribution in a corresponding neighborhood ${{\mathcal {N}}}_{i}$. For this purpose, the factor ${{\check{\delta }}}_{i}$ is introduced

$$\begin{aligned}&{{\check{\delta }}}_{i}= {{\check{\alpha }}}\cdot \left( \dfrac{1}{n_{\text {ne}}} \sum _{\ell =1}^{n_{\text {ne}}} { v_{\ell }^{\text {e}}} \right) + (1-{{\check{\alpha }}}). \end{aligned}$$

(16)

In this formulation, the average fill volume of $n_{\text {ne}}$ elements in the neighborhood ${{\mathcal {N}}}_{i}$ is included and multiplied with a weighting factor ${{\check{\alpha }}}$, which can modify the influence of material distribution on ${{\check{\delta }}}_{i}$. Here ${{\check{\alpha }}}$  is set to 0.9. The part $\,(1-{{\check{\alpha }}})$ describes the minimum value for ${{\check{\delta }}}_{i}$, and in case of a completely filled neighborhood ${{\mathcal {N}}}_{i}$, the maximum ${{\check{\delta }}}_{i}=1$ results. Using ${{\check{\delta }}}_{i}$, the adapted normal velocity $\check{V}_{\text {n}}$ is defined as

(17)

Thereby, the multiplication of ${{\check{\delta }}}_{i}$ with $\lambda _{k}$ slows the shift of normal velocity values into the negative zone, whereas the multiplication of ${{\check{\delta }}}_{i}$ with $[ {{\hat{\psi }}}_{i}-\lambda _{k}\cdot {{\check{\delta }}}_{i}]$ serves as a scaling in dependence upon the material amount in ${{\mathcal {N}}}_{i}$. It should be noticed that the choice of ${{\mathcal {N}}}_{i}$ is not a trivial task. If a very large neighborhood is considered, the factor ${{\check{\delta }}}_{i}$ makes no significant difference, and in case of a small neighborhood such as a little circle around the node i, updates with undesired local artifacts result. For this reason, in this work, a neighborhood ${{\mathcal {N}}}_{i}$ with a moderate size is selected for each node i. This neighborhood includes the corresponding node row orthogonal to the longitudinal axis and the two element rows adjacent to that. In Fig. 12, this choice is illustrated. Moreover, as an example, in Fig. 13, the distribution function ${{\check{\delta }}}$ for the final design of example 2-C, see also Fig. 11, is shown. It can be seen that the dense areas of the design possess a higher value of ${{\check{\delta }}}$, and due to the chosen neighborhood, all nodes in a row orthogonal to the longitudinal axis are assigned with the same ${{\check{\delta }}}$.

Fig. 12

Neighborhood ${{\mathcal {N}}}_{i}$ of the node i

Fig. 13

Distribution function ${{\check{\delta }}}$ over the final design of example 2-C

Using the adapted normal velocity $\check{V}_{\text {n}}$, the new augmented velocity vector $\check{\varvec{B}}$ for the update of the discretized level set function $\varvec{\phi }$ can be formulated as

$$\begin{aligned}&\check{\varvec{B}}({{\tilde{t}}}_{k}) \\&\quad =[\check{V}_{\text {n}}(\varvec{r}_{1},{{\tilde{t}}}_{k})\cdot {{\hat{\delta }}}(\phi (\varvec{r}_{1},{{\tilde{t}}}_{k})), \ldots , \check{V}_{\text {n}}(\varvec{r}_{n},{{\tilde{t}}}_{k})\cdot {{\hat{\delta }}}(\phi (\varvec{r}_{n},{{\tilde{t}}}_{k}))]^{\top }. \end{aligned}$$

(18)

This vector replaces the former augmented velocity vector $\hat{\varvec{B}}$ from Eq. (3).

4.2 Adaptation V: introduction of the distribution function ${{\tilde{\delta }}}$

In the current work, a stability limit based on the CFL condition is not considered. However, inspired by that, the distribution function ${{\tilde{\delta }}}$ is introduced and multiplied with $\check{\varvec{B}}$, which, among others, helps to cope with issues regarding a coarse discretization and stress concentrations. For each node i, this distribution factor is formulated with the average of augmented velocity values ${| \check{B}_{j}| }$ at $n_{\text {no}}$ nodes in the neighborhood ${{\mathcal {N}}}_{i}$, and a weighting factor ${{\tilde{\beta }}}$ as

$${{\tilde{\delta }}}_{i}= \dfrac{{{\tilde{\beta }}}}{{{{\tilde{\beta }}}}+ \left( \dfrac{1}{n_{\text {no}}} \sum \nolimits _{j=1}^{n_{\text {no}}} {| \check{B}_{j}| }\right) }.$$

(19)

Thereby, the weighting factor ${{\tilde{\beta }}}$ can modify the influence of the average $\frac{1}{n_{\text {no}}}$ $\sum \nolimits _{j=1}^{n_{\text {no}}}$${| \check{B}_{j}| }$ on ${{\tilde{\delta }}}_{i}$. The smaller ${{\tilde{\beta }}}$, the greater is this influence, and in case of large weighting factors ${{\tilde{\beta }}}\gg \frac{1}{n_{\text {no}}}$ $\sum \nolimits _{j=1}^{n_{\text {no}}}$${| \check{B}_{j}| }$, the distribution factor ${{\tilde{\delta }}}_{i}\approx 1$ cannot have any significant effect. To illustrate the construction of ${{\tilde{\delta }}}$ better, again the final design of the example 2-C is considered. For this design, the corresponding augmented velocity $\check{B}$ over the element nodes is shown in Fig. 14. Based on that and with a selected weighting factor ${{\tilde{\beta }}}=0.1$, a distribution function ${{\tilde{\delta }}}$ is developed, which is shown in Fig. 15. Thereby, areas around the fixed edges of the structure on the left side possess a large-augmented velocity value and with that a smaller distribution term ${{\tilde{\delta }}}$ than the rest of the structure. Besides, on the right half of the design domain, a drop of the distribution term ${{\tilde{\delta }}}$ can be observed, which is again due to the high value of the augmented velocity in the corresponding regions. In general, it can be stated that the introduction of ${{\tilde{\delta }}}$ modifies the development of the level set function in the areas of high strain energy density and stress concentration. However, the choice of the neighborhood ${{\mathcal {N}}}_{i}$ and the weighting factor ${{\tilde{\beta }}}$ should be appropriate.

Fig. 14

Augmented velocity $\check{B}$ for the final design of example 2-C

Fig. 15

Distribution function ${{\tilde{\delta }}}$ for the final design of example 2-C

With the introduced adaptations IV and V, a convenient development of the discretized level set function can be performed by the following update scheme

$$\varvec{\phi }({{\tilde{t}}}_{k+1})={\varvec{\phi }}({{\tilde{t}}}_{k})+\varDelta {{\tilde{t}}}_{k}\,\,\big (\tilde{\varvec{\delta }}({{\tilde{t}}}_{k})\odot \check{\varvec{B}}({{\tilde{t}}}_{k})\big ),$$

(20)

where $\tilde{\varvec{\delta }}=[{{\tilde{\delta }}}_{1},\ldots ,{{\tilde{\delta }}}_{n}]^{\top}$ and $\odot$ denotes the element-wise product of two vectors. Compared to the update scheme (2), it can be stated that the augmented velocity vector $\hat{\varvec{B}}$ is replaced by $\tilde{\varvec{\delta }}\odot \check{\varvec{B}}$. Nevertheless, it should be mentioned that the included terms ${{\check{\delta }}}$ and ${{\tilde{\delta }}}$ are developed and utilized within the framework of the compliance minimization problem for slender structures under single forces. Their successful application for other types of optimization problems should be examined separately. However, the more essential point is that such filtering-like terms can be developed to adapt the update scheme (2) based on further considerations. This can, for instance, help to include additional manufacturing or stress constraints into the optimization process.

4.3 Numerical studies

To indicate the high stability and applicability of the optimization algorithm including adaptations I–V, the topology optimizations of the presented slender cantilever beam with width/length ratio 1/10 and different volume limits $v_{\text {max}}=0.5$ (example 3-A), $v_{\text {max}}=0.4$ (example 3-B), $v_{\text {max}}=0.3$ (example 3-C) and $v_{\text {max}}=0.2$ (example 3-D) are considered, see Table 3 for problem definitions and optimization results. Since the included distribution terms ${{\check{\delta }}}$ and ${{\tilde{\delta }}}$ slow the design evolution, the maximum pseudo-time step size $\varDelta {{\tilde{t}}}_{\text {max}}$ and the parameters for the numerical update of the Lagrange multiplier $\lambda$ should be selected larger than in Sects. 2 and 3. The process parameters are here chosen as $n_{\text {E}}=20$, $\mu =5$, $\gamma _{0}=0.5$, $\varDelta \gamma =0.5$, $\varDelta {{\tilde{t}}}_{1}=2$, $\varDelta {{\tilde{t}}}_{\text {max}}=2$. Furthermore, unlike in the last sections, the approximate reinitialization is performed every 10-th iteration to protect thin connections better.

Table 3 Problem definitions and optimization results of demonstration examples in Sect. 4

The optimization histories of the mentioned demonstration examples are shown in Fig. 16, and the corresponding final designs after 200 iterations are represented in Fig. 17. In example 3-A, a final design with a compliance $\psi _{\text {end}}=4.84\cdot {10^{3}}\,{\text {Nm}}$ and a volume fraction $v_{\text {end}}=0.500$ results, which is in the same quality range as the final designs of examples 2-A, 2-B and 2-C. This comparison indicates that the included adaptations IV and V do not impair the quality of the optimization process. On the contrary, due to the added filtering-like terms ${{\check{\delta }}}$ and ${{\tilde{\delta }}}$, the thin struts of the final design in example 3-A are better connected than in examples 2-A, 2-B and 2-C. Nevertheless, the main contribution of the adaptations IV and V is rather the stable optimization course for a wide range of volume limits $v_{\text {max}}$ without changing the process parameters. This potential can be clearly seen in optimization histories in Fig. 16.

Fig. 16

Optimization histories of examples in Sect. 4

Fig. 17

Final designs of examples in Sect. 4

As it can be seen in Fig. 16a, b, the progression of the compliance $\psi$ and the volume fraction v are inversely proportional. The lower the obtained final volume $v_{\text {end}}$, the higher the final compliance $\psi _{\text {end}}$. However, this relationship is not linear, and the compliance increase between the final designs of the examples 3-A  and 3-B is smaller than the compliance increase between the final designs of the examples 3-B and 3-C, and so on. Besides, moving the volume limit from $v_{\text {max}}=0.5$ to 0.2, it can be realized that the struts become thinner, see Fig. 17. The final design of example 3-D with a compliance $\psi _{\text {end}}=1.00\cdot {10^4}\,{\text {Nm}}$ and a volume fraction $v_{\text {end}}=0.206$ represents the most critical case. Thereby, the most struts have a broken pattern. As mentioned before, a broken pattern in the zero-level contour representation shows that the connection is not completely solid, and the fill volume of the underlying FE-elements in the corresponding areas is less than 1. For sure, this indicates that the chosen discretization with only $20 \times 200$ elements is too coarse to achieve a close-to-optimal design with such a low volume limit. However, the more interesting point is that even in such a critical case, where the optimization process starts with a very simple and completely filled initial design, and drives the volume fraction v down toward $v_{\text {max}}=0.2$, the optimization algorithm with the adaptations I–V does not fail and returns meaningful optimization courses with symmetric final designs.

As it is the case for the compliance history, the Lagrange multiplier development is also in phase opposition to the progression of the volume fraction v, see Fig. 16b and  c, respectively. The lower the volume limit $v_{\text {max}}$, the higher ends the Lagrange multiplier $\lambda$. Thereby, among others, the introduced distribution function ${{\check{\delta }}}$ has an influence on the value of the Lagrange multiplier $\lambda$, which leads to a final design with a volume fraction $v_{\text {end}}$ close or equal to $v_{\text {max}}$.

Moreover, for the presented examples, the pseudo-time step size $\varDelta {{\tilde{t}}}$ over the iteration number k is shown in Fig. 16d. It can be observed that in some iterations between $k=1$ and 40, $\varDelta {{\tilde{t}}}$ is reduced to alleviate oscillations in the beginning. This is due to the fact that the optimizations start with a simple initial level set function, $\{\forall i\in \,1(1)n:\phi (\varvec{r}_{i},0)=1\cdot 10^{-3}\}$, which represents a completely filled initial design. Between $k=40$ and 160, only some single pseudo-time step size adaptations are included, and in the final part after $k=160$, $\varDelta {{\tilde{t}}}$ is mostly reduced to obtain a better convergence. If in some examples, frequent adaptations of $\varDelta {{\tilde{t}}}$ from the beginning to the end of the optimization process are observed, it is recommended to reduce $\varDelta {{\tilde{t}}}$. Another remedy is to increase the influence of the distribution functions ${{\check{\delta }}}$ and ${{\tilde{\delta }}}$.

With the considered adaptations and the same process parameters, a stable design evolution for the examples 3-A, 3-B, 3-C and 3-D is shown. However, it should also be mentioned that there are no limitations to the choice of the initial design with a volume $v_{0}<1$. Though, the considered completely filled initial design for different examples in this work should rather be seen as the most general case without any preconditioning, which is here successfully used for a critical examination of the presented optimization algorithm.

In the end, it should also be mentioned that the chosen values for the process parameters of the presented adaptations, such as $\varepsilon _{1}$ in adaptation I, $\tau _{1}$, $\tau _{2}$, $\tau _{3}$, in adaptation II, d in adaptation III, ${{\check{\alpha }}}$ in adaptation IV, and ${{\tilde{\beta }}}$ in adaptation V are given to make the illustrated examples reproducible. Nevertheless, the set of selected values is only a suggestion, and to tune the properties of the presented optimization algorithm, such as the convergence behavior, the interested readers shall change the process parameters included in the adaptations I–V in wide ranges.

5 Validation and 3D extension

As shown in the last sections, the adapted level set method can be successfully used to perform topology optimizations of sparsely-filled and slender cantilever beams. However, it is reasonable to test, whether the presented algorithm leads to results of an appropriate quality. Therefore, in the following, a slender cantilever beam is optimized both with the adapted algorithm and the well-established SIMP method. The histories and results of both optimizations are then briefly compared and discussed. Furthermore, it is important to show for practical use that the algorithm can be employed to treat 3D topology optimization problems. For this reason, in a final application example, it is demonstrated that the adapted level set method can be conveniently extended to 3D design domains.

5.1 A comparison with the SIMP method

As it is described in Sigmund and Maute (2013), the SIMP method is a density approach, which had originally been proposed in Bendsøe (1989), Mlejnek (1992) and Zhou and Rozvany (1991). In this method, the stiffness of each element $\ell$ is penalized by continuous density-like design variables $x_{\ell}$ and an artificial power-law. In the optimization process, such a power-law penalization sustains, among others, the convergence of the optimization toward close-to-optimal designs of low greyness. The penalized stiffness matrix of element $\ell$ is given as

$$\begin{aligned} \varvec{K}_{\ell}&= {x}_\ell ^{p} \varvec{K}_{0}, \quad 0 < x_{{\text{min}}}\le x_{\ell} \le 1. \end{aligned}$$

(21)

Thereby, p is the penalization power, which is typically set to 3, see also Sigmund (2001) and Sigmund and Maute (2013). Besides, to avoid ill-conditioned matrices, a lower limit $x_{\text {min}}$ is assigned to $x_{\ell }$. This is similar to the chosen weak material density $\epsilon$ in the linear penalization addressed in Sect. 2.2. Here $x_{\text {min}}=10^{-3}$ is chosen.

The compliance of a SIMP-parametrized structural analysis model can be formulated as

$$\psi =\sum _{\ell =1}^{n_{\text {e}}}{ x_{\ell} ^{p} \varvec{u}_{\ell }^{\top} \varvec{K}_{0}\,\varvec{u}_{\ell }}.$$

(22)

As mentioned in Sect. 2.2, the vector $\varvec{u}_{{\ell }}$ of nodal displacements for element $\ell$ results from the static equilibrium equation (8). Nevertheless, here the global stiffness matrix $\overline{\varvec{K}}$ is constructed by SIMP-parametrized element stiffness matrices from Eq. (21).

The compliance minimization problem under static loads $\overline{\varvec{F}}$ can be written as

$$\begin{aligned}&\underset{{\varvec{x}\in {{\mathbb {R}}}^{n_{\text {e}}}}}{{\text{minimize}}}\,\, \psi (\varvec{x}) =\sum _{\ell =1}^{n_{\text {e}}}{ x_\ell ^{p} \varvec{u}_{\ell }^{\top} \varvec{K}_{0}\,\varvec{u}_{\ell } } \end{aligned}$$

(23a)

$$\begin{aligned}&\text {subject to} \,\, \left\{ \begin{array}{l}\overline{\varvec{K}}\,\overline{\varvec{U}}-\overline{\varvec{F}}=0\\ h(\varvec{x})=v(\varvec{x})-v_{\text {max}}\le 0\\ 0<x_{\text {min}}<x_{\ell }\le 1,\quad \forall \ell \in 1(1)n_{\text {e}} \end{array}\right. \end{aligned}$$

(23b)

In contrast to the level set-based formulation (9) of the compliance minimization problem, here the density-like design variables $x_{\ell }$ compose the design domain. These are gathered to the vector $\varvec{x}=[x_{1},\ldots ,x_{n_{\text {e}}}]$. Besides, the volume constraint is included as an inequality constraint $h(\varvec{x})\le 0$.

For the efficient solution of the optimization problem (23), a gradient-based optimization algorithm is normally used. In the current work, the SIMP optimization is performed by the well-established Method of Moving Asymptotes (MMA), see Sigmund (2001) for the implementation of the SIMP optimization and Svanberg (1987) for the MMA algorithm. The gradient is typically obtained using an adjoint sensitivity analysis. Based on that, the sensitivity of the compliance $\psi$ with respect to the design variable $x_{\ell }$ can be formulated as

$$\frac{{\text {d}}\psi }{{\text {d}} x_{\ell }}=-px_{\ell }^{(p-1)}\varvec{u}_{\ell }^{\top }\varvec{K}_{0}\varvec{u}_{\ell }.$$

(24)

In order to counter checkerboard patterns, the gradient in the SIMP optimization is mostly modified by filtering techniques, see Sigmund and Maute (2013). To this end, here the mesh-independency filter as proposed in Sigmund (2001) is used.

For the purpose of comparison, topology optimizations of a slender cantilever beam with width/length ratio 1/20 are performed using both the level set algorithm (example 4-A), and the SIMP method (example 4-B), see Table 4 for problem definitions and optimization results.

Table 4 Problem definitions and optimization results of demonstration examples 4-A and 4-B

Since it is difficult to compare optimizations, which rely on different penalization schemes, in both examples the penalization strategy (21) is used to parameterize the finite element model. However, in example 4-A, the design variable $x_{\ell }$ of each element is connected to the discretized level set function $\varvec{\phi }$ as $x_{\ell }={\text {max}}(v_{\ell }(\varvec{\phi }),\,x_{\text {min}})$. Besides, the normal velocity $\check{V}_{\text {n}}$ from Eq. (17) is formulated using the SIMP-parametrized element compliances $\psi _{\ell }=x_{\ell }^{p}\varvec{u}_{\ell }^{\top }\varvec{K}_{0}\varvec{u}_{\ell }$, whereas in example 4-B, the derivatives of the element compliances with respect to the corresponding design variables $x_{\ell }$ serve as the gradient, see Eq. (24). Nevertheless, in the compliance minimization problem, these two sensitivity types are closely linked, see also van Dijk et al. (2013) and Sigmund and Maute (2013).

The slender cantilever beam is here modeled with $20 \times 400$ elements, the volume limit $v_{\text {max}}$ is set to 0.5 and the number of iterations is 200. While the level set optimization in example 4-A starts from a completely filled initial design, the SIMP optimization in example 4-B starts from a homogeneous grey initial design with the volume fraction $v_{0}=v_{\text {max}}$.

Figure 18 shows the final designs of the examples 4-A and 4-B. As argued in Sigmund and Maute (2013), the qualitative comparison of smooth designs represented by zero-level contours with density-based greyscale designs is not meaningful. For this reason, in Fig. 18, the final design of example 4-A is represented not only as contour plot but also as density-based greyscale plot. The corresponding optimization histories of the examples 4-A and 4-B are provided in Fig. 19.

Fig. 18

Final designs of examples 4-A and 4-B

Fig. 19

Optimization histories of examples 4-A and 4-B

It can be observed that the optimization results of both examples are in a good agreement. In example 4-A, a final design with a compliance $\psi _{{\text{end}}}=3.85\cdot 10^{4}\,{\text {Nm}}$ and a volume fraction $v_{\text {end}}=0.500$ is reached by the level set algorithm, whereas the SIMP optimization in example 4-B provides a final design with $\psi _{{\text{end}}}=3.88\cdot 10^{4}\,{\text {Nm}}$ and $v_{\text {end}}=0.498$. Hence, it can be stated that the presented level set method leads to a design with valid quantitative values. Nevertheless, the final designs of both procedures possess clearly different complexities and greynesses. This can be traced back, among others, to the considerable differences of the optimization algorithms, including process parameters and selected initial designs. The optimization histories in Fig. 19 help to understand some similarities and differences of the optimization processes in examples 4-A and 4-B.

As shown in Fig. 19a, the completely filled initial design of example 4-A has the lowest compliance. In contrast, due to the chosen grey initial design in example 4-B, the first designs in the corresponding SIMP optimization possess the largest compliance values. Even so, the optimization process in both examples converges to similar compliance values. Moreover, the development of the volume fraction v in example 4-A is different from example 4-B, see Fig. 19b. In example 4-A the augmented Lagrangian method is used. This method allows to start with a volume fraction $v_{0}=1$ far away from the volume limit $v_{\text {max}}$, and drives the optimization process toward $v_{\text {max}}$. Thereby, due to the large change of the volume and the chosen process parameters, an undershoot of the volume can be observed, which is then gradually decreased. On the contrary, the utilized MMA in example 4-B includes a Lagrange multiplier, which keeps the volume fraction v in the whole optimization process less than or equal to the volume limit $v_{\text {max}}$. Nevertheless, despite different implementations of the volume constraint, here both procedures converge to similar volume fractions.

It is known that the greyness in a level set-based topology optimization is limited to elements intersected by the zero-level set, whereas the SIMP method normally leads to a higher number of grey intermediate elements. This difference can qualitatively be seen in the final designs of examples 4-A and 4-B in Fig. 18, which speaks in favor of less grey final design of example 4-A using the level set algorithm. Besides, for a quantitative comparison, the normalized greyness g can be defined as

$$g=\dfrac{1}{n_{\text {e}}}\sum _{\ell =1}^{n_{\text {e}}}{4\,x_{\ell }(1-x_{\ell })},$$

(25)

see also Sigmund (2007). In Fig. 19c, the greyness histories of examples 4-A and 4-B are shown. In example 4-A, the greyness is in the beginning equal to 0, increases slightly with the creation of new boundaries, and reaches a final value $g_{\text {end}}=0.13$ in the end of the optimization process. On the other hand, in example 4-B, the SIMP optimization starts with the maximum greyness 1. The greyness decreases during the optimization process and reaches a final value $g_{\text {end}}=0.25$ in the end, which is about 92% higher than the greyness of the final design obtained with the level set algorithm.

The mentioned comparisons with the well-known SIMP method show that the proposed level set algorithm provides valid optimization results for the compliance minimization problem of sparsely-filled and slender structures.

5.2 3D cantilever beam

The topology optimization of 3D large-scale problems is of great interest. In particular, in industrial applications, 3D models with a fine discretization are usually required. To this end, the adapted optimization algorithm including all adaptations I–V is extended to 3D problems, and tested for the compliance minimization of a 3D slender cantilever beam.

For the extension of the proposed optimization algorithm to 3D problems, only few changes are required, which are due to the dimension change self-descriptive. First, a cuboid design domain is considered, which is discretized by 8-node unit hexahedron elements. Thereby, the same material properties $E_{0}=1\,{\text {Pa}}$ and $\nu =0.3$ as in the 2D examples are used to formulate the stiffness matrix $\varvec{K}_{0}$ of the reference element with the maximum fill volume. The stiffness matrix $\varvec{K}_{\ell }$ of each element $\ell$ is then penalized linearly as described in Sect. 2.2. Since the number of element nodes is different from the 2D case, the map of energy densities from elements to nodes in Eq. (17) has to be adjusted.

Furthermore, it is clear that the level set function $\phi$ is here defined over a 3D design domain. Hence, the calculation of the element volumes $v_{\ell }$, and also the numerical computation of the spatial derivative $|\nabla \phi |$ for the approximate reinitialization should be extended. Besides, to check the structural cohesion of 3D examples, in adaptation I the Matlab functions bwlabeln or bwconncomp can be utilized. Due to a lower memory use, bwconncomp is preferred. Moreover, for the adaptations IV and V, a 3D neighborhood is taken into account. Analogous to the 2D case in Fig. 12, the considered neighborhood ${{\mathcal {N}}}_{i}$ of each node i in 3D examples consists of the corresponding node section orthogonal to the longitudinal axis, and two element sections adjacent to that. The other parts of the proposed algorithm can remain unchanged.

The cuboid design domain of the 3D slender cantilever beam has the width/depth/length ratio 1/1/10, and is here discretized by $30 \times 30 \times 300$ elements (example 5). The nodes on its left end are all fixed, and the structure is loaded by the single force $F=1\,{\text {N}}$ at the middle node on its right end, see Fig. 20. As in the 2D examples, a completely filled initial design is considered. Using adaptations I–V, the process parameters can be chosen in wide ranges. To obtain an appropriate convergence speed, here $n_{\text {E}}=20$, $\mu =0.05$, $\gamma _{0}=0.02$, $\varDelta \gamma =0.02$, $\varDelta {{\tilde{t}}}_{1}=10$, $\varDelta {{\tilde{t}}}_{\text {max}}=20$ are selected. The volume limit $v_{\text {max}}$ is set to 0.1, and the optimization is performed within 100 iterations.

Fig. 20

Final design of example 5

After 100 optimization iterations, a final design with a compliance $\psi _{\text {end}}=533.3\,{\text {Nm}}$ and a volume fraction $v_{\text {end}}=0.100$ is obtained. In Fig. 20, the final design is shown using the final level set function $\phi _{\text {end}}$ and the Matlab functions isosurface, isocaps and patch, see The MathWorks (2014) for more details. The optimization histories depicted in Fig. 21 confirm the stability and smoothness of the 3D optimization process.

Fig. 21

Optimization histories of example 5

Lastly, the computational effort of the presented 3D example should be mentioned. The performed topology optimization within 100 iterations takes a computation time of $310\,{\text {min}}$. Thereby, the 100 FE-analyses make up the major part with $304\,{\text {min}}$ calculation time, whereas the rest of the adapted optimization algorithm takes only $6\,{\text {min}}$ and, hence, less than 2% of the whole computation time. This indicates the high potential of the presented algorithm to provide an efficient large-scale topology optimization of 3D examples.

6 Summary and conclusion

In this work a set of adaptations are introduced and assigned to an approximate level set method, which make it proper for the topology optimization of sparsely-filled and slender structures. These adaptations can roughly be divided into two types. Adaptations I–III shall be deemed as algorithmic and numerical, whereas the adaptations IV and V are rather filtering-like. For demonstration and testing purposes, the compliance minimization problem of a slender cantilever beam is considered to indicate the functionality of the developed adaptations.

In the case that the structural cohesion is lost, the adaptation I adjusts the Lagrange multiplier $\lambda$ to reconstruct the load path. Adaptation II is intended to control the pseudo-time step size $\varDelta {{\tilde{t}}}$ based on compliance changes, and alleviates in this way compliance jumps and oscillations. Moreover, adaptation III includes numerical changes of the normal velocity formulation, which help to avoid instabilities due to corrupted design updates, and leads to a smoother convergence of the optimization process.

The filtering-like adaptations IV and V are proposed to maintain the optimization stability, and decrease the influence of the chosen process parameters on the topology optimization process. Adaptation IV adjusts the level set function evolution depending on the average material distribution in each region, in this way a better material distribution and connection are achieved. Moreover adaptation V is motivated by the CFL condition, and modifies the level set function evolution depending on the average normal velocity in each region. This helps to alleviate issues regarding coarse discretizations and stress concentrations.

The level set algorithm with the adaptations I–V is successfully applied for a topology optimization of slender structures with different volume limits $v_{\text {max}}$, which indicates, among others, the contribution of the included adaptations to the optimization stability. Besides, to test the quality of results obtained with the level set algorithm, a comparison with the SIMP optimization is considered. Thereby, both the presented level set algorithm and the SIMP method are used to perform the topology optimization of a slender cantilever beam. Despite clear differences in the optimization histories and shapes of final designs, in both cases similar compliance values are reached. This indicates that the presented level set algorithm works properly. After all, the extension of the optimization process to 3D problems, and its efficient application for a 3D cantilever beam are shortly discussed, which reveals its potential for the topology optimization of large-scale 3D problems.

It can be expected that the introduced adaptations in this work also help to handle issues in other types of level set-based optimizations beyond the considered compliance minimization problem under static loads. Hence, in a future work, the modified level set algorithm should be studied for further topology optimization types, among others, within the framework of stress-constrained topology optimization on irregularly shaped design domains, e.g., L-beams, see also Cai and Zhang (2015) for practical stress-constrained topology optimizations on free-form design domains. In another future work, the presented level set algorithm should be investigated for the topology optimization of dynamically loaded components in flexible multibody systems, see for instance Held et al. (2016) and Moghadasi et al. (2018). Thereby, the presented level set algorithm can, among others, help to retain the load path of dynamically loaded structures, which is a challenging task, especially in case of high frequency related optimization problems.