A general fidelity transformation framework for reliability-based design optimization with arbitrary precision

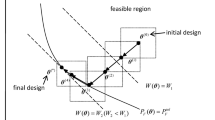
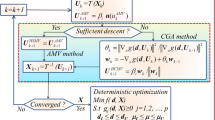
Abstract

Reliability-based design optimization (RBDO) offers a powerful tool to handle optimization problems with inherently unavoidable uncertainty factors. However, solving the engineering systems with high fidelity remains a great challenge. In this study, a novel fidelity transformation framework is proposed to address this issue, where an arbitrary high-fidelity RBDO method can be converted into an arbitrary low-fidelity RBDO method without sacrificing the accuracy. The fidelity transformation factor plays the central role. Furthermore, two fidelity transformation strategies are developed to solve the RBDO problem efficiently and accurately. In addition, the well-known performance measure approach and sequential optimization and reliability assessment method are employed as the low-fidelity RBDO methods. In this way, six new methods are developed based on three high-fidelity RBDO methods and two low-fidelity RBDO methods. One highly mathematical example, two numerical examples, and a stiffened panel with cutouts are used to demonstrate the generality, fidelity, and superiority of the proposed methods.

Appendix

For the Kriging model, the stochastic field ${\mathcal{G}}({\mathbf{x}})$ contains two parts: deterministic function ${\mathbf{F}}({\mathbf{x}},{\varvec{\beta}})$ and stationary Gaussian process $z({\mathbf{x}}),$ which can be expressed as follows:

$${\mathcal{G}}({\mathbf{x}}) = {\mathbf{F}}({\mathbf{x}},{\varvec{\beta}}) + z({\mathbf{x}}),$$

(37)

where the term ${\mathbf{F}}({\mathbf{x}},{\varvec{\beta}})$ is always selected as the regression model.

$${\mathbf{F}}({\mathbf{x}},{\varvec{\beta}}) = {\mathbf{f}}({\mathbf{x}})^{{\text{T}}} {\varvec{\beta}},$$

(38)

where ${\mathbf{f}}({\mathbf{x}})^{{\text{T}}} {{ = \{ }}f_{1} ({\mathbf{x}}),f_{2} ({\mathbf{x}}),...,f_{k} {(}{\mathbf{x}}{{)\} }}$ is the basis function vector and ${\varvec{\beta}}{{ = \{ }}\beta_{1} {,}\beta_{2} {,}...{,}\beta_{k} {{\} }}$ is the regression coefficient vector. The mean of $z({\mathbf{x}})$ is zero, and the covariance function between two arbitrary points ${\mathbf{x^{\prime}}}$ and ${\mathbf{x^{\prime\prime}}}$ is formulated as follows:

$$Cov(z({\mathbf{x^{\prime}}}),z({\mathbf{x^{\prime\prime}}})) = \sigma_{z}^{2} R_{\theta } ({\mathbf{x^{\prime}}},{\mathbf{x^{\prime\prime}}}),$$

(39)

where $\sigma_{z}$ is the standard deviation and $R_{\theta } ( \cdot )$ is the correlation function that is computed using the vector ${{\varvec{\uptheta}}}.$ For the Kriging model, the squared-exponential function is always selected to represent the correlation.

$$R_{\theta } ({\mathbf{x^{\prime}}},{\mathbf{x^{\prime\prime}}}) = \prod\limits_{i = 1}^{p} {\exp [ - \theta_{i} (x^{\prime}_{i} - x^{\prime\prime}_{i} )^{2} ]},$$

(40)

where $x^{\prime}_{i}$ and $x^{\prime\prime}_{i}$ are the jth coordinate values of the points ${\mathbf{x^{\prime}}}$ and ${\mathbf{x^{\prime\prime}}},$ Assuming that we have a DOE $[{\mathbf{x}}^{(1)} ,{\mathbf{x}}^{(2)},\ldots,{\mathbf{x}}^{(p)} ]$ with ${\mathbf{x}}^{(i)} \in {\mathbf{R}}_{\theta }^{p},\;\hat{\beta },$ and $\hat{\sigma }_{z}^{2}$ can be computed as follows:

$$\begin{gathered} \hat{\beta } = \frac{{{\mathbf{1}}^{{\text{T}}} {\mathbf{R}}_{\theta }^{ - 1} {\mathbf{Y}}}}{{{\mathbf{1}}^{{\text{T}}} {\mathbf{R}}_{\theta }^{ - 1} {\mathbf{1}}}} \hfill \\ \hat{\sigma }_{z}^{2} = \frac{{({\mathbf{Y}} - \beta {\mathbf{1}})^{{\text{T}}} {\mathbf{R}}_{\theta }^{ - 1} ({\mathbf{Y}} - \beta {\mathbf{1}})}}{p} \hfill \\ \end{gathered},$$

(41)

where ${\mathbf{Y}}$ is the p-dimensional vector, 1 is the p-dimensional vector of 1. ${\mathbf{R}}_{\theta }$ is the p × p correlation matrix, in which the parameter ${{\varvec{\uptheta}}}$ is evaluated by the maximum likelihood estimation (Echard et al. 2011).

$${{\varvec{\uptheta}}} = \arg \mathop {\min }\limits_{\theta } (det{\mathbf{R}}_{\theta } )^{\frac{1}{p}} \hat{\sigma }_{z}^{2}.$$

(42)

Based on the existing DOE, the Kriging model can predict the response $g({\mathbf{x}})$ for the arbitrarily unknown point x, and the unbiased predictor of $g({\mathbf{x}})$ can be expressed as follows:

$$\hat{g}({\mathbf{x}}) = \hat{\beta } + {\mathbf{r}}({\mathbf{x}})^{{\text{T}}} {\mathbf{R}}_{\theta }^{ - 1} ({\mathbf{Y}} - \beta {\mathbf{1}}),$$

(43)

where ${\mathbf{r}}({\mathbf{x}}) = R_{\theta } ({\mathbf{x}},{\mathbf{x}}^{(i)} ),$$(i = 1,2, \ldots ,p)$ denotes the correlation function. The variance $\sigma_{{\hat{g}}}^{2}$ between the actual response $g({\mathbf{x}})$ and Kriging response $\hat{g}({\mathbf{x}})$ can be estimated using the following formulation.

$${\sigma_{\hat{g}}^{2}} = {\sigma_{z}^{2}} \left( {1 - {\mathbf{r}}({\mathbf{x}})^{{\text{T}}} {\mathbf{R}}_{\theta}^{ - 1} {\mathbf{r}}({\mathbf{x}}) + \frac{{(1 - {\mathbf{1}}^{{\text{T}}} {\mathbf{R}}_{\theta}^{- 1} {\mathbf{r}}({\mathbf{x}}))^{2} }}{{{\mathbf{1}}^{{\text{T}}} {\mathbf{R}}_{\theta } {\mathbf{1}}}}} \right).$$

(44)

Therefore, the predicted response at ${\mathbf{x}}$ follows the normal distribution $\hat{g}({\mathbf{x}}) \sim N(\hat{g}({\mathbf{x}}),\sigma_{\hat{g}}^{2} ).$ In general, the active learning strategy is commonly implemented based on $\hat{g}({\mathbf{x}})$ and ${\sigma}_{\hat{g}}.$