Approximating solution spaces as a product of polygons

Abstract

Solution spaces are regions of good designs in a potentially high-dimensional design space. Good designs satisfy by definition all requirements that are imposed on them as mathematical constraints. In previous work, the complete solution space was approximated by a hyper-rectangle, i.e., the Cartesian product of permissible intervals for design variables. These intervals serve as independent target regions for distributed and separated design work. For a better approximation, i.e., a larger resulting solution space, this article proposes to compute the Cartesian product of two-dimensional regions, so-called 2d-spaces, that are enclosed by polygons. 2d-spaces serve as target regions for pairs of variables and are independent of other 2d-spaces. A numerical algorithm for non-linear problems is presented that is based on iterative Monte Carlo sampling.

1 Introduction

Some technical systems, such as vehicles or airplanes, are difficult to design because of complexity: many interacting components from different technical disciplines with uncertain properties are to be arranged and adjusted such that the overall system behavior satisfies overall system requirements and the system reaches its design goal (Zimmermann et al. 2017).

Established methods such as sensitivity analysis (Saltelli et al. 2000) or multidisciplinary design optimization (Martins and Lambe 2013) address design complexity due to many design variables, however without uncertainty treatment. Uncertainty is considered in robust design optimization (Beyer and Sendhoff 2007) or reliability-based design optimization (Rackwitz 2001; Youn et al. 2004). These methods are, however, only applicable when a detailed uncertainty model is available and is equipped with appropriate data, e.g., on the density distribution of random variables.

Development procedure models, such as the so-called V-model, see Haskins (2006), provide a framework for so-called top-down design without uncertainty model. Technical systems are decomposed into smaller and more manageable parts. These parts may be seen as sub-systems or sub-sub-systems, etc., and will be referred to as components. In order to direct the design work on components toward the overall design goals, component requirements are formulated. They have to be such that they are (1) sufficient for reaching the overall system goal, (2) as little restrictive for component design as possible, and (3) independent of component interaction.

Requirements can be expressed quantitatively as so-called solution spaces (Zimmermann and von Hoessle 2013). Solution spaces are sets of good designs, i.e., design points that satisfy all system level-requirements. They are also known as feasible regions (Zeng and Duddeck 2001), permissible design spaces (Graf et al. 2018), or reduced design spaces (Hannapel and Vlahopoulos 2014; Shallcross et al. 2020). Solution spaces are typically approximated as axis-parallel hyper-rectangles, called solution boxes. They are maximized in order to enclose uncertainty and provide design flexibility. Note that this is a different view of systems design: while typically the objective function measures the performance of one design, it quantifies the size of the solution space in this approach. Large solution spaces are essential for a successful design process, as design work is typically subject to uncontrollable uncertainy (Graff et al. 2014) and restrictions from other disciplines (Haberfellner et al. 2019) (in particular some that cannot be quantified). The edges of a solution box represent permissible regions for each design variable. As long as each uncertain design variable assumes a value from within its associated permissible interval the overall system goal is reached. Design variables on components are considered to be decoupled in a particular sense: their interaction is not relevant anymore as long as they stay within their intervals.

Expressing decoupled component requirements with solution spaces enables separated component development in different teams. The interval widths provide room for design flexibility and to cope with uncertainty. Tedious coordination and iteration between teams may be thus avoided. Practical applications can be found for vehicle crash design in Fender et al. (2017) and Graff et al. (2014), for the design of vibrating systems in Königs and Zimmermann (2017) and Münster et al. (2014), for chassis components in Eichstetter et al. (2015) and Zimmermann and Wahle (2015), for product family design in Eichstetter et al. (2015), and for control systems design in Korus et al. (2018, 2019).

There are several algorithms that compute solution spaces as high-dimensional axis-parallel solution boxes. A detailed analysis of the basic algorithm introduced in Zimmermann and von Hoessle (2013) can be found in Graff et al. (2016). In Fung et al. (2005), linear support vector machines are utilized to find hyperplanes that represent the good design space. Then, hypercubes are computed that lie within this good design space. In Rocco et al. (2003), a combination of a cellular evolutionary strategy and interval arithmetic is applied to find a hyper-rectangle. However, this technique requires that the objective function is known explicitly, which is not the case in this article. An algorithm proposed in Beer and Liebscher (2007) uses fuzzy set theory and cluster analysis to find a hypercube. On the downside, it requires a so-called membership function, which cannot be given for a design process as presented in this article.

In many cases, solution boxes are too small for practical applications and larger solution spaces are desirable. This is due to the fact that regions of good designs have often irregular shapes, in particular when design variables interact, i.e., they simultaneously have significant influence on system output (Vogt et al. 2019). Then, boxes approximate these regions only poorly and good designs are lost in the design process. Consequently, the aforementioned design flexibility is limited in these cases. Therefore, there is a strong interest in finding better approximations of the solution space that still provides uncoupling between design variables from different components.

One approach to alleviate this problem is to divide the design variables into two groups of so-called early- and late-decision variables and enlarge the solution space for early-decision variables by compensating with late-decision variables, for details see Vogt et al. (2019). This way, the resulting solution space can be significantly enlarged, however, components associated with late-decision variables have to be designed after those associated with early-decision variables are finalized. This results in a longer development process.

Another approach that enlarges the solution space without enforcing sequential development relies on so-called 2d-spaces where only pairs of design variables are decoupled from all other pairs (Erschen et al. 2017): their permissible regions are now two-dimensional. The approach increases the degree of coupling between design variables for an increase in size of the solution space. The total solution space is the Cartesian product of all 2d-spaces that can provide a significantly better fit of the complete solution spaces, i.e., the set of all good designs. Note that coupling is recommended for those design variables that are associated with the same component. This way, different components can still be designed independently.

An algorithm to compute convex and piecewise linear 2d-spaces for linear problems was proposed in Erschen et al. (2017). In Harbrecht et al. (2019), design variables were also coupled and the 2d-spaces were represented as rotated boxes (as opposed to axis-parallel boxes). Both approaches increase the size of the resulting solution space, however, the first only for linear problems and the second only for predefined shapes. This still limits the potential for large solution spaces that are relevant for flexibility during design work.

This paper aims at extending the approach based on 2d-spaces for arbitrary two-dimensional shapes and to further increase the size of solution spaces for irregular shapes. An algorithm will be presented that computes a solution space as the product of arbitrary 2-dimensional polygons. As polytopes are the equivalent of polygons in higher dimensions, the problem addressed in this paper is referred to as polytope optimization. While there is significant research on identifying maximum intervals or boxes within a confined space as previously mentioned, to the best knowledge of the authors, there is no previous work that attempts to maximize the Cartesian product of 2d-spaces defined by arbitrary polygons.

Solution space-based design can be applied to multidisciplinary problems where different components are developed satisfying requirements from different disciplines. For example, in the vehicle design problem presented in Zimmermann et al. (2017), engine mount properties and design variables related to the chassis stiffness and geometrical configuration are designed for requirements from acoustics, comfort and durability. Having demonstrated the applicability to a multidisciplinary setting, this paper will focus for simplicity on problems with fewer requirements. Note, however, that this will not restrict generality as requirements from many disciplines can always be joined into one mathematical expression — which can be treated by the approach presented here.

The rest of this article is structured as follows. The problem statement is introduced in Section 2. Section 3 gives the overview to manipulations of polygons, which are used later in the polytope optimization algorithm. The polytope optimization algorithm is then proposed in Section 4. In Section 5, numerical examples are provided. Finally, conclusions are drawn in Section 6.

2 Problem statement

Properties of product components are measured by design variables $x_{i} \in \mathbb {R}$. The overall design is given by the possibly very high-dimensional vector $\boldsymbol {x} = (x_{1},\dots , x_{d})^{\top }$ $\in \mathbb {R}^d$. The performance of a design is evaluated by an objective function $f:{\varOmega }_{\text {ds}}\to \mathbb {R}$, where ${\varOmega }_{\text {ds}}\subset \mathbb {R}^{d}$ is the space of all admissible designs. The function f measures the performance of the design, e.g., related to passenger safety or vehicle dynamics. This leads to the optimization problem

$$ \text{Minimize}\ f(\boldsymbol{x})\ \text{subject to}\ \boldsymbol{x} \in {\varOmega}_{\text{ds}}. $$

(2.1)

The evaluation of f may be quite expensive, since it describes a complex numerical simulation. Therefore, it is mandatory to keep the number of function evaluations small. Moreover, f is a black-box function. It might be noisy and it is assumed here that no information about its gradient is available.

The box optimization algorithm replaces problem (2.1) and instead tries to find a hyperbox ${\varOmega }_{\text {box}} = {\prod }_{k=1}^{d} [a_{k},b_{k}]$ such that all designs x ∈Ω_box fulfill the relaxed optimality criterion f(x) ≤ c for a given threshold value $c \in \mathbb {R}$. The corresponding optimization problem reads (compare Graff 2013, Harbrecht et al. 2019)

$$ \left\{\begin{array}{c} \text{Maximize the volume}\ \mu\left( {\varOmega}_{\text{box}} \right)\\[1ex] \text{over all axis-parallel boxes ${\varOmega}_{\text{box}} \subset {\varOmega}_{\text{ds}}$}\\[1ex] \text{subject to}\ f(\boldsymbol{x}) \leq c\ \text{for all}\ \boldsymbol{x} \in {\varOmega}_{\text{box}}. \end{array}\right. $$

(2.2)

In order to work with this problem, the following definitions are introduced (compare again Graff 2013, Harbrecht et al.2019):

Definition 1

A design x is called a good design or a good design point if f(x) ≤ c and bad design or bad design point if f(x) > c for a critical threshold value $c\in \mathbb {R}$ which is given. Additionally, the set of all good designs is defined as the complete solution space

$$ {\varOmega}_{c} := \left\lbrace \boldsymbol{x} \in {\varOmega}_{\text{ds}} : f(\boldsymbol{x})\leq c \right\rbrace. $$

For example, if f is the Rosenbrock function,

$$ f(\boldsymbol{x}) = (1-x_{1})^{2} + 100 (x_{2}-{x_{1}^{2}})^{2}, $$

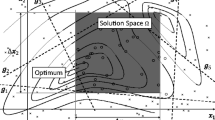
then Ω_c is U–shaped for c = 20, see Fig. 1. An axis-parallel box will settle somewhere in the lower curve of the U–shape, which ignores a large part of the good design space Ω_c (see left plot in Fig. 1). By contrast, a solution space with the shape of a polygon with an arbitrary number of vertices is able to adjust to the U–shape, and approximates the complete solution space better (see right plot in Fig. 1).

Fig. 1

An axis-parallel box (left) and a polygon (right) inside the U-shape

In order to allow for polytopes as solution spaces, the concept of 2d-spaces is utilized. The idea of 2d-spaces is to couple pairs of design variables x_i and x_j. Then, instead of searching for two separate intervals [a_i,b_i] and [a_j,b_j] that satisfy the optimization problem (2.2), one can try to find a joint set S_i,j in the associated 2d-space such that each pair (x_i,x_j) ∈ S_i,j is part of a good design. Formally, a 2d-space can be defined as follows.

Definition 2

The 2d-space Ω_i,j is defined as

$${\varOmega}_{i,j} := \left\lbrace\boldsymbol{y}\in\mathbb{R}^{2}: \boldsymbol{y} = \pi_{i,j}(\boldsymbol{x}), \boldsymbol{x} \in {\varOmega}_{\text{ds}} \right\rbrace,$$

where π_i,j is the projection $(x_{1},\dots ,x_{d}) \mapsto (x_{i},x_{j})$ with 1 ≤ i,j ≤ d. That is, the 2d-space Ω_i,j is the projection of Ω_ds onto the dimensions i and j.

Note that 2d-spaces have already been introduced in Erschen et al. (2017). In the polytope optimization algorithm, this concept of 2d-spaces is utilized and the joint set that is computed on each 2d-space is a polygon. Thus, the axis-parallel hyperbox Ω_box is replaced by a solution space Ω_pol, which is a product of one-dimensional intervals I_k and two-dimensional polygons P_i,j,

$$ {\varOmega}_{\text{pol}} := \prod\limits_{k\in \mathcal{J}_{\text{int}}} I_{k} \times \prod\limits_{(i,j)\in\mathcal{J}_{\text{pair}}} P_{i,j}, $$

(2.3)

where we have

$$ \begin{array}{@{}rcl@{}} \mathcal{J}_{\text{int}} &= \big\{i \in \left\lbrace 1,\dots,d \right\rbrace: i \ \text{is an unpaired dimension}\big\}, \end{array} $$

and, with $\mathcal {J}_{P} = \{1,\ldots ,d\}\setminus \mathcal {J}_{\text {int}}$,

$$ \begin{array}{@{}rcl@{}} \mathcal{J}_{\text{pair}} &&= \big\{(i,j)\in\mathcal{J}_{P}\times\mathcal{J}_{P}: \\ &&\text{the dimensions}\ i\ \text{and} \ j \ \text{are coupled}\big\}. \end{array} $$

The paired and unpaired dimensions are either given by the problem at hand or may be determined through other means, for example by the analysis of covariance, compare Harbrecht et al. (2019). The solution space Ω_pol is thus a specific high-dimensional polytope. As an example, Fig. 2 illustrates a solution space Ω_pol in three dimensions. If Ω_pol is a product of polygons only, i.e.,

$$ {\varOmega}_{\text{pol}} = \prod\limits_{(i,j)\in\mathcal{J}_{\text{pair}}} P_{i,j}, $$

it is a product prism, which is the term for a polytope that is a product of polytopes with two or more dimensions (see Conway et al. 2008). Whereas, we call a polytope that can be written in the fashion of (2.3) a product polytope and we define the space of admissible product polytopes as

$$ {\varOmega}_{\text{prod}}:= \Bigg\{{\varOmega}_{\text{pol}}\subset {\varOmega}_{\text{ds}}:{\varOmega}_{\text{pol}} = \!\prod\limits_{k\in \mathcal{J}_{\text{int}}}\! I_{k} \times \!\!\prod\limits_{(i,j)\in\mathcal{J}_{\text{pair}}}\!\! P_{i,j}\Bigg\}. $$

Finally, (2.2) can be rewritten in the following way:

$$ \left\{\begin{array}{c} \text{Maximize the volume}\ \mu\left( {\varOmega}_{\text{pol}} \right)\\[1ex] \text{over all polytopes ${\varOmega}_{\text{pol}} \in {\varOmega}_{\text{prod}}$}\\[1ex] \text{subject to}\ f(\boldsymbol{x}) \leq c\ \text{for all}\ \boldsymbol{x} \in {\varOmega}_{\text{pol}}. \end{array}\right. $$

(2.4)

Fig. 2

Visualization of a polytope Ω_pol = I₃ × P_1,2 in three dimensions, where I₃ = [0,1.5] and P_i,j = {(0,− 1),(1.5,− 0.5), (2,2),(1,2),(0.7,1),(− 0.3,0.5)}

As explained in Harbrecht et al. (2019), loss of flexibility by coupling pairs of design variables is accepted, because the volume of the polytope is expected to be much larger when compared to an axis-parallel hyperbox. We emphasize that the design problem at hand in general yields a natural choice for the design variables that should be coupled. For example, it is reasonable to couple design variables that one designer has full access to. Design variables are paired with at most one other design variable, and are thus represented on at most one 2d-space. Design variables that have not to be paired with another variable are assigned to an interval I_k. Note that this approach is for a problem of arbitrary dimensions. The coupling, however, is restricted to two variables. Extensions to more variables can be found, e.g., in Daub et al. (2020), however, they are not yet available for arbitrary non-linear problems like the approach presented in this paper.

3 Manipulating two-dimensional polygons

This section intends to give an overview of the basic manipulation steps of two-dimensional polygons. They are the basic ingredients for the polytope optimization algorithm presented in Section 4. A polygon P has a fixed number N of vertices and is represented by the ordered sequence of vertices, that is

$$ P = \left\{ \boldsymbol{v}^{(1)},\dots,\boldsymbol{v}^{(N)} \right\}. $$

3.1 Sample points

A design point inside the polygon P is obtained by constructing a bounding box around P and sampling uniformly distributed random points inside the bounding box until a point $\boldsymbol {x} \in \mathbb {R}^{2}$ is found that also lies within P. Determining whether a point lies within a polygon can be done via the winding number algorithm (compare Hormann and Agathos 2001). After a fixed number of design points have been sampled, all design points x are evaluated with the objective function f and then marked as good and bad points, compare Fig. 3 for an illustration.

Fig. 3

Left: Points are sampled in the dashed bounding box. Right: The points outside the box are removed and the remaining points are marked as good (green circles) and bad (red cross circles)

3.2 Trim polygons

In order to find the good solution space, a polygon needs to be trimmed such that it contains no more bad sample points. This is done by successively removing bad sample points from the polygon. To accomplish this, a bad sample point is specified. A good sample point is chosen (see Fig. 4, top left) and a triangle out of this good sample point and two neighboring vertices is formed, such that the bad sample point is contained in this triangle (see Fig. 4, top right). Then, the vertices are moved toward the good sample point until the bad sample point lies on the edge of the polygon (see Fig. 4, bottom left and right). Thus, the bad sample point lies no longer in the polygon. This procedure is then repeated for each good sample point, yielding multiple polygons that are differently trimmed. From those, the best polygon (according to the quality measures in Section 3.3) is chosen as the new, trimmed polygon. Then, this procedure is repeated again for all bad sample points remaining in the trimmed polygon.

Fig. 4

From a good and a bad point (top left) a triangle is constructed (top right) and the vertices are moved toward the good point for two possible polygons (bottom left and bottom right)

The details of this procedure can be found in Algorithm 1. It requires a polygon P with vertices $\boldsymbol {v}^{(1)},\dots ,\boldsymbol {v}^{(N)}$, a good point x^good and a bad point x^bad as inputs (line 1). For each vertex v^(k), it is checked whether the bad point lies within the convex hull of x^good, v^(k) and v^(k+ 1), which is exactly the triangle formed by those points (lines 3 and 4). If x^bad does lie within the triangle, the polygon is trimmed as explained above by Algorithm 2 (lines 5 and 6). The two possible outcomes are evaluated with the quality measures from Section 3.3 and the better one is kept (line 7). Finally, the best polygon P^(k) is chosen as output in line 10.

Algorithm 2 takes a polygon P, a good point x^good, a bad point x^bad, and two neighboring vertices v₁ and v₂ as input arguments (line 1). It trims the triangle formed by x^good, v₁ and v₂ by moving the edge between v₁ and v₂ such that it lies on x^bad. At first, the edges of the triangle are initialized (lines 3 and 4). Then, in line 5, the system

$$ [\textbf{e}_{1}, -\textbf{e}_{2}] \cdot \textbf{t} = \boldsymbol{v}_{2}-\boldsymbol{v}_{1} $$

is solved and the value t₁ is used to determine how far the vertex v₁ has to be moved (line 6). Finally, the corresponding vertex in the polygon is updated (line 7).

3.3 Evaluation of polygons

As multiple trimmed polygons are obtained at several steps of the optimization algorithm, the best polygon has to be chosen from among those polygons. For this purpose, quality measures for the polygons need to be introduced. A polygon not fulfilling one of these measures is immediately rejected and not used in the algorithm further. The polygons are rated as follows:

3.3.1 Minimum number of self-intersections

Each polygon should be free of self-intersections. Self-intersections lead to unwanted behavior of the algorithms. It is not clear how to trim a polygon with self-intersections, and multiple self-intersections overlaying each other obscure what the inside of the polygon is. Thus, polygons having no self-intersections are preferred over polygons with self-intersections (see Fig. 5).

Fig. 5

The black polygon is preferred over the red polygon because it has no self-intersections

3.3.2 Minimum/maximum size of angles

Polygons with very small angles or very large angles form spikes, see Fig. 6. When a spike is trimmed, it is very likely that a self-intersection is induced. Additionally, there is only a small chance for a point to be sampled within a spike, which in turn means that the spike will not be removed in a trimming step, making the vertex in the corner of the spike redundant. For these reasons, polytopes with no or only a few spikes are preferred. For a fixed threshold angle α, polygons which satisfy α < ϕ < 2π − α for as many vertex angles ϕ as possible (see Fig. 6) are favored over others.

Fig. 6

The black polygon is preferred over the red polygon because it has less spikes

3.3.3 Maximum number of good points

Finally, after rejecting all polygons with a bad shape, the size of the good design space is considered. Therefore, the numbers of good points within the polygons are compared and the polygon containing the most is chosen. If that polygon is not unique because several polygons contain the same highest number of points, then one from among those is chosen at random (see Fig. 7).

Fig. 7

The black polygon is preferred over the red polygon because it contains more good points

3.4 Remove spikes

After trimming and evaluating the polygon, it might still contain spikes. If this is the case, i.e., if there are vertices whose angles ϕ violate the condition α < ϕ < 2π − α, then these vertices are relocated, as seen in Fig. 8. Because the shape of the polygon is only trimmed and not modified further, it is not possible that bad designs are reintroduced to the polygon. After this step, the polygon has no spikes any more while losing not too much of its volume.

Fig. 8

Relocating vertices in order to remove spikes (red) from a polygon

3.5 Relocate vertices

A further manipulation step consists of relocating vertices. The idea behind this step is to avoid degeneration of the polygon, especially to avoid regions where vertices form clusters. This reduces the risk of a polygon developing new spikes.

The strategy of the relocation is as follows: The shortest edge of the polygon is removed by replacing its endpoints by the midpoint of the edge. Hence, one vertex is removed from the polygon. To keep the number of vertices constant, a new vertex is placed at the midpoint of the longest edge of the polygon (see Fig. 9).

Fig. 9

Two short edges (red) are removed from a polygon, then two vertices are added on the longest edges

By default, one vertex is relocated. Depending on the problem, one may either increase the number of short edges that are removed or remove only edges that are shorter than a given threshold.

3.6 Grow polygon

In this step, the polygon is grown in all directions. This allows the polygon to extend into regions of good design space. Every vertex of the polygon is moved by the same factor g along its outward pointing angle bisector (see Fig. 10). The vector of the angle bisector is normalized to 1.

Fig. 10

Growing a polygon

3.7 Remove self-intersections

Sometimes, the trimming, growing, and relocating steps might introduce self-intersections of the polygon, despite the quality measures trying to prevent this. Therefore, Graham’s scan method is applied, which finds the convex hull of a finite set of points, compare Graham (1972). It is used to remove interior self-intersections by finding the hull of the polygon, whose vertices coincide with all vertices of the original polygon which do not lie within that polygon, compare Fig. 11 for an illustration of this procedure. However, the remaining polygon might consist of multiple components. Therefore, the largest of these components is chosen as the new polygon and all the smaller components are removed. Afterwards, vertices are added or removed to maintain the total number of vertices.

Fig. 11

A polygon with self-intersections (left) and its counterpart without self-intersections (right)

In detail, the algorithm consists of the following steps:

Starting with the vertex that has the smallest y-coordinate (it is for sure a vertex of the new polygon), those line segments are considered that directly connect the vertex to other vertices and intersections. From these line segments, the one that encloses the smallest angle with the x-axis and its endpoint is chosen as an edge of the new polygon. This procedure is repeated from the endpoint of that edge, compare Fig. 12.

Fig. 12

Finding the polygon hull. The possible line segments to choose from in each step are blue, the discarded line segments are red, and the chosen segment is green

When the algorithm arrives at the starting vertex again, it has found the hull of the polygon and terminates, see Fig. 13.

Fig. 13

Final hull of the polygon

Nonetheless, the polygon might still consist of multiple different connected components. Thus, the polygon hull algorithm is implemented such that the list of vertices of the hull is given as an output. All vertices that appear more than once in the list are points where at least two different connected components are touching. If the polygon consists of more than two connected components, this information can be used to recursively find all connected components of the polygon hull. Then, the largest of the connected components is chosen as the new polygon. Finally, vertices are added like in the relocate vertices step (cf. Section 3.5) to regain the prescribed amount of vertices. We refer to Fig. 14 for an illustration.

Fig. 14

Finding and choosing the largest connected component of the polygon’s hull

4 Polytope optimization algorithm

The steps in the polytope optimization algorithm are very similar to those of the box optimization algorithm and the rotated box optimization algorithm (see Harbrecht et al. 2019). An overview of the most important steps of the polytype optimization algorithm can be found in Fig. 15. It is similar to the flowchart in Harbrecht et al. (2019), however, the steps “Trim polytope” and “Grow polytope” are much more involved than the related steps of the rotated box optimization algorithm.

Fig. 15

Flowchart for the polytope optimization algorithm

The initial polytope is usually given. If no specific polytope is given, one can use genetic algorithms (Graff et al. 2016) to find points around which a polytope could be constructed. All polygons P_i,j have a fixed number N of vertices, and, in the algorithm, each polygon is represented by an ordered sequence of vertices, that is

$$ P_{i,j} = \left\{ \boldsymbol{v}_{i,j}^{(1)},\dots,\boldsymbol{v}_{i,j}^{(N)} \right\}. $$

4.1 Exploration phase

In the exploration phase, those parts of the initial polytope are trimmed that contain bad design points. Then, the polytope is grown again. These steps are repeated $n^{\exp }$ times. This allows the polytope to move through the design space Ω in order to find a spot with a large volume of good design space. After going through all $n^{\exp }$ steps of the exploration phase, the algorithm switches to the consolidation phase.

4.1.1 Sample points

For each sample point x, all entries x_k, $k\in \mathcal {J}_{\text {int}}$, and x_i, x_j, $(i,j)\in \mathcal {J}_{\text {pair}}$, are sampled separately. The entries x_k can easily be drawn from the interval I_k. The entries (x_i,x_j) are obtained by sampling a point inside the polygon P_i,j as described in Section 3.1. After the sample points are found, they are evaluated. All of the sample points x with an objective value f(x) ≤ c are collected in the set

$$ \mathcal{X}^{\text{good}} := \left\{ {~}_{(1)}\boldsymbol{x}^{\text{good}}, \dots, {~}_{(n^{\text{good}})}\boldsymbol{x}^{\text{good}}\right\}, $$

and all of the sample points x with an objective value f(x) > c are collected in the set

$$ \mathcal{X}^{\text{bad}} := \left\{ {~}_{(1)}\boldsymbol{x}^{\text{bad}}, \dots, {~}_{(n^{\text{bad}})}\boldsymbol{x}^{\text{bad}}\right\}, $$

compare Fig. 16. The sets are sorted by the objective values of the sample points, from highest to lowest.

Fig. 16

A polytope consisting of two polygons and an interval with good and bad sample points

4.1.2 Trim polytope

After the sampling step, the bad points are removed by trimming the polytope. The framework of this step is outlined in Algorithm 3. As input, a polytope Ω_pol and ordered sets of good sample points $\mathcal {X}^{\text {good}}$ and bad sample points $\mathcal {X}^{\text {bad}}$ (line 1) are required. The output (line 2) is a polytope Ω_pol that contains no more bad sample points.

Because the bad sample points have to be removed successively, a loop over the bad sample points is initialized in line 3. Since as many good sample points as possible should be kept, the good sample points are iterated and each sample point ${~}_{(m)}\boldsymbol {x}^{\text {good}}$ is set as an anchor point once (line 4). For each anchor, the current bad sample point ${~}_{(\ell )}\boldsymbol {x}^{\text {bad}}$ is removed from the polytope such that at least the anchor point ${~}_{(m)}\boldsymbol {x}^{\text {good}}$ remains within the polytope. The bad sample point ${~}_{(\ell )}\boldsymbol {x}^{\text {bad}}$ is removed by moving the boundary of an interval I_k or a polygon P_i,j onto ${~}_{(\ell )}\boldsymbol {x}^{\text {bad}}$, thereby trimming the polytope. Thus, all intervals I_k and polygons P_i,j are iterated (see lines 5-10). For each interval I_k and polygon P_i,j, the boundary is moved onto ${~}_{(\ell )}\boldsymbol {x}^{\text {bad}}$ via the trim_interval and trim_polygon algorithms and the resulting polytope is stored in a new variable Ω^(k) or Ω_i,j, respectively, leaving all other intervals and polygons untouched. Note that the algorithm trim_polygon coincides with Algorithm 1 except for needing the coordinates (i,j) of the respective polygon P_i,j as input arguments. The algorithm trim_interval operates on the interval I_k and simply relocates one of the end points onto the bad sample point such that the good sample point remains in the output interval.

Then, in line 11, the function evaluate is applied to all polytopes Ω^(k) and Ω_i,j. It returns the result Ω^(ℓ) that maximizes the quality measures, applied in the same order as listed in Section 3.3. The quality measures are modified for polytopes such that the polytope with the most polygons that fulfill the self-intersection and angle-size measures that also contains as many good design points as possible is chosen as the optimum.

After every good point has been set as anchor once, the polytopes Ω^(ℓ) (line 13) are evaluated and the best of them is used to replace Ω_pol. Following this, the next iteration of the loop starts, where the next bad design point is removed. The polygon trimming is completed when all of the bad points are removed.

In order to avoid degenerate polytopes, finally spikes are removed and vertices are relocated by the function reshape in line 15. This function consists of the operations remove spikes (see Section 3.4) and relocate vertices (see Section 3.5), which are applied to each polygon P_i,j individually as explained in Sections 3.4 and 3.5, respectively.

4.1.3 Grow polytope

The polytope is grown as the final operation of a single step of the exploration phase. To this end, the end points a_k and b_k of each interval I_k are moved by a factor g^(ℓ) in order to grow the polytope in each dimension k. Each polygon P_i,j is grown by the factor g^(ℓ) as explained in Section 3.6.

The factor g^(ℓ) is the growth rate in the ℓ-th step of the exploration phase. It can either be constant or dynamic. A constant growth factor means that $g^{(0)} = g^{(1)} = \dots = g^{(n^{\exp })}$. A dynamic growth factor depends on the number of good design points and the growth rate of the previous step (see Graff et al. 2016):

$$ g^{(\ell)} = \frac{a_{\ell}^{\text{good}}}{a^{\text{target}}} g^{(\ell-1)}. $$

Here, $a_{\ell }^{\text {good}} = n^{\text {good}} / (n^{\text {good}} + n^{\text {bad}})$ is the percentage of good points in the ℓ-th exploration step before trimming the polytope and a^target is the desired percentage of good design points inside the polytope during the exploration phase.

The growth factor is large when many good design points have been found in the sampling step before trimming the polytope. This indicates that the polytope lies in a region with good design space and it could gain potentially more good design space by growing. The growth factor is small when the polytope contains many bad design points, because this implies that the polytope grew out of the good design space into bad design space. Thus, the growth rate should be kept small in order to ensure that the polytope, after having been trimmed, can probe for the potential border between the good and the bad design space.

4.2 Consolidation phase

Having completed the exploration phase, the candidate polytope might still contain some bad design space. The goal of the consolidation phase is to remove as much bad design space as possible. Thus, one step of the consolidation phase consists of the execution of sample points (see Section 4.1.1) and trim polytope (see Section 4.1.2). During this phase, the polytope is no longer grown. The consolidation phase is terminated after either a fixed number of n^con steps or when no bad design points have been sampled three times in series. The resulting polytope is returned as final output for the polytope optimization algorithm.

5 Numerical experiments

5.1 Problem 1: 2d polygon

We consider a simple two-dimensional test example where the solution space is representative for technical problems, e.g., in vehicle dynamics in Erschen et al. (2017). Here, the good design space is bounded by linear constraints. For

$$ \textbf{A} = \left[\begin{array}{cc} 1/8 & 1/4 \\ 4/17 & 2/17 \\ -1/2 & 1/2 \\ -1/2 & -1/3 \\ -1/3 & -2/3 \\ 1 & -3/2 \end{array}\right] \quad \text{and} \quad \textbf{b} = \left[\begin{array}{c} 1 \\ 1 \\ 1 \\ -1 \\ -1 \\ 1 \end{array}\right], $$

we consider the problem of finding x ∈Ω_ds = [0,4]² such that

$$ f(\boldsymbol{x}) = \textbf{A} \boldsymbol{x} - \textbf{b}\le \textbf{0}. $$

The good design space is a two-dimensional six-sided polygon (compare Fig. 17).

Fig. 17

Problem 1: An axis-parallel solution space (left), a rotated solution space (middle) and a polygonal solution space (right) of normalized volumes 0.15, 0.2 and 0.27, respectively. The green color indicates the good solution space

The problem under consideration shows in a simple manner how the polytope optimization works. Especially, it allows for an easy comparison between the box optimization, the rotated box optimization, and the polytope optimization algorithms. Each of these algorithms has been applied 100 times to the objective function f. Every time, the number of steps in the exploration and the consolidation phase is set to $n^{\exp } = n^{\text {con}} = 100$. Additionally, in every step, 100 design points are sampled. The growth rate is dynamic, with a^target = 0.8 and g⁽⁰⁾ = 0.05. The polytope optimization has been performed with polygons that have 10 vertices, where the required minimum size of angles is α = 20^∘ and the vertex relocation takes place in every tenth step of the exploration phase. The results can be found in Table 1.

Table 1 Results of the different optimization algorithms for Problem 1

As one might have expected, the polytope optimization yields the highest average volume for this problem, with 80% more volume than the box optimization and 42% more volume than the rotated box optimization. Examples for the solution spaces found by the different optimization algorithms are given in Fig. 17. There, the axis-parallel box Ω_box is given by the vertices

$$ {\varOmega}_{\text{box}} = \Big\{ \Big[\begin{array}{cc} 1.07 \\[0.5ex] 1.27 \end{array}\Big], \Big[\begin{array}{cc} 2.70 \\[0.5ex] 1.27 \end{array}\Big], \Big[\begin{array}{cc} 2.70 \\[0.5ex] 2.74 \end{array}\Big], \Big[\begin{array}{cc} 1.07 \\[0.5ex] 2.74 \end{array}\Big] \Big\}, $$

the rotated box Ω_rot is given by the vertices

$$ {\varOmega}_{\text{rot}} = \Big\{ \Big[\begin{array}{cc} 3.18 \\[0.5ex] 1.76 \end{array}\Big], \Big[\begin{array}{cc} 2.03 \\[0.5ex] 0.62 \end{array}\Big], \Big[\begin{array}{cc} 0.63 \\[0.5ex] 2.02 \end{array}\Big], \Big[\begin{array}{cc} 1.79 \\[0.5ex] 3.17 \end{array}\Big] \Big\}, $$

and the polytope Ω_pol is given by the vertices

$$ \begin{array}{@{}rcl@{}} {\varOmega}_{\text{pol}} = \Big\{ & \Big[\begin{array}{cc} 2.22 \\[0.5ex] 2.83 \end{array}\Big], \Big[\begin{array}{cc} 1.17 \\[0.5ex] 3.15 \end{array}\Big], \Big[\begin{array}{cc} 0.59 \\[0.5ex] 2.62 \end{array}\Big], \Big[\begin{array}{cc} 0.63 \\[0.5ex] 2.04 \end{array}\Big], \Big[\begin{array}{cc} 0.71 \\[0.5ex] 2.05 \end{array}\Big],\\ & \Big[\begin{array}{cc} 1.52 \\[0.5ex] 0.81 \end{array}\Big], \Big[\begin{array}{cc} 1.84 \\[0.5ex] 0.56 \end{array}\Big], \Big[\begin{array}{cc} 3.43 \\[0.5ex] 1.69 \end{array}\Big], \Big[\begin{array}{cc} 2.80 \\[0.5ex] 2.50 \end{array}\Big], \Big[\begin{array}{cc} 2.45 \\[0.5ex] 2.79 \end{array}\Big]\Big\}. \end{array} $$

It should be noted, however, that the polytope optimization algorithm is generally slower than the box optimization and rotated box optimization algorithms. As stated in Graff (2013), by checking the for-loops of the algorithms, one infers that the number of trimming operations that have to be carried out in both, the box optimization and rotated box optimization algorithms, is O(N³d), where N is the number of design points and d the number of dimensions. For the polytope optimization algorithm, this amounts to O(N³dv), where v is the number of vertices of the polygons in the 2d-spaces. This means that the polytope optimization algorithm usually requires more time to find a solution space.

5.2 Problem 2: 4d Rosenbrock function

The Rosenbrock function is a popular test function for optimization techniques. For x ∈Ω_ds = ([− 2, 2] × [− 2, 3])^d/2, where d is even, it is given by the formula

$$ f(\boldsymbol{x}) = \sum\limits_{i=1}^{d/2} (1-x_{2i-1})^{2} + 100(x_{2i}-x_{2i-1}^{2})^{2}. $$

The rotated box optimization and the polytope optimization are applied 100 times on the problem, with d = 4 and c = 120. The 2d-spaces for the rotated box optimization and the polytope optimization are set to Ω_1,2 = Ω_3,4 = [− 2, 2] × [− 2, 3]. The parameters are set as in Problem 1, except that, for the dynamic growth rate, a^target = 0.6 and the minimum interior angle of the polygons is set to 10^∘. The mean absolute volume of the rotated box optimization is 3.26 (mean normalized volume: 0.0082) and the mean absolute volume of the polytope optimization is 16.4 (mean normalized volume: 0.041). This means that solution spaces found by the polytope optimization have approximately 400% more volume than those found by the rotated box optimization.

In Fig. 18, a rotated box Ω_rot with absolute volume 3.2 and a polytope Ω_pol with volume 16.77 are plotted. The rotated box Ω_rot is the product of two boxes, Ω_rot = B_1,2 × B_3,4, where

$$ \begin{array}{@{}rcl@{}} B_{1,2} &=& \left\{ \left[\begin{array}{cc} 0.79 \\[0.5ex] 1.45 \end{array}\right], \left[\begin{array}{cc} 1.33 \\[0.5ex] 0.70 \end{array}\right], \left[\begin{array}{cc} 0.03 \\[0.5ex] -0.76 \end{array}\right], \left[\begin{array}{cc} -0.51 \\[0.5ex] -0.01 \end{array}\right] \right\}, \\ B_{3,4} &=& \left\{ \left[\begin{array}{cc} 0.89 \\[0.5ex] 1.59 \end{array}\right], \left[\begin{array}{cc} 1.37 \\[0.5ex] 0.92 \end{array}\right], \left[\begin{array}{cc} -0.14 \\[0.5ex] -0.77 \end{array}\right], \left[\begin{array}{cc} -0.62 \\[0.5ex] -0.10 \end{array}\right] \right\}. \end{array} $$

The polytope Ω_pol = P_1,2 × P_3,4 is given by the polygons

$$ \begin{array}{@{}rcl@{}} P_{1,2} &=& \left\{ \left[\begin{array}{cc} 1.19 \\[0.5ex] 0.62 \end{array}\right], \left[\begin{array}{cc} 1.71 \\[0.5ex] 1.95 \end{array}\right], \left[\begin{array}{cc} 1.18 \\[0.5ex] 1.97 \end{array}\right], \left[\begin{array}{cc} 0.17 \\[0.5ex] 0.78 \end{array}\right], \left[\begin{array}{cc} -0.57 \\[0.5ex] 1.15 \end{array}\right],\right.\\ &&\left.~~\left[\begin{array}{cc} -1.16 \\[0.5ex] 2.21 \end{array}\right], \left[\begin{array}{cc} -1.68 \\[0.5ex] 2.30 \end{array}\right], \left[\begin{array}{cc} -1.26 \\[0.5ex] 0.58 \end{array}\right], \left[\begin{array}{cc} -0.17 \\[0.5ex] -0.61 \end{array}\right], \left[\begin{array}{cc} 0.38 \\[0.5ex] -0.44 \end{array}\right] \right\}\!, \\ P_{3,4} &=& \left\{ \left[\begin{array}{cc} -0.95 \\[0.5ex] 0.13 \end{array}\right], \left[\begin{array}{cc} 0.28 \\[0.5ex] -0.79 \end{array}\right], \left[\begin{array}{cc} 1.37 \\[0.5ex] 1.10 \end{array}\right], \left[\begin{array}{cc} 1.54 \\[0.5ex] 1.66 \end{array}\right], \left[\begin{array}{cc} 1.78 \\[0.5ex] 2.62 \end{array}\right],\right.\\ &&\left.~~\left[\begin{array}{cc} 1.33 \\[0.5ex] 2.38 \end{array}\right], \left[\begin{array}{cc} 0.65 \\[0.5ex] 1.07 \end{array}\right], \left[\begin{array}{cc} -0.32 \\[0.5ex] 0.87 \end{array}\right], \left[\begin{array}{cc} -1.58 \\[0.5ex] 1.98 \end{array}\right], \left[\begin{array}{cc} -1.19 \\[0.5ex] 0.63 \end{array}\right] \right\}. \end{array} $$

Fig. 18

Problem 2: A rotated box with volume 3.2 (top) and a polytope with volume 16.77 (bottom). Note that these are projections of the 4d-objects into 2d-spaces

Note that the visualization in Fig. 18 is different than before. On each 2d-space Ω_i,j, 1000 design points $\boldsymbol {x} = (x_{1},\dots ,x_{4})$ are sampled with x_k ∈Ω_box or x_k ∈Ω_pol, respectively, for k≠i,j and x_k ∈Ω_i,j for k = i,j. This means that every design point is inside of Ω_pol, except for the coordinates x_i and x_j, which may be distributed anywhere on the 2d-space Ω_i,j. In a certain way, this illustrates the region around Ω_pol from the “inside” of Ω_pol. This visualization makes clear that the results are reasonable and not much more good design space could be gained by the polytope optimization, Ω_pol fills out most of the U-shaped good design space, whereas the rotated box only fills one side on each 2d-space.

5.3 Problem 3: Application to an optimal control problem

Consider the following problem: Five heat sources have to be designed such that they keep the temperature in a control volume on a given constant level. Each heat source has a fixed position x_i = (x_i,1,x_i,2) in the control volume and a circular shape with radius r_i. The temperature at the i-th heat source is given by the constant factor t_i. For the sake of simplicity, we omit physical units. The distribution of the heat emitted by the heat sources throughout the control volume is modelled by the steady-state heat equation (compare Tröltzsch (2009) for example)

$$ \begin{aligned} -{\Delta} u({\boldsymbol{x}}) &= g_{\boldsymbol{r},\boldsymbol{t}}({\boldsymbol{x}}), \ &&{\boldsymbol{x}} \in D := (0,1)^{2},\\ u({\boldsymbol{x}}) &=0, && {\boldsymbol{x}} \in {\Gamma}:=\partial D, \end{aligned} $$

(5.1)

where

$$ g_{\boldsymbol{r},\boldsymbol{t}}(\boldsymbol{x}) = \sum\limits_{i=1}^{5} t_{i} \cdot \mathcal{X}_{B_{r_{i}}(\boldsymbol{x}_{i})}(\boldsymbol{x}). $$

Here, $\mathcal {X}_{B}$ is the characteristic function

$$\mathcal{X}_{B} (\boldsymbol{x}) = \begin{cases} 1, \ & \boldsymbol{x}\in B, \\ 0, & \text{else,} \end{cases} $$

and $B_{r_{i}}(\boldsymbol {x}_{i})$ denotes the ball with radius r_i around the center x_i. The positions of the centers x_i are given by x₁ = (0.15,0.4), x₂ = (0.45,0.9), x₃ = (0.87,0.7), x₄ = (0.88,0.25), and x₅ = (0.5,0.3).

We prefer designs where the variables r and t are such that the maximum deviation from the desired temperature, i.e.,

$$ f(\boldsymbol{r},\boldsymbol{t}) = \|u^{\star}_{\boldsymbol{r},\boldsymbol{t}} - u_{d}\|_{L^{\infty}(K)}, $$

is as small as possible. Here, u_d = 0.5 is the desired constant temperature and K := [0.3,0.7]² ⊂ D the region inside the control volume where that temperature should be close to u_d (Fig. 19). In the context of classical optimization, the problem under consideration is an optimal control problem, where r and t are the control variables to be determined such that they minimize the cost function f, see Tröltzsch (2009) for example.

Fig. 19

Problem 3: A temperature field that is a solution of the heat equation represented by a design point taken from within the polytope seen in Fig. 20. The region K is marked with a black square and the radii of the heat sources are marked with black circles

In the context of the polytope optimization, however, f is the objective function and r and t are the design variables, where we choose Ω_ds := Ω_r ×Ω_t as design space with

$$ \begin{array}{@{}rcl@{}} {\varOmega}_{\boldsymbol{r}} &=& [0.01, 0.17] \times [0.01, 0.2]\times [0.01,0.2]\\ &&{\kern2.0675cm}\times [0.01,0.18]\times [0.01,0.15],\\ {\varOmega}_{\boldsymbol{t}} &=& [0,100] \times [0,80] \times [0,150] \times [0,180] \times [0,100]. \end{array} $$

The radius and temperature of each heat source are coupled by a 2d-space such that

$$ \begin{array}{@{}rcl@{}} {\varOmega}_{1,2} &= [0.01, 0.17] \times [0,100],\\ {\varOmega}_{3,4} &= [0.01, 0.2] \times [0,80],\\ {\varOmega}_{5,6} &= [0.01,0.2] \times [0,150],\\ {\varOmega}_{7,8} &= [0.01,0.18] \times [0,180],\\ {\varOmega}_{9,10} &= [0.01,0.15] \times [0,100]. \end{array} $$

Again, the algorithm is applied 100 times with 100 steps in the exploration and consolidation phases and 100 sampled design points in each step. Each polygon on a 2d-space has 10 vertices, the minimum angle is 10^∘ and the vertices are relocated every 10 steps. The growth rate is dynamic with a_target = 0.6 and g⁽⁰⁾ = 0.05. Moreover, as critical value, we choose c = 0.15, which means that the temperature generated by the heat sources is allowed to deviate by up to 30% from the desired temperature.

The resulting mean absolute volume of the solution spaces is 11.37 and the mean normalized volume is 1.37 ⋅ 10^− 6. Figure 20 shows a polytope Ω_pol = P_1,2 × P_3,4 × P_5,6 × P_7,8 × P_9,10 with absolute volume 11.88, plotted in the same way as in Fig. 18. The particular polygons are given by

$$ \begin{array}{@{}rcl@{}} P_{1,2} &=& \left\{ \left[\begin{array}{cc} 0.14 \\[0.5ex] 31.41 \end{array}\right], \left[\begin{array}{cc} 0.15 \\[0.5ex] 41.54 \end{array}\right], \left[\begin{array}{cc} 0.12 \\[0.5ex] 52.94 \end{array}\right], \left[\begin{array}{cc} 0.12 \\[0.5ex] 57.16 \end{array}\right], \left[\begin{array}{cc} 0.10 \\[0.5ex] 87.23 \end{array}\right],\right.\\ &&~\left.\left[\begin{array}{cc} 0.10 \\[0.5ex] 89.20 \end{array}\right], \left[\begin{array}{cc} 0.09 \\[0.5ex] 86.08 \end{array}\right], \left[\begin{array}{cc} 0.09 \\[0.5ex] 71.33 \end{array}\right], \left[\begin{array}{cc} 0.13 \\[0.5ex] 42.08 \end{array}\right], \left[\begin{array}{cc} 0.12 \\[0.5ex] 38.86 \end{array}\right] \right\}, \\ P_{3,4} &=& \left\{ \left[\begin{array}{cc} 0.15 \\[0.5ex] 34.80 \end{array}\right], \left[\begin{array}{cc} 0.17 \\[0.5ex] 29.07 \end{array}\right], \left[\begin{array}{cc} 0.16 \\[0.5ex] 48.81 \end{array}\right], \left[\begin{array}{cc} 0.16 \\[0.5ex] 45.32 \end{array}\right], \left[\begin{array}{cc} 0.15 \\[0.5ex] 59.75 \end{array}\right],\right.\\ &&~\left.\left[\begin{array}{cc} 0.14 \\[0.5ex] 57.17 \end{array}\right], \left[\begin{array}{cc} 0.13 \\[0.5ex] 72.76 \end{array}\right], \left[\begin{array}{cc} 0.11 \\[0.5ex] 67.02 \end{array}\right], \left[\begin{array}{cc} 0.11 \\[0.5ex] 58.29 \end{array}\right], \left[\begin{array}{cc} 0.13 \\[0.5ex] 43.79 \end{array}\right] \right\},\\ P_{5,6} &=& \left\{ \left[\begin{array}{cc} 0.08 \\[0.5ex] 69.55 \end{array}\right], \left[\begin{array}{cc} 0.10 \\[0.5ex] 39.30 \end{array}\right], \left[\begin{array}{cc} 0.12 \\[0.5ex] 30.21 \end{array}\right], \left[\begin{array}{cc} 0.13 \\[0.5ex] 51.80 \end{array}\right], \left[\begin{array}{cc} 0.10 \\[0.5ex] 84.91 \end{array}\right], \right.\\ &&~\left.\left[\begin{array}{cc} 0.09 \\[0.5ex] 115.54 \end{array}\right], \left[\begin{array}{cc} 0.07 \\[0.5ex] 127.01 \end{array}\right], \left[\begin{array}{cc} 0.07 \\[0.5ex] 117.81 \end{array}\right], \left[\begin{array}{cc} 0.07 \\[0.5ex] 78.90 \end{array}\right], \left[\begin{array}{cc} 0.09 \\[0.5ex] 54.47 \end{array}\right] \right\},\\ P_{7,8} &=& \left\{ \left[\begin{array}{cc} 0.12 \\[0.5ex] 44.81 \end{array}\right], \left[\begin{array}{cc} 0.12 \\[0.5ex] 79.16 \end{array}\right], \left[\begin{array}{cc} 0.11 \\[0.5ex] 101.98 \end{array}\right], \left[\begin{array}{cc} 0.10 \\[0.5ex] 109.40 \end{array}\right], \left[\begin{array}{cc} 0.10 \\[0.5ex] 142.45 \end{array}\right],\right.\\ &&~\left. \left[\begin{array}{cc} 0.08 \\[0.5ex] 139.10 \end{array}\right], \left[\begin{array}{cc} 0.07 \\[0.5ex] 111.54 \end{array}\right], \left[\begin{array}{cc} 0.08 \\[0.5ex] 88.51 \end{array}\right], \left[\begin{array}{cc} 0.08 \\[0.5ex] 97.50 \end{array}\right], \left[\begin{array}{cc} 0.10 \\[0.5ex] 61.46 \end{array}\right] \right\}, \\ P_{9,10} &=& \left\{ \left[\begin{array}{cc} 0.05 \\[0.5ex] 65.38 \end{array}\right], \left[\begin{array}{cc} 0.03 \\[0.5ex] 50.46 \end{array}\right], \left[\begin{array}{cc} 0.04 \\[0.5ex] 19.14 \end{array}\right], \left[\begin{array}{cc} 0.07 \\[0.5ex] 9.84 \end{array}\right], \left[\begin{array}{cc} 0.09 \\[0.5ex] 6.34 \end{array}\right],\right.\\ &&~\left.\left[\begin{array}{cc} 0.12 \\[0.5ex] 15.62 \end{array}\right], \left[\begin{array}{cc} 0.10 \\[0.5ex] 19.73 \end{array}\right], \left[\begin{array}{cc} 0.09 \\[0.5ex] 19.93 \end{array}\right], \left[\begin{array}{cc} 0.06 \\[0.5ex] 49.61 \end{array}\right], \left[\begin{array}{cc} 0.07 \\[0.5ex] 49.85 \end{array}\right] \right\}. \end{array} $$

Ω_pol fills most of the pocket of good design space it has found. A solution of (5.1) with a design taken from within that polytope is plotted in Fig. 19. Figure 21 shows each 2d-space as a heat map of the 100 solution spaces. The brighter a region, the more solution spaces cover that region. The picture suggests that they usually stay within the same region, so it can be concluded that the algorithm delivers robust results.

Fig. 20

Problem 3: A solution space with volume 11.88

Fig. 21

Problem 3: Heat map for 100 solution spaces

6 Conclusion

The algorithm presented in this article utilizes the concept of 2d-spaces, introduced in Erschen et al. (2017), to form a coupling between the coordinates. It replaces the box-shaped solution space on each 2d-space by a polygonal solution space, whose product results in a high-dimensional polytope. Numerical results confirm that this setting allows the algorithm to find solution spaces of larger volume than those found by its predecessors from Harbrecht et al. (2019) and Zimmermann and von Hoessle (2013) while the cost, i.e., the number of sample points, is the same. Additionally, the algorithm works well with up to 10 dimensions. Note that more applications and numerical results of the algorithm can be found in Tröndle (2020).

Future work could explore the performance of the algorithm in higher dimensions. Another relevant extension would be the coupling of more than two variables into one separated region of permissible designs.