Sequential mixture of Gaussian processes and saddlepoint approximation for reliability-based design optimization of structures

Abstract

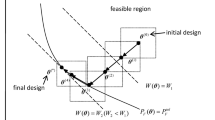
This paper presents an efficient optimization procedure for solving the reliability-based design optimization (RBDO) problem of structures under aleatory uncertainty in material properties and external loads. To reduce the number of structural analysis calls during the optimization process, mixture models of Gaussian processes (MGPs) are constructed for prediction of structural responses. The MGP is used to expand the application of the Gaussian process model (GPM) to large training sets for well covering the input variable space, significantly reducing the training time, and improving the overall accuracy of the regression models. A large training set of the input variables and associated structural responses is first generated and split into independent subsets of similar training samples using the Gaussian mixture model clustering method. The GPM for each subset is then developed to produce a set of independent GPMs that together define the MGP as their weighted average. The weight vector computed for a specified input variable contains the probability that the input variable belongs to the projection of each subset onto the input variable space. To calculate the failure probabilities and their inverse values required during the process of solving the RBDO problem, a novel saddlepoint approximation is proposed based on the first three cumulants of random variables. The original RBDO problem is replaced by a sequential deterministic optimization (SDO) problem in which the MGPs serve as surrogates for the limit-state functions in probabilistic constraints of the RBDO problem. The SDO problem is strategically solved for exploring a promising region that may contain the optimal solution, improving the accuracy of the MGPs in that region, and producing a reliable solution. Two design examples of a truss and a steel frame demonstrate the efficiency of the proposed optimization procedure.

Appendices

Appendix 1 Gaussian process model

Based on the training data set $\mathcal{D}=\left\{\mathbf{X},\mathbf{y}\right\}={\left\{{\mathbf{x}}_i,{y}_i\right\}}_{i=1}^N$, we seek to construct an input-output mapping y = f(x): ℝ^d → ℝ, where f(x) is an unknown regression function.

A semi-parametric GPM defines f(x) using the following probabilistic regression model (Rasmussen and Williams 2006):

$$ f\left(\mathbf{x}\right)=\sum \limits_{i=1}^p{h}_i\left(\mathbf{x}\right){\beta}_i+Z\left(\mathbf{x}\right)={\mathbf{h}}^T\left(\mathbf{x}\right)\boldsymbol{\upbeta} +Z\left(\mathbf{x}\right) $$

(A.1)

where h^T(x) = [h₁(x), …, h_q(x)]^T is a q-dimensional vector of known basis function of x; q is derived from d according to the form of the basis function; β = [β₁, …, β_q]^T is a vector of unknown coefficients; h^T(x)β represents the mean function of f(x); and Z(x) is a correlation function modeling the residual.

Since the prediction performance of GPM is mainly evaluated via the covariance function (Rasmussen and Williams 2006), the basis function in the mean function of the GPM is not the main focus of the method. Thus, there may not exist a criterion to choose a basis function. A zero-basis function is often used to avoid expensive computations of the GPM. However, there are several reasons for explicitly using a non-zero mean function such as interpretability of the regression model and convenience of expressing prior information (Rasmussen and Williams 2006). For this, it is convenient to describe the GP mean function using a few fixed basis functions such as linear or quadratic functions. In this study, the basis function is a quadratic function of the input variables x.

The GPM assumes that the marginal likelihood, i.e., p(y| X), is an N-variate Gaussian with a mean vector $\mathbf{f}={\left\{f\left({\mathbf{x}}_i\right)\right\}}_{i=1}^N$ and covariance matrix. The covariance matrix is determined based on the following two facts. First, its (i, j)th element explains the cosine similarity between two points f(x_i) and f(x_j), both are unknowns and drawn from p(y| X). Second, we expect that the smoothness of any continuous functions also well operates on the regression function f(x), i.e., a small variation in x leads to a small variation in f(x), or vice versa. Therefore, the cosine similarity between two input vectors x_i and x_j, which are known in advance, can be used to characterize the cosine similarity between the two points f(x_i) and f(x_j), which are unknown in advance.

Let the PDF p(Z| X) of the vector of residuals $\mathbf{Z}={\left\{Z\left({\mathbf{x}}_i\right)\right\}}_{i=1}^N$ be an N-variate Gaussian with a zero mean and a covariance matrix explaining the similarity between any two input vectors as

(A.2)

where K ∈ ℝ^N × N is the covariance matrix with the element K_ij = k(x_i, x_j ) is a positive definite kernel function to explain the cosine similarity between two input vectors x_i and x_j. This study uses the squared exponential kernel as

$$ k\left({\mathbf{x}}_i,{\mathbf{x}}_j\ \right)={\theta}_{\mathrm{y}}^2\exp \left[-\frac{{\left({\mathbf{x}}_i-{\mathbf{x}}_j\right)}^T\left({\mathbf{x}}_{\mathrm{i}}-{\mathbf{x}}_j\right)}{2{\theta}_{\mathrm{l}}^2}\right] $$

(A.3)

where θ = {θ_y, θ_l} are unknown parameters of the kernel function.

Since the covariance matrix of p(y| X) is identical to that of p(Z| X) in (A.2), the marginal likelihood can be represented by

(A.4)

where H(X) = [h^T(x₁), …, h^T(x_N)]^T, and H(X)β is the mean vector of f.

The coefficient vector β is the least-squares solution as follows:

$$ \boldsymbol{\upbeta} \left(\boldsymbol{\uptheta} \right)={\left[{\mathbf{H}}^T\left(\mathbf{X}\right){\mathbf{K}}^{-1}\left(\boldsymbol{\uptheta} \right)\mathbf{H}\left(\mathbf{X}\right)\right]}^{-1}{\mathbf{H}}^T\left(\mathbf{X}\right){\mathbf{K}}^{-1}\left(\boldsymbol{\uptheta} \right)\mathbf{y} $$

(A.5)

To determine the kernel parameters θ, the marginal likelihood, or equivalently, its logarithm is maximized with respect to θ as (Rasmussen and Williams 2006)

$$ \mathcal{L}\left(\boldsymbol{\upbeta}, \boldsymbol{\uptheta} \right)=\log p\left(\mathbf{y}|\mathbf{X}\right)=-\frac{1}{2}{\left[\mathbf{y}-\mathbf{H}\left(\mathbf{X}\right)\boldsymbol{\upbeta} \right]}^T{\mathbf{K}}^{-1}\left(\boldsymbol{\uptheta} \right)\left[\mathbf{y}-\mathbf{H}\left(\mathbf{X}\right)\boldsymbol{\upbeta} \right]-\frac{1}{2}\log \left|\mathbf{K}\left(\boldsymbol{\uptheta} \right)\right|-\frac{1}{2}N\log 2\uppi $$

(A.6)

Substituting β in (A.5) into (A.6), $\mathcal{L}$ becomes a function of θ and is maximized using an optimization algorithm. In this study, the DACE toolbox (Lophaven et al. 2002) is used to determine θ.

Once θ and β are determined, to predict the responses ${\mathbf{y}}^{\ast}={\left\{{y}_l^{\ast}\right\}}_{l=1}^M$ for a new test set of a total M input variables ${\mathbf{X}}^{\ast}={\left\{{\mathbf{x}}_l^{\ast}\right\}}_{l=1}^M$, the joint PDF of y ∣ X and y^∗ ∣ X^∗ is established as

(A.7)

where K^∗ ∈ ℝ^N × M with ${K}_{il}^{\ast }=k\left({\mathbf{x}}_i,{\mathbf{x}}_l^{\ast}\ \right)$, and K^∗∗ ∈ ℝ^M × M with ${K}_{lh}^{\ast \ast }=k\left({\mathbf{x}}_l^{\ast},{\mathbf{x}}_h^{\ast}\ \right)$.

Applying the rule of the posterior conditional to the joint PDF in (A.7), the conditional PDF used to predict y^∗ for the test set X^∗ is given by (Rasmussen and Williams 2006)

(A.8)

where

$$ {\boldsymbol{\upmu}}_{{\mathbf{y}}^{\ast }}=\mathbf{H}\left({\mathbf{X}}^{\ast}\right)\boldsymbol{\upbeta} +{\mathbf{K}}^{\ast T}{\mathbf{K}}^{-1}\left[\mathbf{y}-\mathbf{H}\left(\mathbf{X}\right)\boldsymbol{\upbeta} \right] $$

(A.9)

$$ {\boldsymbol{\Sigma}}_{{\mathbf{y}}^{\ast }}={\mathbf{K}}^{\ast \ast }-{\mathbf{K}}^{\ast T}{\mathbf{K}}^{-1}{\mathbf{K}}^{\ast } $$

(A.10)

Appendix 2. Clustering training set using Gaussian mixture model

Clustering a training set aims at distributing its similar samples to an independent group in which the samples share a general property. Two fundamental steps of clustering a training set include measuring the similarity of the samples and selecting a clustering algorithm. Different similarity measures and clustering algorithms can be found in Xu and Wunsch (2005). Here, we premise that two training samples are similar if they emerge from the same PDF. Therefore, it is convenient to split the joint PDF of the input-output variables p(x, y) into different Gaussian components using the GMM (Hastie et al. 2009), assign component as a subset, and then distribute the training samples into each subset accordingly.

The GMM describes the joint PDF p(x, y) by a convex combination of Gaussians as follows:

$$ p\left(\mathbf{x},y|\boldsymbol{\Theta} \right)=\sum \limits_{k=1}^K{\pi}_k\phi \left({\mathbf{x}}_i,{y}_i|{\boldsymbol{\upmu}}_k,{\boldsymbol{\Sigma}}_k\right) $$

(B.1)

$$ \sum \limits_{k=1}^K{\pi}_k=1,\kern0.75em 0\le {\pi}_k\le 1 $$

(B.2)

$$ {\boldsymbol{\upmu}}_k={\left[{\boldsymbol{\upmu}}_{\mathbf{X},k}^T,{\mu}_{y,k}\right]}^T $$

(B.3)

$$ {\boldsymbol{\Sigma}}_k=\left[\begin{array}{cc}{\boldsymbol{\Sigma}}_{\mathbf{X}\mathbf{X},k}& {\boldsymbol{\Sigma}}_{\mathbf{X}y,k}\\ {}{\boldsymbol{\Sigma}}_{y\mathbf{X},k}& {\boldsymbol{\Sigma}}_{yy,k}\end{array}\right] $$

(B.4)

where denote the kth (d + 1)-variate Gaussian; K is the number of Gaussians; and $\boldsymbol{\Theta} ={\left\{{\pi}_k,{\boldsymbol{\upmu}}_k,{\boldsymbol{\Sigma}}_k\right\}}_{k=1}^K$ are unknown parameters of the GMM with π_k, μ_k, and Σ_k represent the mixing proportion, mean vector, and covariance matrix of the kth Gaussian, respectively.

Let z = [z₁, …, z_N]^T denote a latent random vector, where z_i ∈ {1, …, K}, and z_ik denote the probability that the sample (x_i, y_i) belongs to the kth Gaussian (or the kth subset), i.e.,

$$ {z}_{ik}=\left\{\begin{array}{c}1,\kern0.75em \mathrm{if}\ {z}_i=k\\ {}0,\kern0.75em \mathrm{if}\ {z}_i\ne k\end{array}\right. $$

(B.5)

Since z is unknown in advance, z_ik cannot be specified exactly. Instead, its expectation, denoted by $\mathbbm{E}\left[{z}_{ik}\right]$, can be determined by using Bayes’ rule as follows:

$$ \mathbbm{E}\left[{z}_{ik}\right]=\mathrm{\mathbb{P}}\left[{z}_i=k|{\mathbf{x}}_i,{y}_i,\boldsymbol{\Theta} \right]=\frac{p\left({z}_i=k|\boldsymbol{\Theta} \right)p\left({\mathbf{x}}_i,{y}_i|{z}_i=k,\boldsymbol{\Theta} \right)}{\sum_{h=1}^Kp\left({z}_i=h|\boldsymbol{\Theta} \right)p\left({\mathbf{x}}_i,{y}_i|{z}_i=h,\boldsymbol{\Theta} \right)} $$

(B.6)

where p(z_i = k| Θ) = π_k is the prior and p(x_i, y_i| z_i = k, Θ) = ϕ(x_i, y_i| μ_k, Σ_k) is the likelihood. Thus, (B.6) can be rewritten as

$$ \mathbbm{E}\left[{z}_{ik}\right]=\mathrm{\mathbb{P}}\left[{z}_i=k|{\mathbf{x}}_i,{y}_i,\boldsymbol{\Theta} \right]=\frac{\pi_k\phi \left({\mathbf{x}}_i,{y}_i|{\boldsymbol{\upmu}}_k,{\boldsymbol{\Sigma}}_k\right)}{\sum_{h=1}^K{\pi}_h\phi \left({\mathbf{x}}_i,{y}_i|{\boldsymbol{\upmu}}_h,{\boldsymbol{\Sigma}}_h\right)} $$

(B.7)

To determine Θ, the posterior of the following log-likelihood ${\mathcal{L}}_c$ of the training set is maximized using an iterative expectation-maximization (EM) algorithm (Hastie et al. 2009).

$$ {\mathcal{L}}_c=\sum \limits_{i=1}^N\sum \limits_{k=1}^K\mathbbm{E}\left[{z}_{ik}\right]\log \left[{\pi}_k\phi \left({\mathbf{x}}_i,{y}_i|{\boldsymbol{\upmu}}_k,{\boldsymbol{\Sigma}}_k\right)\right] $$

(B.8)

The EM algorithm starts with initial parameters ${\boldsymbol{\Theta}}^{(0)}={\left\{{\pi}_k^{(0)},{\boldsymbol{\upmu}}_k^{(0)},{\boldsymbol{\Sigma}}_k^{(0)}\right\}}_{k=1}^K$, computes $\mathbbm{E}\left[{z}_{ik}\right]$ using (B.7), maximizes ${\mathcal{L}}_c$ in (B.8) with respect to Θ for obtaining a new value of Θ, and moves on to the next iteration with the new Θ. For a given K, the initial mixing proportions ${\pi}_k^{(0)}$ are uniform, the initial mean vectors ${\boldsymbol{\upmu}}_k^{(0)}$ are randomly selected from K vectors of the training set, and the initial variance matrices ${\boldsymbol{\Sigma}}_k^{(0)}$ are diagonal, where the ith element on the diagonal is the variance of the ith input variable. The algorithm is assured to converge at a finite number of iterations since it always reduced ${\mathcal{L}}_c$ after each iteration. Detailed derivations and convergence properties of the EM algorithm can be found in Hastie et al. (2009). Here, we summarize two main steps of the EM as follows:

• E step:

$$ \mathbbm{E}\left[{z}_{ik}^{(t)}\right]=\frac{\pi_k^{(t)}\phi \left({\mathbf{x}}_i,{y}_i|{\boldsymbol{\upmu}}_k^{(t)},{\boldsymbol{\Sigma}}_k^{(t)}\right)}{\sum_{h=1}^K{\pi}_h^{(t)}\phi \left({\mathbf{x}}_i,{y}_i|{\boldsymbol{\upmu}}_h^{(t)},{\boldsymbol{\Sigma}}_h^{(t)}\right)} $$

(B.9)

• M step:

$$ {\pi}_k^{\left(t+1\right)}=\frac{\sum_{i=1}^N\mathbbm{E}\left[{z}_{ik}^{(t)}\right]}{N} $$

(B.10)

$$ {\boldsymbol{\upmu}}_k^{\left(t+1\right)}=\frac{\sum_{i=1}^N\mathbbm{E}\left[{z}_{ik}^{(t)}\right]{\mathbf{d}}_i}{\sum_{i=1}^N\mathbbm{E}\left[{z}_{ik}^{(t)}\right]} $$

(B.11)

$$ {\boldsymbol{\Sigma}}_k^{\left(t+1\right)}=\frac{\sum_{i=1}^N\mathbbm{E}\left[{z}_{ik}^{(t)}\right]\left({\mathbf{d}}_i-{\boldsymbol{\upmu}}_k^{\left(t+1\right)}\right){\left({\mathbf{d}}_i-{\boldsymbol{\upmu}}_k^{\left(t+1\right)}\right)}^T}{\sum_{i=1}^N\mathbbm{E}\left[{z}_{ik}^{(t)}\right]} $$

(B.12)

where t denote the iteration counter and ${\mathbf{d}}_i={\left[{\mathbf{x}}_i^T,{y}_i\right]}^T$.

After Θ is obtained, the probability that the training sample (x_i, y_i) belongs to the kth Gaussian, i.e., $\mathbbm{E}\left[{z}_{ik}\right]$, is determined using (B.7), thereby producing K values of $\mathbbm{E}\left[{z}_{ik}\right]$. The maximum value among these K values indicates which Gaussian (or subset) contains the sample (x_i, y_i).

By projecting all subsets in (d + 1)-dimensional space onto the d-dimensional space of input variables, the probability that an input variable x emerges from the kth projected subset can be determined (without knowing the corresponding output variable y) by

$$ \mathrm{\mathbb{P}}\left[{z}_i=k|\mathbf{x},\boldsymbol{\Theta} \right]=\frac{\pi_k\phi \left(\mathbf{x}|{\boldsymbol{\upmu}}_{\mathbf{X},k},{\boldsymbol{\Sigma}}_{\mathbf{X}\mathbf{X},k}\right)}{\sum_{h=1}^K{\pi}_h\phi \left(\mathbf{x}|{\boldsymbol{\upmu}}_{\mathbf{X},h},{\boldsymbol{\Sigma}}_{\mathbf{X}\mathbf{X},h}\right)} $$

(B.13)

where μ_{X, k} and Σ_{XX, k} are derived from (B.3) and (B.4), respectively.

As a model selection task, the number of Gaussians K should be determined before employing the EM algorithm for obtaining Θ. Detailed discussions on criteria used for selecting the best model among available GMMs can be found in McLachlan and Rathnayake (2014). Here, the Bayesian information criterion (BIC) is chosen since its effectiveness has been confirmed by many authors in the statistical learning field (McLachlan and Rathnayake 2014). To produce a set of GMM candidates for the model selection, we simply increase K step by step from 1 to 50. The best GMM among these candidates minimizes BIC as (Hastie et al. 2009)

$$ \mathrm{BIC}=-\mathcal{L}+\frac{1}{2}{n}_{\mathrm{p}}\log N $$

(B.14)

where $\mathcal{L}={\sum}_{i=1}^N\log \left[{\sum}_{k=1}^K{\pi}_k\phi \left({\mathbf{x}}_i,{y}_i|{\boldsymbol{\upmu}}_k,{\boldsymbol{\Sigma}}_k\right)\right]$ is the log-likelihood of the training set and n_p is the number of free parameters required for a total of K Gaussians.