Tabu efficient global optimization with applications in additive manufacturing

Abstract

Methods based on Gaussian stochastic process (GSP) models and expected improvement (EI) functions have been promising for box-constrained expensive optimization problems. These include robust design problems with environmental variables having set-type constraints. However, the methods that combine GSP and EI sub-optimizations suffer from the following problem, which limits their computational performance. Efficient global optimization (EGO) methods often repeat the same or nearly the same experimental points. We present a novel EGO-type constraint-handling method that maintains a so-called tabu list to avoid past points. Our method includes two types of penalties for the key “infill” optimization, which selects the next test runs. We benchmark our tabu EGO algorithm with five alternative approaches, including DIRECT methods using nine test problems and two engineering examples. The engineering examples are based on additive manufacturing process parameter optimization informed using point-based thermal simulations and robust-type quality constraints. Our test problems span unconstrained, simply constrained, and robust constrained problems. The comparative results imply that tabu EGO offers very promising computational performance for all types of black-box optimization in terms of convergence speed and the quality of the final solution.

1 Introduction

Engineering design optimization problems often involve expensive black-box functions such as finite element methods (FEM), computational fluid dynamics (CFD), or thermal simulations based on Green’s functions. The computational times required to build and run these simulations could be minutes, hours, or even days. Therefore, methods based on Gaussian stochastic process (GSP) or Kriging meta-models provide computationally inexpensive approaches to speed up the optimization by providing surrogates for more expensive simulations (Matheron 1963; Santner et al. 2018). GSP meta-models have been incorporated into the so-called efficient global optimization (EGO) to solve unconstrained (Jones et al. 1998), simply constrained (Audet et al. 2000; Sasena et al. 2002; Sasena 2002), and robust constrained (ur Rehman and Langelaar 2017) optimization problems. In all these cases, the EGO algorithm selects the next expensive (in terms of computation time) function evaluation or sample using an “infill” optimization involving the GSP meta-model. These infill optimizations involve some form of expected improvement (EI, Jones et al. 1998) formula or other infill sampling criterion (ISC) such as mode-pursuing sampling (Wang et al. 2004) to balance exploration and exploitation.

EGO applications have been extended to “noisy” problems involving either stochastic simulations or real-world experiments (e.g., Huang and Allen, 2005). The term “noisy” in optimization referring to the problem affected by uncertainties, and it is often called the robust optimization problem. Ben-Tal et al. (2009) summarized the recent progress of robust optimization for linear, convex-quadratic, conic-quadratic, and semidefinite problems. However, literature related to robust optimization of non-convex problems affected by uncertainties is relatively limited. Bertsimas et al. (2010) proposed an algorithm for robust optimization of non-convex problems with constraints, but the method is aimed at identifying local robust optima only. In 2015, Reman and Langelaar proposed the first Kriging-based constrained optimization for addressing efficient global robust optimization of unconstrained problems affected by parametric uncertainties, and they expanded to the constrained optimization problem (ur Rehman and Langelaar 2017). This paper utilizes the framework introduced by Reman and Langelaar to solve the constrained optimization problem with max/min-typed constraints, which will be explained in detail in Section 2.1, by dividing the optimization problem into two sub-optimization problems.

EGO methods often suffer from repeating the same or nearly the same experimental points, which limits their computational performance. Huang et al. (2005) addressed the “diminishing return of addition replicates” in creating a new EI-based infill sampling formula; i.e., they addressed the unfortunate tendency of the EI methods to return to the same points for noisy problems. The associated relatively slow convergence rates were noted even for noisy cases in which repeated sampling could be (hypothetically) beneficial. Those authors created a so-called augmented expected improvement (AEI) to reduce resampling. Here, we propose methods that directly and explicitly increase the probability of avoiding returns to or near previously sampled points using a so-called tabu list. Our proposed lists comprise previously sampled points, and points predicted to be infeasible identified during infill optimizations.

Tabu searches (TS) are highly regarded meta-heuristics for the optimization of inexpensive black-box functions (Glover 1986, 1989, 1990; Chelouah and Patrick 2000). Generating variants of TS methods continues to be an active area of research for inexpensive functions, including new types of “hybrid” optimization (Duarte et al. 2011). TS methods have been combined with other meta-heuristics, such as particle swarm methods (Lin et al. 2019). However, TS methods have not been applied to expensive black-box functions and have not been combined with EGO methods. Although the idea of tabu search could be applied to most of the sequential global optimization methods, combining TS and EGO to address expensive black-box optimization is our primary objective here.

It should be noted that Forrester et al. (2006) also observed the repetition tendency in noisy black-box methods of EGO. They proposed that nontrivial regression models should be included in the Kriging modeling to avoid repetition. Even though our problem here is noiseless, we include the so-called superEGO methods with first-order regression in our comparison.

The method for performing infill optimizations using the inexpensive GSP meta-models is generally not a major concern in the context of the EGO method because the computational overhead often has less importance than the costs of the expensive black-box runs. Therefore, many types of non-linear programming approaches can be applied, including DIRECT methods (Jones 2009a; Liu et al. 2017), constraint importance mode-pursuing sampling for continuous global optimization (CIMPS, Kazemi et al. 2010), and constrained local metric stochastic radial-based function (ConstrLMSRBF, Regis 2011) methods. In our implementation, we use DIRECT for our infill optimization; a brief introduction of the DIRECT method can be found in Section 2.4. However, non-linear programming approaches have been proposed to apply to expensive black-box functions (e.g., Liu et al. 2017). We also included MATLAB’s build-in constrained non-linear optimization algorithm fmincon (The Math Works, Inc 2020), and Tree Parzen Estimator (Bergstra et al. 2013) from a python package hyperopt is included in the results comparison study. Therefore, the methods mentioned above are included in our computational comparison together with the pre-existing EGO-type methods.

The motivating application for this work is the optimal design of additive manufacturing process parameters informed by point-based thermal simulations (Frazier 2014; Schwalbach et al. 2019). These thermal simulation outputs derive from a sum over Green’s function evaluations evaluated at discrete points in a physical two-dimensional layer (Schwalbach et al. 2019). This type of simulation differs from usual FEM or CFD simulations in that it is possible to obtain values at discrete X-Y points only. The FEM and CFD methods almost unavoidably generate outputs at all X-Y points in the part geometry. Therefore, the use of discrete thermal simulations motivates the application of a robust formulation in which the part thermal quality must be guaranteed at all X-Y points in the process parameter optimization. This is challenging because potentially the worst X-Y point might differ depending on the process parameter values. We address the decision problem posed for robust EGO methods (ur Rehman and Langelaar 2017).

The remainder of this article is organized as follows. Section 2 reviews the decision problems in unconstrained (Jones et al. 1998), simply constrained (Audet et al. 2000; Sasena et al. 2002; Sasena 2002), and robust constrained (ur Rehman and Langelaar 2017) optimization and provides a brief introduction to the DIRECT method. The first two problems are described as a special case of the third. Also, the mechanics of GSP meta-models and pseudo-code for EGO methods are reviewed, again with unconstrained and simply constrained methods described as special cases of robust EGO methods. Further, TS method concepts and methods are briefly described. In Section 3, we propose the novel tabu EGO methods building on robust EGO and concepts from TS methods. Sections 4 and 5 compare the performance of tabu EGO with three alternative methods on nine numerical test problems and two additive manufacturing process parameter optimization problems. Finally, Section 6 discusses the implications and suggests multiple opportunities for future research.

2 Review of alternative methods

2.1 Decision problems

The general robust decision problem was explored by ur Rehman and Langelaar (2017). The controllable decision variables are x_c which are restricted to the set ${\mathbbm{X}}_{\mathrm{c}}$. In addition, there are environmental or noise variables, x_e, restricted to the set ${\mathbbm{X}}_{\mathrm{e}}$. In our additive example, the process parameter variables are controllable, and the noise variables are the X-Y positions because our part must have acceptable quality at all points in each layer. The objective function is f(x_c, x_e), and the q constraints are g_j(x_c, x_e), j = 1, ⋯, q. In our example, the objective is the processing speed times, and the constraints related to part quality at all points. The general formulation is

$$ {\displaystyle \begin{array}{c}\underset{{\boldsymbol{x}}_{\mathrm{c}}}{\min}\underset{{\boldsymbol{x}}_{\mathrm{e}}}{\max }f\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}\right)\\ {}s.t.\underset{{\boldsymbol{x}}_{\mathrm{e}}}{\max }{\mathrm{g}}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}\right)\le 0\kern0.5em \forall j=1,\dots, q\\ {}{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}.\end{array}} $$

(1)

Note that “simply” constrained formulations are special cases for which the environmental variable is a constant, i.e., $\left|{\mathbbm{X}}_{\mathrm{e}}\right|=1$. Unconstrained problems are special cases with q = 0.

Two potentially significant quantities are the worst environmental conditions at iteration t, ${\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast }$, for a given set of control parameters ${\boldsymbol{x}}_{\mathrm{c}}^{\ast }$ and the best control parameters at iteration t, ${\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast }$, for a given environmental set of conditions ${\boldsymbol{x}}_{\mathrm{e}}^{\ast }$. These quantities are

$$ {\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast }=\underset{{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_e}{\mathrm{argmax}}f\left({\boldsymbol{x}}_{\mathrm{c}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)\mid {g}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)\le 0\forall j=1,\dots, q,{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}. $$

(2)

and

$$ {\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast }=\underset{{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}}}{\mathrm{argmin}}f\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}^{\ast}\right)\mid {g}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}^{\ast}\right)\le 0\forall j=1,\dots, q,{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}}. $$

(3)

The two quantities in (2) and (3) relate to the two sub-optimizations of the robust EGO algorithm (ur Rehman and Langelaar 2017). For methods without robustness constraints, (2) is not relevant (e.g., Jones et al. 1998; Sasena 2002).

2.2 Gaussian stochastic process models

Gaussian stochastic process (GSP) or “Kriging” meta-models have proven useful for the modeling and optimization of expensive black-box functions (Matheron 1963; Santner et al. 2018). The derived empirical models can generate surrogate predictors, ${\mathcal{F}}_{\mathrm{f}}$ and G_j, for the objectives and constraint functions, f and g_j, in (1).

We assume that the decision vector x has d dimensions, and n is the current total number of data points. The assumptions of GSP models are often expressed in terms of outputs, Y(x), regression terms, h(x), and random terms Z(x). The assumed model is

$$ Y\left(\boldsymbol{x}\right)=h\left(\boldsymbol{x}\right)+Z\left(\boldsymbol{x}\right). $$

(4)

Where Z(x) is a zero mean stationary Gaussian process with Cov(Z(x_i ), Z(x_j) = σ²R_{i, j}(θ, p), where R_{i, j}(θ, p) is defined in (5).

In our numerical examples, we make the common assumption that the regression terms are constant, i.e., h(x) = β₀. However, detrending data using regression can be critical in some problems.

The GSP model parameters are d dimensional vectors of correlation parameters, θ, and exponents, p. A critical model quantity is the correlation matrix, R, between the responses at the points, x₁, ⋯, x_n. Here, we assume the standard Gaussian correlation function R with i, jth entry R_{i, j}:

$$ {R}_{\mathrm{i},\mathrm{j}}\left(\boldsymbol{\theta}, \boldsymbol{p}\right)={\prod}_{k=1}^m{e}^{-{\theta}_{\mathrm{k}}{\left({x}_{\mathrm{k}}-{x}_{\mathrm{i},\mathrm{k}}\right)}^{p_{\mathrm{k}}}}. $$

(5)

where R_{i, j}(θ, p) is only a valid correlation function when 0 < p_k ≤ 2 for all k. And the Gaussian correlation function assumes all p_k= 2.

The best linear unbiased predictor for the regression coefficients in h(x) = β₀ is

$$ {\beta}_{\mathrm{est}}\left(\boldsymbol{\theta}, \boldsymbol{p}\right)={\left({\mathbf{1}}^{\prime }{\boldsymbol{R}}^{-1}\mathbf{1}\right)}^{-1}{\mathbf{1}}^{\prime }{\boldsymbol{R}}^{-1}\boldsymbol{y} $$

(6)

where 1 is an n-dimensional vector of 1s. This coefficient is used for estimating the point-specific variance ${s}_{\mathrm{est}}^2\left(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{p}\right)$ and optimizing the likelihood. The standard formula to predict the variance of the GSP at point x is

$$ {s}_{\mathrm{est}}^2\left(\boldsymbol{x}|\boldsymbol{\theta}, \boldsymbol{p}\right)={n}^{-1}{\left(\boldsymbol{y}-\mathbf{1}{\beta}_{\mathrm{est}}\right)}^{\prime }{\boldsymbol{R}}^{-1}\left(\boldsymbol{y}-\mathbf{1}{\beta}_{\mathrm{est}}\right). $$

(7)

The valued of θ and p that maximize the right-hand side of (8) are the MLEs:

$$ \underset{\boldsymbol{\uptheta}, \mathbf{p}}{\max}\ln L\left(\boldsymbol{\theta}, \boldsymbol{p}\right)=-\underset{\boldsymbol{\uptheta}, \mathbf{p}}{\max}\frac{n\ln {s}_{\mathrm{est}}^2+\ln \left[\det \left(\boldsymbol{R}\right)\right]}{2}. $$

(8)

Predictions from the derived meta-model are then generated using the best linear unbiased predictor (BLUP, Santner et al. 2018):

$$ \mathcal{F}\left(\boldsymbol{x}\right)={\beta}_{\mathrm{est}}+{\boldsymbol{r}}^{\prime}\left(\boldsymbol{x}\right){\boldsymbol{R}}^{-1}\left(\boldsymbol{y}-\mathbf{1}{\beta}_{\mathrm{est}}\right) $$

(9)

where r(x) = [R(x, x₁), ⋯, R(x, x_n)]^′ with R(x_i, x_j) given by $R\left({\boldsymbol{x}}_{\mathbf{i}},{\boldsymbol{x}}_{\mathbf{j}}\right)={\prod}_{k=1}^m{e}^{-{\theta}_{\mathrm{k}}{\left({x}_{\mathrm{i},\mathrm{k}}-{x}_{\mathrm{j},\mathrm{k}}\right)}^{p_{\mathrm{k}}}}$. The BLUP is a predictor with pleasing properties, including that it passes through the design points and provides a smooth interpolation between the points when p_k = 2. Far from the points (depending on the estimated correlation parameters, θ), the BLUP returns to the regression model. In our examples, this means that the model returns to a constant value.

2.3 Efficient global optimization and variants

The method proposed by ur Rehman and Langelaar (2017) to solve (1) is called robust EGO. Because the worst possible environmental conditions are not precisely known at any iteration for a given set of control variables, x_c, the current best estimate for the objective value, ${\hat{u}}_{\mathrm{t}}$, is needed. Also, the estimated worst possible objective value for a given set of environmental variables, x_e, is needed ${\hat{l}}_{\mathrm{t}}$. Formulas to estimate these quantities given the meta-models ${\mathcal{F}}_{\mathrm{f}}$ and ${\mathcal{G}}_{\mathrm{j}}$ are

$$ {\hat{u}}_{\mathrm{t}}=\left.\underset{{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}}}{\min }{\mathcal{F}}_{\mathrm{f}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)\right|{\mathcal{G}}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)\le 0\forall j=1,\cdots, q,{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}} $$

(10)

and

$$ {\hat{l}}_{\mathrm{t}}=\left.\underset{{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}}{\max }{\mathcal{F}}_{\mathrm{f}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)\right|{\mathcal{G}}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)\le 0\forall j=1,\cdots, q,{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}. $$

(11)

At iteration t, two quantities are successively estimated corresponding to the environmental conditions to study, ${\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast }$, and control conditions to study, ${\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast }$. Intermediate quantities are the improvement function, I_c(x_c) at the point x_c, which is defined as ${I}_{\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)=\max \left({\hat{u}}_{\mathrm{t}}-{\mathcal{F}}_{\mathrm{f}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)\right)$ and the constraint violation function, V_{j, c}(x_c) at the point x_c, which is defined as ${V}_{\mathrm{j},\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)=\max \left({\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{e}}\right)-0\right),j=1,\cdots, q$. Similar definitions hold for I_e(x_e) and V_{j, e}(x_e), j = 1, ⋯, q. The so-called worst-case Kriging functions are ${\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)={\mathcal{F}}_{\mathrm{f}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)$, ${\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{c}}\right)={\mathcal{G}}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)\forall j=1,\cdots, q$, ${\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)={\mathcal{F}}_{\mathrm{f}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right),{\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{e}}\right)={\mathcal{G}}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)\forall j=1,\cdots, q.$ Then, the intermediate quantities are

$$ E\left[{I}_{\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)\right]=-\left({\hat{u}}_{\mathrm{t}}-{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)\right)\Phi \left(\frac{{\hat{u}}_{\mathrm{t}}-{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)}{s\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)}\right)-s\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)\phi \left(\frac{{\hat{u}}_{\mathrm{t}}-{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)}{s\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)}\right) $$

(12)

and

$$ E\left[{V}_{\mathrm{j},\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)\right]=\left({\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{c}}\right)-0\right)\Phi \left(\frac{{\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{c}}\right)-0}{s_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)}\right)+{s}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)\phi \left(\frac{{\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{c}}\right)-0}{s_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right)}\right). $$

$$ E\left[{I}_{\mathrm{e}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)\right]=\left({\hat{l}}_{\mathrm{t}}-{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)\right)\Phi \left(\frac{{\hat{l}}_{\mathrm{t}}-{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)}{s\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)}\right)+s\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)\phi \left(\frac{{\hat{l}}_{\mathrm{t}}-{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)}{s\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)}\right) $$

(13)

and

$$ E\left[{V}_{\mathrm{j},\mathrm{e}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)\right]=\left({\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{e}}\right)-0\right)\Phi \left(\frac{{\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{e}}\right)-0}{s_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)}\right)+{s}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)\phi \left(\frac{{\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{e}}\right)-0}{s_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right)}\right). $$

The two expected improvement optimizations for infill candidate selections are

$$ {\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast }=\underset{{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}}}{\mathrm{argmin}}E{I}_{\mathrm{c}\mathrm{g}}=\underset{{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_c}{\mathrm{argmin}}\left\{\left.E\left[{I}_{\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)\right]\right|E\left[{V}_{\mathrm{j},\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)\right]\right\}. $$

(14)

and

$$ {\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast }=\underset{{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}}{\mathrm{argmax}}E{I}_{\mathrm{e}\mathrm{g}}=\underset{{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}}{\mathrm{argmax}}\left\{\left.E\left[{I}_{\mathrm{e}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)\right]\right|E\left[{V}_{\mathrm{j},\mathrm{e}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)\right]\right\}. $$

(15)

With these definitions, the robust EGO from ur Rehman and Langelaar 2017 is defined in Algorithm 1. Therefore, the method progressively identifies undesirable environmental conditions and desirable controllable parameters. The stopping conditions may relate to convergence, termination of a computational budget (as in our numerical examples), or the attainment of quality objectives.

Note that Algorithm 1 reduces to superEGO from Sasena et al. (2002) if $\left|{\mathbbm{X}}_{\mathrm{e}}\right|=1$ and the environmental variables are fixed. Then, step 6 is trivial, and step 7 is the constrained EI optimization. Also, if there are no constraints, i.e., q = 0, then (12) reduces to the standard unconstrained EI formula (Jones et al. 1998). The reduction to standard unconstrained EGO is not exact because EGO originally used the best-obtained prediction value for ${\hat{r}}_{\upkappa}$ rather than attempting to predict that value using the GSP model in (9). Here, we seek a further generalization of Algorithm 1 to include a tabu list for the infill optimization.

2.4 Tabu search methods

Tabu search (TS) is an evolving topic, but the core method elements persist (Glover 1986, 1989, 1990; Chelouah and Patrick 2000). An initial solution is generated, perhaps using a pre-procedure. Then, candidate solutions of interest are identified. The restrictions from an updating list of off-limits or “tabu” solutions are considered in selecting which candidate is to be sampled. If the sampled candidate offers an improvement, then it becomes the current best solution. Stopping criteria are checked. If the criteria are not met, then the restriction list is potentially updated, adding or removing items depending on the specific rules chosen.

Note that this structure is already similar to EGO methods. Both methods identify desirable candidates and take single steps, preserving their best solutions so far. The infill optimizations in EGO promise to provide a desirable way to identify and screen candidates. The major difference is the application of tabu lists during candidate screening. This is the difference that we seek to address in our proposed methods.

2.5 The DIRECT method

DIRECT is a derivative-free method for constrained (or unconstrained), non-linear optimization (Jones 2009b). DIRECT works by using Lipschitz theory to divide up the design space into hyper-rectangles. At each iteration, the set of hyper-rectangles most likely to contain good function values are further subdivided.

DIRECT is used by superEGO and tabu EGO to find optimal Kriging model parameters and to solve the infill sampling criterion (ISC) sub-optimization problem.

3 Proposed methods

As mentioned previously, both EGO and tabu searches share a common structure of initialization followed by single steps leading to evaluations and iteration. A key difference for our proposed tabu EGO methods compared with other EGO methods relates to the infill optimizations being restricted by a list of “tabu” solutions. As for ordinary EGO, the expected improvement functions are successively optimized to obtain the corresponding environmental conditions, ${\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast }$, and control conditions, ${\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast }$. However, the closest relevant point, ${\boldsymbol{c}}_{\mathrm{t}}^{\ast}\left({\boldsymbol{x}}_{\mathrm{c}}\right)$ (which will be written as ${\boldsymbol{c}}_{\mathrm{t}}^{\ast }$ for simplification), on the tabu list is considered in a penalty term involving weights μ₁ and closeness ε as follows:

$$ {\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast }=\underset{{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}}}{\mathrm{argmin}}E{I}_{\mathrm{c}\mathrm{g}}=\underset{{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}}}{\mathrm{argmin}}\left\{\left.E\left[{I}_{\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)\right]\right|E\left[{V}_{\mathrm{j},\mathrm{c}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)\right]+{\mu}_1\left(\varepsilon -\min \left(d\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{c}}_{\mathrm{t}}^{\ast}\right),\varepsilon \right)\right)\right\}. $$

(16)

where $d\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{c}}_{\mathrm{t}}^{\ast}\right)=\sqrt{\sum_{i=1}^N{\left({\boldsymbol{x}}_{\mathrm{c}}-{\boldsymbol{c}}_{\mathrm{t},\mathrm{i}}\right)}^2},{\boldsymbol{c}}_{\mathrm{t}}\in {\mathbbm{X}}_{\mathrm{t},\mathrm{c}}$.

$$ {\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)={\mathcal{F}}_{\mathrm{f}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right);{\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{c}}\right)={\mathcal{G}}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast}\right),\forall j=1,\cdots, q,{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}, $$

${\mu}_1=\frac{{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{c}}\right)}{\varepsilon },{\mathbbm{X}}_{\mathrm{t},\mathrm{c}}$ :

is the tabu list for the control variables.

Similarly, for the environmental variable optimization phase, we have

$$ {\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast }=\underset{{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}}{\mathrm{argmax}}E{I}_{\mathrm{e}\mathrm{g}}=\underset{{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}}{\mathrm{argmax}}\left\{\left.E\left[{I}_{\mathrm{e}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)\right]\right|E\left[{V}_{\mathrm{j},\mathrm{e}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)\right]+{\mu}_2\left(\varepsilon -\min \left(d\left({\boldsymbol{x}}_{\mathrm{e}},{\boldsymbol{e}}_{\mathrm{t}}^{\ast}\right),\varepsilon \right)\right)\right\}. $$

(17)

where $d\left({\boldsymbol{x}}_{\mathrm{e}},{\boldsymbol{e}}_{\mathrm{t}}\right)=\sqrt{\sum_{i=1}^N{\left({\boldsymbol{x}}_{\mathrm{e}}-{\boldsymbol{e}}_{\mathrm{t},\mathrm{i}}\right)}^2},{\boldsymbol{e}}_{\mathrm{t}}\in {\mathbbm{X}}_{\mathrm{t},\mathrm{e}}.$

$$ {\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)={\mathcal{F}}_{\mathrm{f}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right);{\hat{g}}_{\mathrm{j},\max}\left({\boldsymbol{x}}_{\mathrm{e}}\right)={\mathcal{G}}_{\mathrm{j}}\left({\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast },{\boldsymbol{x}}_{\mathrm{e}}\right),\forall j=1,\cdots, q,{\boldsymbol{x}}_{\mathrm{c}}\in {\mathbbm{X}}_{\mathrm{c}},{\boldsymbol{x}}_{\mathrm{e}}\in {\mathbbm{X}}_{\mathrm{e}}, $$

${\mu}_2=\frac{{\hat{f}}_{\mathrm{max}}\left({\boldsymbol{x}}_{\mathrm{e}}\right)}{\varepsilon },{\mathbbm{X}}_{\mathrm{t},\mathrm{e}}$ :

is the tabu list for the environmental variables.

Equations (16) and (17) are simple generalizations of the previous equations with the penalties included for points being similar to previous points. In terms of these equations, Algorithm 2 provides a detailed description of the proposed tabu EGO method for unconstrained, simple constrained, or robust design problems. In our examples, we use $\varepsilon =\underset{{\mathbf{x}}_{\mathrm{i}},{\mathbf{x}}_{\mathrm{j}}\in \chi }{\min}\left|{\mathbf{x}}_{\mathrm{i}}-{\mathbf{x}}_{\mathrm{j}}\right|$, i ≠ j, 1 ≤ , i, j ≤ N, the minimum possible distance between the points in the tabu list, for our tuning parameter. Random Latin hypercubes with n = 11d runs are applied by default.

It is noted that your algorithm only uses points at which the black-box function has been evaluated for purposes of estimating the optimum which is consistent with superEGO algorithm. Therefore, tabu EGO differs from other forms of EGO, including superEGO (Sasena et al. 2002) and robust EGO (ur Rehman and Langelaar 2017):

• A tabu list is included within the infill optimizations to screen candidates for novelty.

• Specifically, our penalty is either μ₁ε/μ₂ε, or a value that linearly decreases to zero depending on the sub-optimization problem as points differ from those on the tabu list.

• In addition, our method carefully updates and applies the apparent best solution, ${\boldsymbol{x}}_{\mathrm{c},\mathrm{t}}^{\ast \ast }$, and worst environmental condition, ${\boldsymbol{x}}_{\mathrm{e},\mathrm{t}}^{\ast \ast }$ in lines (12) and (13). This does not directly relate to the tabu search aspects, but we have found that it improves the method performance.

4 Numerical comparisons

4.1 Illustrations of tabu EGO

We illustrate the behavior of tabu EGO and its comparison to the traditional EGO method with the Ackley, Rastrigin, and G06 functions. Figure 1 shows the 3D and contour plots of Ackley, Rastrigin, and G06 benchmark functions. Both Ackley and Rastrigin functions pose a risk for optimization algorithms, particularly iterative algorithm algorithms, to be trapped in one of its many local minima. Note in Fig. 2 that, by employing the tabu search method, tabu EGO converges very quickly to the optimum with high accuracy (0.0046) for Ackley function at cycle 20, while superEGO obtained a minimum of 1.5245 when the maximum function evaluation reached. In addition, if we let tabu EGO to continue with the exploration, the meta-model quality is continuously improved.

Fig. 1

3D and contour plots of Ackley, Rastrigin, and G06 benchmark functions. a Ackley, b Rastrigin, (c.1) G06 Objective function, (c.2) G06 Constraints function

Fig. 2

Evolution of approximation of Ackley function (2 variables) with tabu EGO and superEGO. a Cycle 01 – tabuEGO, b Cycle 02 – tabuEGO, c Cycle 03 – tabuEGO, d Cycle 06 – tabuEGO, e Cycle 20 – tabuEGO, f Cycle 01 – superEGO, g Cycle 02 – superEGO, h Cycle 03 – superEGO, i Cycle 06 – superEGO, j Cycle 20 – superEGO

We observed the same performance of tabu EGO for other functions as well. For instance is the evolution of the Rastrigin and G06 function in Figs. 3 and 4. In those cases, tabu EGO has found the optimum points within high accuracy at cycle 26 (0.0258) and cycle 27 (−6.36E+03) compared to superEGO.

Fig. 3

Evolution of approximation of Rastrigin function (2 variables) with tabu EGO and superEGO. a Cycle 01 – tabuEGO, b Cycle 02 – tabuEGO, c Cycle 16 – tabuEGO, d Cycle 20 – tabuEGO, e Cycle 26 – tabuEGO, f Cycle 01 – superEGO, g Cycle 02 – superEGO, h Cycle 16 – superEGO, i Cycle 20 – superEGO, j Cycle 26 – superEGO

Fig. 4

Evolution of approximation of G06 function (2 variables) with tabu EGO and superEGO. a Cycle 01 – tabuEGO, b Cycle 02 – tabuEGO, c Cycle 04 – tabuEGO, d Cycle 06 – tabuEGO, e Cycle 27 – tabuEGO, f Cycle 01 – superEGO, g Cycle 02 – superEGO, h Cycle 04 – superEGO, i Cycle 06 – superEGO, j Cycle 27 – superEGO

Based on these preliminary results with unconstrained and constrained functions, we can conclude that tabu EGO has a good performance on driving EGO algorithm, with a single infill point per cycle. Note as more infill points are added per cycle, the faster is the convergence to the global optimum (exploitation), and the quality improvement (predictability) of the meta-model is visioned. Future work could improve the convergence rate of tabu EGO by including multiple infill points method.

4.2 Comparative study

The test problems in Table 1 include the Ackley, Griewank, Rastrigin, Eggholder, Schaffer, Rosenbrock, Mishra’s Bird function, and other standard global optimization benchmarks (Ma and Simon 2017). We also adapted the test functions G04, G09, and G09 from standard global optimization benchmarks (Ma and Simon 2017) to the robust constrained problem by setting controllable and environmental variables. Therefore, problems 1–5 are unconstrained, problems 6–10 are simply constrained, and problems 11–13 are robust design problems. The feasibility ratio of the constrained problems is generally small such that it is challenging for black-box methods to find optimal or even feasible solutions.

Table 1 Test problems for the numerical comparisons

We used the same n = 11d runs from a Latin hypercube for all EGO methods in each test problem. As noted previously, the penalty parameter $\varepsilon =\underset{{\mathbf{x}}_{\mathrm{i}},{\mathbf{x}}_{\mathrm{j}}\in \chi }{\min}\left|{\mathbf{x}}_{\mathrm{i}}-{\mathbf{x}}_{\mathrm{j}}\right|$, i ≠ j, 1 ≤ , i, j ≤ N, was applied for tabu EGO implementations.

For the robust design problems (7–9), only robust EGO offers a valid peer method. Therefore, we only compare these results with robust EGO results. For the comparison, the stopping criterion for all methods was a fixed budget of runs. This is an excellent way to simulate engineering applications restricted by expensive simulation (e.g., FEA, CFD, and thermal simulation in additive manufacturing). We permitted n = 50 evaluations for test problems 1–6, n = 100 evaluations for test problems 7–8, and n = 150 evaluations for test problem 9.

Tables 2 and 3 show the resulting solutions of mean, best, and standard deviation for each method and test problem. The best results are marked in bold. All the test problems are repeated 20 times with different DOE seeds. The sample means and standard deviations for comparison are provided. The DIRECT method does not require any experimental design or other random inputs, so the standard deviation is not fitted for this case.

Table 2 Numerical test results for solutions after 50 evaluations for test problems 1–6. The responses and design variables are dimensionless except for problem 10. Problem 10 has outputs in centimeters³ and inputs in centimeters

Table 3 Numerical test results for solutions after 100 evaluations for test problems 7–8, and 150 evaluations for test problem 9. The responses and design variables are dimensionless

In ten of the thirteen cases, tabu EGO obtains the best mean solution. For all the cases in which it does not, fmincon and superEGO get a better solution. In terms of best results over ten different runs, the tabu EGO algorithm wins in eight of the thirteen cases. Also, for the cases it does not, fmincon and TPE obtain a better one. The success rate (SR) of each algorithm for every test function is 1, except for test problems #7 and #13. For test problem #7, both tabu EGO and superEGO with constant regression got a 0.9 SR while superEGO with first-order regression got a 0.95 SR. This also suggests that the Kriging optimization method with higher-order regression could increase its success rate and algorithm performance (Forrester et al. 2006). However, except for test functions #2 and #9, tabu EGO tends to achieve superior results compared with the higher-order regression version of EGO. For test problem #13, the SR is 0.85 for robust EGO while SR is 1 for tabu EGO, which also implies tabu EGO has the potential of improving success rate by decrease the probability of returning to points in the tabu list.

Figure 5 presents the boxplots of the optimization results for twenty experimental designs for tabu EGO comparison with superEGO for the Ackley, Griewank, Rastrgin, and G06 test functions. Note that as the objective function is minimized as the function optimization cycles evolve, the dispersion is comparatively smaller in tabu EGO than superEGO.

Fig. 5

Comparison of the convergence of tabu EGO (left boxplots) vs. superEGO (right boxplots), over 10 different initial DOE in each case for the functions Ackley, Griewank, Rastrigin, and G06. a Ackley, tabuEGO, b Griewank, tabuEGO, c Rastrigin, tabuEGO, d G06, tabuEGO, e Ackley, superEGO, f Griewank, superEGO, g Rastrigin, superEGO, h G06, superEGO

In the same direction as the results presented by Viana et al. (2013), we found that by using tabu EGO with a penalty added in expected improvement function, a reduction in the dispersion of the results (minimum of the objective function) can be achieved as long as the optimization cycles evolve. For the Ackley case and Griewank case, the dispersion tends higher for tabu EGO than superEGO for the first 1–2 iterations. However, the dispersion for tabu EGO will be lower after 4 iterations for Ackley case and 3 iterations for Griewank case than superEGO as the algorithm evolves. This trend is more distinct for Griewank case than Ackley which maintain a slightly better dispersion from iterations 10–28 for tabu EGO than superEGO. For the Rastrigin and G06 function, the dispersion is similar for both tabu EGO and superEGO algorithm; however, the algorithm gets a better average result after 27 iterations for tabu EGO.

Figure 6 a‑c present a comparison among tabu EGO and superEGO for Ackley, Griewank, and G06 functions. For both cases, the superEGO algorithm appears to outperform the tabu EGO algorithm except at cycle 23 for Ackley and Griewank function and the very last point for G06 function. Overall, the final performance of tabu EGO is better over all the alternative methods. For both cases, tabu EGO was faster in convergence rate than superEGO.

Fig. 6

Comparison of tabu EGO vs. other alternatives on the averaged results (a‑c) and level of improvement (d‑f) in each iteration. a Ackley, b Griewank, c G06, d Ackley, e Griewank, f G06

In order to compare the level of improvement (L_imp) vs. optimization cycles, for all test problems, it was considered ${f}_{\mathrm{eval}}^{\mathrm{max}}$= 50. In this case, L_imp is calculated for each cycle k as

$$ {L}_{\mathrm{imp}}=100\%\times \left|\frac{y_{\mathrm{min}}^k-{y}_{\mathrm{min}}^0}{y_{\mathrm{min}}^{\mathrm{exact}}-{y}_{\mathrm{min}}^0}\right| $$

(18)

where ${y}_{\mathrm{min}}^0$ is the minimum for the initial sample, ${y}_{\mathrm{min}}^k$ is the minimum value at cycle k, and ${y}_{\mathrm{min}}^{\mathrm{exact}}$ is the exact minimum value. Figure 6 d‑f are to compare tabu EGO and superEGO in terms of computational costs, measured by the number of optimization cycles (function evaluations) required for the same level of improvement on the objective function at each optimization cycle.

As shown in the curves of Fig. 6d‑f, we can observe that for Ackley and Griewank at the beginning of the optimization cycles, superEGO has lower cost in terms of the number of function evaluations than tabu EGO for the same level of improvement, but at some point (e.g., around 91% for Ackley and 95% for Griewank), the situation is more favorable to tabu EGO. In the case of the G06 function, the computational cost of both methods is quite similar before 55% of L_imp while tabu EGO outperforms superEGO when L_imp is around 67%. These results confirm the fact that tabu EGO, in general, is beneficial in terms of delivering results in reasonable processing time.

Note that additional experimental work is done on the effect of the initial sample size for the algorithm’s results, and the results are summarized in Table 4. The results indicated that the performance of the tabu EGO does not always enhance as the number of initial samples increases. Specifically, the algorithm got its best results for problem #2 when n = 8d, problem #3 when n = 8d, problem #4 when n = 10d, and problem #6 when n = 16d. For problems #1 and #5, the algorithm results are optimal when n = 11d. However, the performance of tabu EGO is not monotonously increased as the initial sample size increased those two cases, which obtain their second better results for n = 6d (problem #1) and n = 8d (problem #6).

Table 4 Results of tabu EGO for test functions #1‑#6 based on different LHC design variables

By changing the stopping criterion to relative error $E=\left|\frac{{\hat{f}}_{\mathrm{min}}-{f}_{\mathrm{min}}}{f_{\mathrm{min}\mathrm{s}}}\right|$ and set E < 0.01 for tabu EGO, we can compare the results of G06, G08, and three-bar truss function to the results from eDIRECT-C method (Liu et al. 2017). It can see that the tabu EGO has the potential of saving function runs as suggested by G08 function, which saves more than 50 runs to get a result with an error around 0.01(Table 5). For the three-bar truss case, the algorithm requires slightly large function runs than eDIRECT-C but better than all the other methods while maintaining a high level of accuracy. However, for G06 test function, the result from tabu EGO got stuck by a local minimum, meaning that tabu EGO has the threat of preventing the algorithm from finding the exact minimum. This issue will be discussed in detail in Section 6.

Table 5 Simple constrained comparison based on a 1% stopping criterion. In the table, f_min is the minimum objective value. The average number of evaluations and the success rate (SR) are estimated using 10 problem instances

5 Additive manufacturing case studies

Additive manufacturing (AM) or 3D printing has become one of the most promising commercial manufacturing techniques. Benefits of AM include delivery savings as parts are made on-site, lower environmental wastes with less warehousing, and (in some cases) improved product quality and performance. The principal barriers of AM include cost, speed, quality, range of materials, and size limitations (Frazier 2014). Here, we focus on additive manufacturing process design with the objective of reducing costs and increasing the speed with quality constraints.

For our case studies, the Green’s function thermal simulation method is used for evaluating the part quality constraints at different points in the X-Y space (Schwalbach et al. 2019). The thermal simulations identify a lattice of source and measurement points and estimate the temperature histories. The parameter T₀ is the initial temperature, σ is the physical size over which the energy is deposited, τ_i is the actual power deposit time, p_i is the laser power at point i, ρ is the power (Ti-6Al-4 V) density, and α is the thermal diffusivity. The temperature field is expressed by

$$ T\left({r}_{\mathrm{j}},t\right)={T}_0+{\sum}_i^N{C}_{\mathrm{i}}\Theta \left(t-{\tau}_{\mathrm{i}}\right){\lambda}_{\mathrm{i}}^{-3/2}{\mathrm{e}}^{\left(-\frac{R_{\mathrm{i}\mathrm{j}}^2}{2{\lambda}_{\mathrm{i}}}\right)}. $$

(19)

where ${C}_{\mathrm{i}}=\frac{p_{\mathrm{i}}\Delta t}{\rho {c}_{\mathrm{p}}\sqrt{2}{\pi}^{\frac{3}{2}}},{\lambda}_{\mathrm{i}}={\sigma}^2+2\alpha \left(t-{\tau}_{\mathrm{i}}\right),{R}_{\mathrm{i}\mathrm{j}}=\left|{\overrightarrow{r}}_{\mathrm{j}}-{\overrightarrow{r}}_{\mathrm{i}}\right|=\sqrt{x_{\mathrm{i}\mathrm{j}}^2+{y}_{\mathrm{i}\mathrm{j}}^2+{z}_{\mathrm{i}\mathrm{j}}^2},{\overrightarrow{r}}_{\mathrm{i}}=\left\langle {x}_{\mathrm{i},}{y}_{\mathrm{i}},{z}_{\mathrm{i}}\right\rangle, {\overrightarrow{r}}_{\mathrm{j}}=\left\langle {x}_{\mathrm{j},}{y}_{\mathrm{j}},{z}_{\mathrm{j}}\right\rangle$, and $\alpha =\frac{\kappa }{\rho {c}_{\mathrm{p}}}$.

Figure 7 shows the thermal history at an arbitrary point in the X-Y space for a given layer and scan pattern. The temperature reaches a maximum when the laser is closest to the point.

Fig. 7

The thermal temperature of a discrete point changes with time. The horizontal line shows the melting temperature of Ti-6Al-4 V in °C

When the thermal temperature is estimated as the function time, two quality measures can be calculated: (1) times molten n_m, i.e., the number of times a discrete point is melted during the laser scanning process and (2) molten duration t_m, i.e., the total time a discrete point melted during the laser scanning process.

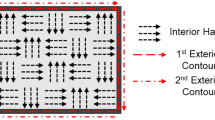
The thermal simulations based on (18) differ from many types of finite element methods in that there is a considerable incremental cost to obtaining results from each point in X-Y space. Finite element methods (FEM) generally provide results across spatial points such as latent stresses or part distortion values, making it relatively easy to identify the worst points on the parts involved. In our simulations, however, the most difficult points on the part must be identified using a spatial optimization. Therefore, (19) involves speeding up the laser path as shown in Fig. 8. The parameters in (19) determine the raster pattern of the beam as indicated in Fig. 9.

Fig. 8

Hypothetical laser path in additive manufacturing

Fig. 9

Standard scan pattern for a rectangular coupon

In our study, we consider two different layer geometries. The first is a rectangular grid indicated in Fig. 9. The second is shown in Fig. 10b.

Fig. 10

a 3D airfoil and b 2D cross section of N-10 with constraints defining the boundary

For the airfoil case, additional constraints defining airfoil boundaries (${A}_{\mathrm{j}}x+{B}_{\mathrm{j}}y+{C}_{\mathrm{j}}\le 0\kern0.5em \forall \mathrm{j}=1,\cdots, N$) are included in the problem constraints. However, no meta-models are fitted on these boundary constraints since its functions are known and given.

With these definitions, the additive process design problem can be written as

$$ {\displaystyle \begin{array}{c}\underset{p,v,{h}_{\mathrm{s}}}{\max }v{h}_{\mathrm{s}}\\ {}\begin{array}{c}s.t.:\underset{x_1,{x}_2}{\min }{n}_{\mathrm{m}}\left(p,v,{h}_{\mathrm{s}},{x}_1,{x}_2\right)\ge 3,\\ {}\underset{x_1,{x}_2}{\min }{t}_{\mathrm{m}}\left(p,v,{h}_{\mathrm{s}},{x}_1,{x}_2\right)\ge 0.001\\ {}\underset{x_1,{x}_2}{\max }{t}_{\mathrm{m}}\left(p,v,{h}_{\mathrm{s}},{x}_1,{x}_2\right)\le 0.02\end{array}\end{array}} $$

(20)

where p is the laser scanning power, v is the laser scanning velocity, and h_s is the hatch spacing of the scanning vector. Therefore, the objective relates to the square of the overall completion rate.

For both cases, the objectives are maximization of vh_s, which can be defined as the laser printing “efficiency”. Similarly, we adapted the other methods where a grid of 16 or 31 environmental variable points was applied so that the robust problem was approximated as a simple constrained problem with constraints for each set of environmental conditions. The results from the rectangular and airfoil cases show that our method offers a promising process parameter combination while satisfying thermal quality constraints. The benefits of the second problem are quite significant.

Figure 11 and Table 6 show the results from a single replication (for time reasons) of the alternative method solution values plotted against iteration. Compared with robust EGO, tabu EGO produces a solution with almost double the velocity × hatch spacing or the square root of two times the production rate (41% faster). Such benefits could make a significant difference in making AM viable for practical problems. Note that we are plotting the proven best solution and not the predicted best, which makes our plot relatively constant (e.g., compared with Ferreira and Serpa 2018).

Fig. 11

f_best vs. iteration of tabu EGO including all alternative methods for 2 application cases. Alternative methods include tabu EGO and superEGO. a and b The comparison plots for applications 1 and 2, respectively. In these problems, the objective is maximization

Table 6 Case study-based comparison of solutions after 100 evaluations for application 1 and 150 evaluations for application 2 (the objectives are maximization)

6 Discussion

We propose the incorporation of tabu list penalties in infill optimization to improve the computational performance of EGO methods for a variety of black-box optimization problems. This approach decreases the possibility that experimental effort is directed at or near previous points in the decision or environmental variable spaces, with an additional sub-step to identify and store the currently relevant conditions. This frees up evaluations to search new points resulting in faster convergence and improved solution quality. To comprehensively evaluate the proposed methods, we compare the performance of the proposed tabu EGO with alternatives, including DIRECT, superEGO, robust EGO, fmincon, TPE and for unconstrained, constrained, and robust constrained problems, selecting the appropriate method alternative for each type of problem.

The results show the generally better performance of tabu EGO in terms of convergence speed and solution quality, given a fixed run size, for the majority of our test problems. For all the tests for which tabu EGO did not perform the best, one other solution method (TPE, fmincon) provided better results. Our applications to thermal-based optimization of additive manufacturing suggest that the benefits from tabu EGO could be quite relevant practical. Tabu EGO produces solutions in one case that produces (almost) 41% improved speed of part production compared with robust EGO. Note that the objective function used is proportional to the square of the speed.

Note that one of the features of the original EGO algorithm is its ability to locate all the minima when there are multiple minima. One concern for the tabu EGO algorithm is that the penalty term will prohibit the algorithm from sampling near these minimums. Thus, it might never discover there are multiple minima. However, with tabu EGO, it is possible to move within the current epsilon value of another point. Such moves are merely penalized. Both the penalty and ε are dynamic. This explains why our new approach often results in an ongoing reduction in the tabu list ε value. More importantly, tabu EGO converges for all instances and all test functions except for test function #4 (G06). Our performance is superior to all the alternatives that we consider except on test function #4. Note that superEGO repeatedly fails to converge on test function #2 (Table 7). This occurs presumably because the failure of the Kriging model based on empirical estimation of the smoothness parameter can cause convergence issues that are mitigated through a more widespread search.

Table 7 Comparison of solutions of tabu EGO and superEGO for Griewank and G08 functions over 10 different DoEs

There are several opportunities for future research. First, tabu EGO can be extended to address noisy optimization problems (e.g., Huang et al. 2006a) and multi-objective optimization problems (e.g., Li et al. 2008 or for variance or quality objectives and exploration Allen et al. 2018). Also, both single objective and multi-objective problems could employ techniques such as parallels computing for speed and efficiency improvement. Second, multiple fidelity optimization (see Huang and Allen 2005; Huang et al. 2006b) and problems involving two or more types of simulation can be studied, e.g., thermal and finite element method (FEM) simulations of additive manufacturing. Third, more elements of the standard tabu search structure can be explicitly incorporated to extend tabu EGO. These elements include short and long-term tabu lists, expiration conditions for points on the tabu list, candidate lists, and filter strategies. We have argued that the EI function approaches are likely to result in better performance than the local search strategies common in tabu searches. However, this can be studied empirically. Fourth, the additive manufacturing application can be explored more thoroughly, including experimental data and addressing layer interactions and part structure ending conditions.