Abstract
By using topology optimization, we consider the problem of designing a passive acoustic device that allows for one-way flow of sound waves; such a device is often colloquially referred to as an acoustic diode. The Helmholtz equation is used to model the time harmonic linear wave propagation together with a Dirichlet-to-Neumann (DtN) type boundary condition, and the finite element method is used for discretization. The objective of this study is to maximize the wave propagation in one direction (from left to right) and minimize the wave propagation in the reverse direction (from right to left) for planar incoming waves. The method of moving asymptotes (MMA) solves the optimization problem, and a continuation approach is used for the penalizing intermediate design variables. The results for the optimized waveguide show that more than 99.8% of the power of planar incoming waves get transmitted from left to right while less than 0.3% gets transmitted in the reverse direction for planar incoming waves in the specified frequency range. Since a true diode is a non-reciprocal device and here we used a linear acoustic wave model, which is basically reciprocal, we discuss details about how it appears to be possible to obtain a one-way waveguiding effect using this linear model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Like an electric diode, which only allows current to flow in one direction, an acoustic diode only allows acoustic waves to propagate in one direction. The magnificent impact of the invention of the electric diode on human life inspired a lot of research work trying to control other forms of energy in the same way. Since ultrasound is widely used in biomedical imaging and non-destructive diagnostics, recently, the concept of acoustic diodes has raised interest among researchers in physics and engineering. One way to get directional acoustic wave propagation in a waveguide, is to use nonlinear materials to break the reciprocity in the transmission (Liang et al. 2009, 2010; Popa and Cummer 2014; Grinberg et al. 2018; Darabi et al. 2019; Li et al. 2019, 2020). This method, however, suffers from low efficiency due to considerable losses in the nonlinear conversion (Chen et al. 2017; Song et al. 2016). It has also other limitations, such as significant alteration and distortion of the frequency content of the transmitted acoustic signal (Grinberg et al. 2018), as well as bandwidth limitations of working frequencies (Zhu et al. 2015b). This motivates the efforts on the investigation of linear and passive acoustic one-way structures, trying to find the design of sound-hard material so that the problem setup works as an acoustic diode (He et al.2011; Li et al. 2012a, 2012b; Zhu et al. 2015a, b; Chen et al. 2017; He and Kang 2018). Here, we use material distribution-based topology optimization to optimize the design of a passive acoustic one-way waveguide.
Topology optimization is one of the most general and effective design optimization methods, where the aim is to find the best layout of material in a design domain such that the objective function is maximized (or minimized). For material distribution-based topology optimization, we divide the design domain into elements, and for each element, the optimization algorithm decides whether it will hold material or not. This method was first introduced for structural mechanics using the homogenization method (Bendsøe and Kikuchi 1988). Since then, researchers have adopted this method in many fields and applications, such as acoustics (Wadbro and Berggren 2006; Dühring et al. 2008; Lee and Kim 2009), electromagnetics (Hassan et al. 2014; Aage and Johansen 2017), optics (Cox and Dobson 1999; Jensen and Sigmund 2011; Mori et al. 2019), and fluid mechanics (Borrvall and Petersson 2002). A summary of early research works on material distribution-based topology optimization can be found in the monograph by Bendsøe and Sigmund (2003). Here, we introduce a novel optimized design of a directionally selective device that provides a one-way waveguiding effect, for the specified frequency range.
Besides the research content, this paper also has an educational message, which will be clear to the reader before the end of the article.
For now, in order not to spoil the intended message, we simply ask the reader to (just as usual) have an open and critical mindset. Moreover, the structure of the presentation in this article is non-standard; the presentation is structured as follows. Sections 2 and 3 provide a brief explanation of the problem description and also present the results for the optimized design. The purpose in these two sections is to give an understanding of the problem and the methods we used to solve it without getting into details. At the end of Section 3, we introduce and discuss conceptual issues regarding the problem setup. The remainder of the paper is spent on resolving these issues. More precisely, Section 4 provides important aspects of the resulting wave propagation and revisits the optimization problem formulation. Sections 5 and 6 contain results in more detail and a discussion on the essential issues mentioned above. Finally, details about the filtering algorithm used in the topology optimization are provided in the Appendix.
2 Brief problem description
Consider the axi-symmetric setup illustrated in Fig. 1. This setup comprises two semi-infinite waveguides and the gray meshed region ΩD, which we will use as our design domain. Some parts of ΩD may be filled with sound-hard material to make this setup a one-way waveguide. From here on, outgoing waves refer to all waves propagating away from the design domain ΩD and incoming waves refer to all waves propagating toward the design domain ΩD.
Consider the following two cases:
- Case 1 :
-
There is an incoming planar acoustic wave in the left waveguide, propagating towards ΩD.
- Case 2 :
-
There is an incoming planar acoustic wave in the right waveguide propagating towards ΩD.
As illustrated in Fig. 1, we seek a design so that the incoming wave in Case 1 propagates to the other side of the setup, while the incoming wave in Case 2 gets reflected.
2.1 Mathematical model
The wave propagation inside the fluid (air) region of the setup in Fig. 2 is governed by the linear wave equation. By considering time harmonic wave propagation, we assume acoustic pressure P(x,t) = Re{p(x)e−iωt}. This gives us Helmholtz equation for the complex amplitude function p of the acoustic pressure. In cylindrical coordinates, we have:
where the wave number k = ω/c, c is the speed of sound in the fluid, ω is the angular frequency, and \(\hat {{\varOmega }}\) is the fluid (air) region of the setup.
The computational domain, Ω, consists of design domain ΩD and two truncated waveguides. The sound-hard material inside ΩD is defined as Ωs, and the rest of the setup filled with fluid (air) is defined as \(\hat {\varOmega }\). The boundaries consist of axi-symmetric Γsym (dash-dotted line), the sound-hard walls Γs (solid line), and artificial truncated boundaries ΓL and ΓR (dashed lines)
For the computational experiment, we consider following dimensions for the setup. The radius and length of the design region ΩD is rD = 50mm and lD = 50mm, respectively. The radius and length of the waveguides are rW = 30mm and lW = 20mm, respectively.
To deal with the infinite waveguides numerically, we truncate them and use a DtN (Dirichlet-to-Neumann) type perfect absorbing (or non-reflecting) boundary condition on the artificial boundaries ΓL and ΓR, as illustrated in Fig. 2. For a general description of the Dirichlet-to-Neumann boundary condition, we refer the reader to the book by Ihlenburg (1998, p. 63). Hence, the state equation reads:
where gL and gR are the incoming waves from the left and right waveguides, respectively. Here, we consider a planar incoming wave for both case 1 and case 2. The variational formulation for the states (2)–(5) is:
Remark 1
Throughout this paper, we do not write symbols for measure such as \(\mathrm {d}\hat {{\varOmega }}\), dΓR, or dΓL in integrals as long as their omission is not a source of confusion.
To model the distribution of sound-hard material in ΩD (that is, the shape of region Ωs), we define a material indicator function, α. The function α ≡ 0 in Ωs and α ≡ 1 in Ω ∖Ωs. By using this function to extend the integration domain of the first two integrals in problem (6), from \(\hat {{\varOmega }}\) to Ω, we obtain the following problem:
where \({\varOmega } = \hat {\varOmega } \cup {\varOmega }^{\text {s}}\) is the extended domain that contains both the air and solid material. To allow gradient-based optimization, the standard approach in material distribution-based topology optimization is to allow α to take values in the range [0,1].
Remark 2
The model of letting the parameter control the design act directly on the domain integral can at least be traced back to 2006 (Wadbro and Berggren 2006) and has been used in many contributions thereafter. For a pure solid–fluid design, where the fluid is represented by α = 1 and the solid scatterer by α = 𝜖, Kasolis et al. (2015) proved that the error in the complex-pressure field converges linearly in 𝜖 to the solution of the problem with an exactly modeled scatterer.
2.2 Discretization
We use the finite element method to discretize and solve problem (7). To discretize the domain Ω, we use a uniform mesh of square elements, and define a functional space Vh that consists of functions that are continuous and bi-quadratic on each element. We denote the basis functions of Vh by φj, j = 1,2,…,NN, where NN is the number of nodes or degrees of freedom in the finite element approximation. We approximate the complex amplitude function p and the test function q by ph ∈ Vh and qh ∈ Vh, respectively. In addition, we use an element-wise constant function αh to approximate material indicator function α. The discretized version of problem (7) reads:
We define the NN × NN stiffness K and mass M matrices with entries
and also NN × 1 vectors bL and bR with entries
respectively.
Furthermore, we define \(\boldsymbol {\alpha }=\left [\alpha _{1},\alpha _{2},\ldots ,\alpha _{N^{\text {D}}}\right ]^{T}\) that holds the element values of αh, where ND is the number of elements in ΩD, and \(\boldsymbol {p}=\left [p_{1},p_{2},\ldots ,p_{N^{N}}\right ]^{T}\) that holds the nodal values of complex pressure amplitude in Ω. By using the definitions above (8) reads:
where the matrix B corresponds to the Dirichlet-to-Neumann boundary conditions (4) and (5). More details about how to compute matrix B can be found in an earlier article by Wadbro (2014, Appendix A).
2.3 Objective function and optimization problem
The transfer parameter TXY from X to Y is defined as:
where X ∈{L,R} and Y ∈{L,R}, in which L and R denote the left and right waveguides, respectively. Section 4 provides detailed information on how the transfer parameters are evaluated for a given design.
Our goal is to maximize the power transmitted to the right in case 1 and minimize the power transmitted to the left in case 2. Which is to minimize the power at ΓL for both cases, based on conservation of power, whether the incoming wave is from the left or right waveguide. So for case 1, we minimize reflection TLL, and for case 2, we minimize transmission TRL. The objective function can thus be written as:
where Nf is the number of frequencies subject to optimization. So, the optimization problem consists of finding the distribution of sound-hard material in ΩD that minimizes the objective function (13).
3 Results
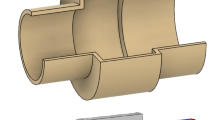
Figure 3 shows the axi-symmetric optimized waveguide, and Fig. 4 is its 3D visualization. For planar incoming waves, this design allows acoustic power to be transmitted from left to right but not from right to left (to within 0.3% of the incident power) with frequencies in the range 8–9 kHz.
Figure 5 shows the transfer parameters as functions of frequency for the optimized design in Fig. 3. The top graph corresponds to case 1, where there is an incoming planar wave at left waveguide, and shows the resulting transmission (TLR) and reflection (TLL) as functions of frequency. This graph shows that throughout the frequency band of interest, the incoming planar wave is transmitted from left to right waveguide and there is essentially no reflection at left waveguide. More precisely, for all integer frequencies in the range 8–9 kHz, TLL < 1.4 × 10− 3, which means that at most 0.2% of the input power is reflected back and thus more than 99.8% of the power is transmitted to the right waveguide. Throughout this paper, by integer frequencies in the range 8–9 kHz, we refer to the frequencies 8000,8001,…,9000Hz. Similarly the bottom graph in Fig. 5 shows the transmission (TRL) and reflection (TRR) as functions of frequency for case 2, when there is an incoming planar wave at right waveguide. In this case for all integer frequencies in the range 8–9 kHz, TRL < 2.8 × 10− 3 which means more than 99.7 % of power is reflected back to the right waveguide and at most 0.3 % of the input power is transmitted to the left waveguide.
The design presented above appears to act as a perfect acoustic diode for the frequency band of interest. However, the observant and critical reader may already have thought about raising the following questions and remarks:
-
What about acoustic reciprocity?
-
The diode is a non-linear device; if so, how and why is it possible to create such a device using a linear model?
The above questions are indeed valid, and we have on purpose withheld some information hoping that the reader would keep a critical mindset. We stress that we have not made any claims that the design in Fig. 3 is an acoustic diode; we stay with the weaker statement that it appears to act as one. We devote the remainder of this paper to describe and detail what we have done to arrive at this result.
4 Detailed problem description
Here, we present details about how our waveguide setup works by including the discussion of modes. In Section 4.1, we will elaborate how to compute these eigenvalues and eigenmodes for the waveguide setup. In Section 4.2, we provide the full optimization problem.
4.1 Wave propagation in a circular duct
Consider semi-infinite waveguides on the left and right sides of ΩD, as illustrated in Fig. 1. Assume that the complex pressure amplitude p satisfies Helmholtz (2) and boundary condition (3). Using separation of variable, we write the general solution in the left waveguide as:
and solution in the right waveguide as:
where zL and zR are the positions of z-axis on ΓL and ΓR, the functions fm(r) are the modes at left and right waveguides (in the continuous case, it is well known that the functions fm are so-called Bessel functions), e is the base of the natural logarithm, i is the imaginary unit, and \(A^{\text {L}}_{m}\) and \(B^{\text {L}}_{m}\) are complex constants that determine the amplitude of incoming and outgoing waves, respectively, at the left waveguide. Similarly, \(A^{\text {R}}_{m}\) and \(B^{\text {R}}_{m}\) are complex constants that determine the amplitude of incoming and outgoing waves, respectively, at the right waveguide, and the constants km are the so-called reduced wave numbers.
To obtain a discrete exact radiating boundary condition, we will, instead of using the Bessel functions, use eigenfunctions to a finite element problem on the boundary mesh on ΓL and ΓR.
In short, we solve one-dimensional eigenproblems in the radial direction on ΓL and ΓR. Both these problems are of the form:
(Note that since the radii of the left and right waveguide are the same, we only need to solve one problem. In the text below, Γ refers to either ΓL or ΓR.) To solve the one-dimensional eigenproblem on Γ, we use a restriction of the finite element mesh on Ω to Γ. We let \(V^{h}_{{\varGamma }}\) be the space of functions that are bi-quadratic on each element of Γ. We solve a discrete version of problem (16) to find the M eigenvalues λm and the corresponding eigenfunctions or modes \({f_{m}^{h}} \in V^{h}_{{\varGamma }}\), where m = 0,1,…,M. We assume that the eigenvalues are sorted and the lowest eigenvalue λ0 = 0. Due to orthonormality of modes, we have:
Since the complex amplitude function p satisfies Helmholtz (2) and boundary condition (3), we conclude that the reduced wavenumbers satisfy:
Note that for the wave to propagate, the reduced wave number km must be real, so λm ≤ k2. That is, for a given frequency f, there is only a finite number \({M^{p}_{f}}\) of so-called propagating modes. Waves of modes higher than \({M^{p}_{f}}\) are geometrically evanescent, and any such outgoing mode decays exponentially in the waveguide.
The Dirichlet-to-Neumann type boundary conditions allow us to set the amplitudes Am of the propagating incoming modes and perfectly absorb all outgoing waves. We set the amplitude \(A_{m}^{\text {L}}\) and \(A_{m}^{\text {R}}\) of the incoming wave as
in case 1, and
in case 2.
Having solved governing equation (11), we can compute the outgoing wave amplitudes \(B_{m}^{\text {L}}\) and \(B_{m}^{\text {R}}\). For X ∈{L, R}, it holds that:
where the first equality follows from expression (14) or (15) and the second equality follows from relation (17).
This expression holds for both ΓL and ΓR, so
where the NN × 1 vectors \(\boldsymbol {c}_{m}^{\text {L}}\) and \(\boldsymbol {c}_{m}^{\text {R}}\) have entries
4.2 Objective function with modes
The outgoing waves can be written as a sum over propagating modes, and the power of each of these modes can be monitored, which enables us to achieve a greater control and understanding of the resulting wave propagation. Thus, for X ∈{L,R}, Y ∈{L,R}, and \(i,j\in \{0,1,2,\ldots ,{M_{f}^{p}}\}\), we define the so-called scattering parameters as:
The power of a propagating wave of mode m is proportional to the square of its amplitude and the corresponding reduced wave number km. Provided that the input wave is of mode i at ΓX, then the corresponding scattering parameters can be evaluated as:
The transfer parameter TXY defined in Section 2.3 is related to scattering parameters \(S_{X_{i}Y_{j}}\) as
Remark that transfer parameters are defined for the planar incoming wave. Hence, only X0 is included in the definition above.
Using the definition above, the objective function (13) can be re-written as:
where we minimize reflection of power over \({M^{p}_{f}}\) modes at left waveguide for case 1, and transmission of power over \({M^{p}_{f}}\) modes at left waveguide for case 2.
In the numerical experiments, we use a combination of filtering and a penalization method to suppress the intermediate values in ND × 1 vector d that defines the material distribution inside ΩD before filtering. To this end, we let \(\boldsymbol {\alpha }:=\mathcal {F}(\boldsymbol {d})\), where \(\mathcal {F}(\boldsymbol {d})\) is a filtered version of d (details in the Appendix) and add a quadratic penalization term (Allaire and Kohn 1993) to the objective function. In summary, we solve the optimization problem:
where γ is a penalty parameter and
is a set of admissible designs in ΩD.
5 Results revisited
Here, we revisit the results from Section 3. In Fig. 5, the frequency response of the optimized design shows transmission and reflection of an incoming planar wave in terms of transfer parameters. In this section, we will present all the details to show transmission and reflection of incoming wave in terms of scattering parameters. That is, how the output power is distributed over the propagating modes. With a given waveguide setup, the propagation of modes depends upon the frequency. For our waveguide setup (recall Fig. 2), the first non-planar mode starts propagating at 7kHz, and the second non-planar mode starts propagating at 13kHz. For the numerical experiments, we consider the size of the device and select frequencies that only allow two modes to propagate in our waveguide setup. That is, only the planar mode (m = 0) and the first non-planar mode (m = 1) propagate.
To obtain the design in Fig. 3, we minimize objective function (28) for the Nf = 11 frequencies 8.0, 8.1, 8.2, …, 9.0 kHz. More precisely, we solve the optimization problem for 25,600 design variables in ΩD using the method of moving asymptotes (MMA) by Svanberg (1987). For penalization of design variables, we use a two-step approach. In the first step, we set γ = 1 and initial design d to the vector with all ones, and solve the optimization problem. The optimization terminates when the residual norm of first order optimality condition computed by the MMA algorithm is less than 10− 3. In the second step, we increase the penalty parameter by setting γ = 102 and solve the updated optimization problem using optimal design from the first step as initial guess to obtain our final optimized design. We use the same termination condition for MMA in both steps.
5.1 Planar mode as incoming wave
Figure 6 presents graphs of transmission and reflection distributed over modes with planar incoming wave at left and right waveguide, respectively. For case 1, the graph shows that nearly all the power of the incoming planar mode at left waveguide is transmitted to the first non-planar mode at the right waveguide, throughout the frequency band of interest. More precisely, more than 99.8% of the power is transmitted to the non-planar mode at the right waveguide for all integer frequencies in the range 8–9 kHz. Due to conservation of power, there is essentially no reflection at left waveguide, as values of \({S}_{\text {L}_{0}\text {L}_{0}}<5.4\times 10^{-4}\) and \({S}_{\text {L}_{0}\text {L}_{1}}<9.0\times 10^{-4}\), respectively, for all integer frequencies in the range 8–9 kHz. Similarly, there is approximately zero transmission at the planar mode at the right waveguide, as value of \({S}_{\text {L}_{0}\text {R}_{0}}<2.2\times 10^{-3}\) for all integer frequencies in the range 8–9 kHz.
For case 2, the graph shows that nearly all the power of incoming planar mode at right waveguide is reflected back throughout the frequency band of interest. More precisely, more than 99.5% of power is reflected back to the planar mode at the right waveguide for all integer frequencies in the range 8–9 kHz. Moreover, there is essentially no transmission to the left waveguide, as values of \({S}_{\text {R}_{0}\text {L}_{0}}<2.2\times 10^{-3}\) and \({S}_{\text {R}_{0}\text {L}_{1}}<4.2\times 10^{-4}\), respectively, for all integer frequencies in the range 8–9 kHz. Similarly, there is approximately zero reflection at the first non-planar mode of the right waveguide, as value of \({S}_{\text {R}_{0}\text {R}_{1}}<2.3\times 10^{-3}\) for all integer frequencies in the range 8–9 kHz.
For case 1, the wave propagation is essentially in one direction, that is, from left to right waveguide throughout the frequency band of interest. Similarly, for case 2, there is essentially no wave propagation in the left waveguide, and incoming planar mode is reflected back to the right waveguide throughout the frequency band of interest. By using mode conversion for both case 1 and case 2, the numerical experiment successfully minimizes the objective function (28), and the waveguide setup appears to act as an acoustic diode for an incoming planar wave at the left and right waveguides, respectively.
5.2 First non-planar mode as incoming wave
To test if the optimized design in Fig. 3 acts as an acoustic diode for the first non-planar mode as incoming wave, we define two more cases:
- Case 3 :
-
There is an incoming wave of the first non-planar mode in the left waveguide, propagating towards ΩD.
- Case 4 :
-
There is an incoming wave of the first non-planar mode in the right waveguide, propagating towards ΩD.
Figure 7 presents graphs of transmission and reflection distributed over modes with the first non-planar mode as incoming wave at the left and right waveguides, respectively. For case 3, the graph shows that nearly all the power of incoming first non-planar mode is reflected back throughout the frequency band of interest. More precisely, more than 99.7% of the power is reflected back to the left waveguide for all integer frequencies in the range 8–9 kHz. Moreover, there is essentially no transmission towards the right waveguide, as values of \({S}_{\text {L}_{1}\text {R}_{0}}<4.2\times 10^{-4}\) and \({S}_{\text {L}_{1}\text {R}_{1}}<9.9\times 10^{-4}\), respectively, for all integer frequencies in the range 8–9 kHz. Similarly, there is approximately zero reflection at planar mode of the left waveguide, as value of \({S}_{\text {L}_{1}\text {L}_{0}}<9.0\times 10^{-4}\) for all integer frequencies in the range 8–9 kHz.
For case 4, nearly all the power is transmitted to planar mode at left waveguide with an incoming first non-planar mode of the right waveguide throughout the frequency band of interest. More precisely, more than 99.6% of the power is transmitted to the left waveguide for all integer frequencies in the range 8–9 kHz. There is essentially no reflection at the right waveguide, as values of \({S}_{\text {R}_{1}\text {R}_{0}}<2.3\times 10^{-3}\) and \({S}_{\text {R}_{1}\text {R}_{1}}<5.4\times 10^{-4}\), respectively, for all integer frequencies in the range 8–9 kHz. Similarly, there is approximately zero transmission towards the first non-planar mode of the left waveguide, as value of \({S}_{\text {R}_{1}\text {L}_{1}}<9.9\times 10^{-4}\) for all integer frequencies in the range 8–9 kHz.
For both case 3 and case 4, the device does not appear to act as an acoustic diode (from left to right) and there is wave propagation from right to left. Similarly, like case 1 and case 2, here the device uses mode conversion to achieve one-way waveguiding effect in reverse (from right to left). Thus, the one-way waveguiding effect depends on the input mode.
6 Concluding discussion
The results of the numerical experiments presented in Fig. 6 show that the waveguide setup appears to act as an acoustic diode allowing the incoming planar wave to propagate from left to right. However, Figs. 7 and 8 show that for the first non-planar mode as incoming wave, it appears to act as an acoustic diode in reverse, allowing propagation from right to left. Hence, the device designed in this paper is in fact a high-quality mode-converter or a four-port network, illustrated in Fig. 9, instead of a diode.
Four-port network: In case 1, the incoming planar mode (L0) input is converted to the first non-planar mode (R1). Similarly in case 4, the incoming first non-planar mode (R1) is converted to planar mode (L0). On the other hand, incoming planar (R0) and non-planar modes (L1) are reflected back in case 2 and case 3, respectively
Recall that the diode is a non-linear device that allows one-way transmission of any incoming wave. This is not possible for a linear device due to reciprocity. The reciprocal property of this setup is due to Helmholtz equation, where the time-harmonic approximation of acoustic pressure for the incoming \(P(x,t)=\text {Re}\left \{\mathrm {e}^{-\mathrm {i}\omega t} p(x)\right \}\) and the outgoing wave \(P(x,t)=\text {Re}\left \{\mathrm {e}^{\mathrm {i}\omega t} p(x)\right \}\) are the time-reverse of each other. Thus, \(S_{X_{i}Y_{j}}=S_{Y_{j}X_{i}}\). For example, \(S_{\text {L}_{0}\text {R}_{1}}\) (case 1) is equal to \(S_{\text {R}_{1}\text {L}_{0}}\) (case 4) where the optimized design inside the design domain converts planar mode to non-planar mode and vice versa. It is in fact not possible to design a true acoustic diode in reciprocal systems.
Generally, all so-called linear acoustic diodes in the literature are just mode converters which work as multi-port networks, connecting different modes to each other. Despite all possible applications for a linear directional waveguide, diode is just the wrong term for it, as a diode is a non-linear device and to achieve that, we need to break reciprocity, which is an innate property of linear wave propagation. That being said, it is indeed possible to design a highly efficient linear directional waveguide. The results show that by using topology optimization and selecting frequency band that allow two or more propagating modes, we can design a multi-port network that works as an efficient directional waveguide for an incoming planar wave.
Thus, an executive summary of the above reads:
-
The optimized design in this paper is a high-quality mode converter, but not an acoustic diode.
-
Diodes are non-linear devices—there is no such thing as a diode in a reciprocal system.
-
The so-called linear diodes presented in the literature are in fact mode converters. (They should thus be treated and addressed as such and not as diodes.)
References
Aage N, Johansen V E (2017) Topology optimization of microwave waveguide filters. Int J Numer Methods Eng 112(3):283–300. https://doi.org/10.1002/nme.5551
Allaire G, Kohn R V (1993) Topology optimization and optimal shape design using homogenization. In: Topology Design of Structures. Springer, Netherlands, pp 207–218
Bendsøe M P, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. COMMA4 71:197–224. https://doi.org/10.1016/0045-7825(88)90086-2
Bendsøe M P, Sigmund O (2003) Topology optimization. theory, methods, and applications. Springer
Borrvall T, Petersson J (2002) Topology optimization of fluids in Stokes flow. Int J Numer Methods Fluids 41(1):77–107. https://doi.org/10.1002/fld.426
Chen Y, Meng F, Sun G, Li G, Huang X (2017) Topological design of phononic crystals for unidirectional acoustic transmission. J Sound Vib 410:103–123. https://doi.org/10.1016/j.jsv.2017.08.015
Cox S J, Dobson D C (1999) Maximizing band gaps in two-dimensional photonic crystals. SIAM J Appl Math 59(6):2108–2120. https://doi.org/10.2307/118418
Darabi A, Fang L, Mojahed A, Fronk M D, Vakakis A F, Leamy M J (2019) Broadband passive nonlinear acoustic diode. Phys Rev B 99(21). https://doi.org/10.1103/physrevb.99.214305
Dühring M B, Jensen J S, Sigmund O (2008) Acoustic design by topology optimization. J Sound Vib 317(3-5):557–575. https://doi.org/10.1016/j.jsv.2008.03.042
Grinberg I, Vakakis A F, Gendelman O V (2018) Acoustic diode: Wave non-reciprocity in nonlinearly coupled waveguides. Wave Motion 83:49–66. https://doi.org/10.1016/j.wavemoti.2018.08.005
Hägg L, Wadbro E (2017) Nonlinear filters in topology optimization: existence of solutions and efficient implementation for minimum compliance problems. STRMO 55(3):1017–1028. https://doi.org/10.1007/s00158-016-1553-8
Hassan E, Wadbro E, Berggren M (2014) Topology optimization of metallic antennas. IEEE Trans Antennas Propag 63(5):2488–2500. https://doi.org/10.1109/TAP.2014.2309112
He J, Kang Z (2018) Achieving directional propagation of elastic waves via topology optimization. Ultrasonics 82:1–10. https://doi.org/10.1016/j.ultras.2017.07.006
He Z, Peng S, Ye Y, Dai Z, Qiu C, Ke M, Liu Z (2011) Asymmetric acoustic gratings. Appl Phys Lett 98(8):083505. https://doi.org/10.1063/1.3562306
Ihlenburg F (1998) Finite element analysis of acoustic scattering. Springer
Jensen JS, Sigmund O (2011) Topology optimization for nano-photonics. Laser Photon Rev 5(2):308–321. https://doi.org/10.1002/lpor.201000014
Kasolis F, Wadbro E, Berggren M (2015) Analysis of fictitious domain approximations of hard scatterers. SIAM J Numer Anal 53(5):2347–2362. https://doi.org/10.1137/140981630
Lee J W, Kim Y Y (2009) Topology optimization of muffler internal partitions for improving acoustical attenuation performance. Int J Numer Methods Eng 80(4):455–477. https://doi.org/10.1002/nme.2645
Li R-Q, Liang B, Li Y, Kan W-W, Zou X-Y, Cheng J-C (2012a) Broadband asymmetric acoustic transmission in a gradient-index structure. Appl Phys Lett 101(26):263502. https://doi.org/10.1063/1.4773481
Li Y, Tu J, Liang B, Guo X S, Zhang D, Cheng J C (2012b) Unidirectional acoustic transmission based on source pattern reconstruction. J Appl Phys 112(6):064504. https://doi.org/10.1063/1.4752407
Li Z-N, Yuan B, Wang Y-Z, Shui G-S, Zhang C, Wang Y-S (2019) Diode behavior and nonreciprocal transmission in nonlinear elastic wave metamaterial. Mech Mater 133:85–101. https://doi.org/10.1016/j.mechmat.2019.03.010
Li Z-N, Wang Y-Z, Wang Y-S (2020) Three-dimensional nonreciprocal transmission in a layered nonlinear elastic wave metamaterial. Int J Non-Linear Mech 125:103531. https://doi.org/10.1016/j.ijnonlinmec.2020.103531
Liang B, Yuan B, chun Cheng J (2009) Acoustic diode: Rectification of acoustic energy flux in one-dimensional systems. Phys Rev Lett 103(10). https://doi.org/10.1103/physrevlett.103.104301
Liang B, Guo X S, Tu J, Zhang D, Cheng J C (2010) An acoustic rectifier. Nat Mater 9(12):989–992. https://doi.org/10.1038/nmat2881
Mori K, Morimoto K, Tanaka T, Iguchi A, Tsuji Y (2019) Topology optimization of nonlinear optical waveguide devices considering output signal phase. Opt Commun 439:290–294. https://doi.org/10.1016/j.optcom.2019.01.034
Popa B-I, Cummer S A (2014) Non-reciprocal and highly nonlinear active acoustic metamaterials. Nat Commun 5(1). https://doi.org/10.1038/ncomms4398
Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidiscip Optim 33:401–424. https://doi.org/10.1007/s00158-006-0087-x
Song A-L, Chen T-N, Wang X-P, Wan L-L (2016) Waveform-preserved unidirectional acoustic transmission based on impedance-matched acoustic metasurface and phononic crystal. J Appl Phys 120(8):085106. https://doi.org/10.1063/1.4961659
Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. INTJN2 24:359–373. https://doi.org/10.1002/nme.1620240207
Svanberg K, Svärd H (2013) Density filters for topology optimization based on the pythagorean means. STRMO 48(5):859–875. https://doi.org/10.1007/s00158-013-0938-1
Wadbro E, Berggren M (2006) Topology optimization of an acoustic horn. Comput Methods Appl Mech Eng 196(1-3):420–436. https://doi.org/10.1016/j.cma.2006.05.005
Wadbro E (2014) Analysis and design of acoustic transition sections for impedance matching and mode conversion. STRMO 50(3):395–408. https://doi.org/10.1007/s00158-014-1058-2
Wadbro E, Hägg L (2015) On quasi-arithmetic mean based filters and their fast evaluation for large-scale topology optimization. STRMO 52(5):879–888. https://doi.org/10.1007/s00158-015-1273-5
Zhu Y-F, Zou X-Y, Liang B, Cheng J-C (2015a) Acoustic one-way open tunnel by using metasurface. Appl Phys Lett 107(11):113501. https://doi.org/10.1063/1.4930300
Zhu Y-F, Zou X-Y, Liang B, Cheng J-C (2015b) Broadband unidirectional transmission of sound in unblocked channel. Appl Phys Lett 106(17):173508. https://doi.org/10.1063/1.4919537
Funding
Open Access funding provided by Umea University. This work was partially supported by National Natural Science Foundation of China (No. 51975087); the Fundamental Research Funds for the Central Universities (No. DUT20JC23); STINT, The Swedish Foundation for International Cooperation in Research and Higher Education (No. IB2018-7470); the Swedish strategic research programme eSSENCE; and by the Higher Education Commission (HEC) of Pakistan.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Replication of results
Please contact Prof. Krister Svanberg for MMA (optimization algorithm). The code listings for the filtering method are available in Hägg and Wadbro (2017). The remaining parts of the code are available from the corresponding author on request. All the details necessary to reproduce the results have been defined in the paper.
Additional information
Responsible Editor: Jianbin Du
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Filtering
In this work, we use non-linear density filters that are based on morphological operators (Sigmund 2007). To use gradient-based optimization algorithm, these morphological operators are approximated by harmonic means-based filters (Svanberg and Svärd 2013).
For optimization, we use the design domain ΩD; however, for filtering, we extend the domain on three sides, illustrated in Fig. 10. The extended domain for filtering is ΩF = ΩD ∪ΩW ∪ΩM, where ΩW represents the left and right waveguides, and ΩM is the domain with solid material. The material distribution is fixed in ΩW and ΩM, that is, αh(x) = 1 (air) in ΩW and αh(x) = 0 (solid) in ΩM. The discretization in ΩF consists of NF square elements of the same size as those in Ω. The elements in ΩF are arranged such that elements of ΩD come first, ΩM second, and ΩW last.
Furthermore, we define neighborhood \(\mathcal {N}_{r,i}\) of radius r around element i with centroid xi, where \(\mathcal {N}_{r,i}\) consists of j elements with centroid xj. We assemble a matrix Gr with binary entries, where gij = 1 if \(j \in \mathcal {N}_{r,i}\), else gij = 0. If the distance between element i and j is less than r, that is, \(\left \| x_{i} - x_{j} \right \| \leq r\) then element j belongs to Nr,i. We define a weight matrix \(\boldsymbol {W}_{r}=\boldsymbol {D}^{-1}_{r}\boldsymbol {G}_{r}\), where Dr = Gr1N and 1N is a N × 1 matrix with all entries equal to 1.
We define functions \(f(x)_{\mathcal {E}_{r}}=1/(x+\beta )\) and \(f(x)_{\mathcal {D}_{r}}=f_{\mathcal {E}_{r}}(1-x)\) to compute discrete harmonic mean, where β > 0, and \(f^{-1}_{\mathcal {E}_{r}}\) and \(f^{-1}_{\mathcal {D}_{r}}\) are inverse of these functions.
Using notation of fW-mean filters (Wadbro and Hägg 2015), we define discrete erode and dilate operators of the NF × 1 vector ρ with entries in the range [0, 1] by
where \(\boldsymbol {f}(\boldsymbol {\rho })_{\mathcal {E}_{\beta }}= \big [f(\rho _{1})_{\mathcal {E}_{\beta }},\ldots ,f(\rho _{N^{\text {f}}})_{\mathcal {E}_{\beta }}\big ]\), and \(\boldsymbol {f}(\boldsymbol {\rho })_{\mathcal {D}_{\beta }}=\big [f(\rho _{1})_{\mathcal {D}_{\beta }},\ldots ,f(\rho _{N^{\text {f}}})_{\mathcal {D}_{\beta }}\big ]\) are element-wise functions.
Using the definition of harmonic erode and dilate in expression (30), we define harmonic close that acts on ND × 1 vector d
where \(\boldsymbol {I}_{N^{\text {d}}}\) is an identity matrix, \(\boldsymbol {0}_{N^{\text {d}}\times (N^{\text {W}}+N^{\text {M}})}\) is a zero matrix. Similarly, \(\boldsymbol {0}_{N^{\text {M}}}\) is a zero vector and \(\boldsymbol {1}_{N^{\text {W}}}\) is a vector with all entries equal to 1. The \(\mathcal {F}(\boldsymbol {d})\) gives us filtered version of design vector d that holds element values of αh in ΩD.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bokhari, A.H., Mousavi, A., Niu, B. et al. Topology optimization of an acoustic diode?. Struct Multidisc Optim 63, 2739–2749 (2021). https://doi.org/10.1007/s00158-020-02832-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-020-02832-9